Efficient Sensor Placement Optimization for Shape Deformation Sensing of Antenna Structures with Fiber Bragg Grating Strain Sensors
Abstract
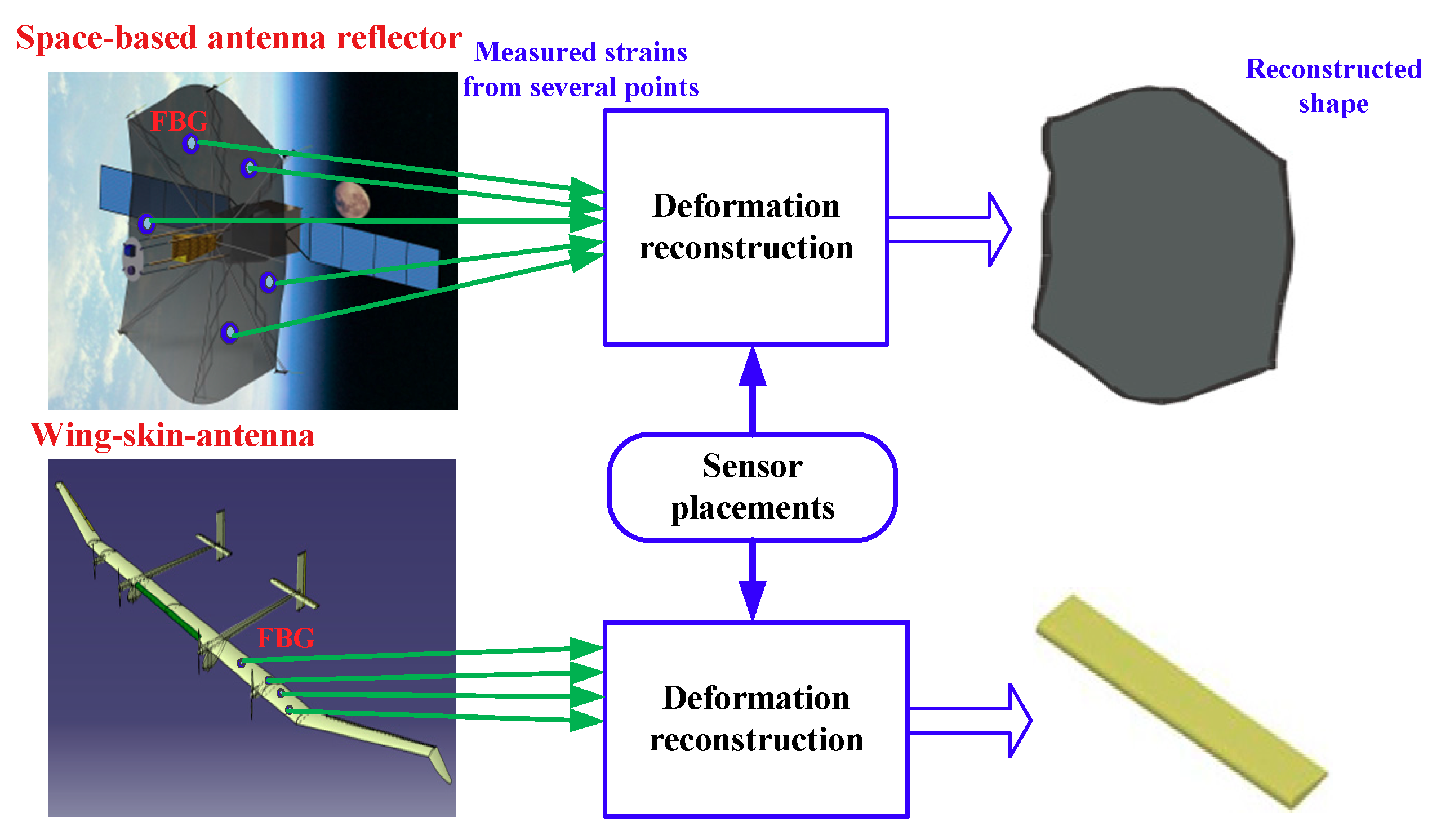
1. Introduction
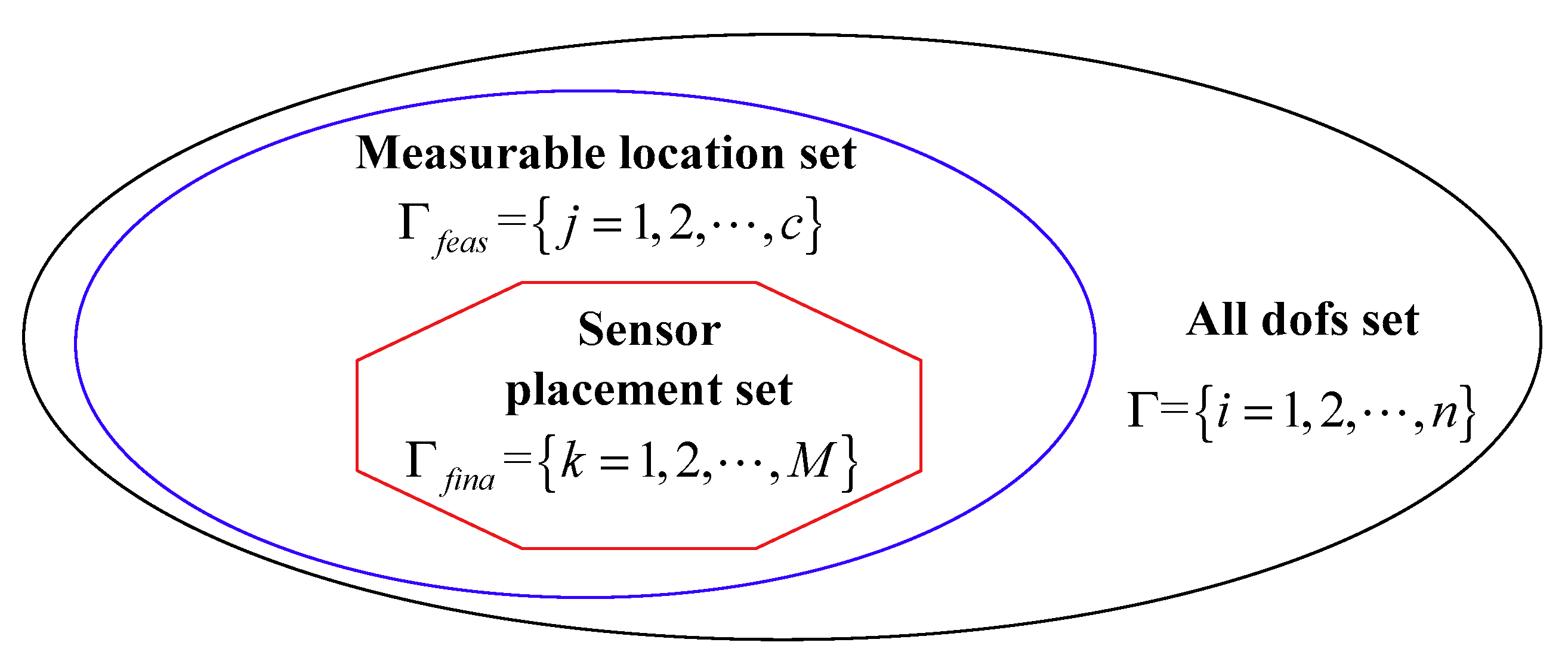
2. Problem Statements
3. Deformation Reconstruction
3.1. Strain–Displacement Transformation
3.2. Relative Reconstruction Error Equation
4. Two-Stage Sensor Placement
4.1. Initial Sensor Placement at the First Stage
4.2. Sequential Sensor Placement at the Second Stage
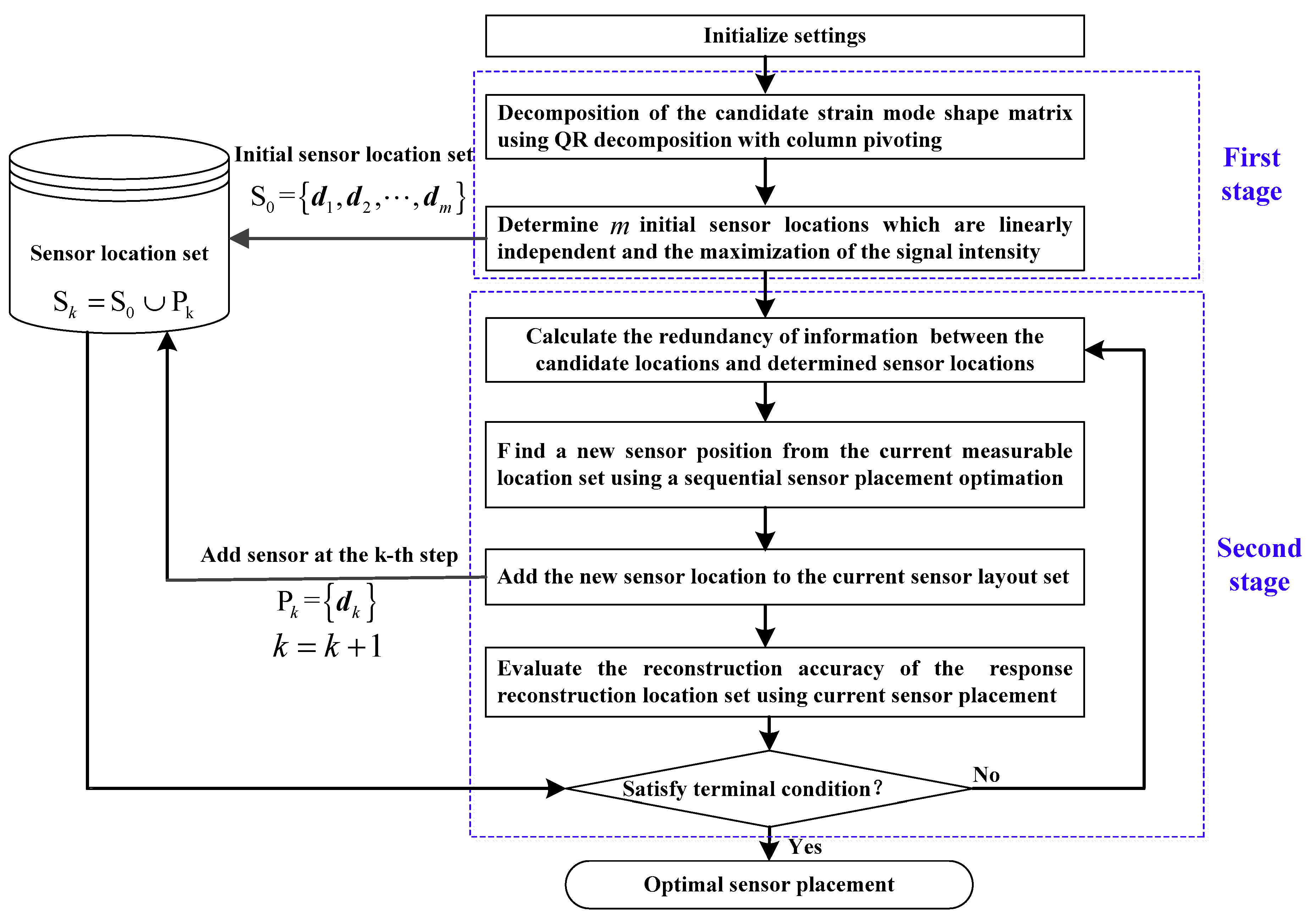
4.3. Implementation Procedure
- (1)
- Specify the mode truncation number , the total sensor number and the allowed maximum reconstruction error . In addition, the measurable location set , the response reconstruction location set and the number of the candidate sensor locations are also determined.
- (2)
- Perform QR decomposition of the matrix using Equation (15), and select the first columns. The column numbers with respect to are extracted from the matrix , and we choose the initial sensor locations corresponding to the sequence of the elements with the value 1 in the unit conversion matrix .
- (3)
- Utilize Equation (18) to calculate the redundancy of information between all of the remaining candidate locations and the previously determined sensor locations.
- (4)
- Select an optimal sensor location satisfying Equation (20) from the current measurable location set.
- (5)
- Add the newly selected sensor location to the current sensor placement set , and update the current measurable location set and the allowable remaining sensor numbers in the second stage.
- (6)
- If the termination conditions are satisfied, the program is terminated, otherwise repeat the steps (3)~(6). In this paper, the termination conditions are as follows:
- (a)
- Whether the requirements of the specified reconstruction accuracy is satisfied;
- (b)
- Whether the allowed maximum sensor number is reached.
5. Numerical Experiment
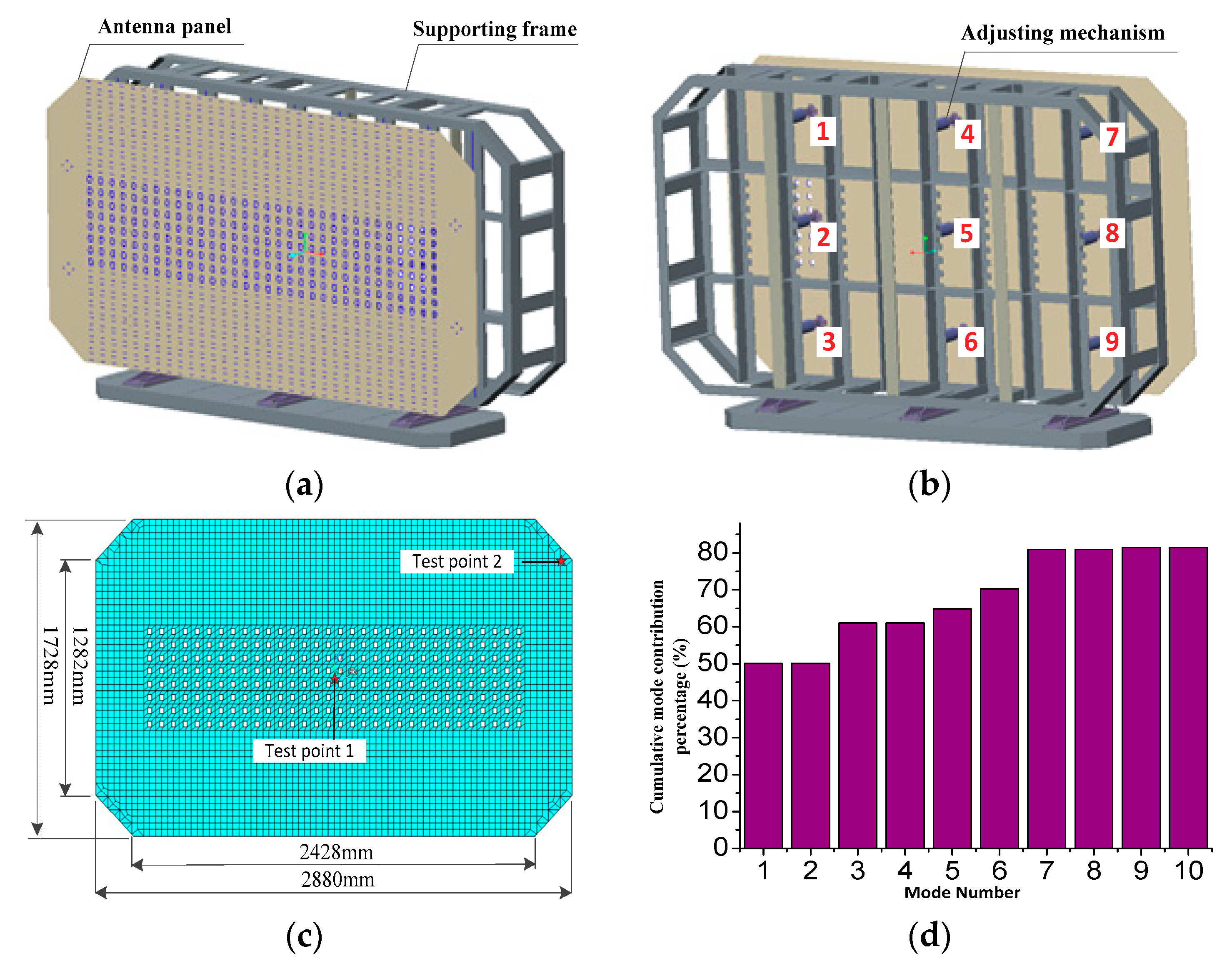
5.1. FEM of the Antenna Experimental Platform
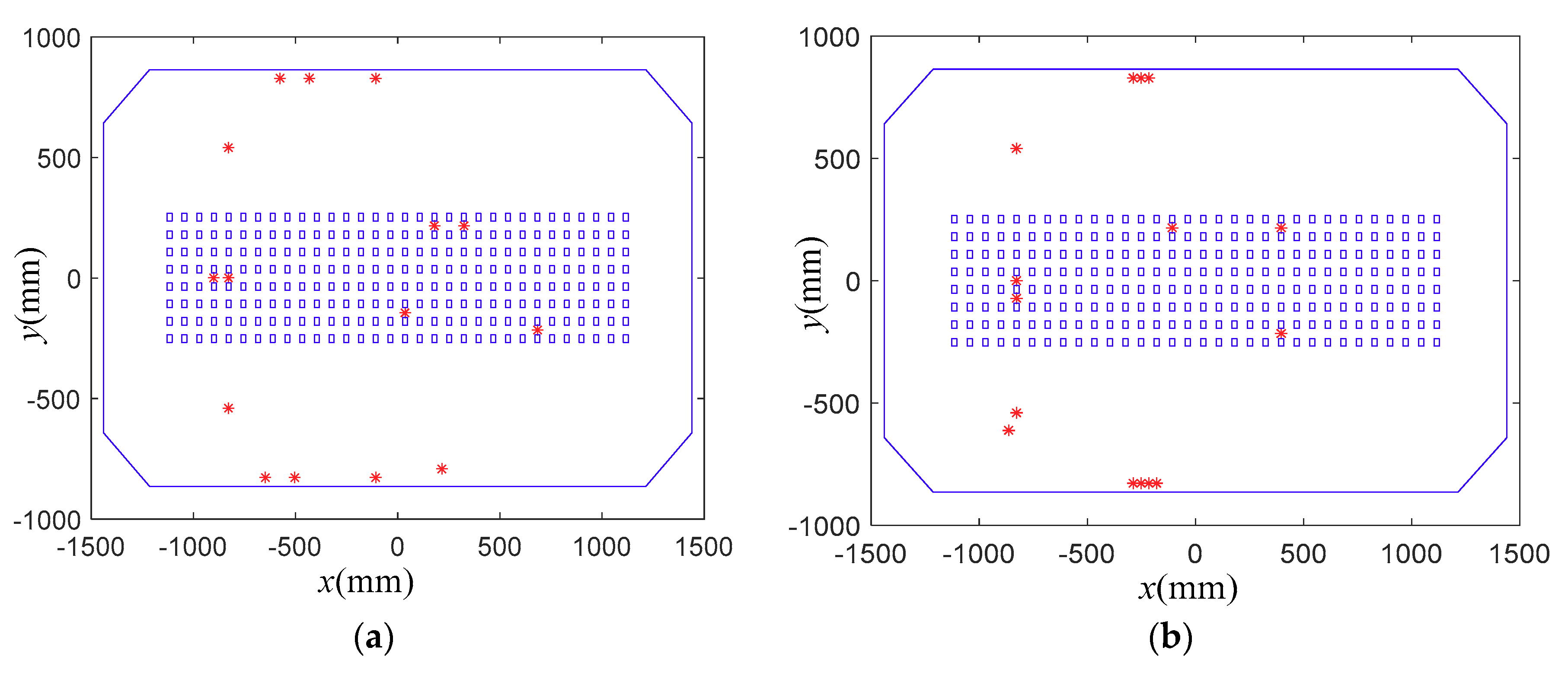
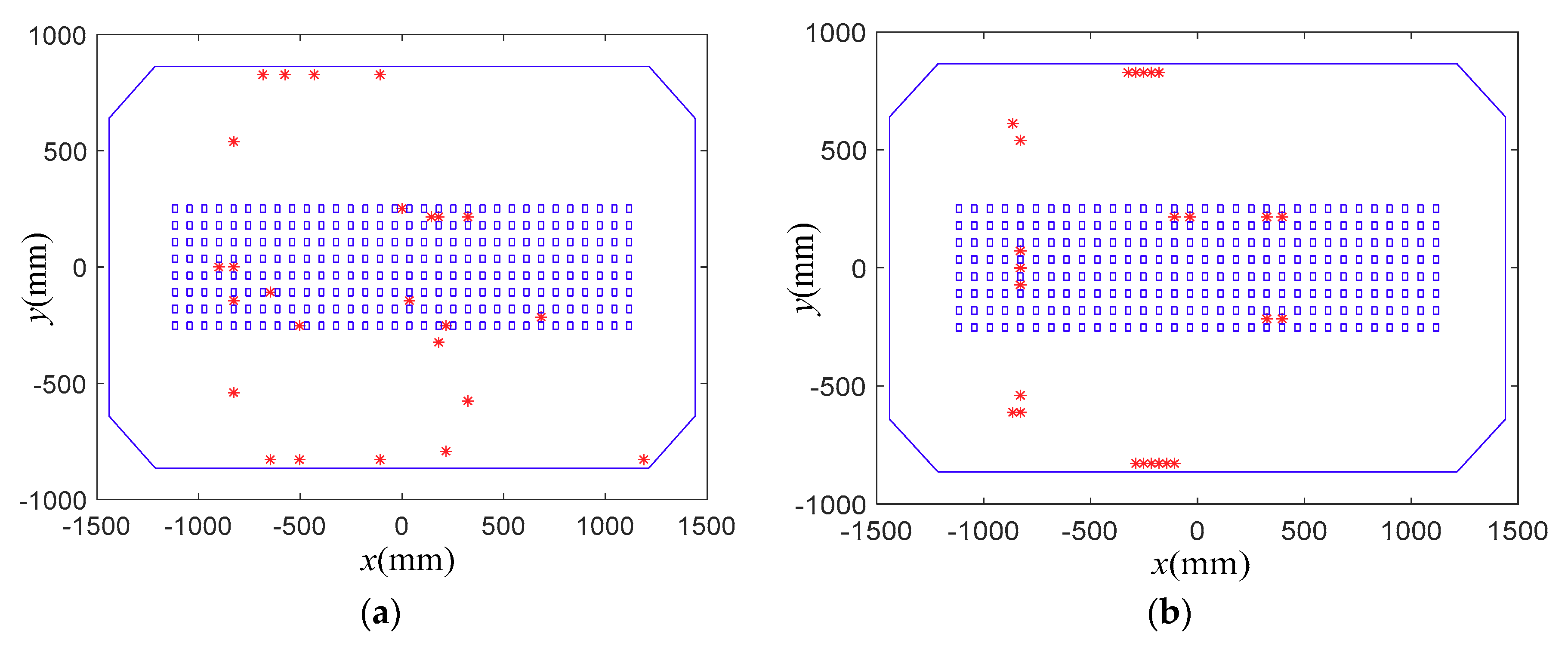
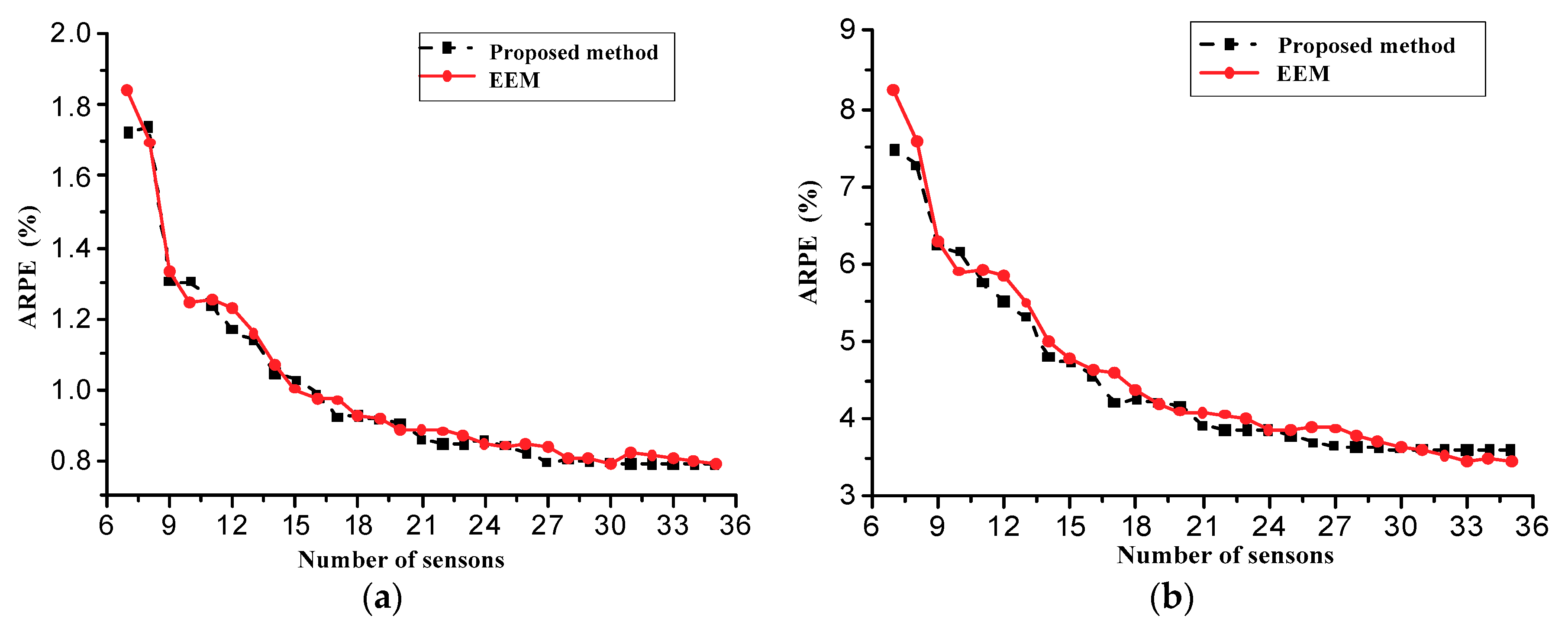
5.2. Superiority of Sensor Placement Method
6. Experimental Results
6.1. Experimental System
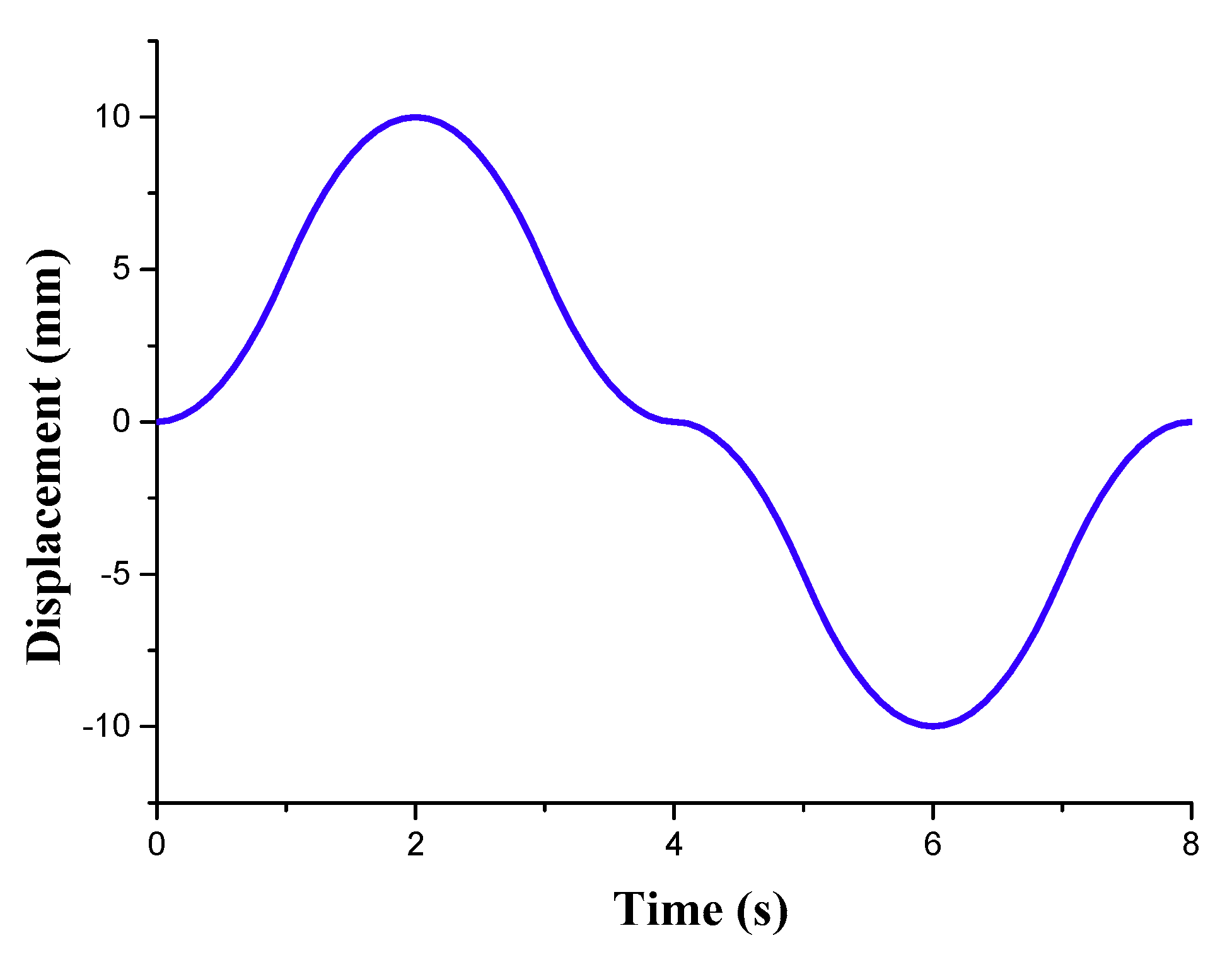
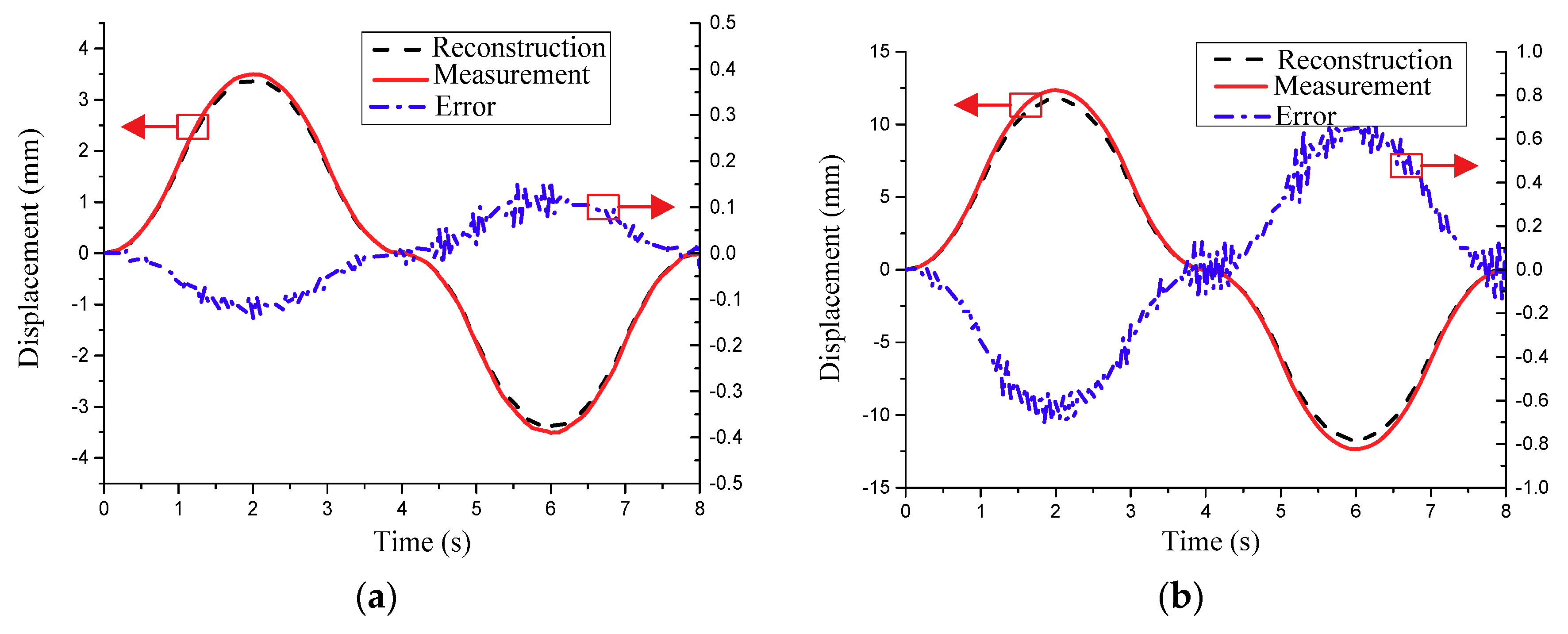
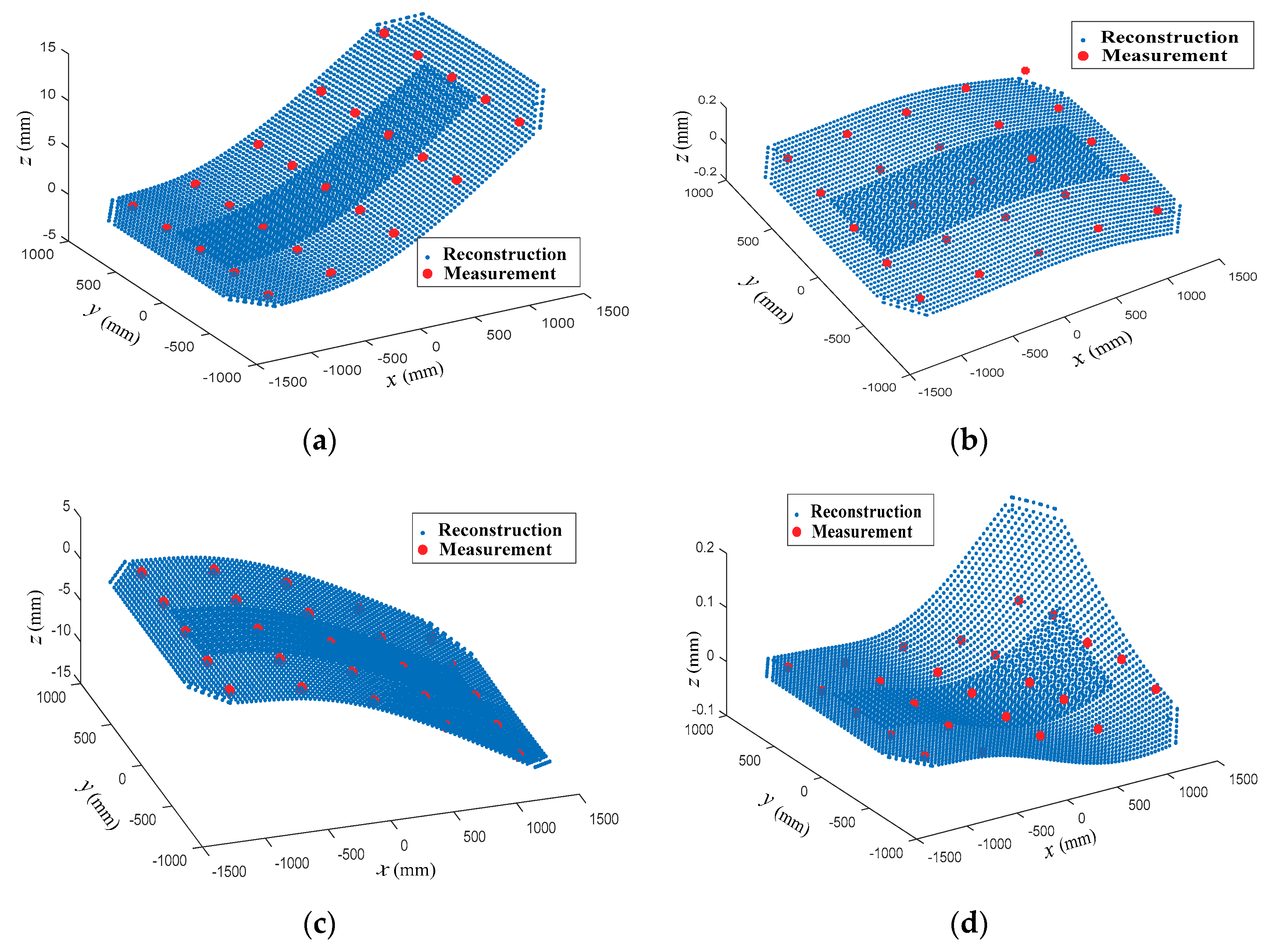
6.2. Reconstruction Results
6.3. Result Discussions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Z.W.; Li, T.J. Optimal piezoelectric sensor/actuator placement of cable net structures using H2-norm measures. J. Vib. Control 2014, 20, 1257–1268. [Google Scholar] [CrossRef]
- Hajrya, R.; Mechbal, N. Principal component analysis and perturbation theory-based robust damage detection of multifunctional aircraft structure. Struct. Health Monit. 2013, 12, 263–277. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, X.P.; Huang, X.Q.; Cheng, Z.A.; Zhang, X.H.; Hou, X.B. Optimal sensor placement for deployable antenna module health monitoring in ssps using genetic algorithm. Acta Astronaut. 2017, 140, 213–224. [Google Scholar] [CrossRef]
- Li, N.-L.; Jiang, S.-F.; Wu, M.-H.; Shen, S.; Zhang, Y. Deformation monitoring for chinese traditional timber buildings using fiber bragg grating sensor. Sensors 2018, 18, 1968. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.S.; Zhu, X.J.; Gao, Z.Y.; Liu, K.N.; Jiang, F. Fiber bragg grating plate structure shape reconstruction algorithm based on orthogonal curve net. J. Intell. Mater. Syst. Struct. 2016, 27, 2416–2425. [Google Scholar] [CrossRef]
- Yi, J.C.; Zhu, X.J.; Zhang, H.S.; Shen, L.Y.; Qiao, X.P. Spatial shape reconstruction using orthogonal fiber bragg grating sensor array. Mechatronics 2012, 22, 679–687. [Google Scholar] [CrossRef]
- Derkevorkian, A.; Masri, S.F.; Alvarenga, J.; Boussalis, H.; Bakalyar, J.; Richards, W.L. Strain-based deformation shape-estimation algorithm for control and monitoring applications. AIAA J. 2013, 51, 2231–2240. [Google Scholar] [CrossRef]
- Wang, Z.F.; Wang, J.; Sui, Q.M.; Li, S.C.; Jia, L. In-situ calibrated deformation reconstruction method for fiber bragggrating embedded smart geogrid. Sens. Actuators A Phys. 2016, 250, 145–158. [Google Scholar] [CrossRef]
- Kefal, A.; Yildiz, M. Modeling of sensor placement strategy for shape sensing and structural health monitoring of a wing-shaped sandwich panel using inverse finite element method. Sensors 2017, 17, 2775. [Google Scholar] [CrossRef] [PubMed]
- Tessler, A.; Spangler, J.L. A least-squares variational method for full-field reconstruction of elastic deformations in shear-deformable plates and shells. Comp. Methods Appl. Mech. Eng. 2005, 194, 327–339. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. An inverse finite element method for beam shape sensing: Theoretical framework and experimental validation. Smart Mater. Struct. 2014, 23, 045027. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Shape sensing of 3D frame structures using an inverse finite element method. Int. J. Solids Struct. 2012, 49, 3100–3112. [Google Scholar] [CrossRef]
- Zheng, S.J.; Zhang, N.; Xia, Y.J.; Wang, H.T. Research on non-uniform strain profile reconstruction along fiber bragg grating via genetic programming algorithm and interrelated experimental verification. Opt. Commun. 2014, 315, 338–346. [Google Scholar] [CrossRef]
- Sławomir, C.; Piotr, K. Inverse problem of determining periodic surface profile oscillation defects of steel materials with a fiber bragg grating sensor. Appl. Opt. 2016, 55, 1412–1420. [Google Scholar]
- Kang, L.H.; Kim, D.K.; Han, J.H. Estimation of dynamic structural displacements using fiber bragg grating strain sensors. J. Sound Vib. 2007, 305, 534–542. [Google Scholar] [CrossRef]
- Davis, M.A.; Kersey, A.D.; Sirkis, J.; Friebele, E.J. Shape and vibration mode sensing using a fiber optic bragg grating array. Smart Mater. Struct. 1996, 5, 759. [Google Scholar] [CrossRef]
- Rapp, S.; Kang, L.H.; Han, J.H.; Mueller, U.C.; Baier, H. Displacement field estimation for a two-dimensional structure using fiber bragg grating sensors. Smart Mater. Struct. 2009, 18, 025006. [Google Scholar] [CrossRef]
- Kim, H.I.; Kang, L.H.; Han, J.H. Shape estimation with distributed fiber bragg grating sensors for rotating structures. Smart Mater Struct 2011, 20, 035011. [Google Scholar] [CrossRef]
- Kammer, D.C. Sensor placement for on-orbit modal identification and correlation of large space structures. J. Guid. Control Dyn. 1991, 14, 251–259. [Google Scholar] [CrossRef]
- Li, D.S.; Li, H.N.; Fritzen, C.P. The connection between effective independence and modal kinetic energy methods for sensor placement. J. Sound Vib. 2007, 305, 945–955. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Beck, J.L.; Au, S.K. Entropy-based optimal sensor location for structural model updating. J. Vib. Control 2000, 6, 781–800. [Google Scholar] [CrossRef]
- Yuen, K.V.; Kuok, S.C. Efficient bayesian sensor placement algorithm for structural identification: A general approach for multi-type sensory systems. Earthq. Eng. Struct. Dyn. 2015, 44, 757–774. [Google Scholar] [CrossRef]
- Bertola, N.; Papadopoulou, M.; Vernay, D.; Smith, I. Optimal multi-type sensor placement for structural identification by static-load testing. Sensors 2017, 17, 2094. [Google Scholar] [CrossRef] [PubMed]
- Yao., L.; Sethares, W.A.; Kammer., D.C. Sensor placement for on-orbit modal identification via a genetic algorithm. AIAA J. 1993, 31, 1922–1928. [Google Scholar] [CrossRef]
- Akbarzadeh, V.; Levesque, J.C.; Gagne, C.; Parizeau, M. Efficient sensor placement optimization using gradient descent and probabilistic coverage. Sensors 2014, 14, 15525–15552. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Jia, J.Q. 3D sensor placement strategy using the full-range pheromone ant colony system. Smart Mater. Struct. 2016, 25, 075003. [Google Scholar]
- Zhang, X.; Li, J.L.; Xing, J.C.; Wang, P.; Yang, Q.L.; Wang, R.H.; He, C. Optimal sensor placement for latticed shell structure based on an improved particle swarm optimization algorithm. Math. Probl. Eng. 2014. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, W.G.; Zhu, H.P.; Chen, J.F. Optimal sensor placement for structural response estimation. J. Cent. South Univ. 2014, 21, 3993–4001. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhu, S.; Xu, Y.L.; Homg, X.J. Integrated optimal placement of displacement transducers and strain gauges for better estimation of structural response. Int. J. Struct. Stab. Dyn. 2011, 11, 581–602. [Google Scholar] [CrossRef]
- Zhang, X.H.; Xu, Y.L.; Zhu, S.Y.; Zhan, S. Dual-type sensor placement for multi-scale response reconstruction. Mechatronics 2014, 24, 376–384. [Google Scholar] [CrossRef]
- Zhang, C.D.; Xu, Y.L. Optimal multi-type sensor placement for response and excitation reconstruction. J. Sound Vib. 2016, 360, 112–128. [Google Scholar] [CrossRef]
- Wang, J.; Law, S.S.; Yang, Q.S. Sensor placement method for dynamic response reconstruction. J. Sound Vib. 2014, 333, 2469–2482. [Google Scholar] [CrossRef]
- Stephan, C. Sensor placement for modal identification. Mech. Syst. Signal Process. 2012, 27, 461–470. [Google Scholar] [CrossRef]
- Lian, J.J.; He, L.J.; Ma, B.; Li, H.K.; Peng, W.X. Optimal sensor placement for large structures using the nearest neighbour index and a hybrid swarm intelligence algorithm. Smart Mater. Struct. 2013, 22, 095015. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, J.; He, Q.; Tang, B.; Song, L. Development and coupling analysis of active skin antenna. Smart Mater. Struct. 2016, 26, 025011. [Google Scholar] [CrossRef]
- Zhou, J.; Song, L.; Huang, J.; Wang, C. Performance of structurally integrated antennas subjected to dynamical loads. Int. J. Appl. Electromagn. Mech. 2015, 48, 409–422. [Google Scholar] [CrossRef]
- Wang, H.S.C. Performance of phased-array antennas with mechanical errors. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 535–545. [Google Scholar] [CrossRef]
- Zhu, L.H.; Dai, J.; Bai, G.L. Sensor placement optimization of vibration test on medium-speed mill. Shock Vib. 2015. [Google Scholar] [CrossRef]
- Sharma, A.; Paliwal, K.K.; Imoto, S.; Miyano, S. Principal component analysis using QR decomposition. Int. J. Mach. Learn. Cybern. 2013, 4, 679–683. [Google Scholar] [CrossRef]
- Friswell, M.I.; Castro-Triguero, R. Clustering of sensor locations using the effective independence method. AIAA J. 2015, 53, 1388–1390. [Google Scholar] [CrossRef]





| Modal | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Frequency (Hz) | 0.45 | 1.47 | 2.78 | 5.05 | 6.03 | 6.40 | 8.52 |
| Locations | RMSE (mm) | MAE (mm) | ARPE |
|---|---|---|---|
| Test point 1 | 0.0741 | 0.1587 | 3.43% |
| Test point 2 | 0.3977 | 0.7240 | 5.22% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Cai, Z.; Zhao, P.; Tang, B. Efficient Sensor Placement Optimization for Shape Deformation Sensing of Antenna Structures with Fiber Bragg Grating Strain Sensors. Sensors 2018, 18, 2481. https://doi.org/10.3390/s18082481
Zhou J, Cai Z, Zhao P, Tang B. Efficient Sensor Placement Optimization for Shape Deformation Sensing of Antenna Structures with Fiber Bragg Grating Strain Sensors. Sensors. 2018; 18(8):2481. https://doi.org/10.3390/s18082481
Chicago/Turabian StyleZhou, Jinzhu, Zhiheng Cai, Pengbing Zhao, and Baofu Tang. 2018. "Efficient Sensor Placement Optimization for Shape Deformation Sensing of Antenna Structures with Fiber Bragg Grating Strain Sensors" Sensors 18, no. 8: 2481. https://doi.org/10.3390/s18082481
APA StyleZhou, J., Cai, Z., Zhao, P., & Tang, B. (2018). Efficient Sensor Placement Optimization for Shape Deformation Sensing of Antenna Structures with Fiber Bragg Grating Strain Sensors. Sensors, 18(8), 2481. https://doi.org/10.3390/s18082481





