Research on Transmission Line Voltage Measurement Method of D-Dot Sensor Based on Gaussian Integral
Abstract
:1. Introduction
2. The Principle and Structure of D-Dot Sensors
3. Calculation of the Transmission Line Voltage Based on the Gaussian Integral
3.1. Integral Algorithm of Transmission Line Voltage
3.2. Voltage Solving Method Based on Gaussian Integrals
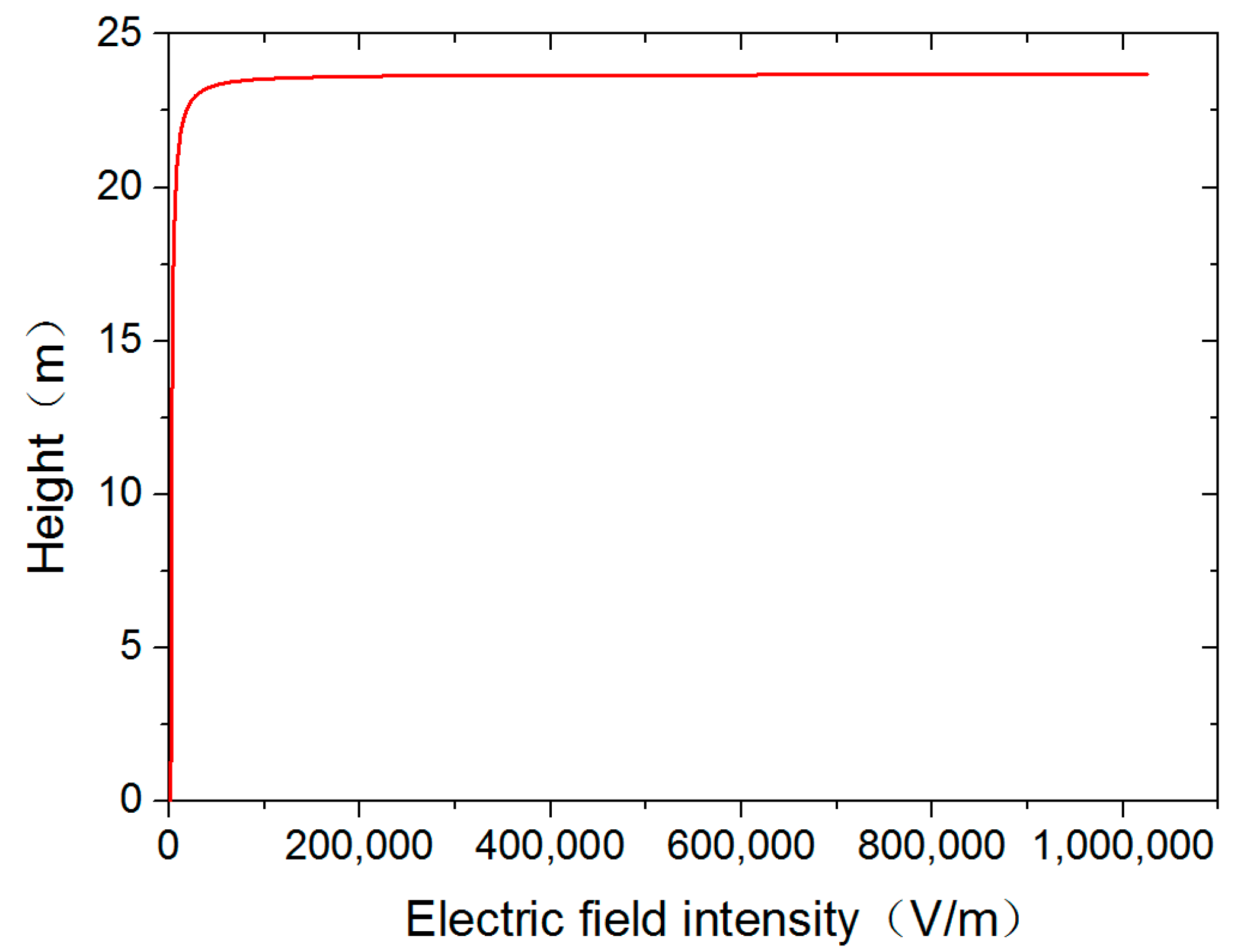
3.3. Solving Transmission Line Voltage
4. Experiment Analysis and Verification
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A. Matlab Code
References
- Huiskamp, T.; Beckers, F.J.C.M.; Heesch, E.J.M.V.; Pemen, A.J.M. B-Dot and D-Dot Sensors for (Sub)Nanosecond High-Voltage and High-Current Pulse Measurements. IEEE Sens. J. 2016, 16, 3792–3801. [Google Scholar] [CrossRef]
- Wang, J.; Gao, C.; Yang, J. Design, Experiments and Simulation of Voltage Transformers on the Basis of a Differential Input D-dot Sensor. Sensors 2014, 14, 12771–12783. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Ban, S.; Yang, Y. A Differential Self-Integration D-Dot Voltage Sensor and Experimental Research. IEEE Sens. J. 2015, 15, 3846–3852. [Google Scholar] [CrossRef]
- Al Agry, A.; Schill, R.A. Calibration of Electromagnetic Dot Sensor—Part 2: D-Dot Mode. IEEE Sens. J. 2014, 14, 3111–3118. [Google Scholar] [CrossRef]
- Wagoner, T.C.; Stygar, W.A.; Ives, H.C.; Gilliland, T.L.; Spielman, R.B.; Johnson, M.F.; Reynolds, P.G.; Moore, J.K.; Mourning, R.L.; Fehl, D.L. Differential-output B-dot and D-dot monitors for current and voltage measurements on a 20-MA, 3-MV pulsed-power accelerator. Phys. Rev. Spec. Top. Accel. Beams 2007, 11, 232. [Google Scholar]
- Wang, J.; Fan, Y.; Zhu, L.; Bai, Y. Design and research of a three-phase voltage sensor based on D-dot principle. IEEJ Trans. Electr. Electr. Eng. 2017, 12, 55–61. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, J.; Xie, X.; Zhao, H.; Zhong, J.; Xiao, D. Optimization algorithm of inverse problem for a power-frequency electric field. Int. Trans. Electr. Energy Syst. 2015, 25, 89–98. [Google Scholar] [CrossRef]
- Ouwerling, G.J.L. A problem-specific inverse method for two-dimensional doping profile determination from capacitance-voltage measurements. Solid-State Electron. 1991, 34, 197–214. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, G.; Luo, C.; Wang, P.; Zhang, S.; Qian, Z. Application and Error Analysis of the Quadrature Methods in the Voltage Transformer. High Volt. Eng. 2008, 34, 919–924. [Google Scholar]
- Schlemmer, E.; Steffan, J.; Rucker, W.M.; Richter, K.R. Accuracy improvement using a modified Gauss-quadrature for integral methods in electromagnetics. IEEE Trans. Magn. 1992, 28, 1755–1758. [Google Scholar] [CrossRef]
- Behroozifar, M.; Habibi, N. A numerical approach for solving a class of fractional optimal control problems via operational matrix Bernoulli polynomials. J. Vib. Control 2018, 24, 2494–2511. [Google Scholar] [CrossRef]
- Zhao, Z.; Cui, X.; Lu, T.; Li, L. An Integral Algorithm to Evaluate the Electric Fields Associated with HVDC Power Transmission Lines. In Proceedings of the 2010 9th International Symposium on Antennas Propagation and EM Theory (ISAPE2010), Guangzhou, China, 29 November–2 December 2010; pp. 852–855. [Google Scholar]
- Head-Gordon, M.; Pople, J.A. A method for two-electron Gaussian integral and integral derivative evaluation using recurrence relations. J. Chem. Phys. 1988, 89, 5777–5786. [Google Scholar] [CrossRef]
- Rahmatian, F.; Chavez, P.P.; Jaeger, N.A.F. 230 kV Optical Voltage Transducers Using Multiple Electric Field Sensors. IEEE Power Eng. Rev. 2002, 17, 417–422. [Google Scholar]
- Chavez, P.P.; Jaeger, N.A.F.; Rahmatian, F. Accurate voltage measurement by the quadrature method. IEEE Trans. Power Deliv. 2002, 18, 14–19. [Google Scholar] [CrossRef]
- Huang, L.; Xu, Q. A New Method of Improving the Electric Field Distributions in Electro-optical Crystal Used in OVT. In Proceedings of the Sixth International Symposium on Computational Intelligence and Design, Hangzhou, China, 28–29 October 2013; IEEE: Piscataway, NJ, USA, 2014; pp. 157–159. [Google Scholar]
- Santos, J.C.; Taplamacioglu, M.C.; Hidaka, K. Pockels high-voltage measurement system. IEEE Trans. Power Deliv. 2000, 15, 8–13. [Google Scholar] [CrossRef]
- Wang, H.; Li, K.; Ding, H.; Ma, K.; Feng, S. Research on Improvement of Temperature Stability of Optical Voltage Transducer. In Proceedings of the International Conference on Intelligent Computation Technology and Automation, Changsha, China, 25–26 October 2014; IEEE: Piscataway, NJ, USA, 2015; pp. 534–538. [Google Scholar]
- Luo, S.N.; Ye, M.Y.; Xu, Y. Stability research on optical fiber voltage transformer. Proc. CSEE 2000, 20, 15–19. [Google Scholar]
- Oh, M.C.; Heo, S.W.; Chu, W.S. Polymeric Integrated-Optic Bias Chip for Optical Voltage Transducers. J. Lightwave Technol. 2014, 32, 4128–4131. [Google Scholar]
- Barbieri, L.; Gondola, M.; Potenza, M.; Villa, A.; Malgesini, R. A sensor for vector electric field measurements through a nonlinear anisotropic optical crystal. Rev. Sci. Instrum. 2017, 88. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Xu, Q.F.; Tan, Q.; Xu, Z. An OVT Based on Conoscopic Interference and Position Sensitive Detector. IEEE Sens. J. 2016, 17, 340–346. [Google Scholar] [CrossRef]
- Zeng, X.; Li, H.; Lu, Y.; Chen, Y. Online monitoring of partial discharge in high voltage switchgear using a differential electric field sensor. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomenon, Fort Worth, TX, USA, 22–25 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 385–388. [Google Scholar]
- Lynn, H.B. Image-log calibration of fracture-azimuth and fracture-density attributes from OVT prestack depth-migrated data. Lead. Edge 2016, 35, 164–169. [Google Scholar] [CrossRef]
- Lin, C.; Li, C.; He, J.; Zhang, B.; Hu, J. Surface charge inversion algorithm based on bilateral surface potential measurements of cone-type spacer. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1905–1912. [Google Scholar] [CrossRef]
- Yangyang, F.U.; Qiang, W.; Zhang, G.; Wang, X. Inverse Calculation of Surface Charge Based on Surface Potential Measurement. High Volt. Eng. 2013, 39, 88–95. [Google Scholar]
- Farah, A.A.M.; Afonso, M.M.; Vasconcelos, J.A.; Schroeder, M.A.O. A Finite-Element Approach for Electric Field Computation at the Surface of Overhead Transmission Line Conductors. IEEE Trans. Magn. 2017, PP, 1–4. [Google Scholar] [CrossRef]
- Zhu, K.; Lee, W.K.; Pong, P.W.T. Non-contact electric-coupling-based and magnetic-field-sensing-assisted technique for monitoring voltage of overhead power transmission lines. In Proceedings of the 2015 IEEE Sensors, Busan, Korea, 1–4 November 2015; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Neumaier, A. Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]











| Parameter | Number | R/mm | h/mm | D/mm | d/mm |
|---|---|---|---|---|---|
| Top electrode | 15 | 44 | 0.035 | 0.1524 | 0.1524 |
| Bottom electrode | 12 | 49.08 | 0.035 | 0.254 | 0.254 |
| Integral Point Coordinates (m) | Integral Point Field Intensity (V/m) | Integral Point Weight | Numerical Integral Voltage (kV) | Actual Voltage (kV) | Relative Error |
|---|---|---|---|---|---|
| 23.06 | 31,028.60 | 3.9138 | 179.94 | 179.63 | 0.17% |
| 14.23 | 3383.27 | 11.9956 | |||
| 3.44 | 2430.33 | 7.3718 |
| Integral Point Coordinates (m) | Integral Point Field Intensity (V/m) | Integral Point Weight | Numerical Integral Voltage (kV) | Actual Voltage (kV) | Relative Error |
|---|---|---|---|---|---|
| 1.44 | 40,370.27 | 0.2505 | 16.353 | 16.330 | 0.14% |
| 0.90 | 5946.42 | 0.7396 | |||
| 0.22 | 3975.56 | 0.4634 |
| Valid Value of Line Voltage (kV) | Integral Point Coordinates (m) | Integral Point Field Intensity (V/m) | Integral Point Weight | Numerical Integral Voltage (kV) | High-Voltage Probe (kV) | Relative Error |
|---|---|---|---|---|---|---|
| 5 | 1.44 | 10,095.43 | 0.2516 | 4.102 | 4.09 | 0.31% |
| 0.90 | 1482.72 | 0.7425 | ||||
| 0.22 | 995.02 | 0.4635 | ||||
| 10 | 1.44 | 20,183.46 | 0.2516 | 8.201 | 8.18 | 0.25% |
| 0.90 | 2964.35 | 0.7426 | ||||
| 0.22 | 1989.31 | 0.4635 | ||||
| 15 | 1.44 | 30,138.90 | 0.2530 | 12.33 | 12.3 | 0.27% |
| 0.90 | 4439.03 | 0.7443 | ||||
| 0.22 | 2999.42 | 0.4667 | ||||
| 20 | 1.44 | 40,560.46 | 0.2505 | 16.43 | 16.4 | 0.18% |
| 0.90 | 5971.06 | 0.7396 | ||||
| 0.22 | 3995.73 | 0.4634 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhao, Y.; Li, W.; Zeng, X.; Tang, J.; Wang, Y.; Deng, X. Research on Transmission Line Voltage Measurement Method of D-Dot Sensor Based on Gaussian Integral. Sensors 2018, 18, 2455. https://doi.org/10.3390/s18082455
Wang J, Zhao Y, Li W, Zeng X, Tang J, Wang Y, Deng X. Research on Transmission Line Voltage Measurement Method of D-Dot Sensor Based on Gaussian Integral. Sensors. 2018; 18(8):2455. https://doi.org/10.3390/s18082455
Chicago/Turabian StyleWang, Jingang, Yanhang Zhao, Wenjiang Li, Xianglong Zeng, Juan Tang, Yao Wang, and Xudong Deng. 2018. "Research on Transmission Line Voltage Measurement Method of D-Dot Sensor Based on Gaussian Integral" Sensors 18, no. 8: 2455. https://doi.org/10.3390/s18082455
APA StyleWang, J., Zhao, Y., Li, W., Zeng, X., Tang, J., Wang, Y., & Deng, X. (2018). Research on Transmission Line Voltage Measurement Method of D-Dot Sensor Based on Gaussian Integral. Sensors, 18(8), 2455. https://doi.org/10.3390/s18082455





