Accurate Collaborative Globally-Referenced Digital Mapping with Standard GNSS
Abstract
1. Introduction
2. Previous Work
3. GNSS Error Analysis
3.1. Low-Cost GNSS in Urban Areas
3.2. Pseudorange Measurement
3.3. Error Sources
3.3.1. Thermal Noise
3.3.2. Satellite Orbit and Clock Errors
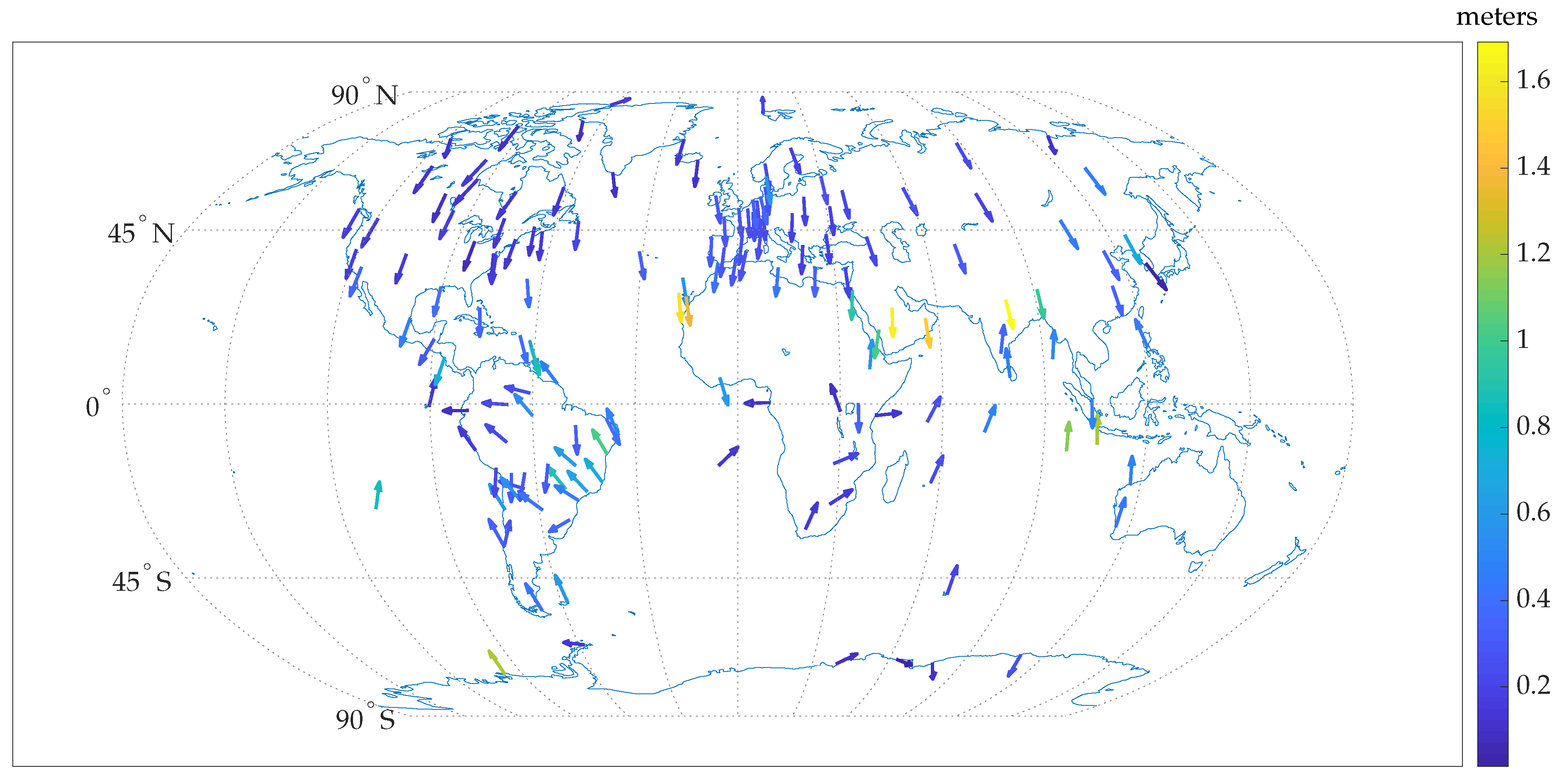
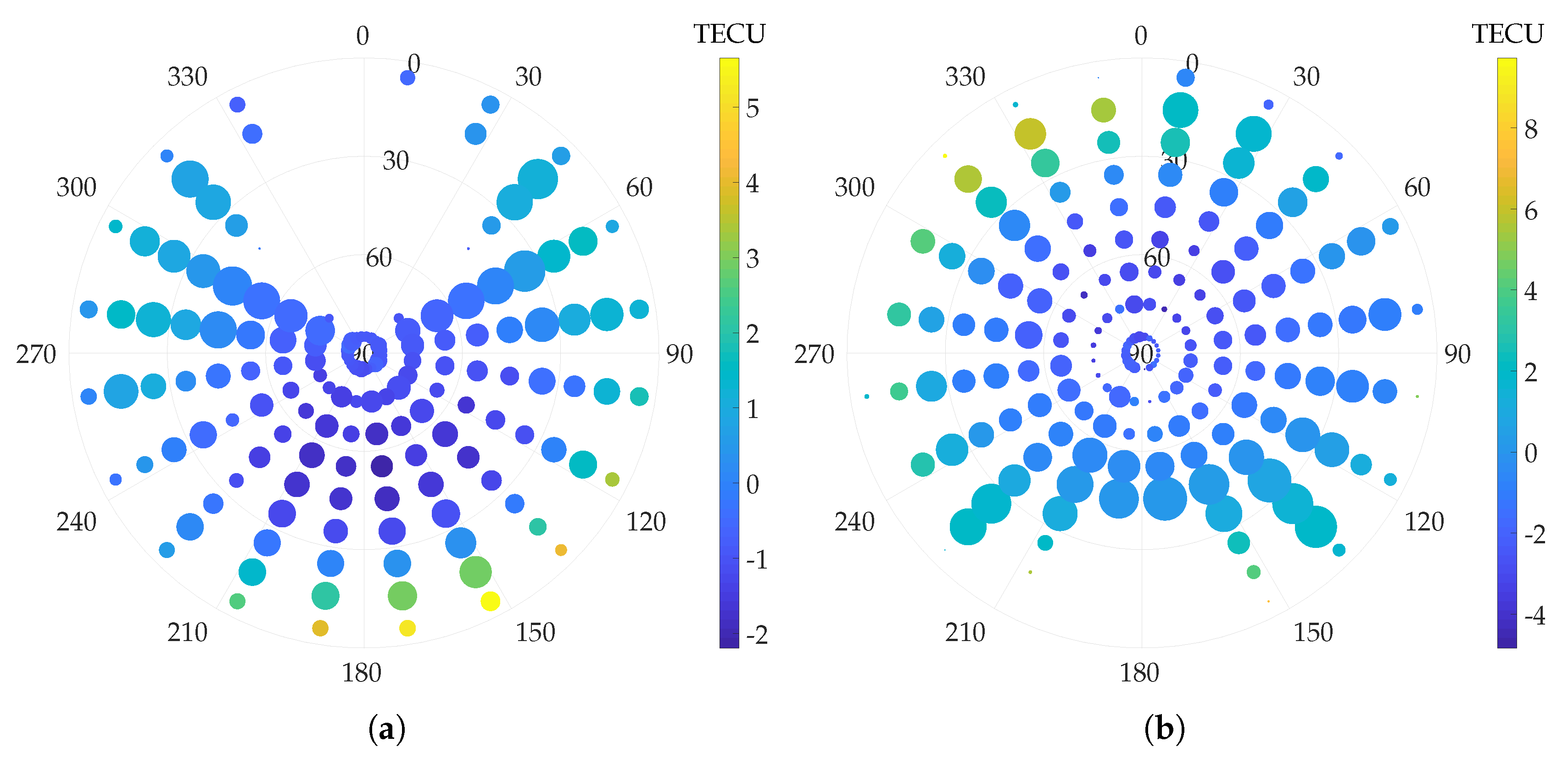
3.3.3. Ionospheric Modeling Errors
3.3.4. Tropospheric Modeling Errors
3.3.5. Multipath Error
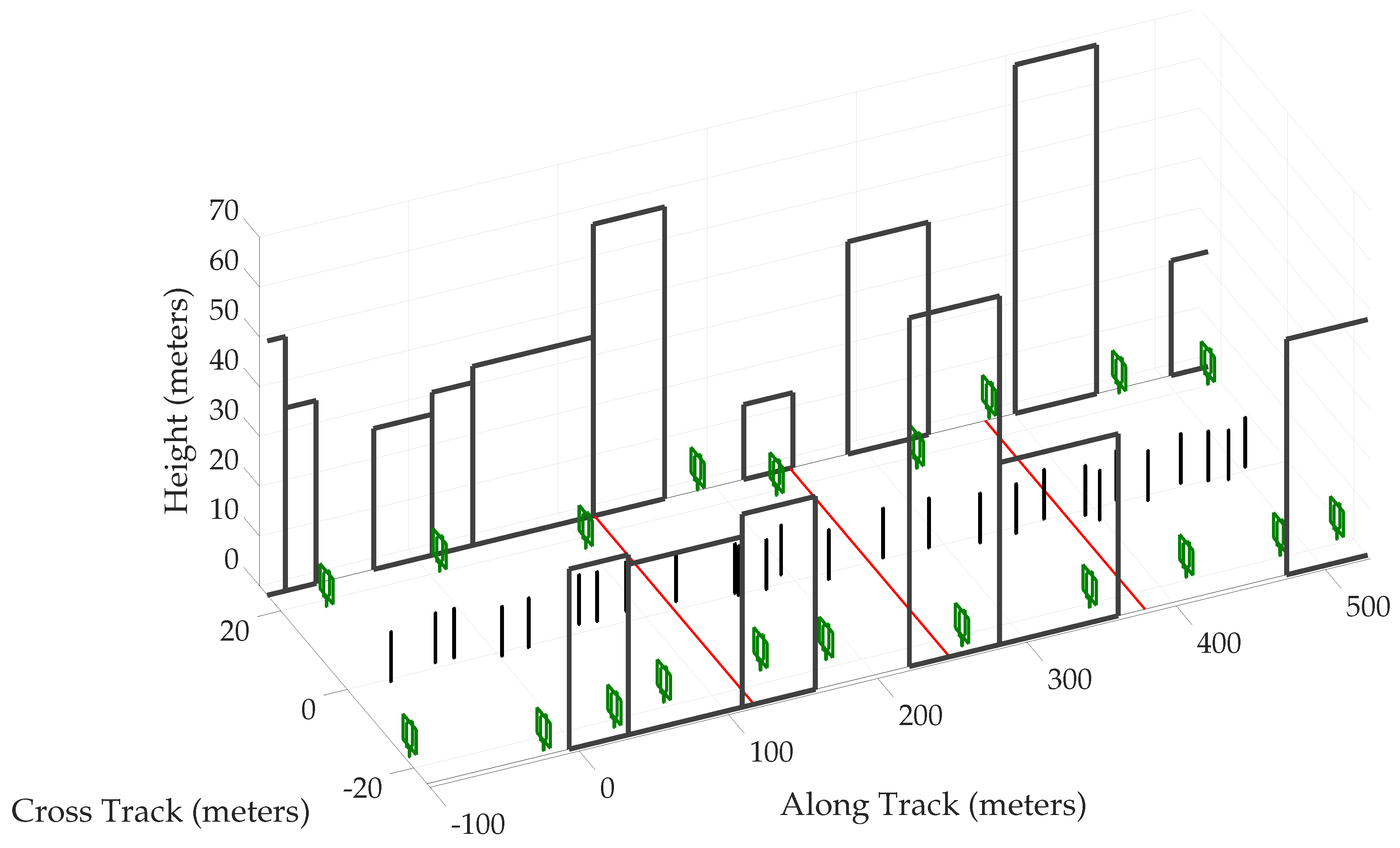
Scenario Setup
Multipath Simulation
Receiver
Navigation Filter
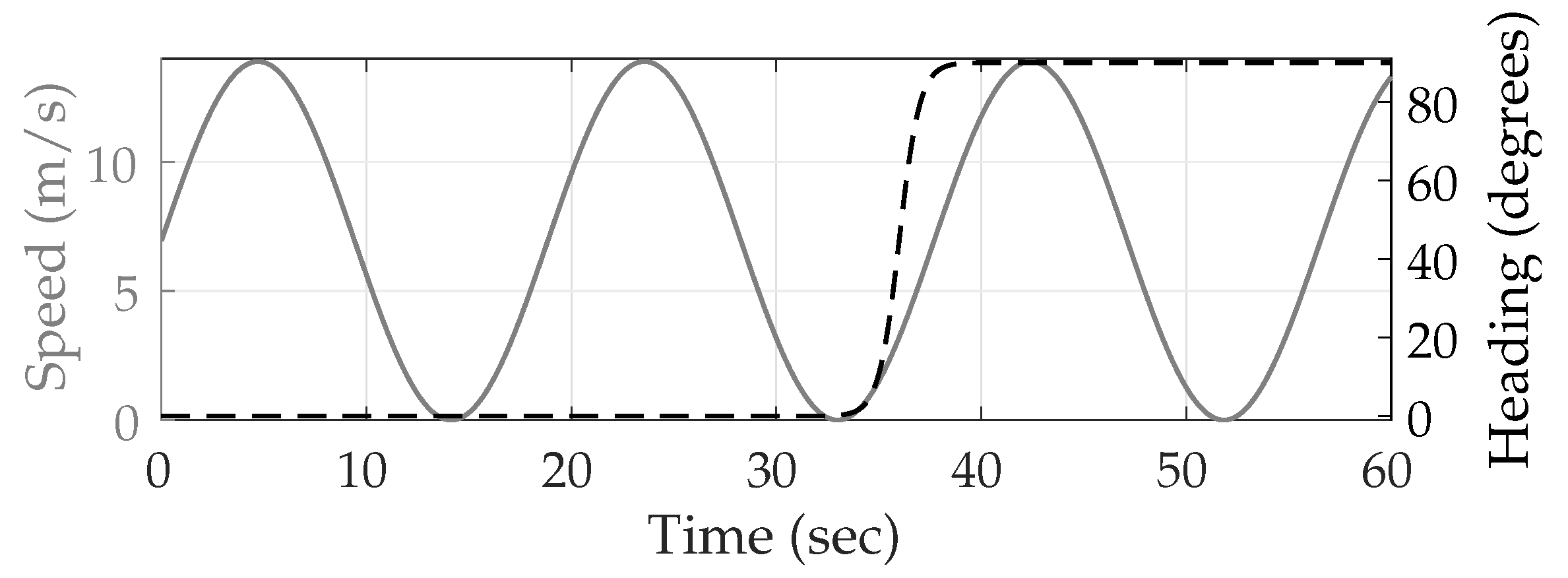
Simulation Results
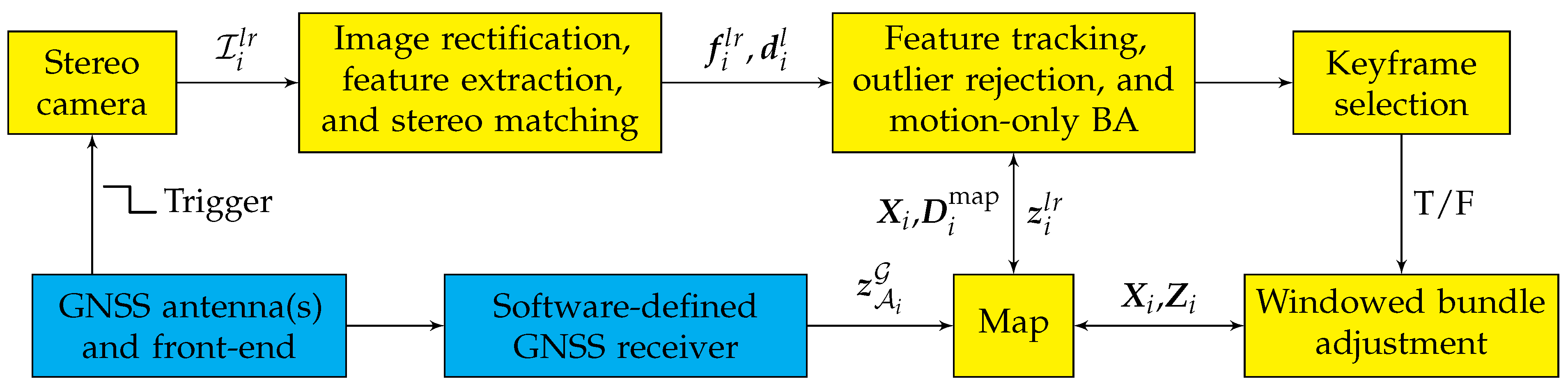
4. Globally-Referenced Electro-Optical SLAM (GEOSLAM)
4.1. Visual SLAM
4.2. GNSS Aiding
4.2.1. Coordinate Frames
4.2.2. Initialization in GNSS-Aided SLAM
4.3. Multi-Session Mapping
4.3.1. Map Database
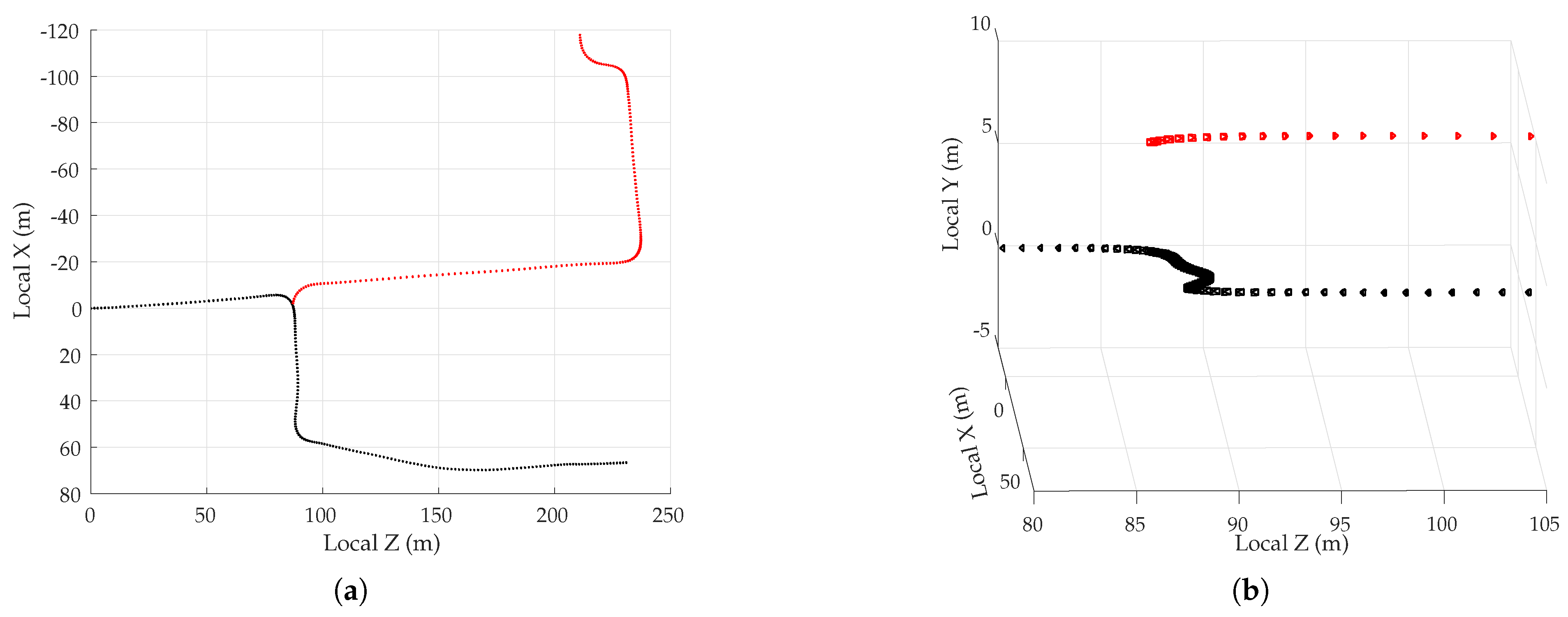
4.3.2. Map Merging
5. Empirical Results
5.1. Rover and Reference Platforms
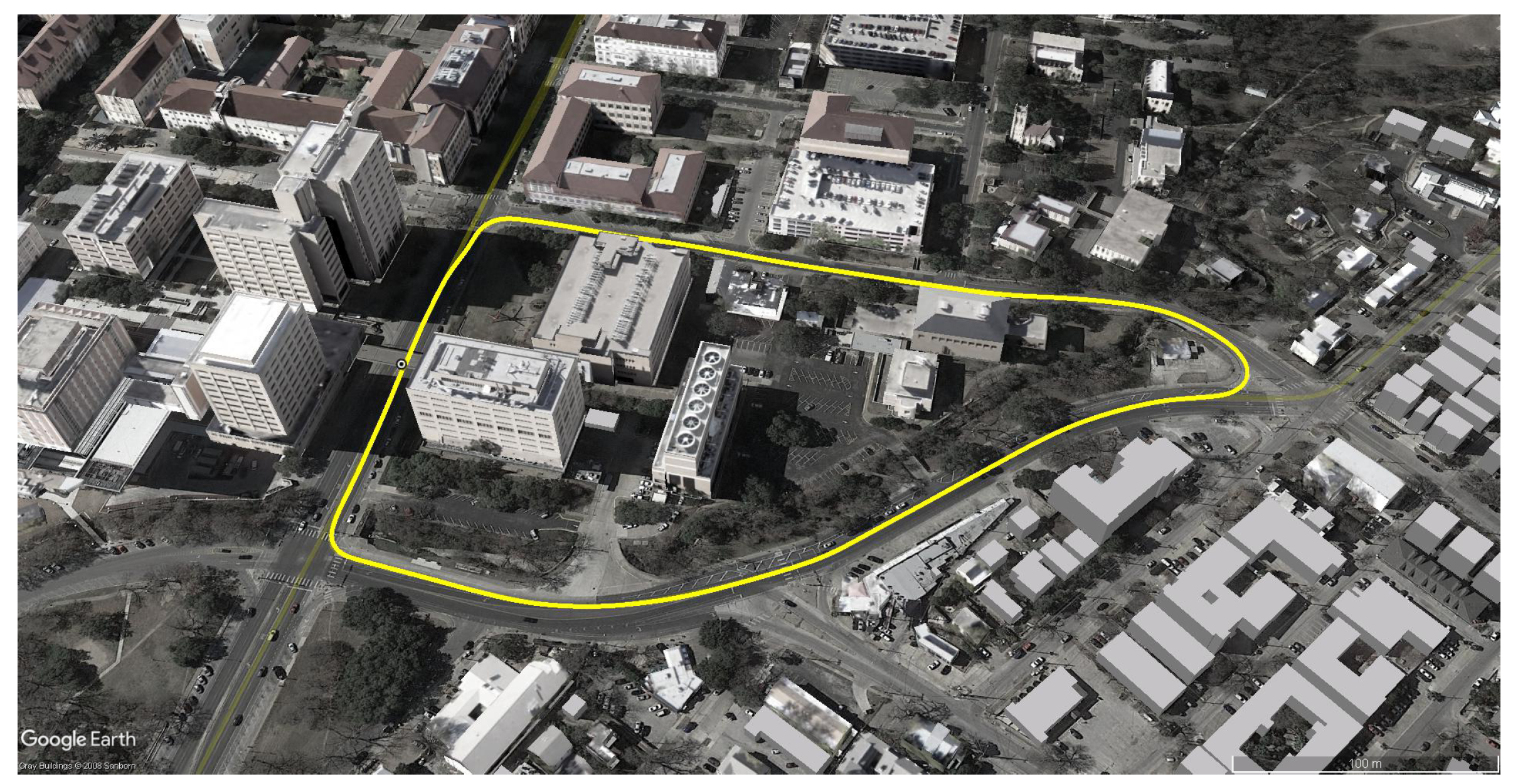
5.2. Test Route
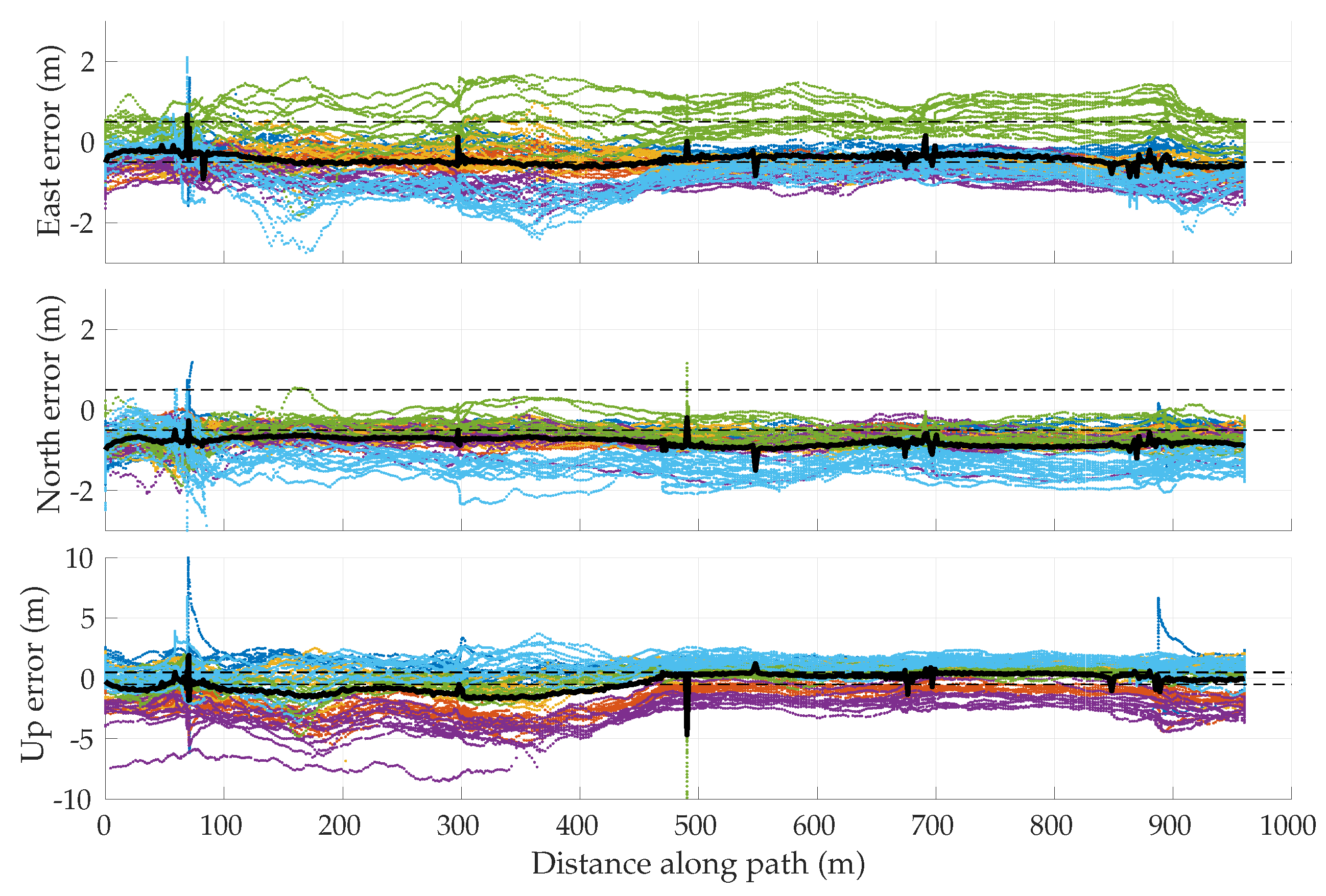
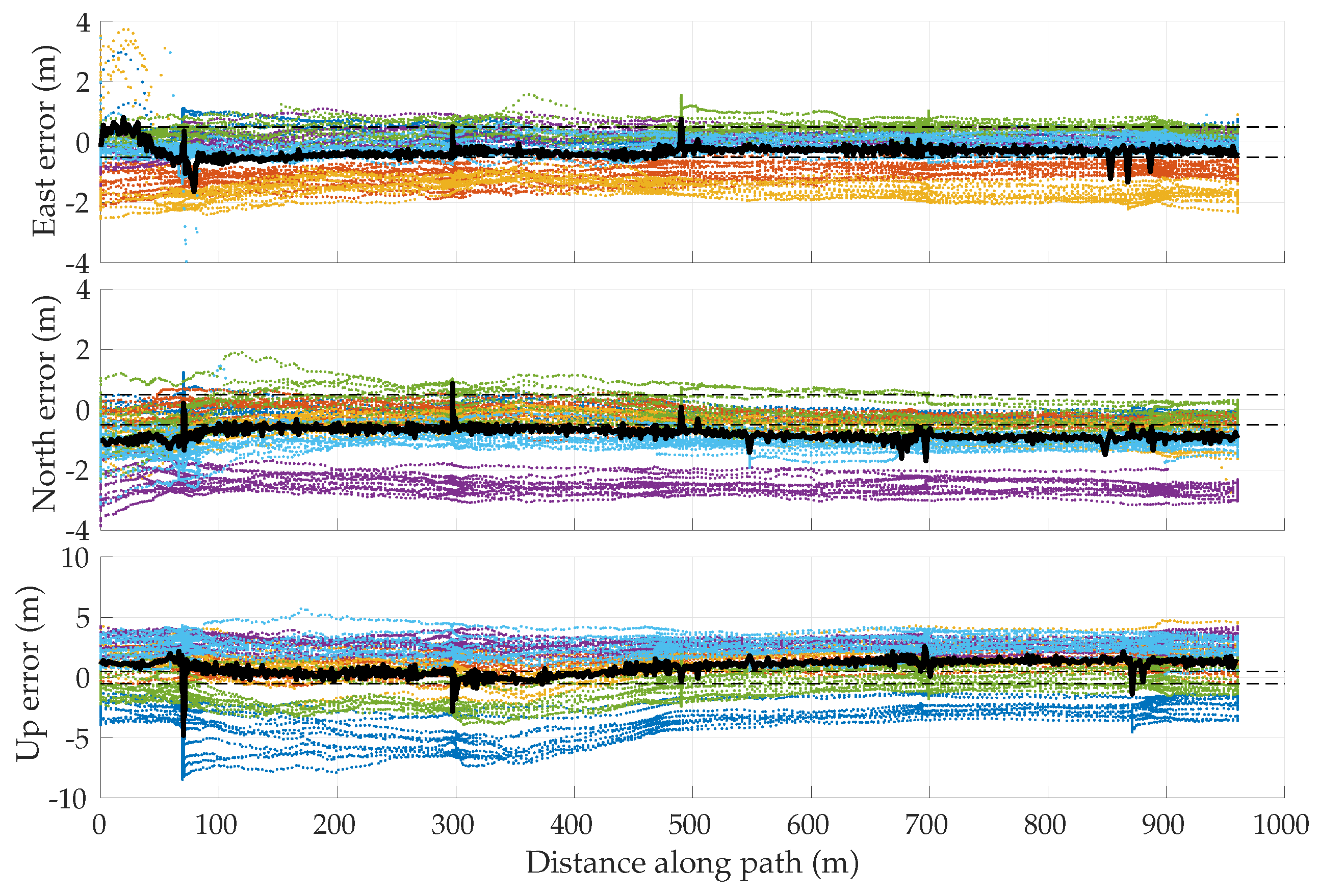
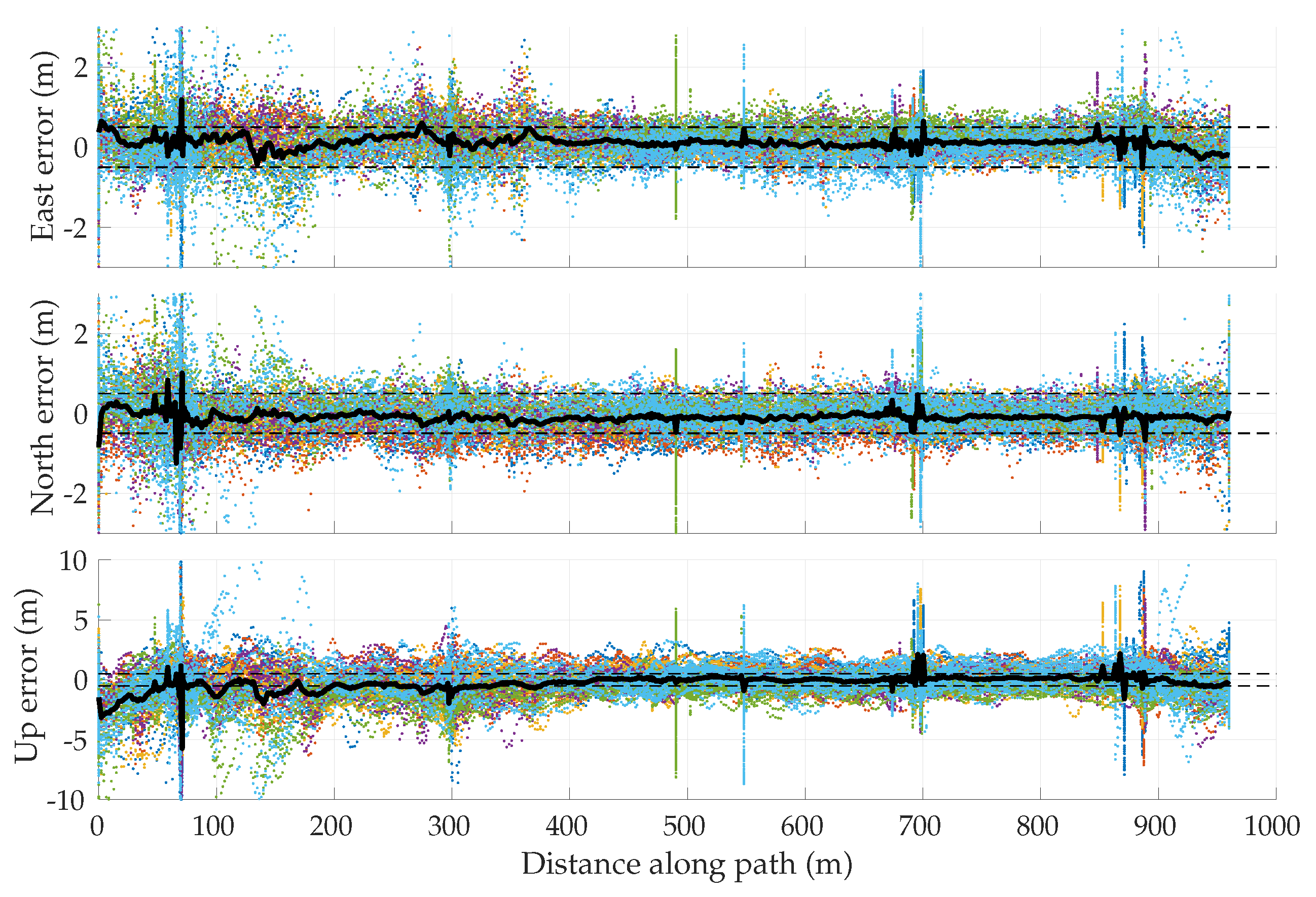
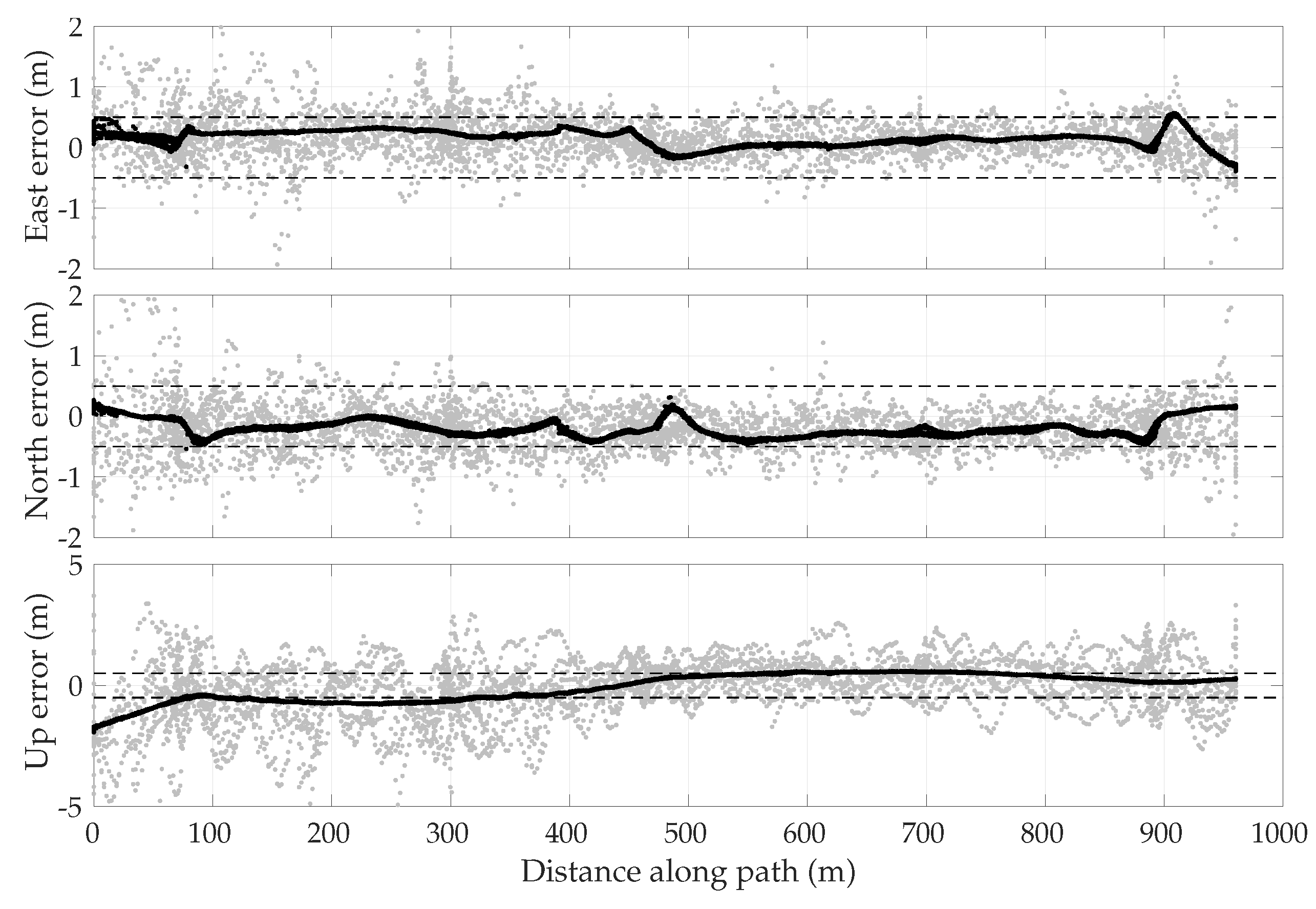
5.3. Empirical GNSS Error Analysis
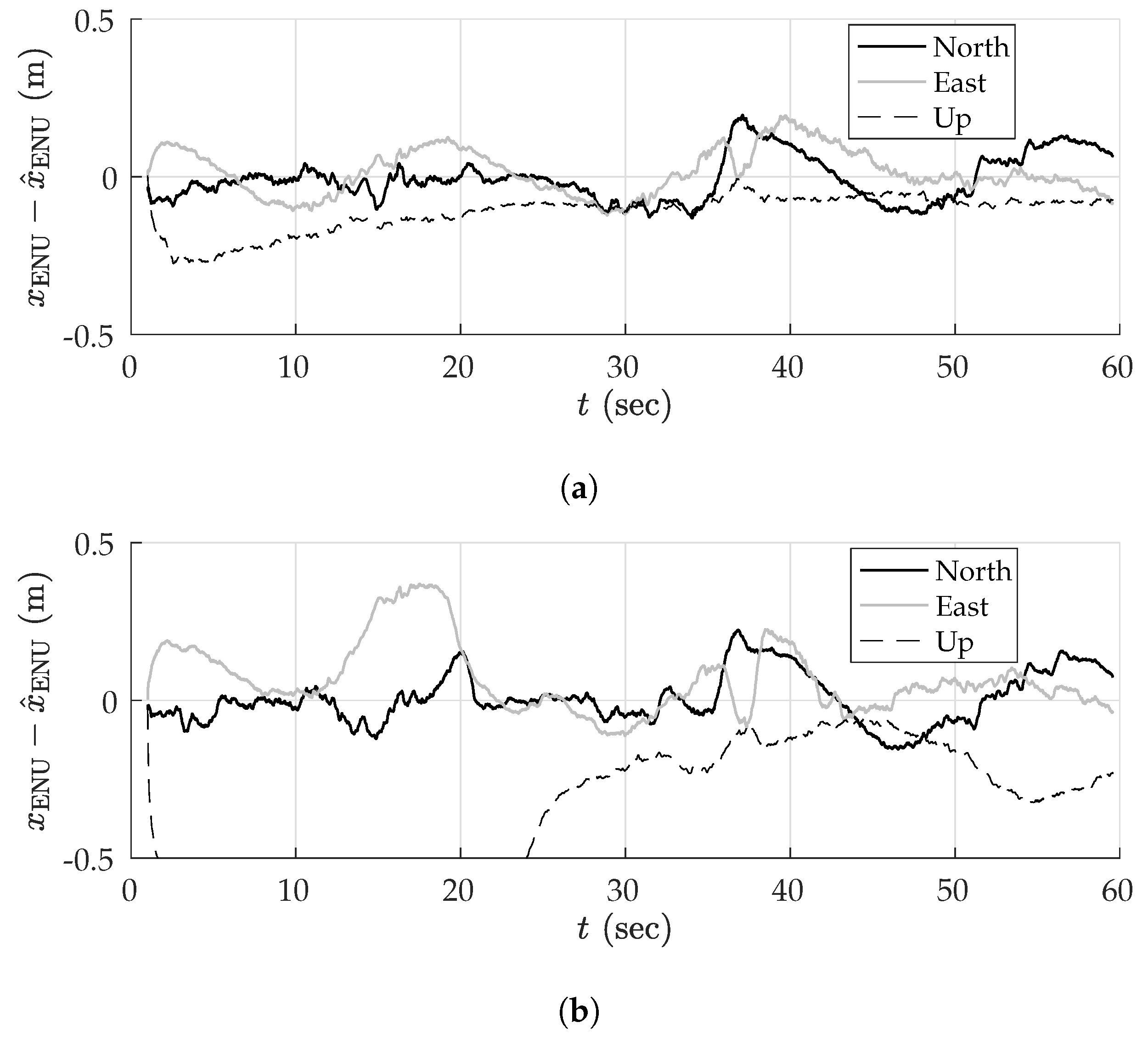
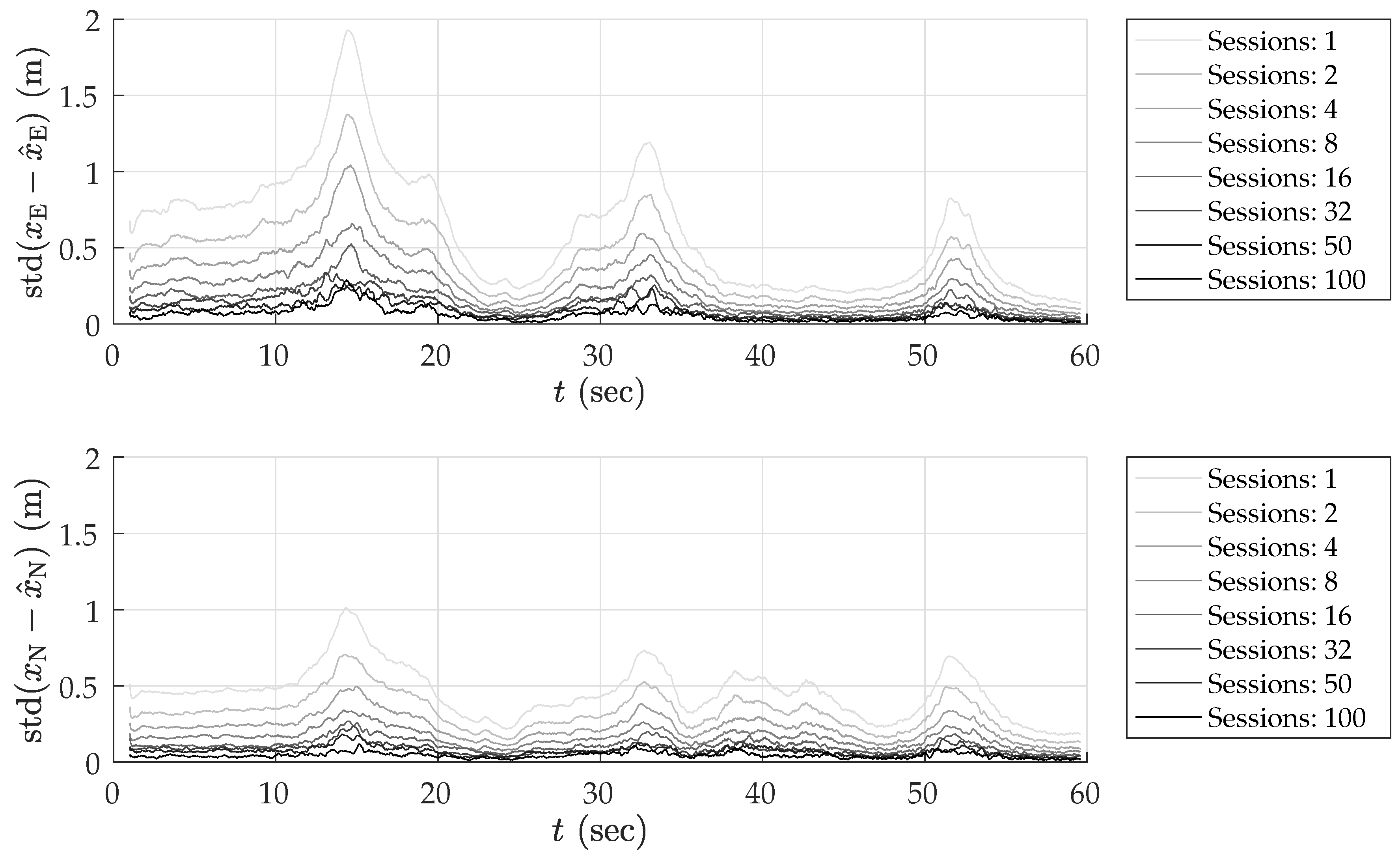
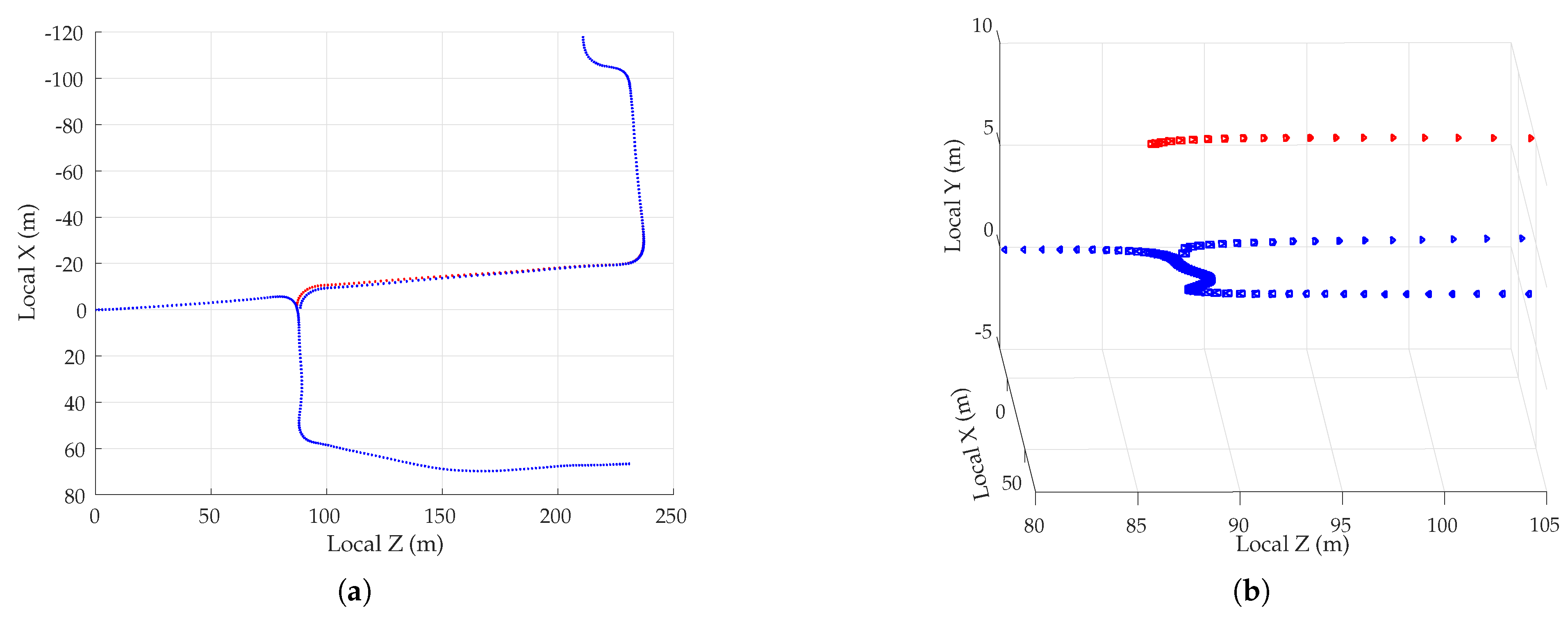
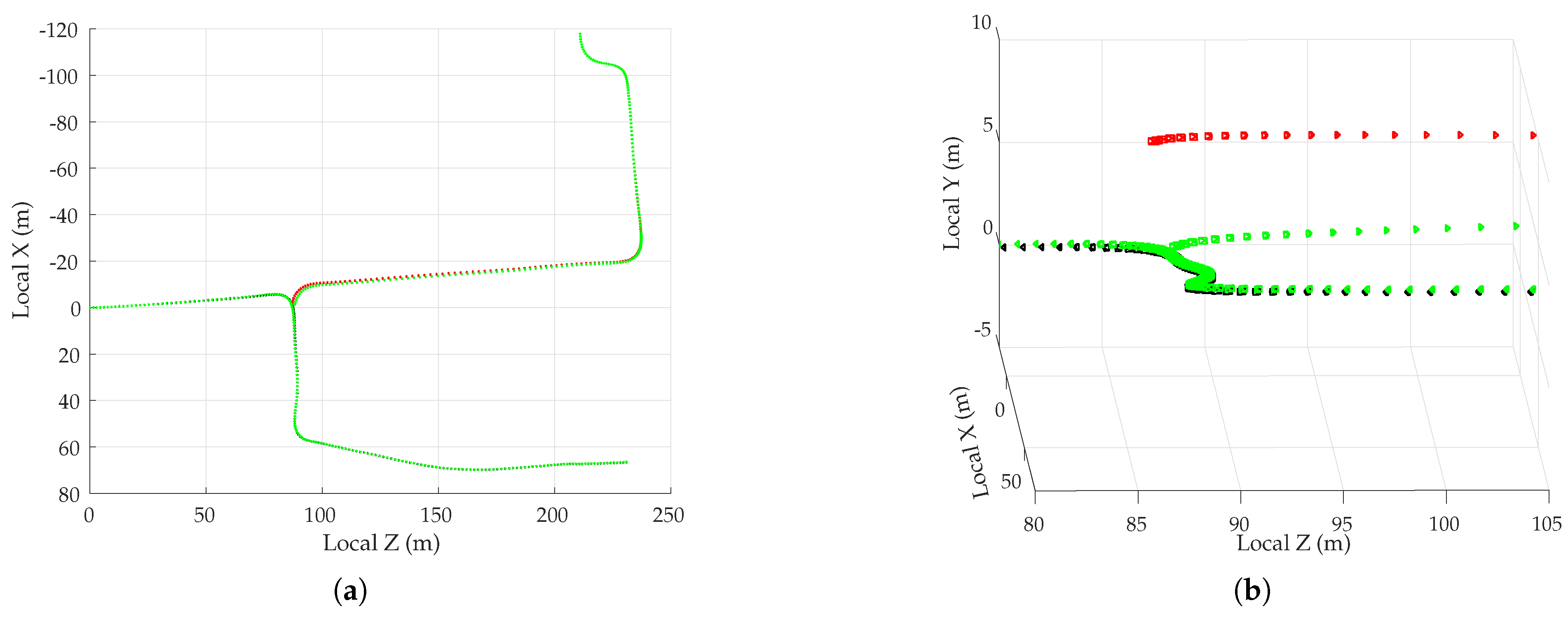
5.4. Multi-Session Mapping Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wymeersch, H.; Seco-Granados, G.; Destino, G.; Dardari, D.; Tufvesson, F. 5G mmWave Positioning for Vehicular Networks. IEEE Wirel. Commun. 2017, 24, 80–86. [Google Scholar] [CrossRef]
- Kenney, J.B. Dedicated short-range communications (DSRC) standards in the United States. Proc. IEEE 2011, 99, 1162–1182. [Google Scholar] [CrossRef]
- Choi, J.; Va, V.; Gonzalez-Prelcic, N.; Daniels, R.; Bhat, C.R.; Heath, R.W. Millimeter-wave vehicular communication to support massive automotive sensing. IEEE Commun. Mag. 2016, 54, 160–167. [Google Scholar] [CrossRef]
- Levinson, J.; Montemerlo, M.; Thrun, S. Map-Based Precision Vehicle Localization in Urban Environments; Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2007; Volume 4, p. 1. [Google Scholar]
- Levinson, J.; Thrun, S. Robust vehicle localization in urban environments using probabilistic maps. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, Alaska, 3–8 May 2010; pp. 4372–4378. [Google Scholar]
- Humphreys, T.E.; Murrian, M.; Narula, L. Low-cost Precise Vehicular Positioning in Urban Environments. In Proceedings of the IEEE/ION PLANS Meeting, Monterey, CA, USA, 23–26 April 2018. [Google Scholar]
- Hutton, J.J.; Gopaul, N.; Zhang, X.; Wang, J.; Menon, V.; Rieck, D.; Kipka, A.; Pastor, F. Centimeter-Level Robust Gnss-Aided Inertial Post-Processing for Mobile Mapping without Local Reference Stations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B3, 819–826. [Google Scholar] [CrossRef]
- Rogers, S. Creating and evaluating highly accurate maps with probe vehicles. In Proceedings of the 2000 IEEE Intelligent Transportation Systems, Dearborn, MI, USA, 1–3 October 2000; pp. 125–130. [Google Scholar]
- Guo, T.; Iwamura, K.; Koga, M. Towards high accuracy road maps generation from massive GPS traces data. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 667–670. [Google Scholar]
- Knoop, V.L.; de Bakker, P.F.; Tiberius, C.C.; van Arem, B. Lane determination with GPS precise point positioning. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2503–2513. [Google Scholar] [CrossRef]
- Circiu, M.S.; Meurer, M.; Felux, M.; Gerbeth, D.; Thölert, S.; Vergara, M.; Enneking, C.; Sgammini, M.; Pullen, S.; Antreich, F. Evaluation of GPS L5 and Galileo E1 and E5a Performance for Future Multifrequency and Multiconstellation GBAS. Navigation 2017, 64, 149–163. [Google Scholar] [CrossRef]
- Kos, T.; Markezic, I.; Pokrajcic, J. Effects of multipath reception on GPS positioning performance. In Proceedings of the ELMAR-2010, Zadar, Croatia, 15–17 September 2010; pp. 399–402. [Google Scholar]
- Le Marchand, O.; Bonnifait, P.; Ibañez-Guzmán, J.; Betaille, D.; Peyret, F. Characterization of GPS multipath for passenger vehicles across urban environments. ATTI dell’Istituto Italiano di Navigazione 2009, 189, 77–88. [Google Scholar]
- Xie, P.; Petovello, M.G. Measuring GNSS multipath distributions in urban canyon environments. IEEE Trans. Instrum. Meas. 2015, 64, 366–377. [Google Scholar]
- Rovira-Garcia, A.; Juan, J.; Sanz, J.; González-Casado, G.; Ibáñez, D. Accuracy of ionospheric models used in GNSS and SBAS: Methodology and analysis. J. Geod. 2016, 90, 229–240. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Shepard, D.P.; Humphreys, T.E. Scalable Sub-Decimeter-Accurate 3D Reconstruction. 2017. Available online: https://ctr.utexas.edu/wp-content/uploads/138.pdf (accessed on 28 July 2018).
- Shepard, D.P.; Humphreys, T.E. High-Precision Globally-Referenced Position and Attitude via a Fusion of Visual SLAM, Carrier-Phase-Based GPS, and Inertial Measurements. In Proceedings of the IEEE/ION PLANS Meeting, Monterey, CA, USA, 5–8 May 2014. [Google Scholar]
- Pesyna, K.M., Jr. Advanced Techniques for Centimeter-Accurate GNSS Positioning on Low-Cost Mobile Platforms. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2015. [Google Scholar]
- Bryson, M.; Sukkarieh, S. A Comparison of Feature and Pose-Based Mapping using Vision, Inertial and GPS on a UAV. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Ellum, C. Integration of raw GPS measurements into a bundle adjustment. IAPRS Ser. 2006, 35, 3025. [Google Scholar]
- Kume, H.; Taketomi, T.; Sato, T.; Yokoya, N. Extrinsic Camera Parameter Estimation Using Video Images and GPS Considering GPS Positioning Accuracy. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 3923–3926. [Google Scholar] [CrossRef]
- Lhuillier, M. Incremental Fusion of Structure-from-Motion and GPS Using Constrained Bundle Adjustments. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2489–2495. [Google Scholar] [CrossRef] [PubMed]
- Lhuillier, M. Fusion of GPS and structure-from-motion using constrained bundle adjustments. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 3025–3032. [Google Scholar] [CrossRef]
- Soloviev, A.; Venable, D. Integration of GPS and Vision Measurements for Navigation in GPS Challenged Environments. In Proceedings of the IEEE/ION PLANS Meeting, IEEE/Institute of Navigation, Indian Wells, CA, USA, 4–6 May 2010; pp. 826–833. [Google Scholar]
- Aumayer, B.M. Ultra-tightly Coupled Vision/GNSS for Automotive Applications. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2016. [Google Scholar]
- Chu, T.; Guo, N.; Backén, S.; Akos, D. Monocular camera/IMU/GNSS integration for ground vehicle navigation in challenging GNSS environments. Sensors 2012, 12, 3162–3185. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.J.; Kodagoda, S.; Dissanayake, G. Vision Aided GPS/INS System for Robust Land Vehicle Navigation. In Proceedings of the ION International Technical Meeting, Anaheim, CA, USA, 26–28 January 2009; pp. 600–609. [Google Scholar]
- Sajad, S.; Michael, T.; Mae, S.; Howard, L. Multiple-robot Simultaneous Localization and Mapping: A Review. J. Field Robot. 2016, 33, 3–46. [Google Scholar] [CrossRef]
- Zou, D.; Tan, P. CoSLAM: Collaborative Visual SLAM in Dynamic Environments. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 354–366. [Google Scholar] [CrossRef] [PubMed]
- Forster, C.; Lynen, S.; Kneip, L.; Scaramuzza, D. Collaborative monocular SLAM with multiple Micro Aerial Vehicles. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3962–3970. [Google Scholar] [CrossRef]
- Piasco, N.; Marzat, J.; Sanfourche, M. Collaborative localization and formation flying using distributed stereo-vision. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1202–1207. [Google Scholar] [CrossRef]
- Indelman, V.; Nelson, E.; Michael, N.; Dellaert, F. Multi-robot pose graph localization and data association from unknown initial relative poses via expectation maximization. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 593–600. [Google Scholar] [CrossRef]
- Cunningham, A.; Wurm, K.M.; Burgard, W.; Dellaert, F. Fully distributed scalable smoothing and mapping with robust multi-robot data association. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1093–1100. [Google Scholar] [CrossRef]
- Andersson, L.A.A.; Nygards, J. C-SAM: Multi-Robot SLAM using square root information smoothing. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 2798–2805. [Google Scholar] [CrossRef]
- Dabeer, O.; Ding, W.; Gowaiker, R.; Grzechnik, S.K.; Lakshman, M.J.; Lee, S.; Reitmayr, G.; Sharma, A.; Somasundaram, K.; Sukhavasi, R.T.; Wu, X. An end-to-end system for crowdsourced 3D maps for autonomous vehicles: The mapping component. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 634–641. [Google Scholar] [CrossRef]
- u blox. u-blox Announces U-Blox F9 Robust and Versatile High Precision Positioning Technology for Industrial and Automotive Applications. 2018. Available online: https://bit.ly/2GoXaOm (accessed on 27 July 2018).
- Murrian, M.J.; Gonzalez, C.W.; Humphreys, T.E.; Pesyna, K.M., Jr.; Shepard, D.P.; Kerns, A.J. Low-cost precise positioning for automated vehicles. GPS World 2016, 27, 32–39. [Google Scholar]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd rev. ed.; Ganga-Jumana Press: Lincoln, MA, USA, 2012. [Google Scholar]
- GPS Satellite Ephemerides/Satellite & Station Clocks. Available online: http://www.igs.org/products (accessed on 30 March 2018).
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; González-Casado, G. A Worldwide Ionospheric Model for Fast Precise Point Positioning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4596–4604. [Google Scholar] [CrossRef]
- Yunck, T.P. Chapter 21: Orbit Determination. In Global Positioning System: Theory and Applications; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1996; Volume 2, pp. 559–592. [Google Scholar]
- van Bree, R.J.P.; Tiberius, C.C.J.M. Real-time single-frequency precise point positioning: Accuracy assessment. GPS Solut. 2012, 16, 259–266. [Google Scholar] [CrossRef]
- Le, A.Q.; Tiberius, C. Single-frequency precise point positioning with optimal filtering. GPS Solut. 2007, 11, 61–69. [Google Scholar] [CrossRef]
- Odijk, D. Fast Precise GPS Positioning in the Presence of Ionospheric Delays; No. 52 in Fast Precise GPS Positioning in the Presence of Ionospheric Delays, NCG, Nederlandse Commissie voor Geodesie; Delft University of Technology: Delft, The Netherlands, 2002. [Google Scholar]
- Shi, C.; Gu, S.; Lou, Y.; Ge, M. An improved approach to model ionospheric delays for single-frequency Precise Point Positioning. Adv. Space Res. 2012, 49, 1698–1708. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Lehner, A.; Steingass, A. A novel channel model for land mobile satellite navigation. In Proceedings of the ION GNSS Meeting, Long Beach, CA, USA, 13–16 September 2005; pp. 13–16. [Google Scholar]
- Lehner, A.; Steingass, A. Technical Note on the Land Mobile Satellite Channel Model—Interface Control Document; Association of Radio Industries and Businesses: Tokyo, Japan, 2008. [Google Scholar]
- Psiaki, M.; Mohiuddin, S. Modeling, analysis, and simulation of GPS carrier phase for spacecraft relative navigation. J. Guid. Control Dyn. 2007, 30, 1628. [Google Scholar] [CrossRef]
- Braasch, M.S. Springer Handbook of Global Navigation Satellite Systems; Chapter Multipath; Springer: Cham, Switzerland, 2017; pp. 443–468. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley and Sons: New York, NY, USA, 2001. [Google Scholar]
- Mur-Artal, R.; Tardos, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo and RGB-D Cameras. arXiv, 2016; arXiv:1610.06475. [Google Scholar]
- Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R.; Furgale, P. Keyframe-based visual–inertial odometry using nonlinear optimization. Int. J. Robot. Res. 2015, 34, 314–334. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 834–849. [Google Scholar]
- Strasdat, H.; Montiel, J.; Davison, A.J. Visual SLAM: Why filter? Image Vis. Comput. 2012, 30, 65–77. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Muja, M.; Lowe, D.G. Fast approximate nearest neighbors with automatic algorithm configuration. In Proceedings of the VISAPP (1), Lisboa, Portugal, 5–8 February 2009; Volume 2, p. 2. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Lightsey, E.G.; Humphreys, T.E.; Bhatti, J.A.; Joplin, A.J.; O’Hanlon, B.W.; Powell, S.P. Demonstration of a Space Capable Miniature Dual Frequency GNSS Receiver. Navig. J. Inst. Navig. 2014, 61, 53–64. [Google Scholar] [CrossRef]
- Sorkine-Hornung, O.; Rabinovich, M. Least-squares rigid motion using SVD. Computing 2017, 1, 1. [Google Scholar]
- Mühlfellner, P.; Bürki, M.; Bosse, M.; Derendarz, W.; Philippsen, R.; Furgale, P. Summary maps for lifelong visual localization. J. Field Robot. 2016, 33, 561–590. [Google Scholar] [CrossRef]
- Strasdat, H.; Davison, A.J.; Montiel, J.M.; Konolige, K. Double window optimisation for constant time visual SLAM. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2352–2359. [Google Scholar]

| Ionosphere Model | Region | East (m) | North (m) | Up (m) |
|---|---|---|---|---|
| IGS | 0.0107 | −0.2129 | 0.6733 | |
| −0.0651 | −0.0692 | 1.5467 | ||
| 0.0237 | 0.2450 | 0.3355 | ||
| WAAS | CONUS | −0.0048 | −0.2916 | −0.1248 |
| Fast PPP IONEX | −0.0042 | −0.0099 | −0.0122 | |
| −0.0390 | 0.0013 | −0.3053 | ||
| −0.0325 | −0.0087 | 0.0309 |
| Distance from road center to buildings | 24 m | Distance from road center to vehicle | 5 m |
| Mean distance between road center and trees | 20 m | Antenna height | 2 m |
| Mean building width | 30 m | Building width standard deviation | 25 m |
| Mean building height | 40 m | Building height standard deviation | 20 m |
| Probability of gap between buildings | 0.5 | Mean gap width | 30 m |
| Mean distance between trees | 60 m | Mean distance between poles | 25 m |
| Averaging Ensemble Size: | 1 | 2 | 4 | 8 | 16 | 32 | 50 | 100 | |
|---|---|---|---|---|---|---|---|---|---|
| Ideal | 0–60 s average (m) | 1.5910 | 1.1262 | 0.7902 | 0.5488 | 0.4078 | 0.3090 | 0.2696 | 0.2147 |
| 13–19 s average (m) | 2.5925 | 1.7809 | 1.2136 | 0.8927 | 0.6416 | 0.4145 | 0.3544 | 0.2609 | |
| NIS | 0–60 s average (m) | 1.7851 | 1.2795 | 0.9245 | 0.6588 | 0.5169 | 0.4175 | 0.3920 | 0.3526 |
| 13–19 s average (m) | 3.1217 | 2.1953 | 1.5467 | 1.1720 | 0.8456 | 0.6470 | 0.5950 | 0.4702 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narula, L.; Wooten, J.M.; Murrian, M.J.; LaChapelle, D.M.; Humphreys, T.E. Accurate Collaborative Globally-Referenced Digital Mapping with Standard GNSS. Sensors 2018, 18, 2452. https://doi.org/10.3390/s18082452
Narula L, Wooten JM, Murrian MJ, LaChapelle DM, Humphreys TE. Accurate Collaborative Globally-Referenced Digital Mapping with Standard GNSS. Sensors. 2018; 18(8):2452. https://doi.org/10.3390/s18082452
Chicago/Turabian StyleNarula, Lakshay, J. Michael Wooten, Matthew J. Murrian, Daniel M. LaChapelle, and Todd E. Humphreys. 2018. "Accurate Collaborative Globally-Referenced Digital Mapping with Standard GNSS" Sensors 18, no. 8: 2452. https://doi.org/10.3390/s18082452
APA StyleNarula, L., Wooten, J. M., Murrian, M. J., LaChapelle, D. M., & Humphreys, T. E. (2018). Accurate Collaborative Globally-Referenced Digital Mapping with Standard GNSS. Sensors, 18(8), 2452. https://doi.org/10.3390/s18082452





