UAV Based Relay for Wireless Sensor Networks in 5G Systems
Abstract
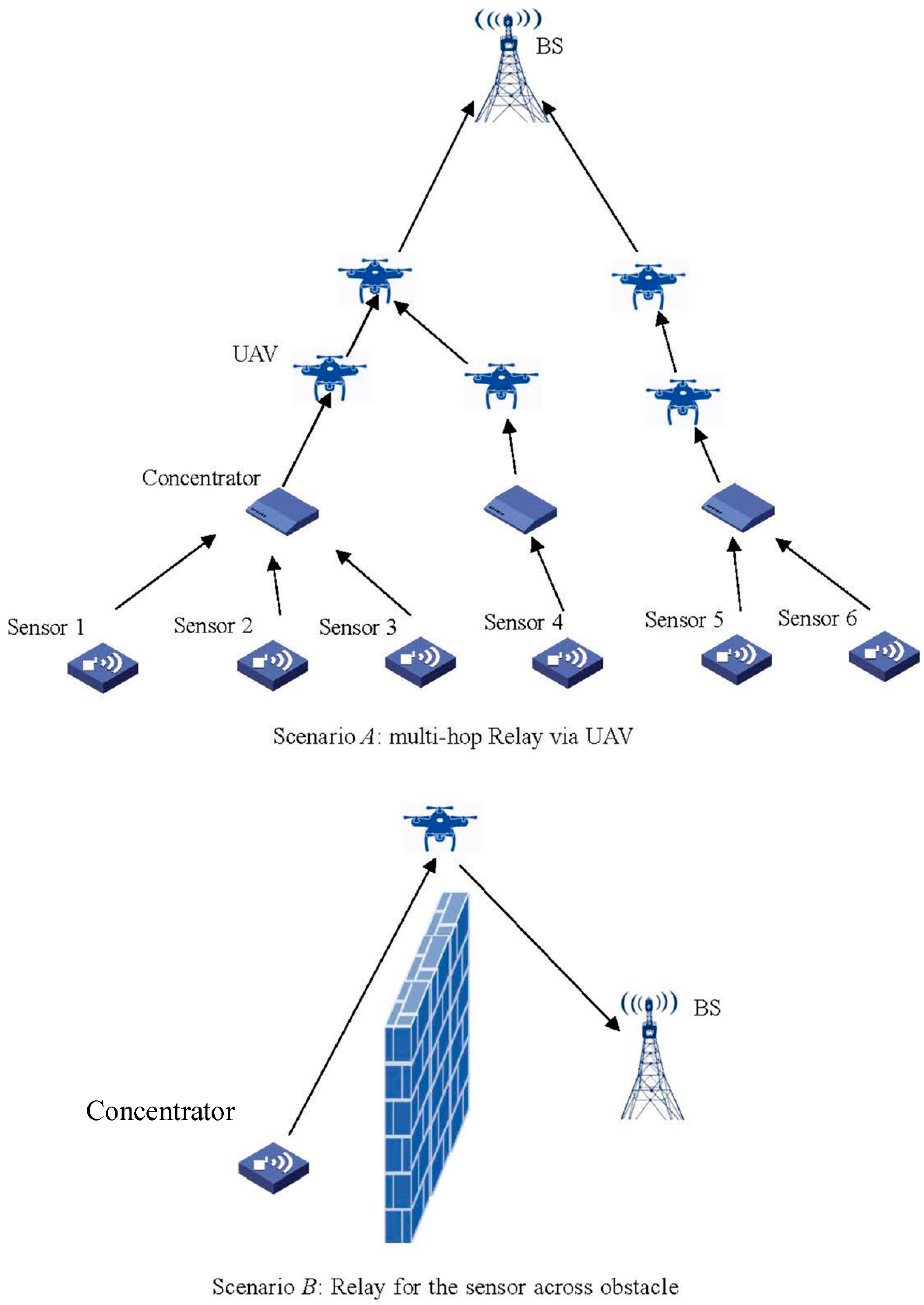
1. Introduction
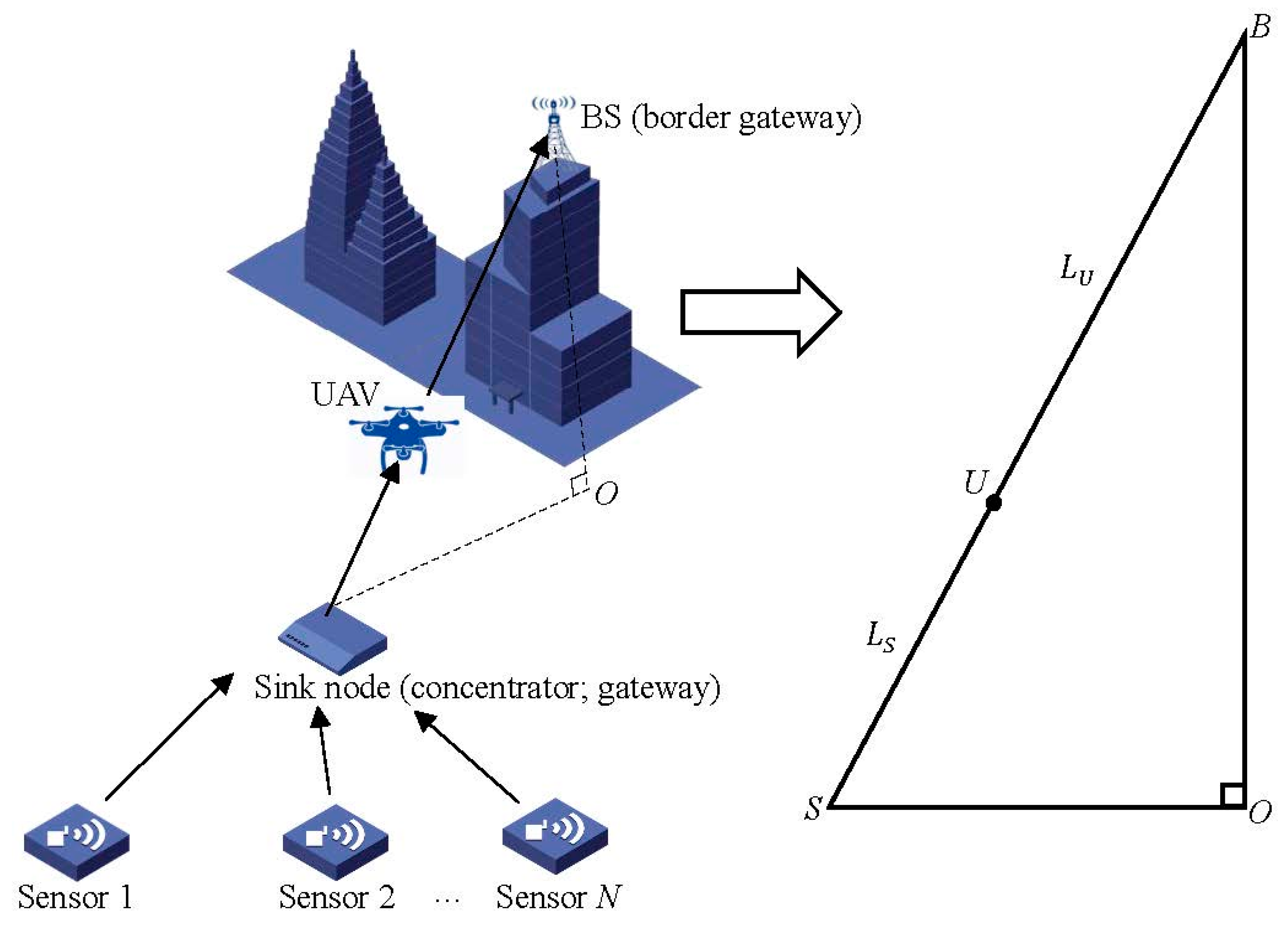
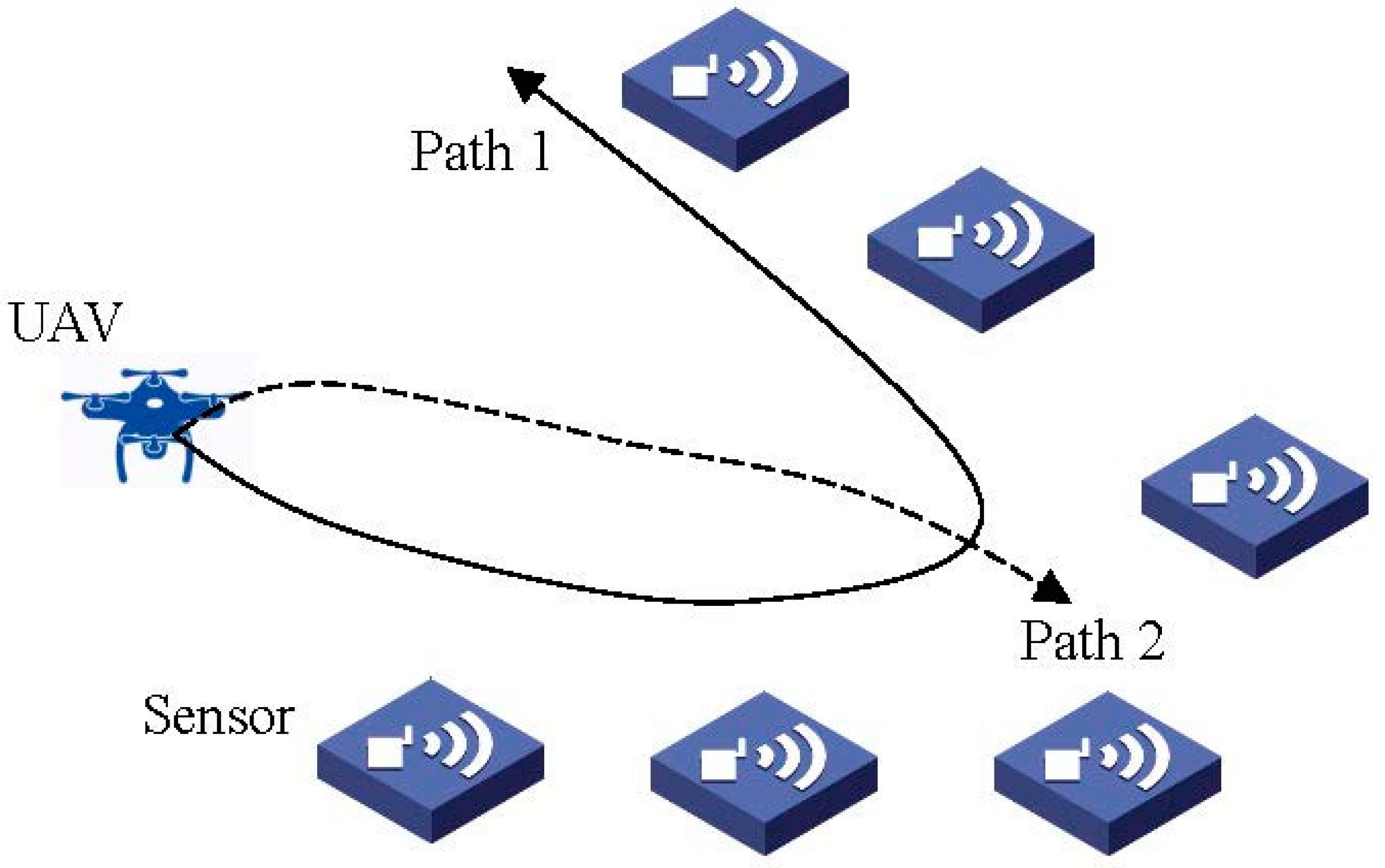
2. System Model and the Problem Formulation
3. Convex Optimization Based Position of Unmanned Aerial Vehicle
| Algorithm 1. Location of UAV (LU) algorithm. |
| Input: location of the concentrator, location of BS, the length of and , respectively; C, , , , , and . |
| Output: the optimal for minimizing system power consumption. |
| 1. Determine by (3). 2. Obtain the optimization model in (9). 3. Obtain the optimal value of as in (11). Return: . |
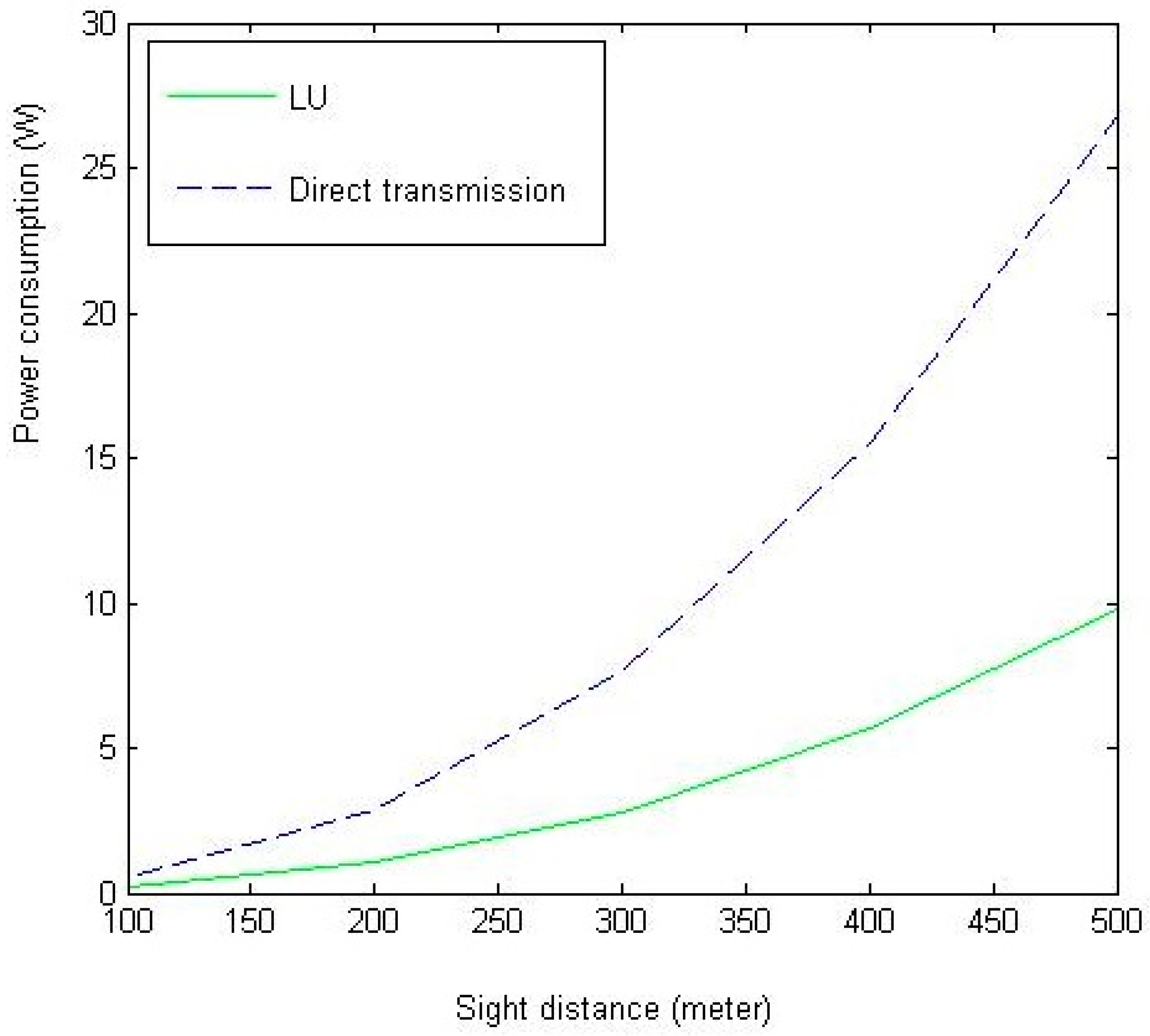
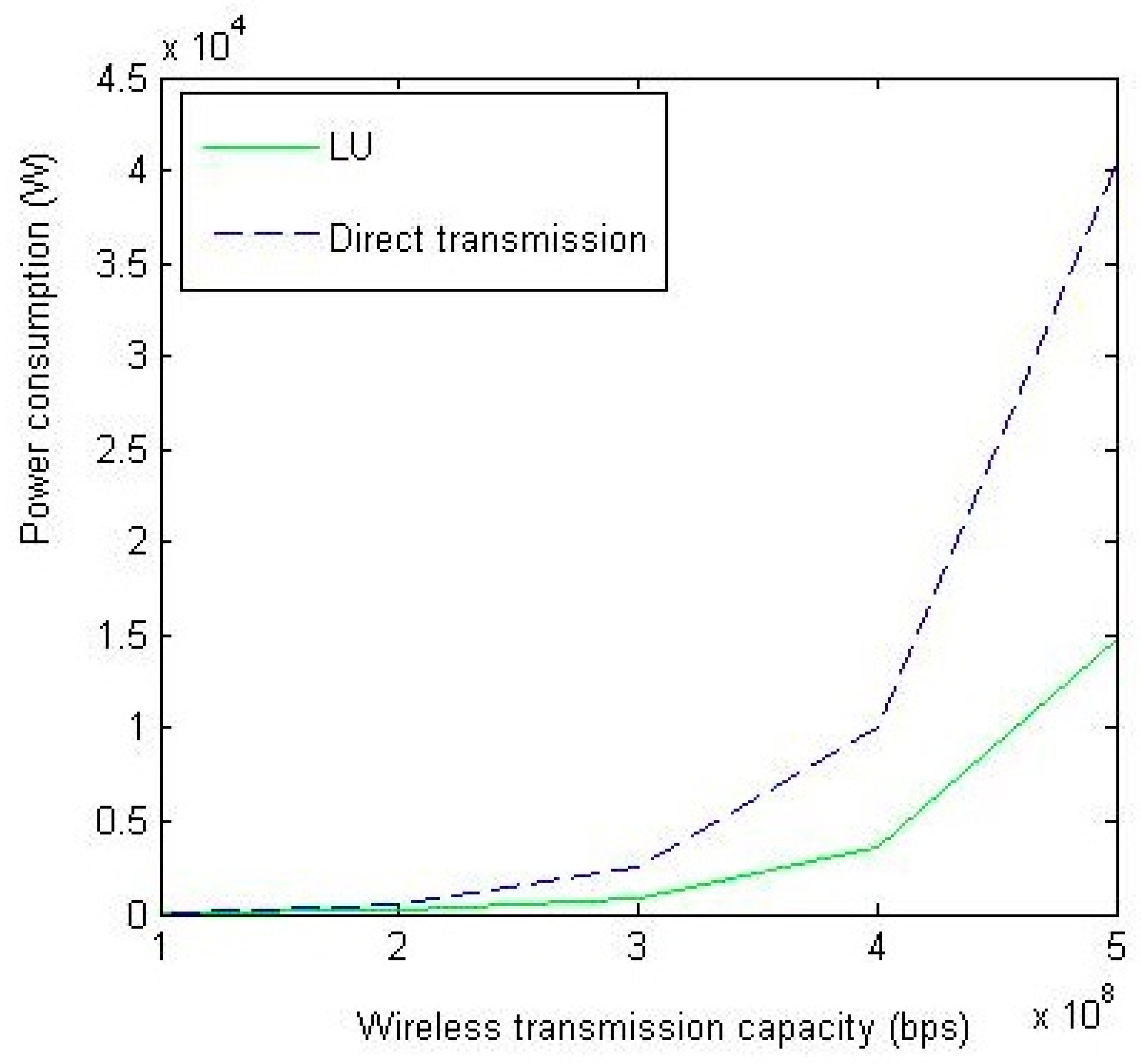
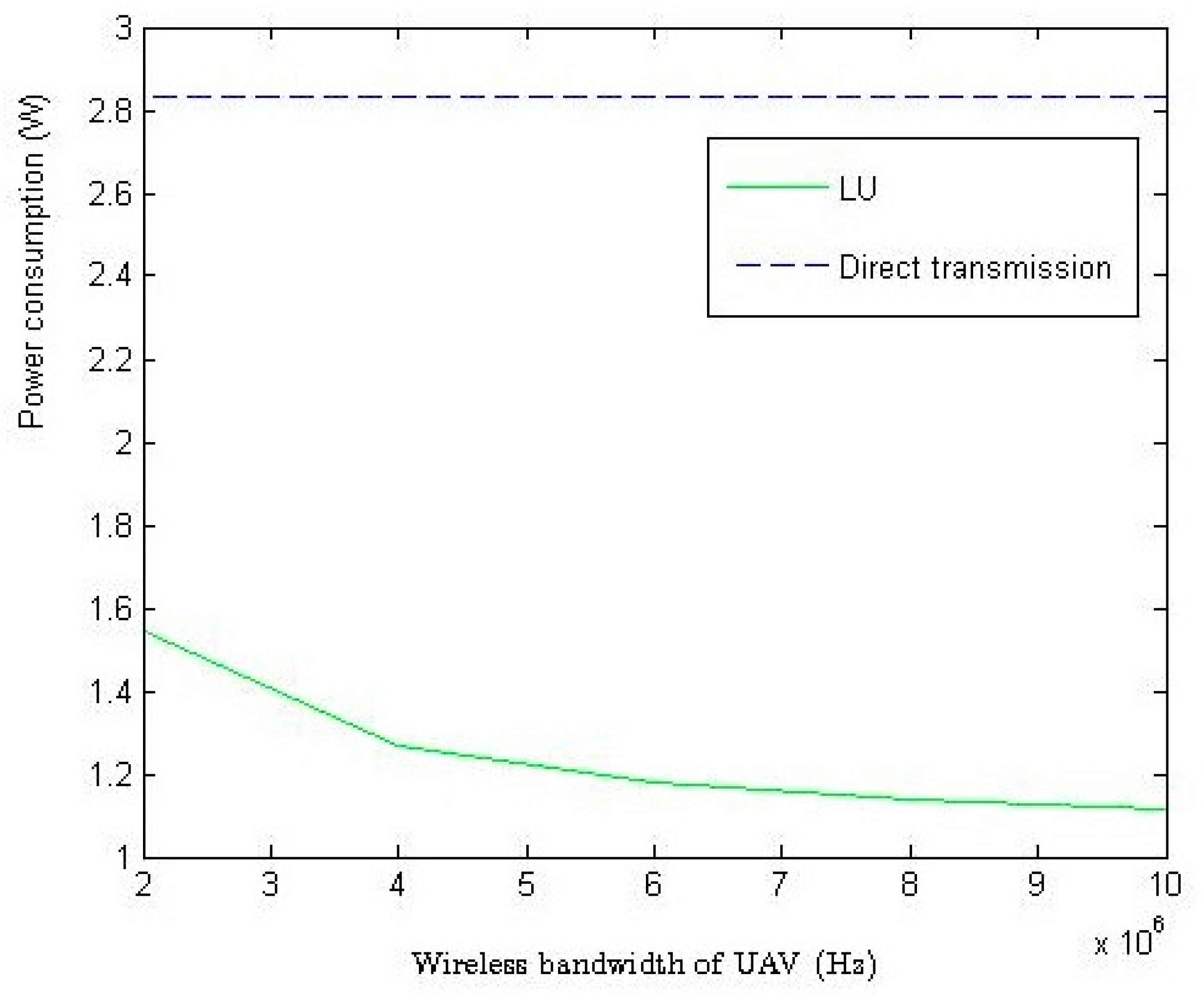
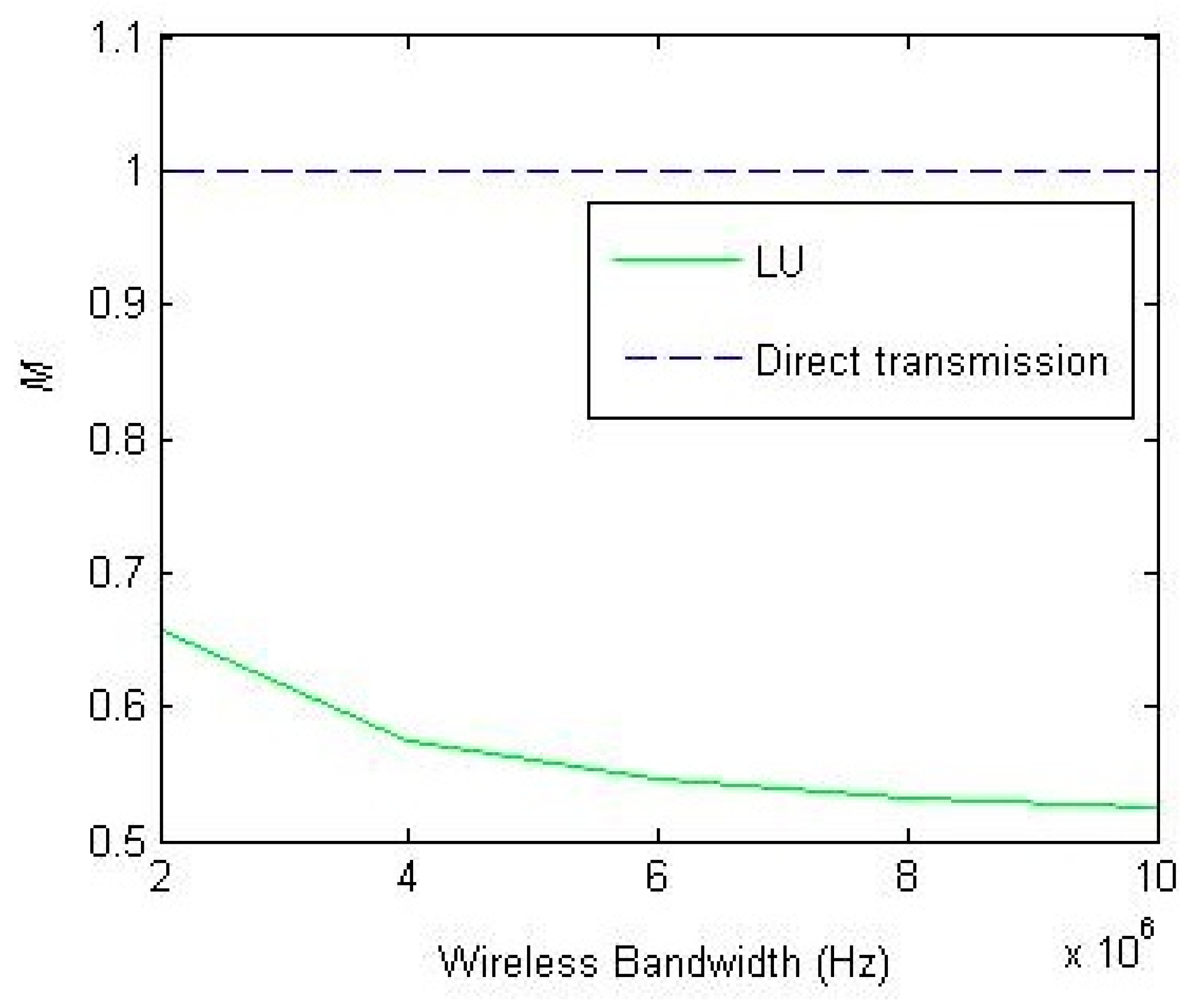
4. Simulation
5. Research Direction and Conclusions
- (1)
- When frequency subchannels, fast fading, and slow fading are considered, the optimal position for a specific UAV differs across the frequency of subchannels. How to determine the optimal position will be an intractable problem.
- (2)
- Considering the power consumption of UAV flight, how does the optimal position of a UAV change.
- (3)
- How to determine the optimal flightpath. This is a key issue for the UAV based relay due to the moving feature of a UAV.
- (4)
- How to achieve the tradeoff between the number of UAV and the performance of the WSN. This should be appropriately determined by an optimization tool, such as geometric programming optimization, etc.
- (5)
Author Contributions
Funding
Conflicts of Interest
References
- Martínez, I.; Salcedo, I.; Daza, I. IoT application of WSN on 5G infrastructure. In Proceedings of the International Symposium on Networks, Computers and Communications (ISNCC), Marrakech, Morocco, 16–18 May 2017; pp. 1–6. [Google Scholar]
- Duan, Y.; Li, W.; Fu, X.; Luo, Y.; Yang, L. A methodology for reliability of WSN based on software defined network in adaptive industrial environment. IEEE/CAA J. Autom. Sin. 2018, 5, 74–82. [Google Scholar] [CrossRef]
- Khalil, N.; Abid, M.; Benhaddou, D.; Gerndt, M. Wireless sensors networks for Internet of Things. In Proceedings of the IEEE Ninth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Singapore, 21–24 April 2014; pp. 1–6. [Google Scholar]
- Si, P.; He, Y.; Yao, H.; Yang, R.; Zhang, Y. DaVe: Offloading delay-tolerant data traffic to connected vehicle networks. IEEE Trans. Veh. Technol. 2016, 65, 3941–3953. [Google Scholar] [CrossRef]
- Xu, L.; Collier, R.; O’Hare, G. A survey of clustering techniques in WSNs and consideration of the challenges of applying such to 5G IoT scenarios. IEEE Int. Things J. 2017, 4, 1229–1249. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication, 1st ed.; Cambridge University: New York, NY, USA, 2005. [Google Scholar]
- Goparaju, A.K. Superposition Coding Based Co-Operative Diversity Schemes. Master’s Thesis, Louisiana State University, Baton Rouge, LA, USA, October 2005. [Google Scholar]
- Men, J.J.; Ge, J.H.; Zhang, C.S. Performance analysis of nonorthogonal multiple access for relaying networks over Nakagami-m fading channels. IEEE Trans. Veh. Technol. 2017, 66, 1200–1208. [Google Scholar] [CrossRef]
- Shi, S.L.; Yang, L.X.; Zhu, H. Outage balancing in downlink nonorthogonal multiple access with statistical channel state information. IEEE Trans. Wirel. Commun. 2016, 15, 4718–4731. [Google Scholar]
- Bhanumathi, V.; Sangeetha, C.P. A guide for the selection of routing protocols in WBAN for healthcare applications. Hum. Centric Comput. Inf. Sci. 2017, 7, 24. [Google Scholar] [CrossRef]
- Costa, F.G.; Ueyama, J.; Braun, T.; Pessin, G.; Osório, F.S.; Vargas, P.A. The use of unmanned aerial vehicles and wireless sensor network in agricultural applications. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 12 November 2012; pp. 5045–5048. [Google Scholar]
- Valente, J.; Sanz, D.; Barrientos, A.; del Cerro, J.; Ribeiro, Á.; Rossi, C. An air-ground wireless sensor network for crop monitoring. Sensors 2011, 11, 6088–6108. [Google Scholar] [CrossRef]
- Aslan, Y.E.; Korpeoglu, I.; Ulusoy, Ö. A framework for use of wireless sensor networks in forest fire detection and monitoring. Comput. Environ. Urban Syst. 2012, 36, 614–625. [Google Scholar] [CrossRef]
- Quaritsch, M.; Kruggl, K.; Wischounig-Strucl, D.; Bhattacharya, S.; Shah, M.; Rinner, B. Networked UAVs as aerial sensor network for disaster management applications. E & I Elektrotechnik Und Informationstechnik 2010, 127, 56–63. [Google Scholar]
- Ueyama, J.; Freitas, H.; Faical, B.S.; Filho, G.P.R. Exploiting the use of unmanned aerial vehicles to provide resilience in wireless sensor networks. IEEE Commun. Mag. 2014, 52, 81–87. [Google Scholar] [CrossRef]
- Kułakowski, P.; Calle, E.; Marzo, J.L. Performance study of wireless sensor and actuator networks in forest fire scenarios. Int. J. Commun. Syst. 2013, 26, 515–529. [Google Scholar] [CrossRef]
- Erman, A.T.; van Hoesel, L.; Havinga, P.; Wu, J. Enabling mobility in heterogeneous wireless sensor networks cooperating with UAVs for mission-critical management. IEEE Wirel. Commun. 2008, 15, 38–46. [Google Scholar] [CrossRef]
- Rangan, S.; Rappaport, T.S.; Erkip, E. Millimeter-wave cellular wireless networks: Potentials and challenges. Proc. IEEE 2014, 102, 366–385. [Google Scholar] [CrossRef]
- Su, Z.; Xu, Q.; Luo, J.; Pu, H.; Peng, Y.; Lu, R. A secure content caching scheme for disaster backup in fog computing enabled mobile social networks. IEEE Trans. Ind. Inform. 2018, PP, 1. [Google Scholar] [CrossRef]
- Su, Z.; Hui, Y.; Xu, Q.; Yang, T.; Liu, J.; Jia, Y. An edge caching scheme to distribute content in vehicular networks. IEEE Trans. Veh. Technol. 2018, 67, 5346–5356. [Google Scholar] [CrossRef]
- Xu, Q.; Su, Z.; Zheng, Q.; Luo, M.; Dong, B. Secure content delivery with edge nodes to save caching resources for mobile users in green cities. IEEE Trans. Ind. Inform. 2018, 14, 2550–2559. [Google Scholar] [CrossRef]
| 50 MHz | |
| 50 MHz | |
| T | 200 m |
| C | 500 Mbps |
| Noise power spectral density | −174 dBm/Hz |
| The omnidirectional path model | |
| Link | Uplink |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, S.; Zhao, L.; Su, Z.; Jian, X. UAV Based Relay for Wireless Sensor Networks in 5G Systems. Sensors 2018, 18, 2413. https://doi.org/10.3390/s18082413
Fu S, Zhao L, Su Z, Jian X. UAV Based Relay for Wireless Sensor Networks in 5G Systems. Sensors. 2018; 18(8):2413. https://doi.org/10.3390/s18082413
Chicago/Turabian StyleFu, Shu, Lian Zhao, Zhou Su, and Xin Jian. 2018. "UAV Based Relay for Wireless Sensor Networks in 5G Systems" Sensors 18, no. 8: 2413. https://doi.org/10.3390/s18082413
APA StyleFu, S., Zhao, L., Su, Z., & Jian, X. (2018). UAV Based Relay for Wireless Sensor Networks in 5G Systems. Sensors, 18(8), 2413. https://doi.org/10.3390/s18082413







