Dissimilarity Metric Based on Local Neighboring Information and Genetic Programming for Data Dissemination in Vehicular Ad Hoc Networks (VANETs)
Abstract
:1. Introduction
1.1. Problem Statement
1.2. Our Contribution
2. Related Works
2.1. Data Dissemination Algorithms in VANETs
2.2. Probabilistic Data Dissemination Algorithms for VANETs Based on Distance
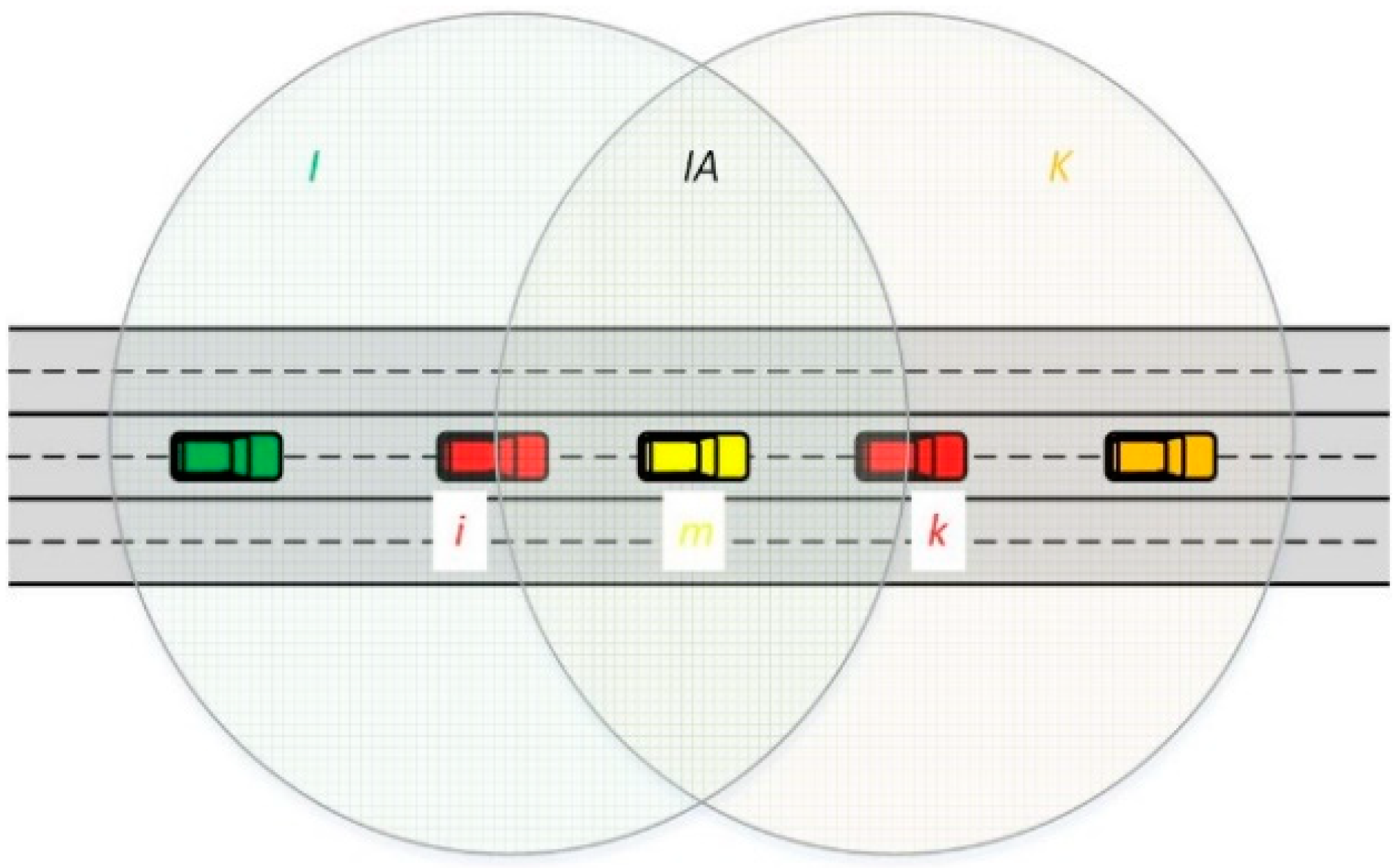
3. Dissimilarity Metrics Based on Neighboring Information
3.1. Definition of Classical Dissimilarity Metrics
3.2. New Dissimilarity Metrics
4. Genetic Programming
| Algorithm 1. Genetic programming. |
| 1: Objective function = PCC(M, D) |
| 2: Encode the solution into a tree (string) |
| 3: Generate the initial population |
| 4: Set crossover (pc) and mutation (pm) probabilities |
| 5: While (t < Max. of generations) |
| 6: Parents selection |
| 7: Crossover with pc |
| 8: Mutation with pm |
| 9: Evaluate offspring |
| 10: Update t = t + 1 |
| 11: End While |
| 12: Decode the results and visualization |
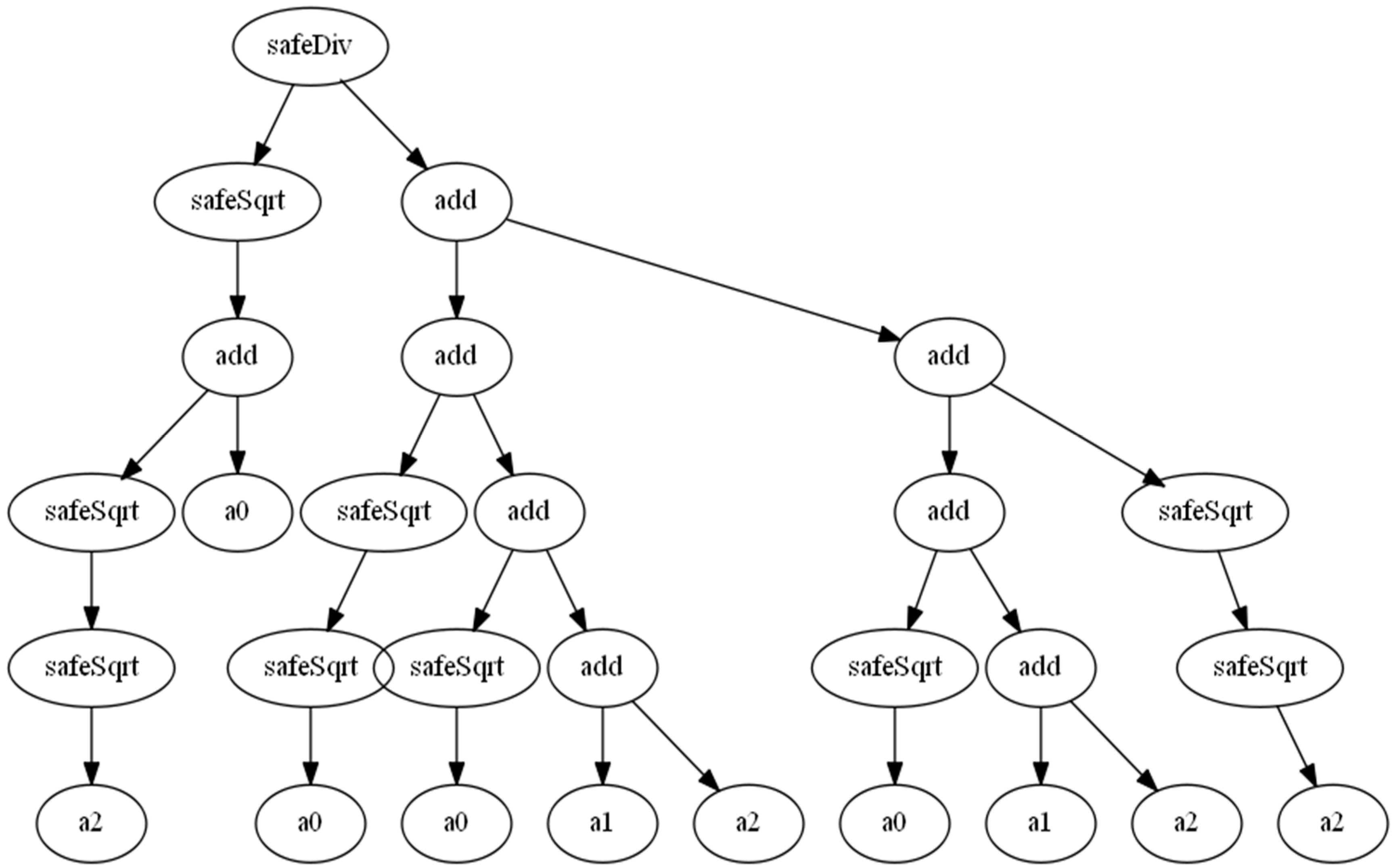
4.1. Representation of the Solutions
4.2. Fitness Function
4.3. Genetic Operators
4.4. Stopping Criterion and Time Complexity
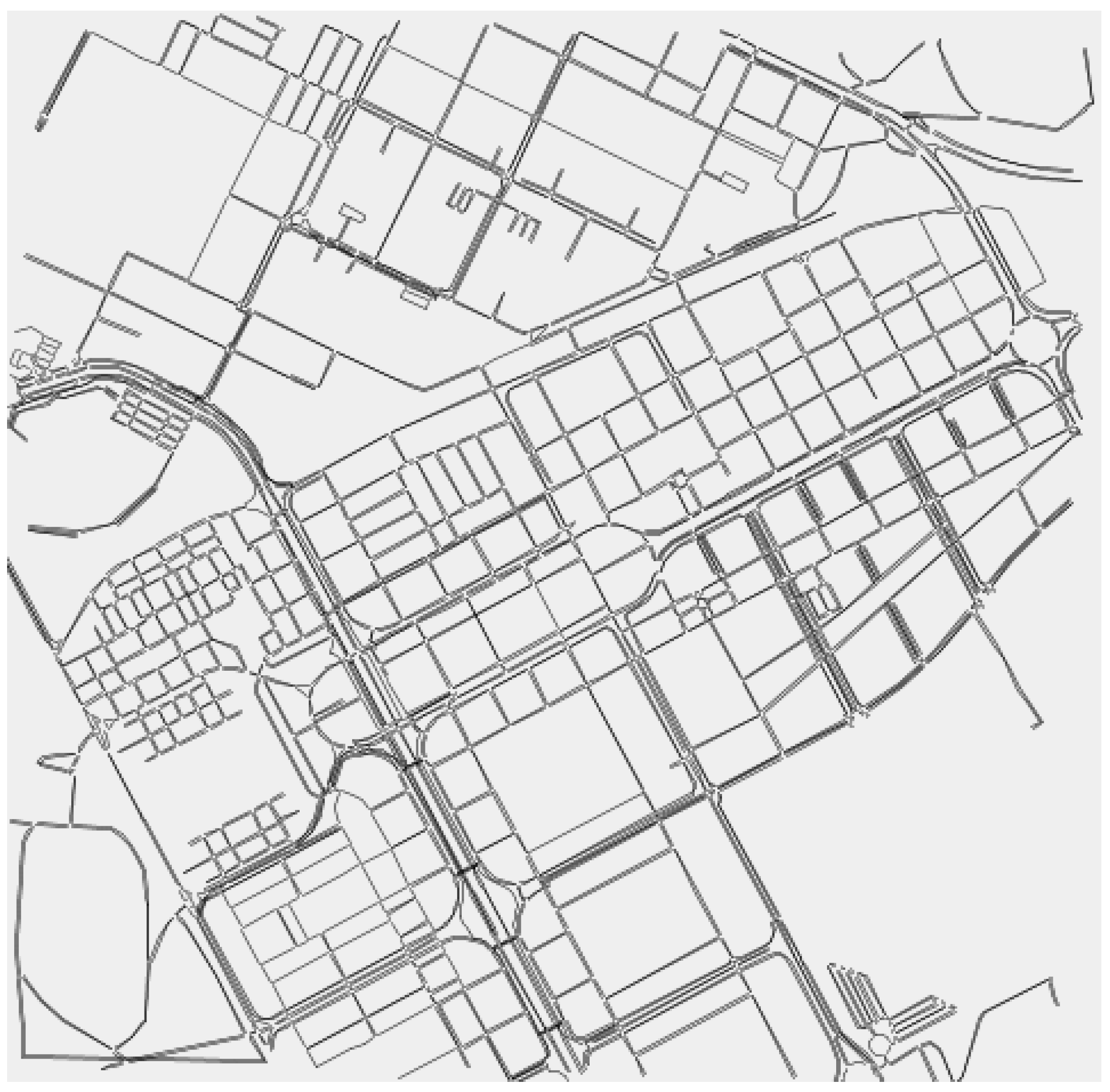
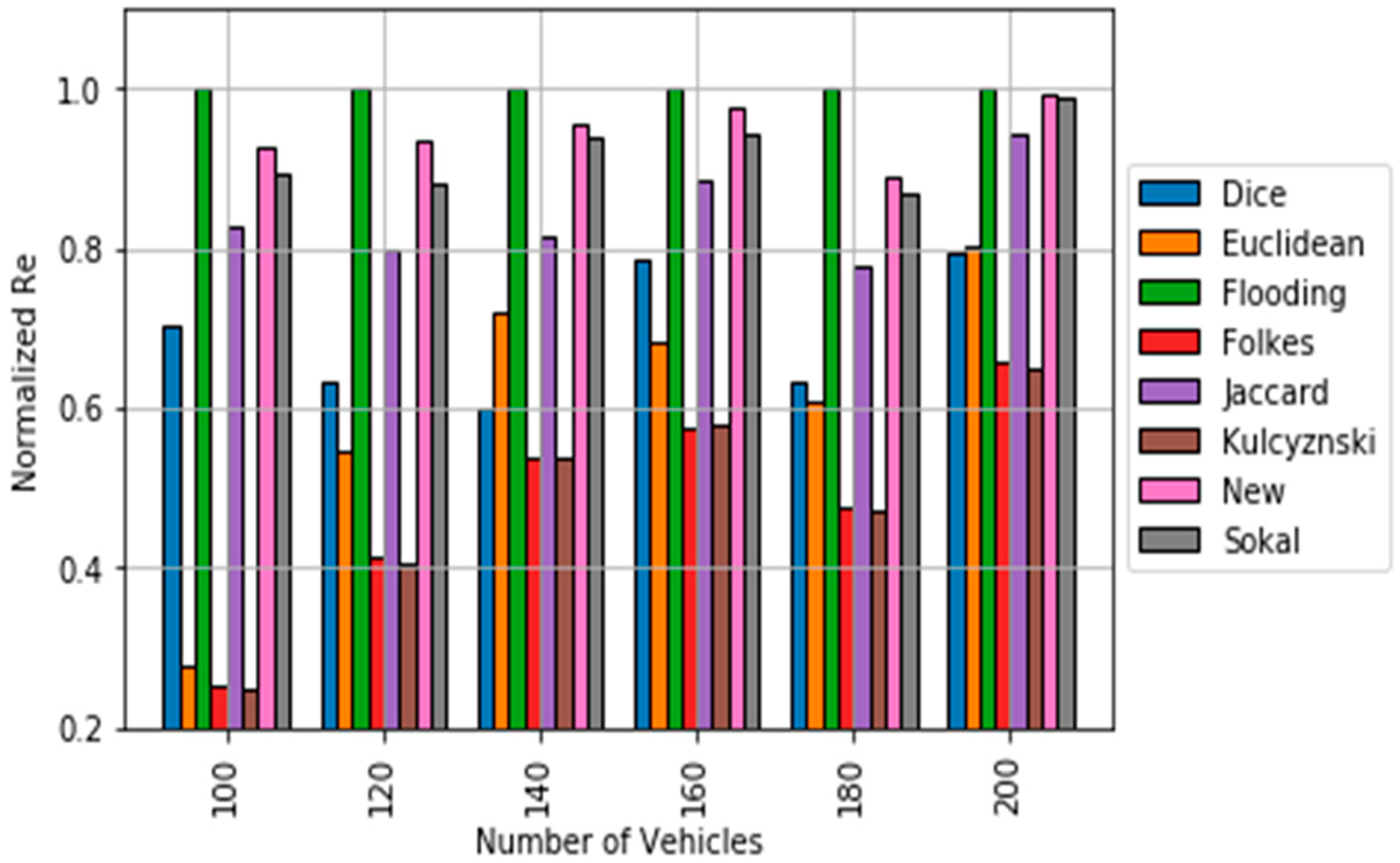
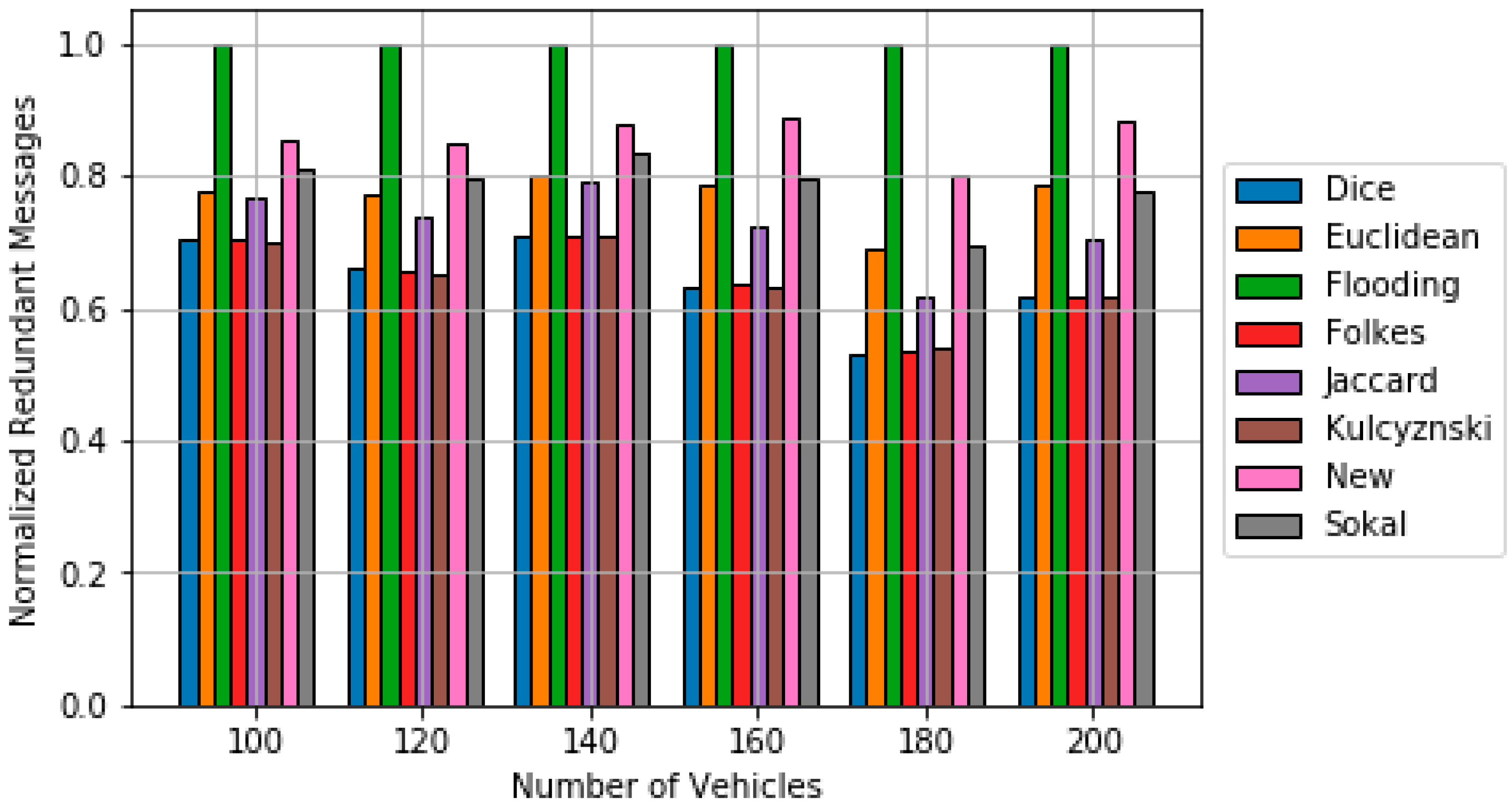
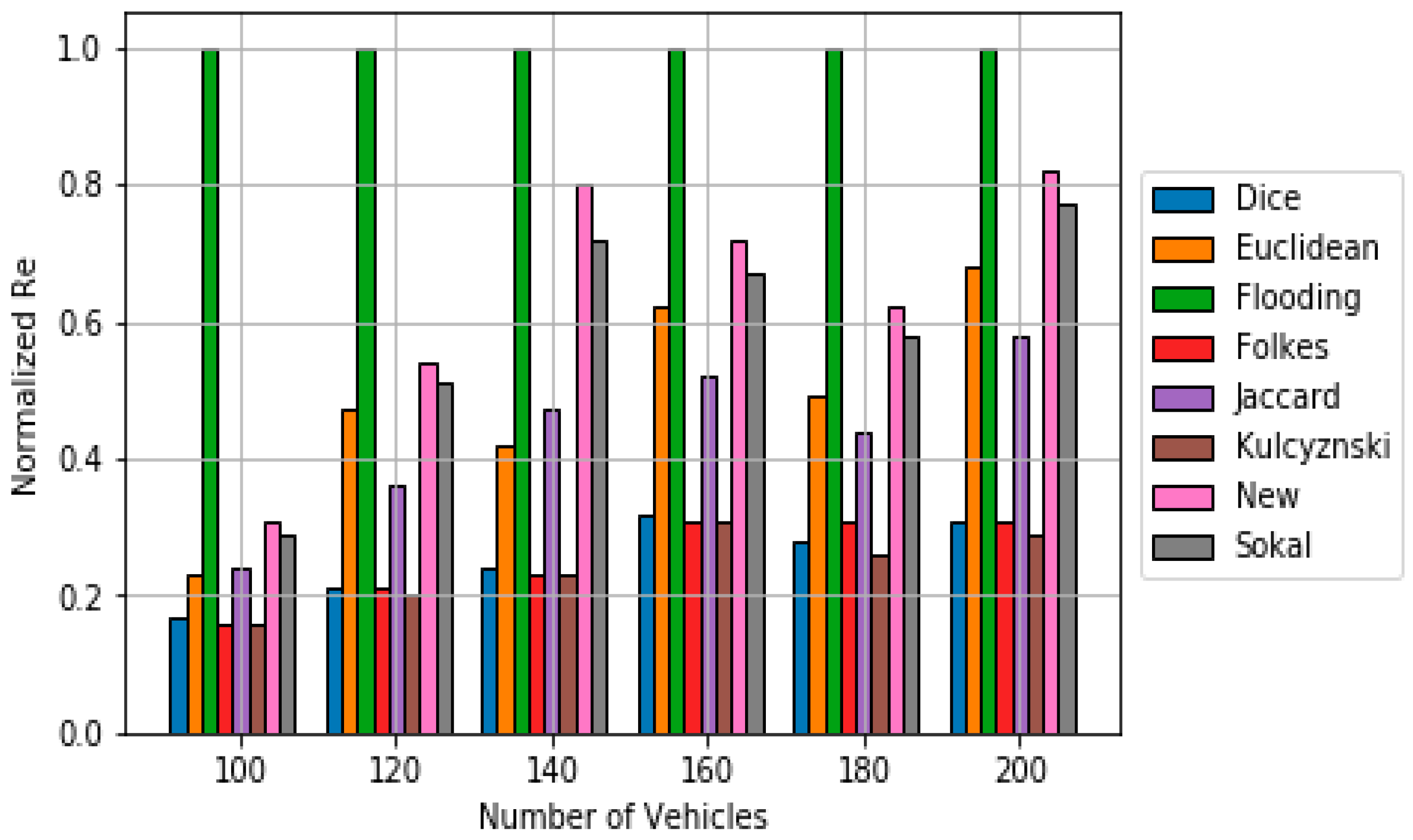
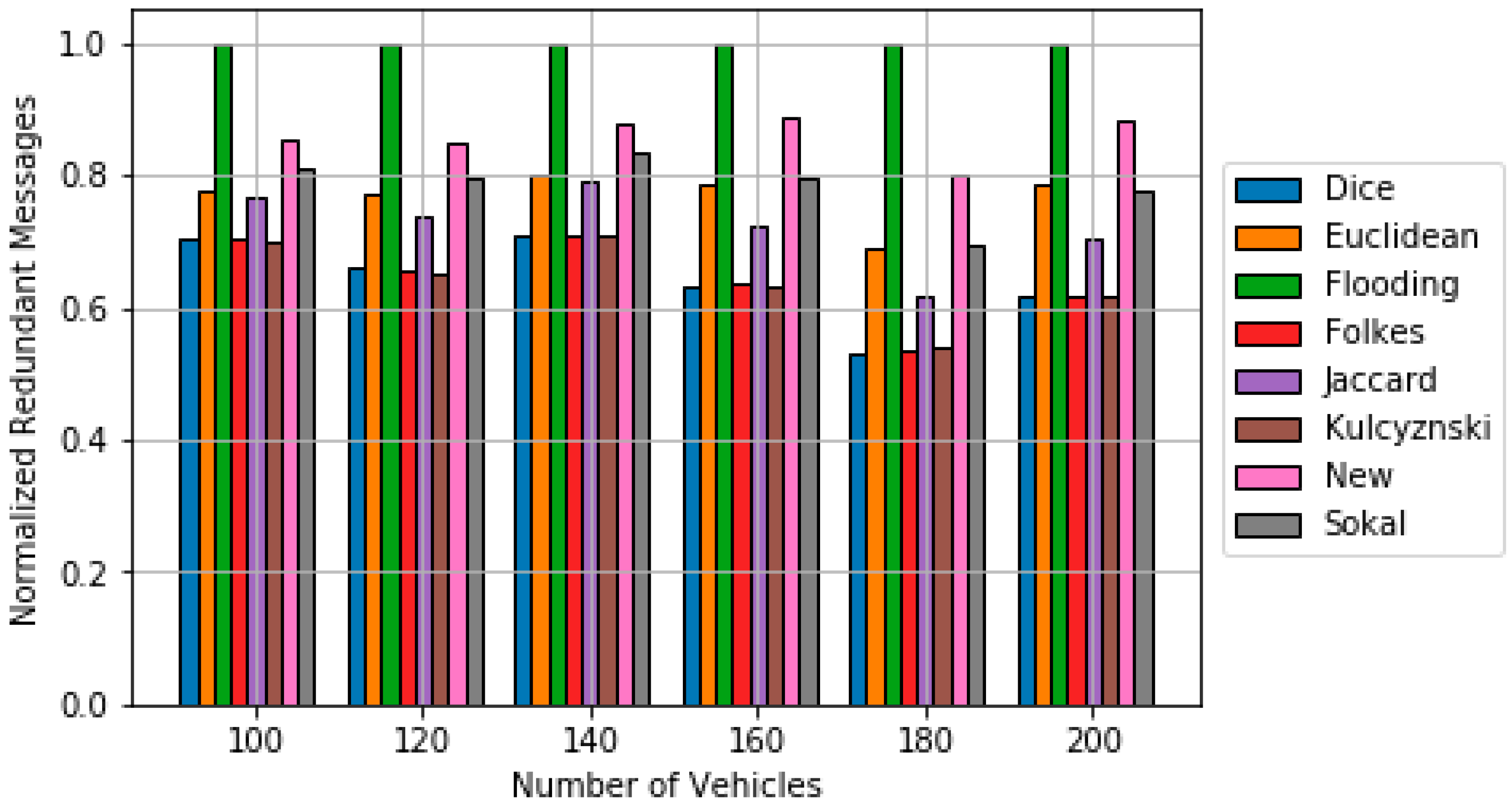
5. Simulation Results
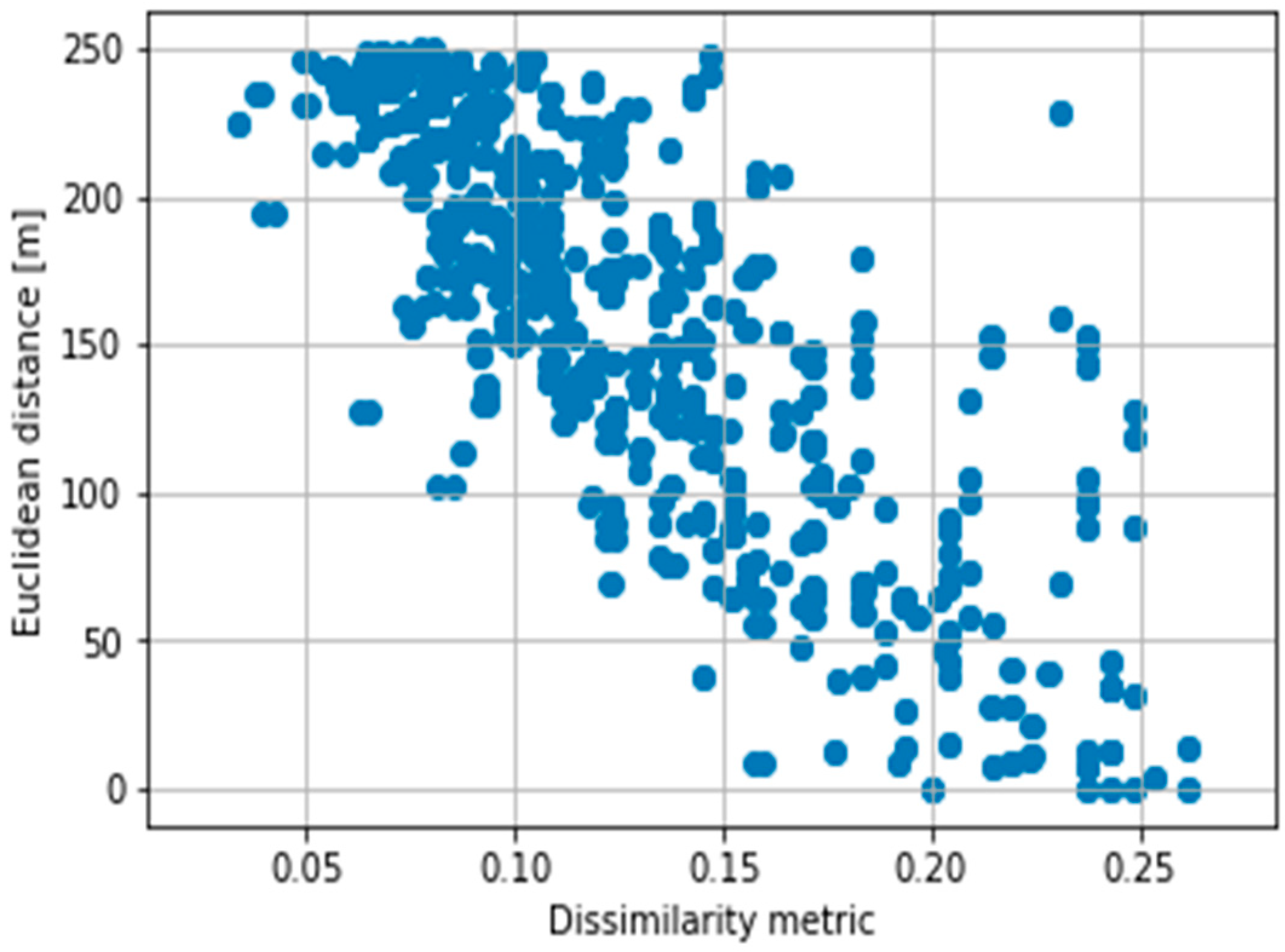
5.1. Correlation Results
5.2. Data Dissemination Results
| Algorithm 2. P-persistence algorithm based on dissimilarity metric. |
| 1: Whenever a message g is received |
| 1: If g is new: |
| 3: Retrieve neighboring list from g |
| 4: Calculate aik, ai, ak |
| 5: Calculate p as |
| 6: If p ≥ Rand [0,1] |
| 7: Include neighboring list in g |
| 8: Rebroadcast g |
| 9: Else: |
| 10: Eliminate g |
| 11: End if |
| 12: Else: |
| 13: Eliminate g |
| 12: End if |
| Algorithm 3. Polynomial algorithm based on dissimilarity metric. |
| 1: Whenever a message g is received |
| 1: If g is new: |
| 3: Retrieve neighboring list from g |
| 4: Calculate aik, ai, ak |
| 5: Calculate p as |
| 6: If p ≥ Rand [0,1] |
| 7: Include neighboring list in g |
| 8: Rebroadcast g |
| 9: Else: |
| 10: Eliminate g |
| 11: End if |
| 12: Else: |
| 13: Eliminate g |
| 12: End if |
| Algorithm 4. Irresponsible algorithm based on dissimilarity metric. |
| 1: Whenever a message g is received |
| 2: If g is new: |
| 3: Retrieve neighboring list from g |
| 4: Calculate aik, ai, ak |
| 5: Calculate p as |
| 6: If p ≥ Rand [0,1] |
| 7: Include neighboring list in g |
| 8: Rebroadcast g |
| 9: Else: |
| 10: Eliminate g |
| 11: End if |
| 12: Else: |
| 13: Eliminate g |
| 12: End if |
5.3. Future Work
- Combine the proposed approach with online approaches based on learning policies like [35]. The idea is to reduce the number of messages exchanged among nodes by updating the hyper-parameters of learning models.
- Evaluate the proposed approach under different wireless and sensor technologies for VANETs, such as IEEE 802.11p, IEEE 802.11ax, and IEEE 802.15.4, among others.
- Since in majority of cases the proposed approach outperforms the other algorithms in terms of Re, but with an increase of redundancy, we plan to extend the work by considering a multi-objective genetic programming approach [40]. Therefore, both reachability and redundancy can be balanced.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Panichpapiboon, S.; Pattara-atikom, W. A Review of Information Dissemination Protocols for Vehicular Ad Hoc Networks. IEEE Commun. Surv. Tutor. 2012, 14, 784–798. [Google Scholar] [CrossRef]
- Sharma, V.; Chen, H.C.; Kumar, R. Driver behaviour detection and vehicle rating using multi-UAV coordinated vehicular networks. J. Comput. Syst. Sci. 2017, 86, 3–32. [Google Scholar] [CrossRef]
- Sharma, V.; You, I.; Kumar, R. Energy efficient data dissemination in multi-UAV coordinated wireless sensor networks. Mob. Inf. Syst. 2016, 2016, 8475820. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, S.; Mao, X.; Chen, K.; Li, J. Insight of the protection for data security under selective opening attacks. Inf. Sci. 2017, 412, 223–241. [Google Scholar] [CrossRef]
- Kimura, T.; Premachandra, C. Optimal Relay Node Selection in Two-Hop Routing for Intermittently Connected MANETs. JoWUA 2016, 7, 23–38. [Google Scholar]
- Bhargava, B.K.; Johnson, A.M.; Munyengabe, G.I.; Angin, P. A Systematic Approach for Attack Analysis and Mitigation in V2V Networks. JoWUA 2016, 7, 79–96. [Google Scholar]
- Sanchez-Iborra, R.; Sánchez-Gómez, J.; Santa, J.; Fernández, P.J.; Skarmeta, A. Integrating LP-WAN communications within the vehicular ecosystem. J. Internet Serv. Inf. Secur. 2017, 7, 45–56. [Google Scholar]
- Reina, D.G.; Toral, S.L.; Johnson, P.; Barrero, F. A Survey on Probabilistic Broadcast Schemes for Wireless Ad Hoc Networks. Ad Hoc Netw. 2015, 25, 263–292. [Google Scholar] [CrossRef]
- Latif, S.; Mahfooz, S.; Jan, B.; Ahmand, N.; Cao, Y.; Asif, M. A Comparative Study of Scenario-driven Multi-hop Broadcast Protocols for VANETs. Veh. Commun. 2018, 12, 88–109. [Google Scholar] [CrossRef]
- Chaqfeh, M.; Lakas, A.; Jawhar, I. A survey on data dissemination in vehicular ad hoc networks. Veh. Commun. 2014, 1, 214–225. [Google Scholar] [CrossRef]
- Kakkasageri, M.S.; Manvi, S.S. Information management in vehicular ad hoc networks: A review. J. Netw. Comput. Appl. 2014, 39, 334–350. [Google Scholar] [CrossRef]
- Aliyu, A.; Abdullah, A.H.; Kaiwartya, O.; Cao, Y.; Lloret, J.; Aslam, N.; Joda, U.M. Towards video streaming in IoT Environments: Vehicular communication perspective. Comput. Commun. 2018, 118, 93–119. [Google Scholar] [CrossRef]
- Xu, B.; Zheng, J.; Wang, Q.; Xiao, Y.; Ozdemir, S. An Adaptive Vehicle Detection Algorithm Based on Magnetic Sensors in Intelligent Transportation Systems. Ad Hoc Sens. Wirel. Netw. 2017, 36, 211–232. [Google Scholar]
- Yang, H.; Huang, L.; Xu, H. Distributed Compressed Sensing in Vehicular Ad-hoc Network. Ad Hoc Sens. Wirel. Netw. 2015, 24, 121–145. [Google Scholar]
- Perez-Garrancho, V.; Garcia, L.; Sendra, S.; Lloret, J. Mobile Low Cost system for Environmental Monitoring in Emergency Situations. In Proceedings of the Seventh International Conference on Ambient Computing, Applications, Services and Technologies (AMBIENT 2017), Barcelona, Spain, 12–16 November 2017; pp. 28–33. [Google Scholar]
- Sohail, M.; Wang, L. 3VSR: Three Valued Secure Routing for Vehicular Ad Hoc Networks using Sensing Logic in Adversarial Environment. Sensors 2018, 18, 856. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, P.; Bouvry, P. Survey on broadcast algorithms for mobile ad hoc networks. ACM Comput. Surv. 2015, 48, 1–35. [Google Scholar] [CrossRef]
- Wisitpongphan, N.; Tonguz, O.K.; Parikh, J.S.; Mudalige, P.; Bai, F.; Sadekar, V. Broadcast storm mitigation techniques in vehicular ad hoc networks. IEEE Wirel. Commun. 2007, 14, 84–94. [Google Scholar] [CrossRef]
- Mostafa, A.; Vegni, A.M.; Agrawal, D.P. A probabilistic routing by using multi-hop retransmission forecast with packet collision-aware constraints in vehicular networks. Ad Hoc Netw. 2014, 14, 118–129. [Google Scholar] [CrossRef]
- Reina, D.G.; Toral, S.L.; Jonhson, P.; Barrero, F. Hybrid flooding scheme for mobile ad hoc networks. IEEE Commun. Lett. 2013, 17, 592–595. [Google Scholar] [CrossRef]
- Mylonas, Y.; Lestas, M.; Pitsillides, A.; Ioannou, P.; Papadopoulou, V. Speed Adaptive Probabilistic Flooding for Vehicular Ad-Hoc Networks. IEEE Trans. Veh. Technol. 2015, 64, 1973–1990. [Google Scholar] [CrossRef]
- Busanelli, S.; Ferrari, G.; Gruppini, R. Recursive analytical performance evaluation of broadcast protocols with silencing: Application to VANETs. EURASIP J. Wirel. Commun. Netw. 2012, 10, 1–21. [Google Scholar] [CrossRef]
- Gorrieri, A.; Ferrari, G. DiSIF: A Distance-Based Silencing Technique for Multi-Hop Broadcast Communications in Pedestrian Ad-Hoc Networks. IEEE Trans. Mob. Comput. 2015, 15, 2706–2718. [Google Scholar] [CrossRef]
- Reina, D.G.; Günes, M.; Toral, S.L. Real experimentation of probabilistic broadcasting algorithms based on dissimilarity metrics for multi-hop ad hoc networks. Ad Hoc Netw. 2016, 47, 1–15. [Google Scholar] [CrossRef]
- Reina, D.G.; Toral, S.L.; Johnson, P.; Barrero, F. Improving Discovery Phase of Reactive Ad Hoc Routing Protocols Using Jaccard Distance. J. Supercomput. 2014, 67, 131–152. [Google Scholar] [CrossRef]
- Cartigny, J.; Simplot, D. Border Node Retransmission Based Probabilistic Broadcast Protocols in Ad-Hoc Networks. Telecommun. Syst. 2003, 4, 189–204. [Google Scholar] [CrossRef]
- Hardle, W.; Simar, L. Applied Multivariate Statistical Analysis; Method Data Technologies; Springer: Berlin, Germany, 2003. [Google Scholar]
- Panichpapiboon, S.; Ferrari, G. Irresponsible forwarding. In Proceedings of the International Conference on ITS Telecommunications (ITST), Phuket, Thailand, 24 October 2008; pp. 311–316. [Google Scholar]
- Blywis, B.; Günes, M.; Juraschek, F.; Hahm, O.; Schmittberger, N. Properties and Topology of DES-Testbed (2nd Extended Revision); Telematic and Computer System; Freie Universitát: Berlin, Germany, 2011. [Google Scholar]
- García-Campos, J.M.; Sánchez, J.; Reina, D.G.; Toral, S.L.; Barrero, F. Evaluation of Dissimilarity-based Probabilistic Broadcasting Algorithms in VANETs. In Proceedings of the International Conference on Developments in eSystems Engineering (DESE2015), Duai, United Arab Emirates, 13–14 December2015. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; ISBN 0-262-11170-5. [Google Scholar]
- Available online: https://github.com/Dany503/Genetic-Programming (accessed on 5 May 2018).
- Fortin, F.; de Rainville, F.; Gardner, M.; Parizeau, M.; Gagne, C. DEAP: Evolutionary Algorithms Made Easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Available online: http://www.grc.upv.es/Software/c4r.html (accessed on 5 May 2018).
- Trihinas, D.; Pallis, G. ADMin: Adaptive Monitoring Dissemination for the Internet of Things. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM 2017), Atlanta, GA, USA, 1–4 May 2017. [Google Scholar]
- Granda, F.; Azpilicueta, L.; Vargas-Rosales, C.; Lopez-Iturri, P.; Aguirre, E.; Astrain, J.J.; Villandangos, J.; Falcone, F. Spatial Characterization of Radio Propagation Channel in Urban Vehicle-to-Infrastructure Environments to Support WSNs Deployment. Sensors 2017, 17, 1313. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Chen, X.; Liu, A.; Hu, C. A Latency and Coverage Optimized Data Collection Scheme for Smart Cities Based on Vehicular Ad-hoc Networks. Sensors 2017, 17, 888. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; You, I.; Pau, G.; Collotta, M.; Lim, J.D.; Kim, J.N. LoRaWAN-Based Energy-Efficient Surveillance by Drones for Intelligent Transportation Systems. Energies 2018, 11, 573. [Google Scholar] [CrossRef]
- You, I.; Sharma, V.; Atiquzzaman, M.; Choo, K.K.R. GDTN: Genome-based delay tolerant network formation in heterogeneous 5G using inter-UA collaboration. PLoS ONE 2016, 11, e0167913. [Google Scholar] [CrossRef] [PubMed]
- Cano, A.; Ventura, S. Multi-objective genetic programming for feature extraction and data visualization. Soft Comput. 2017, 21, 2069–2089. [Google Scholar] [CrossRef]



| Metric | Correlation |
|---|---|
| Jaccard | 0.661357 |
| Dice | 0.622318 |
| Kulczynski | 0.616629 |
| Fowlkes-Mallows | 0.620337 |
| Sokal-Sneath | 0.620337 |
| GP Metric (Depth = 4, pc = 0.7, pm = 0.1) | 0.738470 |
| GP Metric (Depth = 5, pc = 0.8, pm = 0.15) | 0.741575 |
| GP Metric (Depth = 6, pc = 0.8, pm = 0.2) | 0.740777 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez-Reina, D.; Sharma, V.; You, I.; Toral, S. Dissimilarity Metric Based on Local Neighboring Information and Genetic Programming for Data Dissemination in Vehicular Ad Hoc Networks (VANETs). Sensors 2018, 18, 2320. https://doi.org/10.3390/s18072320
Gutiérrez-Reina D, Sharma V, You I, Toral S. Dissimilarity Metric Based on Local Neighboring Information and Genetic Programming for Data Dissemination in Vehicular Ad Hoc Networks (VANETs). Sensors. 2018; 18(7):2320. https://doi.org/10.3390/s18072320
Chicago/Turabian StyleGutiérrez-Reina, Daniel, Vishal Sharma, Ilsun You, and Sergio Toral. 2018. "Dissimilarity Metric Based on Local Neighboring Information and Genetic Programming for Data Dissemination in Vehicular Ad Hoc Networks (VANETs)" Sensors 18, no. 7: 2320. https://doi.org/10.3390/s18072320
APA StyleGutiérrez-Reina, D., Sharma, V., You, I., & Toral, S. (2018). Dissimilarity Metric Based on Local Neighboring Information and Genetic Programming for Data Dissemination in Vehicular Ad Hoc Networks (VANETs). Sensors, 18(7), 2320. https://doi.org/10.3390/s18072320







