An Exception Handling Approach for Privacy-Preserving Service Recommendation Failure in a Cloud Environment
Abstract
1. Introduction
- (1)
- A novel LSH variant named converse LSH is developed, which can be utilized to search for the enemy users of a target user, in a time-efficient and privacy-preserving way.
- (2)
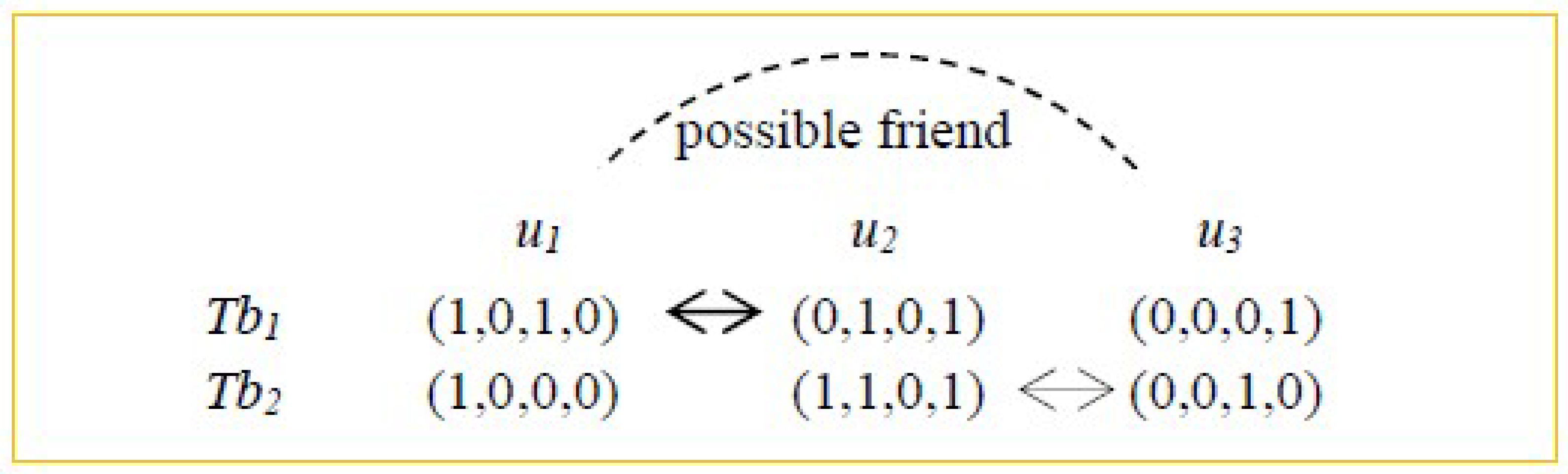
- We utilize converse LSH technique to search for the enemies of a target user and then look for the target user’s similar friends indirectly based on the “enemy’s enemy is a possible friend” inference rule in Social Balance Theory. Afterwards, we generate recommended results by considering the preferences of obtained similar friends, so as to handle the exceptions incurred by recommendation failures.
- (3)
- Comprehensive experiments are simulated based on Movielens dataset, to test the effectiveness of suggested recommendation approach. Experiment results indicate the advantages of our proposal compared to other competitive approaches when a recommendation failure occurs.
2. Related Work
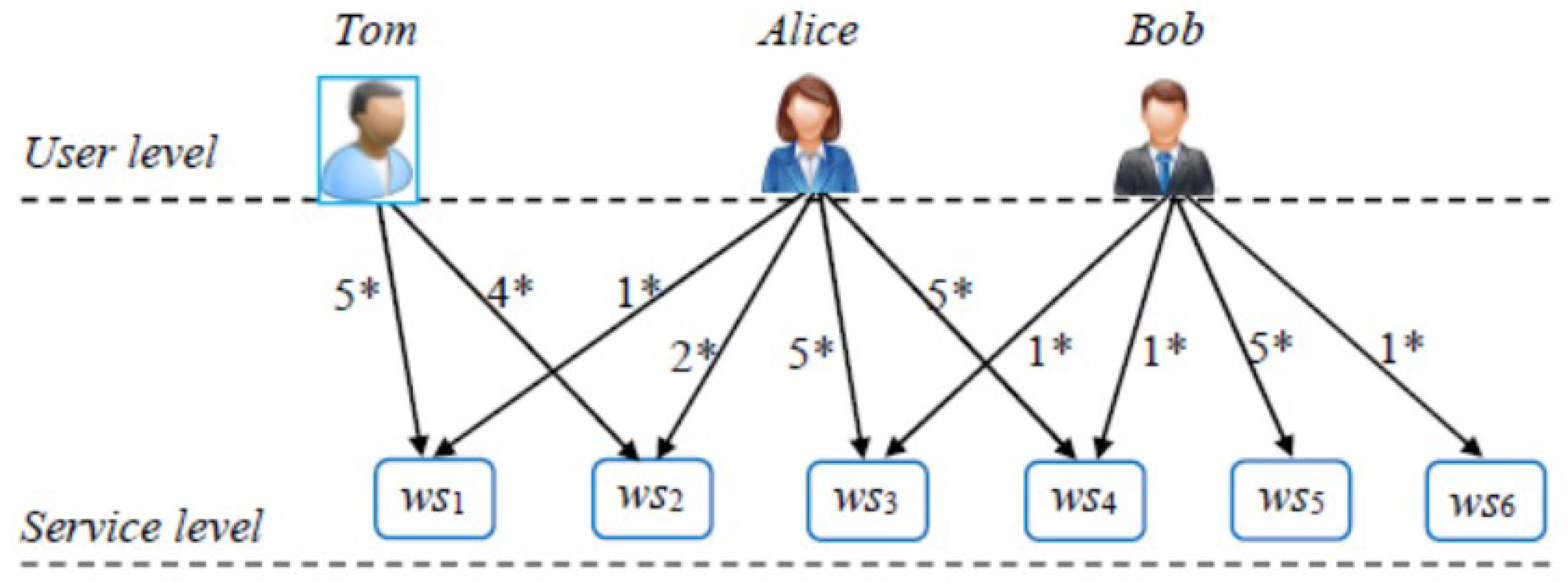
3. Converse Locality-Sensitive Hashing
4. An Exception Handling Approach Based on Converse LSH
- Step-1: Build user indices offline through traditional LSH technique.
- Step-2: Determine the indirect friends of the target user u* based on user indices and converse LSH technique.
- Step-3: Recommend services to u* based on the possible friends of u*.
5. Experiments
5.1. Experiment Configurations
- (1)
- Random: this benchmark approach predicts the missing service quality data based on the quality of a randomly selected service, and returns the service with the optimal predicted quality.
- (2)
- WSRec [23]: it predicts the missing service quality data by two pieces of average quality, i.e., average quality of the service rated by all users and average quality of all services rated by the user. Finally, the optimal service is returned to the target user.
- (3)
- SBT-SR [12]: this approach first looks for the indirect friends of a target user based on Collaborative Filtering and Social Balance Theory, and then recommends appropriate services based on the derived indirect friends.
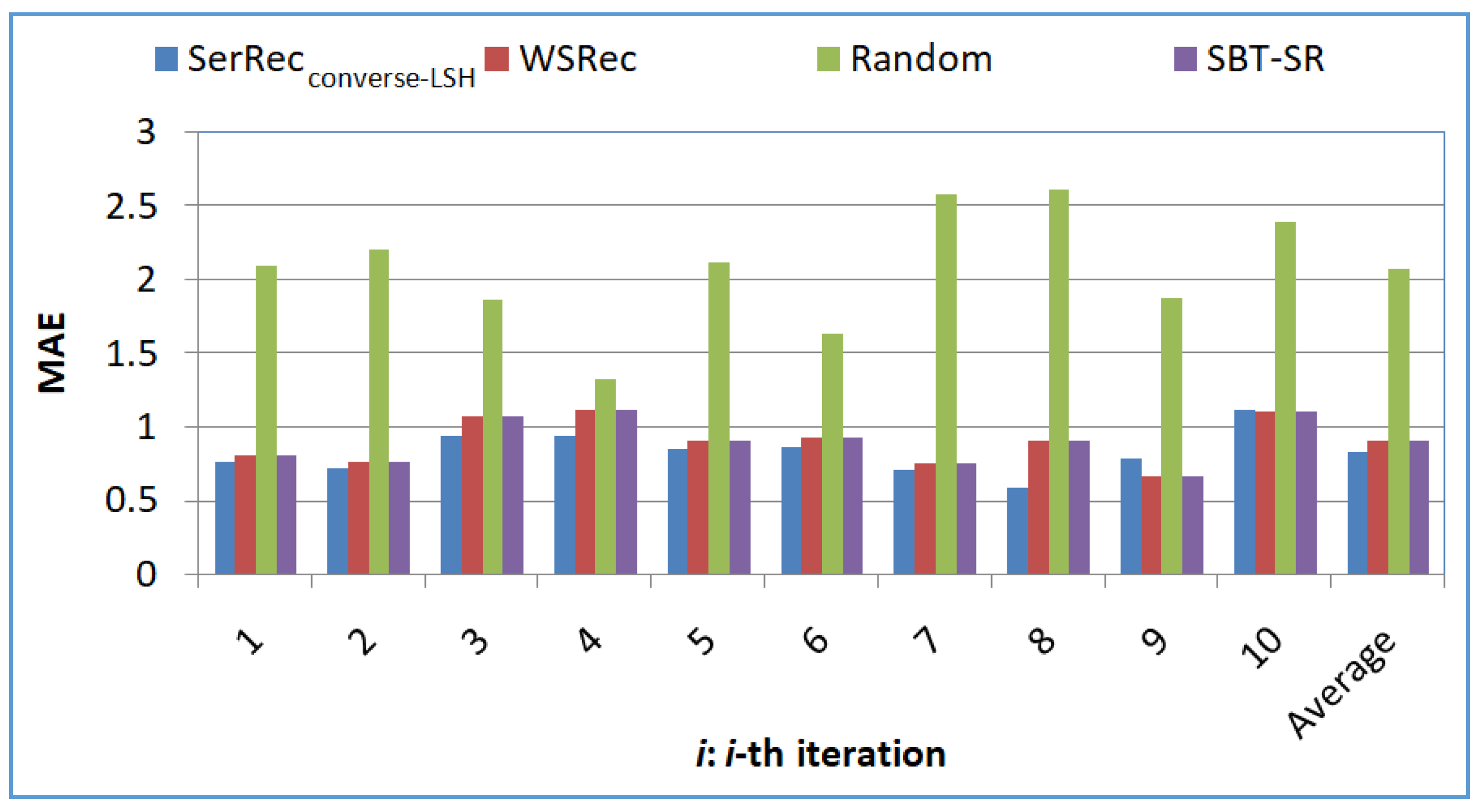
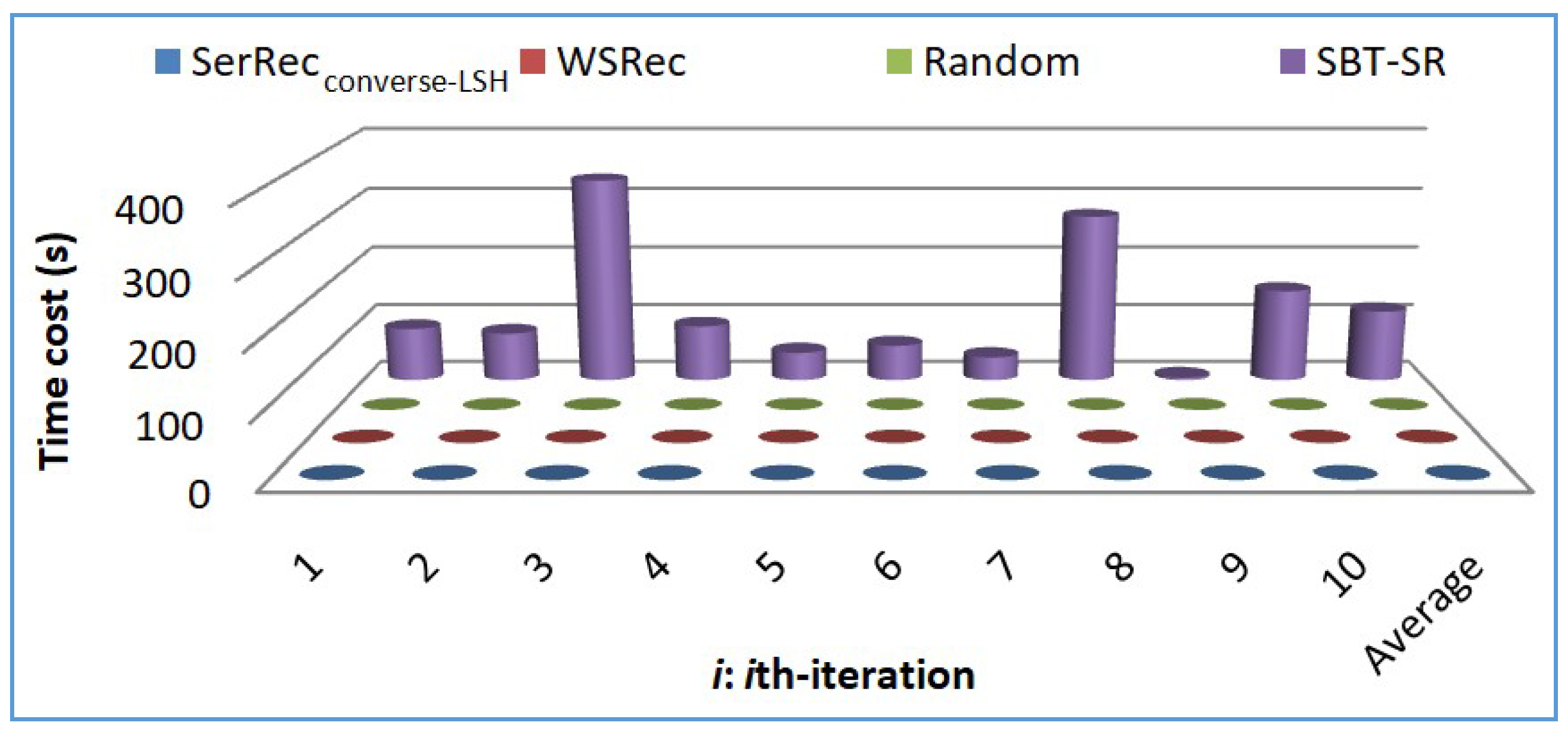
5.2. Experiment Results
- Profile 1: Accuracy comparison of four approaches
- Profile 2: Efficiency comparison of four approaches
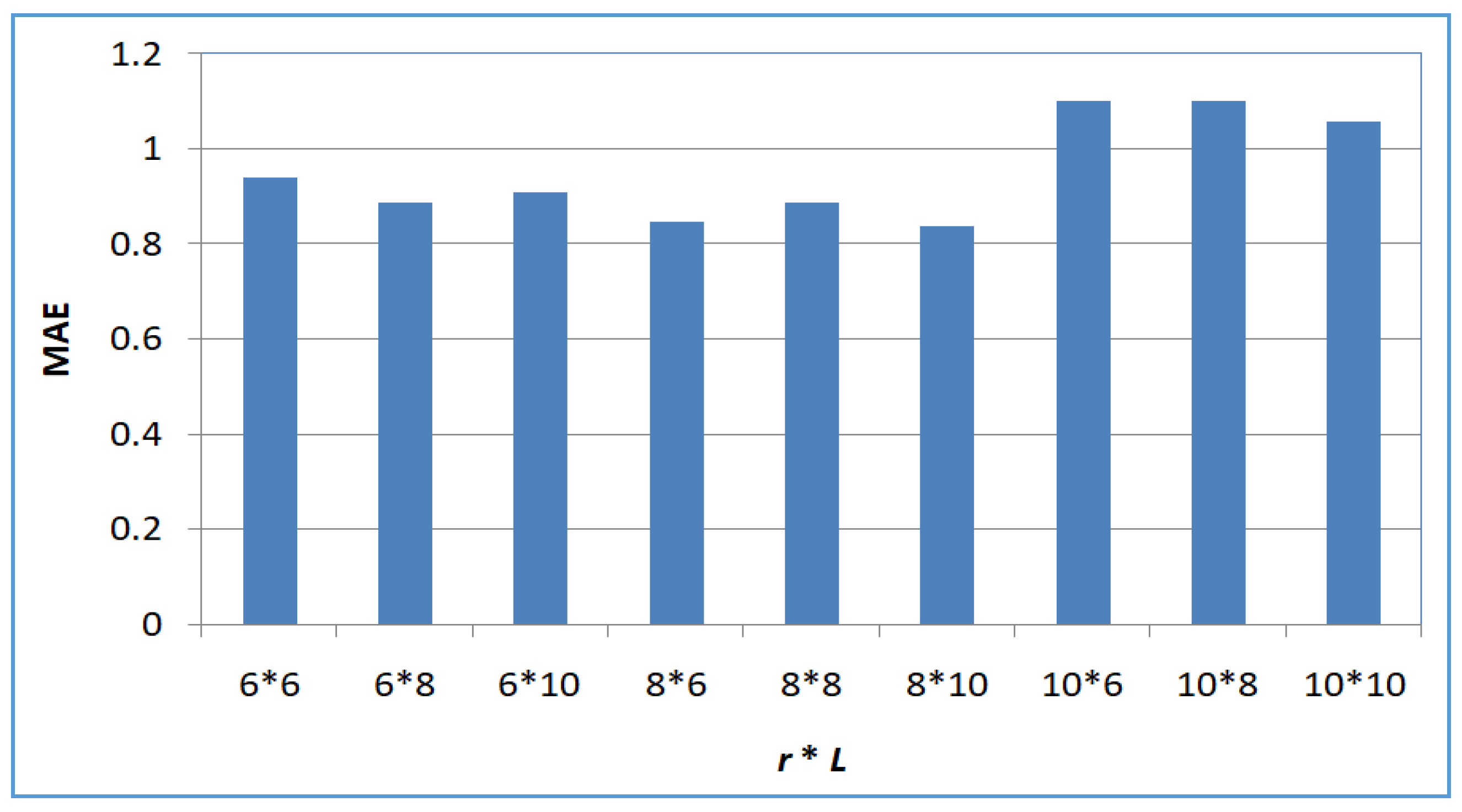
- Profile 3: Accuracy of SerRecconverse-LSH with respect to L and r
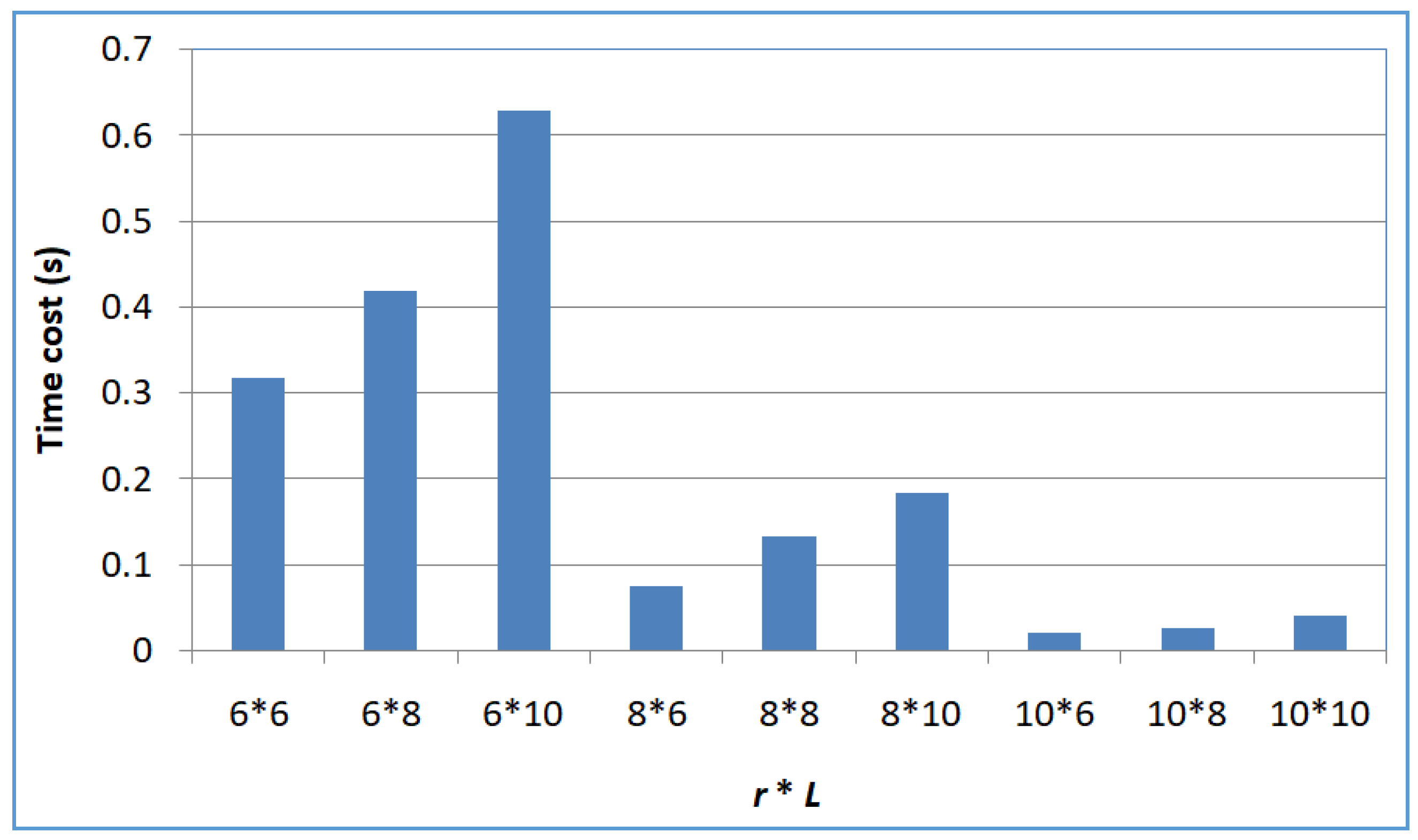
- Profile 4: Efficiency of SerRecconverse-LSH with respect to L and r
5.3. Shortcoming Analyses & Future Work
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Naim, H.; Aznag, M.; Quafafou, M.; Durand, N. Probabilistic approach for diversifying web services discovery and composition. In Proceedings of the International Conference on Web Services (ICWS), San Francisco, CA, USA, 27 June–2 July 2016; pp. 73–80. [Google Scholar]
- Qi, L.; Zhang, X.; Dou, W.; Ni, Q. A distributed locality-sensitive hashing based approach for cloud service recommendation from multi-source data. IEEE J. Sel. Areas Commun. 2017, 35, 2616–2624. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, Y.; Cai, Z.; Liu, A.; Li, Y. Securing display path for security-sensitive applications on mobile devices. Comput. Mater. Contin. 2018, 55, 17–35. [Google Scholar]
- Cao, Y.; Zhou, Z.; Sun, X.; Gao, C. Coverless information hiding based on the molecular structure images of material. Comput. Mater. Contin. 2018, 54, 197–207. [Google Scholar]
- Liu, Y.; Peng, H.; Wang, J. Verifiable diversity ranking search over encrypted outsourced data. Comput. Mater. Contin. 2018, 55, 37–57. [Google Scholar]
- Li, T.; Li, J.; Liu, Z.; Li, P.; Jia, C. Differentially Private Naive Bayes Learning over Multiple Data Sources. Inf. Sci. 2018, 444, 89–104. [Google Scholar] [CrossRef]
- Meng, W.; Tischhauser, E.; Wang, Q.; Wang, Y.; Han, J. When Intrusion Detection Meets Blockchain Technology: A Review. IEEE Access 2018, 6, 10179–10188. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Li, J.; Wong, D.S.; Li, H.; You, I. Ensuring attribute privacy protection and fast decryption for outsourced data security in mobile cloud computing. Inf. Sci. 2017, 379, 42–61. [Google Scholar] [CrossRef]
- Cai, Z.; Yan, H.; Li, P.; Huang, Z.; Gao, C. Towards secure and flexible EHR sharing in mobile health cloud under static assumptions. Cluster Comput. 2017, 20, 2415–2422. [Google Scholar] [CrossRef]
- Li, P.; Li, T.; Ye, H.; Li, J.; Chen, X.; Xiang, Y. Privacy-preserving machine learning with multiple data providers. Future Gener. Comput. Syst. 2018, 87, 341–350. [Google Scholar] [CrossRef]
- Gionis, A.; Indyk, P.; Motwani, R. Similarity search in high dimensions via hashing. VLDB J. 1999, 99, 518–529. [Google Scholar]
- Qi, L.; Zhang, X.; Wen, Y.; Zhou, Y. A social balance theory-based service recommendation approach. In Proceedings of the International Conference on Asia-Pacific Services Computing (APSCC), Bangkok, Thailand, 7–9 December 2015; pp. 48–60. [Google Scholar]
- Qi, L.; Zhou, Z.; Yu, J.; Liu, Q. Data-sparsity tolerant web service recommendation approach based on improved collaborative filtering. IEICE T. Inf. Syst. 2017, E100D, 2092–2099. [Google Scholar] [CrossRef]
- Zheng, X.; Cai, Z.; Li, J.; Gao, H. Location-privacy-aware review publication mechanism for local business service systems. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM), Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Fran, C.; Josep, D.F.; Constantinos, P.; Domènec, P.; Agusti, S. A k-anonymous approach to privacy preserving collaborative filtering. J. Comput. Syst. Sci. 2015, 81, 1000–1011. [Google Scholar]
- Ahila, S.S.; Shunmuganathan, K.L. Role of agent technology in web usage mining: homomorphic encryption based recommendation for e-commerce applications. Wirel. Pers. Commun. 2016, 87, 499–512. [Google Scholar] [CrossRef]
- Zhu, J.; He, P.; Zheng, Z.; Lyu, M.R. A privacy-preserving qos prediction framework for web service recommendation. In Proceedings of the International Conference on Web Services (ICWS), New York, NY, USA, 27 June–2 July 2015; pp. 241–248. [Google Scholar]
- Dou, K.; Guo, B.; Kuang, L. A privacy-preserving multimedia recommendation in the context of social network based on weighted noise injection. Multimed. Tools Appl. 2017, 1–20. [Google Scholar] [CrossRef]
- Xu, Y.; Qi, L.; Dou, W.; Yu, J. Privacy-preserving and scalable service recommendation based on simhash in a distributed cloud environment. Complexity 2017, 2017, 3437854. [Google Scholar] [CrossRef]
- Qi, L.; Zhang, X.; Dou, W.; Hu, C.; Yang, C.; Chen, J. A two-stage locality-sensitive hashing based approach for privacy-preserving mobile service recommendation in cross-platform edge environment. Future Gener. Comput. Syst. 2018. [Google Scholar] [CrossRef]
- Gong, W.; Qi, L.; Xu, Y. Privacy-aware multi-dimensional mobile service quality prediction and recommendation in distributed fog environment. Wirel. Commun. Mob. Commun. 2018, 2018, 3075849. [Google Scholar]
- Zhang, K.; Fan, S.; Wang, H.J. An efficient recommender system using locality sensitive hashing. In Proceedings of the Annual Hawaii International Conference on System Sciences (HICSS), Hawaii, HI, USA, 3–6 January 2018. [Google Scholar]
- Zheng, Z.; Ma, H.; Lyu, M.R.; King, I. QoS-aware web service recommendation by collaborative filtering. IEEE Trans. Serv. Comput. 2011, 4, 140–152. [Google Scholar] [CrossRef]
- Qi, L.; Dou, W.; Zhang, X. An inverse collaborative filtering approach for cold-start problem in web service recommendation. In Proceedings of the Australasian Computer Science Week (ACSW), Geelong, Australia, 31 January–3 February 2017; pp. 46–54. [Google Scholar]
- Movielens. Available online: https://grouplens.org/datasets/movielens/ (accessed on 11 March 2018).
- Tian, G.; Wang, M.; Song, L. Variable selection in the high-dimensional continuous generalized linear model with current status data. J. Appl. Stat. 2014, 41, 467–483. [Google Scholar] [CrossRef]
- Wang, M.; Tian, G. Robust group non-convex estimations for high-dimensional partially linear models. J. Nonparametr. Stat. 2016, 28, 49–67. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M. Variable selection for high-dimensional generalized linear models with the weighted elastic-net procedure. J. Appl. Stat. 2016, 43, 796–809. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, L. Some geometrical properties of convex level sets of minimal graph on 2-dimensional Riemannian manifolds. Nonlinear Anal. 2016, 130, 1–17. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X. The geometric properties of harmonic function on 2-dimensional Riemannian manifolds. Nonlinear Anal. 2014, 103, 2–8. [Google Scholar] [CrossRef]
- Wang, M.; Song, L.; Tian, G. SCAD-penalized least absolute deviation regression in high dimensional models. Commun. Stat.-Theory Methods 2015, 44, 2452–2472. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, X.; Wu, Y.; Liu, L. Global existence and the optimal decay rates for the three dimensional compressible nematic liquid crystal flow. Acta Appl. Math. 2017, 150, 67–80. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, S.; Wang, M. Restricted profile estimation for partially linear models with large-dimensional covariates. Stat. Probabil. Lett. 2017, 128, 71–76. [Google Scholar] [CrossRef]
- Tian, H.; Han, M. Bifurcation of periodic orbits by perturbing high-dimensional piecewise smooth integrable systems. J. Differ. Equ. 2017, 263, 7448–7474. [Google Scholar] [CrossRef]
- Yang, S.; Yao, Z.; Zhao, C. The weight distributions of two classes of p-ary cyclic codes with few weights. Finite Fields Their Appl. 2017, 44, 76–91. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, C.; Zhang, X. Uniform estimate for the tail probabilities of randomly weighted sums. Acta Math. Appl. Sin. E 2014, 30, 1063–1072. [Google Scholar] [CrossRef]
- Cai, J. An implicit sigma(3) type condition for heavy cycles in weighted graphs. Ars Combin. 2014, 115, 211–218. [Google Scholar]
- Liu, H.; Meng, F. Some new generalized volterra-fredholm type discrete fractional sum inequalities and their applications. J. Inequal. Appl. 2016, 2016, 213. [Google Scholar] [CrossRef]
- Li, P.R.; Ren, G.B. Some classes of equations of discrete type with harmonic singular operator and convolution. Appl. Math. Comput. 2016, 284, 185–194. [Google Scholar] [CrossRef]
- Zhang, B. Remarks on the maximum gap in binary cyclotomic polynomials. Bull. Math. Soc. Sci. Math. 2016, 59, 109–115. [Google Scholar]
- Wang, L. The fixed point method for intuitionistic fuzzy stability of a quadratic functional equation. Fixed Point Theory A 2010, 107182. [Google Scholar] [CrossRef]
- Liu, L.L.; Ma, D. Some polynomials related to dowling lattices and x-stieltjes moment sequences. Linear Algebra Appl. 2017, 533, 195–209. [Google Scholar] [CrossRef]
- Li, L.; Meng, F.; Zheng, Z. Oscillation results related to integral average technique for linear hamiltonian systems. Dyn. Syst. Appl. 2009, 18, 725–736. [Google Scholar]
- Xu, A.; Ding, N. Semidualizing bimodules and related gorenstein homological dimensions. J. Algebra Appl. 2016, 15, 1650193. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, L.; Meng, S.; Zhang, X.; Wang, R.; Xu, X.; Zhou, Z.; Dou, W. An Exception Handling Approach for Privacy-Preserving Service Recommendation Failure in a Cloud Environment. Sensors 2018, 18, 2037. https://doi.org/10.3390/s18072037
Qi L, Meng S, Zhang X, Wang R, Xu X, Zhou Z, Dou W. An Exception Handling Approach for Privacy-Preserving Service Recommendation Failure in a Cloud Environment. Sensors. 2018; 18(7):2037. https://doi.org/10.3390/s18072037
Chicago/Turabian StyleQi, Lianyong, Shunmei Meng, Xuyun Zhang, Ruili Wang, Xiaolong Xu, Zhili Zhou, and Wanchun Dou. 2018. "An Exception Handling Approach for Privacy-Preserving Service Recommendation Failure in a Cloud Environment" Sensors 18, no. 7: 2037. https://doi.org/10.3390/s18072037
APA StyleQi, L., Meng, S., Zhang, X., Wang, R., Xu, X., Zhou, Z., & Dou, W. (2018). An Exception Handling Approach for Privacy-Preserving Service Recommendation Failure in a Cloud Environment. Sensors, 18(7), 2037. https://doi.org/10.3390/s18072037








