On the Determination of Uncertainty and Limit of Detection in Label-Free Biosensors
Abstract
1. Introduction and Review of Basic Concepts
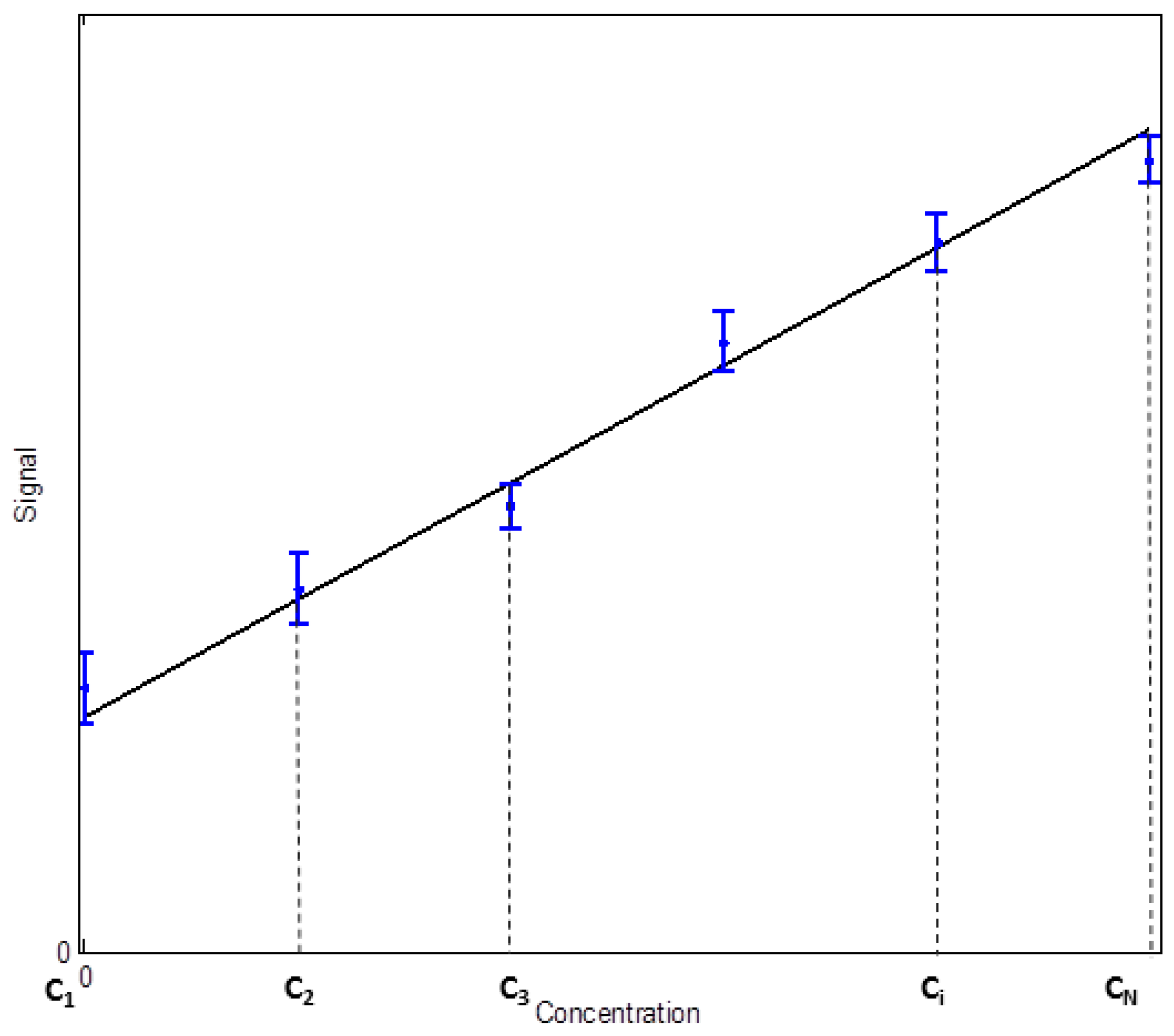
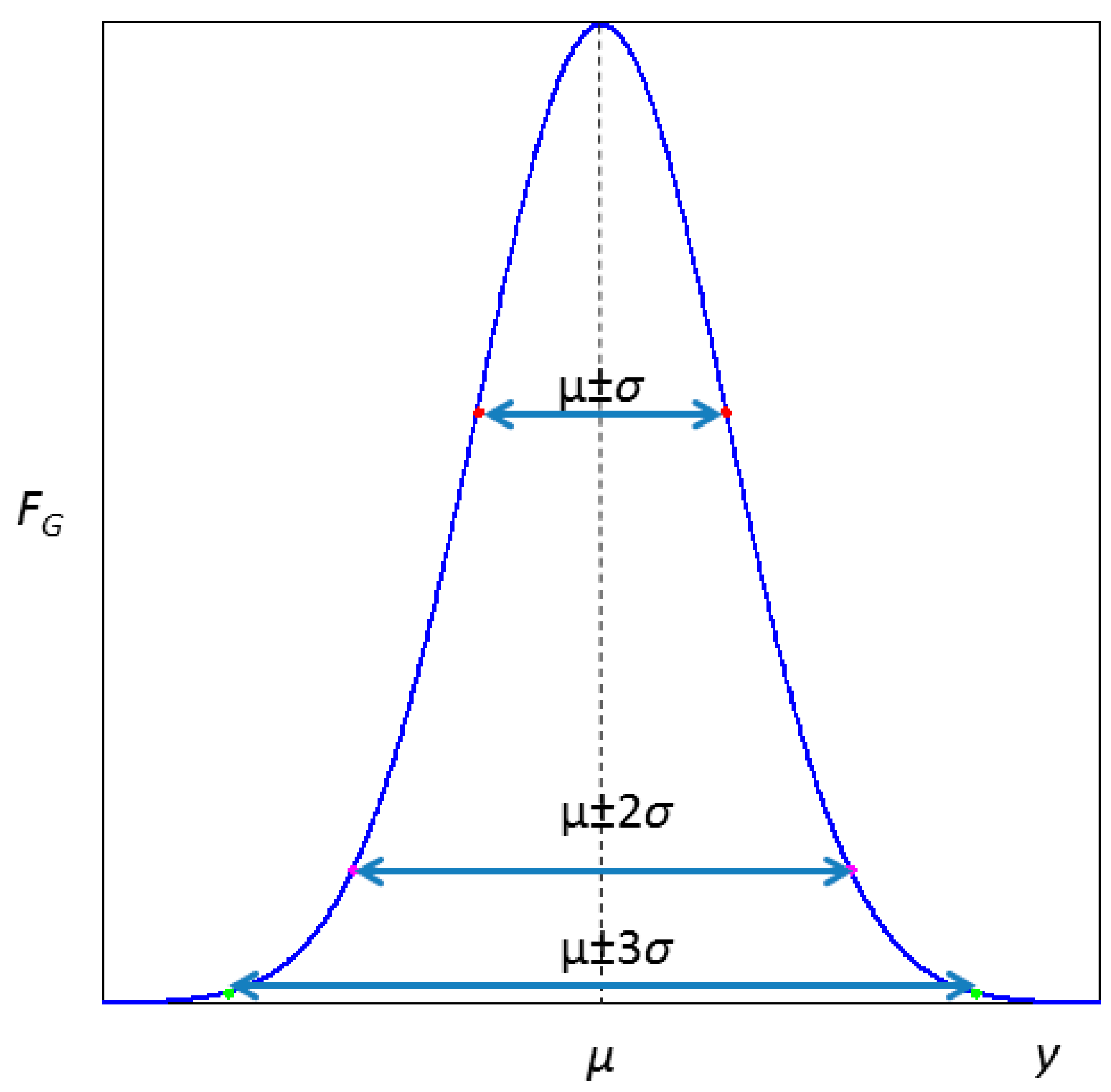
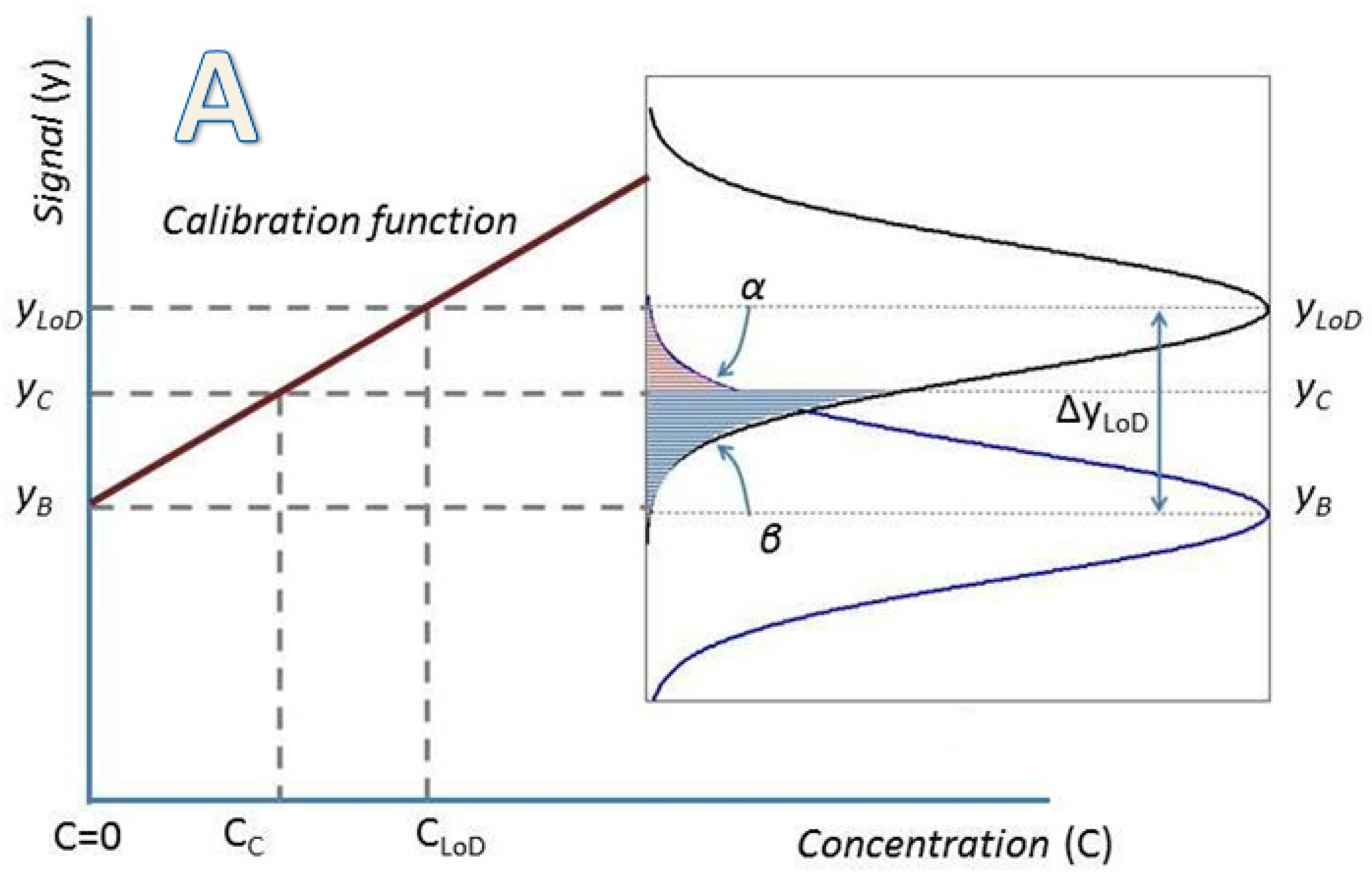
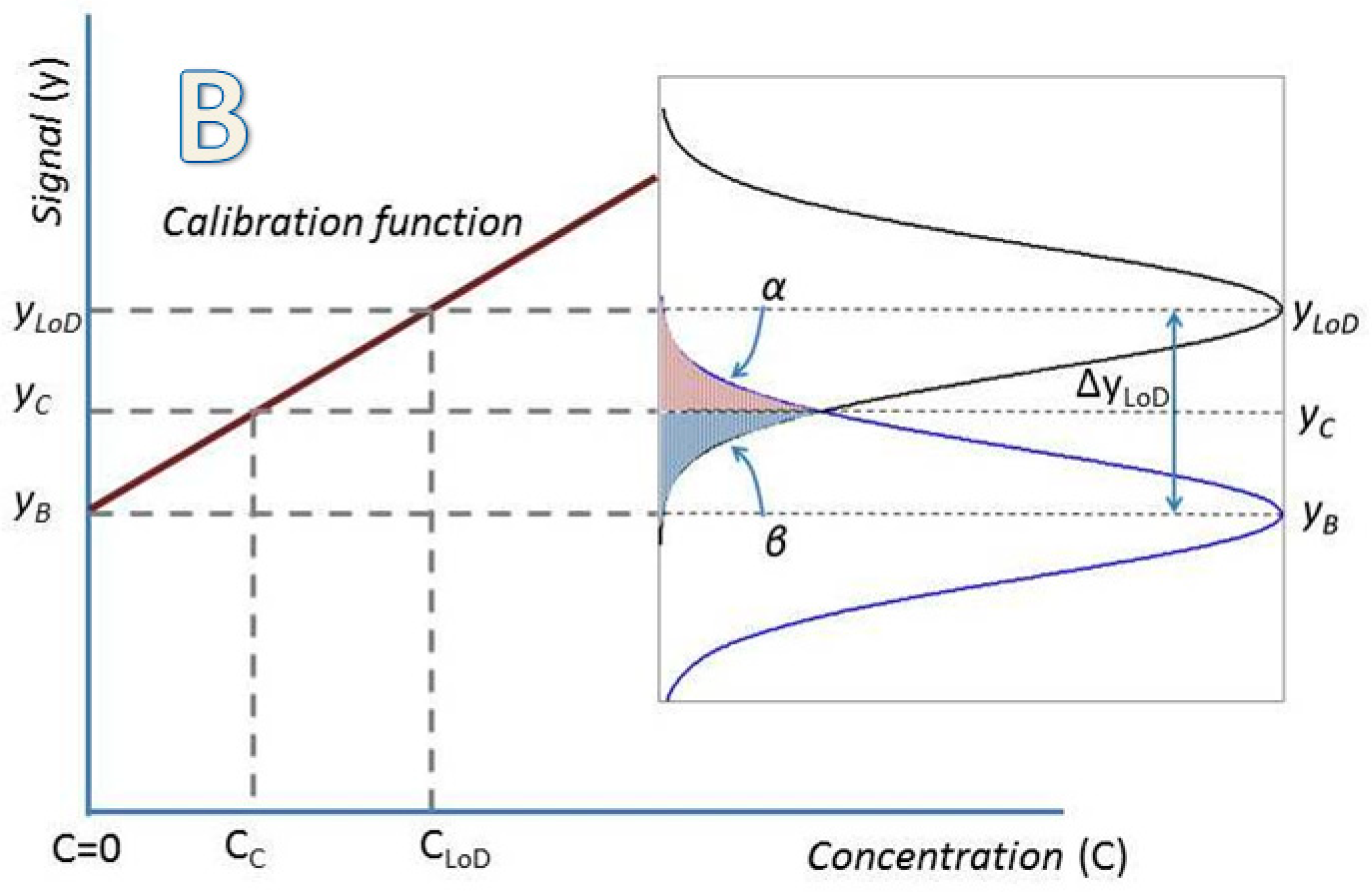
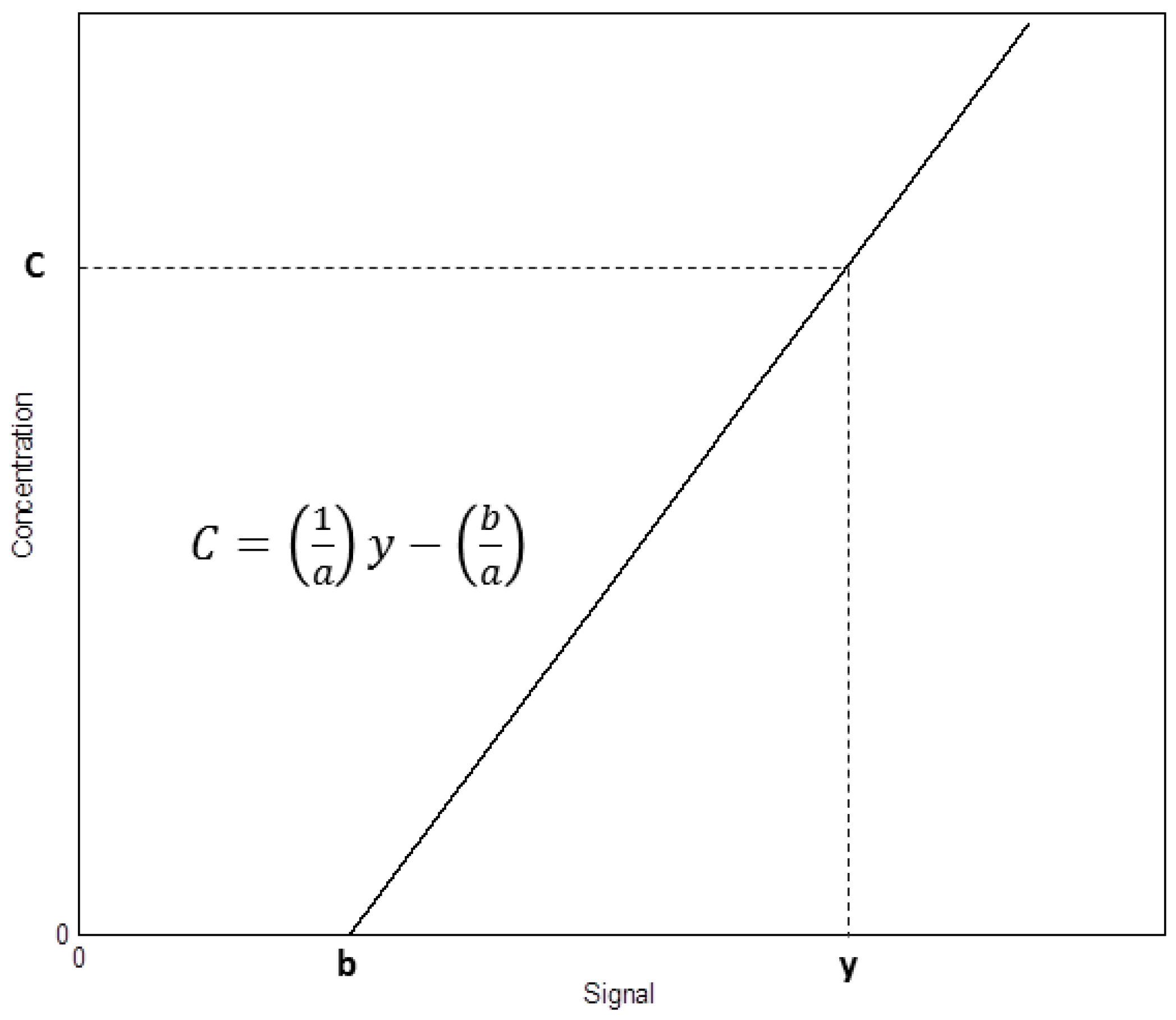
2. Determination of Uncertainty in a Measuring Interval and the Limit of Detection through the Calibration Function Data
3. Analysis of Standard Immunoassay Situations
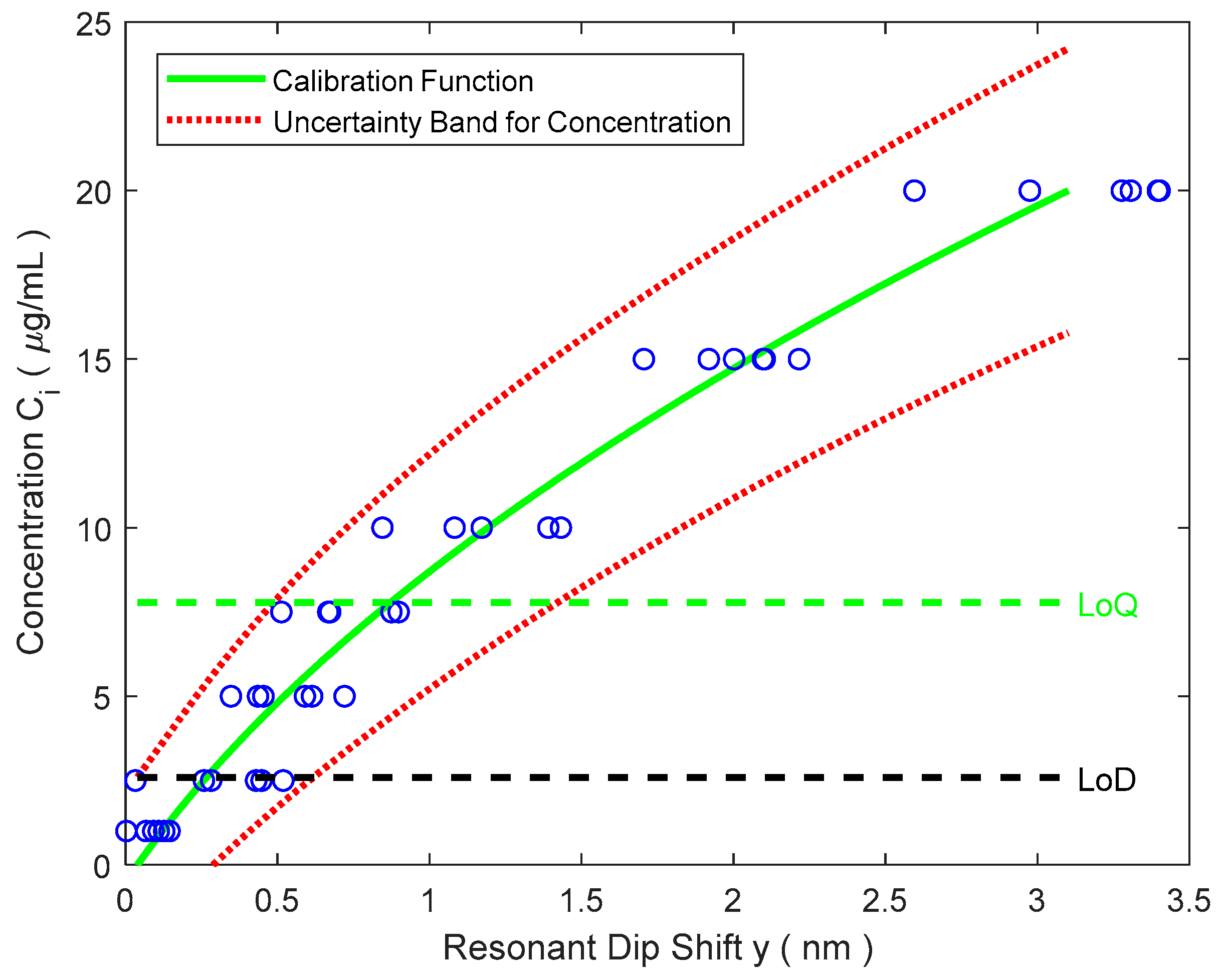
3.1. Simulated Immunoassay
3.2. Experimental Immunoassay
- ○
- The biosensor response is non-linear, with a noticeable lack of repeatability at the end of its scale (over 20 μg/mL).
- ○
- Variability increases with concentration probably due to differences in sensing cells or biofuntionalization performance among other possible factors (standard deviations do not pass the Hartley’s test [29]).
- ○
- The degrees of freedom of the problem , where is the number of the parameters to be determined during the fitting: five for the 5PL, for the polynomials.
- ○
- The weighted sum of squares , where is . is the fitted calibration curve.
- ○
- The critical value of a Chi-square distribution with degrees of freedom corresponding to a confidence level of .
- ○
- .
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zanchetta, G.; Lanfranco, R.; Giavazzi, F.; Bellini, T.; Buscaglia, M. Emerging applications of label-free optical biosensors. Nanophotonics 2017, 6. [Google Scholar] [CrossRef]
- Estevez, M.C.; Alvarez, M.; Lechuga, L.M. Integrated optical devices for lab-on-a-chip biosensing applications. Laser Photonics Rev. 2011, 4, 447–463. [Google Scholar] [CrossRef]
- Homola, J. Surface plasmon resonance sensors for detection of chemical and biological species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; White, I.M.; Shopova, S.I.; Zhu, H.; Suter, J.D.; Sun, Y. Sensitive optical biosensors for unlabeled targets: A review. Anal. Chim. Acta 2008, 620, 8–26. [Google Scholar] [CrossRef] [PubMed]
- United States Pharmacopeia. Validation of Compendial Procedures. Available online: https://hmc.usp.org/about/general-chapters (accessed on 14 May 2018).
- Barwick, V.J.; Prichard, E. (Eds.) Eurachem Guide: Terminology in Analytical Measurement—Introduction to VIM 3. 2011. Available online: www.eurachem.org (accessed on 14 May 2018).
- International Conference on Harmonization of Technical Requirements for the Registration of Pharmaceuticals for Human Use. Validation of Analytical Procedures: Text and Methodology Q2(R1). 2005. Available online: http://www.ich.org/products/guidelines/quality/article/quality-guidelines.html (accessed on 14 May 2018).
- IUPAC. Compendium of Chemical Terminology, 2nd ed.; the “Gold Book”; Blackwell Scientific Publications: Oxford, UK, 1997; ISBN 0-9678550-9-8. [Google Scholar]
- Currie, L.A. Nomenclature in evaluation of analytical methods including detection and quantification capabilities. Pure Appl. Chem. 1995, 67, 1699–1723. [Google Scholar] [CrossRef]
- ISO. Technical Committee ISO/TC 69 Subcommittee SC6 Capability of Detection: Part 1: Terms and Definitions; ISO 11843-1; ISO: Geneva, Switzerland, 1997. [Google Scholar]
- Chiavaioli, F.; Gouveia, C.A.J.; Jorge, P.A.S.; Baldini, F. Towards a uniform metrological assessment of grating- based optical fiber sensors: From refractometers to biosensors. Biosensors 2017, 7, 23. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Ramos, M.D.; Cuadros-Rodríguez, L.; Arroyo-Guerrero, E.; Capitan-Vallvey, L.F. An IUPAC based approach to estimate the detection limit in co-extraction-based optical sensors for anions with sigmoidal response calibration curves. Anal. Bioanal. Chem. 2011, 401, 2881–2889. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Xiaochen, S.; Agarwal, A.; Kimerling, L.C. Design guidelines for optical resonator biochemical sensors. J. Opt. Soc. Am. B 2009, 26, 5. [Google Scholar] [CrossRef]
- Janiga, I.; Mocak, J.; Garaj, I. Comparison of minimum detectable concentration with the IUPAC detection limit. Meas. Scie. Rev. 2008, 8, 5. [Google Scholar] [CrossRef]
- Analytical Methods Committee; Royal Society of Chemistry. Recommendations for the definition, estimation, and use of the detection limit. Analyst 1987, 112, 199–204. [Google Scholar]
- Look, H.P.; Wentzell, D.P. Detection limits of chemical sensors: Applications and misapplications. Sens. Actuator B Chem. 2012, 172, 157–163. [Google Scholar] [CrossRef]
- Evard, H.; Kruve, A.; Leito, I. Tutorial on estimating the limit of detection using LC-MS analysis, Part I: Theoretical review. Anal. Chim. Acta 2016, 942, 23–39. [Google Scholar] [CrossRef] [PubMed]
- Chiavaioli, F.; Trono, C.; Giannetti, A.; Brenci, M.; Baldini, F. Characterisation of a label-free biosensor based on long period grating. J. Biophotonics 2014, 7, 312–322. [Google Scholar] [CrossRef] [PubMed]
- Magnusson, B.; Örnemark, U. Eurachem Guide: The Fitness for Purpose of Analytical Methods—A Laboratory Guide to Method Validation and Related Topics, 2nd ed. 2014. Available online: www.eurachem.org (accessed on 14 May 2018).
- Currie, L.A. Detection and quantification limits: Origins and historical overview. Anal. Chim. Acta 1999, 391, 127–134. [Google Scholar] [CrossRef]
- Ellison, S.L.R.; Williams, A. (Eds.) Eurachem/CITAC Guide: Quantifying Uncertainty in Analytical Measurements. 2012. Available online: https://eurachem.org/images/stories/Guides/pdf/QUAM2012_P1.pdf (accessed on 24 June 2018).
- Cordero, R.R.; Seckmeyer, G.; Labbe, F. Effect of the resolution on the uncertainty evaluation. Metrologia 2006, 43, L33–L38. [Google Scholar] [CrossRef]
- Philips, S.D.; Toman, B.; Estler, W.T. Uncertainty Due to Finite Resolution Measurements. J. Res. Natl. Inst. Stand. Technol. 2008, 113, 143–156. [Google Scholar] [CrossRef]
- JCGM/BIPM. Evaluation of Measurement Data: Guide to the Expression of Uncertainty in Measurements. 2008. Available online: http://www.bipm.org/en/publications/guides/gum.html (accessed on 24 June 2018).
- Bevington, P.R.; Robison, D.K. Data Reduction and Error Analysis for the Physical Sciences; Mc Graw Hill: New York, NY, USA, 1993; ISBN 0-07-247227-8. [Google Scholar]
- JCGM/BIPM. Evaluation of Measurement Data—Supplement 2 to the “Guide to the Expression of Uncertainty in Measurement”—Extension to Any Number of Output Quantities. 2011. Available online: http://www.bipm.org/en/publications/guides/gum.html (accessed on 24 June 2018).
- Rozet, E.; Ziemons, E.; Marini, R.D.; Hubert, P. Usefulness of information criteria for the selection of calibration curves. Anal. Chem. 2013, 85, 6327–6335. [Google Scholar] [CrossRef] [PubMed]
- Hernández, A.; Casquel, R.; Holgado, M.; Cornago, I.; Fernández, F.; Ciaurriz, P.; Sanza, F.; Santamaría, B.; Maigler, M.; Laguna, M.F. Resonant nanopillars arrays for label-free biosensing. Opt. Lett. 2016, 41, 5430–5433. [Google Scholar] [CrossRef] [PubMed]
- Hartley, H.O. The maximum F-ratio as a short cut test for homogeneity of variance. Biometrika 1950, 37, 308–312. [Google Scholar] [PubMed]
- Burnham, K.; Anderson, D. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: Berlin, Germany, 2002; ISBN 0-387-95364-7. [Google Scholar]
- Lavagnini, I.; Magno, F. A statistical overview on multivariate calibration, inverse regression and detection limits: Application to mass chromatography/ mass spectrometry technique. Mass Spectrom. Rev. 2007, 26, 1–18. [Google Scholar] [CrossRef] [PubMed]

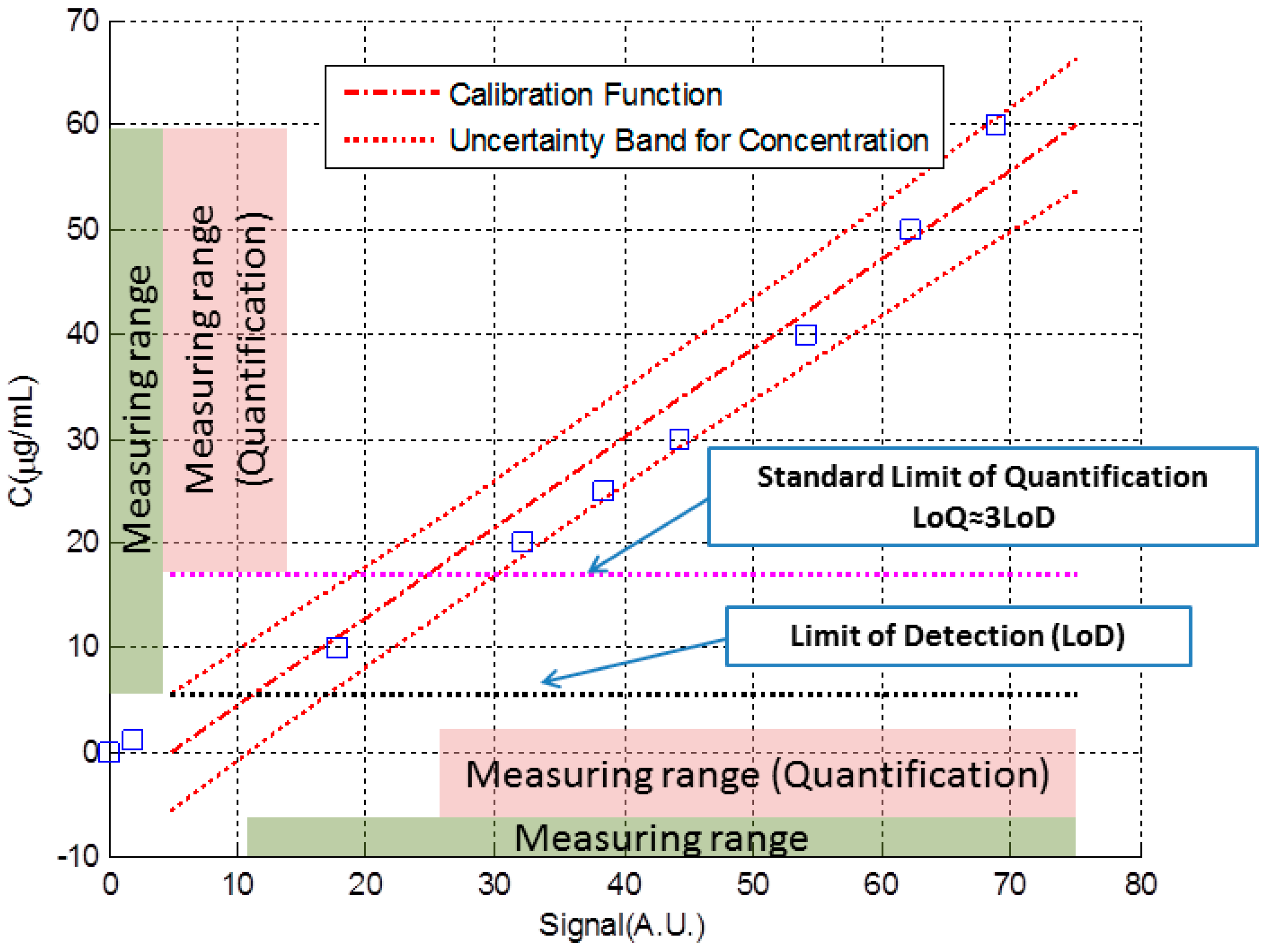

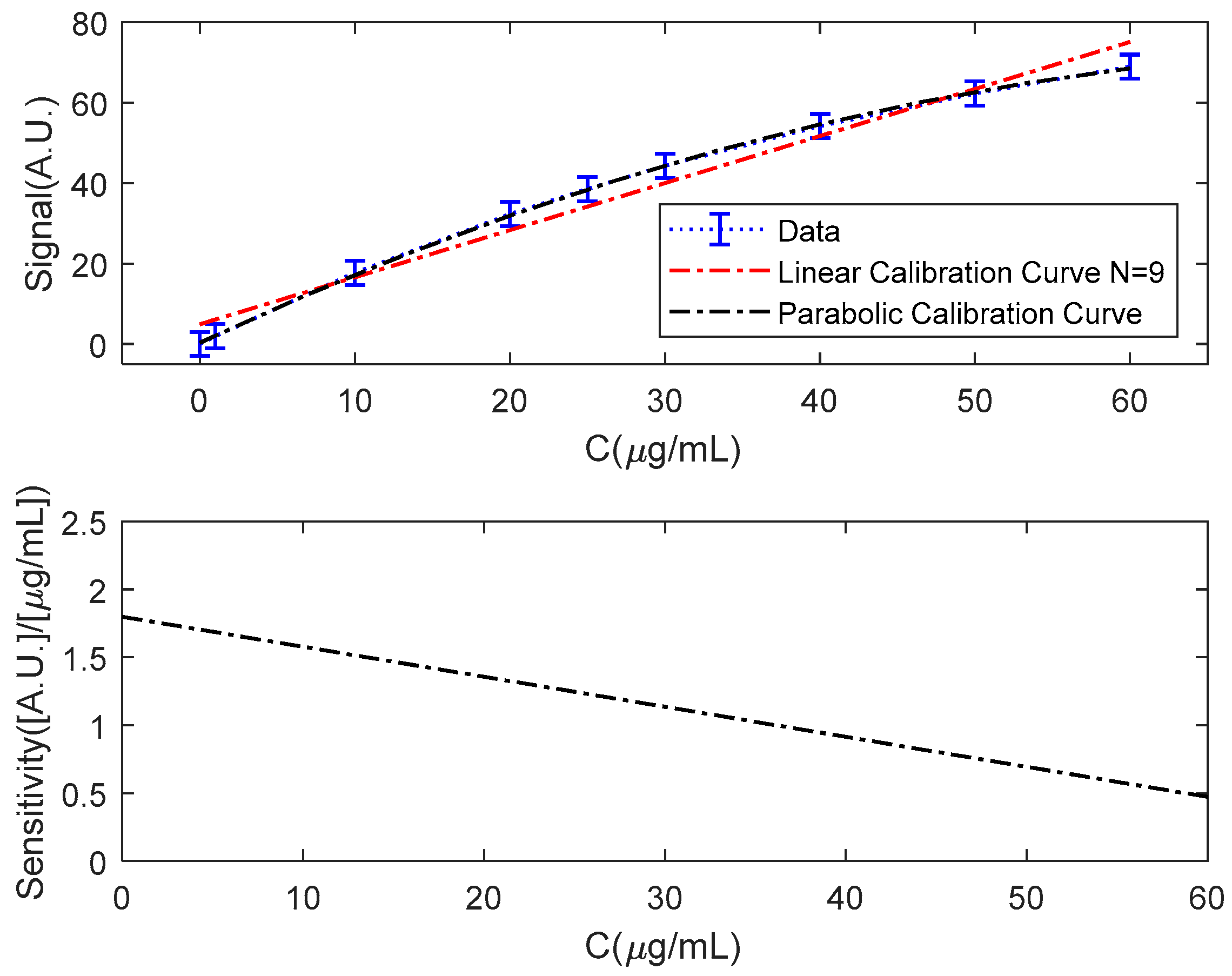
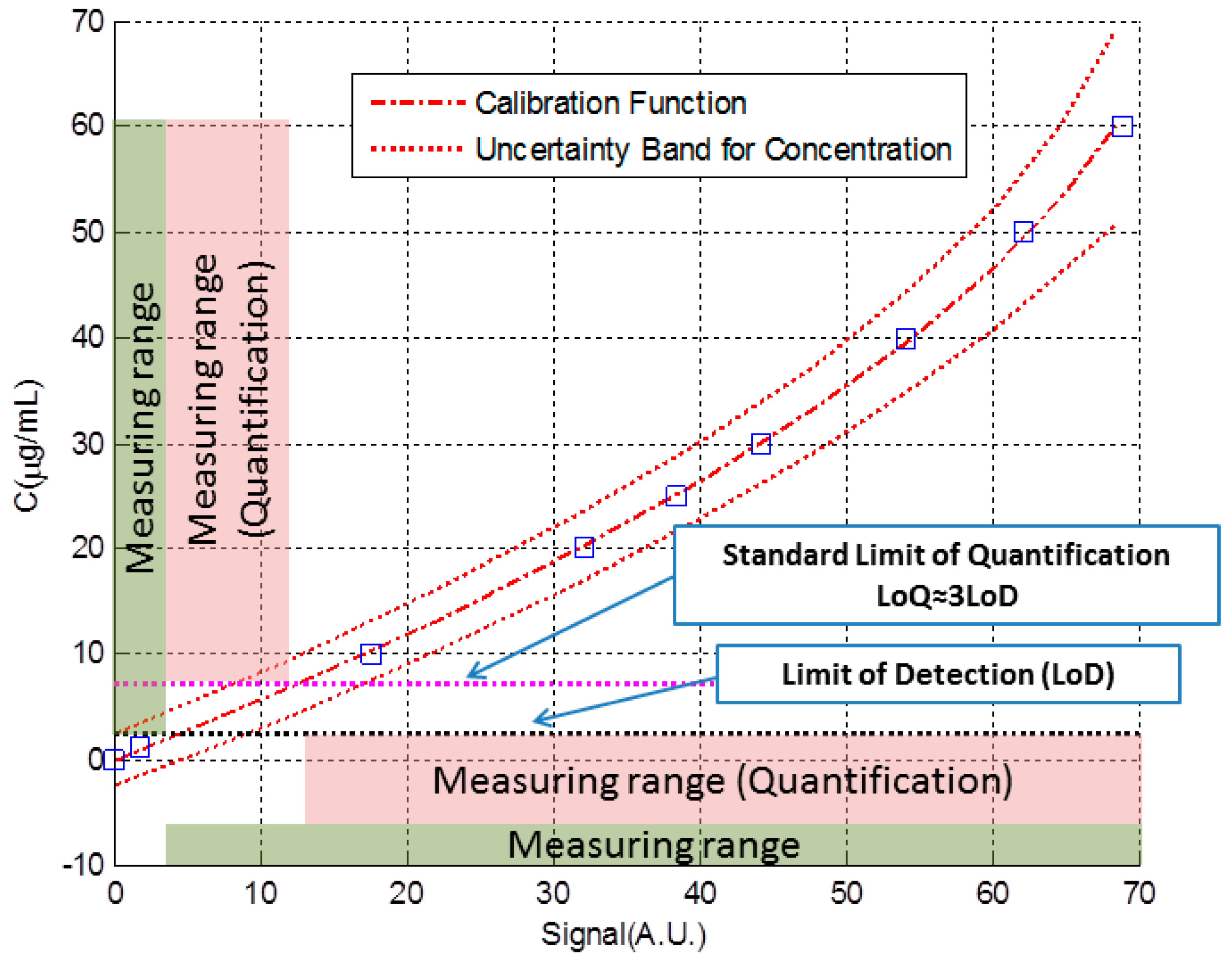

| C (μg/mL) | 0 | 1 | 10 | 20 | 25 | 30 | 40 | 50 | 60 | 100 | 200 | 300 | 400 | 500 |
| Signal (A.U.) | 0 | 1.9 | 17.7 | 32.3 | 38.5 | 44.2 | 54.1 | 62.2 | 68.9 | 85.7 | 97.9 | 99.0 | 99.1 | 99.2 |
| S (A.U.) | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| a([A.U.]/[μg/mL] | b([A.U.]) | ua([A.U.]/[μg/mL] | ub([A.U.]) | r |
| 1.17 | 4.88 | 0.05 | 1.66 | −0.79 |
| LoD (μg/mL) | LoQ (μg/mL) | Umin (μg/mL) | Umax (μg/mL) | CMax(μg/mL) |
| 5.7 | 16.8 | 4.5 | 6.3 | 60 |
| N = 9 | N = 8 | N = 7 | N = 6 | |
|---|---|---|---|---|
| a([A.U.]/[μg/mL] | 1.17 | 1.27 | 1.38 | 1.49 |
| b([A.U.]) | 4.88 | 3.37 | 2.03 | 1.04 |
| LoD (μg/mL) | 5.7 | 5.4 | 5.1 | 4.9 |
| LoQ (μg/mL) | 17.1 | 16.2 | 15.3 | 14.7 |
| Cmax(μg/mL) | 60 | 50 | 40 | 30 |
| Umin (μg/mL) | 4.5 | 4.3 | 4 | 3.8 |
| Umax (μg/mL) | 6.3 | 5.9 | 5.6 | 5.1 |
| Concentration (μg/mL) | Transduction Signal (nm) | Mean (nm) | Si (nm) | |||||
|---|---|---|---|---|---|---|---|---|
| j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | j = 6 | |||
| 1 | 0.13 | 0.15 | 0.00 | 0.09 | 0.11 | 0.07 | 0.09 | 0.05 |
| 2.5 | 0.52 | 0.43 | 0.03 | 0.28 | 0.26 | 0.45 | 0.33 | 0.18 |
| 5 | 0.61 | 0.72 | 0.44 | 0.35 | 0.59 | 0.45 | 0.53 | 0.14 |
| 7.5 | 0.87 | 0.90 | 0.67 | 0.87 | 0.67 | 0.51 | 0.75 | 0.16 |
| 10 | 1.43 | 1.39 | 1.17 | 1.39 | 1.08 | 0.85 | 1.22 | 0.23 |
| 15 | 2.22 | 2.10 | 2.00 | 2.10 | 1.92 | 1.71 | 2.01 | 0.18 |
| 20 | 3.40 | 3.28 | 3.31 | 3.40 | 2.97 | 2.60 | 3.16 | 0.32 |
| 30 | 3.92 | 3.80 | 3.96 | 4.18 | 3.37 | 3.14 | 3.73 | 0.40 |
| 50 | 4.55 | 4.82 | 4.68 | 4.30 | 4.26 | 3.73 | 4.39 | 0.39 |
| 70 | 5.38 | 5.07 | 5.24 | 4.94 | 4.77 | 4.91 | 5.05 | 0.22 |
| 100 | 6.14 | 5.69 | 5.76 | 5.66 | 5.37 | 5.05 | 5.61 | 0.37 |
| Type of Curve | Deegres of Freedom | Weighted Sum of Squares | Chi-Square Critical Value | Akaike Information Criterion AICc |
|---|---|---|---|---|
| Polynomial g = 1 | 5 | 37.1 | 11.1 | 18.7 |
| Polynomial g = 2 | 4 | 8.66 | 9.49 | 15.5 |
| Polynomial g = 3 | 3 | 6.31 | 7.81 | 27.3 |
| Polynomial g = 1 | 2 | 4.16 | 5.99 | 66.4 |
| 5PL | 2 | 2.01 | 5.99 | 61.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lavín, Á.; Vicente, J.D.; Holgado, M.; Laguna, M.F.; Casquel, R.; Santamaría, B.; Maigler, M.V.; Hernández, A.L.; Ramírez, Y. On the Determination of Uncertainty and Limit of Detection in Label-Free Biosensors. Sensors 2018, 18, 2038. https://doi.org/10.3390/s18072038
Lavín Á, Vicente JD, Holgado M, Laguna MF, Casquel R, Santamaría B, Maigler MV, Hernández AL, Ramírez Y. On the Determination of Uncertainty and Limit of Detection in Label-Free Biosensors. Sensors. 2018; 18(7):2038. https://doi.org/10.3390/s18072038
Chicago/Turabian StyleLavín, Álvaro, Jesús De Vicente, Miguel Holgado, María F. Laguna, Rafael Casquel, Beatriz Santamaría, María Victoria Maigler, Ana L. Hernández, and Yolanda Ramírez. 2018. "On the Determination of Uncertainty and Limit of Detection in Label-Free Biosensors" Sensors 18, no. 7: 2038. https://doi.org/10.3390/s18072038
APA StyleLavín, Á., Vicente, J. D., Holgado, M., Laguna, M. F., Casquel, R., Santamaría, B., Maigler, M. V., Hernández, A. L., & Ramírez, Y. (2018). On the Determination of Uncertainty and Limit of Detection in Label-Free Biosensors. Sensors, 18(7), 2038. https://doi.org/10.3390/s18072038










