Two-Dimensional DOA Estimation for Three-Parallel Nested Subarrays via Sparse Representation
Abstract
:1. Introduction
- We propose two kinds of TPNAs so as to estimate more sources than the number of sensors in the 2-D DOA estimation problem. The closed form expressions of sensors positions are presented, and the number of sensors for different subarrays for TPNAs is investigated to achieve the maximization of continuous DOFs.
- The two proposed kinds of TPNAs can achieve continuous DOFs with sensors by using the vectorization operation of cross-correlation matrices, which are larger than a parallel co-prime array or its modifications.
- By optimizing the sensor distributions in two kinds of TPNAs, the effects of mutual coupling are moderately alleviated.
- By using the sparse representation framework and total least squares technique, the 2-D DOA estimation problem is decomposed into two 1-D DOA estimation problems, and the paired DOAs can be obtained automatically. In addition, the continuous DOFs can be fully used via the sparse representation framework.
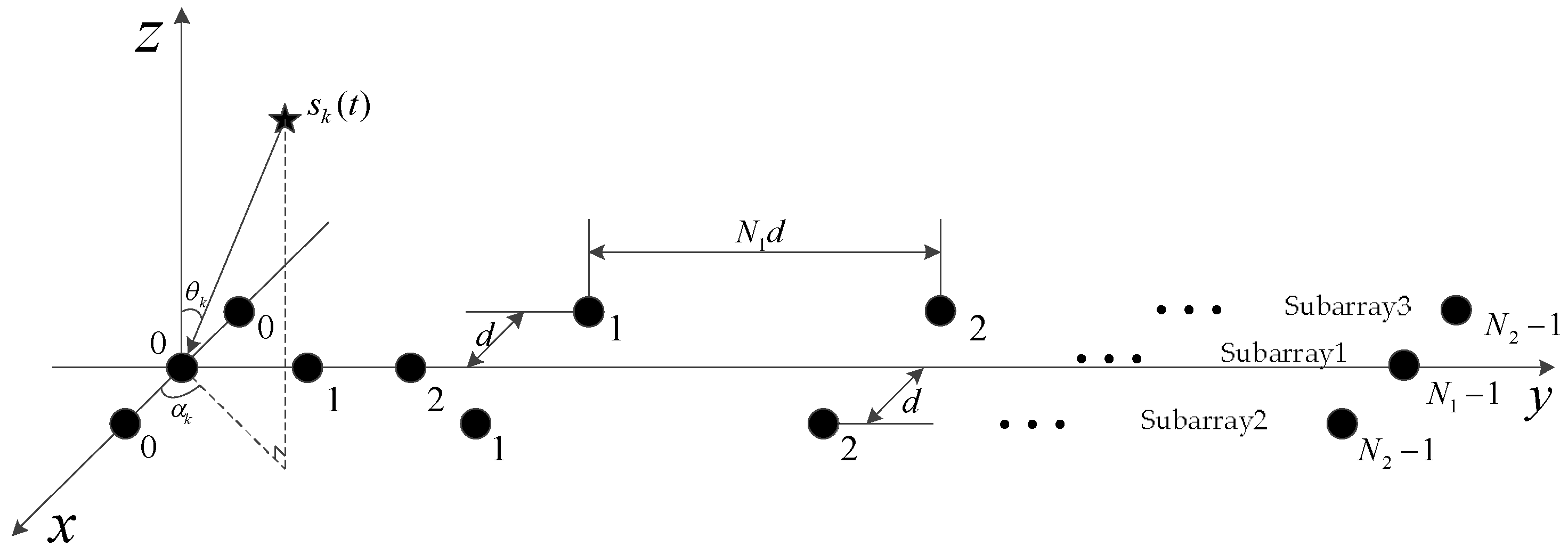
2. System Model
3. The Proposed Three-Parallel Nested Subarrays and 2-D DOA Estimation Method
3.1. The Configurations of TPNAs
3.2. 2-D DOA Estimation Using Cross-Correlation Matrix via Sparse Representation
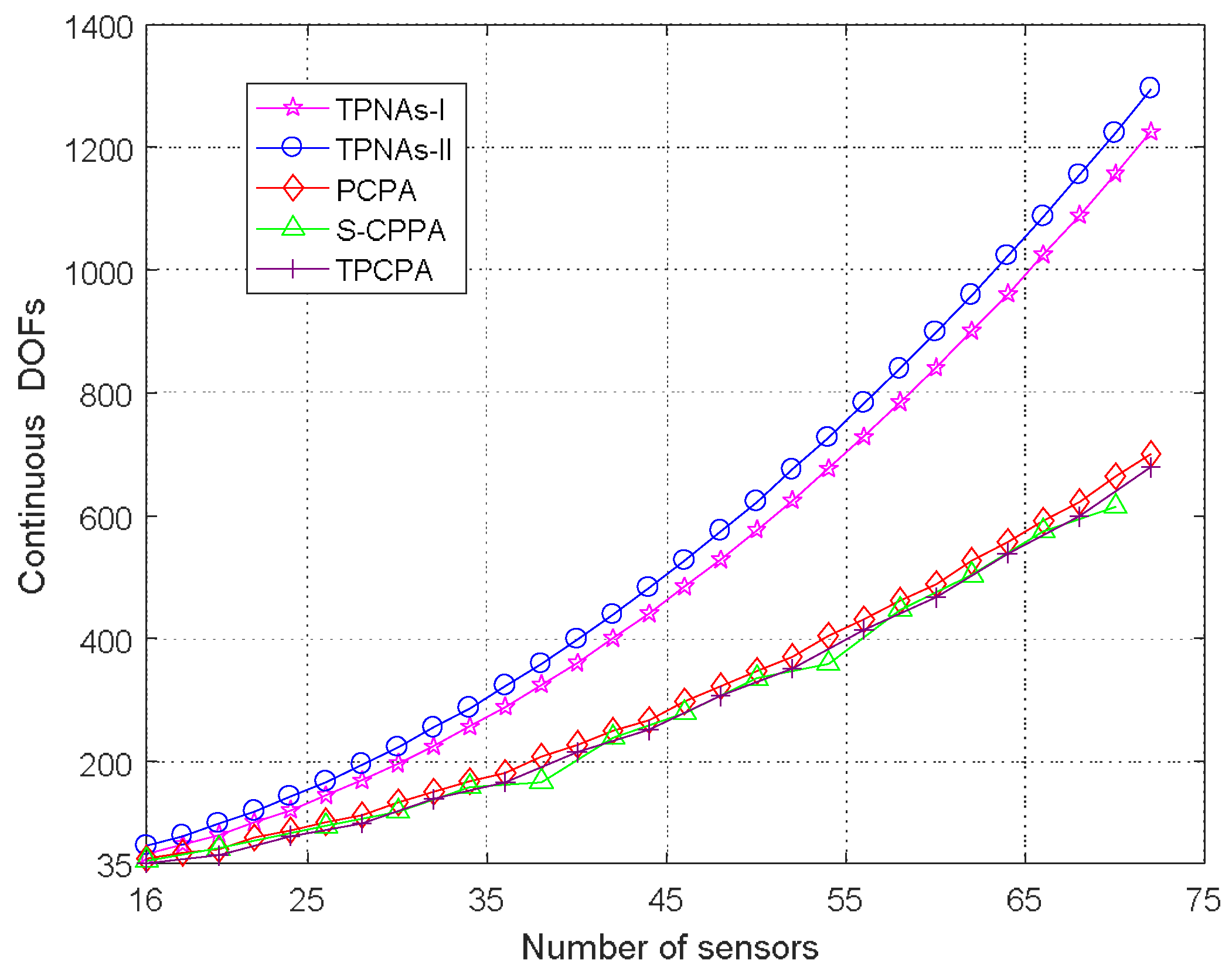
4. Simulation Results
4.1. DOF Comparison
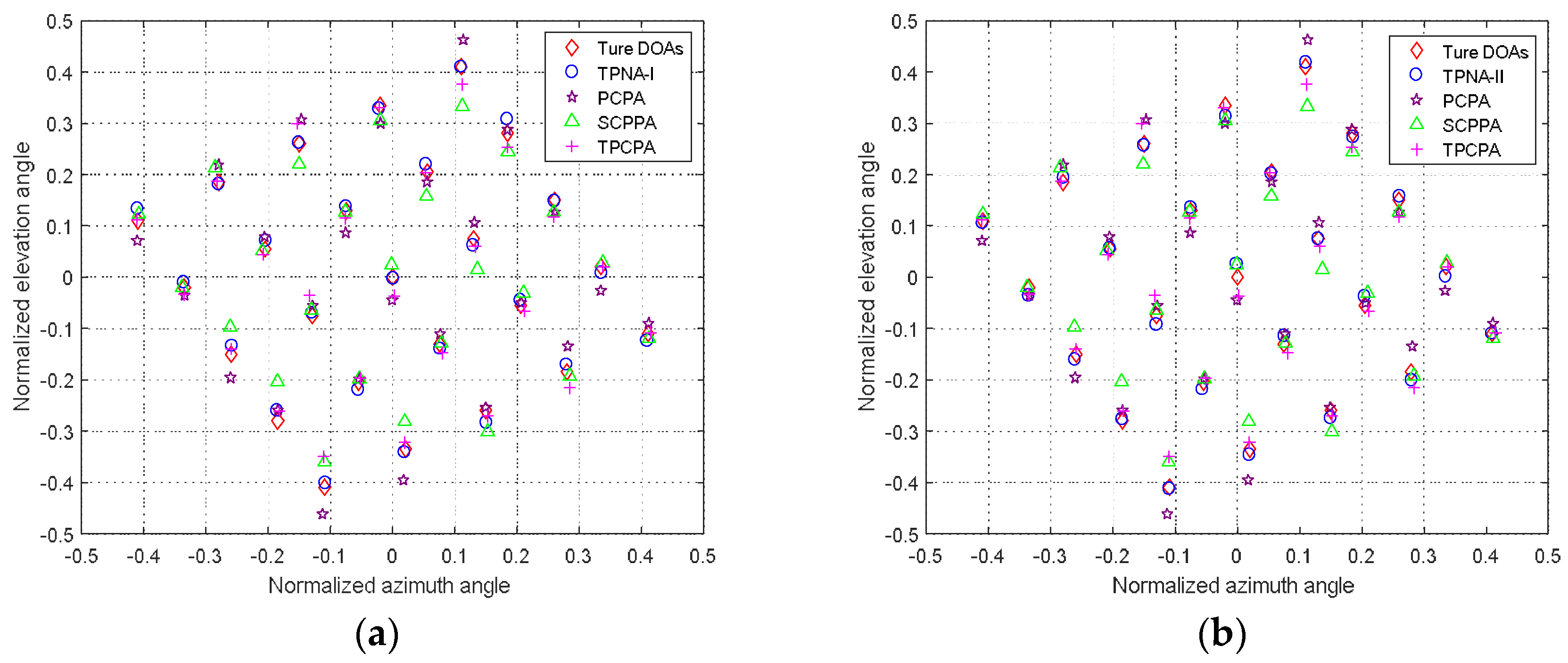
4.2. 2-D DOA Estimation Results
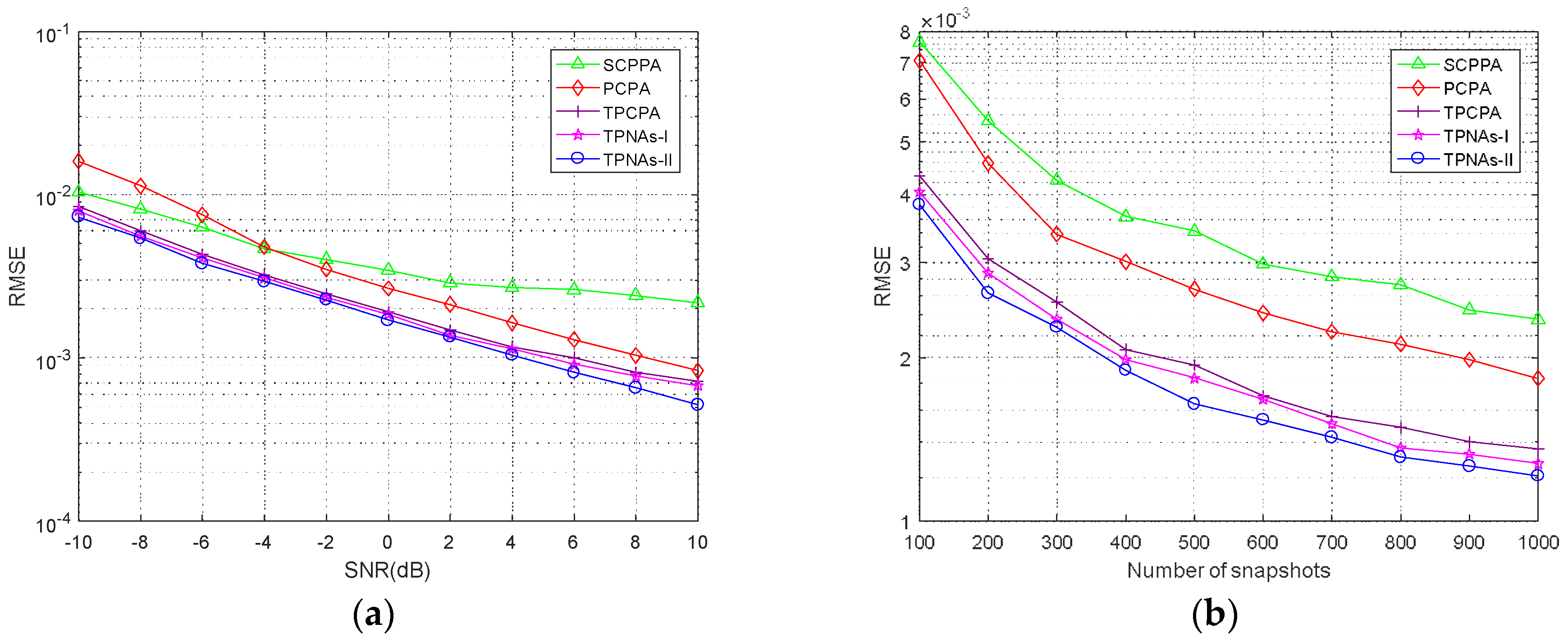
4.3. RMSE Performance
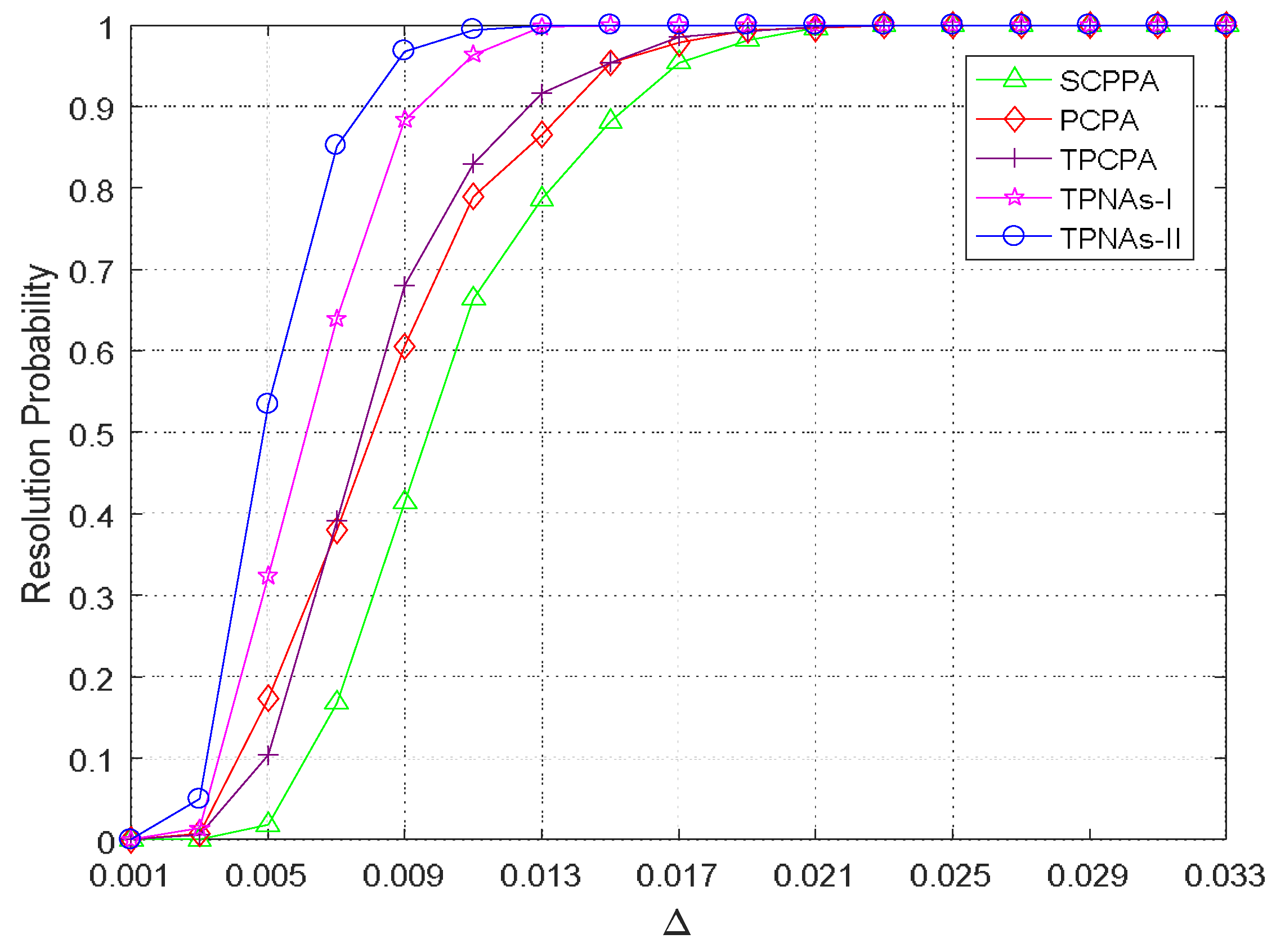
4.4. Resolution Ability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Dai, J.; Xu, W.; Zhao, D. Real-valued DOA estimation for uniform linear array with unknown mutual coupling. Signal Process. 2012, 92, 2056–2065. [Google Scholar] [CrossRef]
- Heidenreich, P.; Zoubir, A.M.; Rubsamen, M. Joint 2-D DOA estimation and phase calibration for uniform rectangular arrays. IEEE Trans. Signal Process. 2012, 60, 4683–4693. [Google Scholar] [CrossRef]
- Mathews, C.P.; Zoltowski, M.D. Eigenstructure techniques for 2-D angle estimation with uniform circular arrays. IEEE Trans. Signal Process. 1994, 42, 2395–2407. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Pal, P.; Vaidyanathan, P.P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Gupta, I.; Ksienski, A. Effect of mutual coupling on the performance of adaptive arrays. IEEE Trans. Antennas Propag. 1983, 31, 785–791. [Google Scholar] [CrossRef]
- Friedlander, B.; Weiss, A.J. Direction finding in the presence of mutual coupling. IEEE Trans. Antennas Propag. 1991, 39, 273–284. [Google Scholar] [CrossRef]
- Pillai, S.U.; Kwon, B.H. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P. Remarks on the spatial smoothing step in coarray music. IEEE Signal Process. Lett. 2015, 22, 1438–1442. [Google Scholar] [CrossRef]
- Si, W.; Wang, Y.; Hou, C.; Wang, H. Real-valued 2D MUSIC algorithm based on modified forward/backward averaging using an arbitrary centrosymmetric polarization sensitive array. Sensors 2017, 17, 2241. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.L.; Vaidyanathan, P.P. Super nested arrays: Linear sparse arrays with reduced mutual coupling-part I: Fundamentals. IEEE Trans. Signal Process. 2016, 64, 3997–4012. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P. Super nested arrays: Linear sparse arrays with reduced mutual coupling-part II: High-order extensions. IEEE Trans. Signal Process. 2016, 64, 4203–4217. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Lu, Y.; Ren, S.; Cao, S. Augmented nested arrays with enhanced DOF and reduced mutual coupling. IEEE Trans. Signal Process. 2017, 65, 5549–5563. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized coprime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P.; Pal, P. Coprime coarray interpolation for DOA estimation via nuclear norm minimization. In Proceedings of the IEEE International Symposium Circuits and Systems, Montreal, QC, Canada, 22–25 May 2016; pp. 2639–2642. [Google Scholar]
- Chen, T.; Guo, M.; Guo, L. A direct coarray interpolation approach for direction finding. Sensors 2017, 17, 2149. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.D.; Amin, M.G.; Himed, B. Sparsity-based DOA estimation using co-prime arrays. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 3967–3971. [Google Scholar]
- Tan, Z.; Eldar, Y.C.; Nehorai, A. Direction of arrival estimation using co-prime arrays: A super resolution viewpoint. IEEE Trans. Signal Process. 2014, 62, 5565–5576. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays in two dimensions, Part I: Geometrical considerations. IEEE Trans. Signal Process. 2012, 60, 4694–4705. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays in two dimensions, part II: Application in two dimensional array processing. IEEE Trans. Signal Process. 2012, 60, 4706–4718. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P. Hourglass arrays and other novel 2-D sparse arrays with reduced mutual coupling. IEEE Trans. Signal Process. 2017, 65, 3369–3383. [Google Scholar] [CrossRef]
- Cheng, Z.; Shui, P.; Li, H.; Zhao, Y. Two-dimensional DOA estimation algorithm with co-prime array via sparse representation. Electron. Lett. 2015, 51, 2084–2086. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Two-dimensional DOA estimation using parallel coprime subarrays. In Proceedings of the 2016 IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM), Rio de Janerio, Brazil, 10–13 July 2016; pp. 1–4. [Google Scholar]
- Shi, J.; Hu, G.; Zhang, X.; Gong, P. Sum and difference coarrays based 2-D DOA estimation with co-prime parallel arrays. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; pp. 1–4. [Google Scholar]
- Gong, P.; Zhang, X.; Shi, J.; Zheng, W. Three-parallel co-prime array configuration for two-dimensional DOA estimation. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; pp. 1–5. [Google Scholar]
- Shi, J.; Hu, G.; Zhang, X.; Sun, F.; Zhou, H. Sparsity-based two-dimensional DOA estimation for coprime array: From sum–difference coarray viewpoint. IEEE Trans. Signal Process. 2017, 65, 5591–5604. [Google Scholar] [CrossRef]
- Gu, J.-F.; Zhu, W.-P.; Swamy, M.N.S. Joint 2-D DOA estimation via sparse L-shaped array. IEEE Trans. Signal Process. 2015, 63, 1171–1182. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Coprime sampling and the MUSIC algorithm. In Proceedings of the 2011 IEEE Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop (DSP/SPE), Sedona, AZ, USA, 4–7 January 2011; pp. 289–294. [Google Scholar]
- Sun, F.; Lan, P.; Gao, B.; Zhang, G. An efficient dictionary learning-based 2-D DOA estimation without pair matching for co-prime parallel arrays. IEEE Access 2018, 6, 8510–8518. [Google Scholar] [CrossRef]
- Cheng, Z.F.; Zhao, Y.B.; Zhu, Y.T.; Shui, P.L.; Li, H. Sparse representation based two-dimensional direction-of-arrival estimation method with L-shaped array. IET Radar Sonar Navig. 2016, 10, 976–982. [Google Scholar] [CrossRef]
- Markovsky, I.; Van Huffel, S. Overview of total least-squares methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef] [Green Version]
- Grant, M.; Boyd, S. CVX: MATLAB Software for Disciplined Convex Programming, Version 2.1. March 2014. Available online: http://cvxr.com/cvx (accessed on 5 May 2018).
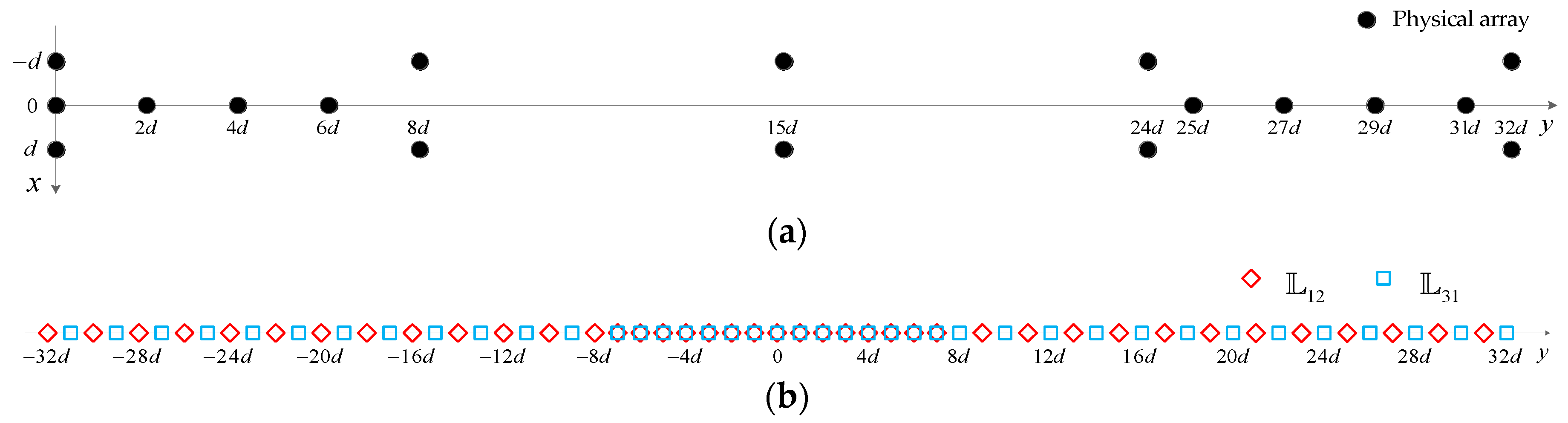
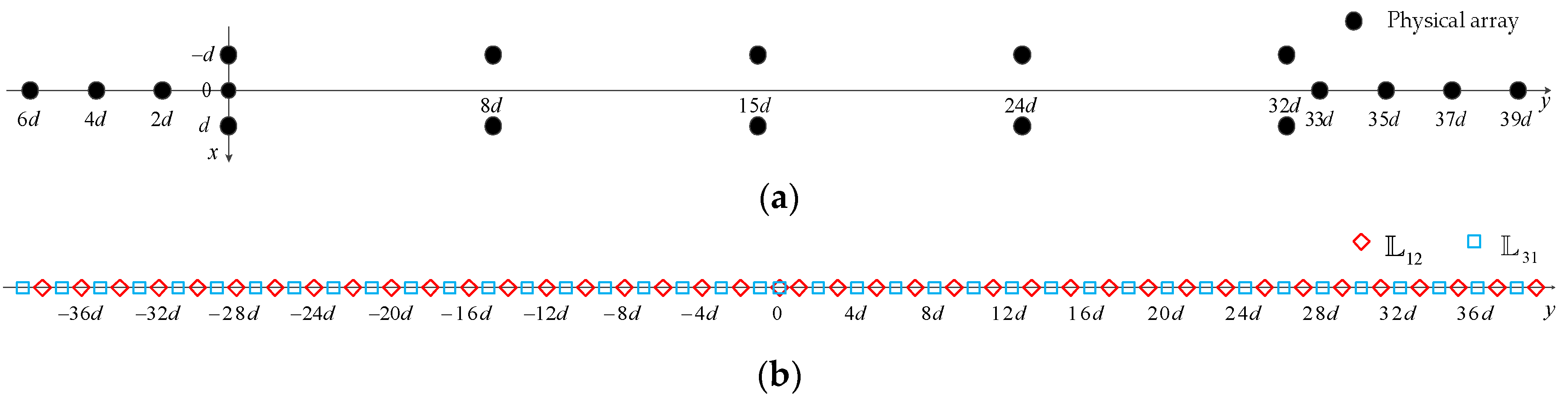
| ( Is an Integer) | Continuous DOFs | ||
|---|---|---|---|
| or | or | ||
| ( Is an Integer) | Continuous DOFs | ||
|---|---|---|---|
| or | or | ||
| Input | The array measurement vectors , and with snapshots. |
| Output | The estimations of normalized 2-D DOAs. |
| Step1 | Calculate the cross-correlation matrices by (27) and (28). |
| Step2 | Construct two received data vectors of virtual array by (31) and (33). |
| Step3 | Obtain the augmented virtual received data vector by (35) and (37). |
| Step4 | Select the regularization parameter according to (43). |
| Step5 | Discretizing the normalized azimuth angle range and perform Equation (41) to obtain the estimations of . |
| Step6 | Calculate the estimations of by (44) and (45). |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, W.; Peng, Z.; Hou, C.; Zeng, F. Two-Dimensional DOA Estimation for Three-Parallel Nested Subarrays via Sparse Representation. Sensors 2018, 18, 1861. https://doi.org/10.3390/s18061861
Si W, Peng Z, Hou C, Zeng F. Two-Dimensional DOA Estimation for Three-Parallel Nested Subarrays via Sparse Representation. Sensors. 2018; 18(6):1861. https://doi.org/10.3390/s18061861
Chicago/Turabian StyleSi, Weijian, Zhanli Peng, Changbo Hou, and Fuhong Zeng. 2018. "Two-Dimensional DOA Estimation for Three-Parallel Nested Subarrays via Sparse Representation" Sensors 18, no. 6: 1861. https://doi.org/10.3390/s18061861
APA StyleSi, W., Peng, Z., Hou, C., & Zeng, F. (2018). Two-Dimensional DOA Estimation for Three-Parallel Nested Subarrays via Sparse Representation. Sensors, 18(6), 1861. https://doi.org/10.3390/s18061861




