Research on a Novel MEMS Sensor for Spatial DC Electric Field Measurements in an Ion Flows Field
Abstract
:1. Introduction
2. Principle of the Sensor
2.1. Principle of the Sensor
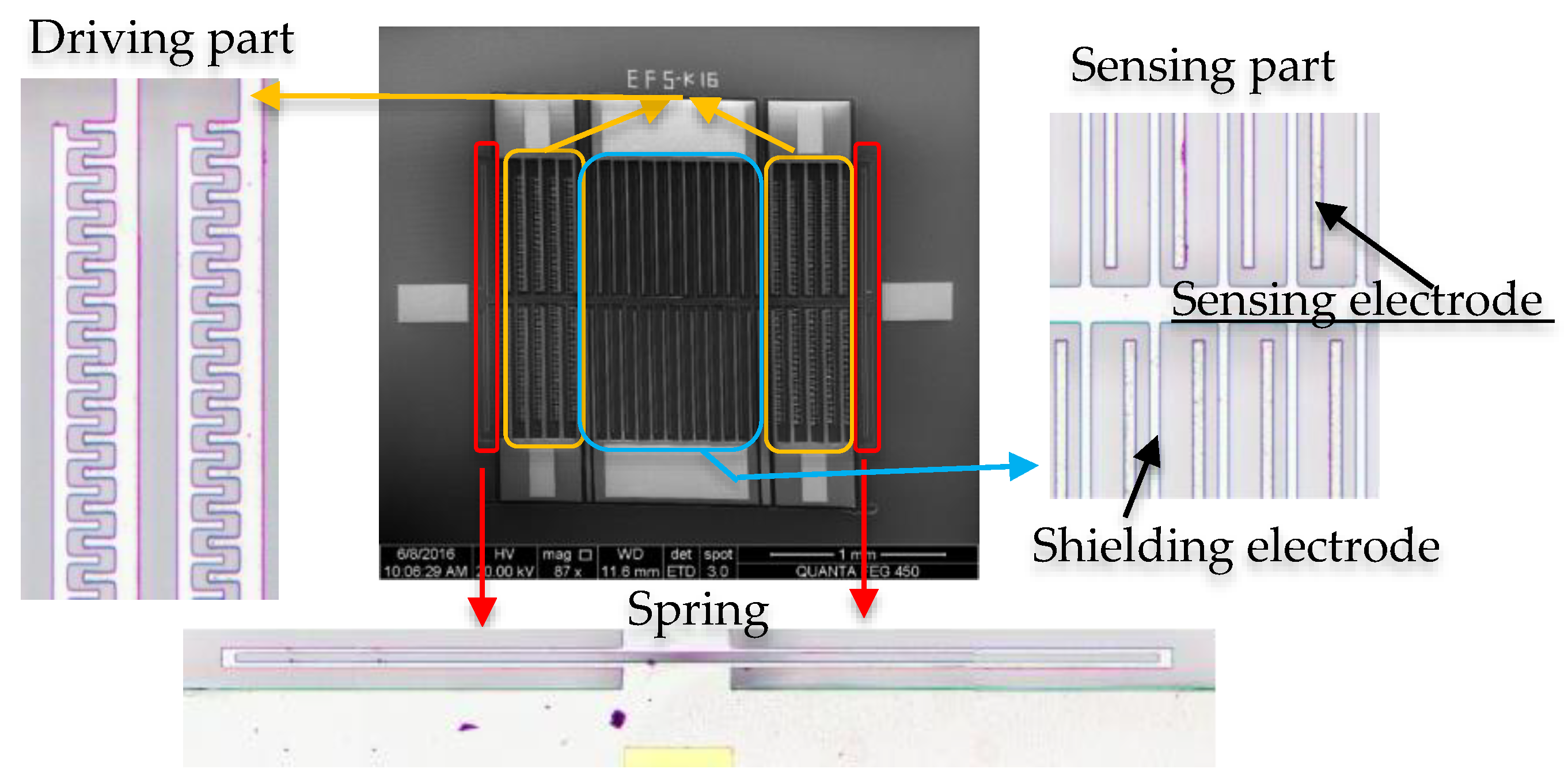
2.2. Driving Part
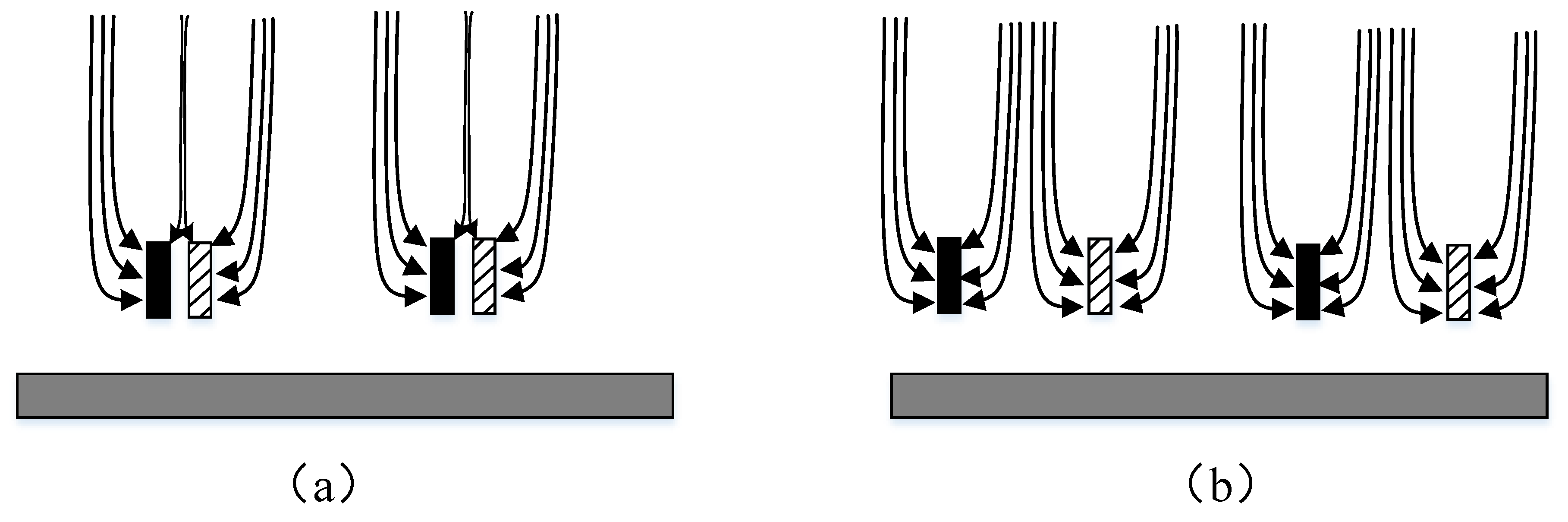
2.3. Sensing Part
2.4. Design and Fabrication
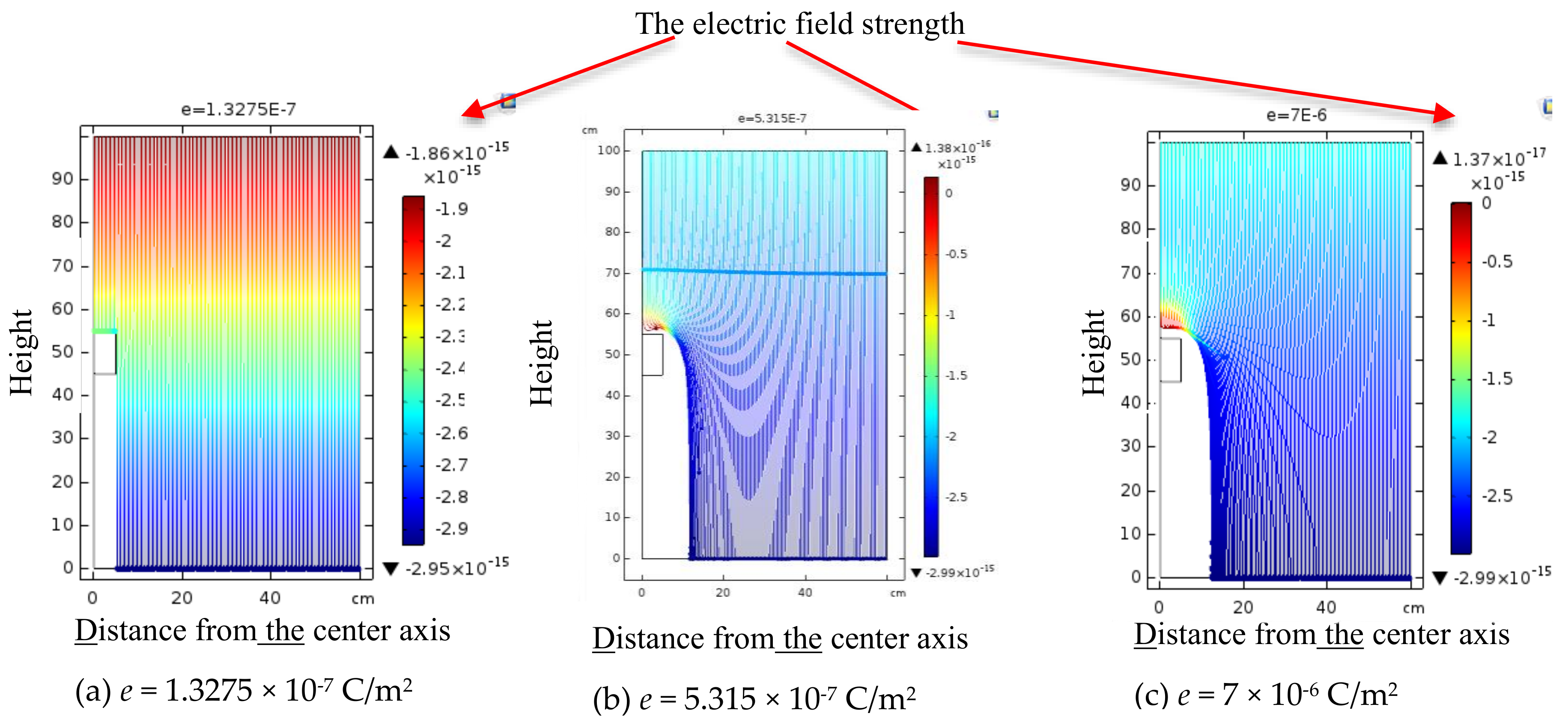
3. Modelling of Ion Flow
3.1. Description of the Sensor
3.2. Analysis of Space Electric Field Injected by Sensor
3.3. Modulation of a Sensor in an Ion Flow Field
- (1)
- The charge density around the sensor is set to a determined value.
- (2)
- The charged particles will move along the electric field lines in the electric field. With time, the particles accumulated on the surface of the package of the sensor will generate a reverse electric field to stop particles of the same polarity from falling on the surface. We assume the charging process completes when no additional particles reach the metal shell of the sensor.
3.4. Field Superposition Model
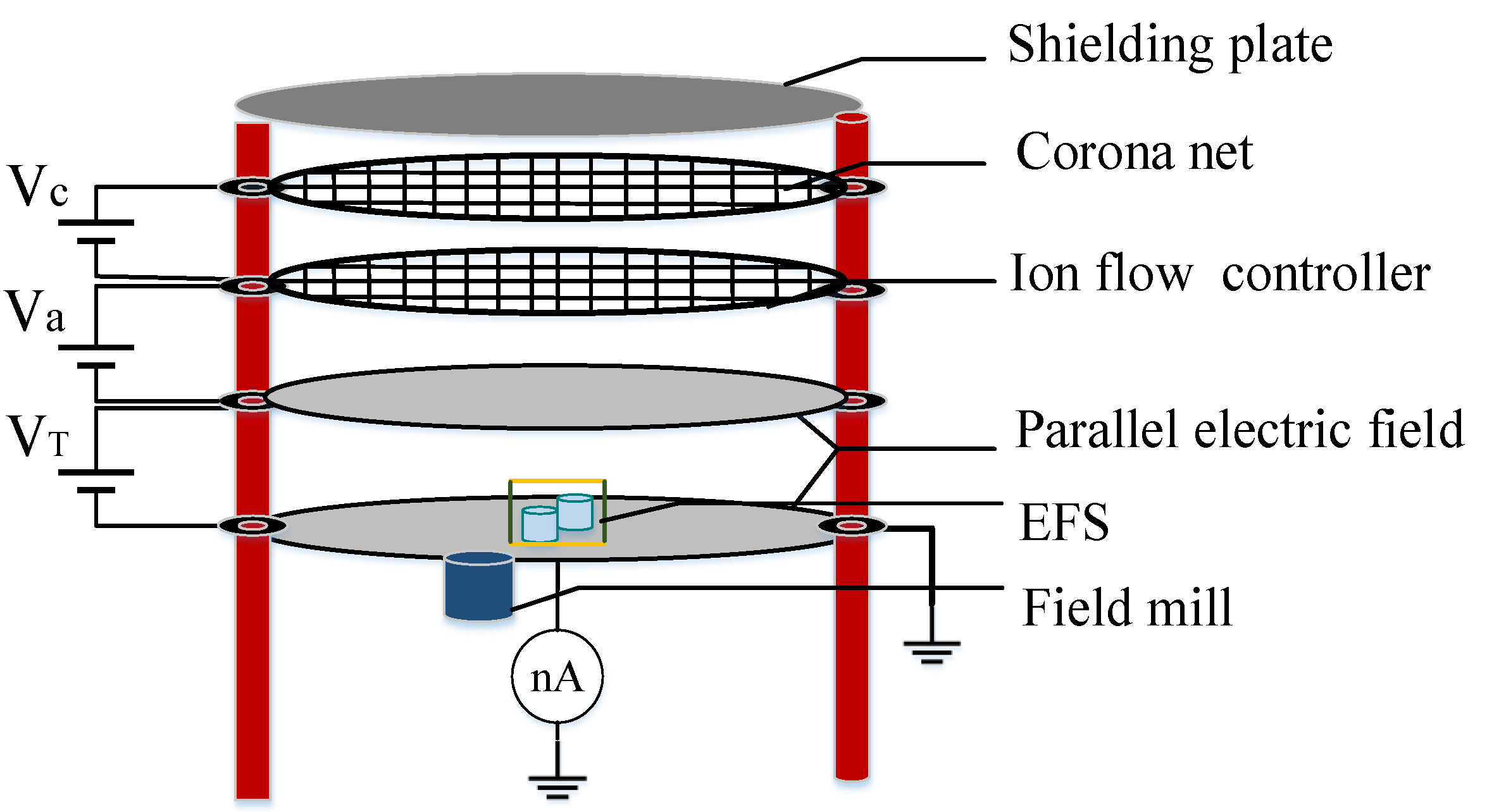
4. Calibration and Measurement in an Electric Ion Flow Field
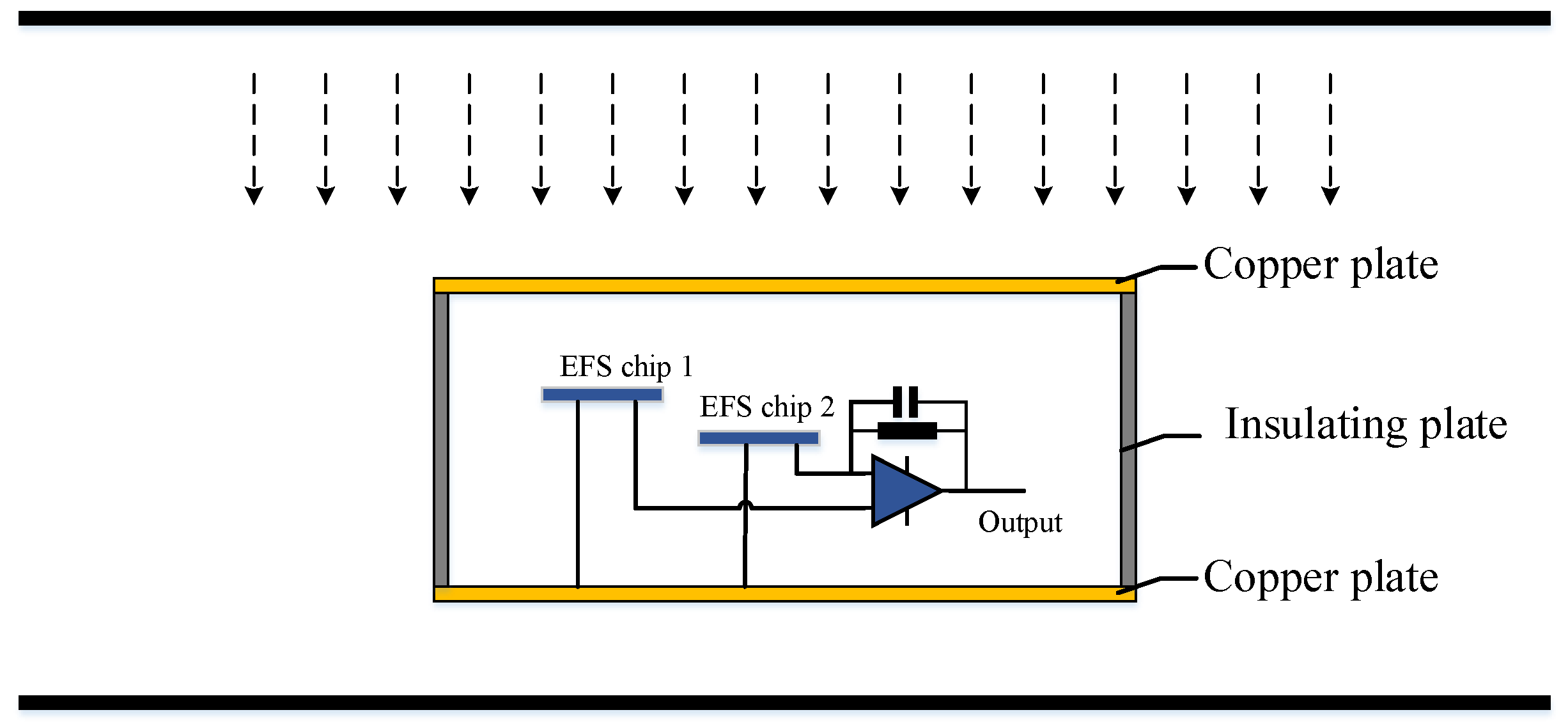
4.1. Introduction of the Parallel-Plate Ion Flow Generator
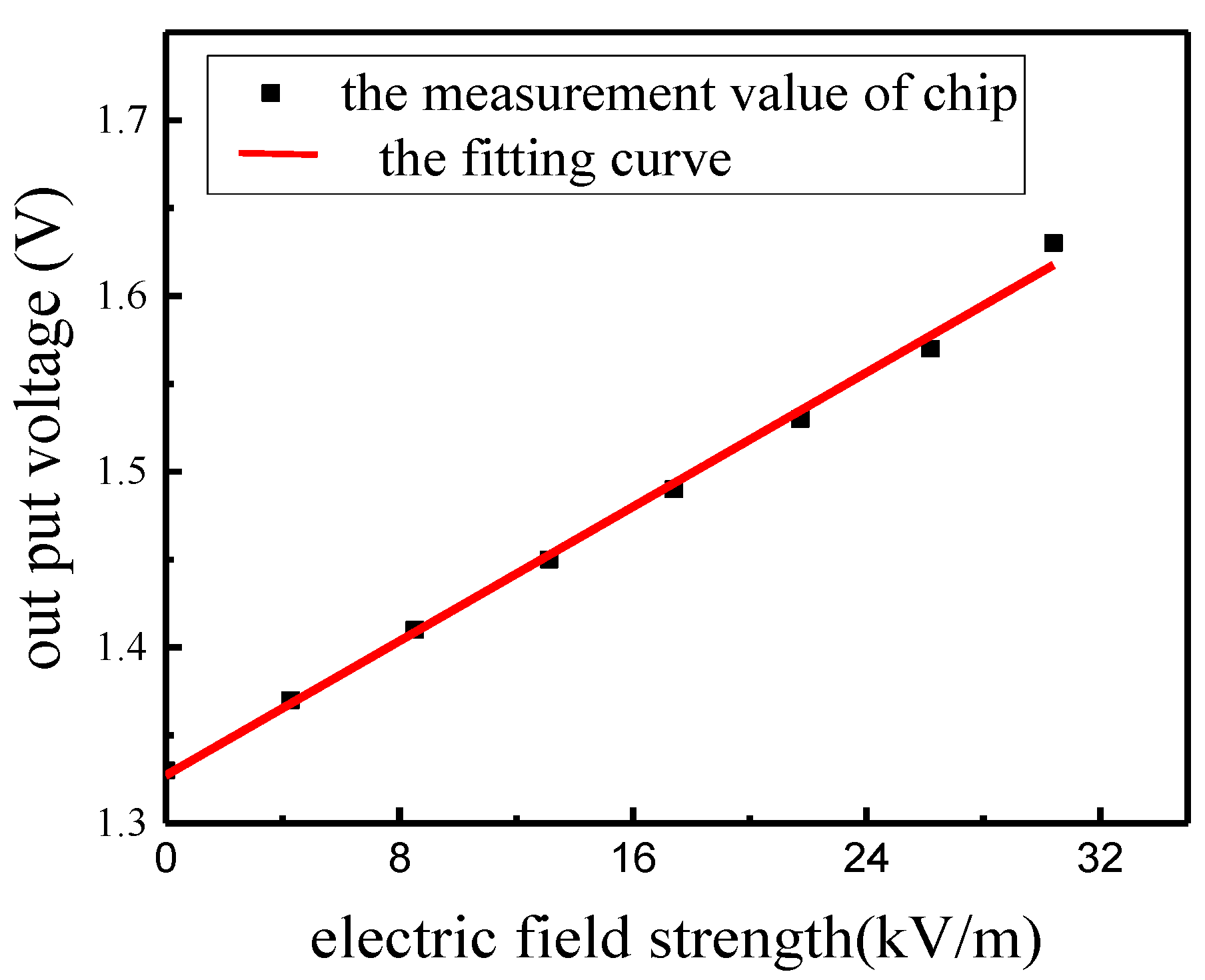
4.2. Measurements of Electrostatic Fields
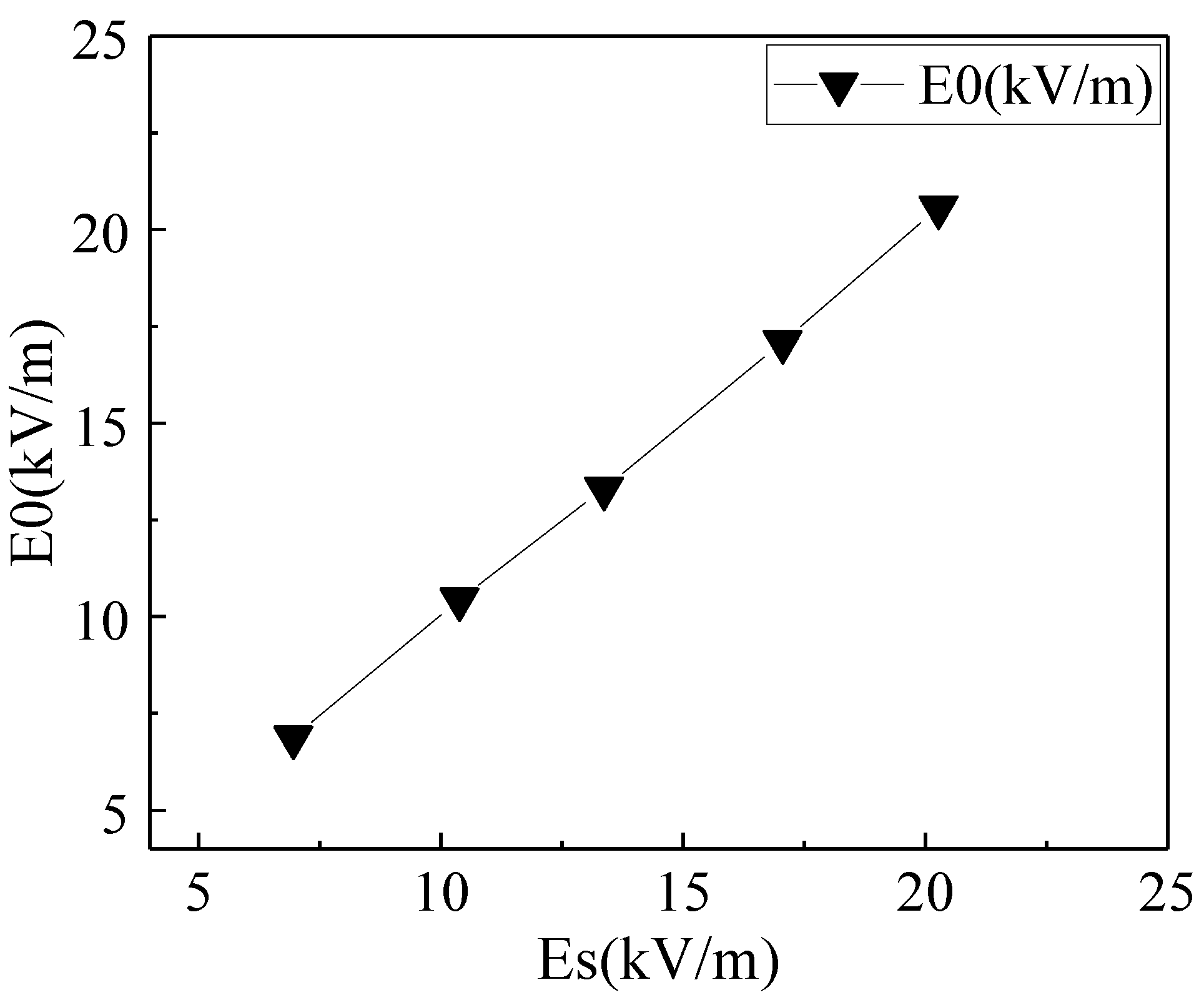
4.3. Calibration of the Electric Field in an Ion Flow Field
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, D.; Zhang, Z.; Jiang, X.; Shu, L.; Wu, B. Simulation Study on the Effects of DC Electric Field on Insulator Surface Pollution Deposit. Energies 2018, 11, 626. [Google Scholar] [CrossRef]
- Hidaka, K. Progress in Japan of space charge field measurement in gaseous dielectrics using a pockels sensor. IEEE Electr. Insul. Mag. 1996, 12, 17–28. [Google Scholar] [CrossRef]
- Cecelja, F.; Bordovsky, M.; Balachandran, W. Electro-optic sensor for measurement of DC fields in the presence of space charge. IEEE Trans. Instrum. Meas. 2002, 51, 282–286. [Google Scholar] [CrossRef]
- Xiao, F.; Zhang, B.; Mo, J.; He, J. Calculation of 3-D Ion Flow Field at the Crossing of HVDC Transmission Lines by Method of Characteristics. IEEE Trans. Power Deliv. 2017, 99, 1611–1619. [Google Scholar]
- Yin, H.; Zhang, B.; He, J.; Zeng, R.; Li, R. Time-domain finite volume method for ion-flow field analysis of bipolar high-voltage direct current transmission lines. IET Gener. Transm. Distrib. 2012, 6, 785–791. [Google Scholar] [CrossRef]
- Xiang, C.; Zhou, X.; Tiebing, L.U. Recent Progress in the Calculation Methods of Ion Flow Field of HVDC Transmission Lines. Proc. Chin. Soc. Electr. Eng. 2012, 32, 130–141. [Google Scholar]
- Tant, P.; Bolsens, B.; Sels, T.; Van Dommelen, D.; Driesen, J.; Belmans, R. Design and application of a field mill as a high-voltage DC meter. IEEE Trans. Instrum. Meas. 2007, 56, 1459–1464. [Google Scholar] [CrossRef]
- Liu, Z.; He, W.; Zhang, H.; Xia, S.; Xiao, B.; Xu, Y. Notice of Retraction Study on the Parameters of UHV DC Electric Field Meter. In Proceedings of the IEEE 2010 Asia-Pacific Power and Energy Engineering Conference (APPEEC), Chengdu, China, 28–31 March 2010. [Google Scholar]
- Hidaka, K. Electric field and voltage measurement by using electro-optic sensor. In Proceedings of the 11th International Symposium on High-Voltage Engineering (ISH 99), London, UK, 23–27 August 1999; Volume 2, pp. 1–14. [Google Scholar]
- Riehl, P.S.; Scott, K.L.; Muller, R.S.; Howe, R.T.; Yasaitis, J.A. Electrostatic charge and field sensors based on micromechanical resonators. J. Microelectromech. Syst. 2003, 12, 577–589. [Google Scholar] [CrossRef]
- Xue, F.; Hu, J.; Wang, S.X.; He, J. Electric Field Sensor Based on Piezoelectric Bending Effect for Wide Range Measurement. IEEE Trans. Ind. Electron. 2015, 62, 5730–5737. [Google Scholar] [CrossRef]
- Gong, C.; Tao, H.; Peng, C.; Bai, Q.; Chen, S.; Xia, S. A novel miniature interlacing vibrating electric field sensor. In Proceedings of the 2005 IEEE Sensors, Irvine, CA, USA, 30 October–3 November 2005; p. 3. [Google Scholar]
- Tang, W. Electrostatic Comb Drive for Resonant Sensor and Actuator Applications. D.S. Thesis, University of California Berkeley, Berkeley, CA, USA, 1990. [Google Scholar]
- Wijeweera, G.; Bahreyni, B.; Shafai, C.; Rajapakse, A.; Swatek, D.R. Micromachined Electric-Field Sensor to Measure AC and DC Fields in Power Systems. IEEE Trans. Power Deliv. 2009, 24, 988–995. [Google Scholar] [CrossRef]
- Ling, B.; Peng, C.; Ren, R.; Chu, Z.; Zhang, Z.; Lei, H.; Xia, S. Design, Fabrication and Characterization of a MEMS-Based Three-Dimensional Electric Field Sensor with Low Cross-Axis Coupling Interference. Sensors 2018, 18, 870–874. [Google Scholar] [CrossRef] [PubMed]
- Chu, Z.; Peng, C.; Ren, R.; Ling, B.; Zhang, Z.; Lei, H.; Xia, S. A High Sensitivity Electric Field Microsensor Based on Torsional Resonance. Sensors 2018, 18, 286. [Google Scholar] [CrossRef] [PubMed]
- Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V. A Ferroelectric-Capacitor-Based Approach to Quasistatic Electric Field Sensing. IEEE Trans. Instrum. Meas. 2010, 59, 641–652. [Google Scholar] [CrossRef]
- Kainz, A.; Steiner, H.; Schalko, J.; Jachimowicz, A.; Kohl, F.; Stifter, M.; Beigelbeck, R.; Keplinger, F.; Hortschitz, W. Distortion-free measurement of electric field strength with a MEMS sensor. Nat. Electron. 2018, 1, 68–73. [Google Scholar] [CrossRef] [PubMed]
- Kotzar, G.; Freas, M.; Abel, P.; Fleischman, A.; Roy, S.; Zorman, C.; Moran, J.M.; Melzak, J. Evaluation of MEMS materials of construction for implantable medical devices. Biomaterials 2002, 23, 2737–2750. [Google Scholar] [CrossRef]
- Grau, A.; Romeu, J.; Lee, M.J.; Blanch, S.; Jofre, L.; De Flaviis, F. A Dual-Linearly-Polarized MEMS-Reconfigurable Antenna for Narrowband MIMO Communication Systems. IEEE Trans. Antennas Propag. 2009, 58, 4–17. [Google Scholar] [CrossRef]
- Iannacci, J.; Huhn, M.; Tschoban, C.; Pötter, H. RF-MEMS Technology for 5G: Series and Shunt Attenuator Modules Demonstrated up to 110 GHz. IEEE Electron Device Lett. 2016, 37, 1336–1339. [Google Scholar] [CrossRef]
- Loconto, D.P. High-Sensitivity Micromechanical Electrostatic Voltmeter. Master’s Thesis, University of California, Berkeley, CA, USA, 1992. [Google Scholar]
- Peng, C.; Yang, P.; Zhang, H.; Guo, X.; Xia, S. Design of a SOI MEMS Resonant Electric Field Sensor for Power Engineering Applications. In Proceedings of the 2010 IEEE Sensors, Kona, HI, USA, 1–4 November 2010; Volume 143, pp. 1183–1186. [Google Scholar]
- Ji, Y. Measurement of Air Ion Mobility and Analysis of Its Impact Factors. Master’s Thesis, Tsinghua University, Beijing, China, 2013. [Google Scholar]
- Ma, Q.; Huang, K.; Yu, Z.; Wang, Z. A MEMS-Based Electric Field Sensor for Measurement of High-Voltage DC Synthetic Fields in Air. IEEE Sens. J. 2017, 17, 7866–7876. [Google Scholar] [CrossRef]
- Misakian, M. Generation and measurement of dc electric fields with space charge. J. Appl. Phys. 1998, 52, 3135–3144. [Google Scholar] [CrossRef]
- Zhang, B.; He, J.; Ji, Y. Dependence of the average mobility of ions in air with pressure and humidity. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 923–929. [Google Scholar] [CrossRef]


| Properties | Field Mill [7,8] | MEMS Sensor [14] | Distortion-Free Probe [16] | In This Paper Differential EFS |
|---|---|---|---|---|
| Schematic Diagram | 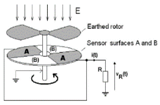 | 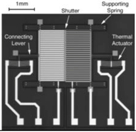 | 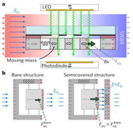 | 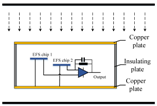 |
| Distortion | large | small | small | large |
| Measures of ion flow | Yes | No | No | Yes |
| Grounding | Yes | No | No | No |
| Cost | low | low | high | low |
| Spatial electric filed in ion flow measurement | No | No | No | Yes |
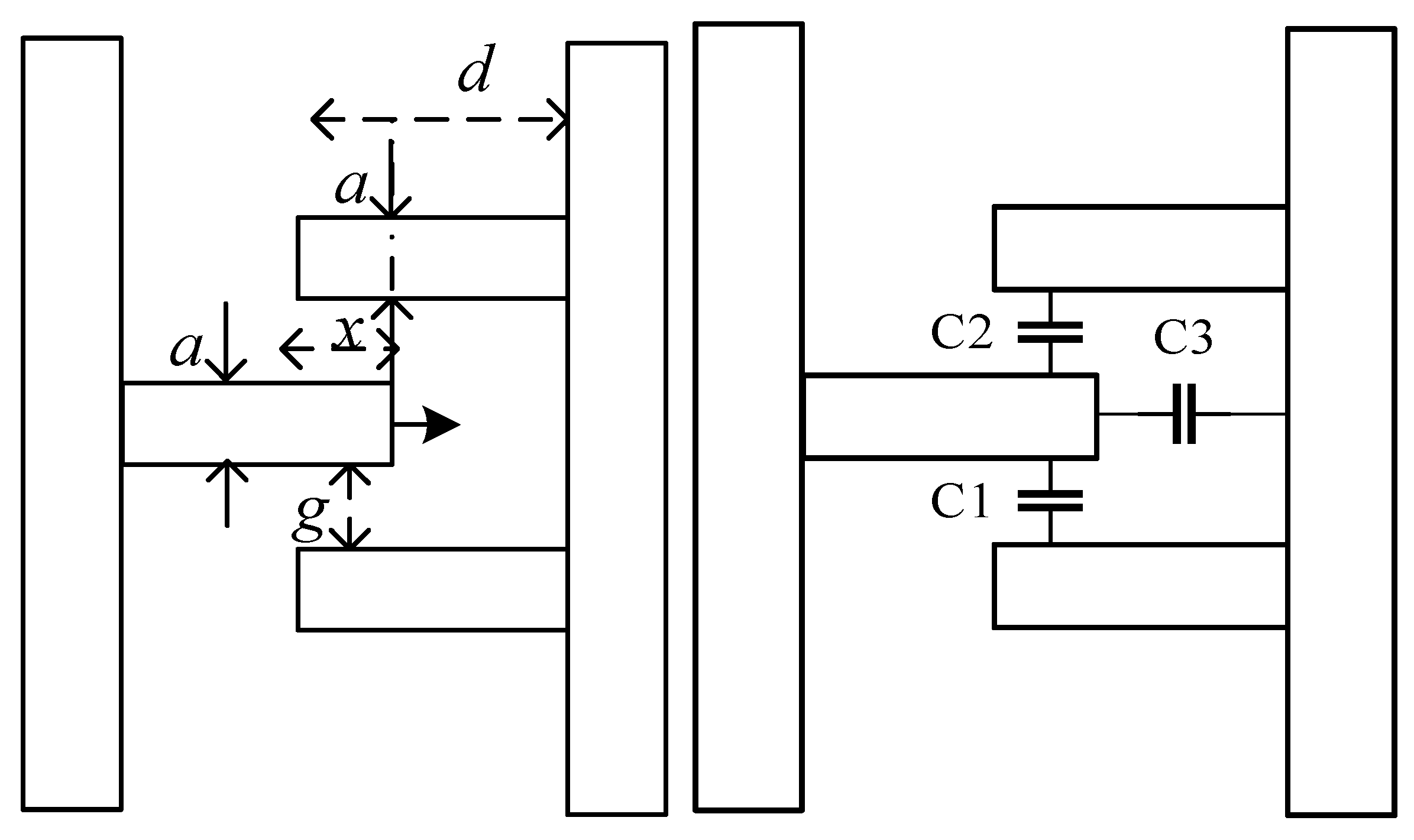
| The width of the shielding electrode | 10 μm | a (as shown in Figure 3) | 5 μm |
| The length of the shielding electrode | 900 μm | d (as shown in Figure 3) | 12 μm |
| The width of the sensing electrode | 10 μm | g (as shown in Figure 3) | 5 μm |
| The width of the sensing electrode | 900 μm | The number of driving electrodes | 250 |
| The gap between the adjacent sensing and shielding electrodes | 15 μm | The thickness of the device layer | 20 μm |
| The number of sensing electrodes | 50 |
| VT (kV) | I (nA) | En (kV/m) | Es (kV/m) | Ein1 (kV/m) | Ein2 (kV/m) | λ |
|---|---|---|---|---|---|---|
| 0.63 | 1.3 | 5.31 | 3.478 | 8.66 | 6.56 | 1.861 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, Y.; Yu, Z.; Huang, K.; Ma, Q.; Zeng, R.; Wang, Z. Research on a Novel MEMS Sensor for Spatial DC Electric Field Measurements in an Ion Flows Field. Sensors 2018, 18, 1740. https://doi.org/10.3390/s18061740
Mou Y, Yu Z, Huang K, Ma Q, Zeng R, Wang Z. Research on a Novel MEMS Sensor for Spatial DC Electric Field Measurements in an Ion Flows Field. Sensors. 2018; 18(6):1740. https://doi.org/10.3390/s18061740
Chicago/Turabian StyleMou, Ya, Zhanqing Yu, Kaitian Huang, Qing Ma, Rong Zeng, and Zheyao Wang. 2018. "Research on a Novel MEMS Sensor for Spatial DC Electric Field Measurements in an Ion Flows Field" Sensors 18, no. 6: 1740. https://doi.org/10.3390/s18061740
APA StyleMou, Y., Yu, Z., Huang, K., Ma, Q., Zeng, R., & Wang, Z. (2018). Research on a Novel MEMS Sensor for Spatial DC Electric Field Measurements in an Ion Flows Field. Sensors, 18(6), 1740. https://doi.org/10.3390/s18061740




