Energy Efficient GNSS Signal Acquisition Using Singular Value Decomposition (SVD)
Abstract
1. Introduction
2. Theoretical of Compressed Sensing
The Design of SVD-C-GNSS
- Improve acquisition performance of the GNSS signal by using a compressive sensing algorithm based on minimization with non-restrictive isometric property RIP analysis. This method will allow finding the best anti-noise performance measurement matrix, given that it is not restricted to random Gaussian or random Bernoulli measurement matrices.
- Develop a robust method for situations in which the receiver needs broader bandwidth to handle all types of navigation positioning signals using the non-RIP approach to compressive sensing which means the use of prior information to improve the acquisition stage.
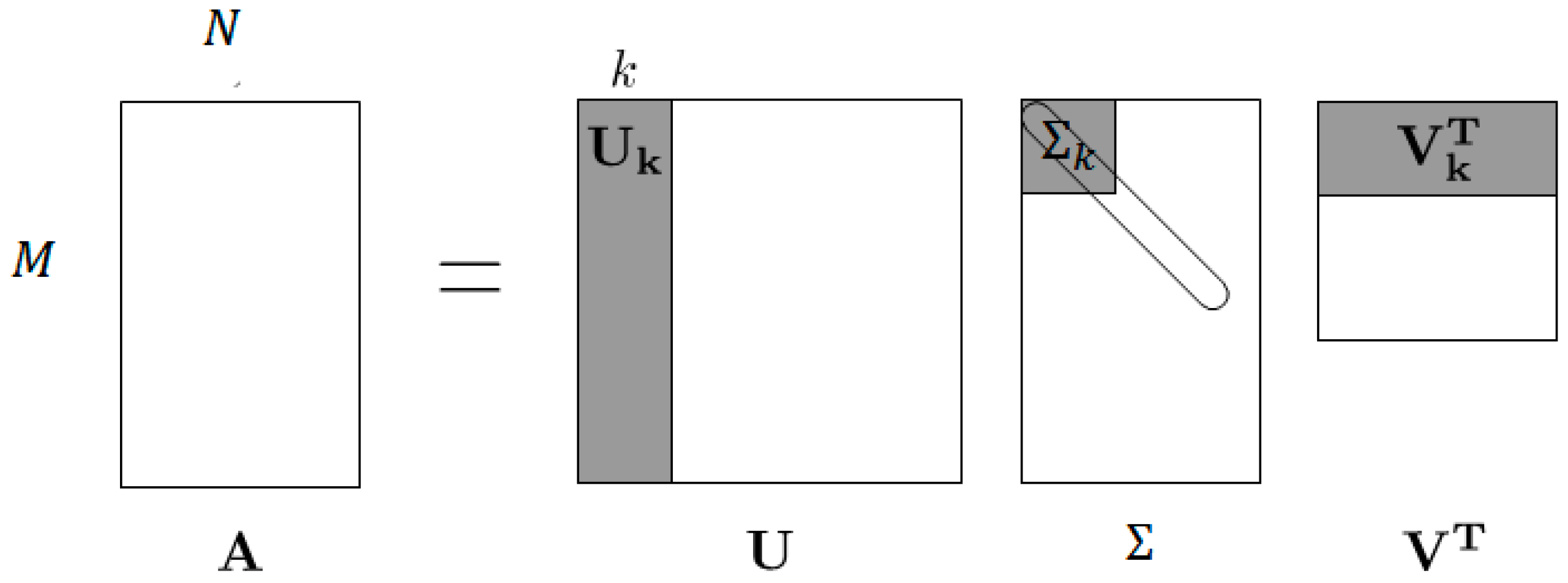
3. Singular Value Decomposition (SVD)
3.1. Theorem 1
- Compute .
- Keep only the top right singular vectors: set equal to the rows of (a matrix).
- Keep only the top left singular vectors: set equal to the first columns of U (an matrix).
- Keep only the top k singular values: set equal to the first rows and columns of (a matrix), corresponding to the largest singular values of .
3.2. SVD Properties
3.2.1. Energy Packaging
3.2.2. Noise Filtering
3.3. Sensing
3.4. GNSS SVD Compressed Sensing Scheme
3.5. Proper Orthogonal Modes (POD)
3.6. Algorithm
| Algorithm 1. Compressive sensing GNSS-SVD-C. |
| Input: |
| Measurements are segmented into vector of length |
Steps
|
| Return: Once is computed, the original signal is decoded by computing for each one of the buckets or windows compressed on step 7. By using the proposed method, only a small set of measurements is required to recover the vector . |
4. Simulation and Performance
4.1. Performance Metrics
4.1.1. Signal to Noise Ratio (SNR)
4.1.2. Computational Complexity
4.1.3. Acquisition Time
4.1.4. Probability of Detection (Pd) and Probability of False Alarm (Pfa)
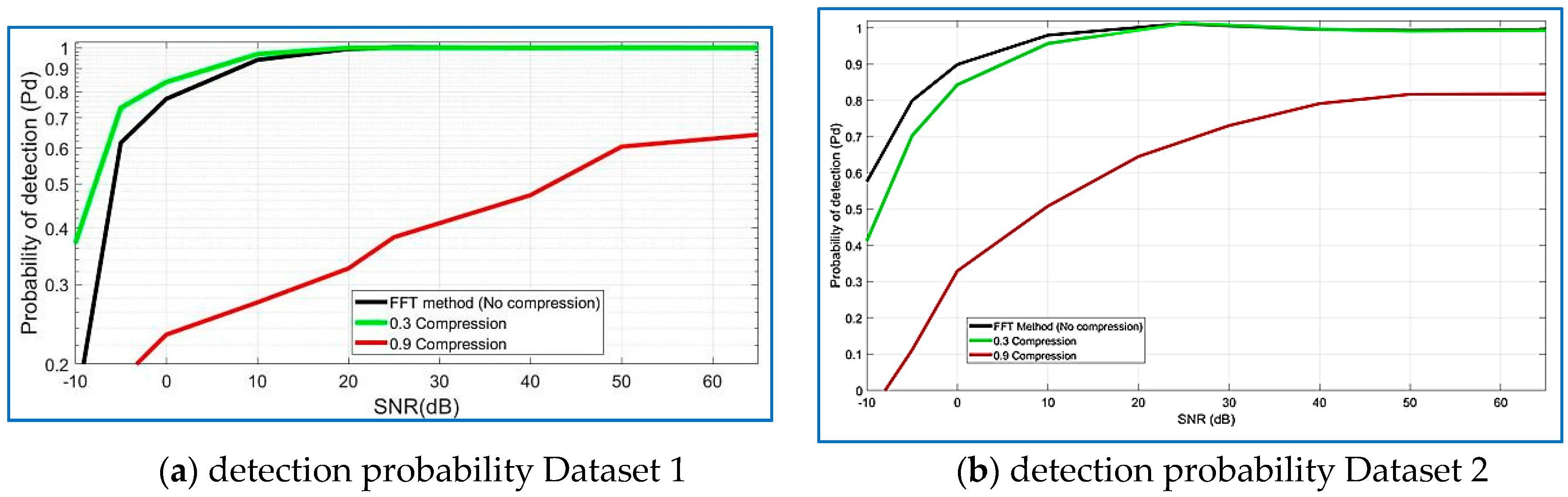
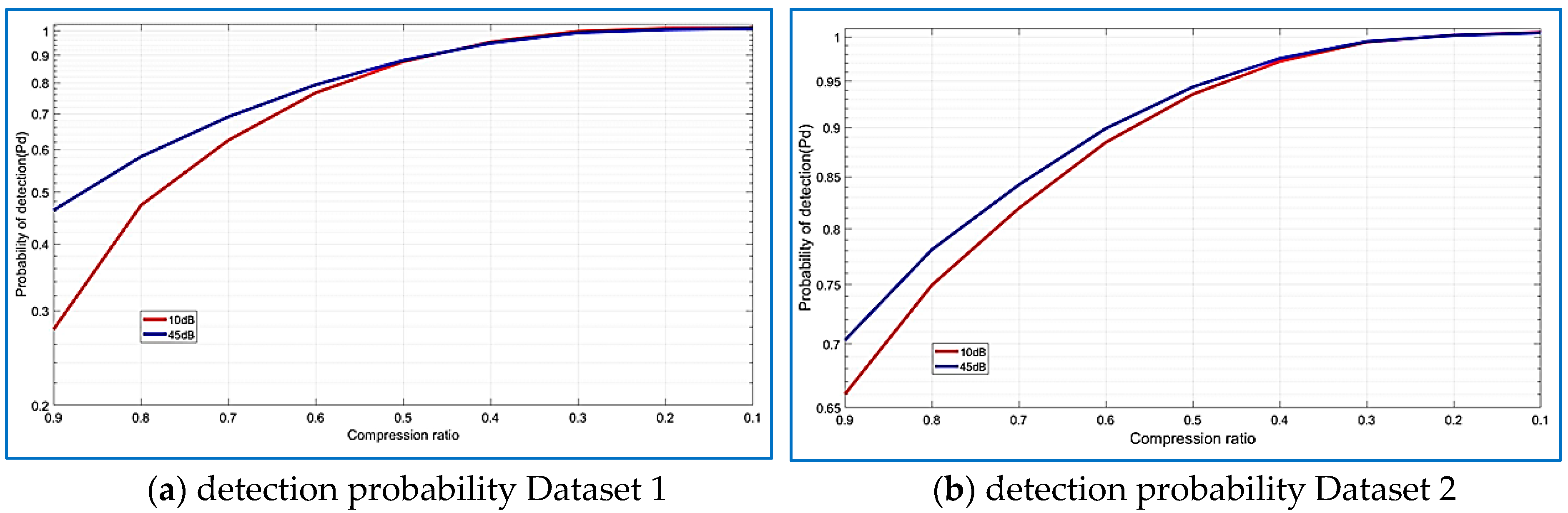
5. Numerical Results
5.1. Datasets
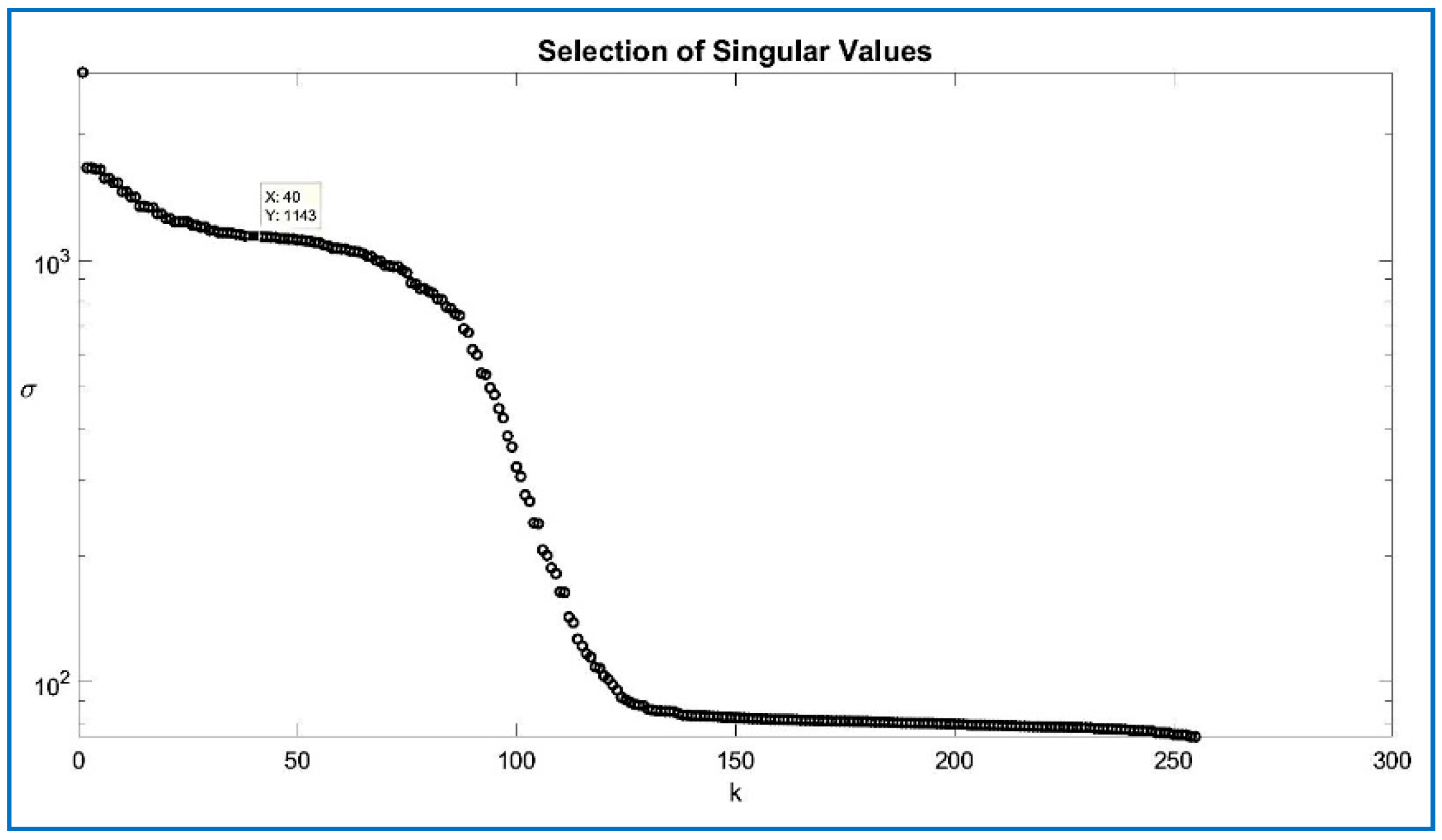
5.2. Compression Performance
6. Conclusions and Future Scope
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Diggelen, F.S.T. A-GPS: Assisted GPS, GNSS, and SBAS; Artech House: Norwood, RI, USA, 2009. [Google Scholar]
- Won, J.-H.; Dötterböck, D.; Eissfeller, B. Performance Comparison of Different Forms of Kalman Filter Approaches for a Vector-Based GNSS Signal Tracking Loop. Navigation 2010, 57, 185–199. [Google Scholar] [CrossRef]
- Downing, B.H. A Method for Comparing the Code Tracking Performance of GNSS Receivers. In Proceedings of the Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 25–28 January 2016. [Google Scholar]
- Panny, T.; Gohler, E.; Irsigler, M.; Winkel, J. On the State-of-the-Art of Real-Timer GNSS Signal Acquisition—A Comparison of Time and Frequency Domain Methods; IEEE: Zurich, Switzerland, 2010; ISBN 978-4244-5864-6/10. [Google Scholar]
- Borre, K.; Akos, D.; Bertelsen, N.; Rinder, P.; Jensen, S. A Software-Defined GPS and Galileo Receiver. A Single-Frequency Approach; Birkhauser: Basel, Switzerland, 2006; ISBN 0-8176-4390-7. [Google Scholar]
- Grewal, M.S.; Andrews, A.P.; Bartone, C.G. Global Navigation Satellite Systems, Inertial Navigation, and Integration, 3rd ed.; John Wiley & Sons: Somerset, NJ, USA, 2013; Available online: http://www.ebrary.com (accessed on 1 February 2018).
- GPS_Signals. Available online: https://en.wikipedia.org/wiki/GPS_signals (accessed on 1 February 2018).
- Fernández-Prades, C.; Arribas, J.; Esteve-Elfau, L.; Pubill, D.; Closas, P. An Open Source Galileo E1 Software Receiver. In Proceedings of the 6th ESA Workshop on Satellite Navigation Technologies (NAVITEC 2012), Noordwijk, The Netherlands, 5–7 December 2012. [Google Scholar]
- European Space Agency (ESA). 16 August 2007. Available online: http://www.esa.int/Our_Activities/Navigation/Galileo/Galileo_navigation_signals_and_frequencies (accessed on 19 March 2018).
- Miralles, D.; Teixeira, M. Development of a Simulink Library for the Design, Development, Testing and Simulation of Software Define GPS Radios; Polytechnic University of Puerto Rico: Hato Rey, Puerto Rico, 2014. [Google Scholar]
- Katabi, H.H.F.A.D.; Indyk, P. Faster GPS via the Sparse Fourier Transform; MobiCom: Istanbul, Turkey, 2012; ISBN 978-1-4503-1159-5. [Google Scholar]
- Tsui, J. Fundamentals of Global Positioning System Receivers: A Software Approach; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Wireless Infrastructure Calculating-Time-First-Fix. GPS World. Calculating Time-to-First. Available online: http://gpsworld.com/wirelessinfrastructurecalculating-time-first-fix-12258/ (accessed on 15 April 2018).
- Deshpande, S.; Cannon, M.E. Analysis of the Effect of GPS Receiver Acquisition Parameters. In Proceedings of the ION GNSS 2004, Long Beach, CA, USA, 21–24 September 2004. [Google Scholar]
- Peterson, R.L.; Ziemer, R.E.; Borth, D.E. Introduction to Spread Spectrum Communications; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Chang, C.L. Modified Compressive Sensing Approach for GNSS Signal Reception in the Presence of Interference. In GPS Solutions; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–13. ISBN 1080-5370. [Google Scholar]
- Rao, M.V.G.; Ratnam, D.V. Faster Acquisition Technique for Software defined GPS Receivers. Def. Sci. J. 2015, 65, 5–11. [Google Scholar] [CrossRef][Green Version]
- Fortin, M.A.; Landry, R. Implementation Strategies for a Universal Acquisition and Tracking Channel Applied to Real GNSS Signals. Sensors 2016, 16, 624. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. For most large underdetermined systems of linear equations the minimal ℓ1-norm solution is also the sparsest solution. Commun. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Viterbi, A.J. CDMA Principles of Spread Spectrum Communication; Addison-Wesley: Redwood City, CA, USA, 1995. [Google Scholar]
- Li, X.; Rueetschi, A.; Eldar, Y.C.; Scaglione, A. GPS signal acquisition via compressive multichannel sampling. Phys. Commun. 2012, 5, 173–184. [Google Scholar] [CrossRef]
- Kong, S.-H. A Compressed Sensing Technique for GNSS Acquisition; The Institute of Navigation: Newport Beach, CA, USA, 2012; pp. 356–361. [Google Scholar]
- Ou, S.; Li, J.; Sun, J.; Zeng, D.; Li, J.; Yan, Y. A GNSS Signal Acquisition Scheme Based on Compressed Sensing. In Proceedings of the ION 2015 Pacific PNT Meeting, Honolulu, HI, USA, 20–23 April 2015; pp. 618–628. [Google Scholar]
- Zhang, Y. Theory of Compressive Sensing via L1-Minimization: A Non-RIP Analysis and Extensions; Rice CAAM Department: Houston, TX, USA, 2008. [Google Scholar]
- Bertoni, N.; Senevirathna, B.; Pareschi, F.; Mangia, M.; Rovatti, R.; Abshire, P.; Simon, J.Z. Low-power EEG monitor based on Compressed Sensing with Compressed Domain Noise Rejection. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 522–525, ISBN 978-1-4799-5341-7/16. [Google Scholar]
- Godsoe, D. A Real-Time Software GNSS; University of New Brunswick: Fredericton, NB, Canada, 2010. [Google Scholar]
- Optimized FFT Algorithm and Its Application to Fast Gps. Available online: https://pdfs.semanticscholar.org/d472/3bdc6df62a7be02eca2b0c6193b28e81e5c8.pdf (accessed on 15 April 2018).
- Roughgarden, T.; Valiant, G. The Modern Algorithm Toolbox Lecture 9: The Singular Value Decomposition (SVD) and Low-Rank Matrix Approximations. 2015. Available online: http://theory.stanford.edu/~tim/s15/l/l9.pdf (accessed on 18 April 2018).
- Sadek, R.A. SVD based image processing applications: State of the art, contributions and research challenges. Int. J. Adv. Comput. Sci. Appl. 2012, 3, 26–34. [Google Scholar]
- Misra, P.; Hu, W.; Yang, M.; Jha, S. Efficient Cross-Correlation via Sparse Representation in Sensor Networks; The University of New South Wales: Sydney, Australia, 2012. [Google Scholar]
- Baraniuk, R.; Davenport, M. An Introduction to Compressive Sensing; OpenStax-CNX: Houston, TX, USA, 2011. [Google Scholar]
- Candes, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Cattel, R.B. The scree test for the number of factors. Multivar. Behav. Res. 1996, 1, 613–627. [Google Scholar] [CrossRef] [PubMed]
- Mattingley, J.; Boyd, S. Real-Time Convex Optimization in Signal Processing. IEEE Signal Process. Mag. 2010, 27, 50–61. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.0 Beta. Available online: http://cvxr.com/cvx (accessed on 18 April 2018).
- Grant, B.M.; Boyd, S.P. Graph implementations for non-smooth convex programs. In Recent Advances in Learning and Control; Boyd, S., Kimura, H., Blondel, V., Eds.; Lecture Notes in Control and Information Sciences; Springer: London, UK, 2008; pp. 95–110. Available online: https://web.stanford.edu/~boyd/papers/pdf/graph_dcp.pdf (accessed on 18 April 2018).
- Misra, P.; Hu, W.; Jin, Y.; Liu, J.; de Paula, A.S.; Wirström, N.; Voigt, T. Energy efficient GPS acquisition with Sparse-GPS. In Proceedings of the 13th International Symposium on Information Processing in Sensor Networks, Berlin, Germany, 15–17 April 2014; pp. 155–166. [Google Scholar] [CrossRef]
- Holmes, J.K.; Morgan, N.; Dafesh, P. A Theoretical Approach to Determining the 95% Probability of TTFF for the P(Y) Code Utilizing Active Code Acquisition. In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS), Fort Worth, TX, USA, 26–29 September 2006. [Google Scholar]
- Anghileri, M.; Paonini, M.; Wallner, S.; Avila, J.; Eissfeller, B. Ready to navigate a methodology of the estimation of the time-to-first-fix. Inside GNSS Mag. 2016, 5, 47–56. [Google Scholar]
- Lowe, S. Voltage Signal-to-Noise Ratio SNR Nonlinearity Resulting from Incoherent Summations; JPL-NASA: La Cañada Flintridge, CA, USA, 1999. [Google Scholar]
- Miralles, D.; Ortiz, M.; Sandoval, J.; Teixeira, M. Software Defined GPS API: Development and Implementation of GPS Correlator Architectures Using MATLAB with Focus on SDR Implementations; Polytechnic University of Puerto Rico: San Juan, Puerto Rico, 2014. [Google Scholar]
- Breed, P. Unreasonable Rocket. 6 February 2016. Available online: http://unreasonablerocket.blogspot.ca/ (accessed on 23 January 2018).
- Hahn, P. Software Define GPS. 5 July 2016. Available online: http://sdrgps.blogspot.ca/2016/07/paul-breed-rocket-test-flight-data-4.html (accessed on 23 January 2018).
- Wall, M.E.; Rechtsteiner, A.; Rocha, L.M. Singular Value Decomposition and Principal Component Analysis. 2002. Available online: http://public.lanl.gov/mewall/kluwer2002.html (accessed on 1 February 2018).
- Thomas, S. Removing noise in biomedical signal recordings by singular value decomposition. Curr. Dir. Biomed. Eng. 2017, 3, 253–256. [Google Scholar]
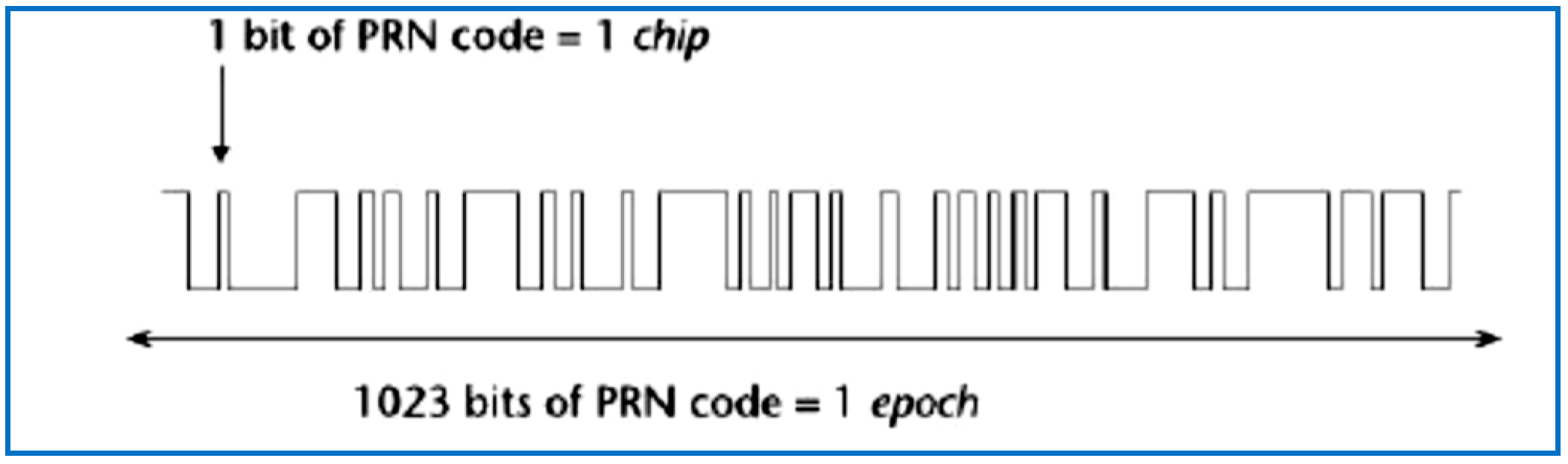
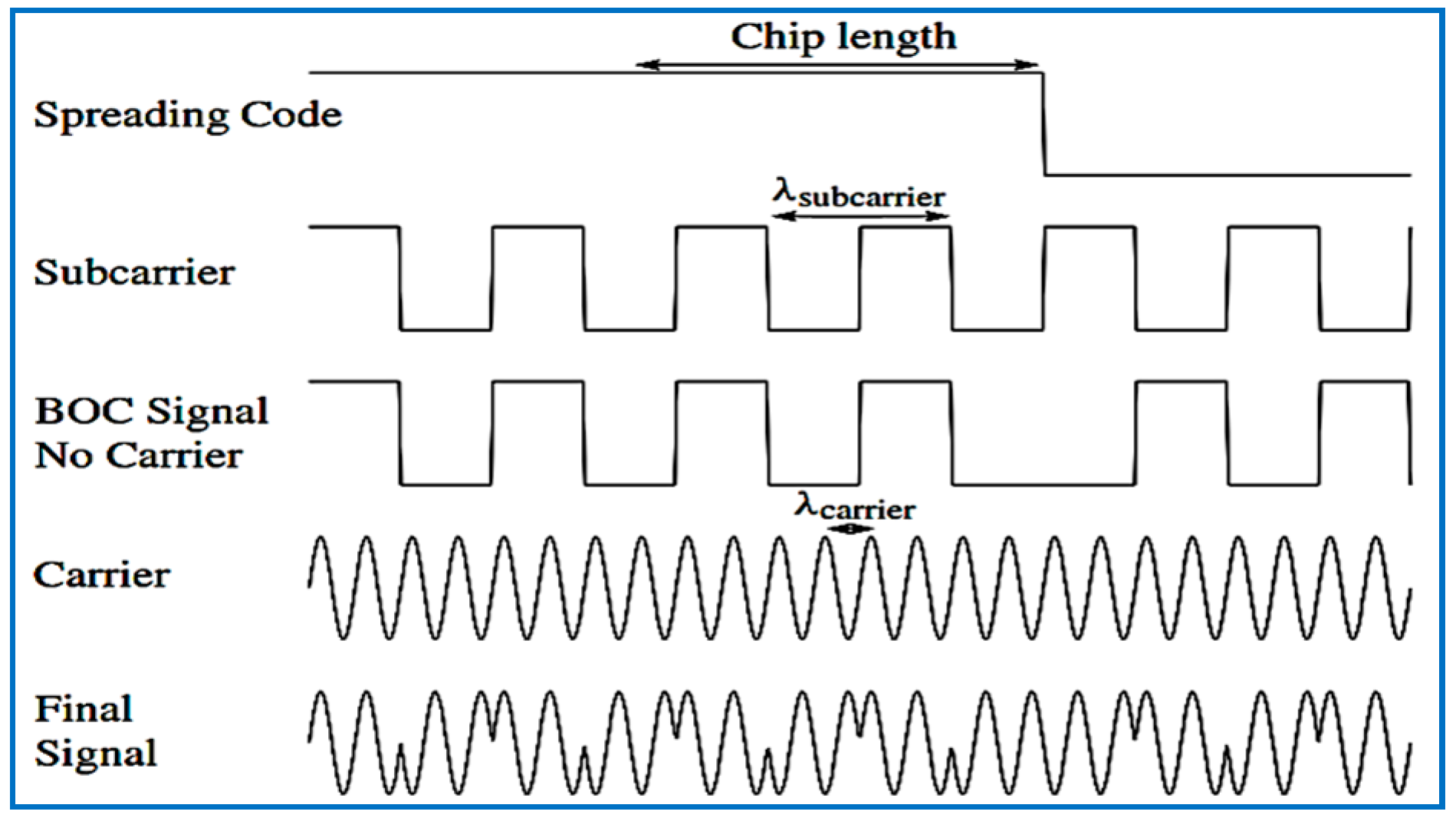
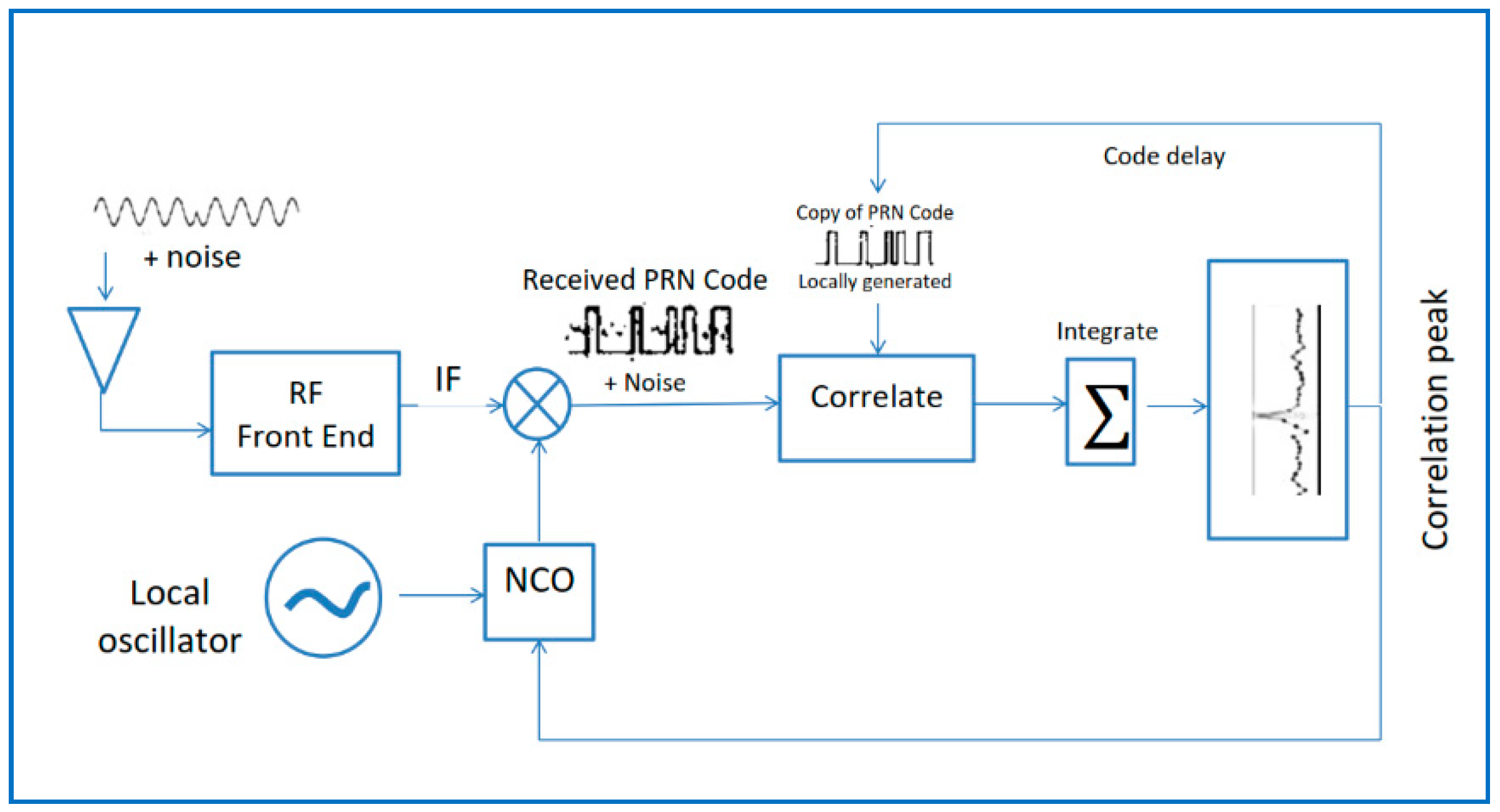
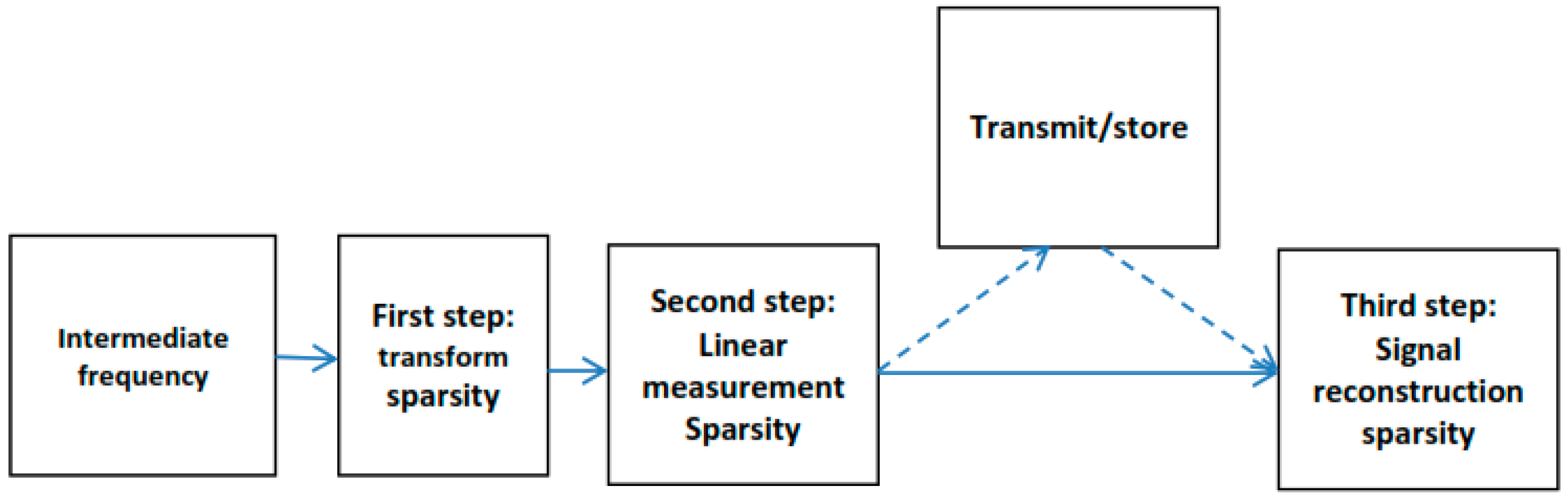
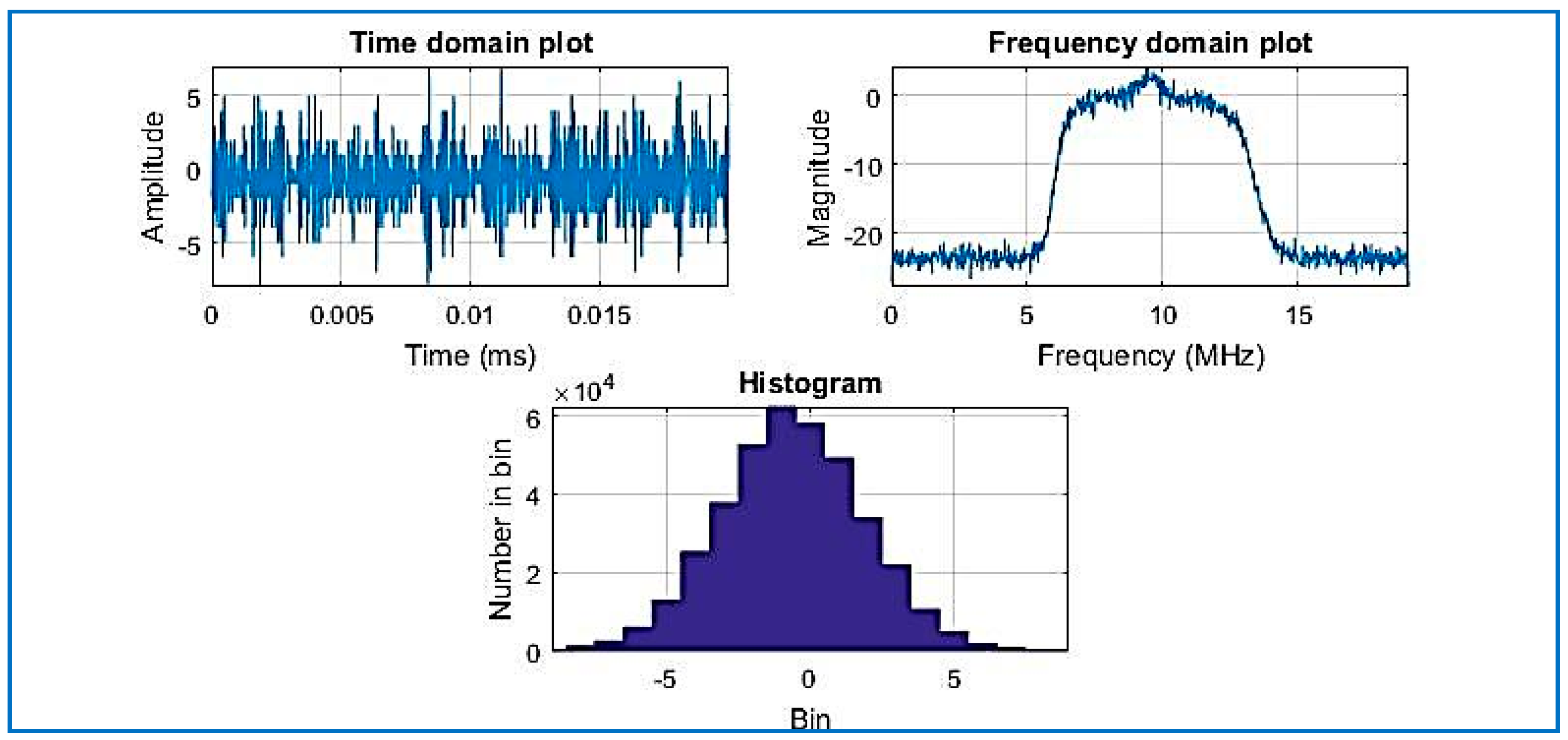
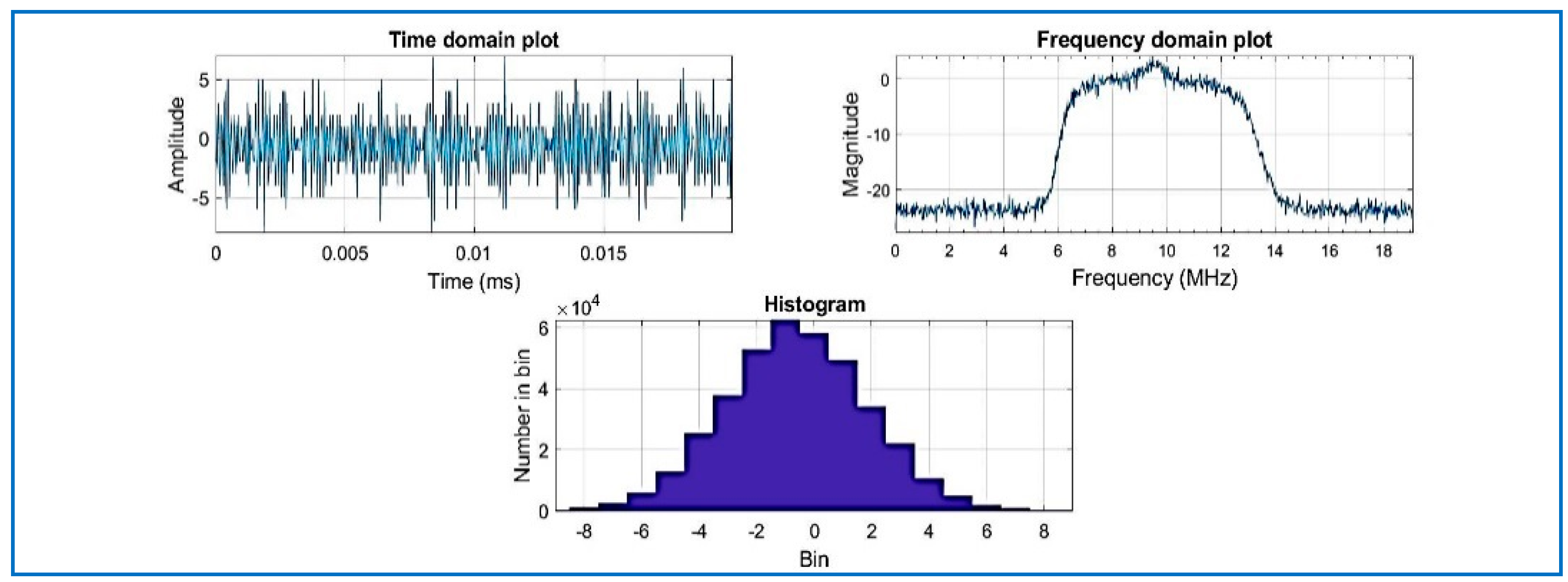
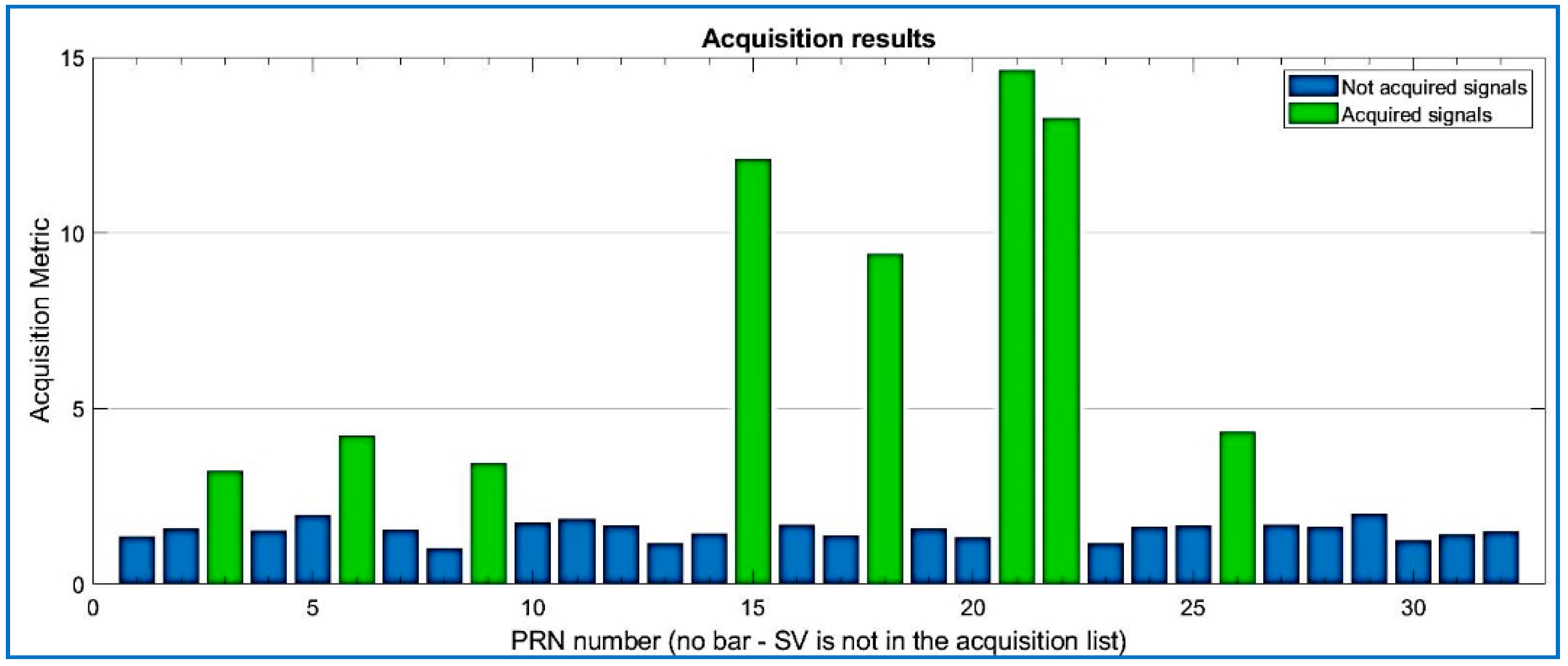
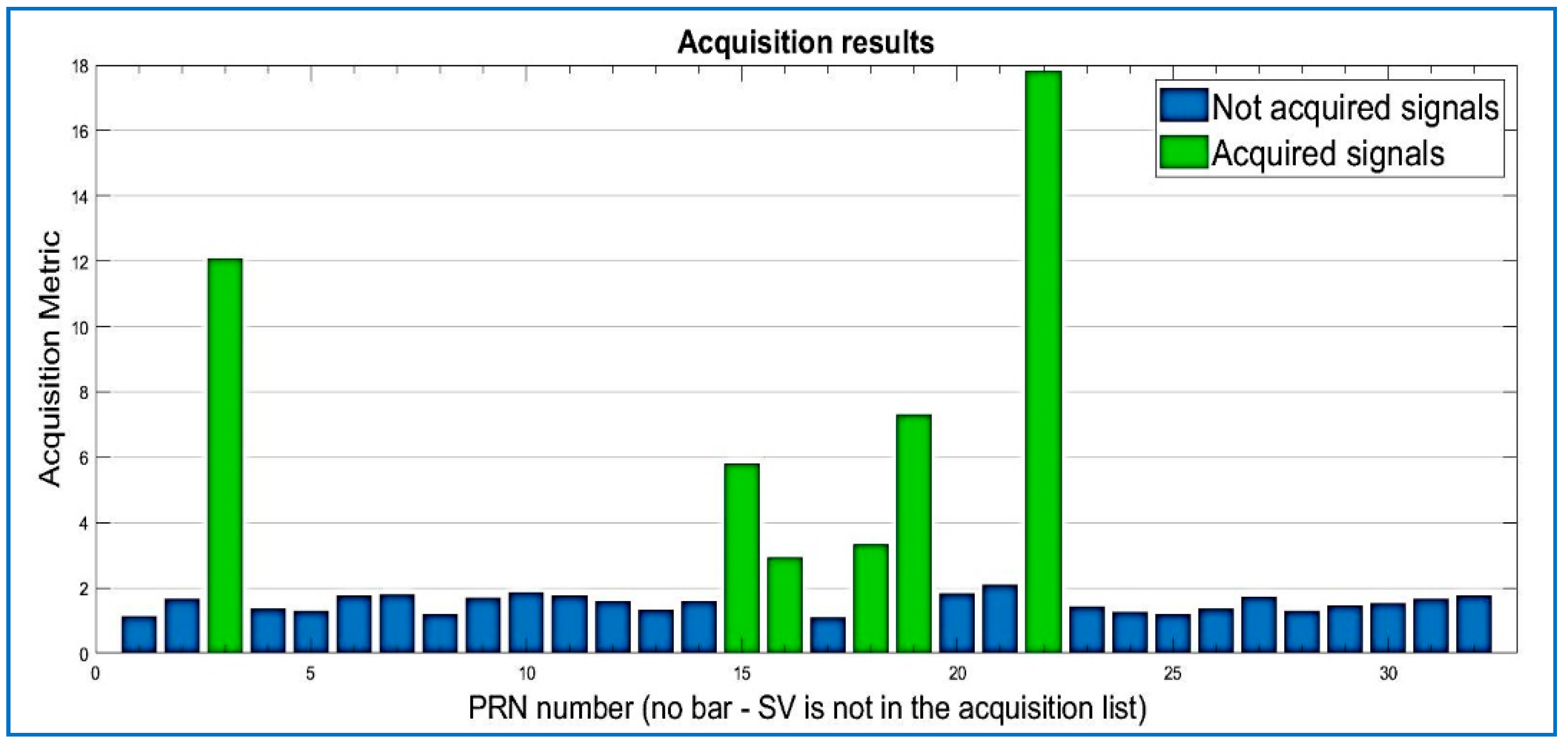
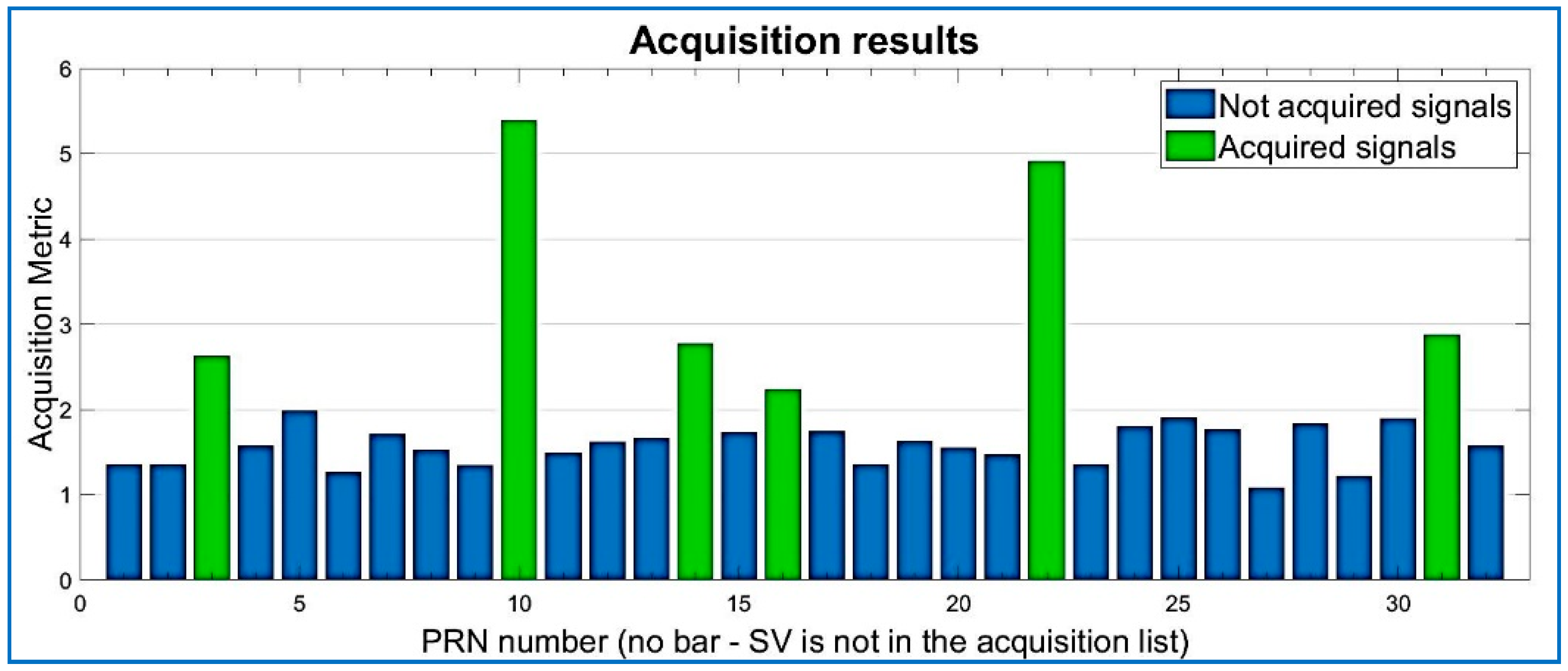
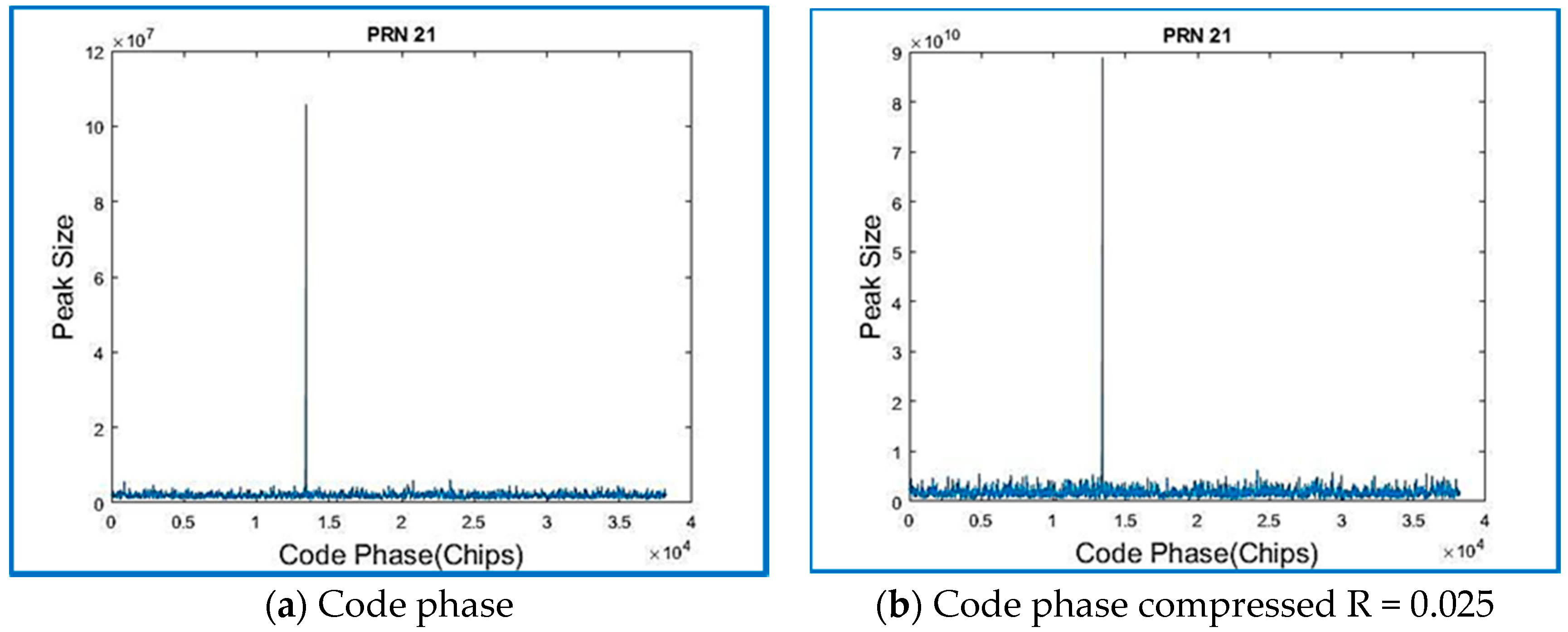
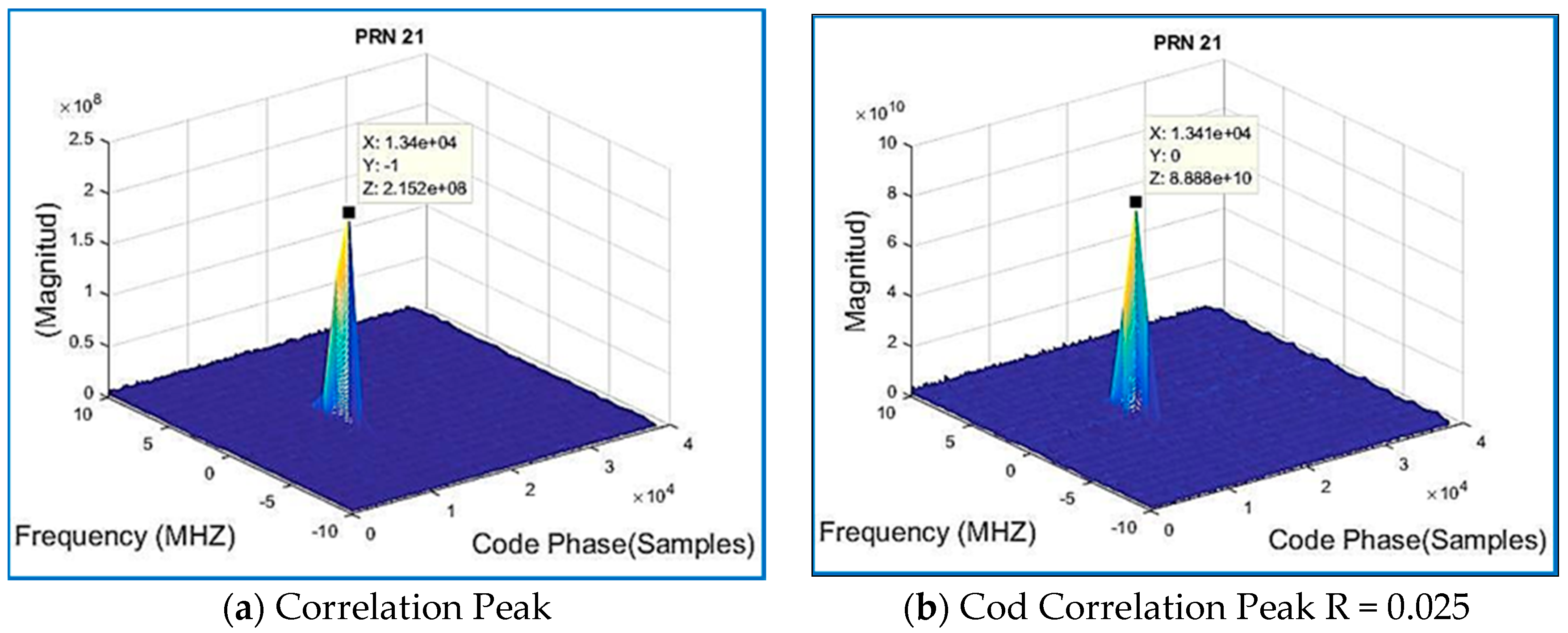
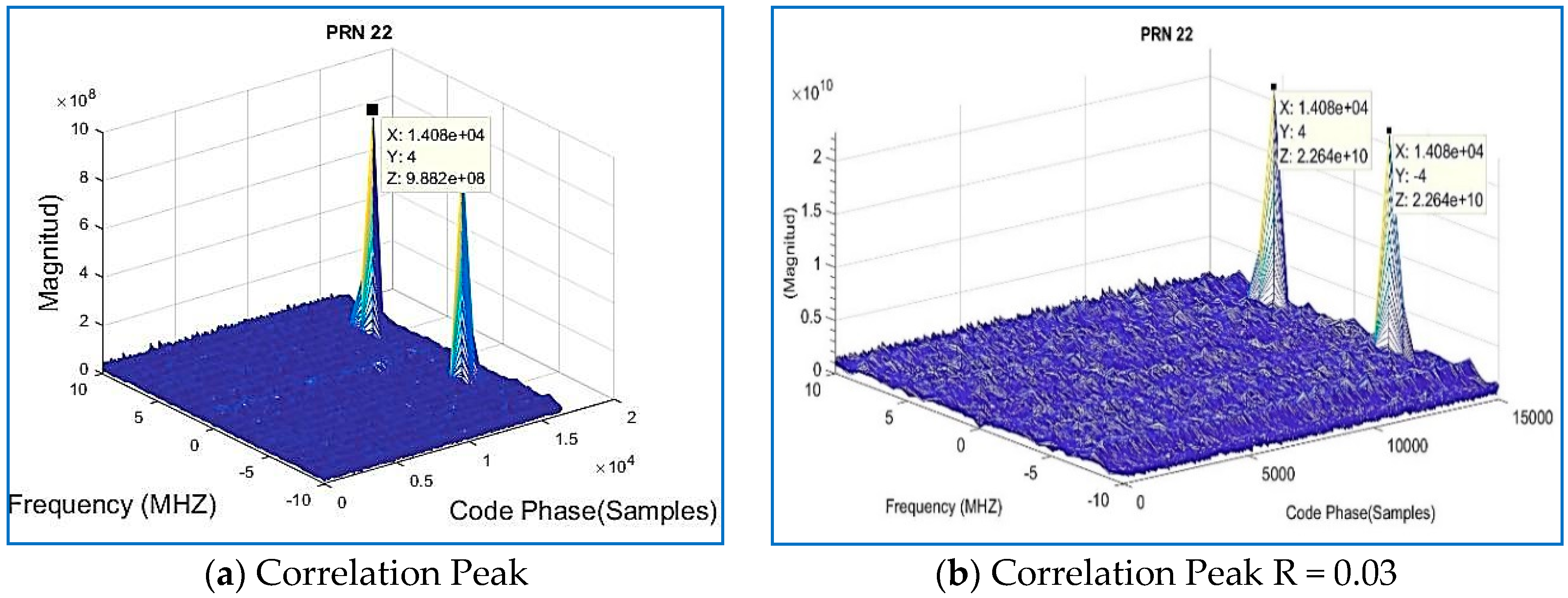
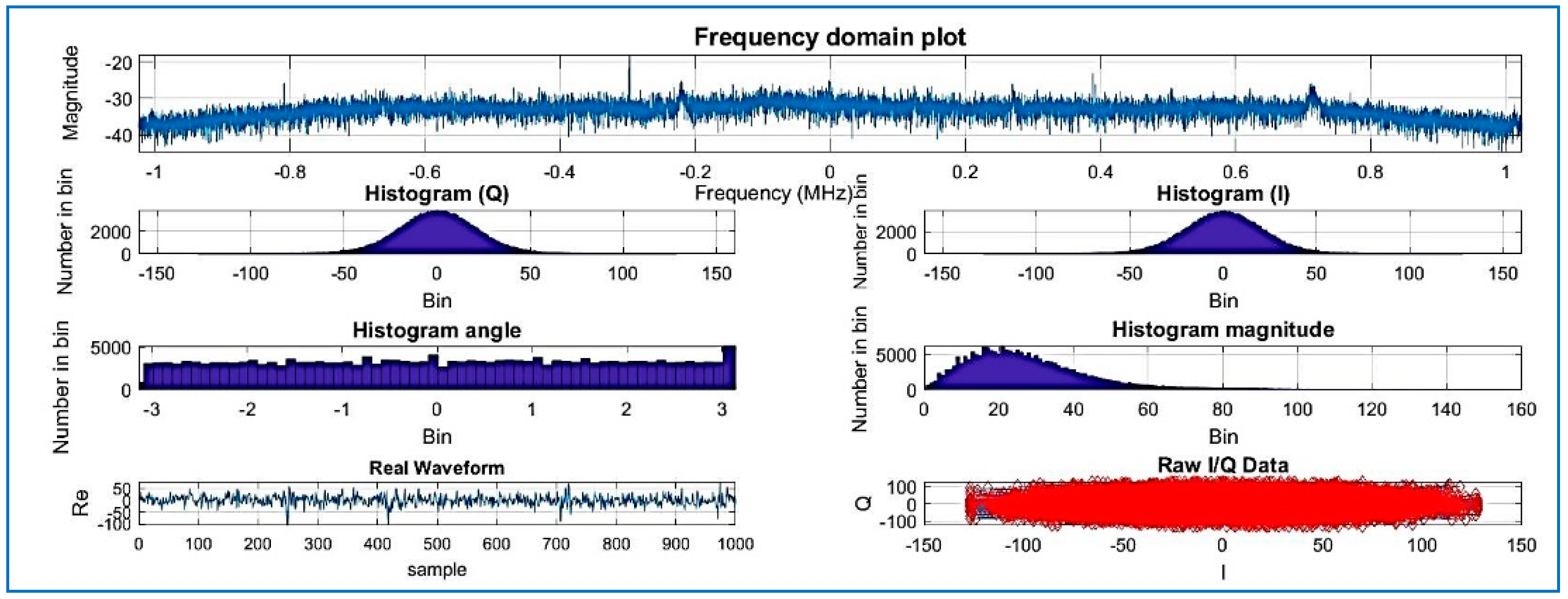
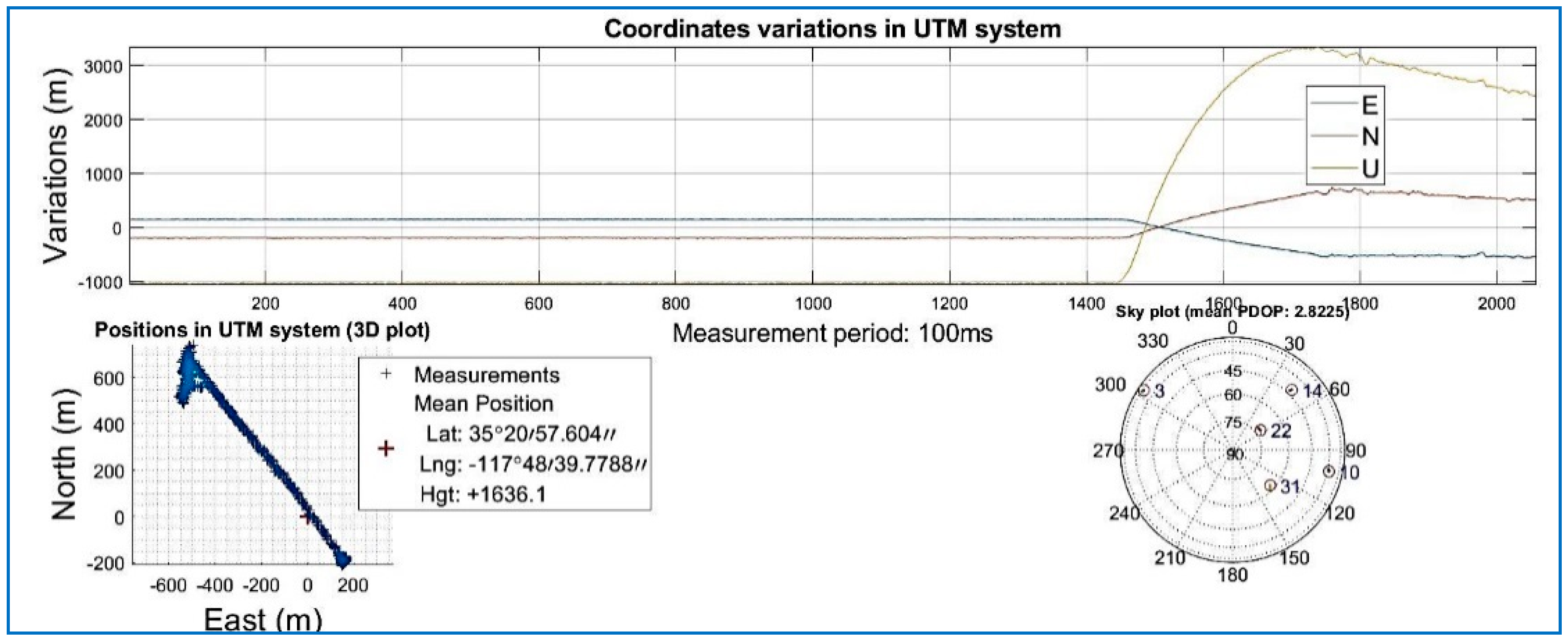
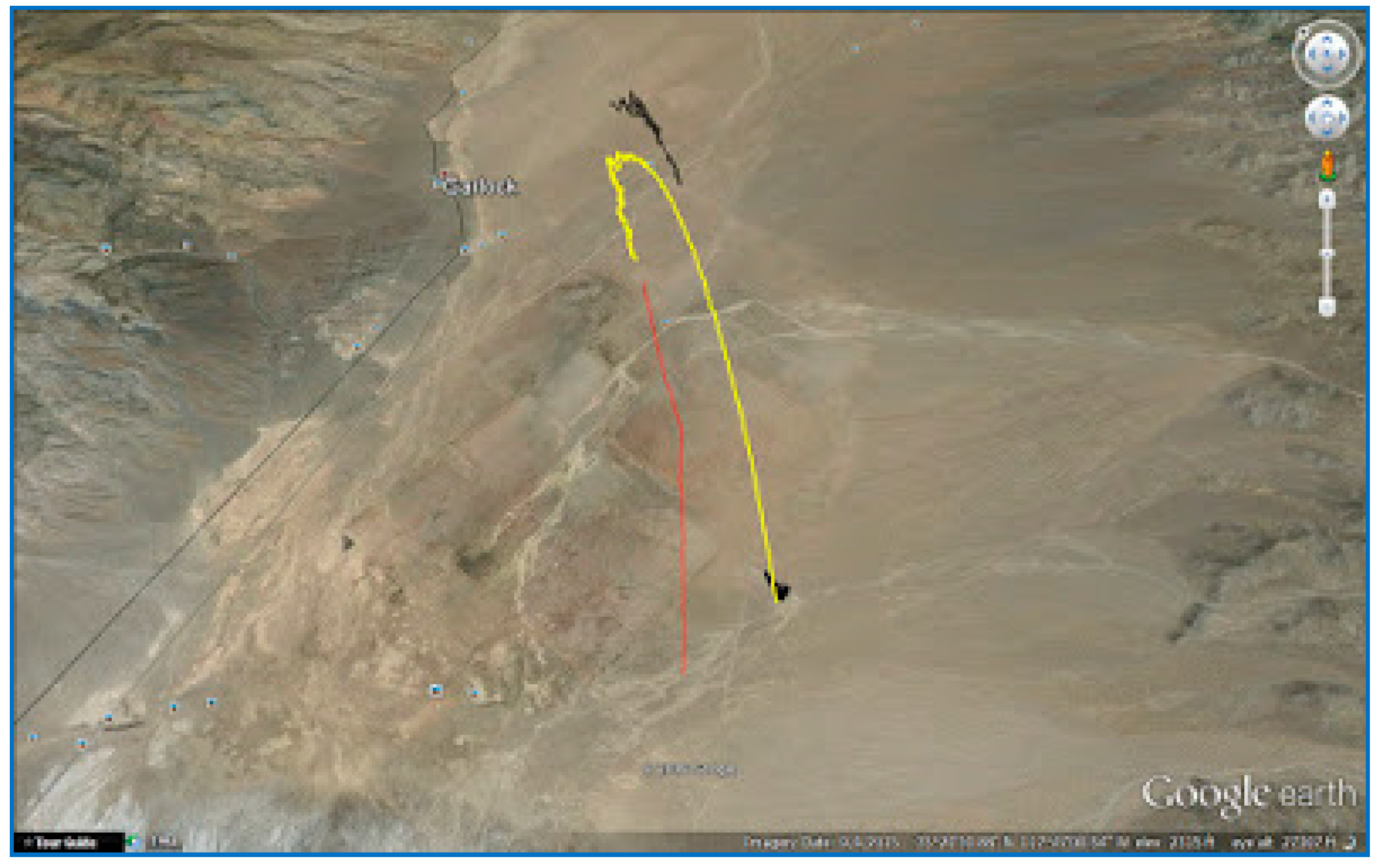
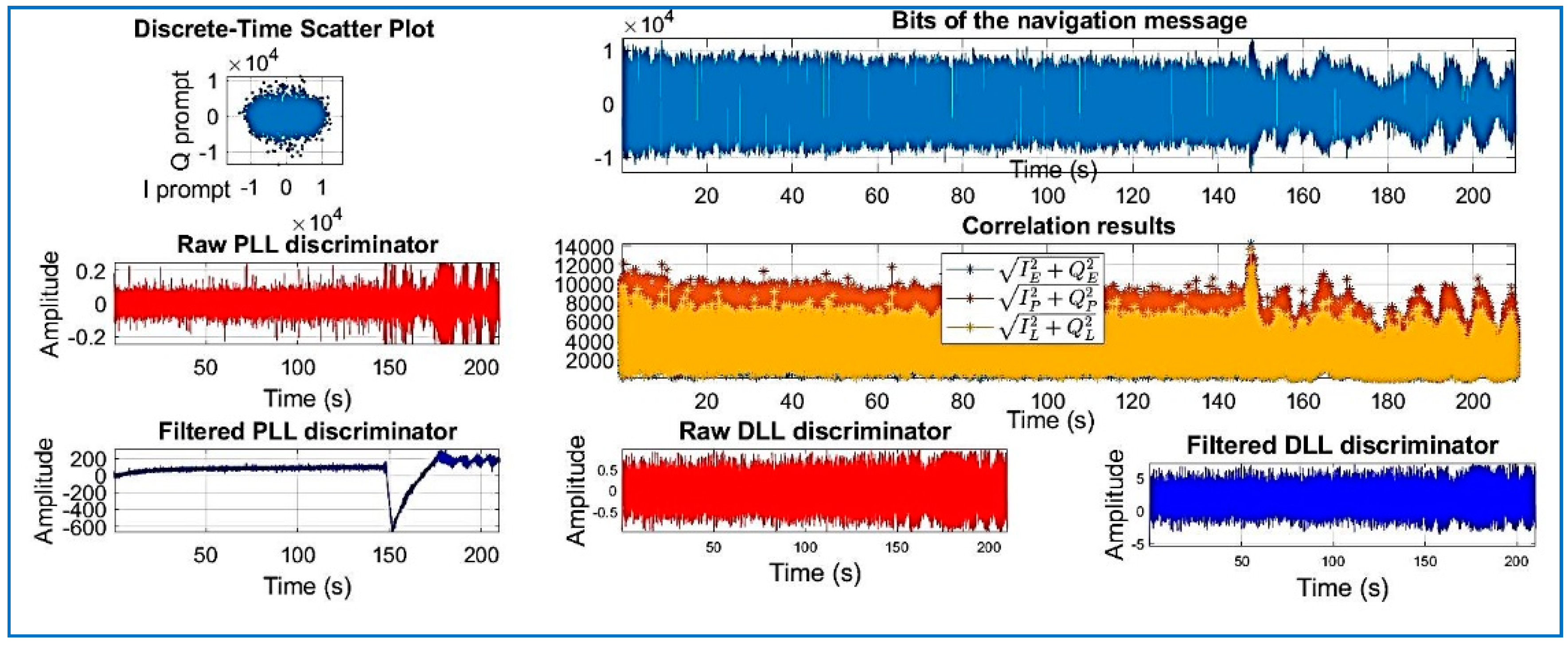
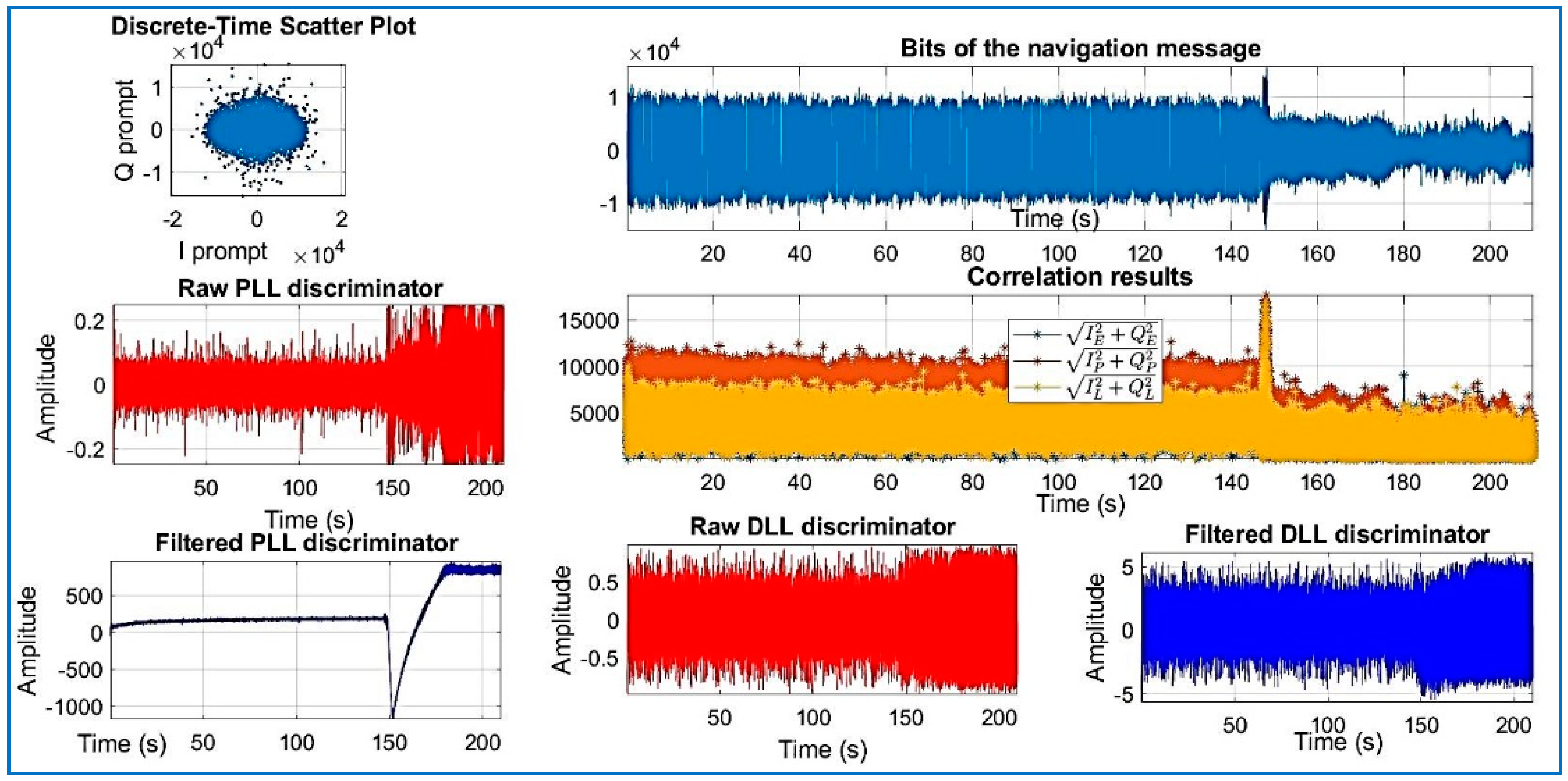
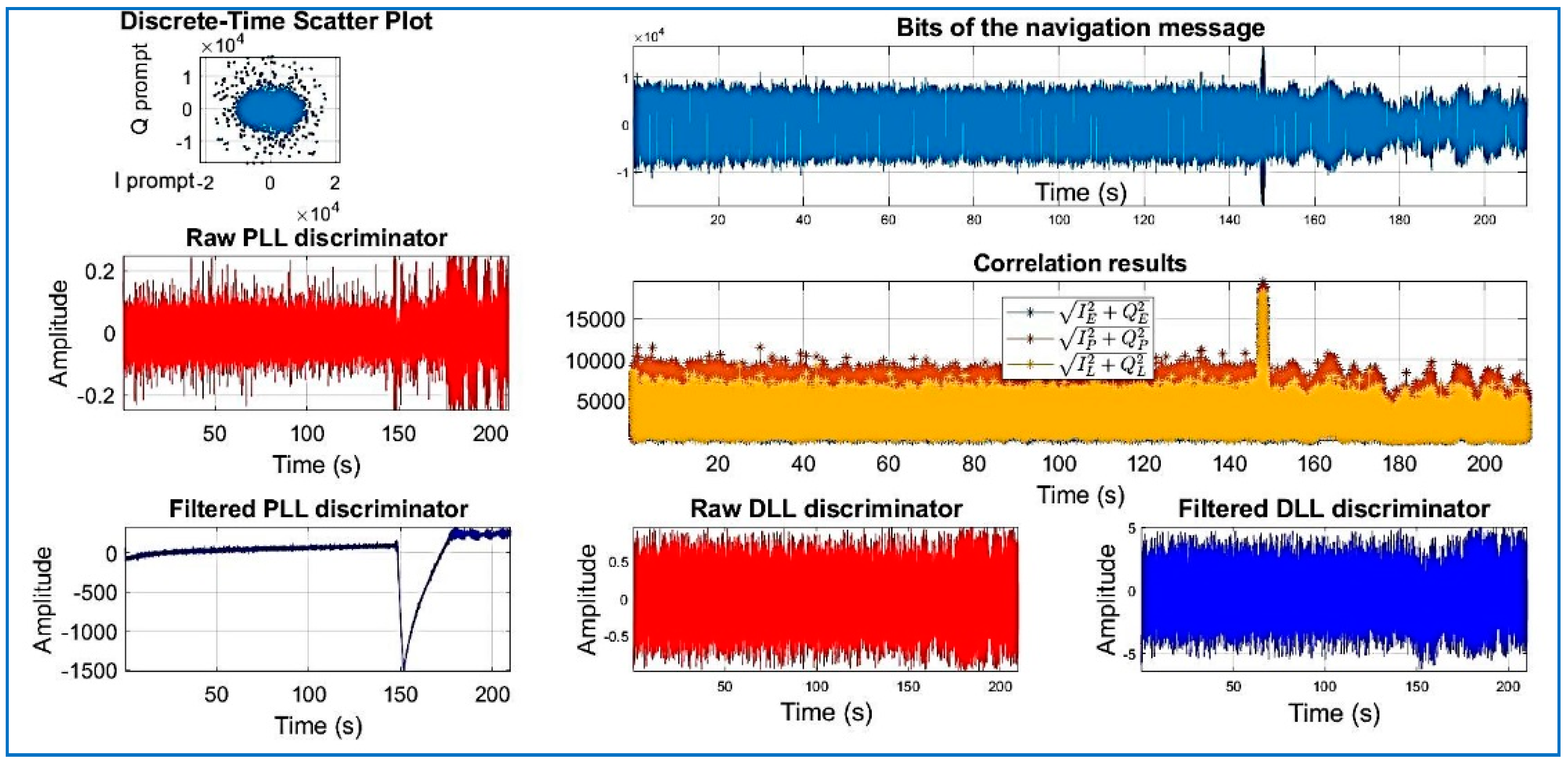
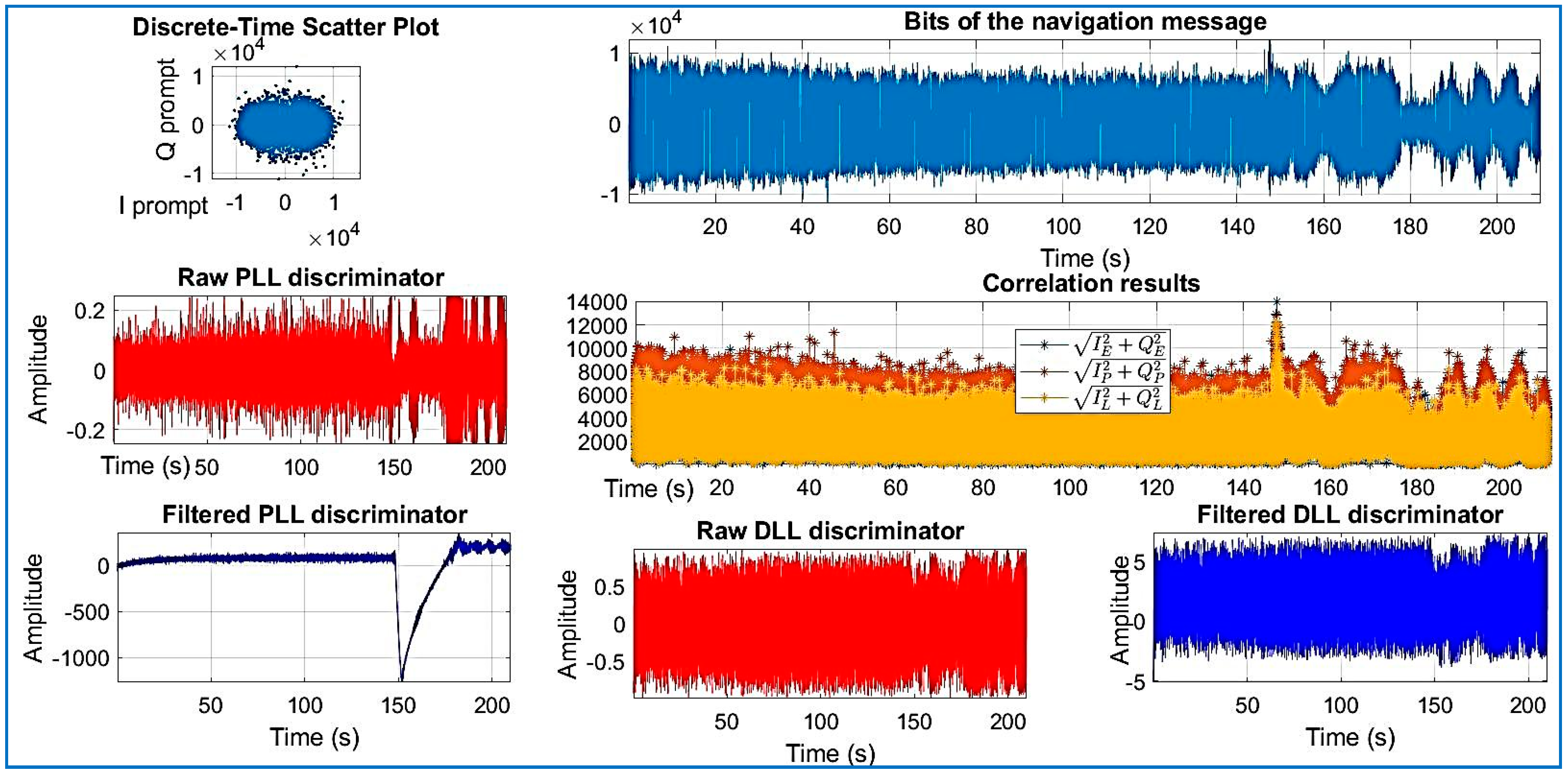
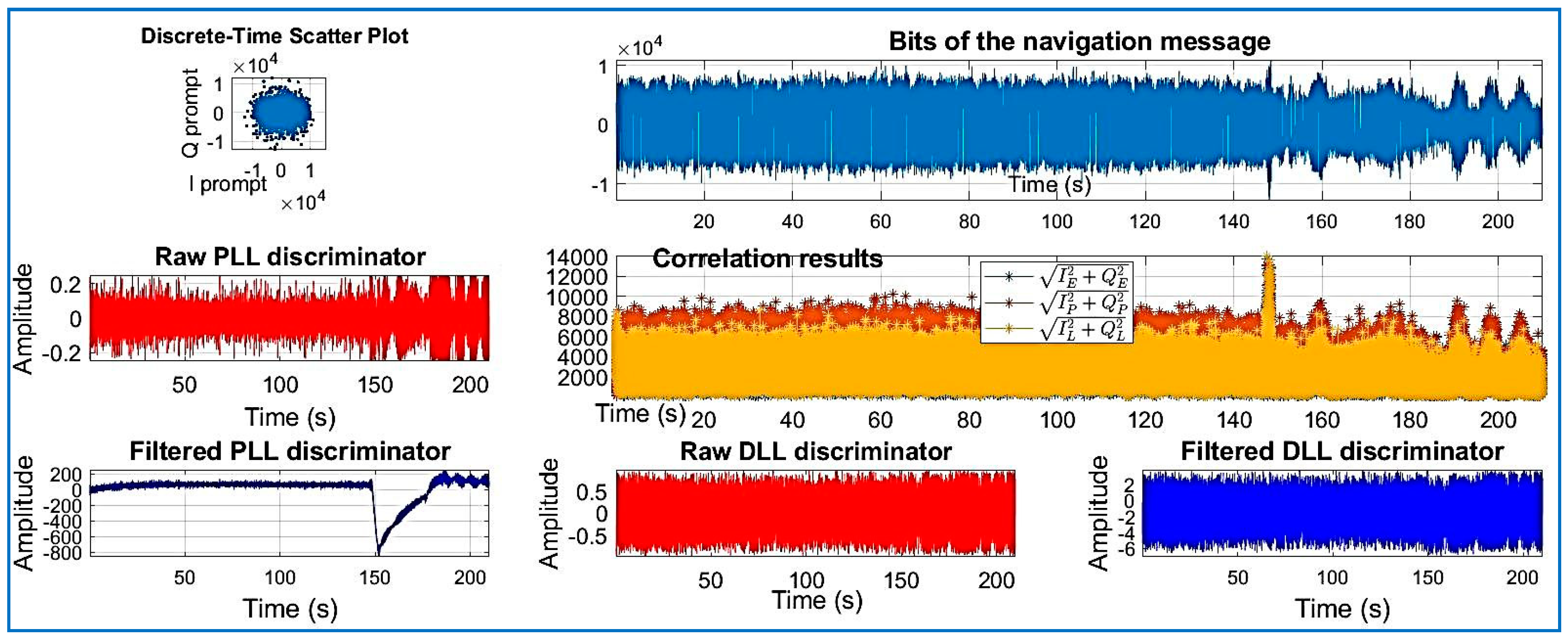
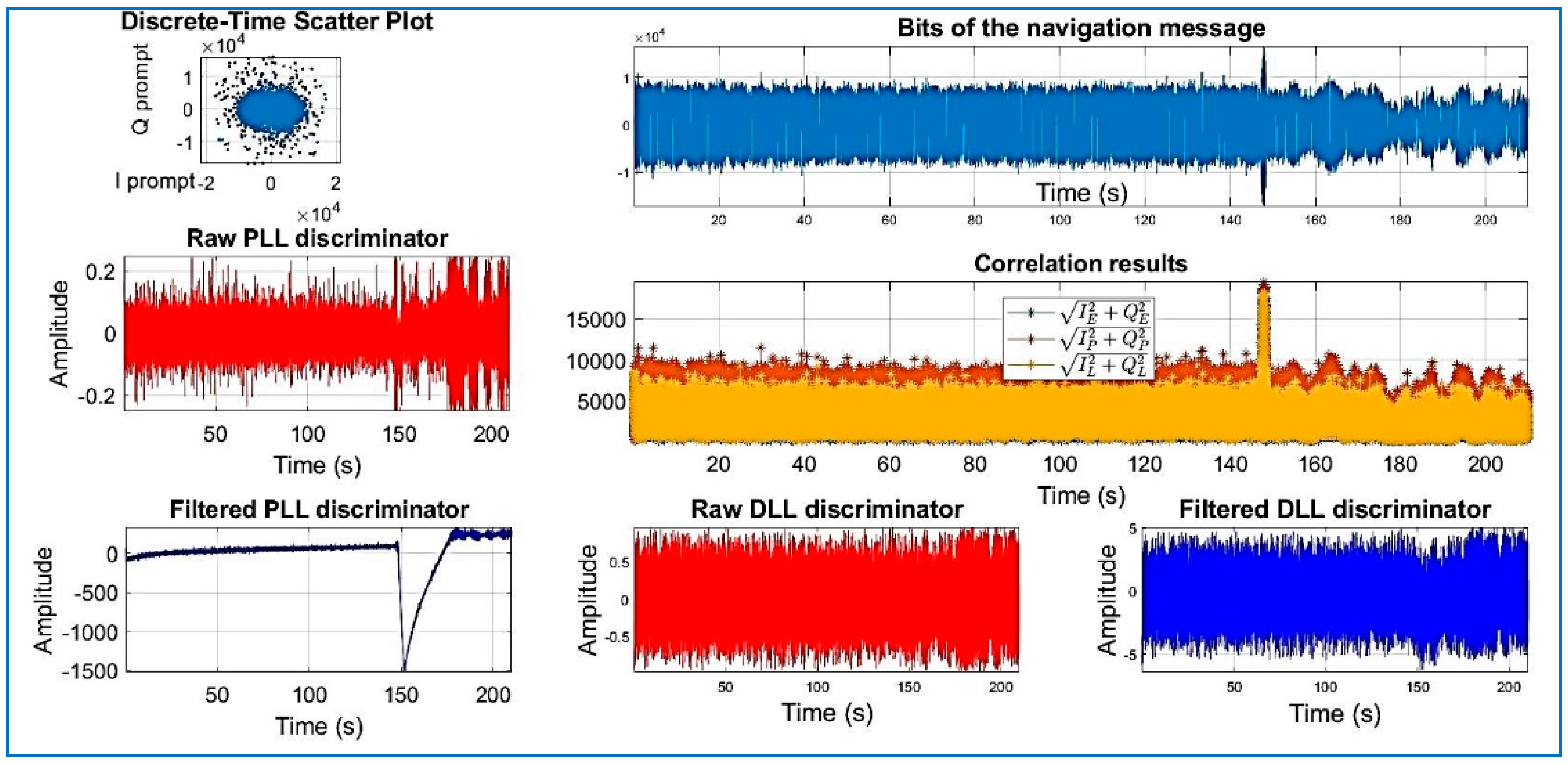
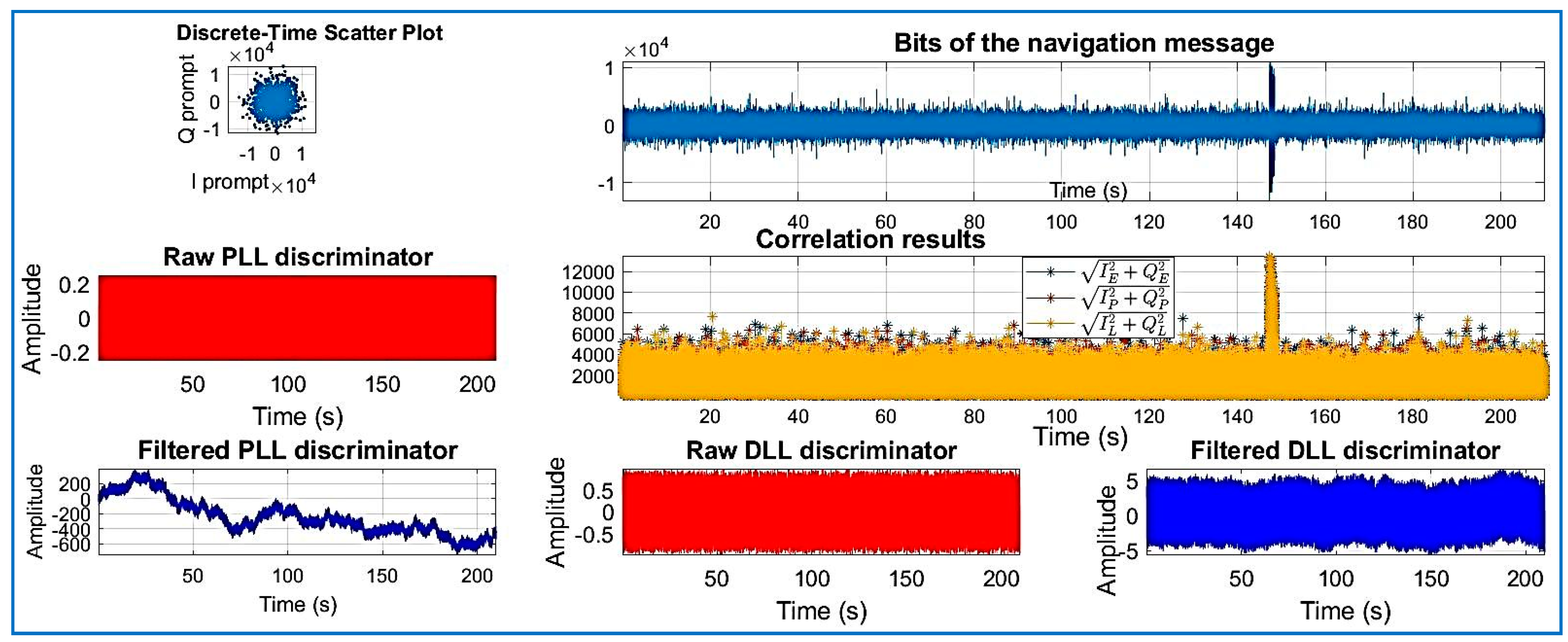
| Data Set | File Name/Reference | Sample Frequency (MHz) | Intermediate Frequency | Signed Character | Doppler Frequency Search |
|---|---|---|---|---|---|
| 1 | GPSdata-DiscreteComponents-fs38_192-if9_55.bin/ [42] | 38.192 | 9.55 MHz | Bit8 | kHz |
| 2 | GPS_and_GIOVE_A-NN-fs16_3676-if4_1304.bin/ [42] | 16.3676 | 4.1304 MHz | Bit8 | kHz |
| 3 | Feb6.u8.bin/ [43] | 2.048 | 2210.53 Hz | uchar | kHz |
| Channel | PRN | Frequency | Doppler | Code Offset |
|---|---|---|---|---|
| 1 | 21 | 9.54742 × 106 | −583 | 13,404 |
| 2 | 22 | 9.54992 × 106 | 1921 | 6288 |
| 3 | 15 | 9.54992 × 106 | 1921 | 36,321 |
| 4 | 18 | 9.54843 × 106 | 428 | 20,724 |
| 5 | 26 | 9.54492 × 106 | −3078 | 26,827 |
| 6 | 6 | 9.54443 × 106 | −3569 | 28,202 |
| 7 | 9 | 9.55092 × 106 | 2923 | 4696 |
| 8 | 3 | 9.54992 × 106 | 1921 | 34,212 |
| Channel | PRN | Frequency | Doppler | Code Offset |
|---|---|---|---|---|
| 1 | 22 | 4.13468 × 106 | 4277 | 14,077 |
| 2 | 03 | 4.13440 × 106 | 4004 | 7363 |
| 3 | 19 | 4.13694 × 106 | 6541 | 6341 |
| 4 | 15 | 4.13209 × 106 | 1686 | 1492 |
| 5 | 18 | 4.13247 × 106 | 2069 | 1528 |
| 6 | 16 | 4.13125 × 106 | 851 | 2071 |
| Channel | PRN | Frequency | Doppler | Code Offset |
|---|---|---|---|---|
| 1 | 10 | 2.39844 × 103 | 188 | 1523 |
| 2 | 22 | 3.90625 × 10 | −2171 | 1680 |
| 3 | 31 | −1.03906 × 103 | −3250 | 512 |
| 4 | 14 | 2.31250 × 103 | 102 | 358 |
| 5 | 03 | −2.76563 × 103 | −4976 | 1729 |
| 6 * | 16 | 2.30398 × 105 | 228,188 | 1252 |
| Columns | Peak Size | Noise Floor Power | Mean Detection Time | SNR |
|---|---|---|---|---|
| 5 | 3.49 × 108 | 3.30 × 1014 | 2.65 | 22.60 |
| 10 | 1.00 × 109 | 3.29 × 1015 | 2.70 | 25.48 |
| 20 | 4.55 × 109 | 5.93 × 1016 | 2.73 | 23.43 |
| 30 | 1.11 × 1010 | 3.88 × 1017 | 2.70 | 24.39 |
| 40 | 2.08 × 1010 | 1.37 × 1018 | 2.70 | 29.31 |
| 50 | 3.27 × 1010 | 3.10 × 1018 | 2.79 | 22.95 |
| 80 | 8.73 × 1010 | 1.77 × 1019 | 2.76 | 22.37 |
| 150 | 3.09 × 1011 | 2.73 × 1020 | 4.31 | 27.82 |
| 300 | 1.15 × 1012 | 4.42 × 1021 | 14.97 | 28.10 |
| 350 | 1.62 × 1012 | 9.04 × 1021 | 144.09 | 23.89 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bermúdez Ordoñez, J.C.; Arnaldo Valdés, R.M.; Gómez Comendador, F. Energy Efficient GNSS Signal Acquisition Using Singular Value Decomposition (SVD). Sensors 2018, 18, 1586. https://doi.org/10.3390/s18051586
Bermúdez Ordoñez JC, Arnaldo Valdés RM, Gómez Comendador F. Energy Efficient GNSS Signal Acquisition Using Singular Value Decomposition (SVD). Sensors. 2018; 18(5):1586. https://doi.org/10.3390/s18051586
Chicago/Turabian StyleBermúdez Ordoñez, Juan Carlos, Rosa María Arnaldo Valdés, and Fernando Gómez Comendador. 2018. "Energy Efficient GNSS Signal Acquisition Using Singular Value Decomposition (SVD)" Sensors 18, no. 5: 1586. https://doi.org/10.3390/s18051586
APA StyleBermúdez Ordoñez, J. C., Arnaldo Valdés, R. M., & Gómez Comendador, F. (2018). Energy Efficient GNSS Signal Acquisition Using Singular Value Decomposition (SVD). Sensors, 18(5), 1586. https://doi.org/10.3390/s18051586






