Sparsity-Driven Reconstruction Technique for Microwave/Millimeter-Wave Computational Imaging
Abstract
:1. Introduction
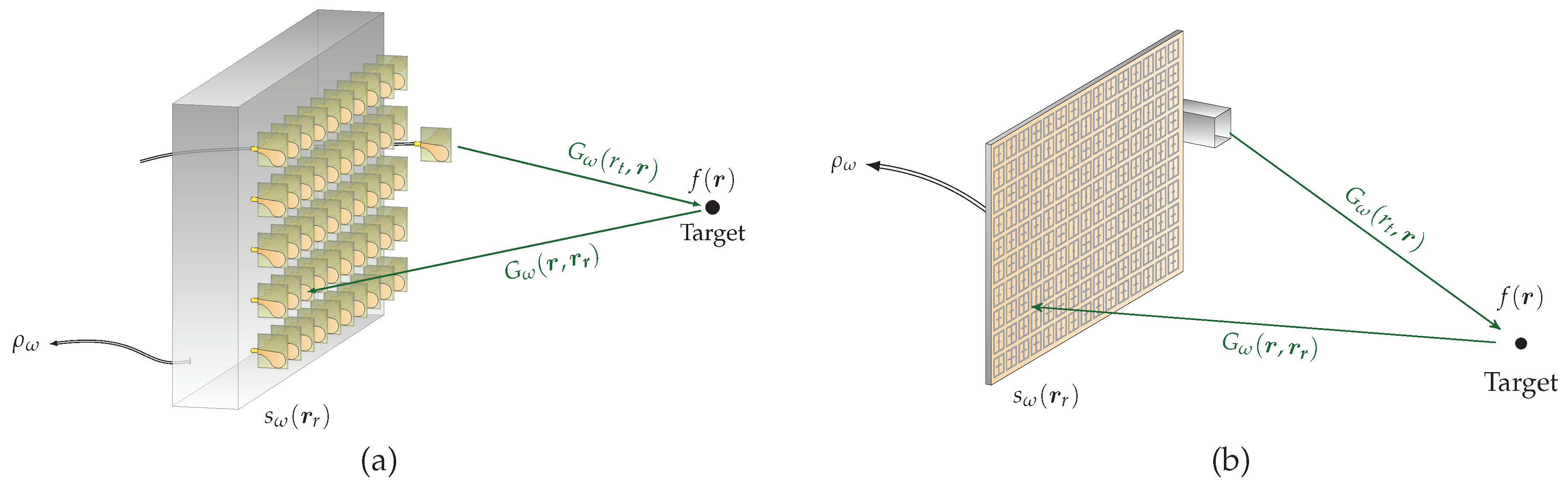
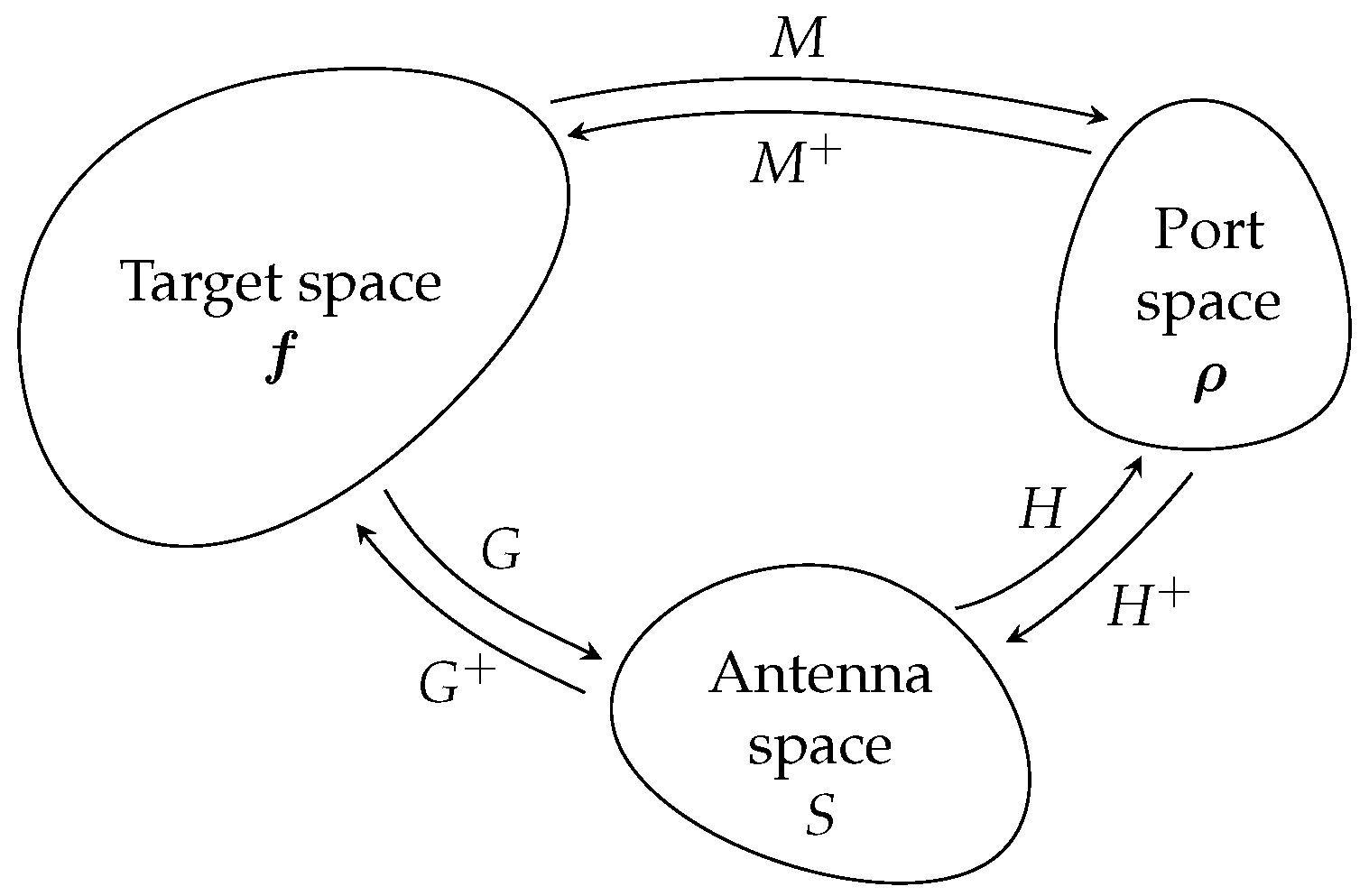
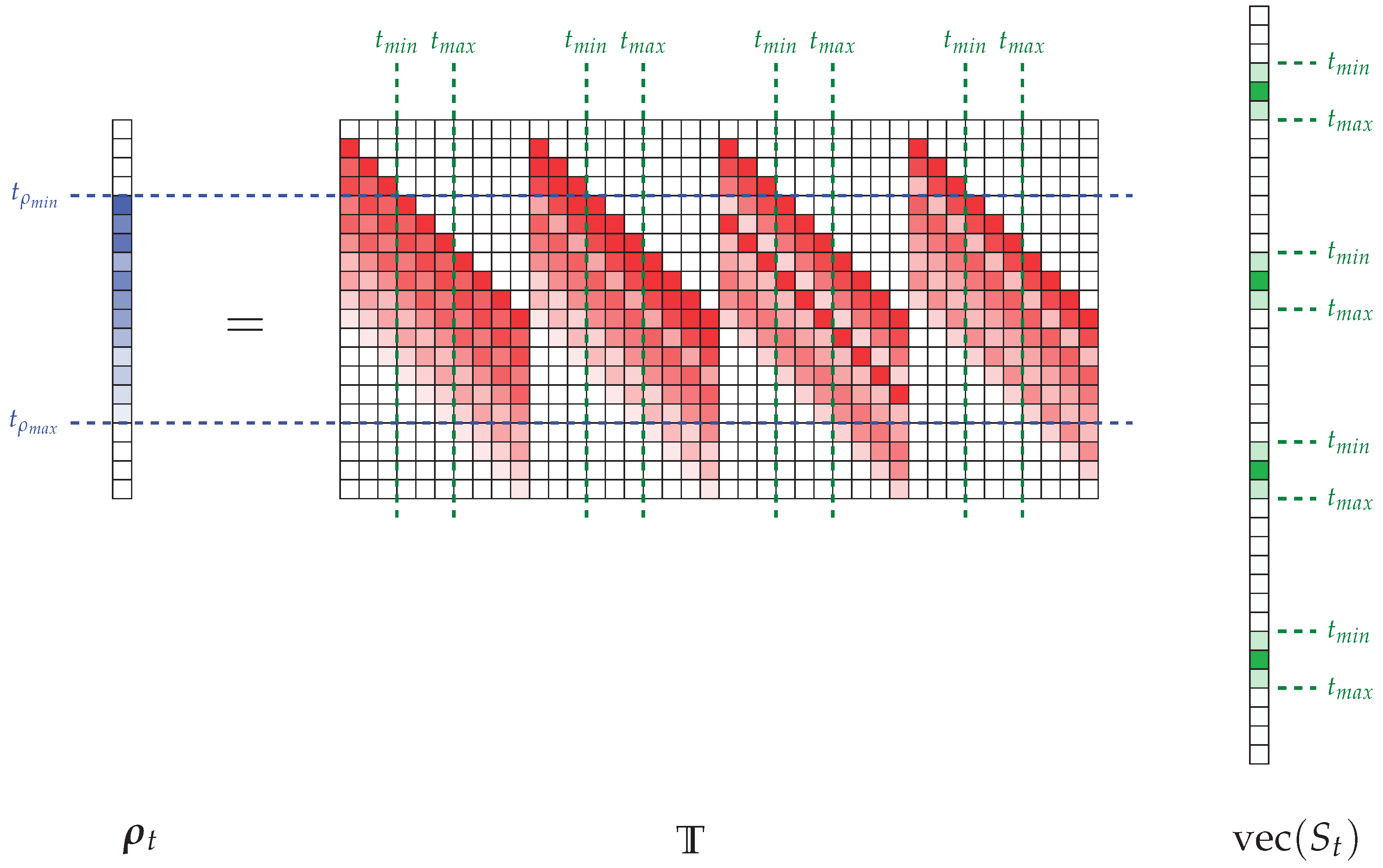
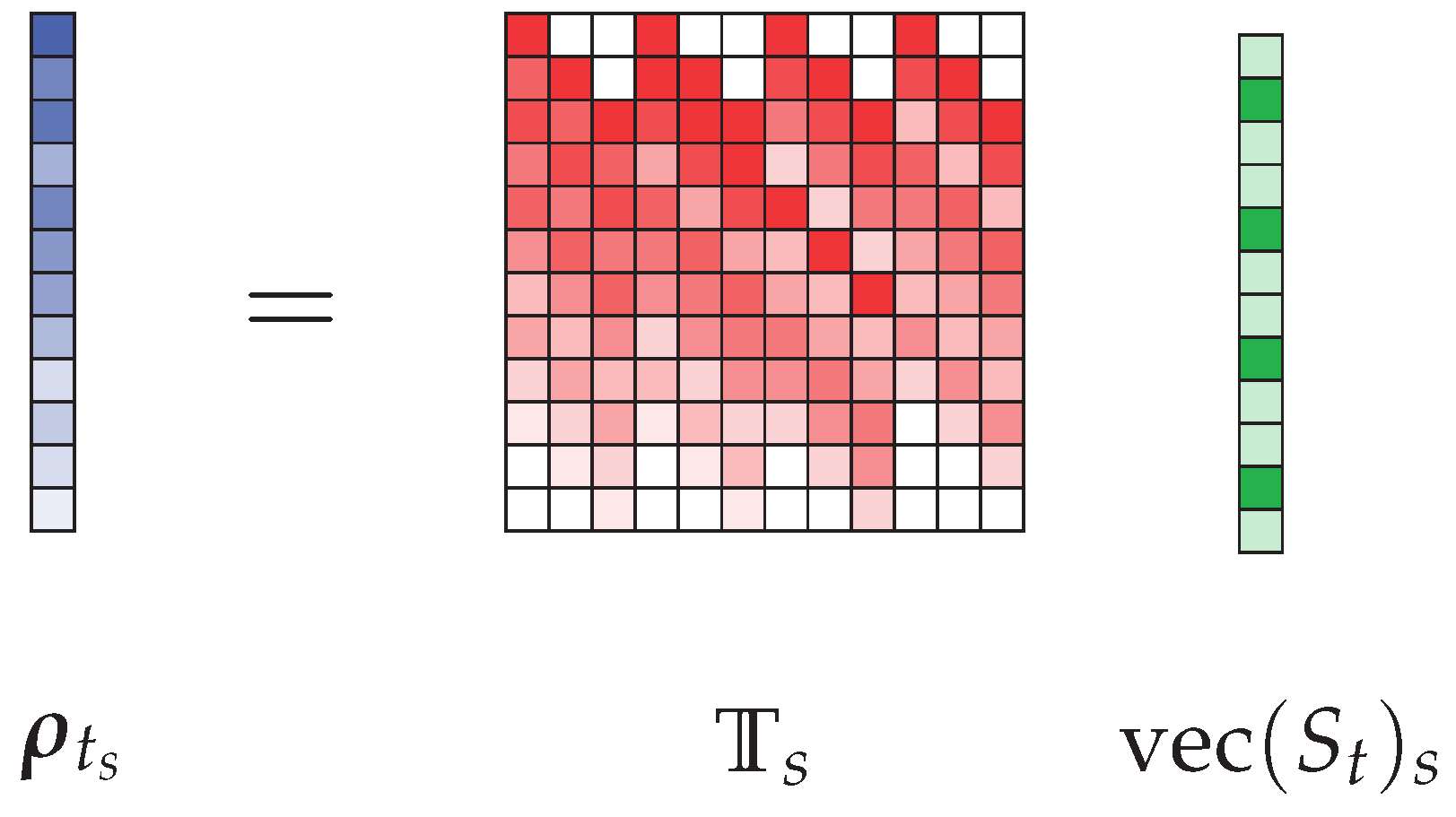
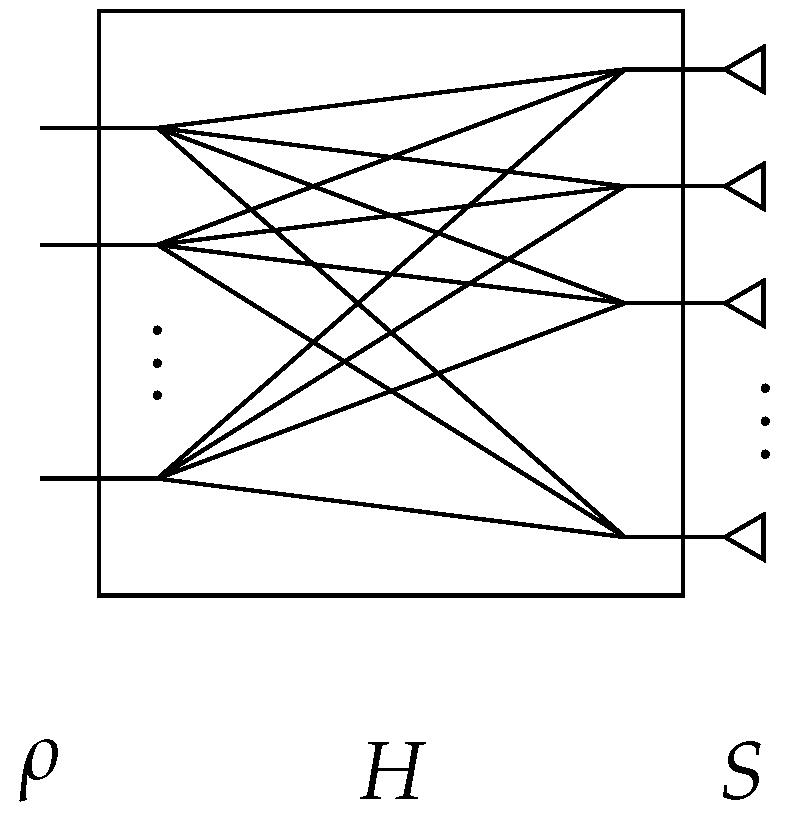
2. Theoretical Principle of a Sparsity-Based Time-Domain Signal Estimation
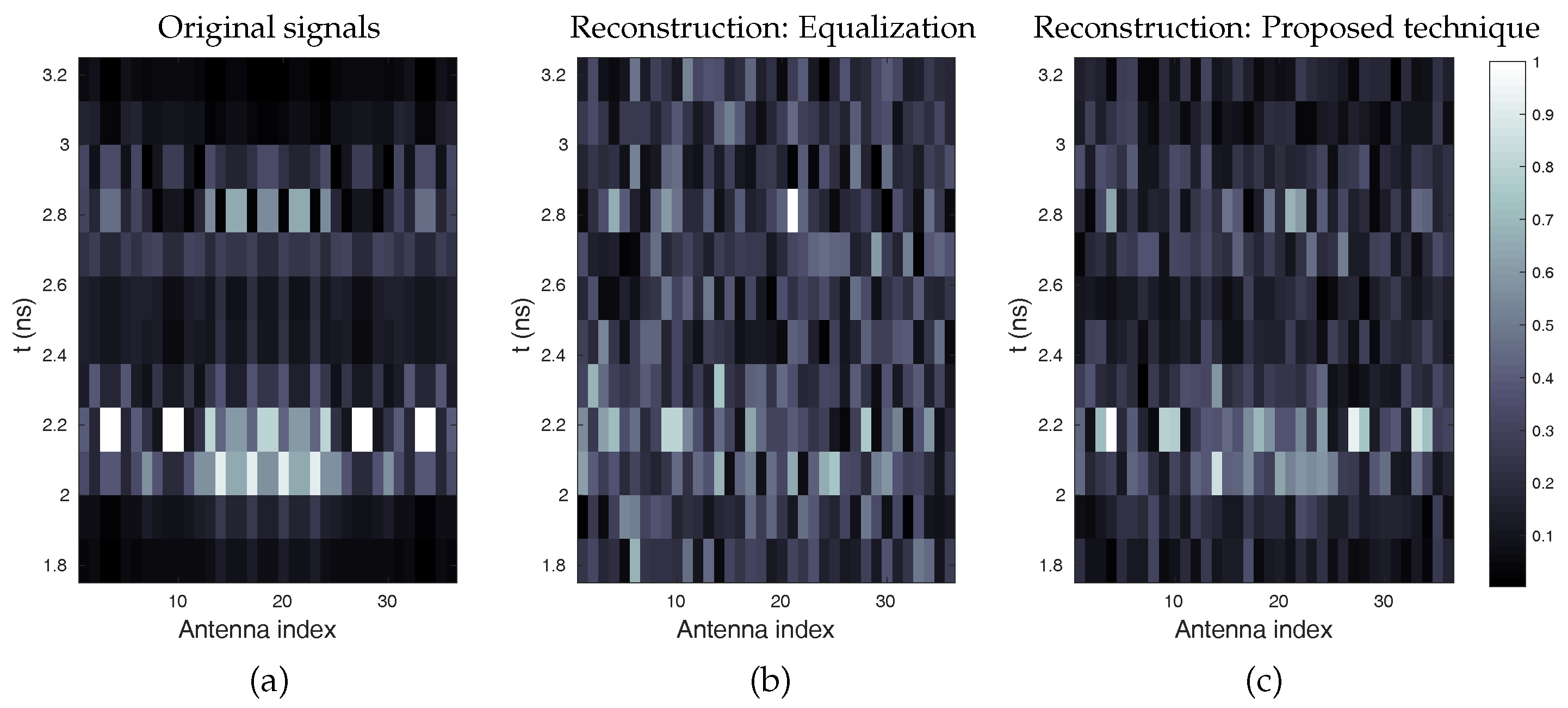
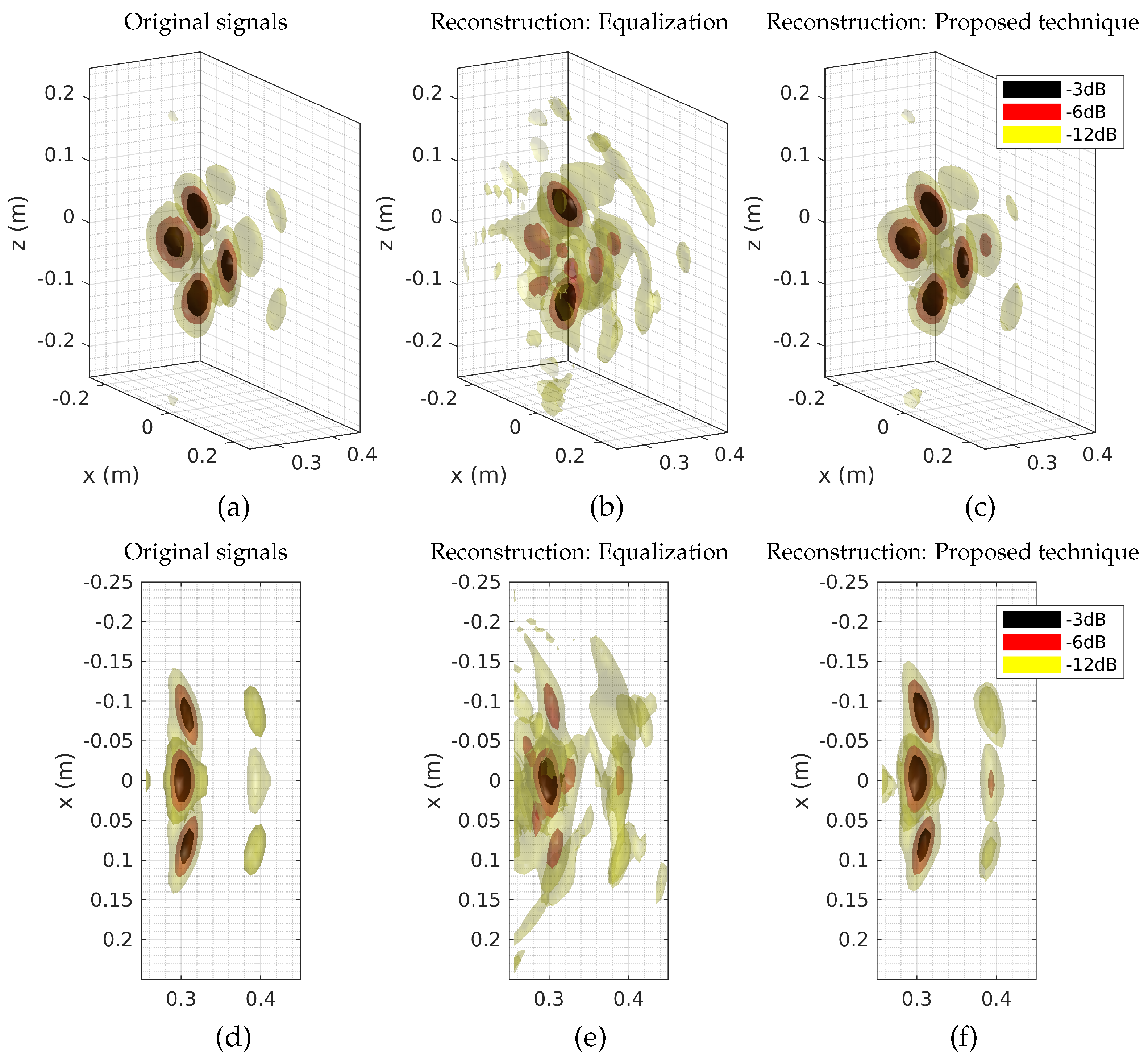
3. Numerical Validation
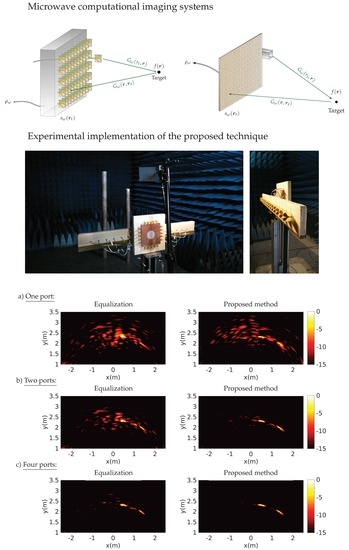
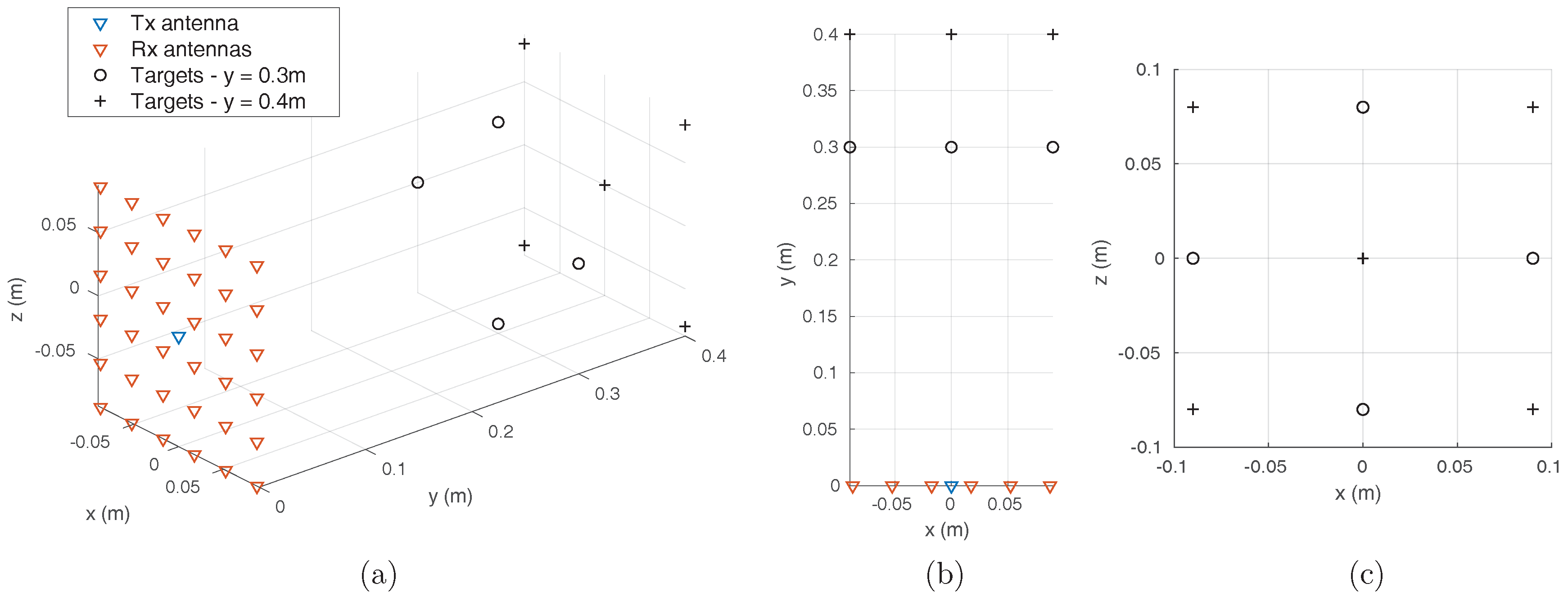
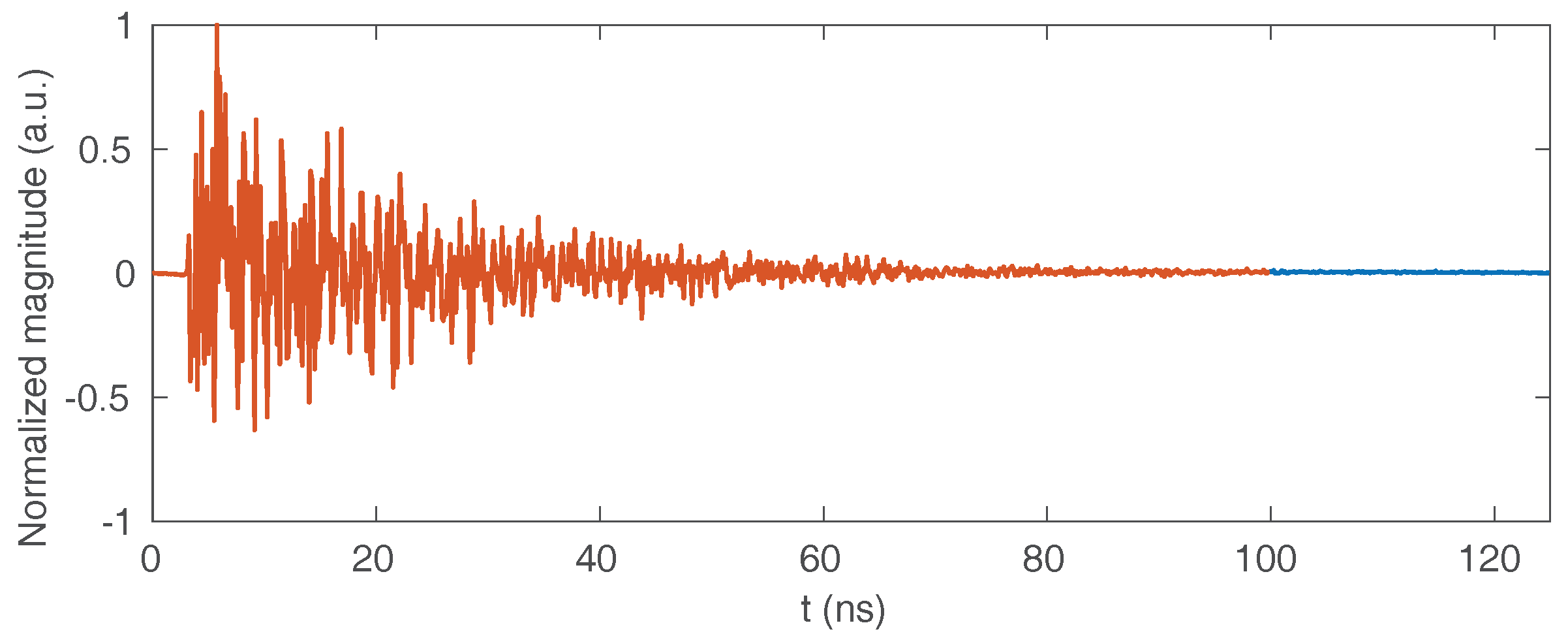
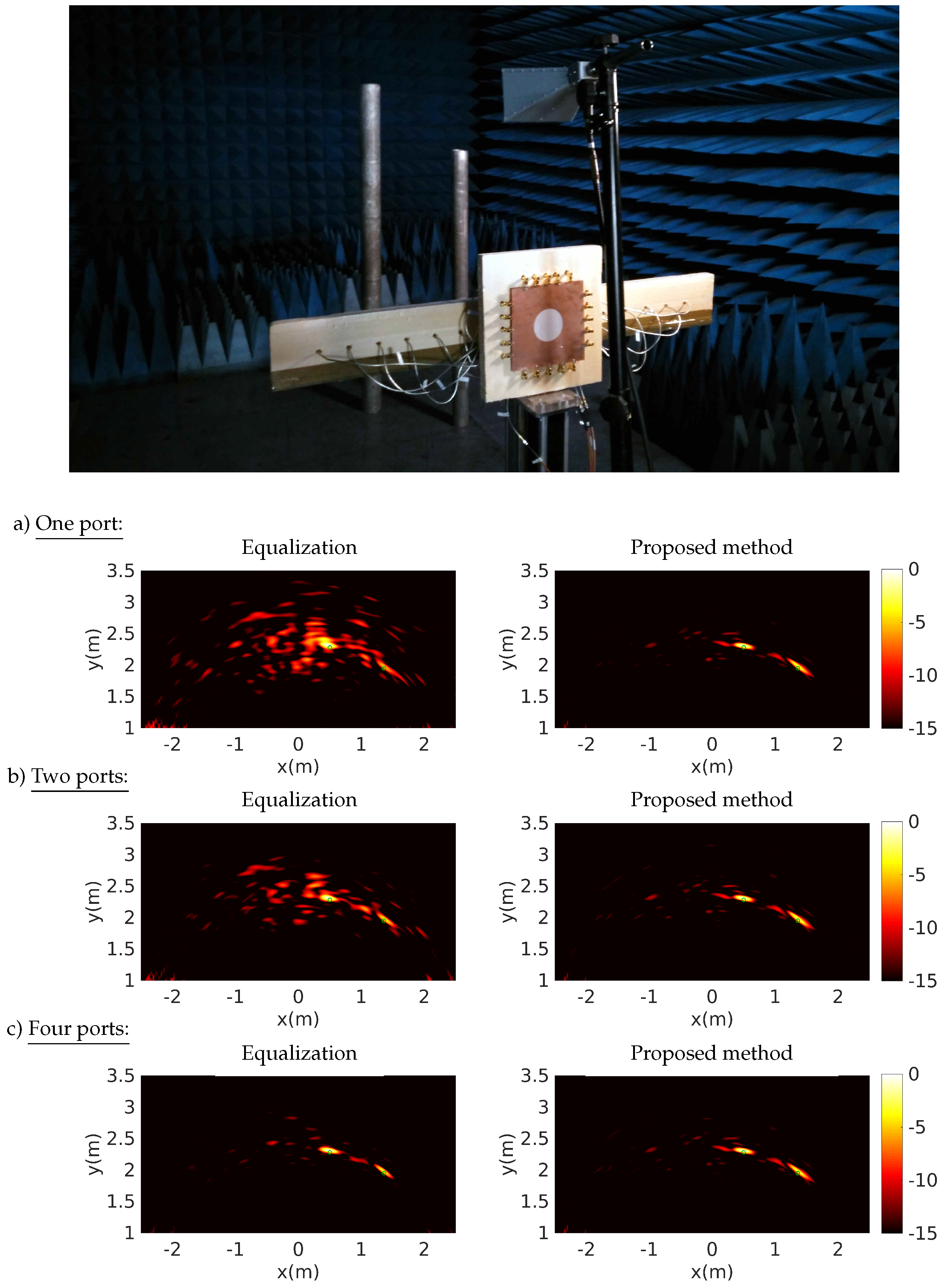
4. Experimental Validation
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Fear, E.C.; Li, X.; Hagness, S.C.; Stuchly, M.A. Confocal microwave imaging for breast cancer detection: Localization of tumors in three dimensions. IEEE Trans. Biomed. Eng. 2002, 49, 812–822. [Google Scholar] [CrossRef] [PubMed]
- Bond, E.J.; Li, X.; Hagness, S.C.; Van Veen, B.D. Microwave imaging via space-time beamforming for early detection of breast cancer. IEEE Trans. Antennas Propag. 2003, 51, 1690–1705. [Google Scholar] [CrossRef]
- Nikolova, N.K. Microwave imaging for breast cancer. IEEE Microw. Mag. 2011, 12, 78–94. [Google Scholar] [CrossRef]
- Bevacqua, M.T.; Scapaticci, R. A compressive sensing approach for 3D breast cancer microwave imaging with magnetic nanoparticles as contrast agent. IEEE Trans. Med. Imaging 2016, 35, 665–673. [Google Scholar] [CrossRef] [PubMed]
- Schajer, G.S.; Orhan, F.B. Microwave non-destructive testing of wood and similar orthotropic materials. Subsurf. Sens. Technol. Appl. 2005, 6, 293. [Google Scholar] [CrossRef]
- Hasar, U. Non-destructive testing of hardened cement specimens at microwave frequencies using a simple free-space method. NDT E Int. 2009, 42, 550–557. [Google Scholar] [CrossRef]
- Mohamed, I.; Dudley, R.; Gregory, A.; Mouthaan, R.; Tian, Z.; Andrews, P.; Mellonie, A. Non-destructive testing for black heart cavities in potatoes with microwave radiation. In Proceedings of the 46th European Microwave Conference, London, UK, 4–6 October 2016; pp. 815–818. [Google Scholar]
- Ahmed, S.S.; Genghammer, A.; Schiessl, A.; Schmidt, L.P. Fully Electronic E-Band Personnel Imager of 2mx2m Aperture Based on a Multistatic Architecture. IEEE Trans. Microw. Theory Tech. 2013, 61, 651–657. [Google Scholar] [CrossRef]
- Gonzalez-Valdes, B.; Álvarez, Y.; Rodriguez-Vaqueiro, Y.; Arboleya-Arboleya, A.; García-Pino, A.; Rappaport, C.M.; Las-Heras, F.; Martinez-Lorenzo, J.A. Millimeter wave imaging architecture for on-the-move whole body imaging. IEEE Trans. Antennas Propag. 2016, 64, 2328–2338. [Google Scholar] [CrossRef]
- Laviada, J.; Arboleya-Arboleya, A.; Las-Heras, F. Multistatic Millimeter-Wave Imaging by Multiview Portable Camera. IEEE Access 2017, 5, 19259–19268. [Google Scholar] [CrossRef]
- Carsenat, D.; Decroze, C. UWB antennas beamforming using passive time-reversal device. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 779–782. [Google Scholar] [CrossRef]
- Fromenteze, T.; Decroze, C.; Carsenat, D. Waveform coding for passive multiplexing: Application to microwave imaging. IEEE Trans. Antennas Propag. 2015, 63, 593–600. [Google Scholar] [CrossRef]
- Fromenteze, T.; Kpré, E.L.; Carsenat, D.; Decroze, C.; Sakamoto, T. Single-shot compressive multiple-inputs multiple-outputs radar imaging using a two-port passive device. IEEE Access 2016, 4, 1050–1060. [Google Scholar] [CrossRef]
- Hunt, J.; Driscoll, T.; Mrozack, A.; Lipworth, G.; Reynolds, M.; Brady, D.; Smith, D.R. Metamaterial apertures for computational imaging. Science 2013, 339, 310–313. [Google Scholar] [CrossRef] [PubMed]
- Gollub, J.; Yurduseven, O.; Trofatter, K.; Arnitz, D.; Imani, M.; Sleasman, T.; Boyarsky, M.; Rose, A.; Pedross-Engel, A.; Odabasi, H.; et al. Large metasurface aperture for millimeter wave computational imaging at the human-scale. Sci. Rep. 2017, 7, 42650. [Google Scholar] [CrossRef] [PubMed]
- Yurduseven, O.; Marks, D.L.; Fromenteze, T.; Gollub, J.N.; Smith, D.R. Millimeter-wave spotlight imager using dynamic holographic metasurface antennas. Opt. Express 2017, 25, 18230–18249. [Google Scholar] [CrossRef] [PubMed]
- Fromenteze, T.; Yurduseven, O.; Imani, M.F.; Gollub, J.; Decroze, C.; Carsenat, D.; Smith, D.R. Computational imaging using a mode-mixing cavity at microwave frequencies. Appl. Phys. Lett. 2015, 106, 194104. [Google Scholar] [CrossRef]
- Fromenteze, T.; Liu, X.; Boyarsky, M.; Gollub, J.; Smith, D.R. Phaseless computational imaging with a radiating metasurface. Opt. Express 2016, 24, 16760–16776. [Google Scholar] [CrossRef] [PubMed]
- Fromenteze, T.; Yurduseven, O.; Boyarsky, M.; Gollub, J.; Marks, D.L.; Smith, D.R. Computational polarimetric microwave imaging. Opt. Express 2017, 25, 27488–27505. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Lopez, Y.; Garcia-Gonzalez, C.; Vazquez-Antuna, C.; Ver-Hoeye, S.; Las Heras Andres, F. Frequency scanning based radar system. Prog. Electromagn. Res. 2012, 132, 275–296. [Google Scholar] [CrossRef]
- Alvarez, Y.; Camblor, R.; Garcia, C.; Laviada, J.; Vazquez, C.; Ver-Hoeye, S.; Hotopan, G.; Fernandez, M.; Hadarig, A.; Arboleya, A. Submillimeter-wave frequency scanning system for imaging applications. IEEE Trans. Antennas Propag. 2013, 61, 5689–5696. [Google Scholar] [CrossRef]
- Laviada, J.; Álvarez-López, Y.; García-González, C.; Vázquez-Antuña, C.; Ver-Hoeye, S.; Fernández-García, M.; Hotopan, G.; Camblor, R.; Las-Heras, F. A novel phaseless frequency scanning based on indirect holography. J. Electromagn. Waves Appl. 2013, 27, 430–438. [Google Scholar] [CrossRef]
- Fromenteze, T.; Kpré, E.L.; Decroze, C.; Carsenat, D.; Yurduseven, O.; Imani, M.; Gollub, J.; Smith, D.R. Unification of compressed imaging techniques in the microwave range and deconvolution strategy. In Proceedings of the 2015 European Radar Conference (EuRAD), Paris, France, 9–11 September 2015; pp. 161–164. [Google Scholar]
- Van Den Berg, E.; Friedlander, M.P. Probing the Pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 2008, 31, 890–912. [Google Scholar] [CrossRef]
- Van Den Berg, E.; Friedlander, M.P. SPGL1: A solver for large-scale sparse reconstruction, 2007. Available online: http://www.cs.ubc.ca/labs/scl/spgl1 (accessed on 12 May 2018).
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef] [PubMed]
- Figueiredo, M.A.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Fromenteze, T.; Kpre, E.; Carsenat, D.; Decroze, C. Clean deconvolution applied to passive compressed beamforming. Prog. Electromagn. Res. C 2015, 56, 163–172. [Google Scholar] [CrossRef]
- Pulido-Mancera, L.; Fromenteze, T.; Sleasman, T.; Boyarsky, M.; Imani, M.F.; Reynolds, M.; Smith, D. Application of range migration algorithms to imaging with a dynamic metasurface antenna. JOSA B 2016, 33, 2082–2092. [Google Scholar] [CrossRef]
- Holland, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Commun. Stat. Theory Methods 1977, 6, 813–827. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Gray, R.M. Toeplitz and circulant matrices: A review. Found. Trends Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar] [CrossRef]
- Fromenteze, T.; Kpré, E.L.; Decroze, C.; Carsenat, D. Passive UWB beamforming: AN to M compression study. In Proceedings of the 2015 European Radar Conference (EuRAD), Paris, France, 9–11 September 2015; pp. 169–172. [Google Scholar]
- Fromenteze, T.; Kpré, E.L.; Decroze, C.; Carsenat, D. Passive compression technique applied to UWB beamforming and imaging architectures. Int. J. Microw. Wirel. Technol. 2016, 8, 815–823. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, W. Sparse signal reconstruction via iterative support detection. SIAM J. Imaging Sci. 2010, 3, 462–491. [Google Scholar] [CrossRef]
- Liang, D.; DiBella, E.V.; Chen, R.R.; Ying, L. k-t ISD: Dynamic cardiac MR imaging using compressed sensing with iterative support detection. Magn. Reson. Med. 2012, 68, 41–53. [Google Scholar] [CrossRef] [PubMed]
- Draeger, C.; Fink, M. One-channel time reversal of elastic waves in a chaotic 2D-silicon cavity. Phys. Rev. Lett. 1997, 79, 407. [Google Scholar] [CrossRef]
- Montaldo, G.; Palacio, D.; Tanter, M.; Fink, M. Building three-dimensional images using a time-reversal chaotic cavity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 1489–1497. [Google Scholar] [CrossRef] [PubMed]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fromenteze, T.; Decroze, C.; Abid, S.; Yurduseven, O. Sparsity-Driven Reconstruction Technique for Microwave/Millimeter-Wave Computational Imaging. Sensors 2018, 18, 1536. https://doi.org/10.3390/s18051536
Fromenteze T, Decroze C, Abid S, Yurduseven O. Sparsity-Driven Reconstruction Technique for Microwave/Millimeter-Wave Computational Imaging. Sensors. 2018; 18(5):1536. https://doi.org/10.3390/s18051536
Chicago/Turabian StyleFromenteze, Thomas, Cyril Decroze, Sana Abid, and Okan Yurduseven. 2018. "Sparsity-Driven Reconstruction Technique for Microwave/Millimeter-Wave Computational Imaging" Sensors 18, no. 5: 1536. https://doi.org/10.3390/s18051536
APA StyleFromenteze, T., Decroze, C., Abid, S., & Yurduseven, O. (2018). Sparsity-Driven Reconstruction Technique for Microwave/Millimeter-Wave Computational Imaging. Sensors, 18(5), 1536. https://doi.org/10.3390/s18051536