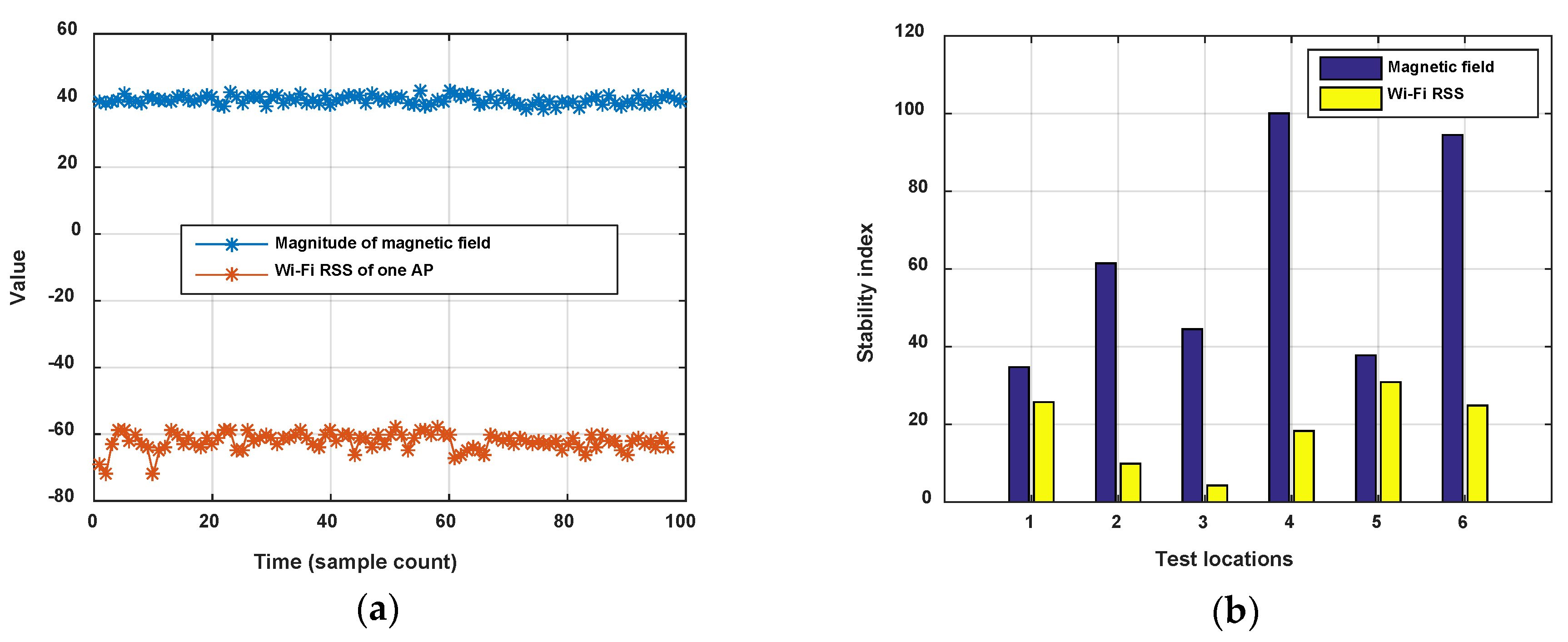
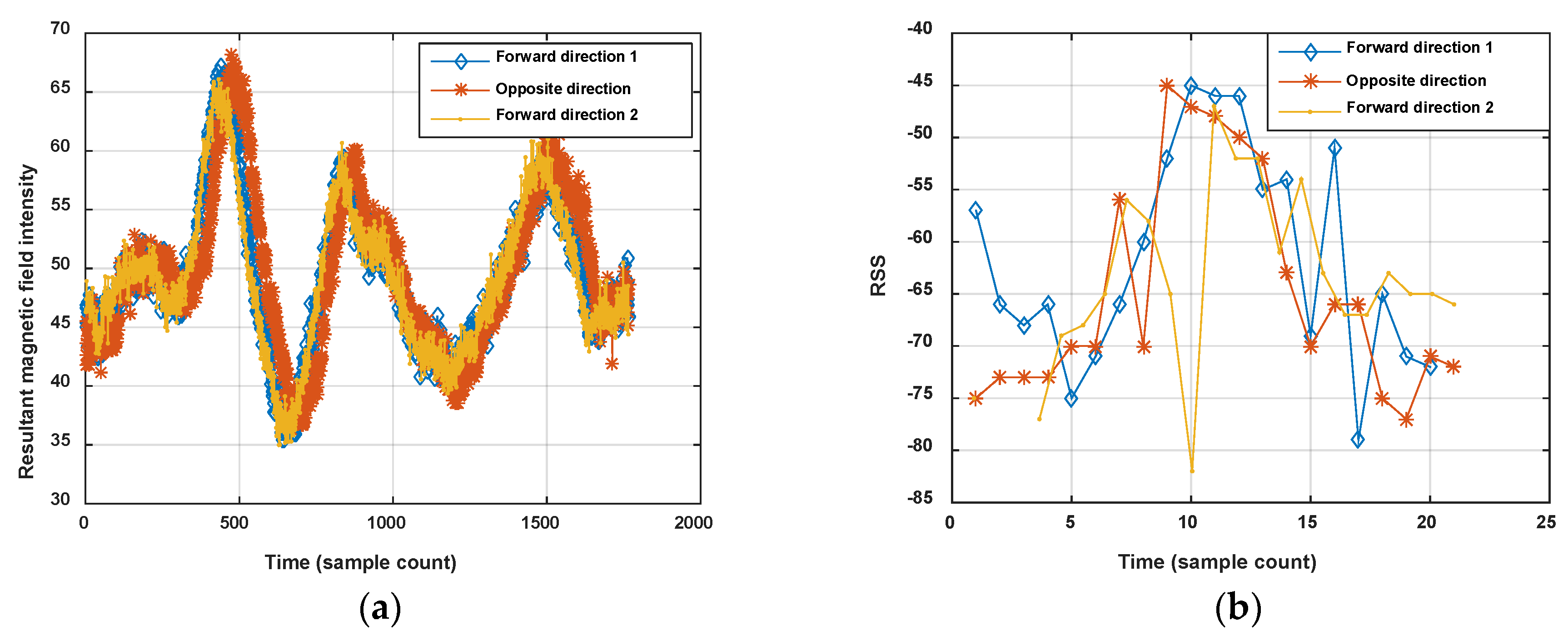
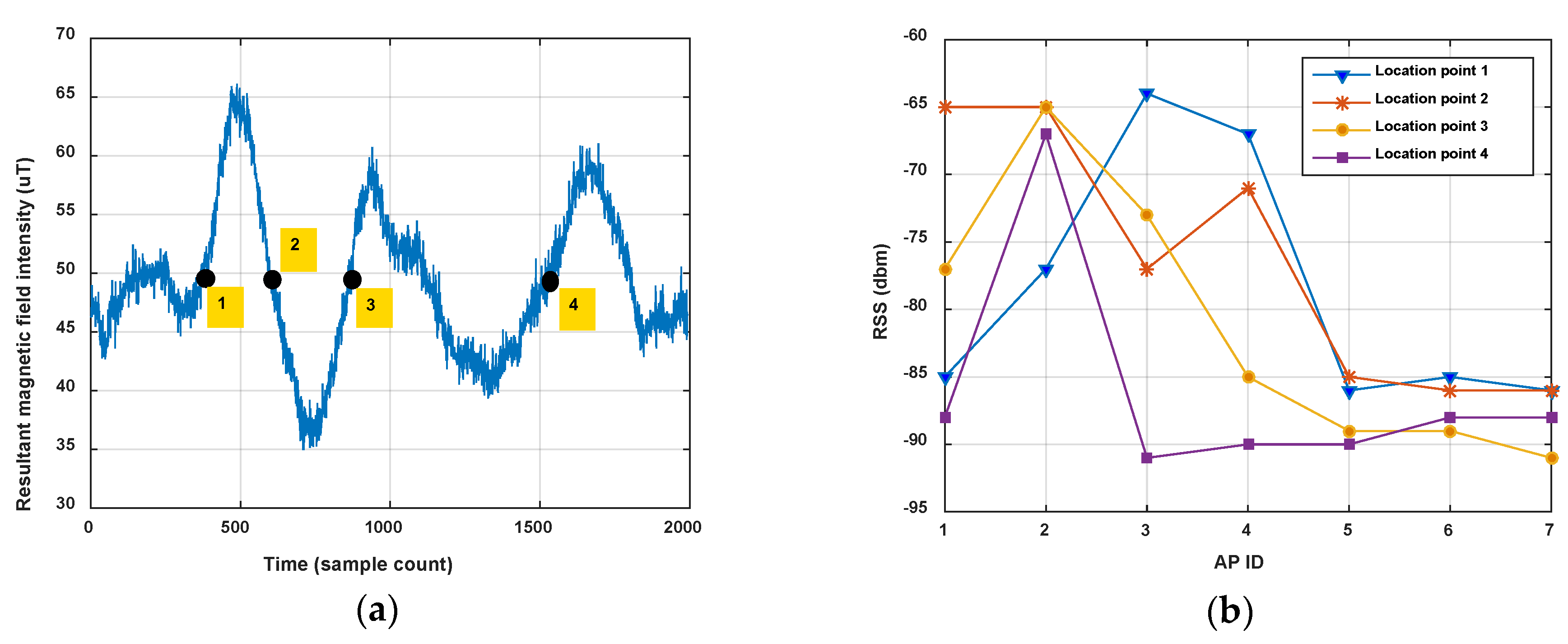
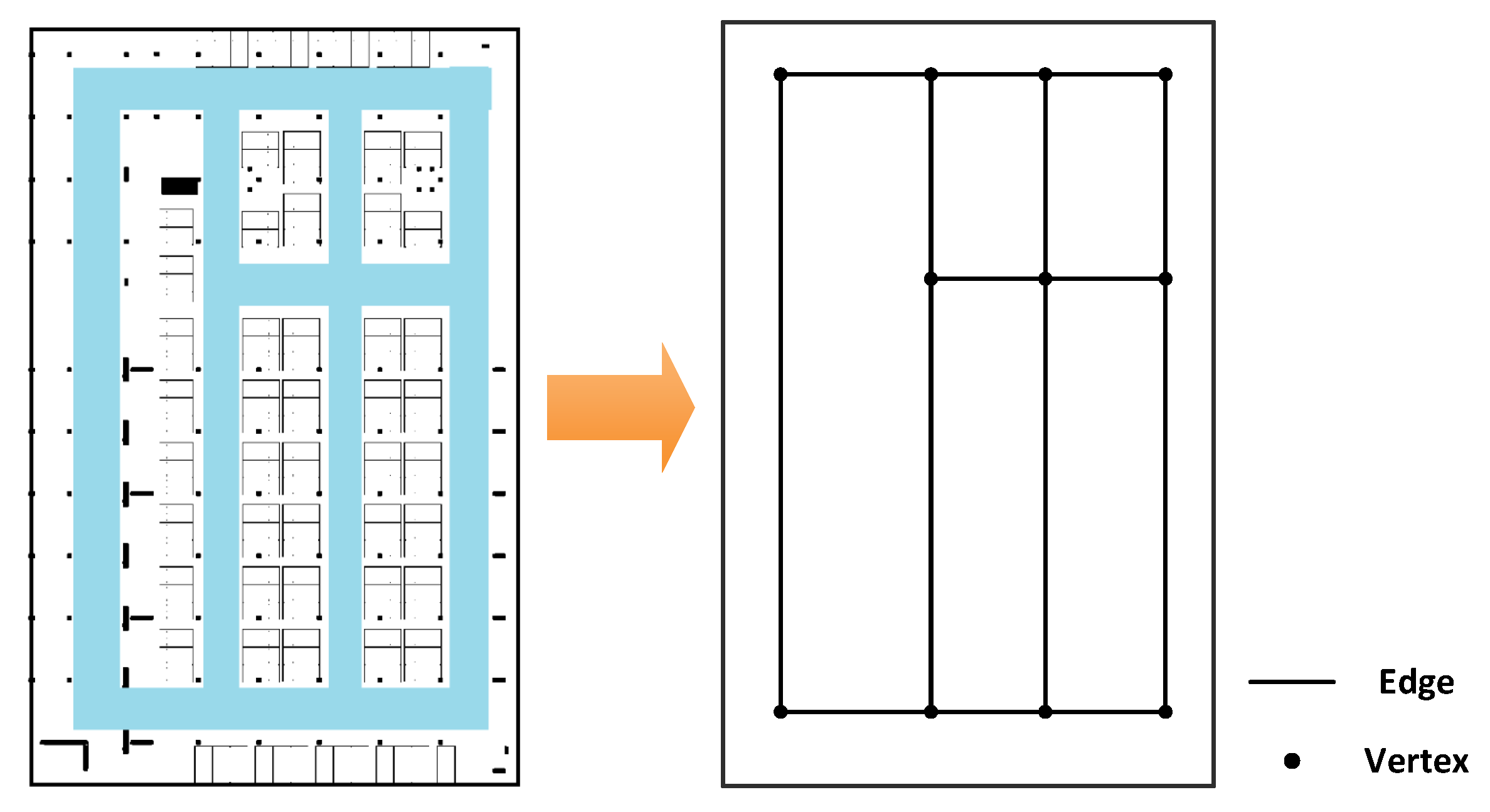
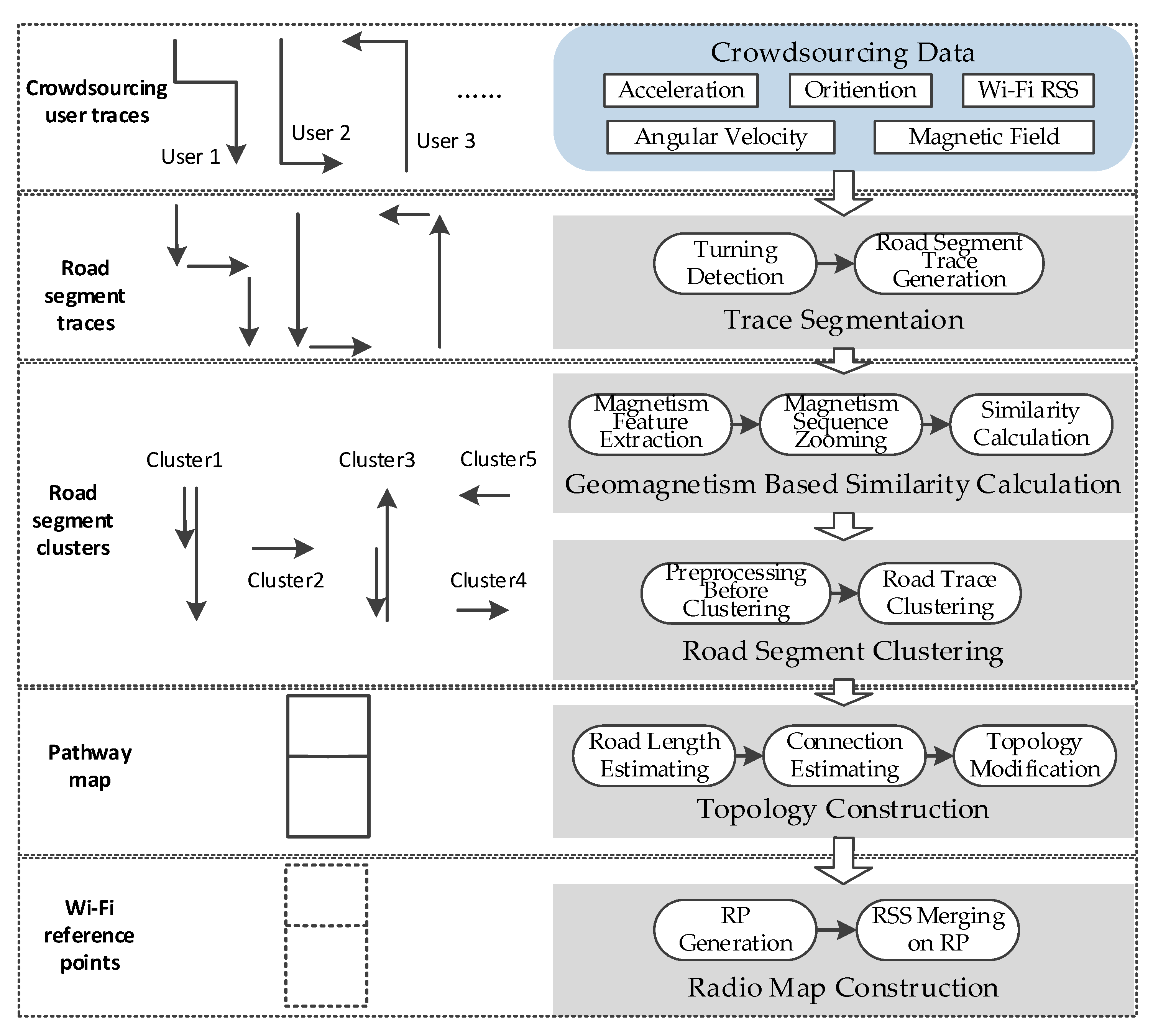
3.2.2. Sequence Zooming
In this part, we propose a method to zoom the distance scale of one magnetism sequence to another through magnetism features in order to match them together. It includes four key steps:
Step 1: First of all, we estimate the movement distance from the start point of the user trace to each magnetic field sampling time using an empirical stride length. Then two pairs of magnetism features from the two sequences are selected randomly as the initial assumed matching feature points, if the ratio of two estimated distances between features in each sequence is within a reasonable range of pedestrian stride length.
Step 2: Secondly, using the distance ratio calculated by the initial matching feature pairs, the remaining part of the second sequence is zoomed to the same stride length as the first one.
Step 3: Thirdly, to deal with the common case of uneven walking speed in one trace, the rest of the feature points from two sequences are matched together based on the initial matched features.
Step 4: Finally, the number of matched feature points is counted, and if the proportion of matched features is greater than the settled threshold, one time of Sequence Zooming is finished.
The details of the above steps will be respectively depicted in the following paragraphs.
(1) Initial Feature Matching
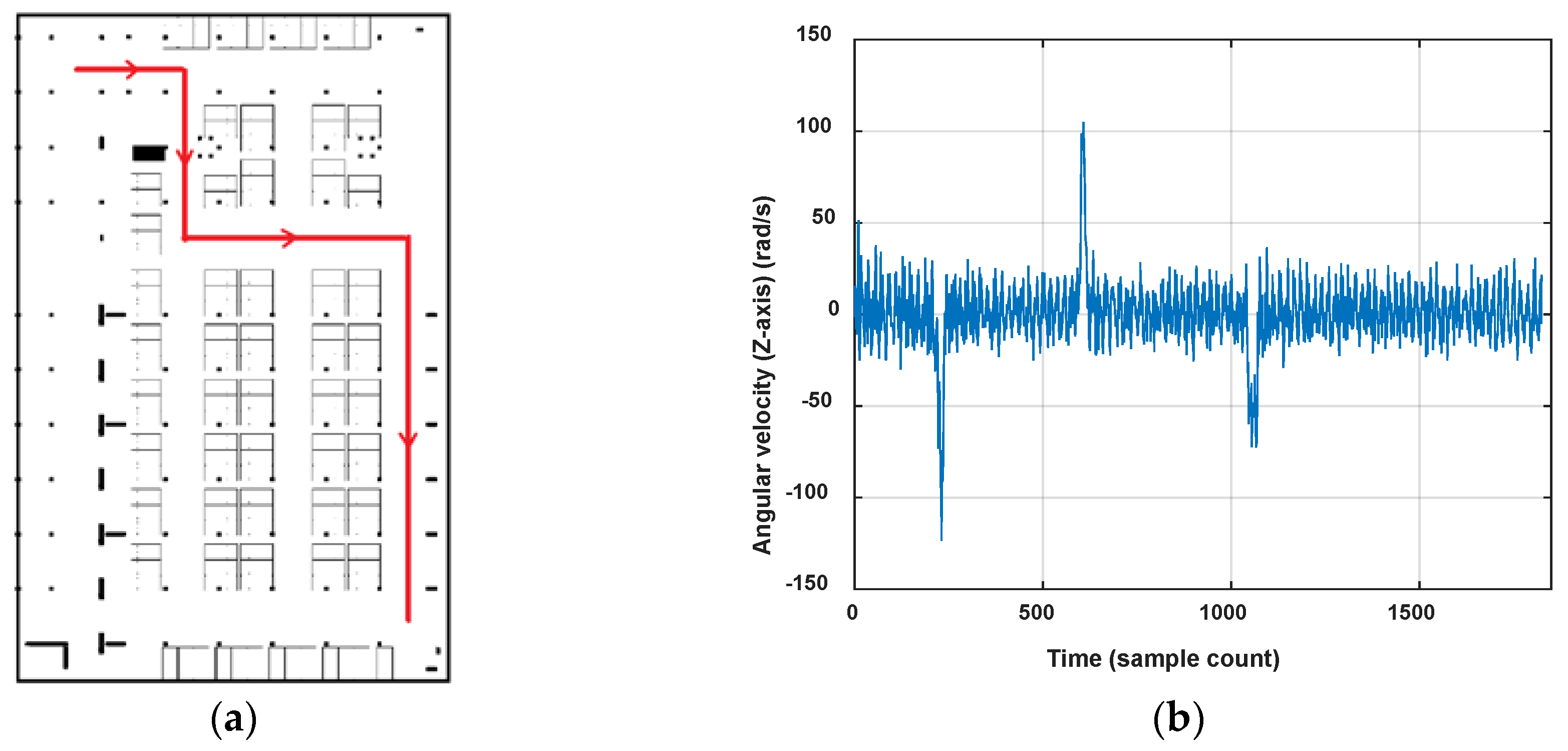
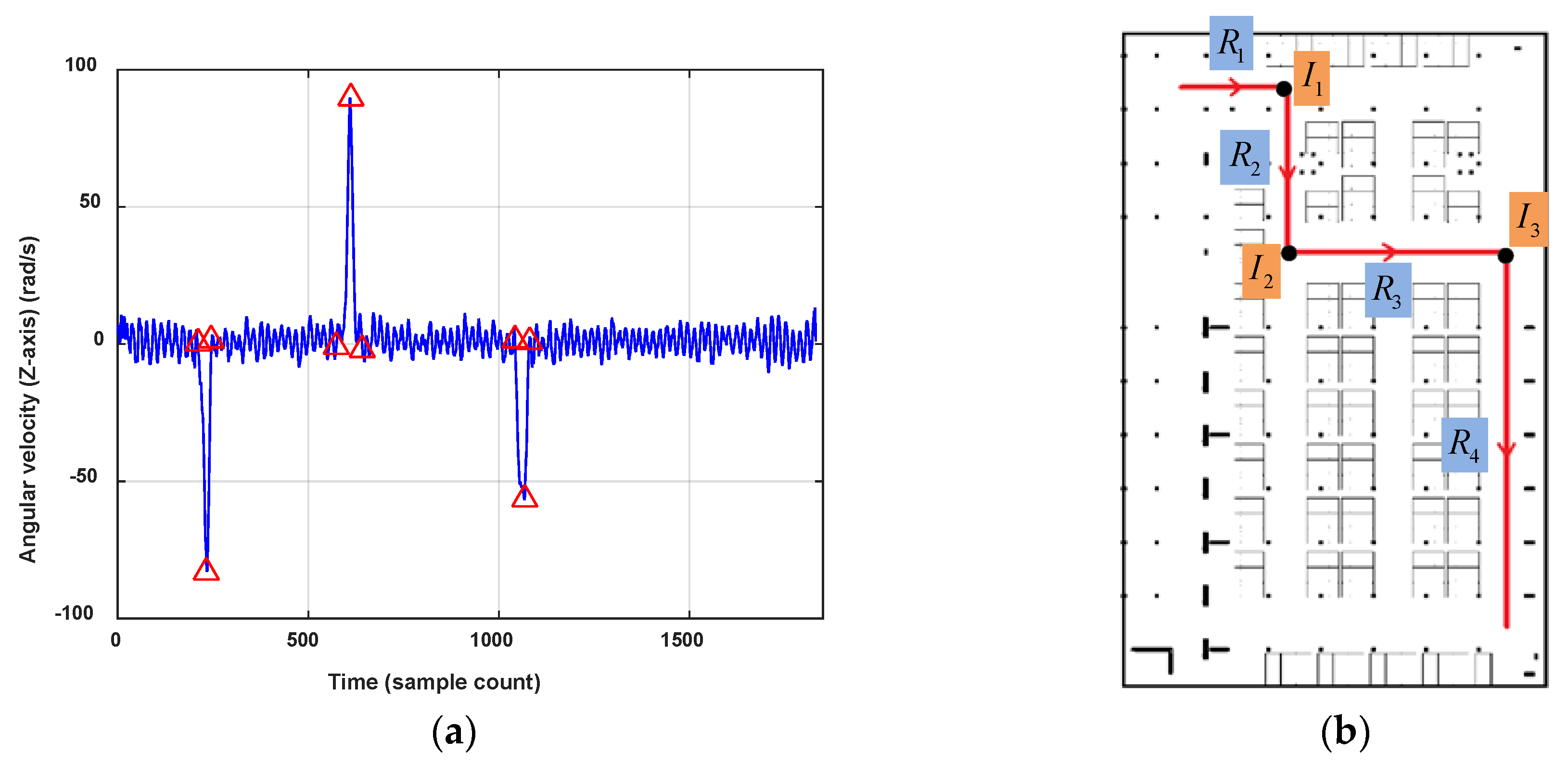
We use detected steps and stride length to estimate the trace length. The acceleration is utilized for step detection. The algorithm for step detection is the same as the Feature Extraction algorithm presented in 3.2.1. The detected peaks of resultant acceleration which satisfy the settled constraint are user steps, and the amount of steps is marked as
. Other algorithms can also be used to realize step detection, like the one described in [
31]. Stride length
is set as an empirical value like 0.6 m, so the length of the user trace is estimated by:
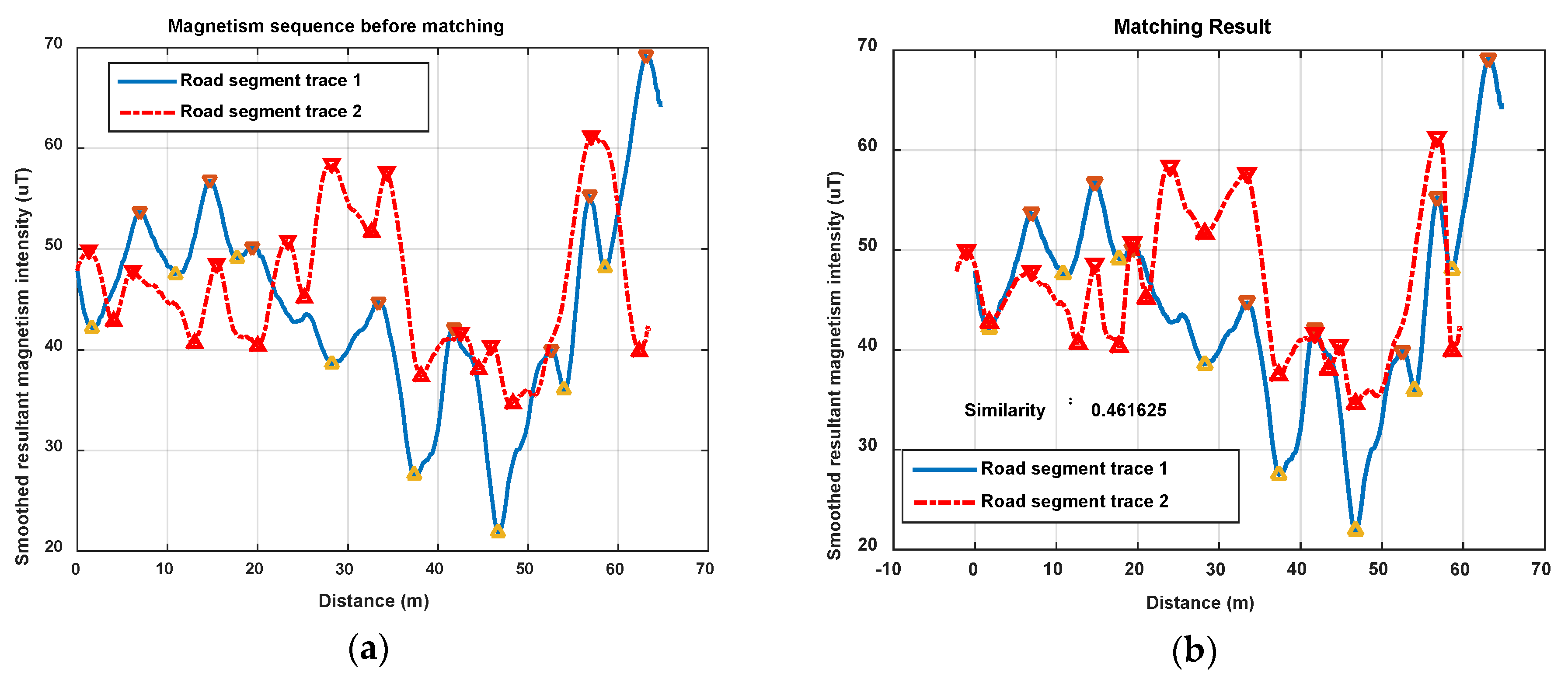
The trace length do not need to be exact, as it is only used to provide a rough distance between each magnetism feature, and the similarity of the queues of magnetism features is the main criterion to estimate whether two traces are generated on the same road segment. The procedures of features alignment and similarity calculation will be proposed in the following context.
When we get the length of the trace, the distances from start point of the trace to each magnetism sampling time, denoted as
, can be estimated by:
Here is the i-th count of magnetic field readings, is the total number of the field data on a road segment trace. We use a linear model here to estimate distance each time, for it is hard to get the exact walking speed of users, and the linear moving model will simplify the procedures to acquire a rough distance sequence. In case of the uneven walking speed in one trace, the magnetism features alignment will be implemented in Step 3.
Considering two road segment data of different users, denoted by and . The magnetism sequences of them are and , denoted as and . The data length of each sequences are respectively and . Though the above mentioned method, the distance sequences corresponding to and are obtained, denoted as and .
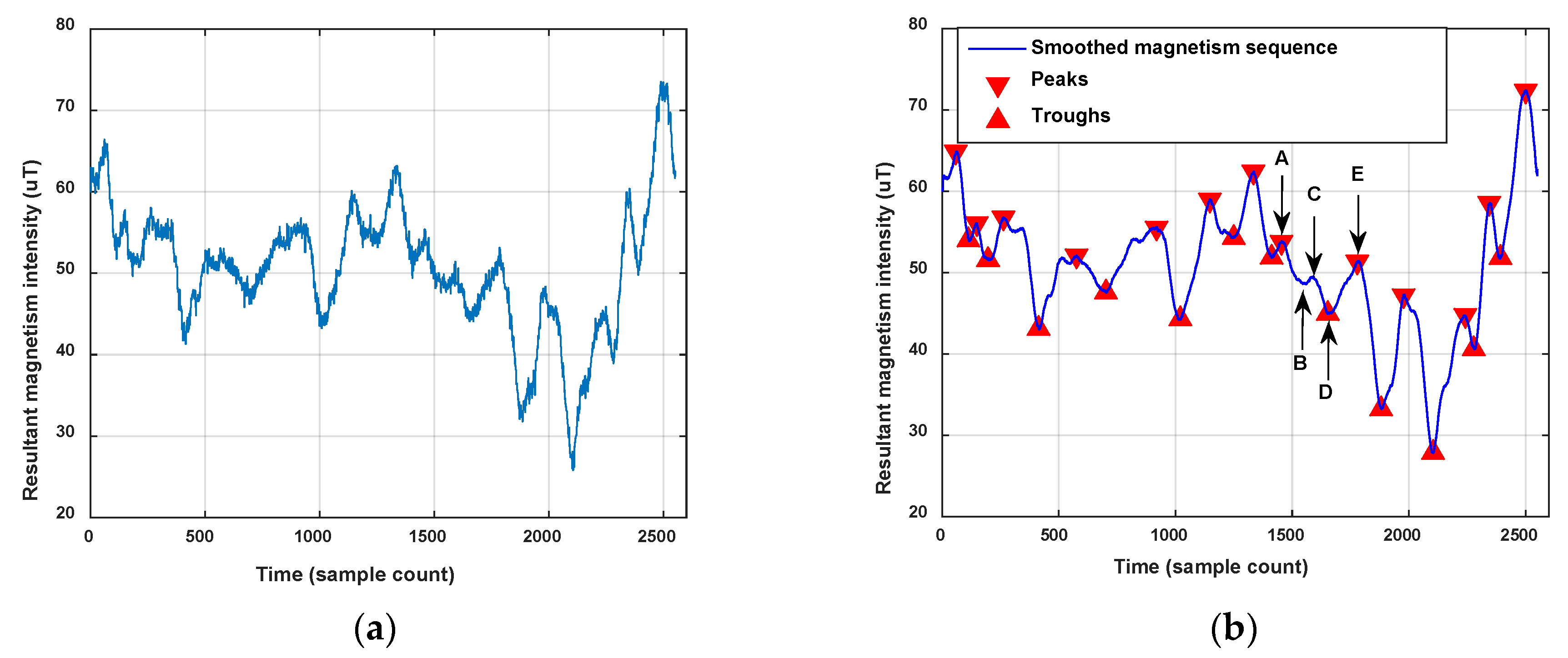
Then the magnetism features are extracted from
and
, recorded by
,
,
and
:
and
are respectively the total numbers of peaks and troughs in
. Similarly,
and
are respectively the total numbers of peaks and troughs in
.
At the beginning of Sequence Zooming, we pick up two couples of magnetism features respectively from
and
randomly. They are recorded by
,
(a feature point pair from
) and
,
(a feature point pair from
). The following constraint should be satisfied in selection of feature point pairs:
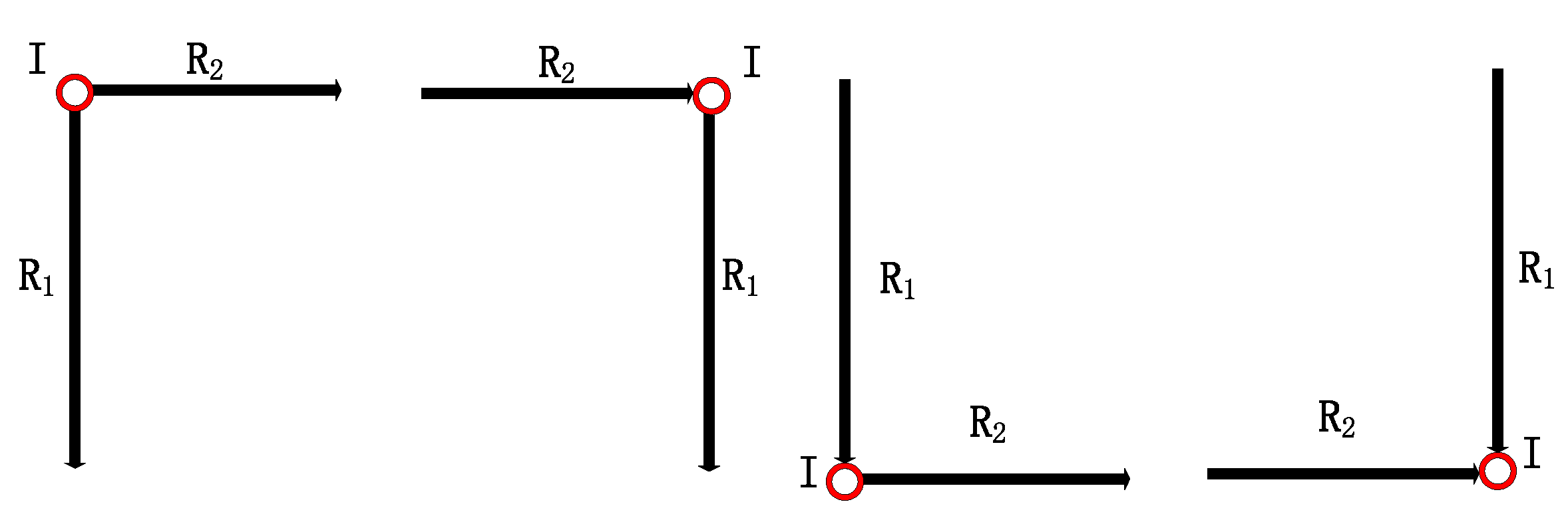
The above equation means that the feature point pairs from and should have the same pattern and same order in their queues. For example, when we choose as feature point couple in , we should use in to match with them. The subscripts a, b, c and d should meet the conditions and .
If
and
are generated at a same location point A, and at the same time,
and
are at a same location point B, the trace distances between
and
, as well as
and
would be equal, assuming that the walking paths on the road segment are unique for users, so we can obtain the following equality:
in which,
and
are respectively the number of detected steps from location A to B on road segment traces R1 and R2.
and
are the real stride length of users on R1 and R2.
is the actual trace length between location A and B. Stride length
is the empirical value that we use to estimate the distances from the start point to each magnetic field sampling point, so it can also be obtained that:
Then the stride length ratio is reckoned as:
The normal range of pedestrian stride lengths is about 0.4 m to 0.8 m, so the stride length ratio should be on the range of [0.5, 2]. When the calculated is in this range, the feature points (,) and (,) can be assumed as the initial matched feature points of R1 and R2. On the contrary, if is out of this range, this procedure will be implemented again for another pair of feature points, until the initial matched points are found.
(2) Rough Zooming
Based on the initial matched feature points (
,
), the data on
will be zoomed using
, and
will be translated to
. The new distance sequence is calculated by the following equation:
here
. Then we get a new distance sequence
for R2.
may have some negative data, for its start point would not be the same as for R1.
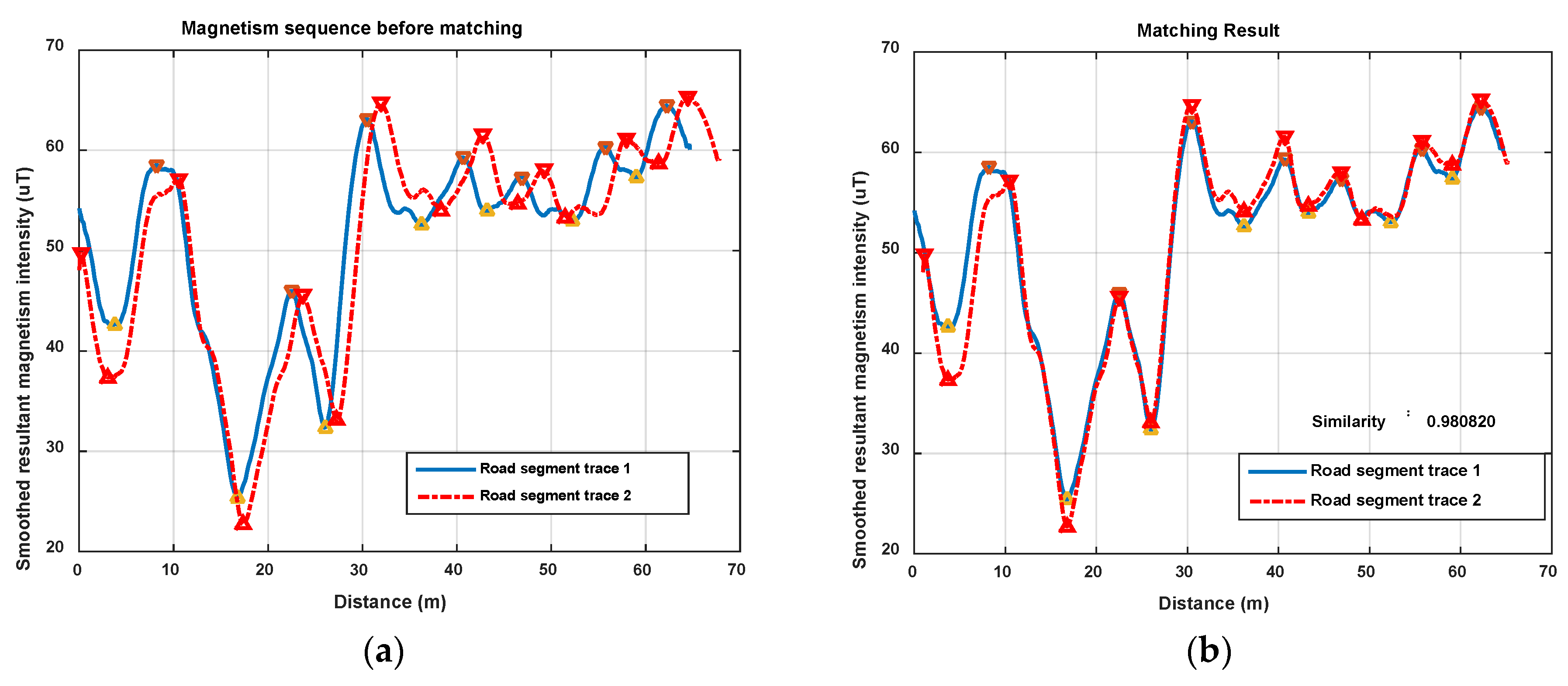
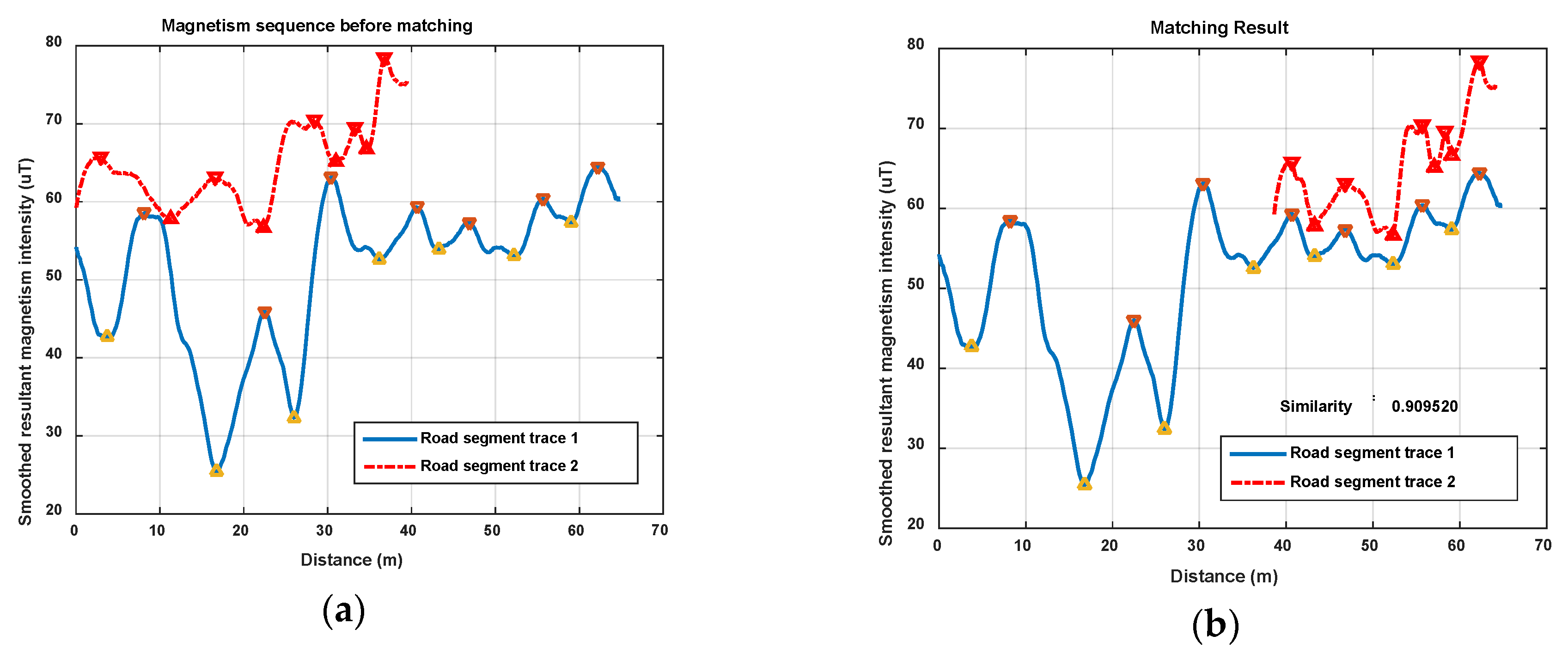
After rough zooming in the above procedure, the magnetism feature points on R2 are basically matched together with those on R1 if the initial matching points (,) are correct. Because of the rough zooming is an even zooming only based on the scalar , if users’ walking speeds are uneven, which is a very common situation, the feature points will not match well only by rough zooming. The following step is designed to deal with this issue.
(3) Features Alignment
In this step, the feature points in R2 are aligned based on the current initial matched feature points ((,) and (,)) and matched with other feature points in R1 using the principle of proximity. Therefore, when the initial matched feature points are really sampled on the same location point, the Features Alignment would make other feature points on R2 and R1 match exactly, so that the magnetism similarity of R1 and R2 can be calculated accurately. When the initial assumed matching feature points are not matched correctly, this procedure will also be carried out and the final matching result will be judged by the result of Similarity Calculation in the following step.
We denote the assemblage of aligned feature points as
. Based on the initial matched feature points, the initial of the assemblage
is shown in the following:
For the peak
, the candidate matching area in R1 is settled at first, which is indicated by
. The edge of matching area is the feature points of R1 in
, whose matched feature points in R2 are the closest ones respectively to left and right side of
. This can be expressed as:
When only has one side neighbor with aligned feature points, then the matching area will be settled as or . is the data length of .
Then all the peaks of R1 in the range of are traversed to find the matching point of . The matching point would satisfy two requirements, including:
The difference between and is minimum compared with other candidate peaks. For the have been accorded with , the difference between them indicates the probable location distance between and , and the closest pair may have the biggest probability to be sampled on a same location.
In case of some feature points are undetected, and R1 and R2 have different trace lengths, we set a distance threshold to restrict the difference of distance between matching points. The in this paper is settled as an empirical value.
The matching qualification is expressed by the following equation:
The matched peak couples would be added into as a new element , and further used for matching area choosing of the new prepared for alignment.
For the troughs , the same method is implemented to find the matching troughs in R1. At the same time, the matched trough couples will also be added into as a new element, recorded by .
For the matched feature couples should be apparent in same order both in R1 and R2, and peaks and troughs should appear alternately, the element in
(all the matched peaks and troughs) will be resolved by the data order of feature points in
(or feature points in
). Finally, we obtained all the matched feature couples in
:
is the total number of matched feature couples between R1 and R2.
Then, based on the matched feature pairs in
, the
would be updated using the following equation:
It means that all the matched feature points in R2 will be aligned to the same distance of in R1 and the distance of other sample points will be zoomed using the local ratio, estimated by the closest two feature point couples. In the start or end part of the R2, only translation is implemented to the , since the zooming ratio cannot be estimated only by one pair of matched feature point. Finally, we get the updated distance sequence for R2.
(4) Matched Features Amount Judgment
In this step we count the amount of matched feature couples in
, and calculate the matching proportion
using the following equation:
and
are respectively total numbers of peaks and troughs in
.
and
are respectively the total numbers of peaks and troughs in
.
is the total number of matched feature pairs between
and
. When
is greater than the settled threshold
, one time of Sequence Zooming is finished.