Non-Invasive Detection of Respiration and Heart Rate with a Vehicle Seat Sensor
Abstract
:1. Introduction
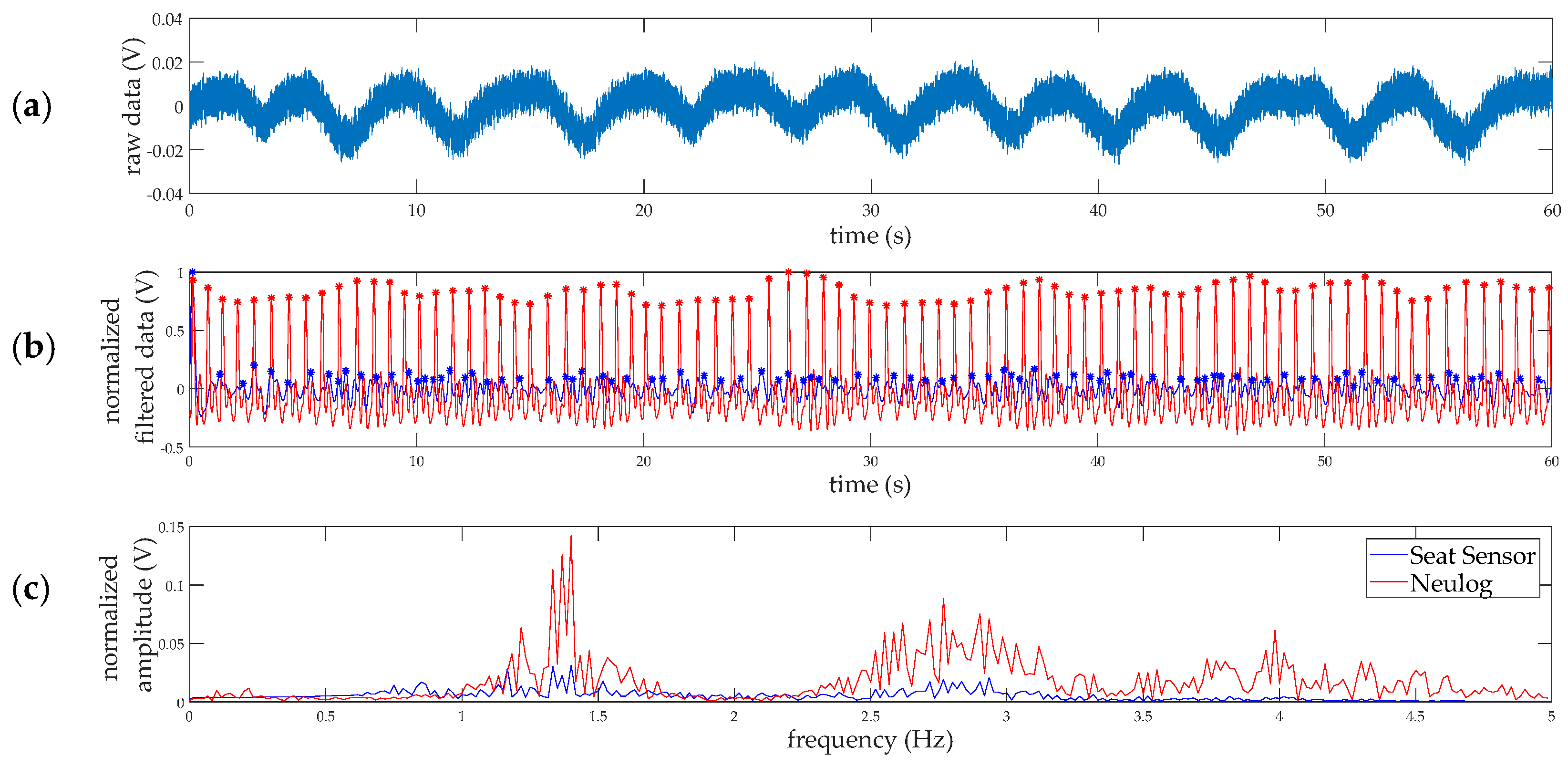
2. Materials and Methods
2.1. Respiration Rate (RR)
2.2. Heart Rate (HR)
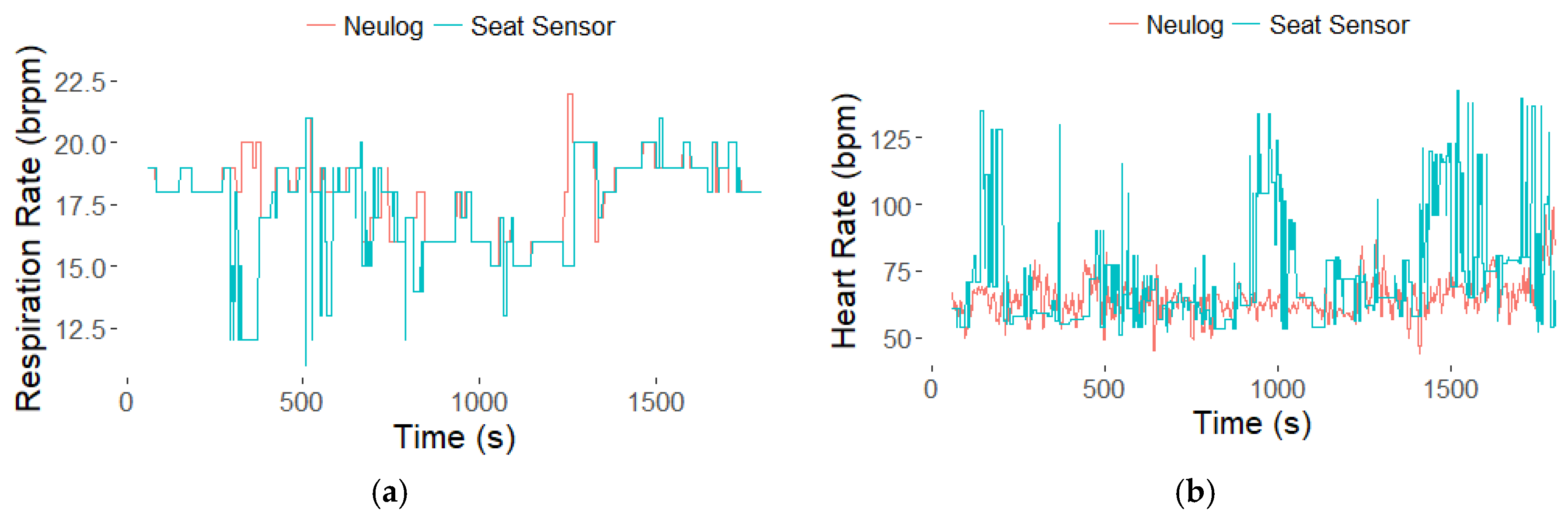
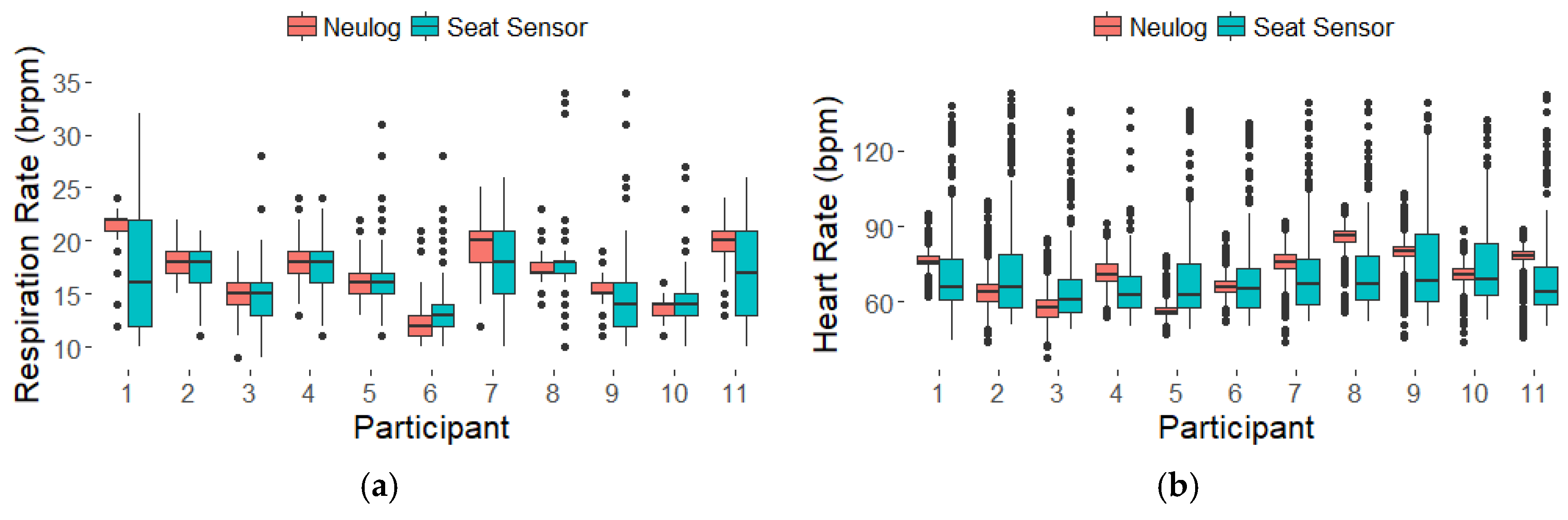
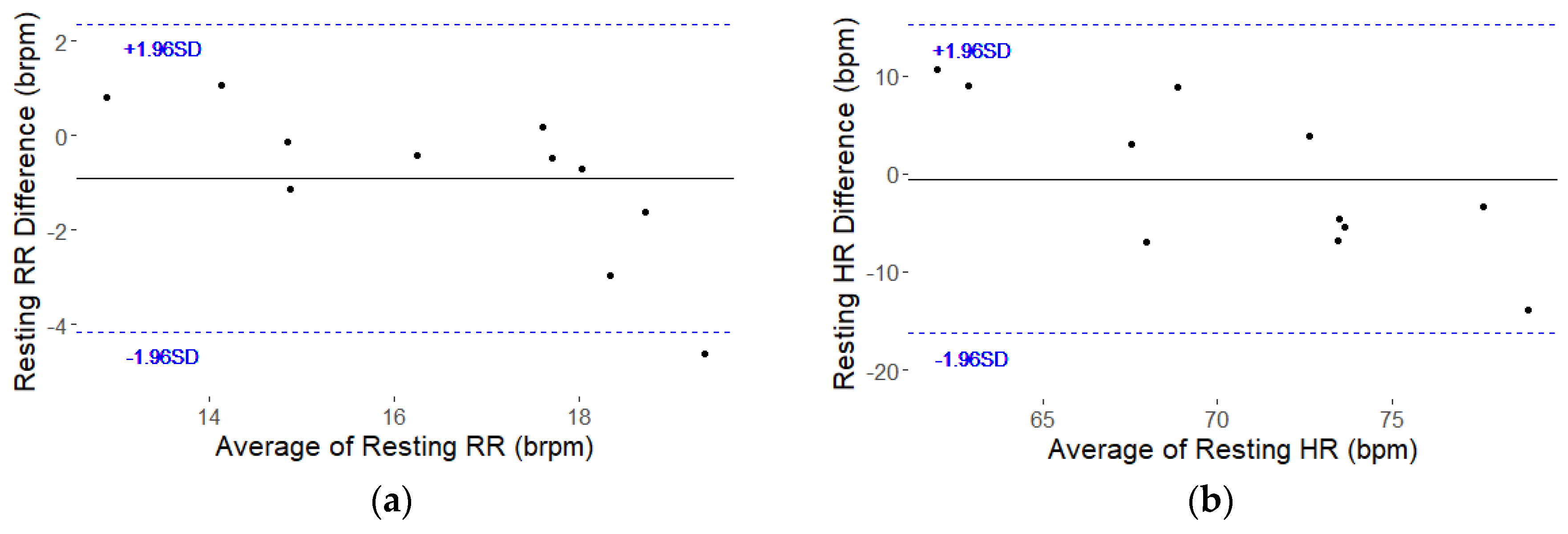
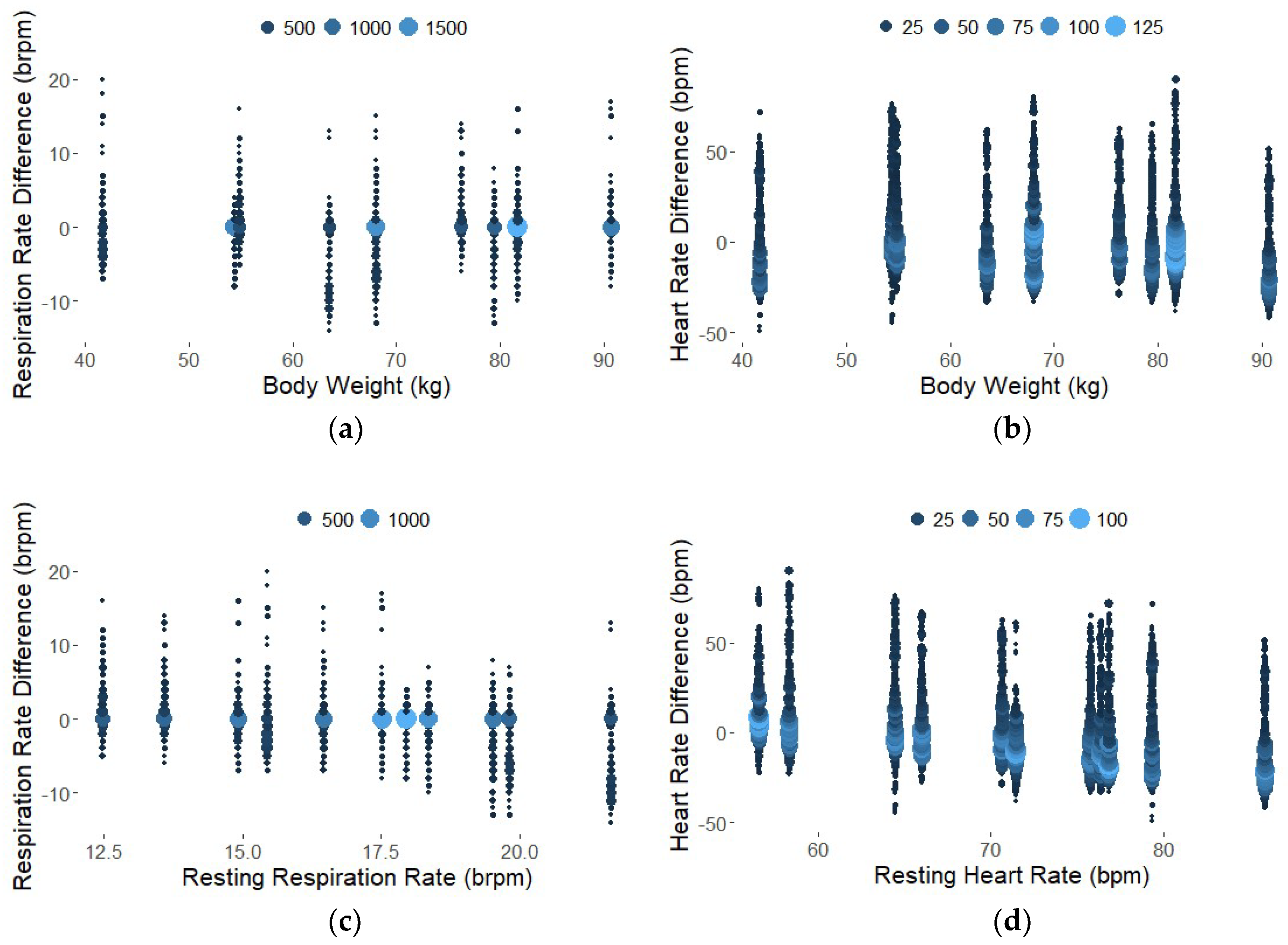
3. Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kusano, K.; Gabler, H.C. Comparison and validation of injury risk classifiers for advanced automated crash notification systems. Traffic Inj. Prev. 2014, 15, 126–133. [Google Scholar] [CrossRef] [PubMed]
- Kusano, K.D.; Gabler, H.C. Automated crash notification: Evaluation of in-vehicle principal direction of force estimations. Transp. Res. C Emerg. Technol. 2013, 32, 116–128. [Google Scholar] [CrossRef]
- Kononen, D.W.; Flannagan, C.A.C.; Wang, S.C. Identification and validation of a logistic regression model for predicting serious injuries associated with motor vehicle crashes. Accid. Anal. Prev. 2011, 43, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Bahouth, G.; Digges, K.; Schulman, C. Influence of injury risk thresholds on the performance of an algorithm to predict crashes with serious injuries. Ann. Adv. Automot. Med. 2012, 56, 223–230. [Google Scholar] [PubMed]
- Weiser, M. The Computer for the 21st Century. Sci. Am. 1991, 265, 94–104. [Google Scholar] [CrossRef]
- Walter, M.; Eilebrecht, B.; Wartzek, T.; Leonhardt, S. The smart car seat: Personalized monitoring of vital signs in automotive applications. Pers. Ubiquitous Comput. 2011, 15, 707–715. [Google Scholar] [CrossRef]
- Kim, C.-S.; Ober, S.L.; Mcmurtry, M.S.; Finegan, B.A.; Inan, O.T.; Mukkamala, R.; Hahn, J.-O. Ballistocardiogram: Mechanism and potential for unobtrusive cardiovascular health monitoring. Sci. Rep. 2016, 6, 31297. [Google Scholar] [CrossRef] [PubMed]
- Inan, O.T.; Migeotte, P.-F.; Park, K.-S.; Etemadi, M.; Tavakolian, K.; Casanella, R.; Zanetti, J.; Tank, J.; Funtova, I.; Prisk, G.K.; et al. Ballistocardiography and seismocardiography: A review of recent advances. IEEE J. Biomed. Health Inform. 2014, 19, 1414–1427. [Google Scholar] [CrossRef] [PubMed]
- Pinheiro, E.; Postolache, O.; Girão, P. Study on ballistocardiogram acquisition in a moving wheelchair with embedded sensors. Metrol. Meas. Syst. 2012, 19, 739–750. [Google Scholar] [CrossRef]
- Inan, O.T.; Etemadi, M.; Widrow, B.; Kovacs, G.T.A. Adaptive cancellation of floor vibrations in standing ballistocardiogram measurements using a seismic sensor as a noise reference. IEEE Trans. Biomed. Eng. 2010, 57, 722–727. [Google Scholar] [CrossRef] [PubMed]
- Junnila, S.; Akhbardeh, A.; Värri, A. An electromechanical film sensor based wireless ballistocardiographic chair: Implementation and performance. J Signal Process. Syst. 2009, 57, 305–320. [Google Scholar] [CrossRef]
- Barleanu, A.; Hagan, M.; Geman, O.; Chiuchisan, I. Wearable ballistocardiography system for heartbeat detection. In Proceedings of the 2016 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 20–22 October 2016; pp. 294–298. [Google Scholar] [CrossRef]
- Mack, D.C.; Patrie, J.T.; Suratt, P.M.; Felder, R.A.; Alwan, M. Development and preliminary validation of heart rate and breathing rate detection using a passive, ballistocardiography-based sleep monitoring system. IEEE Trans. Inform. Technol. Biomed. 2009, 13, 111–120. [Google Scholar] [CrossRef] [PubMed]
- David, H.; Marjorie, S. Monitoring pulse and respiration with a non-invasive hydraulic bed sensor. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 2119–2123. [Google Scholar]
- Magno, M.; Spagnol, C.; Benini, L.; Popovici, E. A low power wireless node for contact and contactless heart monitoring. Microelectron. J. 2014, 45, 1656–1664. [Google Scholar] [CrossRef]
- Neri, B.; Saponara, S. Advances in technologies, architectures, and applications of highly-integrated low-power radars. IEEE Aerosp. Electron. Syst. Mag. 2012, 27, 25–36. [Google Scholar] [CrossRef]
- Sarkar, A.; Abbott, A.L.; Doerzaph, Z. Assessment of psychophysiological characteristics using heart rate from naturalistic face video data. In Proceedings of the IEEE International Joint Conference on Biometrics, Clearwater, FL, USA, 29 September–2 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, H.-Y.; Rubinstein, M.; Shih, E.; Guttag, J.; Durand, F.; Freeman, W. Eulerian video magnification for revealing subtle changes in the world. ACM Trans. Graph. 2012, 31, 1–8. [Google Scholar] [CrossRef]
- Occupant Crash Protection; Federal Motor Vehicle Safety Standards. Federal Register. 2000. Available online: https://www.federalregister.gov/documents/2000/05/12/00-11577/federal-motor-vehicle-safety-standards-occupant-crash-protection (accessed on 7 May 2018).
- Peper, E.; Harvey, R.; Lin, I.-M.; Tylova, H.; Moss, D. Is there more to blood volume pulse than heart rate variability, respiratory sinus arrhythmia, and cardiorespiratory synchrony? Biofeedback 2007, 35, 54–61. [Google Scholar]
- Altman, D.G.; Bland, J.M. Measurement in medicine: The analysis of method comparison studies. Statistician 1983, 32, 307–317. [Google Scholar] [CrossRef]
- Zaki, R.; Bulgiba, A.; Ismail, R.; Ismail, N.A. Statistical methods used to test for agreement of medical instruments measuring continuous variables in method comparison studies: A systematic review. PLoS ONE 2012, 7, e37908. [Google Scholar] [CrossRef] [PubMed]
- Shah, Y.; Dunn, J.; Huebner, E.; Landry, S. Wearables data integration: Data-driven modeling to adjust for differences in Jawbone and Fitbit estimations of steps, calories, and resting heart-rate. Comput. Ind. 2017, 86, 72–81. [Google Scholar] [CrossRef]
- Schmidt, E.; Decke, R.; Rasshofer, R. Correlation between subjective driver state measures and psychophysiological and vehicular data in simulated driving. In Proceedings of the IEEE Intelligent Vehicles Symposium, Gothenburg, Sweden, 19–22 June 2016; pp. 1380–1385. [Google Scholar] [CrossRef]
- Victorino, G.P.; Battistella, F.D.; Wisner, D.H. Does tachycardia correlate with hypotension after trauma? J. Am. Coll. Surg. 2003, 196, 679–684. [Google Scholar] [CrossRef]
- Center for Health Statistics N. Anthropometric Reference Data for Children and Adults: United States. 2011. Available online: https://www.cdc.gov/nchs/data/series/sr_03/sr03_039.pdf (accessed on 7 May 2018).


| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Gender | F | F | M | M | F | F | F | F | F | M | F |
| Weight (kg) | 64 | 54 | 82 | 82 | 68 | 55 | 79 | 91 | 42 | 76 | 68 |
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RR | Seat (brpm) | 17 | 17 | 15 | 18 | 16 | 13 | 18 | 18 | 14 | 15 | 17 |
| Neulog (brpm) | 22 | 18 | 15 | 18 | 16 | 12 | 20 | 18 | 15 | 14 | 20 | |
| Difference (brpm) | −5 | −1 | 0 | 0 | 0 | 1 | −2 | 0 | −1 | 1 | −3 | |
| HR | Seat (bpm) | 71 | 73 | 67 | 65 | 67 | 69 | 71 | 72 | 76 | 75 | 70 |
| Neulog (bpm) | 76 | 64 | 58 | 71 | 57 | 66 | 76 | 86 | 79 | 71 | 77 | |
| Difference (bpm) | −5 | 9 | 9 | −6 | 10 | 3 | −5 | −14 | −3 | 4 | −7 |
| Signal | Units | Analysis Method | Difference Mean | Difference SD | Difference 95% CI | RMSE | R2 |
|---|---|---|---|---|---|---|---|
| RR | brpm | Peaks | −2.5 | 2.9 | (−8.3; 3.3) | 2.5 | 0.16 |
| FFT | −0.91 | 3.3 | (−7.5; 5.7) | 2.8 | 0.22 | ||
| HR | bpm | Peaks | −23 | 13 | (−48; 2.9) | 9.9 | 0.0019 |
| FFT | −0.50 | 19 | (−39; 38) | 9.9 | 0.0043 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wusk, G.; Gabler, H. Non-Invasive Detection of Respiration and Heart Rate with a Vehicle Seat Sensor. Sensors 2018, 18, 1463. https://doi.org/10.3390/s18051463
Wusk G, Gabler H. Non-Invasive Detection of Respiration and Heart Rate with a Vehicle Seat Sensor. Sensors. 2018; 18(5):1463. https://doi.org/10.3390/s18051463
Chicago/Turabian StyleWusk, Grace, and Hampton Gabler. 2018. "Non-Invasive Detection of Respiration and Heart Rate with a Vehicle Seat Sensor" Sensors 18, no. 5: 1463. https://doi.org/10.3390/s18051463
APA StyleWusk, G., & Gabler, H. (2018). Non-Invasive Detection of Respiration and Heart Rate with a Vehicle Seat Sensor. Sensors, 18(5), 1463. https://doi.org/10.3390/s18051463





