Impact Assessment of GNSS Spoofing Attacks on INS/GNSS Integrated Navigation System
Abstract
:1. Introduction
- Based on the authentic and spoofed signal model, a comparison between unsynchronized and synchronized GNSS spoofing attacks is given. A framework for a measurement-level trajectory spoofing simulation is proposed, which simplifies the process of impact assessment for integrated navigation systems.
- We systematically analyze the impact of spoofing on the integrated navigation filter’s error covariance, innovation and inertial sensor bias estimation, revealing how the conventionally used Kalman filer responds to spoofing attacks.
- According to the impact assessment, we make recommendations for the cautious use of (1) error covariance for integrity monitoring, and (2) calibrated inertial sensors for pure INS solutions. Spoofing detection methods based on innovations and inertial sensor bias monitoring are suggested.
2. INS/GNSS Integrated Navigation Model
3. GNSS Spoofing Attacks and Measurement-Level Simulation
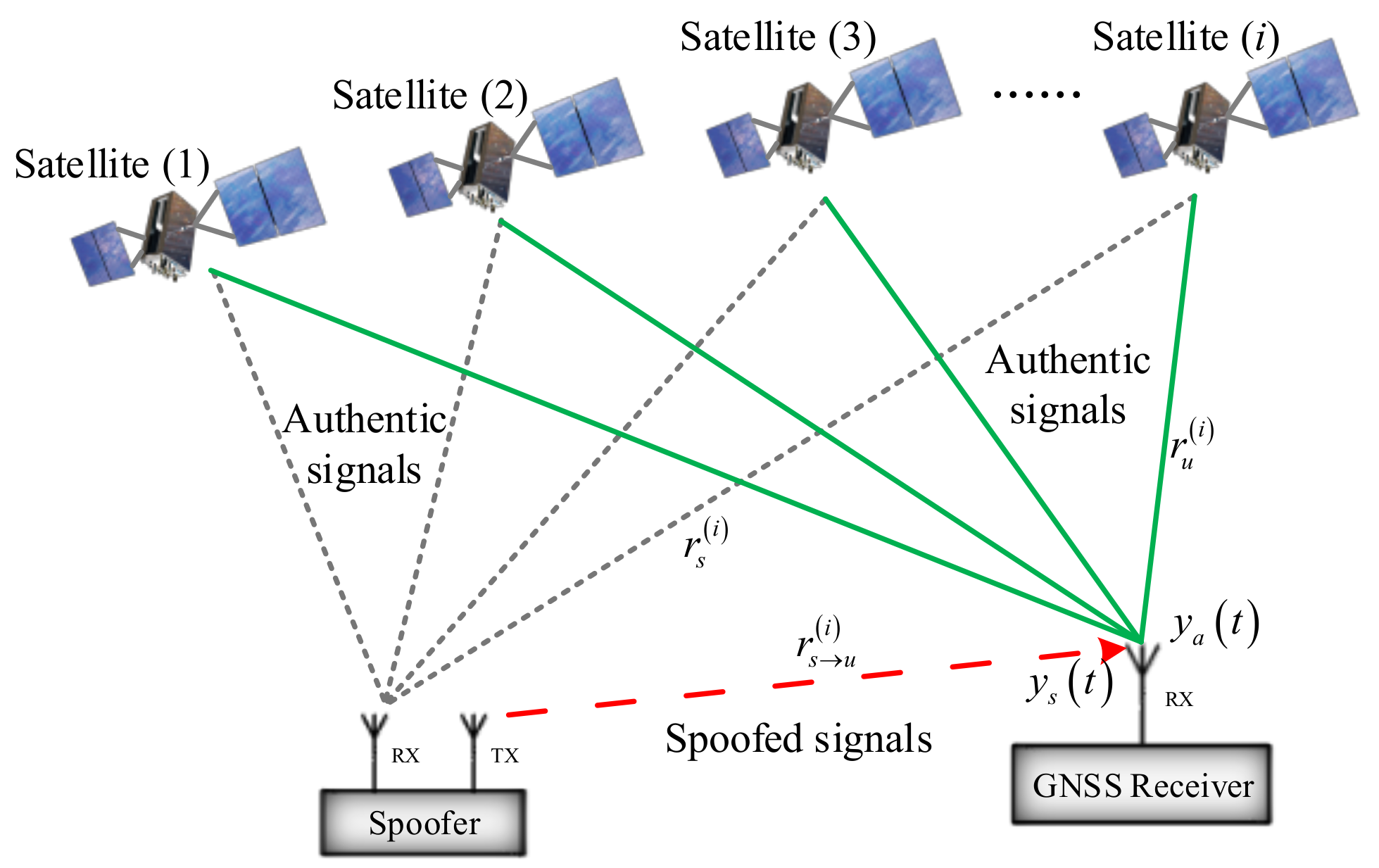
3.1. GNSS Spoofing Attacks
3.2. Measurement-Level Spoofing Attack Simulation
- When is determined, the components and in Equation (13) can be calculated accordingly. They are added to the authentic measurements generated based on to construct the spoofed measurements. In this way, the critical parameters of the spoofer can also be simulated.
- If we only focus on the INS/GNSS integrated navigation system, a simpler method can be used without direct calculation of and . This is done by directly feeding and to the GNSS measurement-level simulator as two independent trajectories. A switch from to during the simulation can easily introduce the spoofed measurements to the integrated navigation system.
4. Impact Assessment and Recommendations
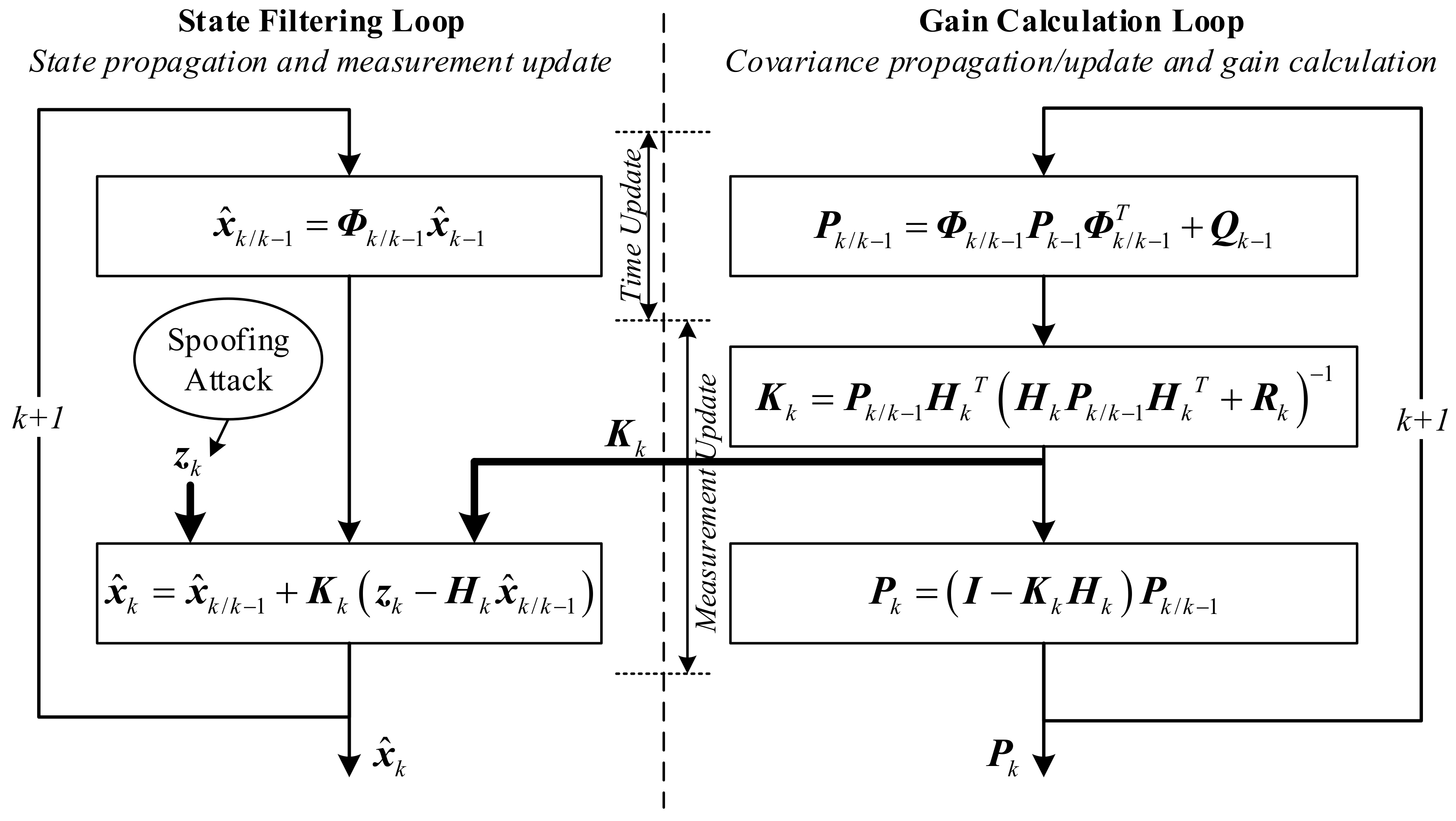
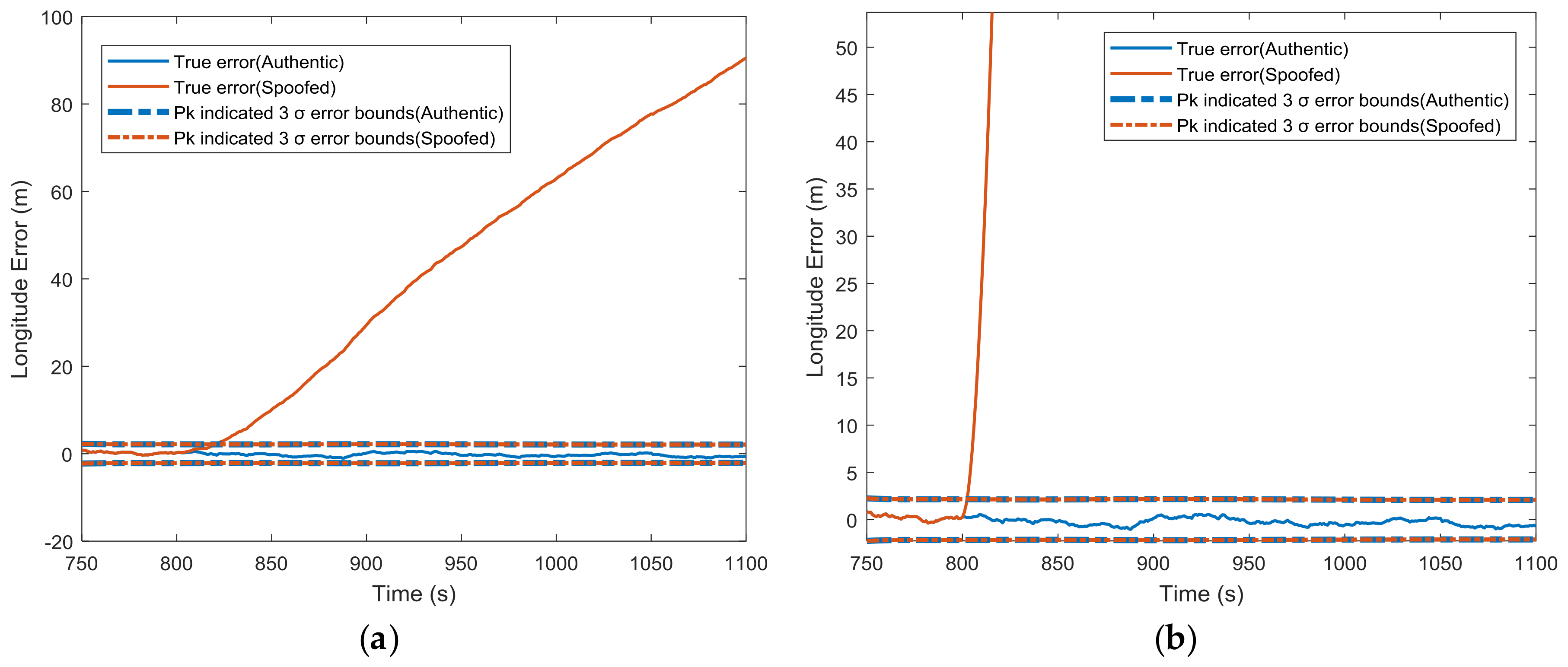
4.1. Error Covariance
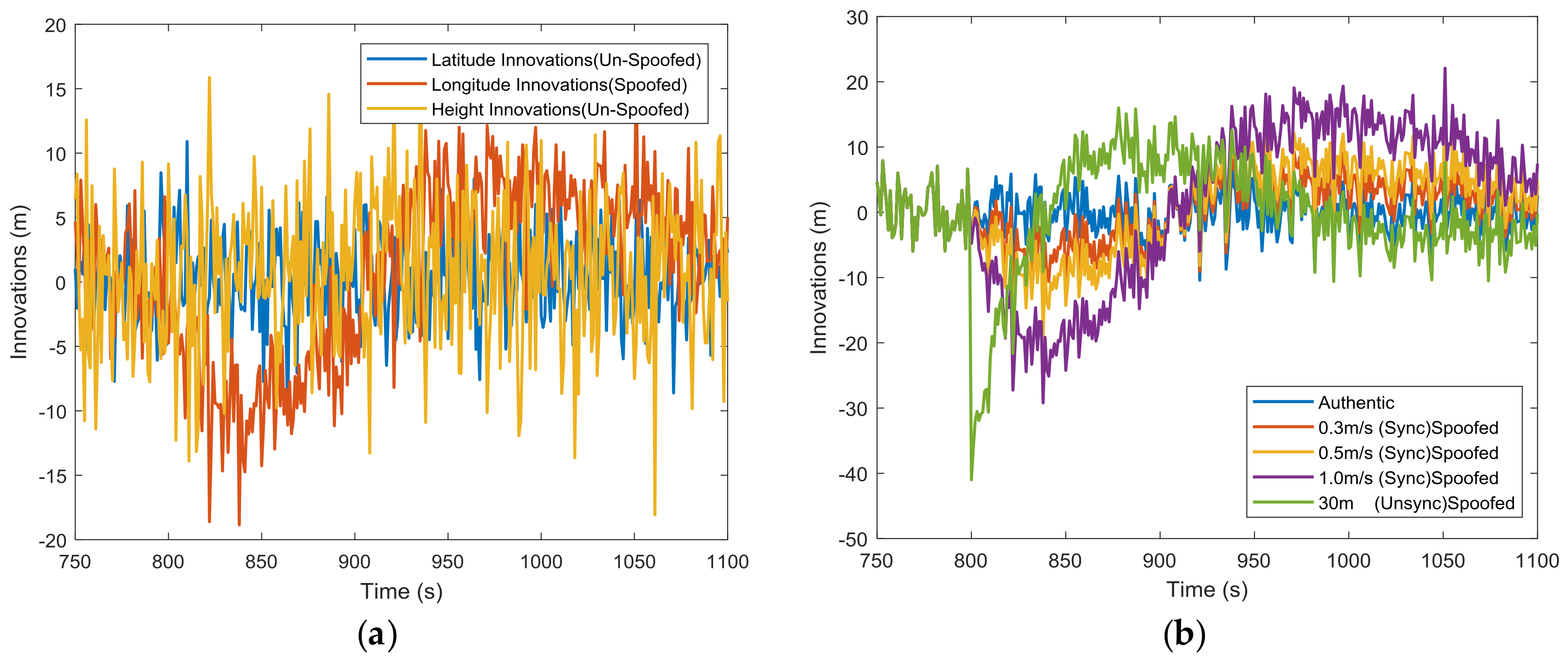
4.2. Kalman Filter Innovation
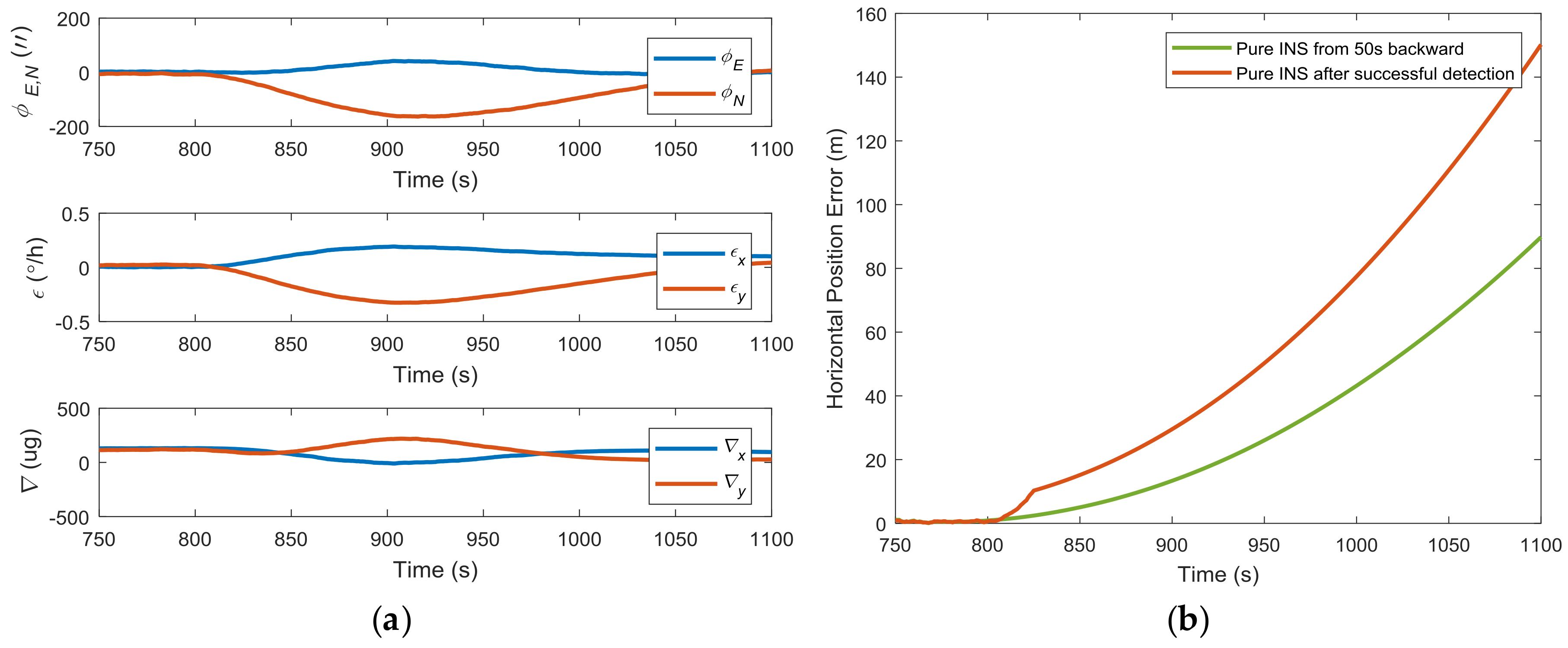
4.3. Inertial Sensor Bias Estimation
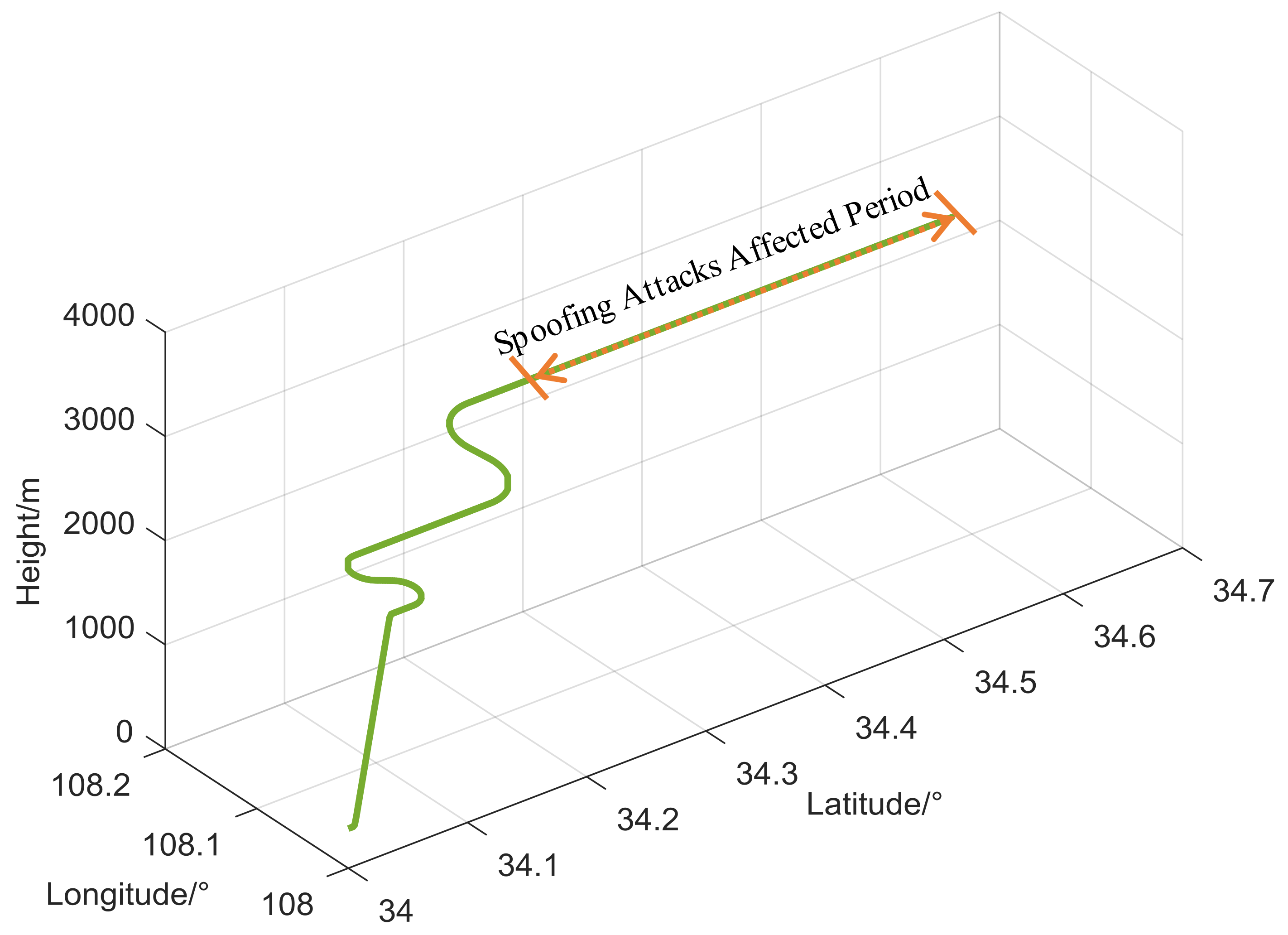
5. Simulation Analysis
6. Conclusions and Future Works
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Parameters | Unsynchronized Spoofing | Synchronized Spoofing | |
|---|---|---|---|
| Signal | Signal power | ||
| Signal delay | Arbitrarily determined for simulator attacks; generally, for meaconing attacks | in the transition process, then determined arbitrarily by the spoofer | |
| Doppler | Consistent with the spoofer’s code phase variations | in the transition process, then varies consistently with the code phase | |
| Visible satellites | Generally, equals | ||
| Data sequence | Same structure as the content can be changed | Same as in the transition process, then the content can be changed | |
| Code sequence | Strictly the same as the authentic signals | ||
| Carrier frequency | Strictly the same as the authentic signals | ||
| Measurement | Pseudorange | Arbitrarily determined | Matched with in the transition process, then determined by the spoofer |
| Carrier phase | Consistent with code phase, hard to align with the authentic signals | ||
| PVT | Position | Arbitrarily determined | Matched with the authentic condition in the transition process, then determined arbitrarily by the spoofer |
| Velocity | Consistent with position | ||
| Time | Arbitrarily determined for simulator attacks; generally earlier than true time for meaconing attacks | ||
| Implementation | Platform | Repeater Simulator | Advanced repeater Receiver/spoofer |
| Requirements | Jam-and-spoof | Know the real-time position of the target receiver | |
Appendix C
- Position: = 34.6887°, = 108.1915°, = 2282.8941 m
- Velocity: = −0.0058 m/s, = 149.9911 m/s, = 0.0081 m/s
- Attitude: = −0.0018°, = 0.0017°, = 359.9941°
- Specific force: = −0.0128 m/s2, = −0.0016 m/s2, = 9.7900 m/s2
- Meridian radius of curvature plus height: = 6,358,383 m
- Transverse radius of curvature plus height: = 6,387,345 m
Appendix D
References
- John, A. Volpe National Transportation Systems Center. In Vulnerability Assessment of the Transportation Infrastructure Relying on the Global Positioning System; John A. Volpe National Transportation Systems Center: Cambridge, MA, USA, 2001. [Google Scholar]
- Psiaki, M.L.; Humphreys, T.E. GNSS Spoofing and Detection. Proc. IEEE 2016, 104, 1258–1270. [Google Scholar] [CrossRef]
- Warner, J.S.; Johnston, R.G. GPS Spoofing Countermeasures. J. Secur. Adm. 2003, 25, 19–27. [Google Scholar]
- Key, E.L. Techniques to Counter GPS Spoofing; The MITRE Corporation: Bedford, MA, USA, 1995. [Google Scholar]
- Humphreys, T.E.; Ledvina, B.M.; Psiaki, M.L.; O’Hanlon, B.W.; Kintner, P.M., Jr. Assessing the Spoofing Threat: Development of a Portable GPS Civilian Spoofer. In Proceedings of the 21st ION GNSS International Technical Meeting of the Satellite Division (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 2314–2325. [Google Scholar]
- Huang, L.; Yang, Q. GPS Spoofing: Low-Cost GPS Simulator. Presented at DEF CON 23, Las Vegas, NV, USA, August 2015. Available online: https://www.researchgate.net/publication/286330869_Low-cost_GPS_simulator_-_GPS_spoofing_by_SDR (accessed on 4 May 2018).
- Kerns, A.J.; Shepard, D.P.; Bhatti, J.A.; Humphreys, T.E. Unmanned Aircraft Capture and Control via GPS Spoofing. J. Field Robot. 2014, 31, 617–636. [Google Scholar] [CrossRef]
- Bhatti, J.; Humphreys, T.E. Hostile Control of Ships via False GPS Signals: Demonstration and Detection. Navig. J. Inst. Navig. 2017, 64, 51–66. [Google Scholar] [CrossRef]
- Wang, K.; Chen, S.; Pan, A. Time and Position Spoofing with Open Source Projects; Black Hat Europe: Amsterdam, The Netherlands, 2015; Available online: https://www.blackhat.com/docs/eu-15/materials/eu-15-Kang-Is-Your-Timespace-Safe-Time-And-Position-Spoofing-Opensourcely-wp.pdf (accessed on 16 April 2018).
- Rothrock, K. The Kremlin Eats GPS for Breakfast: Why Geolocation in Central Moscow Has Become a Real Headache. Available online: https://themoscowtimes.com/articles/the-kremlin-eats-gps-for-breakfast-55823 (accessed on 20 March 2018).
- Goward, D. Mass GPS Spoofing Attack in Black Sea? Available online: http://maritime-executive.com/editorials/mass-gps-spoofing-attack-in-black-sea (accessed on 20 March 2018).
- Borio, D.; Gioia, C. A Sum-of-Squares Approach to GNSS Spoofing Detection. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1756–1768. [Google Scholar] [CrossRef]
- Günther, C. A Survey of Spoofing and Counter-Measures. Navig. J. Inst. Navig. 2014, 61, 159–177. [Google Scholar] [CrossRef]
- Jafarnia-Jahromi, A.; Broumandan, A.; Nielsen, J.; Lachapelle, G. GPS Vulnerability to Spoofing Threats and a Review of Antispoofing Techniques. Int. J. Navig. Obs. 2012, 2012. [Google Scholar] [CrossRef]
- Schmidt, D.; Radke, K.; Camtepe, S.; Foo, E.; Ren, M. A Survey and Analysis of the GNSS Spoofing Threat and Countermeasures. ACM Comput. Surv. 2016, 48. [Google Scholar] [CrossRef]
- Dovis, F. GNSS Interference Threats and Countermeasures; Artech House: Norwood, MA, USA, 2015. [Google Scholar]
- Liu, Y.; Li, S.; Xiao, X.; Fu, Q. INS-Aided GNSS Spoofing Detection Based on Two Antenna Raw Measurements. Gyrosc. Navig. 2016, 7, 178–188. [Google Scholar] [CrossRef]
- Manickam, S.; O’Keefe, K. Using Tactical and MEMS Grade INS to Protect Against GNSS Spoofing in Automotive Applications. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 2291–3001. [Google Scholar]
- Tanil, C.; Khanafseh, S.; Joerger, M.; Pervan, B. Kalman Filter-based INS Monitor to Detect GNSS Spoofers Capable of Tracking Aircraft Position. In Proceedings of the IEEE/ION PLANS 2016, Savannah, GA, USA, 11–14 April 2016; pp. 1027–1034. [Google Scholar]
- Liu, Y.; Fu, Q.; Liu, Z.; Li, S. GNSS Spoofing Detection Ability of a Loosely Coupled INS/GNSS Integrated Navigation System for Two Integrity Monitoring Methods. In Proceedings of the 2017 International Technical Meeting of the Institute of Navigation, Monterey, CA, USA, 30 January–2 February 2017; pp. 912–921. [Google Scholar]
- Tanil, C.; Khanafseh, S.; Joerger, M.; Pervan, B. An INS Monitor to Detect GNSS Spoofers Capable of Tracking Vehicle Position. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 131–143. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, H.; Wang, S. Principles of Kalman Filter and Integrated Navigation; Northwestern Polytechnical University Press: Xi’an, China, 2015. [Google Scholar]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Ioannides, R.T.; Pany, T.; Gibbons, G. Known Vulnerabilities of Global Navigation Satellite Systems, Status, and Potential Mitigation Techniques. Proc. IEEE 2016, 104, 1174–1194. [Google Scholar] [CrossRef]
- Humphreys, T.E. Interference. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing AG: Cham, Switzerland, 2017; pp. 469–503. [Google Scholar]
- Humphreys, T.E.; Bhatti, J.A.; Shepard, D.P.; Wesson, K.D. A Testbed for Developing and Evaluating GNSS Signal Authentication Techniques; International Symposium on Certification of GNSS Systems & Services (CERGAL): Dresden, Germany, 2014; Available online: https://radionavlab.ae.utexas.edu/images/stories/files/papers/tb.pdf (accessed on 16 April 2018).
- Lee, Y.C.; O’Laughlin, D.G. Performance Analysis of a Tightly Coupled GPS/Inertial System for Two Integrity Monitoring Methods. Navig. J. Inst. Navig. 2000, 47, 175–189. [Google Scholar] [CrossRef]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering: Theory and Practice with MATLAB, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zhong, L.; Liu, J.; Li, R.; Wang, R. Approach for Detecting Soft Faults in GPS/INS Integrated Navigation based on LS-SVM and AIME. J. Navig. 2017, 70, 561–579. [Google Scholar] [CrossRef]
- Cho, S. A Study for Detection of Drift in Sensor Measurements. Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, 2012. [Google Scholar]
- Gao, Z. Inertial Navigation System Technology; Tsinghua University Press: Beijing, China, 2012. [Google Scholar]
- Li, W.; Wu, W.; Wang, J.; Lu, L. A Fast SINS Initial Alignment Scheme for Underwater Vehicle Applications. J. Navig. 2013, 66, 181–198. [Google Scholar] [CrossRef]
- U.S. Department of Defense. Global Positioning System Standard Positioning Service Performance Standard, 4th ed.; U.S. Department of Defense: Arlington, VA, USA, 2008.
- Lo, S.; Chen, Y.H.; Reid, T.; Perkins, A.; Walter, T.; Enge, P. The Benefit of Low Cost Accelerometers for GNSS Anti-Spoofing. In Proceedings of the ION 2017 Pacific PNT Meeting, Honolulu, HI, USA, 1–4 May 2017; pp. 775–796. [Google Scholar]
| Sensor | Parameter | Value | Unit |
|---|---|---|---|
| IMU | Gyro bias | 0.01 | °/h |
| Gyro random walk | 0.005 | ||
| Accelerometer bias | 100 | μg | |
| Accelerometer random walk | 20 | ||
| GPS | Residual satellite clock and ephemeris errors | 0.5 | m |
| Residual ionosphere error (single-frequency) | 4.0 | m | |
| Residual troposphere error | 0.2 | m | |
| Tracking noise | 0.67 | m | |
| Short-range multipath error | 0.94 | m |
| State | Absolute (Relative) | State | Absolute (Relative) | State | Absolute (Relative) |
|---|---|---|---|---|---|
| 3.43 × 10−6° (0.20%) | 4.40 × 10−6° (0.26%) | 1.06 × 10−5° (0.19%) | |||
| 1.52 × 10−6 m/s (0.01%) | 1.96 × 10−5 m/s (0.14%) | 8.63 × 10−7 m/s (0.02%) | |||
| 3.69 × 10−4 m (0.05%) | 1.02 × 10−5 m (0.002%) | 2.87 × 10−5 m (0.004%) | |||
| 1.59 × 10−5 °/h (0.11%) | 2.52 × 10−5 °/h (0.18%) | 7.72 × 10−6 °/h (0.03%) | |||
| 6.33 × 10−2 μg (0.29%) | 7.17 × 10−2 μg (0.35%) | 1.14 × 10−3 μg (0.07%) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, S.; Fu, Q.; Liu, Z. Impact Assessment of GNSS Spoofing Attacks on INS/GNSS Integrated Navigation System. Sensors 2018, 18, 1433. https://doi.org/10.3390/s18051433
Liu Y, Li S, Fu Q, Liu Z. Impact Assessment of GNSS Spoofing Attacks on INS/GNSS Integrated Navigation System. Sensors. 2018; 18(5):1433. https://doi.org/10.3390/s18051433
Chicago/Turabian StyleLiu, Yang, Sihai Li, Qiangwen Fu, and Zhenbo Liu. 2018. "Impact Assessment of GNSS Spoofing Attacks on INS/GNSS Integrated Navigation System" Sensors 18, no. 5: 1433. https://doi.org/10.3390/s18051433
APA StyleLiu, Y., Li, S., Fu, Q., & Liu, Z. (2018). Impact Assessment of GNSS Spoofing Attacks on INS/GNSS Integrated Navigation System. Sensors, 18(5), 1433. https://doi.org/10.3390/s18051433






