A Low-Ambiguity Signal Waveform for Pseudolite Positioning Systems Based on Chirp
Abstract
:1. Introduction
2. Mathematical Models
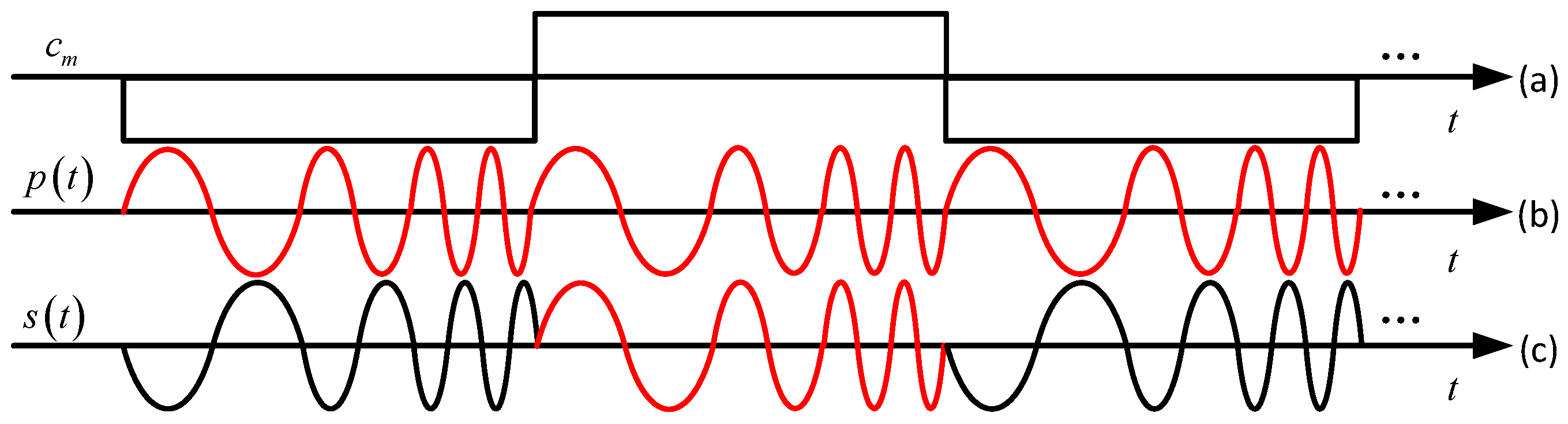
2.1. Modulation Principle
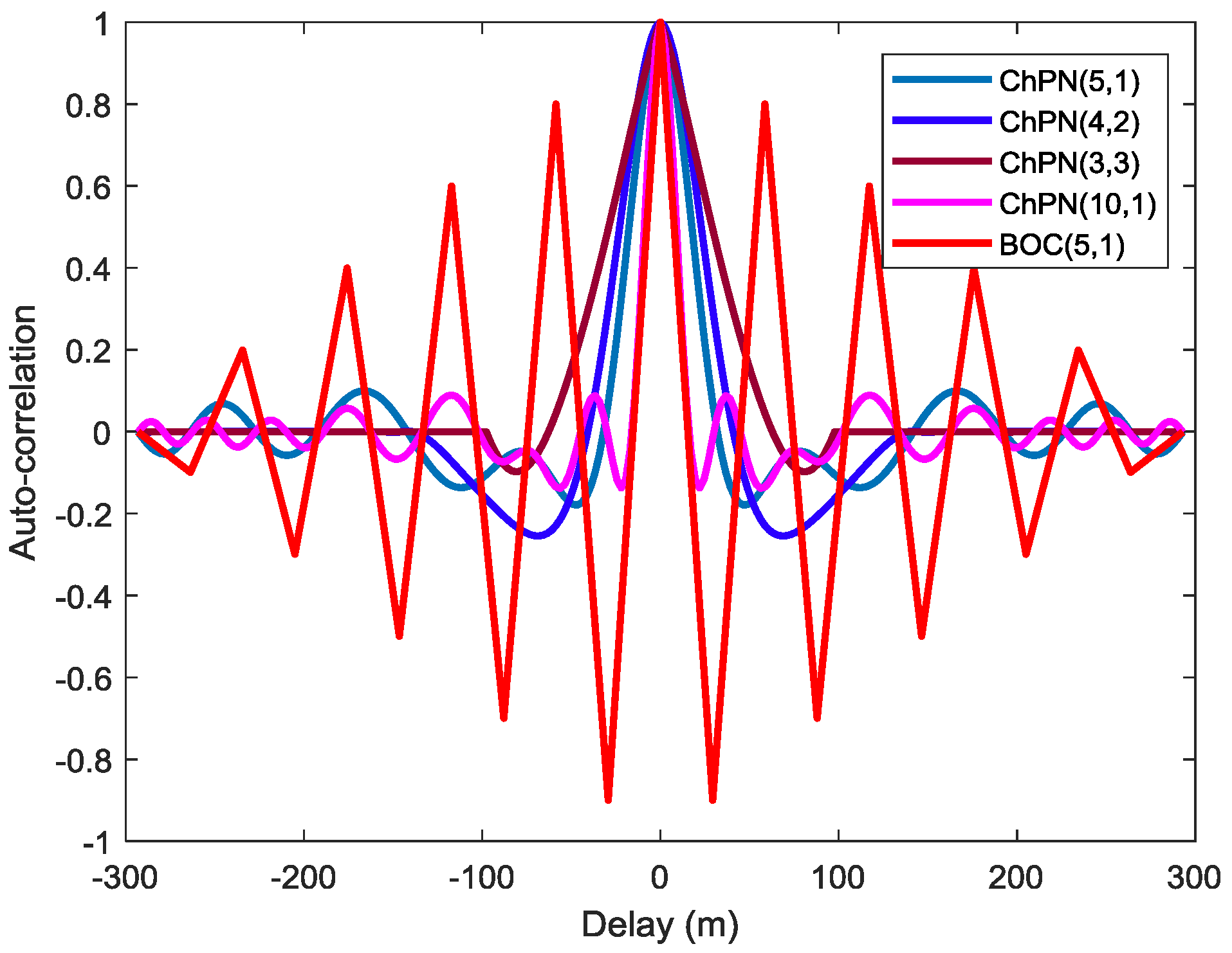
2.2. Auto-Correlation Function
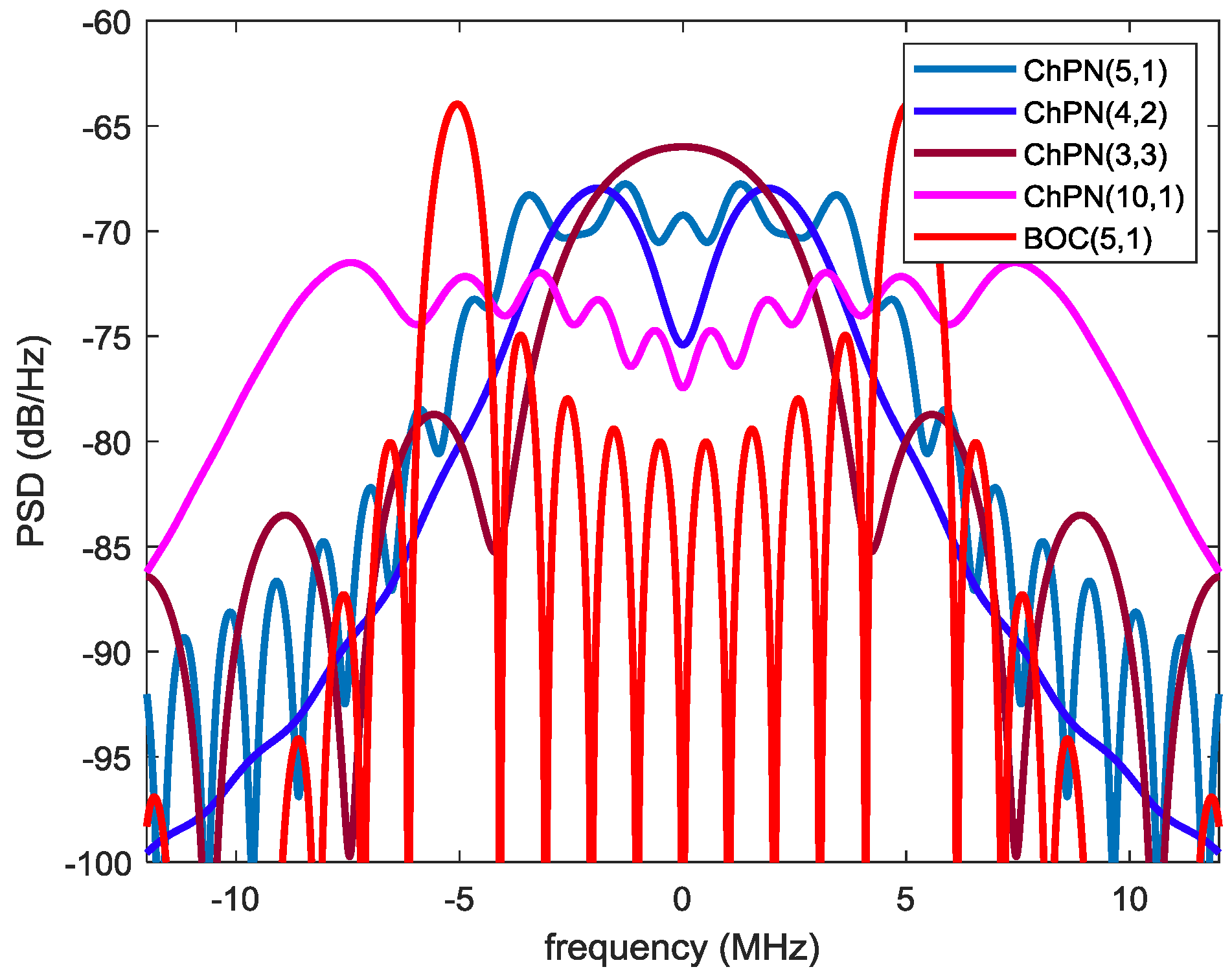
2.3. Power Spectrum Density
2.4. ChPN with Orthogonal Chirps
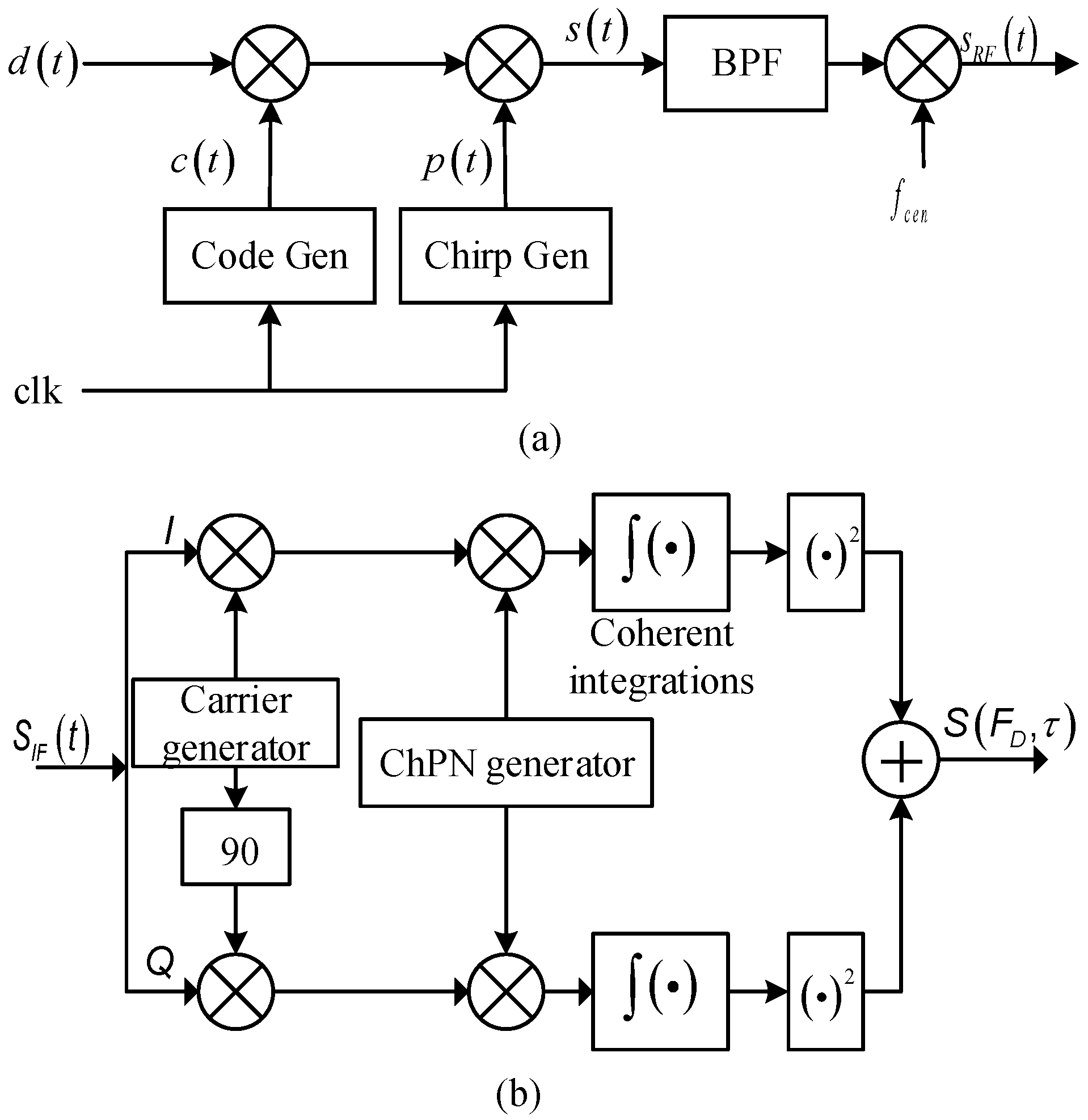
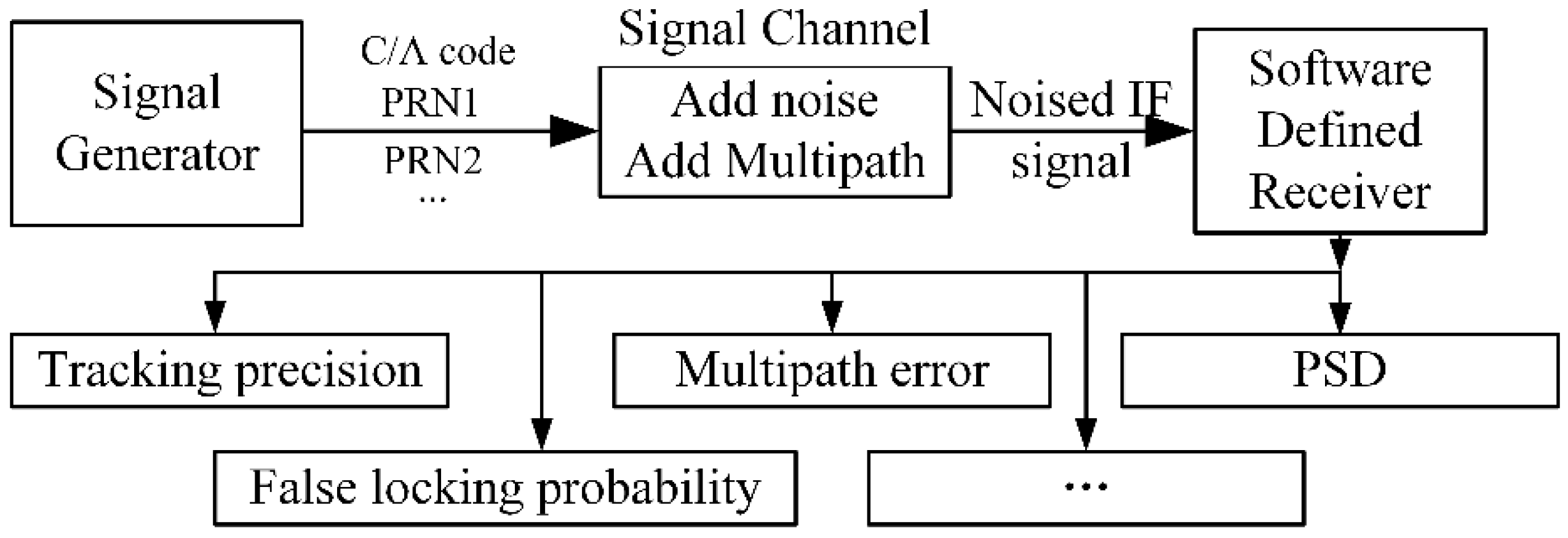
3. Signal Generation and Detection
4. Numerical Results
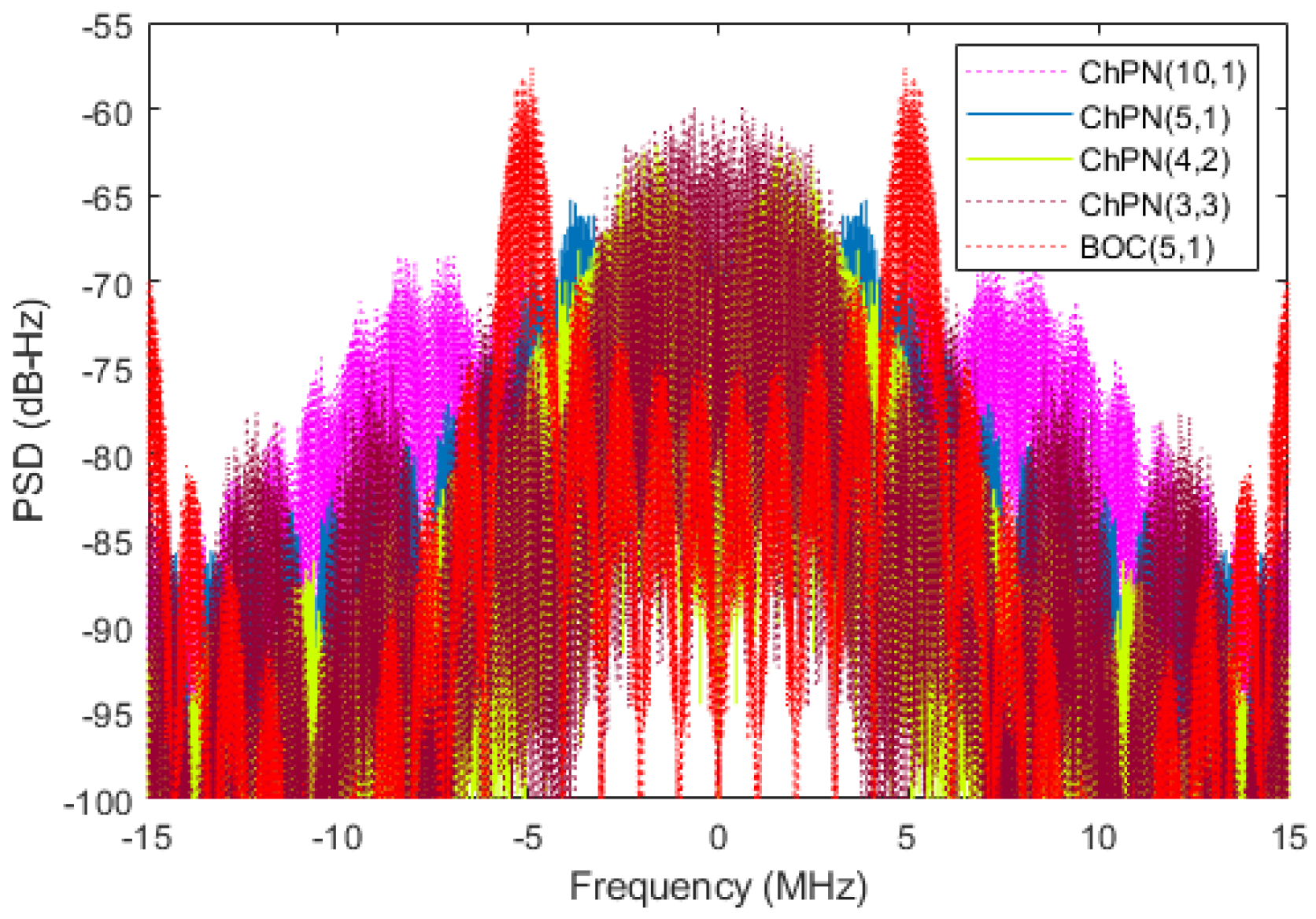
4.1. ACF and PSD
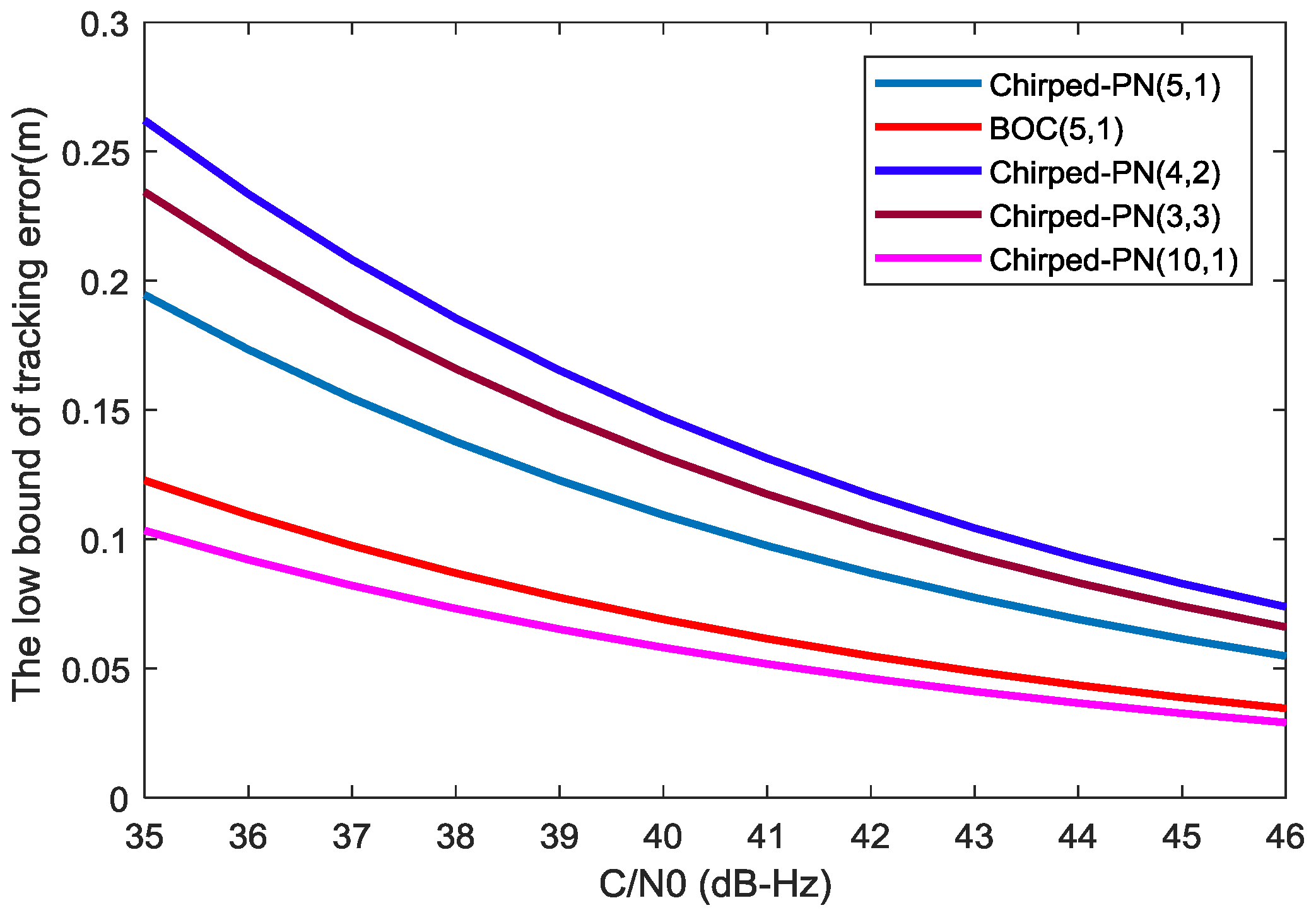
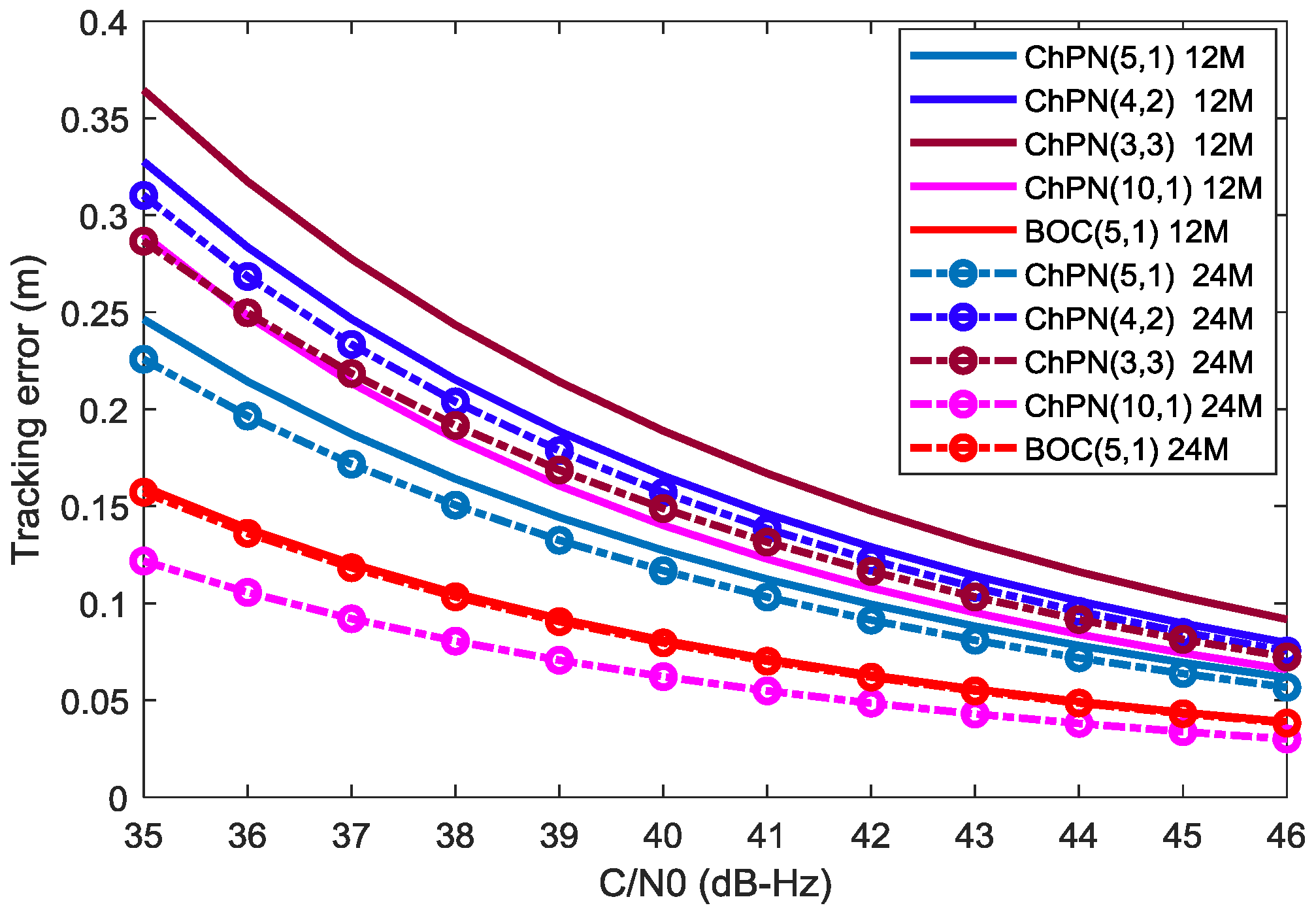
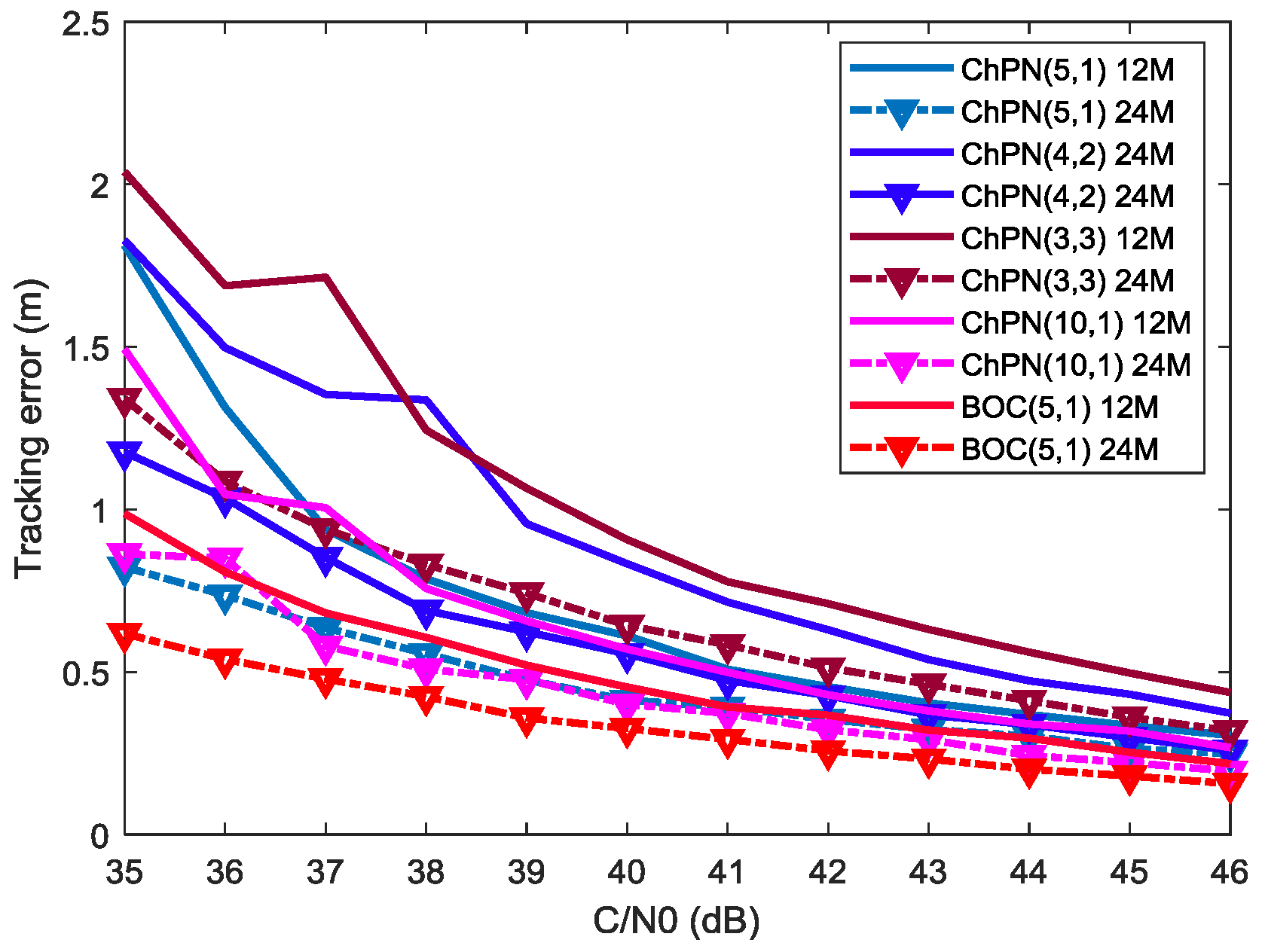
4.2. Tracking Performance
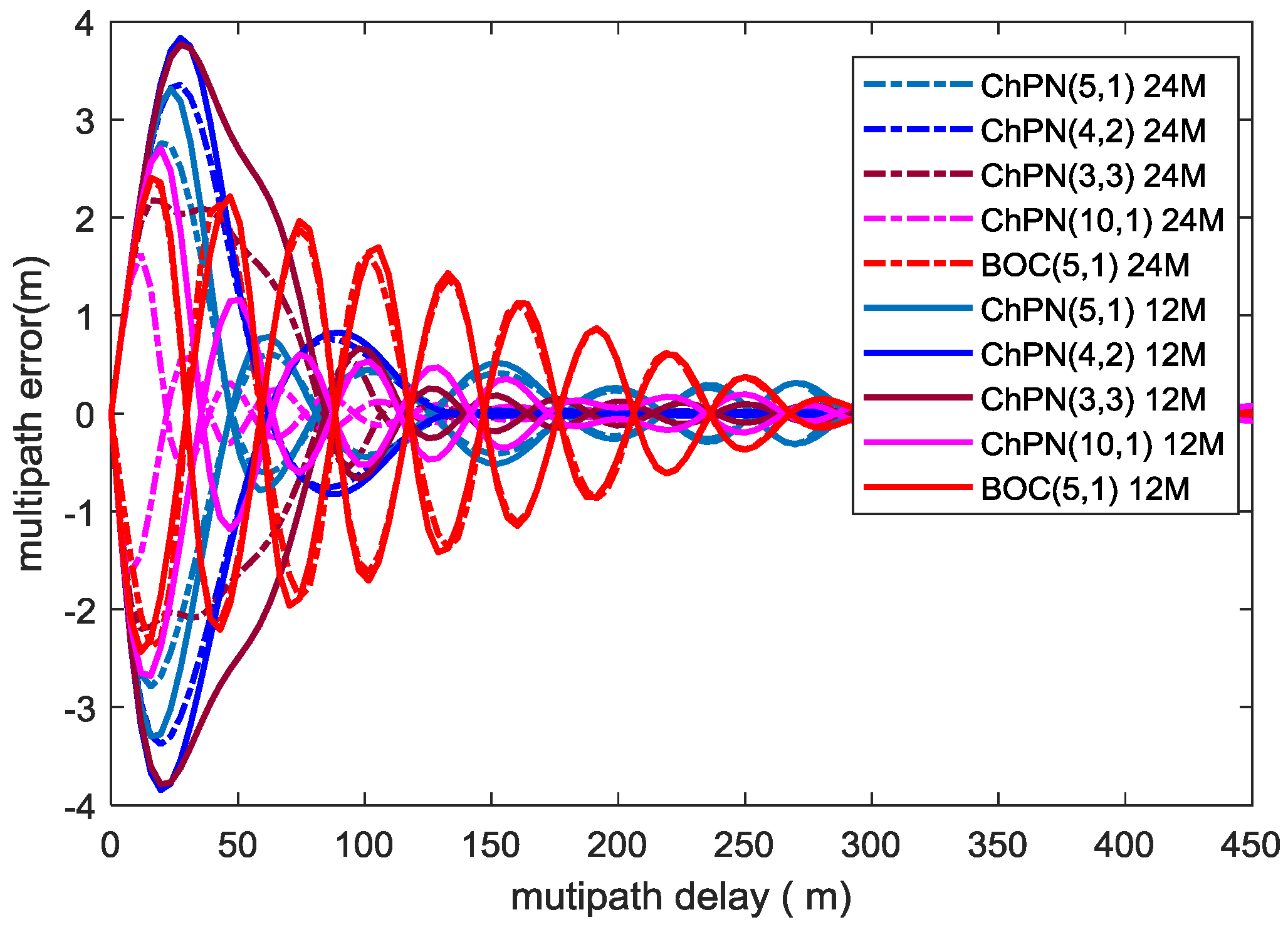
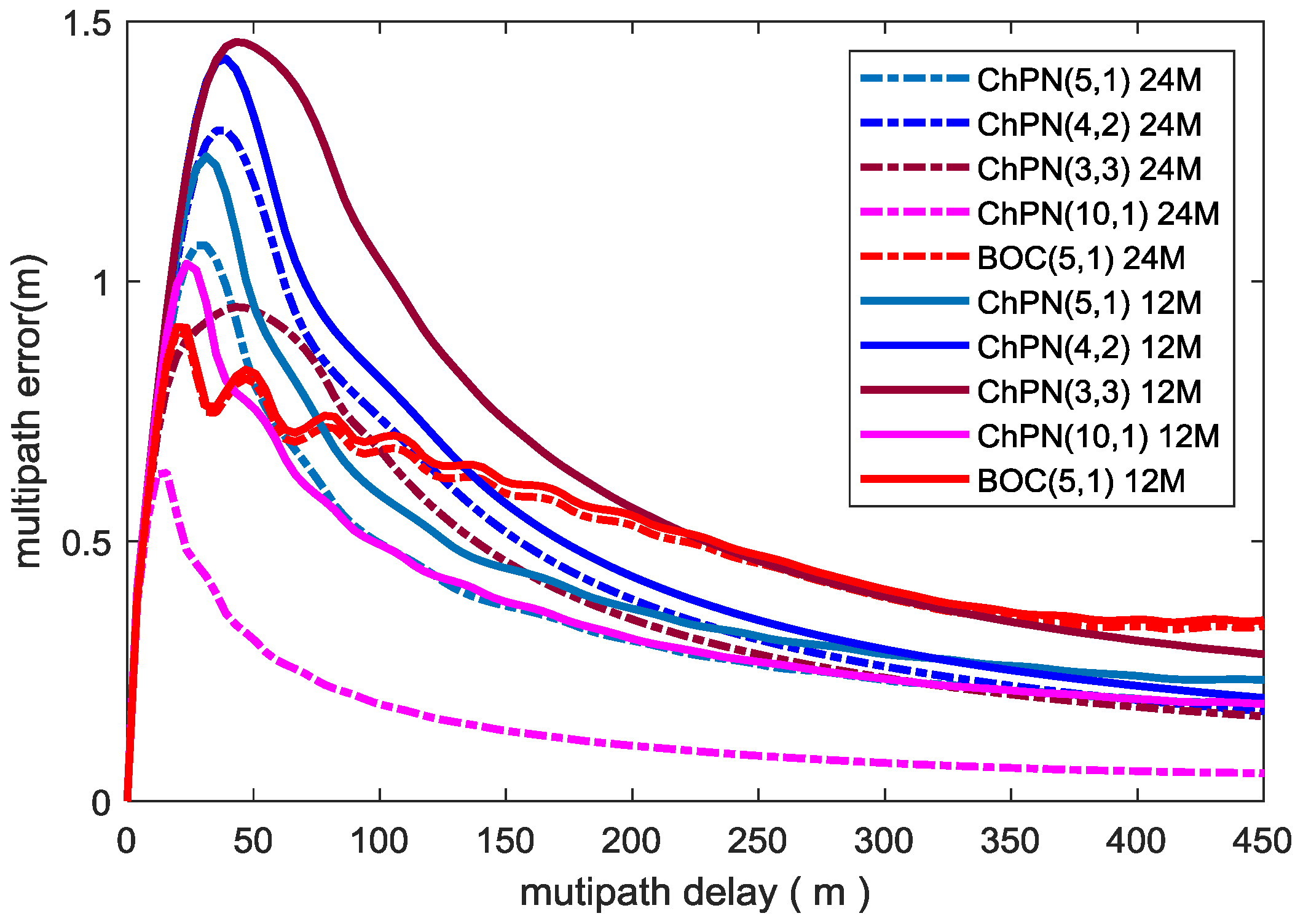
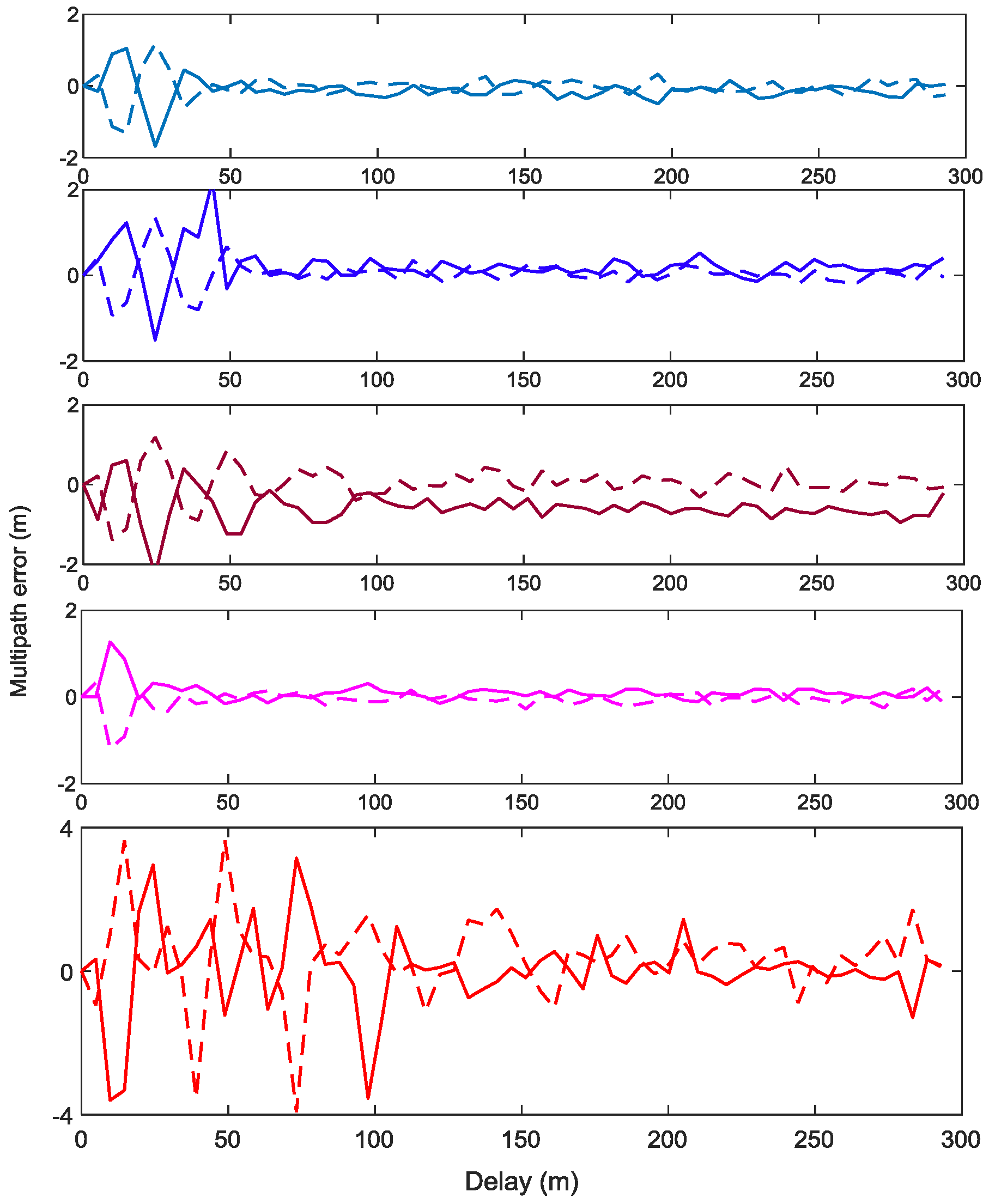
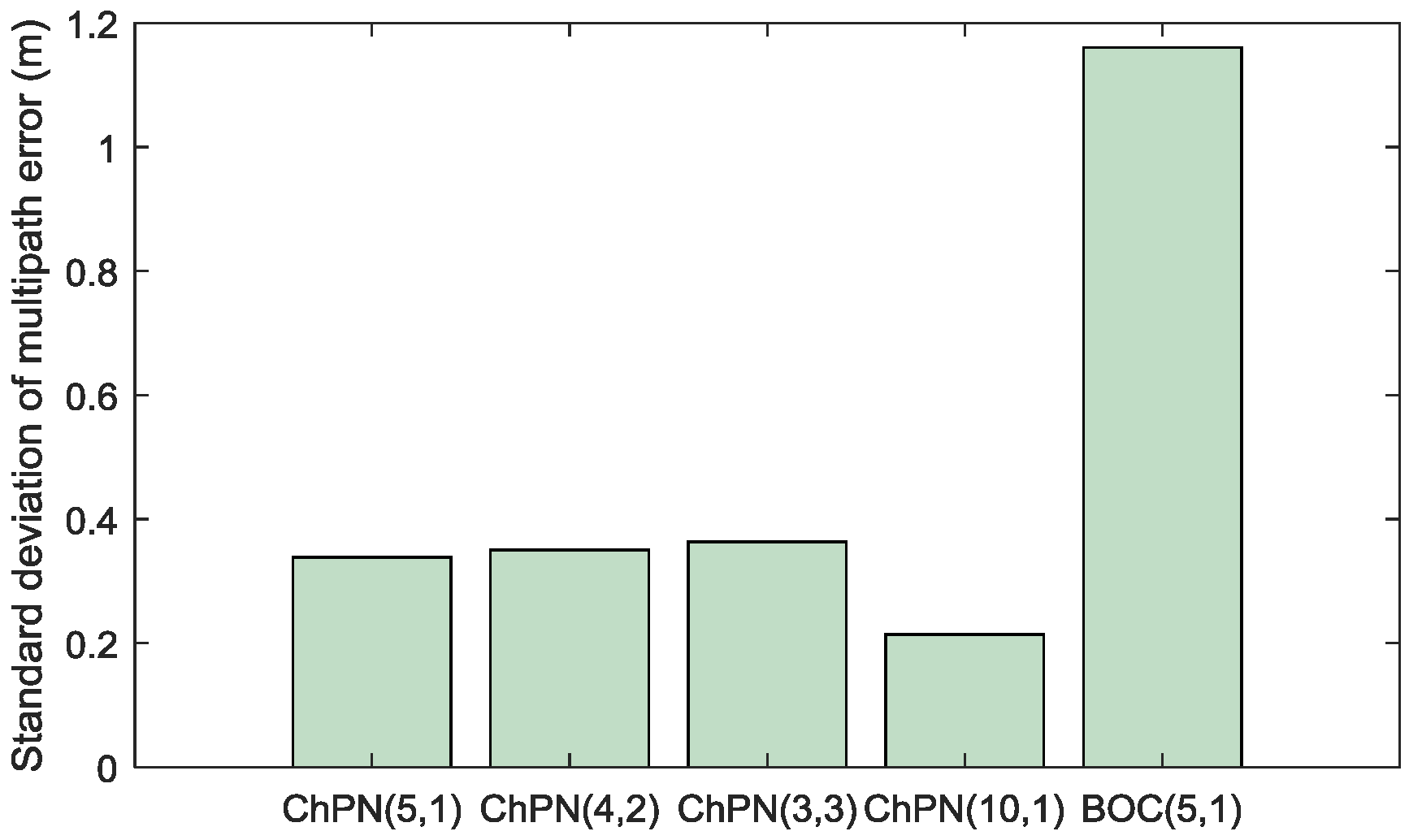
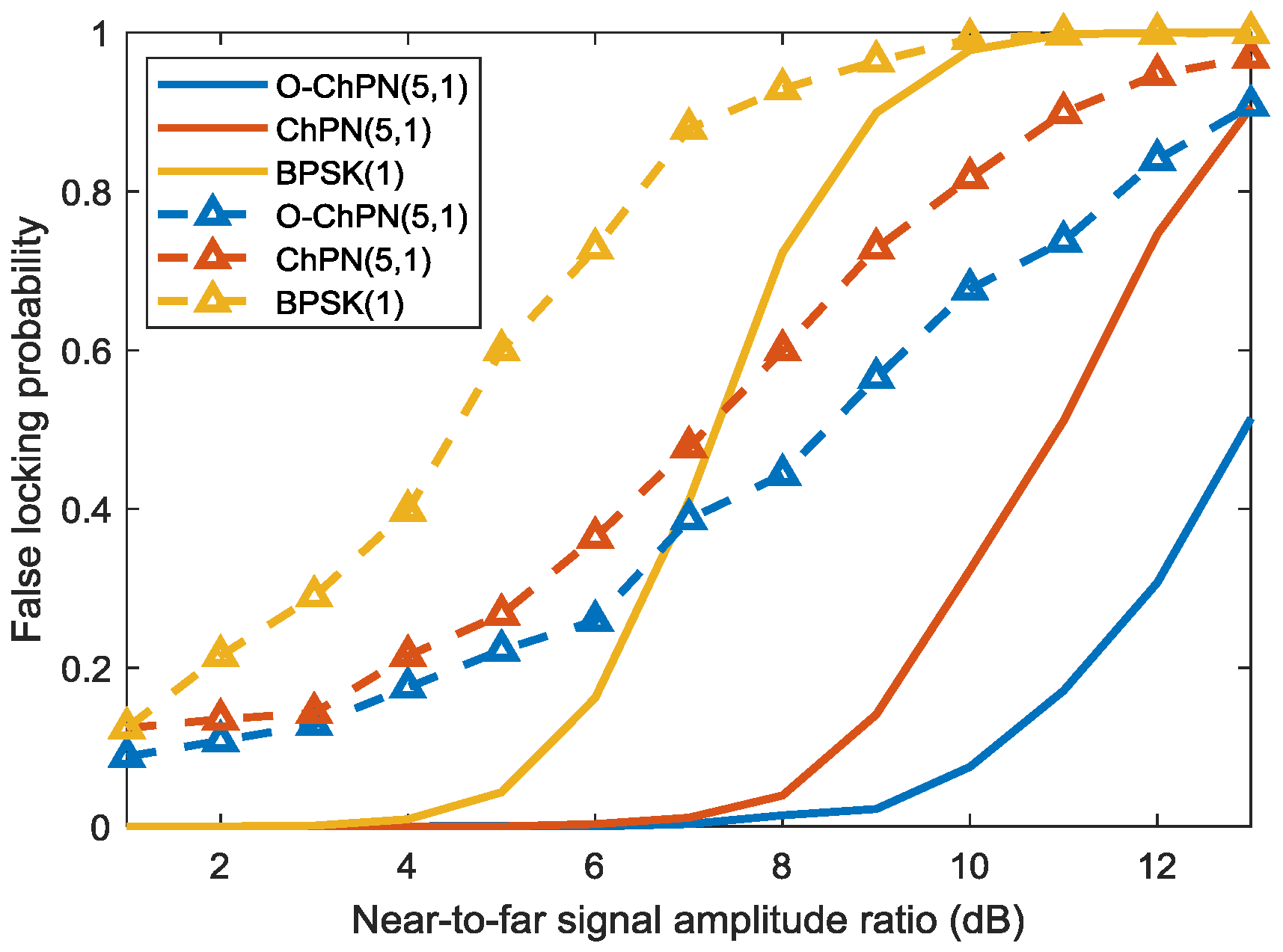
4.3. Multipath Resistance
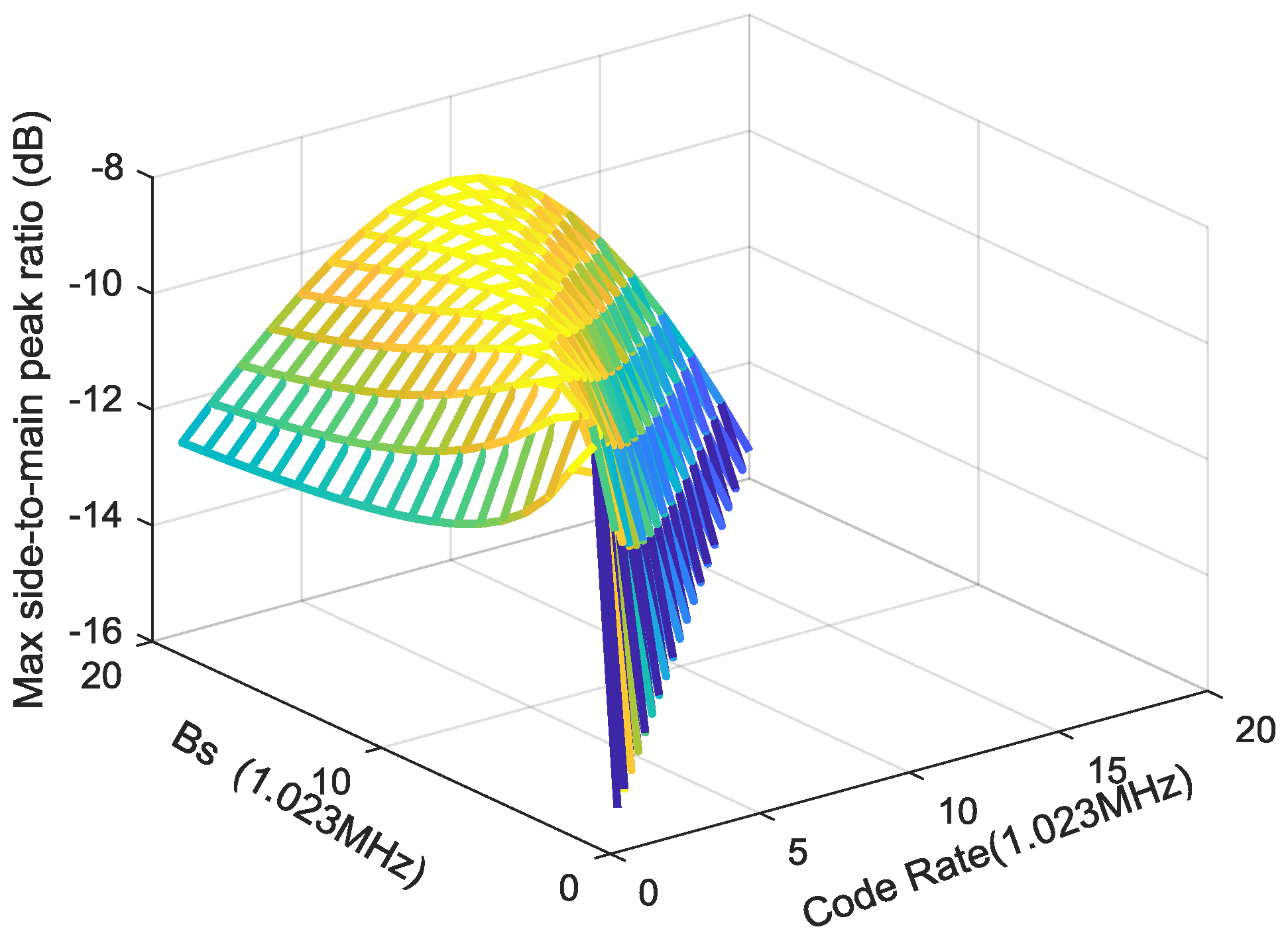
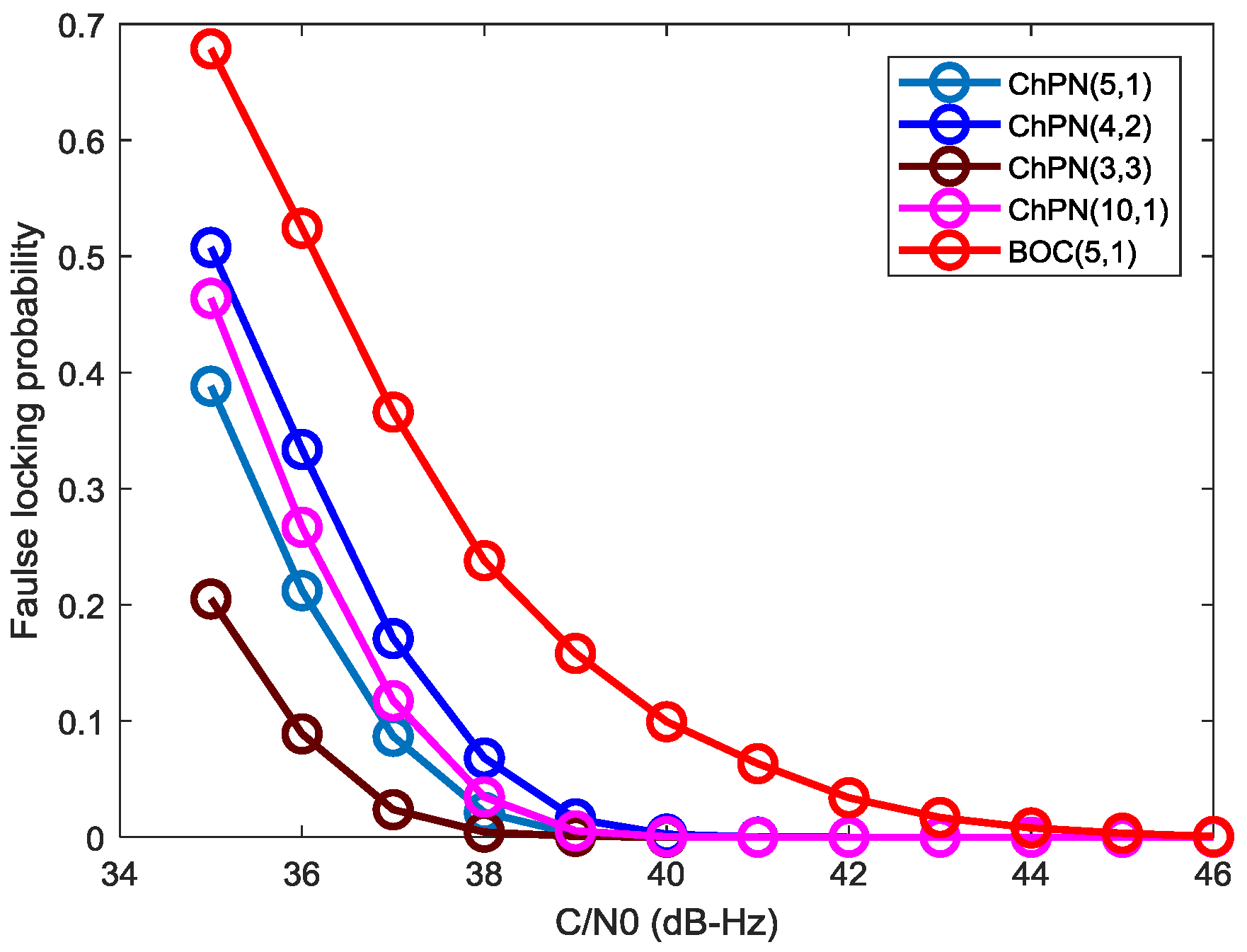
4.4. ACF Peaks Ambiguity
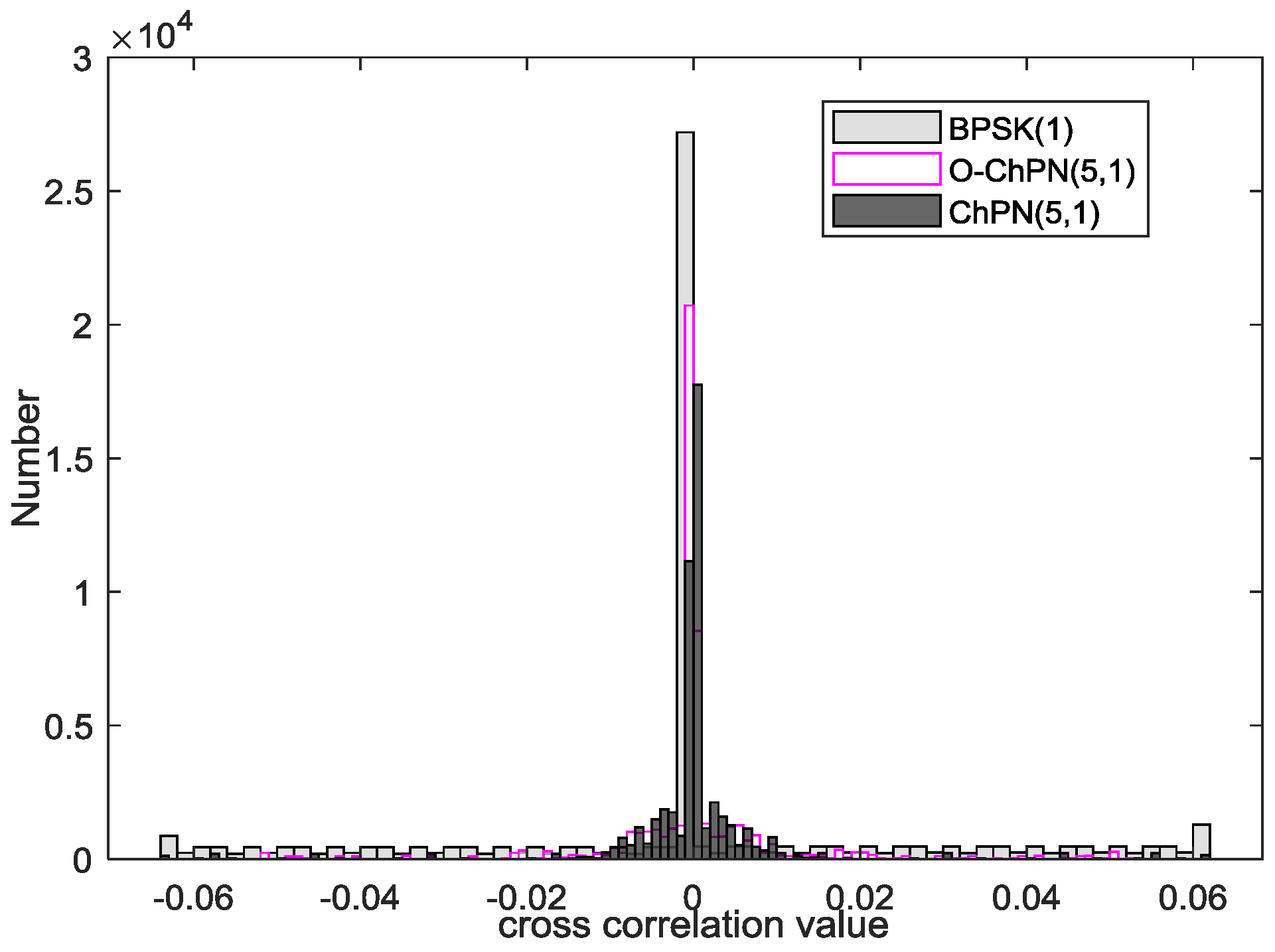
4.5. Cross-Correlation Comparison
5. Simulation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
A.1. The First Term
A.2. The Second Term
A.3. The Expression
References
- Trunzo, A.; Benshoof, P.; Squadron, T.; Afb, H.; Nm, J. The UHARS Non-GPS Based Positioning System. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011. [Google Scholar]
- Rizos, C.; Roberts, G.; Barnes, J.; Gambale, N. Locata: A new high accuracy indoor positioning system. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010. [Google Scholar]
- Rizos, C.; Roberts, G.; Barnes, J.; Gambale, N. Experimental results of Locata: A high accuracy indoor positioning system. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010. [Google Scholar]
- Babu, R.; Wang, J. Ultra-tight GPS/INS/PL integration: A system concept and performance analysis. GPS Solut. 2009, 13, 75–82. [Google Scholar] [CrossRef]
- Progri, I.F.; Michalson, W.R.; Wang, J.; Bromberg, M.C. Indoor geolocation using FCDMA pseudolites: Signal structure and performance analysis. Navigation 2007, 54, 241–256. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, Y.; Wang, J.; Liu, K.; Liu, C. Precise point positioning for ground-based navigation systems without accurate time synchronization. GPS Solut. 2018, 22, 34. [Google Scholar] [CrossRef]
- Li, X.; Zhang, P.; Guo, J.; Wang, J.; Qiu, W. A New Method for Single-Epoch Ambiguity Resolution with Indoor Pseudolite Positioning. Sensors 2017, 17, 921. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Chen, W.; Xu, Y.; Ji, S.; Liu, J. Improved GNSS-based indoor positioning algorithm for mobile devices. GPS Solut. 2017, 21, 1721–1733. [Google Scholar] [CrossRef]
- Kurz, O.; Mongrédien, C.; Rohmer, G. A new multipath detection and mitigation approach for pseudolite systems. In Proceedings of the 26th International Technical Meeting of the ION Satellite Division (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013. [Google Scholar]
- Guo, F.; Yao, Z.; Lu, M. BS-ACEBOC: A generalized low-complexity dual-frequency constant-envelope multiplexing modulation for GNSS. GPS Solut. 2017, 21, 561–575. [Google Scholar] [CrossRef]
- Locata Signal Interface Control Document. Available online: http://www.locata.com/wp-content/uploads/2014/07/Locata-ICD-100E.pdf (accessed on 24 April 2018).
- Ouyang, X.; Zhao, J. Orthogonal chirp division multiplexing. IEEE Trans. Commun. 2016, 64, 3949–3957. [Google Scholar] [CrossRef]
- Meta, A.; Hoogeboom, P.; Ligthart, L.P. Signal Processing for FMCW SAR. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3519–3532. [Google Scholar] [CrossRef]
- Benson, S.; Chen, C.I.H.; Lin, D.M.; Liou, L.L. Digital linear chirp receiver for high chirp rates with high resolution time-of-arrival and time-of-departure estimation. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1146–1154. [Google Scholar] [CrossRef]
- Zeng, T.; Yang, W.; Ding, Z.; Liu, D.; Long, T. A refined two-dimensional nonlinear chirp scaling algorithm for geosynchronous earth orbit SAR. Prog. Electromagn. Res. 2013, 143, 19–46. [Google Scholar] [CrossRef]
- Kanagaratnam, P.; Markus, T.; Lytle, V.; Heavey, B. Ultrawideband Radar Measurements of Thickness of Snow Over Sea Ice. IEEE Trans. Geosc. Remote Sens. 2007, 45, 2715–2724. [Google Scholar] [CrossRef]
- Liu, H. Multicode ultra-wideband scheme using chirp waveforms. IEEE J. Select. Areas Commun. 2006, 24, 885–891. [Google Scholar]
- Segou, O.E.; Thomopoulos, S.C.A. Probabilistic Error Modeling and Topology-Based Smoothing of Indoor Localization and Tracking Data, Based on the IEEE 802.15.4a Chirp Spread Spectrum Specification. Int. J. Distrib. Sens. Netw. 2014, 10, 1–18. [Google Scholar] [CrossRef]
- Ling, H.; Yilong, L.; Liu, W. Using chirp signal for accurate RFID positioning. In Proceedings of the 2010 International Conference on Communications, Circuits and Systems (ICCCAS), Chengdu, China, 28–30 July 2010. [Google Scholar]
- Pivato, P.; Dalpez, S.; Macii, D. Performance evaluation of Chirp Spread Spectrum ranging for indoor embedded navigation systems. In Proceedings of the 7th IEEE International Symposium on Industrial Embedded Systems, Karlsruhe, Germany, 20–22 June 2012. [Google Scholar]
- Yoon, C.; Cha, H. Experimental analysis of IEEE 802.15.4a CSS ranging and its implications. Comput. Commun. 2011, 34, 1361–1374. [Google Scholar] [CrossRef]
- Nunes, F.D.; Leitao, J.M.; Sousa, F.M. Performance analysis of an absolute phase modulation scheme for GNSS signals. In Proceedings of the 8th ESA Workshop onSatellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 14–16 December 2016. [Google Scholar]
- Cook, C. Radar Signals: An Introduction to Theory and Application; Elsevier: New York, NY, USA, 2012. [Google Scholar]
- Kowatsch, M.; Lafferl, J.T. A Spread-Spectrum Concept Combining Chirp Modulation and Pseudonoise Coding. IEEE Trans. Commun. 1983, 31, 1133–1142. [Google Scholar] [CrossRef]
- Rebeyrol, E.; Macabiau, C.; Lestarquit, L.; Ries, L.; Issler, J.L.; Boucheret, M.L.; Bousquet, M. BOC power spectrum densities. In Proceedings of the 2005 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 24–26 January 2005. [Google Scholar]
- Betz, J.W.; Kolodziejski, K.R. Generalized Theory of Code Tracking with an Early-Late Discriminator Part I: Lower Bound and Coherent Processing. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1538–1556. [Google Scholar] [CrossRef]
- Betz, J.W.; Kolodziejski, K.R. Generalized Theory of Code Tracking with an Early-Late Discriminator Part II: Noncoherent Processing and Numerical Results. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1557–1564. [Google Scholar] [CrossRef]
- Kaplan, E. Understanding GPS: Principles & Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Zuping, T. Research on releVant Theory for GNSS Signal Design and Evaluation; HUST: Wuhan, China, 2009. [Google Scholar]
| Situations | Signals | Characteristics |
|---|---|---|
| 1 | ChPN(5,1), ChPN(4,2), ChPN(3,3) | ChPN signals with the same MLB, different sweep bandwidths. |
| 2 | ChPN(5,1), BOC(5,1) | Different waveforms with the same code rate and MLB. |
| 3 | ChPN(10,1), ChPN(5,1) | ChPN signals with the same code rate and different MLBs. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Huang, Z.; Kou, Y.; Wang, J. A Low-Ambiguity Signal Waveform for Pseudolite Positioning Systems Based on Chirp. Sensors 2018, 18, 1326. https://doi.org/10.3390/s18051326
Liu Q, Huang Z, Kou Y, Wang J. A Low-Ambiguity Signal Waveform for Pseudolite Positioning Systems Based on Chirp. Sensors. 2018; 18(5):1326. https://doi.org/10.3390/s18051326
Chicago/Turabian StyleLiu, Qing, Zhigang Huang, Yanhong Kou, and Jinling Wang. 2018. "A Low-Ambiguity Signal Waveform for Pseudolite Positioning Systems Based on Chirp" Sensors 18, no. 5: 1326. https://doi.org/10.3390/s18051326
APA StyleLiu, Q., Huang, Z., Kou, Y., & Wang, J. (2018). A Low-Ambiguity Signal Waveform for Pseudolite Positioning Systems Based on Chirp. Sensors, 18(5), 1326. https://doi.org/10.3390/s18051326





