Printing and Folding: A Solution for High-Throughput Processing of Organic Thin-Film Thermoelectric Devices
Abstract
1. Introduction
2. A TEG on the Human Body
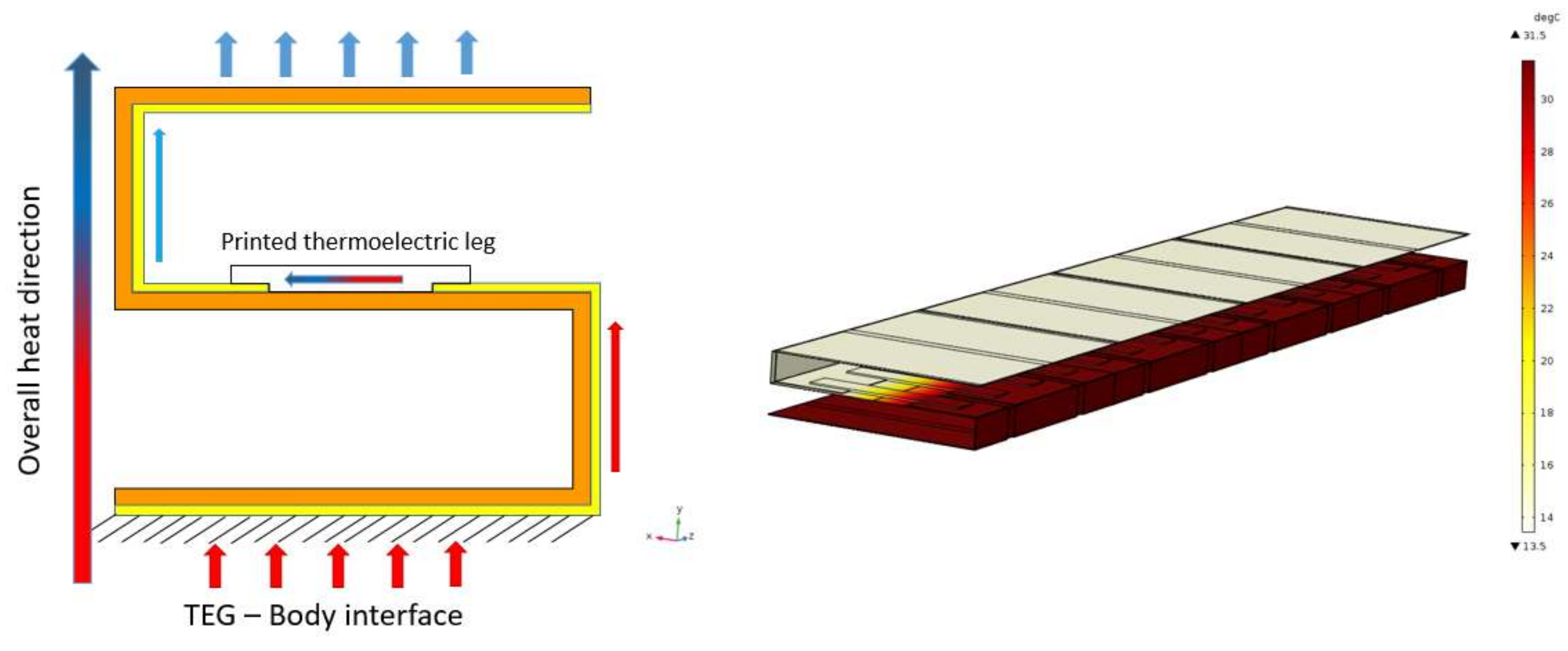
3. Printing and Folding of Thin Film Legs
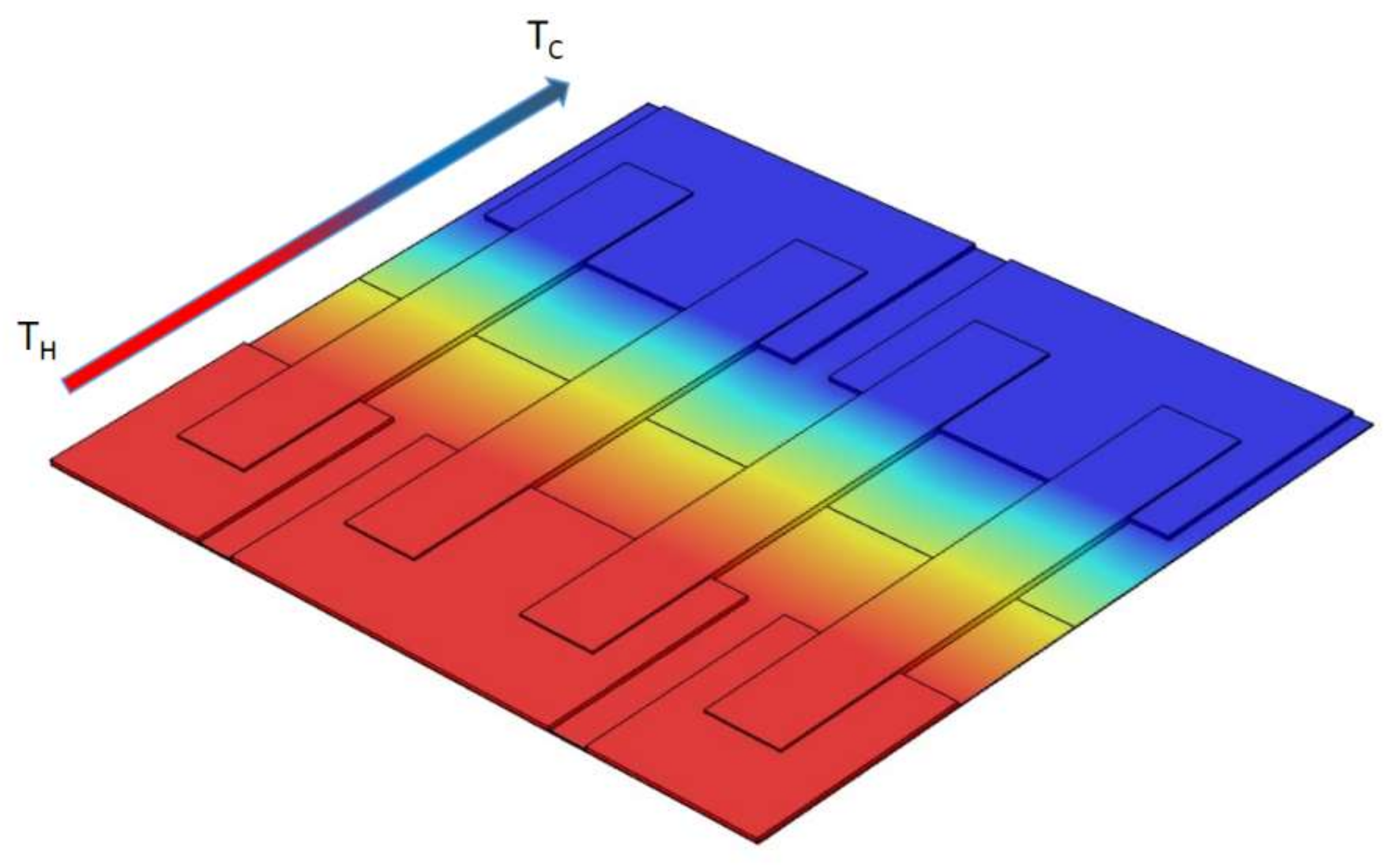
4. Design and Multi-Physics Simulation
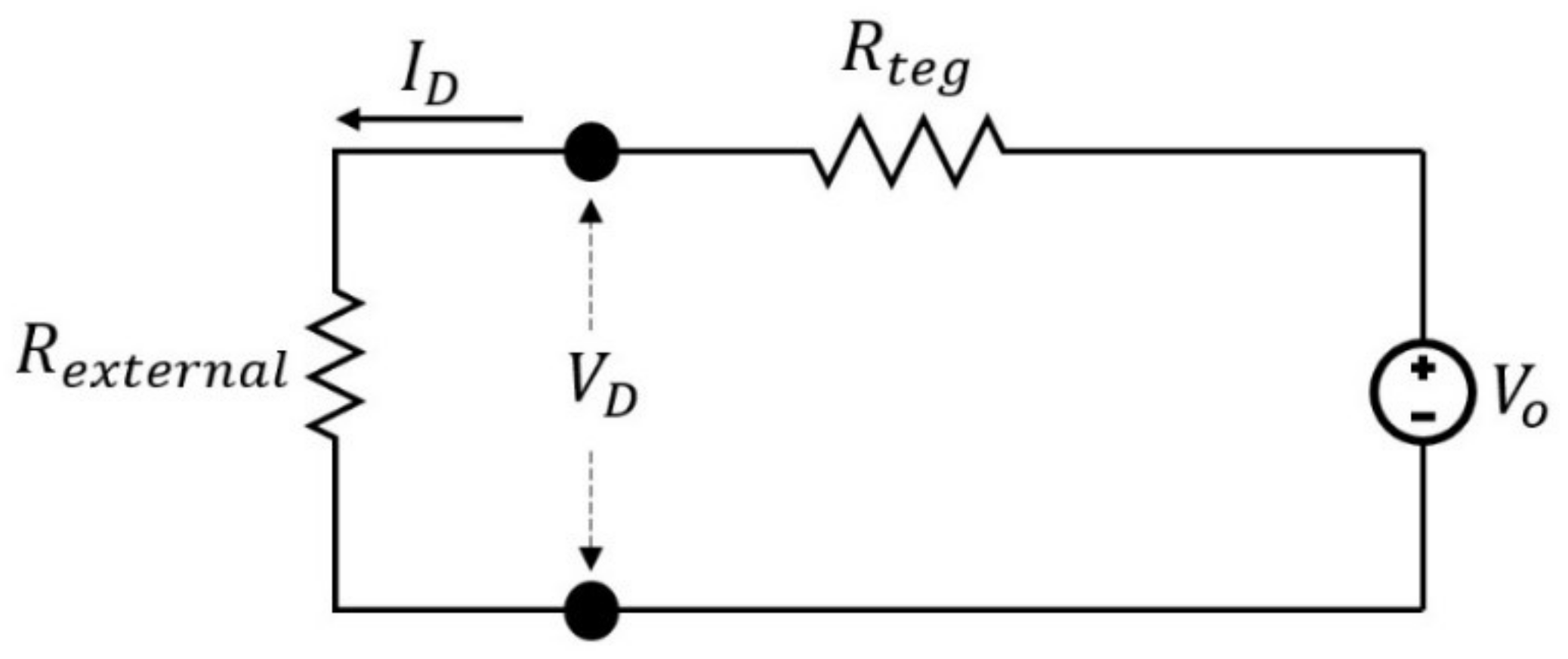
5. Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pillatsch, P.; Yeatman, E.M.; Holmes, A.S. A piezoelectric frequency up-converting energy harvester with rotating proof mass for human body applications. Sens. Actuators A Phys. 2014, 206, 178–185. [Google Scholar] [CrossRef]
- Cheng, X.; Meng, B.; Zhang, X.; Han, M.; Su, Z.; Zhang, H. Wearable electrode-free triboelectric generator for harvesting biomechanical energy. Nano Energy 2015, 12, 19–25. [Google Scholar] [CrossRef]
- Proto, A.; Penhaker, M.; Conforto, S.; Schmid, M. Nanogenerators for Human Body Energy Harvesting. Trends Biotechnol. 2017, 35, 610–624. [Google Scholar] [CrossRef] [PubMed]
- Starner, T. Human-powered wearable computing. IBM Syst. J. 1996, 35, 618–629. [Google Scholar] [CrossRef]
- Leonov, V.; Torfs, T.; Fiorini, P.; van Hoof, C. Thermoelectric converters of human warmth for self-powered wireless sensor nodes. IEEE Sens. J. 2007, 7, 650–656. [Google Scholar] [CrossRef]
- Settaluri, K.T.; Lo, H.; Ram, R.J. Thin thermoelectric generator system for body energy harvesting. J. Electron. Mater. 2012, 41, 984–988. [Google Scholar] [CrossRef]
- Lossec, M.; Multon, B.; Ahmed, H.B.; Goupil, C. Thermoelectric generator placed on the human body: System modeling and energy conversion improvements. Eur. Phys. J. Appl. Phys. 2010, 52, 11103. [Google Scholar] [CrossRef]
- Bahk, J.-H.; Fang, H.; Yazawa, K.; Shakouri, A. Flexible thermoelectric materials and device optimization for wearable energy harvesting. J. Mater. Chem. C 2015, 3, 10362–10374. [Google Scholar] [CrossRef]
- Lossec, M.; Multon, B.; Ahmed, H.B. Sizing optimization of a thermoelectric generator set with heatsink for harvesting human body heat. Energy Convers. Manag. 2013, 68, 260–265. [Google Scholar] [CrossRef]
- Hoang, D.C.; Tan, Y.K.; Chng, H.B.; Panda, S.K. Thermal energy harvesting from human warmth for wireless body area network in medical healthcare system. In Proceedings of the International Conference on Power Electronics and Drive Systems, Taipei, Taiwan, 2–5 November 2009; pp. 1277–1282. [Google Scholar]
- Wahbah, M.; Alhawari, M.; Mohammad, B.; Saleh, H.; Ismail, M. Characterization of Human Body-Based Thermal and Vibration Energy Harvesting for Wearable Devices. IEEE J. Emerg. Sel. Top. Circuits Syst. 2014, 4, 354–363. [Google Scholar] [CrossRef]
- Kim, M.-K.; Kim, M.-S.; Lee, S.; Kim, C.; Kim, Y.-J. Wearable thermoelectric generator for harvesting human body heat energy. Smart Mater. Struct. 2014, 23, 105002. [Google Scholar] [CrossRef]
- Lu, Z.; Layani, M.; Zhao, X.; Tan, L.P.; Sun, T.; Fan, S.; Yan, Q.; Magdassi, S.; Hng, H.H. Fabrication of flexible thermoelectric thin film devices by inkjet printing. Small 2014, 10, 3551–3554. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.J.; We, J.H.; Cho, B.J. A wearable thermoelectric generator fabricated on a glass fabric. Energy Environ. Sci. 2014, 7, 1959–1965. [Google Scholar] [CrossRef]
- Thielen, M.; Sigrist, L.; Magno, M.; Hierold, C.; Benini, L. Human body heat for powering wearable devices: From thermal energy to application. Energy Convers. Manag. 2017, 131, 44–54. [Google Scholar] [CrossRef]
- Suarez, F.; Parekh, D.P.; Ladd, C.; Vashaee, D.; Dickey, M.D.; Öztürk, M.C. Flexible thermoelectric generator using bulk legs and liquid metal interconnects for wearable electronics. Appl. Energy 2017, 202, 736–745. [Google Scholar] [CrossRef]
- Itoigawa, K.; Ueno, H.; Shiozaki, M.; Toriyama, T.; Sugiyama, S. Fabrication of flexible thermopile generator. J. Micromech. Microeng. 2005, 15, S233–S238. [Google Scholar] [CrossRef]
- Francioso, L.; De Pascali, C.; Farella, I.; Martucci, C.; Cretì, P.; Siciliano, P.; Perrone, A. Flexible thermoelectric generator for ambient assisted living wearable biometric sensors. J. Power Sources 2011, 196, 3239–3243. [Google Scholar] [CrossRef]
- Goncalves, L.M.; Rocha, J.G.; Couto, C.; Alpuim, P.; Min, G.; Rowe, D.M.; Correia, J.H. Fabrication of flexible thermoelectric microcoolers using planar thin-film technologies. J. Micromech. Microeng. 2007, 17, S168–S173. [Google Scholar] [CrossRef]
- Glatz, W.; Muntwyler, S.; Hierold, C. Optimization and fabrication of thick flexible polymer based micro thermoelectric generator. Sens. Actuators A Phys. 2006, 132, 337–345. [Google Scholar] [CrossRef]
- Yousef, H.; Hjort, K.; Lindeberg, M. Vertical thermopiles embedded in a polyimide-based flexible printed circuit board. J. Microelectromech. Syst. 2007, 16, 1341–1348. [Google Scholar] [CrossRef]
- Bubnova, O.; Khan, Z.U.; Malti, A.; Braun, S.; Fahlman, M.; Berggren, M.; Crispin, X. Optimization of the thermoelectric figure of merit in the conducting polymer poly(3,4-ethylenedioxythiophene). Nat. Mater. 2011, 10, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Jiao, F.; Di, C.-A.; Sun, Y.; Sheng, P.; Xu, W.; Zhu, D. Inkjet-printed flexible organic thin-film thermoelectric devices based on p- and n-type poly(metal 1,1,2,2-ethenetetrathiolate)s/polymer composites through ball-milling. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130008. [Google Scholar] [CrossRef] [PubMed]
- Besganz, A.; Zöllmer, V.; Kun, R.; Pál, E.; Walder, L.; Busse, M. Inkjet Printing as a Flexible Technology for the Deposition of Thermoelectric Composite Structures. Procedia Technol. 2014, 15, 99–106. [Google Scholar] [CrossRef]
- Søndergaard, R.R.; Hösel, M.; Espinosa, N.; Jørgensen, M.; Krebs, F.C. Practical evaluation of organic polymer thermoelectrics by large-area R2R processing on flexible substrates. Energy Sci. Eng. 2013, 1, 81–88. [Google Scholar] [CrossRef]
- Kim, S.J.; We, J.H.; Kim, J.S.; Kim, G.S.; Cho, B.J. Thermoelectric properties of P-type Sb2Te3 thick film processed by a screen-printing technique and a subsequent annealing process. J. Alloys Compd. 2014, 582, 177–180. [Google Scholar] [CrossRef]
- Rudež, R.; Markowski, P.; Presečnik, M.; Košir, M.; Dziedzic, A.; Bernik, S. Development of thick-film thermoelectric microgenerators based on p-type Ca3Co4O9 and n-type (ZnO)5In2O3 legs. Ceram. Int. 2015, 41, 13201–13209. [Google Scholar] [CrossRef]
- Madan, D.; Wang, Z.; Wright, P.K.; Evans, J.W. Printed flexible thermoelectric generators for use on low levels of waste heat. Appl. Energy 2015, 156, 587–592. [Google Scholar] [CrossRef]
- Chen, A.; Madan, D.; Wright, P.K.; Evans, J.W. Dispenser-printed planar thick-film thermoelectric energy generators. J. Micromech. Microeng. 2011, 21, 104006. [Google Scholar] [CrossRef]
- Cao, Z.; Shi, J.J.; Torah, R.N.; Tudor, M.J.; Beeby, S.P. All dispenser printed flexible 3D structured thermoelectric generators. J. Phys. Conf. Ser. 2015, 660, 12096. [Google Scholar] [CrossRef]
- He, M.; Zhao, Y.; Wang, B.; Xi, Q.; Zhou, J.; Liang, Z. 3D Printing Fabrication of Amorphous Thermoelectric Materials with Ultralow Thermal Conductivity. Small 2015, 11, 5889–5894. [Google Scholar] [CrossRef] [PubMed]
- El-Desouky, A.; Carter, M.; Andre, M.A.; Bardet, P.M.; LeBlanc, S. Rapid processing and assembly of semiconductor thermoelectric materials for energy conversion devices. Mater. Lett. 185, 598–602. [CrossRef]
- Russ, B.; Glaudell, A.; Urban, J.J.; Chabinyc, M.L.; Segalman, R.A. Organic thermoelectric materials for energy harvesting and temperature control. Nat. Rev. Mater. 2016, 1, 16050. [Google Scholar] [CrossRef]
- Sun, T.; Peavey, J.L.; Shelby, M.D.; Ferguson, S.; O’Connor, B.T. Heat shrink formation of a corrugated thin film thermoelectric generator. Energy Convers. Manag. 2015, 103, 674–680. [Google Scholar] [CrossRef]
- Rojas, J.P.; Conchouso, D.; Arevalo, A.; Singh, D.; Foulds, I.G.; Hussain, M.M. Paper-based origami flexible and foldable thermoelectric nanogenerator. Nano Energy 2017, 31, 296–301. [Google Scholar] [CrossRef]
- Qing, S.; Rezania, A.; Rosendahl, L.A.; Enkeshafi, A.A.; Gou, X. Characteristics and parametric analysis of a novel flexible ink-based thermoelectric generator for human body sensor. Energy Convers. Manag. 2018, 156, 655–665. [Google Scholar] [CrossRef]
- ANSI/ASHRAE Standard 55, Thermal Environmental Conditions for Human Occupancy; American Society of Heating, Refrigerating, and Air-Conditioning Engineers. Inc.: Atlanta, GA, USA, 2014.





| Parameter | Symbol | Value |
|---|---|---|
| Seebeck coefficient (p/n-type) | Sp/n | ±215 μV/K |
| Electrical conductivity (p/n-type) | σp/n | 70 S/cm |
| Thermal conductivity (p/n-type) | kp/n | 0.37 W/m-K |
| Hot side temperature | TH | 304.65 K |
| Ambient temperature | TA | 293.15 K |
| Natural heat transfer coefficient | hA | 5.46 W/m2-K |
| TE Leg length | L | 12 mm |
| TE leg width | W | 2 mm |
| TE leg thickness | Tl | 150 μm |
| Copper interconnects thickness | t1 | 100 μm |
| Thickness of Kapton substrate (polyimide) | Tk | 25 μm |
| Thermal conductivity of interconnecters (copper) | Kcu | 400 W/m-K |
| Thermal conductivity of Kapton (polyimide) | Ks | 0.12 W/m-K |
| Electrical conductivity of interconnects | σcu | 5.998 × 107 S/m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mortazavinatanzi, S.; Rezaniakolaei, A.; Rosendahl, L. Printing and Folding: A Solution for High-Throughput Processing of Organic Thin-Film Thermoelectric Devices. Sensors 2018, 18, 989. https://doi.org/10.3390/s18040989
Mortazavinatanzi S, Rezaniakolaei A, Rosendahl L. Printing and Folding: A Solution for High-Throughput Processing of Organic Thin-Film Thermoelectric Devices. Sensors. 2018; 18(4):989. https://doi.org/10.3390/s18040989
Chicago/Turabian StyleMortazavinatanzi, Seyedmohammad, Alireza Rezaniakolaei, and Lasse Rosendahl. 2018. "Printing and Folding: A Solution for High-Throughput Processing of Organic Thin-Film Thermoelectric Devices" Sensors 18, no. 4: 989. https://doi.org/10.3390/s18040989
APA StyleMortazavinatanzi, S., Rezaniakolaei, A., & Rosendahl, L. (2018). Printing and Folding: A Solution for High-Throughput Processing of Organic Thin-Film Thermoelectric Devices. Sensors, 18(4), 989. https://doi.org/10.3390/s18040989







