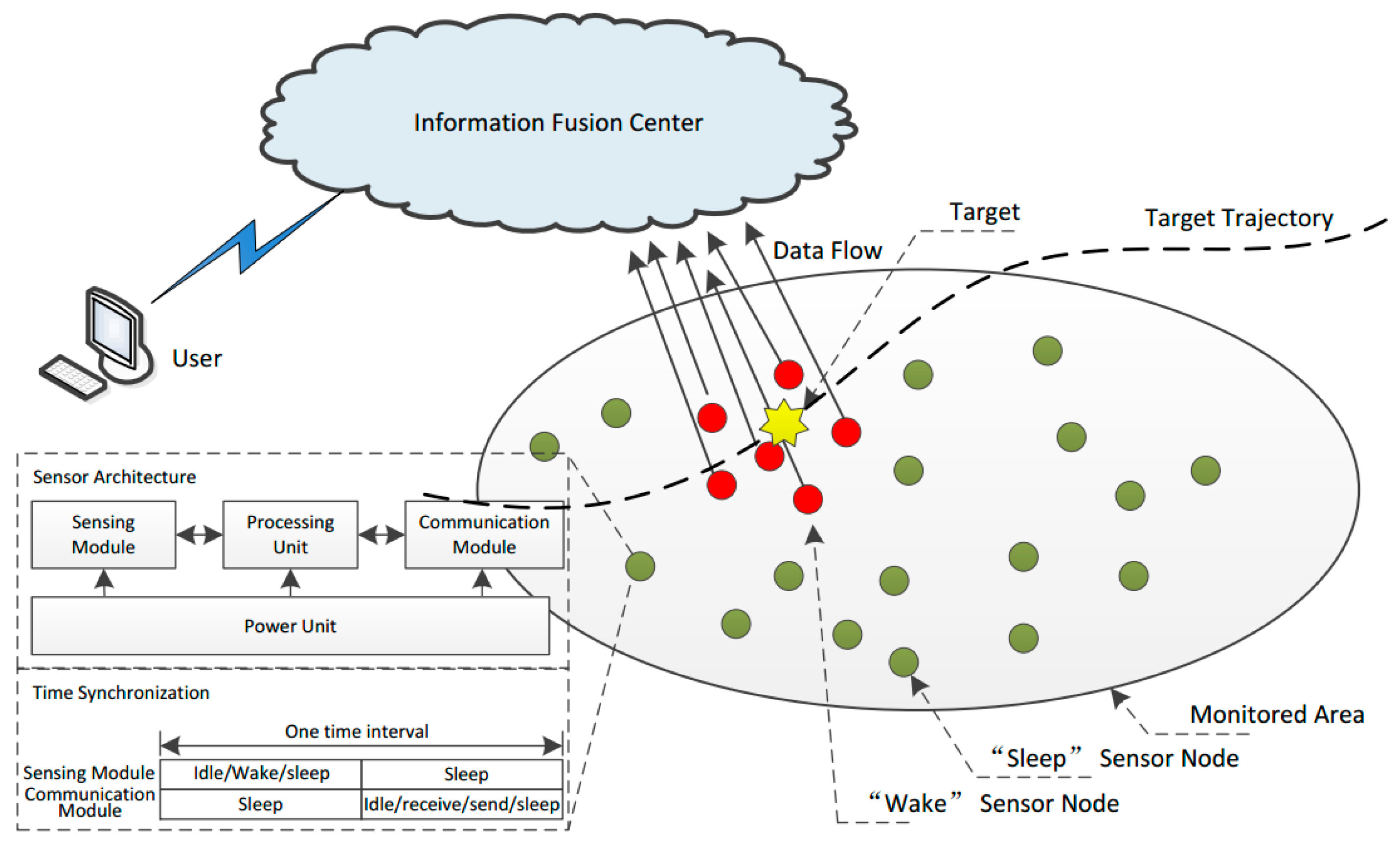
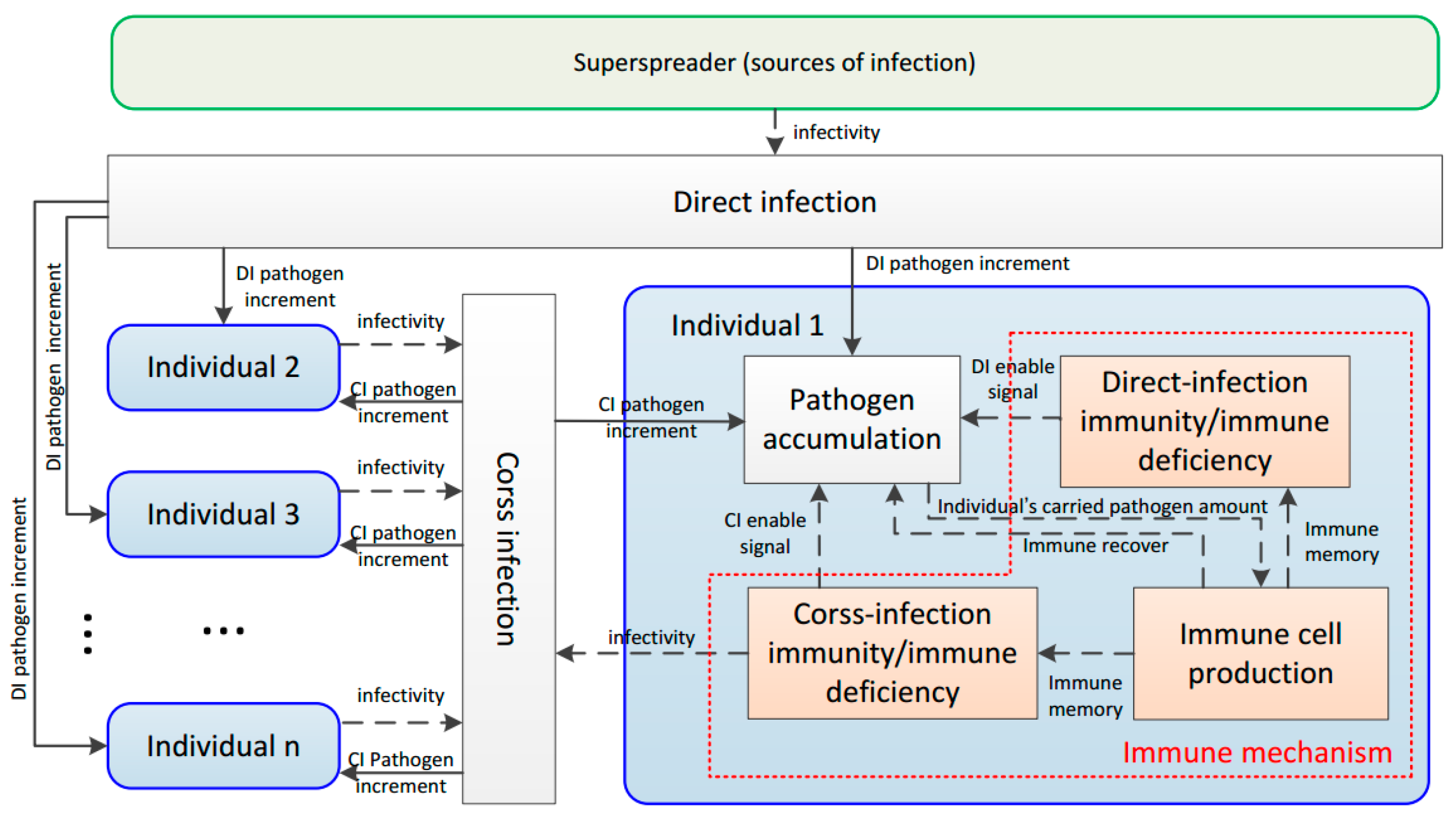
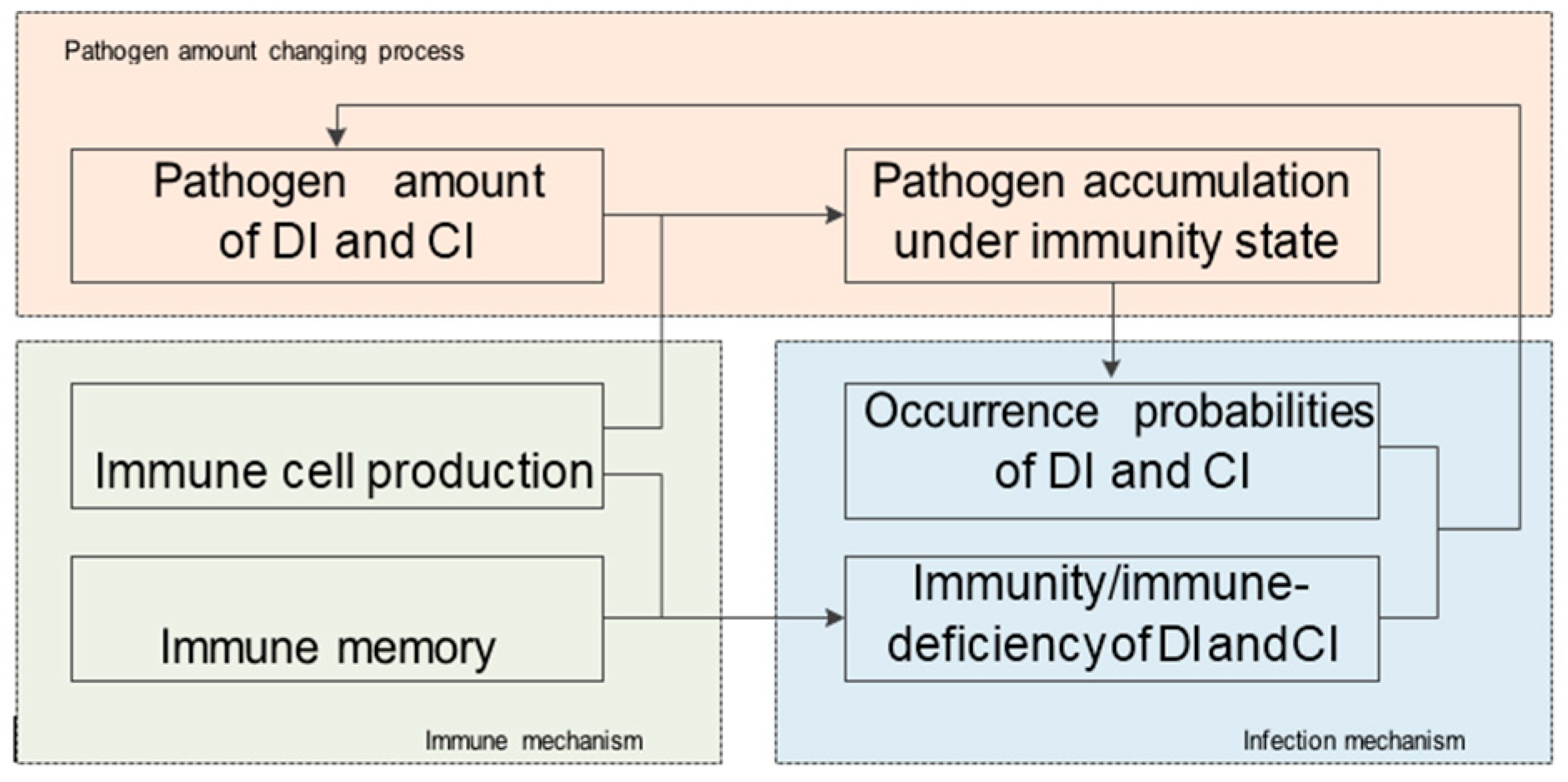
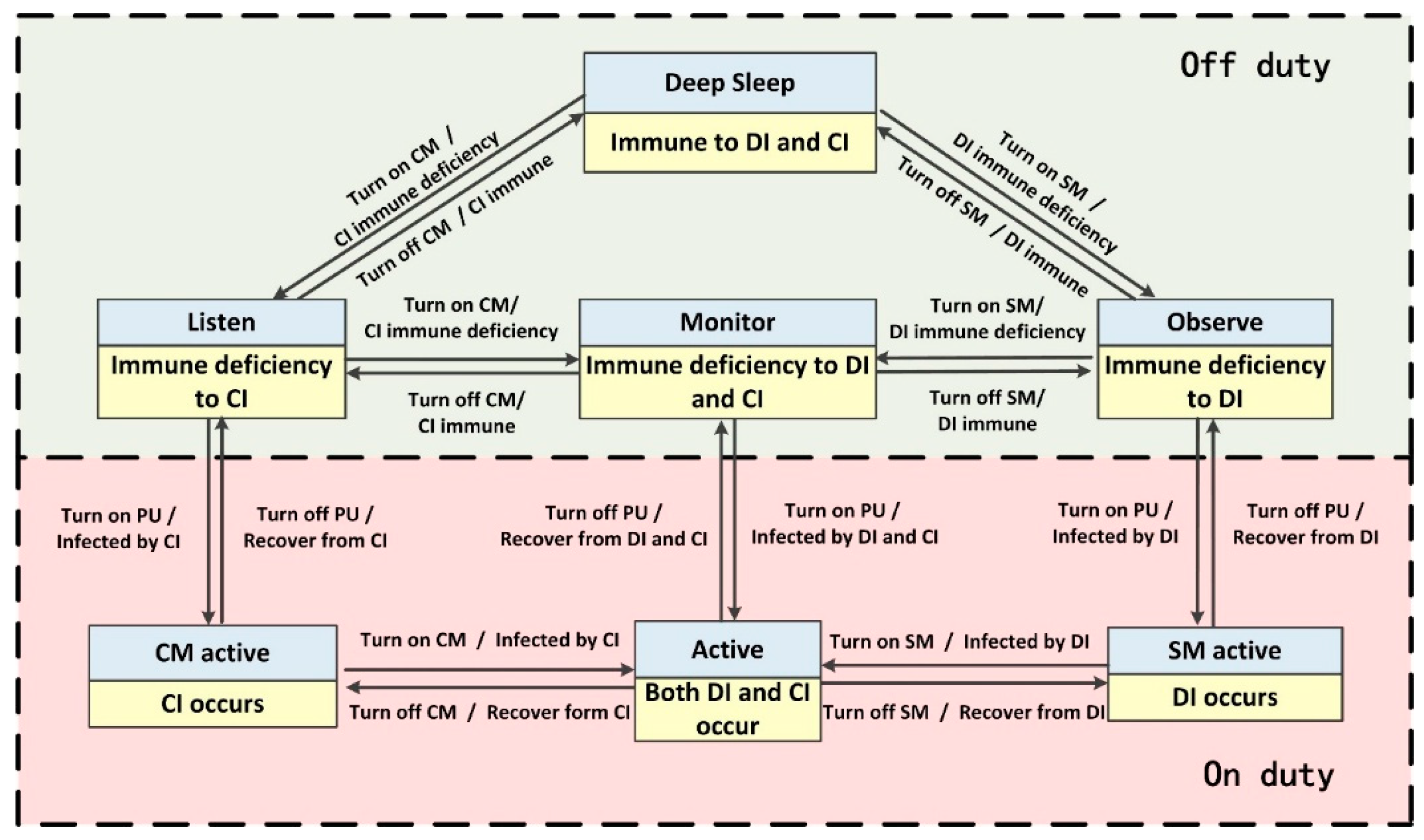
1. Introduction
With the advantages of being low-cost, easy to implement, self-organizing, and highly reliable, multi-sensor fusion networks are widely used for such applications as non-cooperative tracking [
1,
2], forest fire detection [
3], industrial process control [
4], water quality detection [
5], and machine health monitoring [
6], and object state detection [
7,
8]. These sensor networks are composed of a group of cooperating low-power, low-precision, inexpensive sensor nodes equipped with limited transmission range transceivers, a small data processing unit, constrained memory, and limited available energy. However, due to dense sensor node deployment and the infrequent occurrences of the targets for each sensor node, too much energy will be consumed when the targets are absent if wake-up control is not utilized [
9,
10]. The fact that power consumption constraints exist for sensor nodes using un-rechargeable batteries [
11] means that it is essential to balance conflicting performance requirements adaptively between energy consumption and target sensing.
The most widely used technique for lifetime optimization of multi-sensor networks is sensor wake-up control (WC) [
12], which is used to adaptively determine the “wake up” or “sleep” states of each node. A “wake up” sensor node is in charge of collecting and processing the measurements and transferring them to its neighbors or fusion center, while a “sleep” sensor node closes its sensing, communication, and processing modules for energy saving purposes. Currently, two different research methods are employed improve the energy efficiency of the WC of multi-sensor networks. The first mainly focuses on designing different channel assignments [
13,
14,
15], power controls [
16], sampling rates [
17], and MAC/routing protocols [
13,
14,
18]. These methods are usually classified as being in the wireless communication research field of sensor networks, which mainly emphasizes the back-end network protocol design of the system. The second focus of research is primarily interested in establishing different models of multi-sensors themselves and developing corresponding control algorithms. These research methods usually belong to the information fusion field of sensor networks, which theoretically emphasizes the front-end sensor model and fusion algorithm exploration of the system. Further, for the WC strategies viewed from the information fusion field, classical WC scheduling strategies can be divided into three categories: surveillance-oriented, tracking-oriented, and topology-oriented. In the surveillance-oriented category, all sensor nodes are set to randomly “sleep” and “wake” independently, with the aim of achieving homogeneous wide-area coverage with even energy consumption [
19,
20]. For the tracking-oriented WC method, the sensor nodes in the vicinity of the predicted target location are woken up successively along the predicted target track, and, during this process, one or more clusters are formed, and one sensor node will be chosen as the cluster leader in each cluster, which is in charge of gathering target information and controlling the nodes’ states [
21,
22,
23,
24,
25]. The authors of [
22] utilized a PSO algorithm and duty cycling technology in order to let the selected sensors perform tasks. The authors of [
23] proposed a sensor selection strategy based on a multi-objective optimization method to save energy. However, the performance of this method is restricted by localization accuracy of the sensor nodes, as low node localization will lead to poor target positioning and therefore improper wake up clusters. The third category is the topology-oriented WC strategy [
26,
27,
28,
29,
30,
31,
32], which gathers nodes together to form a cluster, in which the node states of “wake” and “sleep” change dynamically. The elected cluster leader keeps the “wake” state to detect the target. A new cluster with two heads was proposed in [
27] to track the targets collaboratively to enhance the robustness and network lifetime. In [
28], two distributed information fusion schemes are proposed in anti-submarine warfare applications. In [
29], an energy-efficient adaptive overlapping clustering method is proposed for continuous monitoring applications. In [
30], a strategy is proposed to track a moving target in an environment with obstacles. This cluster leader will wake up its members once a target is found. Therefore, the decisions regarding target detecting and tracking are dominated completely by a single node. This will inevitably lead to a number of false alarms.
Recently, an artificial ant colony (AAC) approach was proposed to allow distributed sensor WC in WSN to accomplish the joint task of surveillance and target tracking, which in ants is then transformed into information on food location [
9]. The communication, invalidation, and fusion of the target information are modeled as the processes of pheromone diffusion, loss, and accumulation, respectively. Compared with classical wake-up methods, a similar position error is obtained by the AAC method with much lower energy consumption, indicating that swarm intelligence is promising in dealing with the problem of distributed WC in WSNs. However, in the AAC method, the information is modeled as the pheromones that ants release, so whether the information comes from a sensing module (SM) or a communication module (CM) is not distinguishable. Therefore, as in classical wake-up methods, the AAC method is limited to optimizing the energy consumption of the SMs. However, in dynamic power management techniques [
33], the energy consumed by the CM cannot be ignored, which is why we presented a distributed infectious disease model (DIDM) in a prior work [
34]. With four sub-processes and six commonsense rules, the information from the SM and CM was modeled as the pathogen spread by direct infection and cross-infection, respectively. The simulation shows that the DIDM method is more effective than the AAC approach.
On the other hand, the DIDM method placed most emphasis on the infection mechanism. For the immune mechanism, it only introduces a prior identical immunity repairing ratio 0 < q < 1, ignoring the variation tendency in the infectious process. However, in practice, with changes in infection, the biological immune capacity changed correspondingly. Therefore, it is reasonable to design the immune mechanism according to natural processes and dynamical behavior in the biological immune system. With such an immune mechanism, the model deficiency caused by the fixed immunity repairing ratio can be avoided. Motivated by this, a biomimetic distributed infection-immunity model (BDIIM) that includes three sub-processes related to the infection mechanism—the occurrence probabilities of direct-infection and cross-infection, the immunity/immune-deficiency of direct-infection and cross-infection, and the pathogen amount of direct-infection and cross-infection—is proposed. In addition, two sub-processes—immune cell production and immune memory—are added to depict the immune mechanism, and one sub-process—pathogen accumulation under immunity state—is revised. Furthermore, the relationship between sensor wake-up and the BDIIM is established to derive a collaborative wake-up method. A simulation of joint surveillance and target tracking is utilized to show the effectiveness of BDIIM.
The rest of the paper is organized as follows:
Section 2 establishes the BDIIM for node wake-up control and proposes a BDIIM model, and
Section 3 establishes the correspondence between sensor wake-up and disease propagation. The proposed method is evaluated and analyzed by simulations in
Section 4. Finally,
Section 5 concludes the paper.
3. The Corresponding Relationship between the Proposed BDIIM and Node Wake-Up Process
In this section, similarities between sensing nodes in sensor networks and individuals in epidemic areas are established.
Collaboration between the self-organized sensor nodes is similar to the infectious interactions between these individuals.
A sensor node obtains the target information using the SM or CM while an individual is infected through DI or CI.
For the sensor nodes in WSNs, when a sensor node finds a target using its SM, this node then communicates with its neighbors via a CM. For the individuals in an epidemic area, when an individual is infected by DI, this individual then propagates the pathogen to their neighbors by CI.
Using a sensor node SM in a “wake” state, it is possible to find the target, while DI of an individual with immune deficiency may occur with the presence of the superspreader.
A sensor node CM in the sleeping state cannot obtain target information, while CI of an individual with immunity does not occur with their neighbors.
Based on these similarities between the BDIIM and the sensor node wake-up process, parameter correspondence between BDIIM and sensor nodes are established, as listed in
Table 1. Further, for the
kth individual and corresponding
kth sensor node, the corresponding activity relationships between them are listed in
Table 2.
Corresponding relationships composed of seven pairs of states between BDIIM and the sensor’s WC state are shown in
Figure 4. Each pair of states contains a state of the BDIIM and a WC state marked in a yellow and gray box, respectively. Each pair of states denotes the corresponding relationships between the BDIIM and the sensor’s WC states. According to the above proposed algorithm in
Section 2 and the settings in this section, when a target appears, all of these seven groups of states will transform continuously to achieve wake-up control of each sensor node. There are two modes for the sensors: on duty and off duty. When the sensor is in “on duty” mode, the processing unit is powered on, at least one of the SM and/or CM is powered on, and the sensor is capable of processing the sensory messages. On the contrary, when the sensor is in “off duty” mode, the processing unit (PU) is powered off, and the SM and CM are either turned off or turned on to wait for wakeup signals. The corresponding relationships between the WC states and sensors states are listed in
Table 3.
4. Numerical Example
The simulation was formulated in Matlab R2012a and the initial conditions were set as follows: Five hundred micro-sensors are assumed to be randomly planted on the ground in the square region of 40,000 square meters. These sensors integrate CMs receiving and sending modules, and the SMs can detect the target and transfer the target information via the CMs when the target passes by. The time interval was 1 s, and the detailed variables are listed in
Table 4.
The initial values are ∆
Vk(0) = 0 and
Vk(0) =
Vmin.
CIpk(
t) and
RDpk(
t) in Equations (2) and (3) are considered as
The target moves in constant-velocity (CV) driven by a zero-mean Gaussian noise process with a variance of 400 m
2 in 10 consecutive rounds.
Figure 5,
Figure 6 and
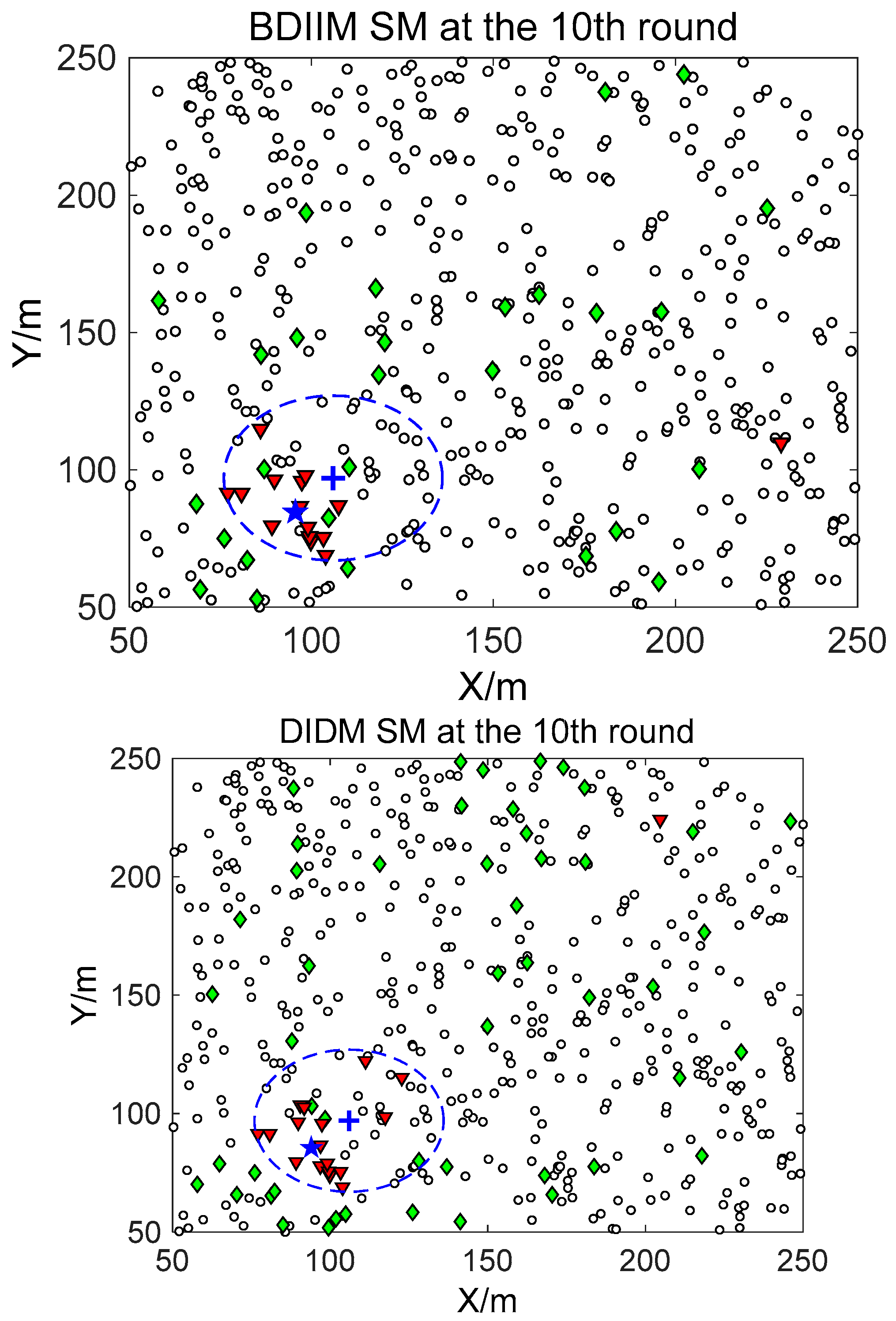
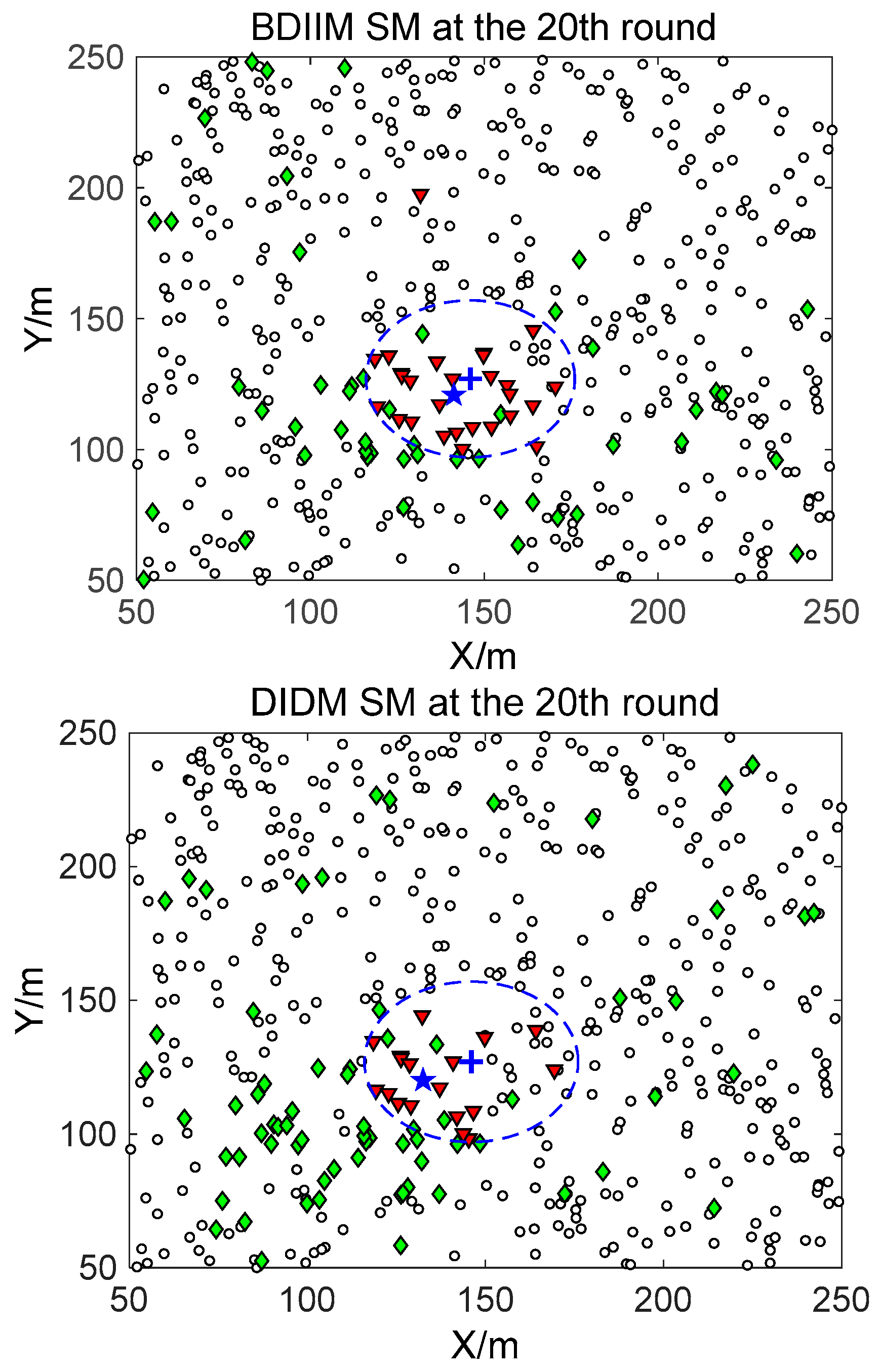
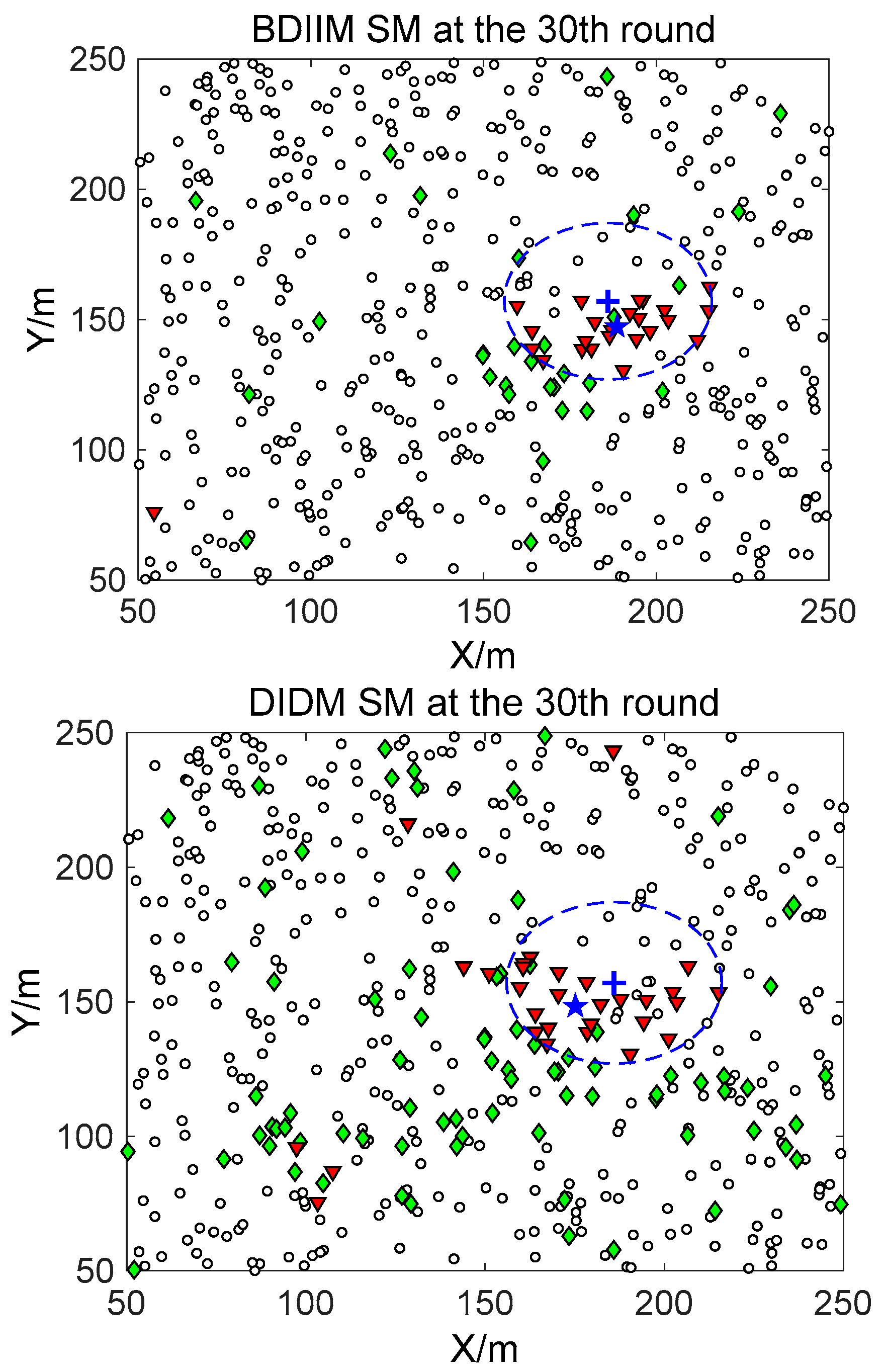
Figure 7 show in detail the state of the SMs at different times during the target movement via the BDIIM and DIDM methods. The target is plotted by a “
+” (blue), which is supposed to have the same track in both methods and move from the left-lower location of the figure to an upper-right location. “★” (blue) represents the estimated target position. The dashed circle (blue) denotes the sensing and communicating area with the radii
Rs and
Rs +
Rc, respectively. “
□” (black) in the smallest size represents the “sleep” SMs. “▼” (red) represents the valid wake-up SMs, which are set to “wake” and successfully find the true target. “◆” (green) represents the invalid wake-up SMs, which are set to “wake” but fail to find the target. The SM states in the 10th, 20th, and 30th time intervals are compared. The results in the other time intervals are similar and are therefore saved. In counting the total number of green “◆” outside the circle at these three time intervals, we find that the number of green “◆” via the proposed BDIIM method is slightly less than the number obtained via the previous DIDM method. Meanwhile, in the area outside the circles where the target passes by, the number of green “◆” via BDIIM is much less than that achieved via DIDM.
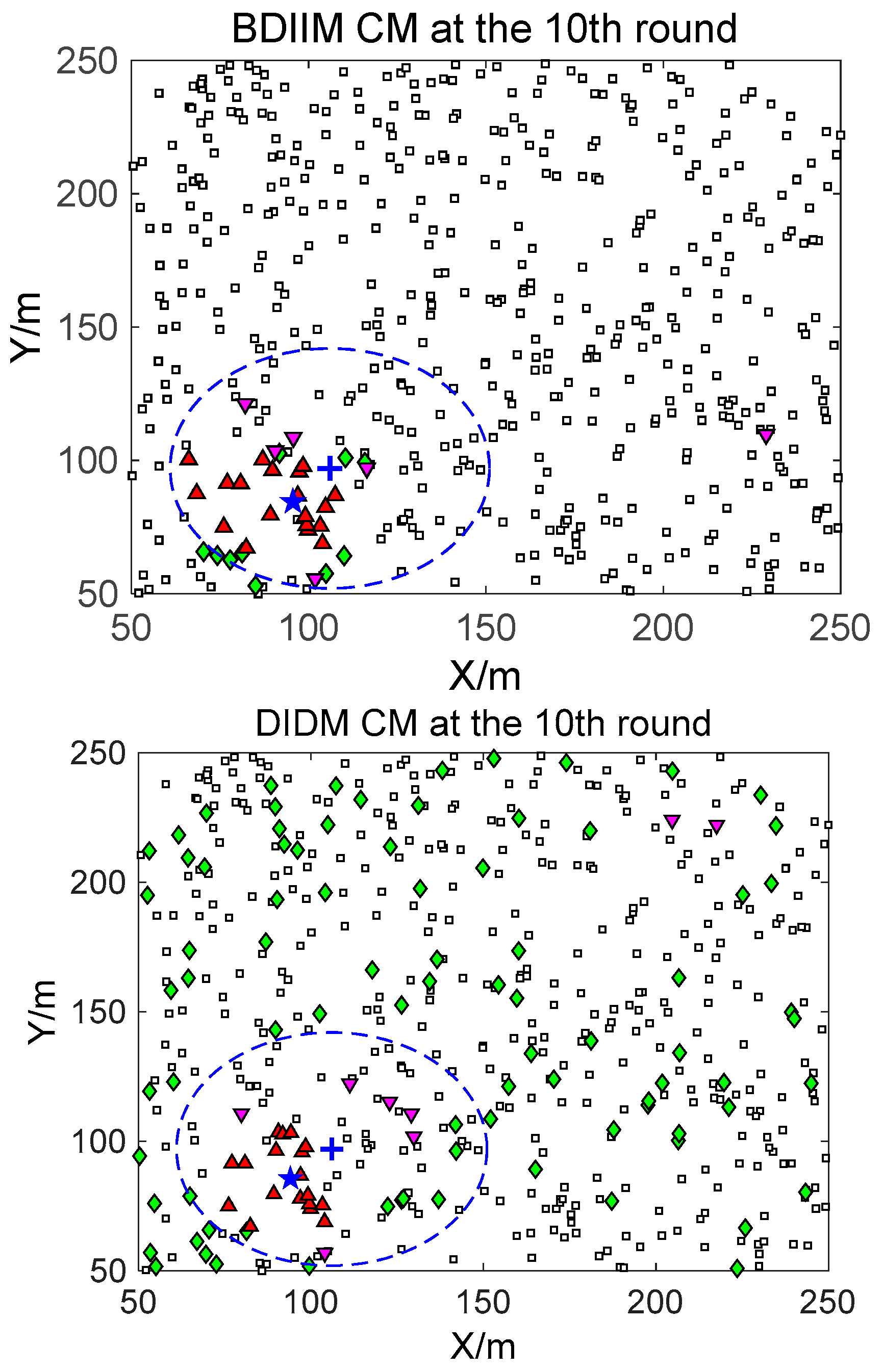
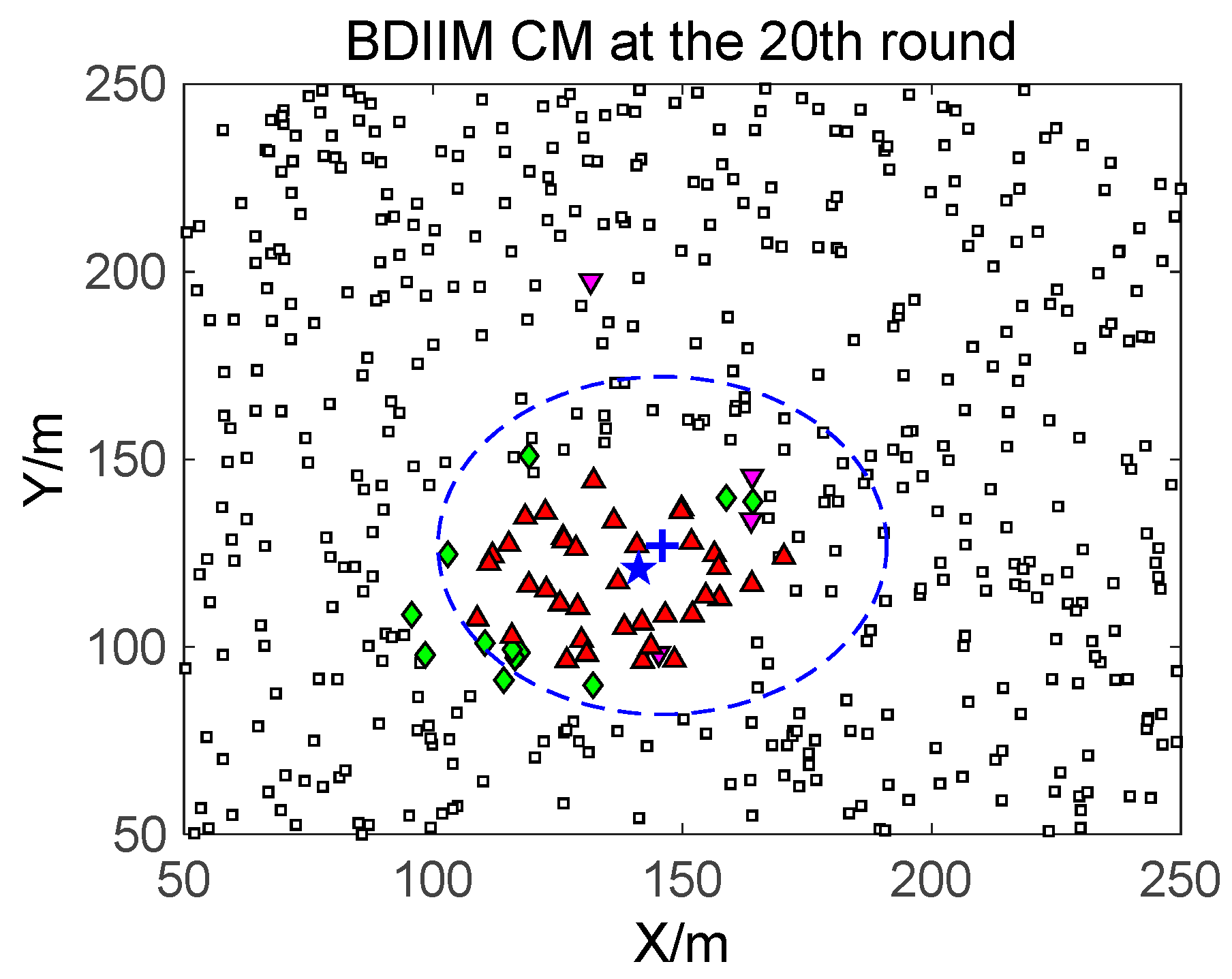
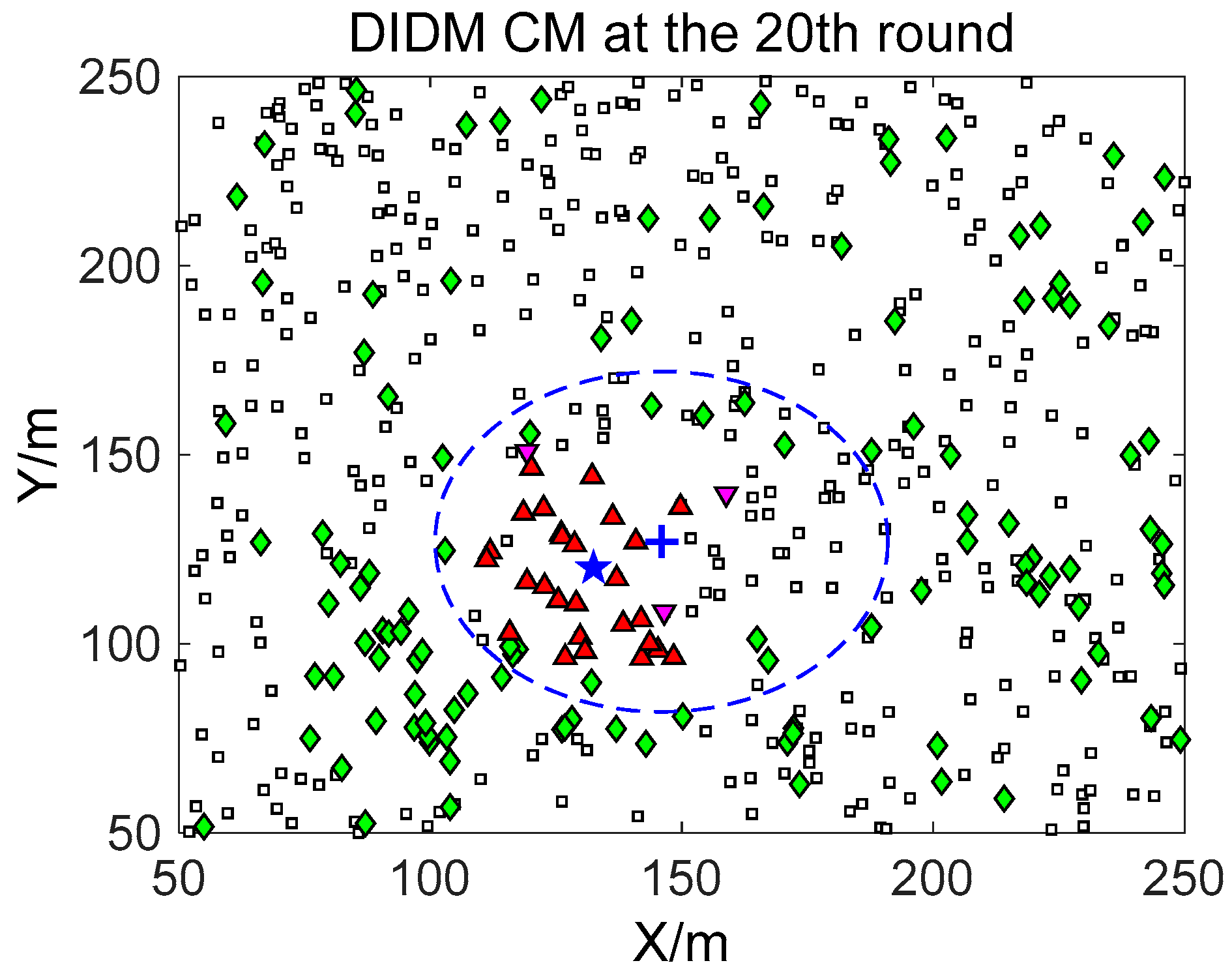
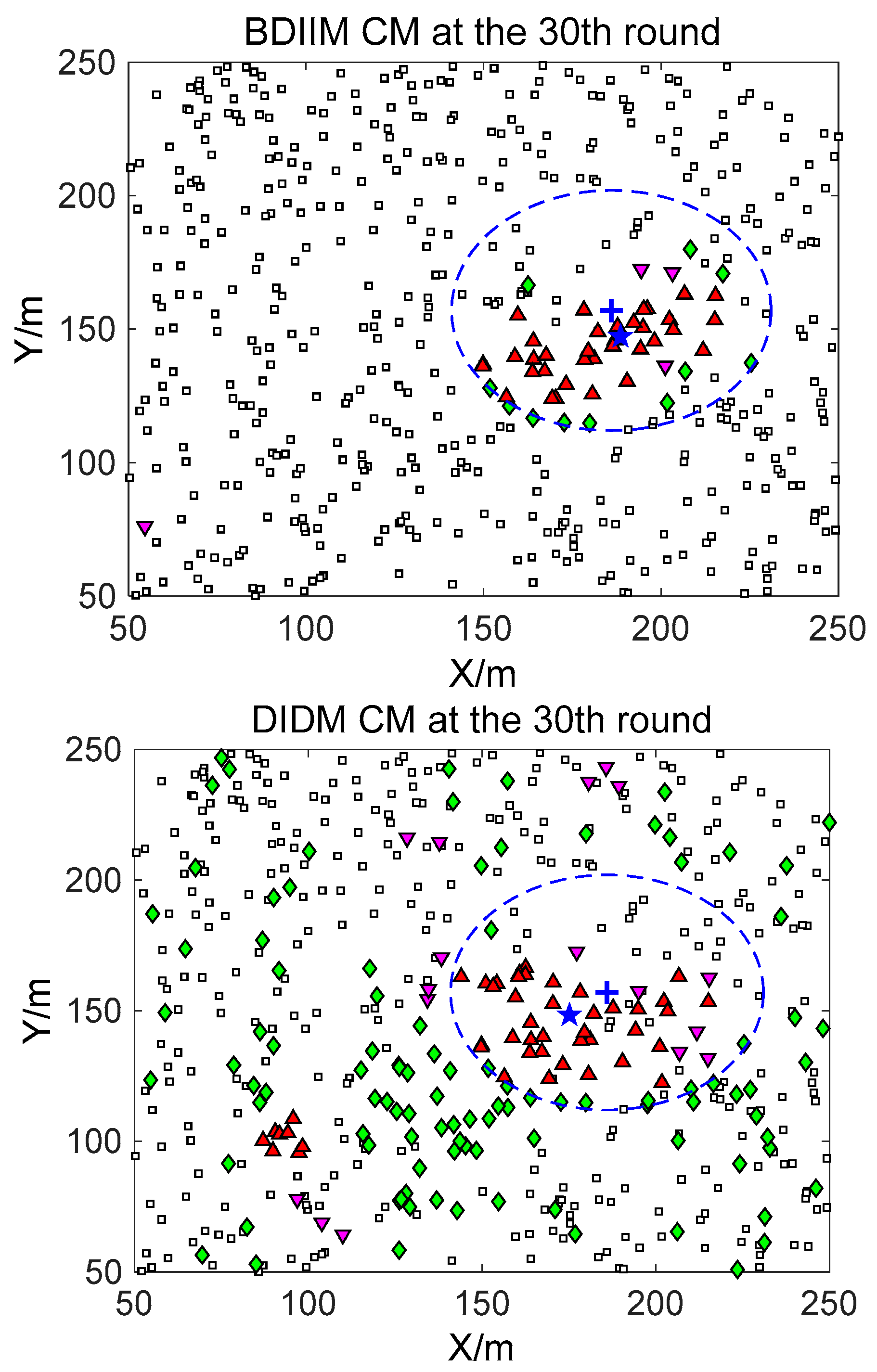
For the state of the CMs, as shown in
Figure 8,
Figure 9 and
Figure 10, the target is plotted by a “+” (blue). “▲” (red) represents the valid wake-up CMs. “▼” (pink) represents the invalid wake-up CMs in which “◆” (green) represents the invalid wake-up CMs in the “send/receive” state. These figures show the detailed states of the CMs at the 10th, 20th, and 30th time intervals during target movement, via the BDIIM and DIDM methods. Especially in the area outside the circles, where the target passes by, the number of green “◆” via the BDIIM is clearly much less than that obtained via the DIDM at each time interval. In other words, the proposed BDIIM method has a higher wake-up efficiency than the DIDM method, and the energy cost of the system is greatly reduced, while the estimation error of the target position also decreases.
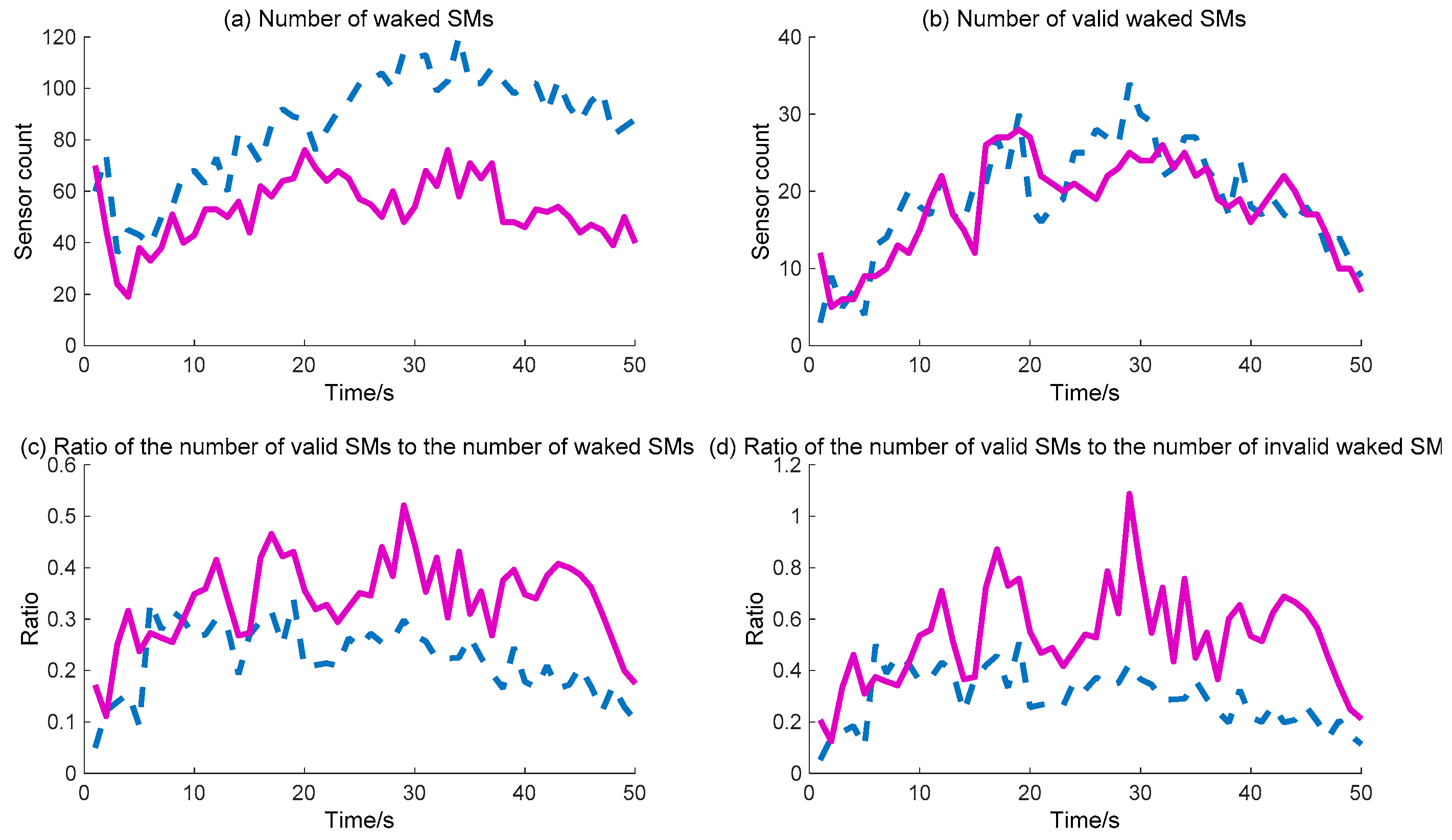
Further, the detailed data regarding the DIDM method and the proposed BDIIM method are curved, as shown in
Figure 11 and
Figure 12. The dashed (blue) and solid (pink) lines represent the DIDM method and the proposed BDIIM method, respectively. The WC performance of the SMs is shown in
Figure 11. The detailed calculation data are listed in
Table 5. It can first be seen from
Figure 11b that, throughout the whole process, there is little difference in the number of valid waked SMs between the two methods. However, it can be clearly seen from
Figure 11a that the number of waked SMs via the BDIIM method is fewer than that achieved via the DIDM method throughout the whole process, especially after 20 s. The ratio of the number of valid waked SMs to the total number of waked SMs is given in
Figure 11c. The average ratio via the proposed method in this work approaches 0.38, while the average ratio via the previous method is about 0.25 during this period. Compared with the previous method, the ratio is improved by approximately 52% by using the proposed method. Furthermore, the ratio of the number of valid waked SMs to the idle number of waked SMs, shown in
Figure 11d, demonstrates that the wake efficiency of SMs via the BDIIM method is higher than that achieved via the DIDM method.
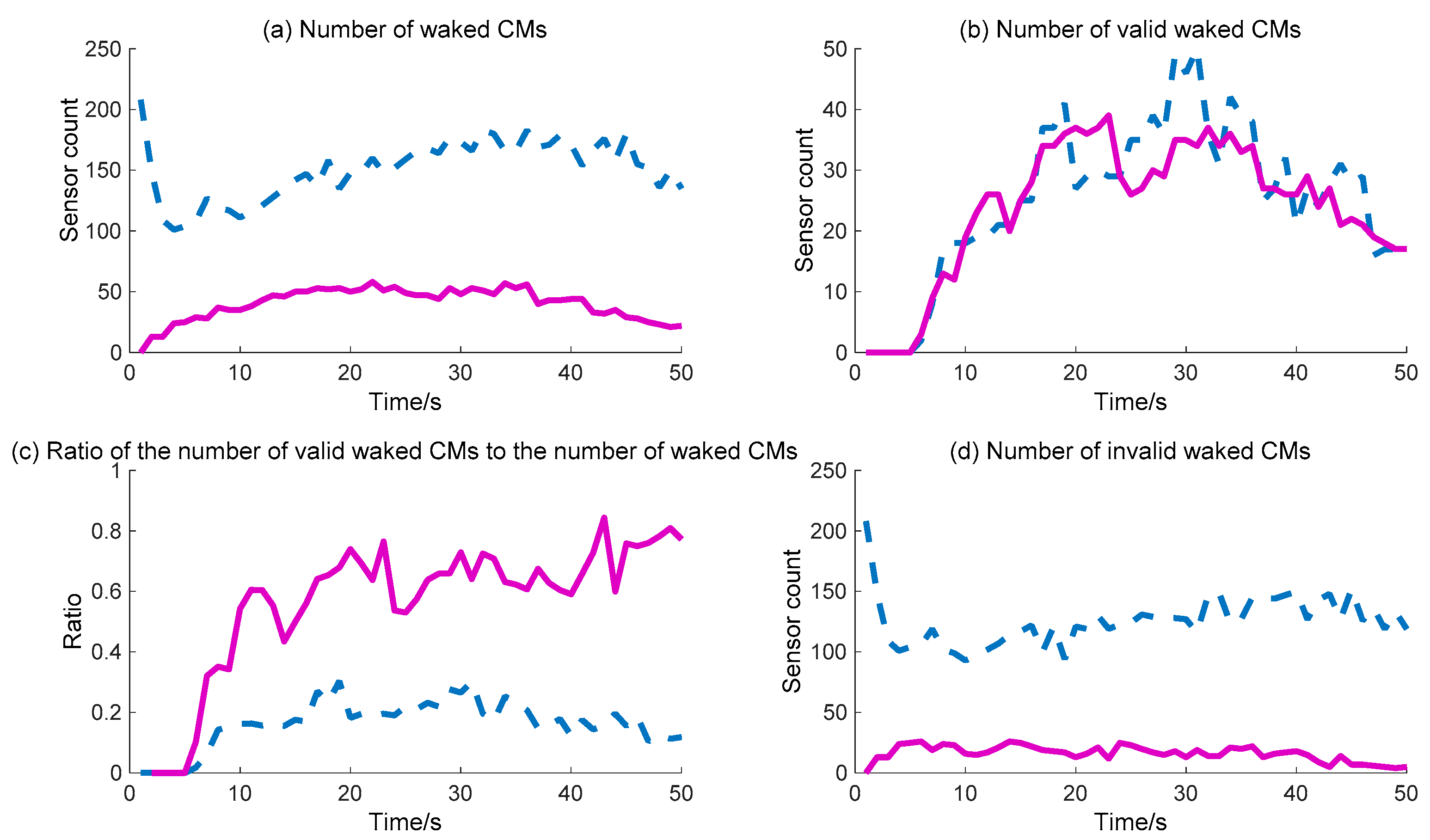
The WC performance of the CMs is shown in
Figure 12. The detailed calculation data are listed in
Table 6.
Figure 12b shows that the number of valid waked CMs is no different across the whole process for the two methods, while
Figure 12a shows that the number of waked CMs via the BDIIM is clearly less than that achieved via the DIDM method. During the whole process, the maximum number of waked CMs via the BDIIM method is approximately 50 after 10 s, while the maximum number via the DIDM method reaches more than 150 much more rapidly. Naturally, the ratio of the number of valid waked CMs to the total number of waked CMs demonstrated by the BDIIM method is much higher than that proposed by the DIDM method, as shown in
Figure 12c, which means that the efficiency of the waked CMs is improved greatly using the BDIIM method. The average efficiency after 10 s using the BDIIM method is estimated to be approximately 65%, compared with an average efficiency of just 21% achieved by the DIDM method. In addition, the number of idle sensor nodes is also given in
Figure 12d, and it can be seen that the average number of idle nodes is 15 in the BDIIM method, which is much less than the 127 that would occur using the DIDM method. The percentage of the number of invalid waked CMs for the BDIIM method compared with the DIDM method is just 12.4%.
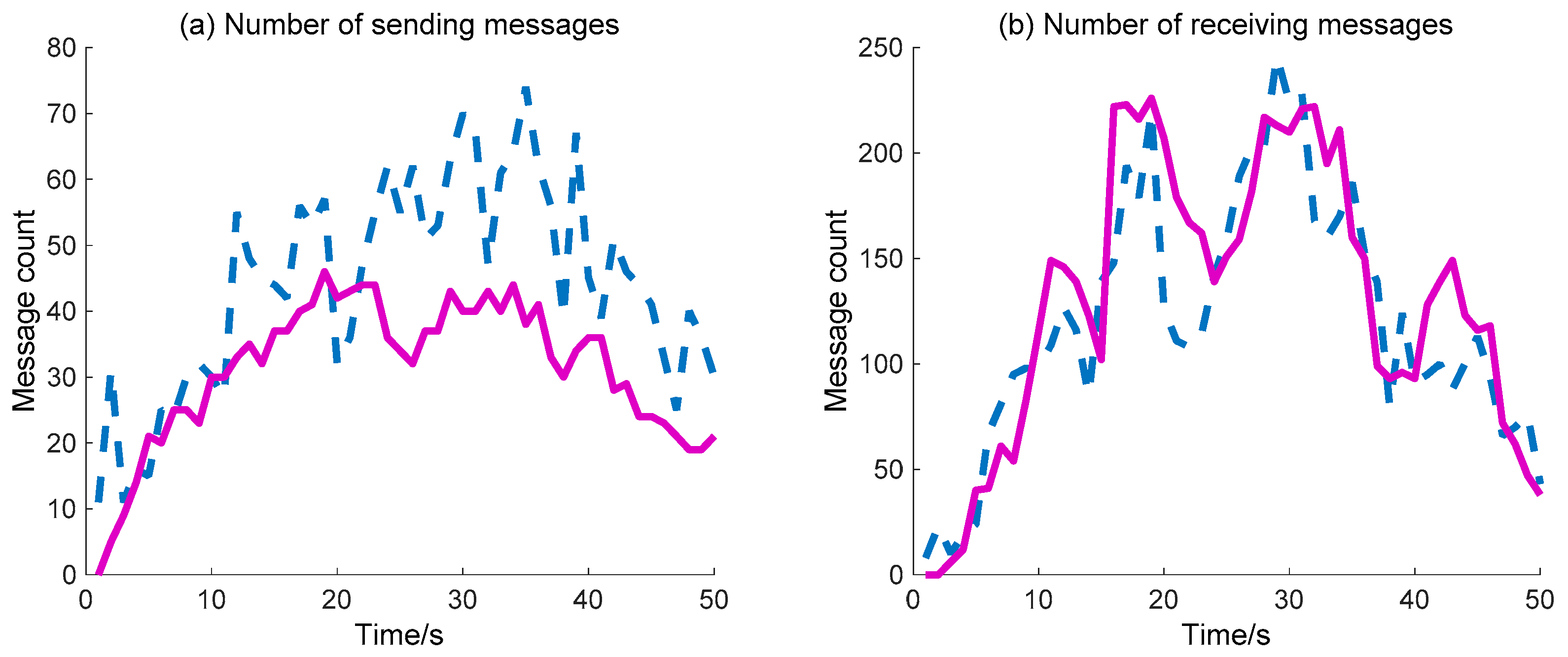
The sending/receiving message number is also considered to compare the WC performance of the two methods (DIDM and BDIIM), as shown in
Figure 13. The detailed calculation data are listed in
Table 7. The sending messages number achieved via the proposed BDIIM method is lower than that achieved via the previous DIDM method. According to the given ratio of receiving messages to sending messages, representing the efficiency of the WC, the improvement in time of the BDIIM method is 1.59 s when compared with the DIDM method.
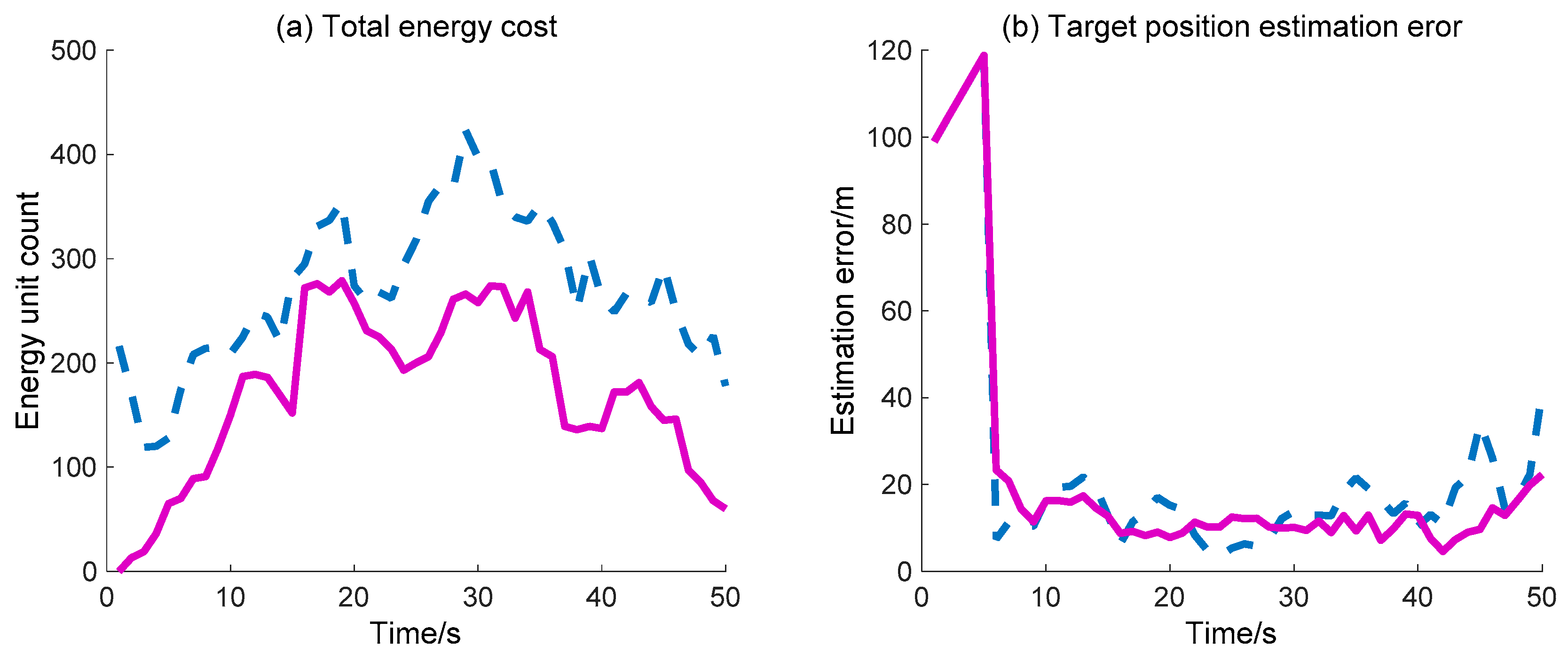
The target position estimation error and total energy cost of WSN are also simulated and compared with the previously mentioned DIDM method. Here, the target position estimation error denotes the distance between the actual target position and the estimate position (the centroid of the valid waked sensor nodes). As for the total energy cost, we consider that the energy consumed by the “idle” sensor node in each time interval is one unit, and one sensor node sending/receiving a message is also considered one unit. Due to the fact that the calculation operation costs much less energy compared with the operation of sending/receiving messages, the calculation cost is not considered. In
Figure 14, the total energy cost across the whole process via the proposed BDIIM method is always less than that obtained via the DIDM method. Finally, the target position estimation error is basically consistent during the first 30 s, while the error via the proposed BDIIM method is slightly less than that obtained via the DIDM method after 30 s. Finally, the total energy cost and position estimation error of the BDIIM method, as listed in
Table 8, are reduced to 50.8% and 78.9% compared with the DIDM method, respectively.