Tightly-Coupled GNSS/Vision Using a Sky-Pointing Camera for Vehicle Navigation in Urban Areas
Abstract
1. Introduction
2. Background and Related Works
3. Vehicle Motion Estimation Using an Upward-Facing Camera
3.1. Camera Calibration and Image Rectification
- denotes the radial lens distortion parameters;
- x and y are the new coordinates of the pixel as a result of the correction;
- is the distance of the distorted coordinates to/from the principal point. and are the coordinates of the principal point.
3.2. Feature Detection, Description and Matching
3.2.1. Feature from Accelerated Segment Test Feature Detector
3.2.2. Binary Robust Independent Elementary Features Descriptor
3.3. Outlier Rejection
3.4. Motion Estimation Process
- k denotes the image frame number;
- ;
- is the rotation matrix;
- and , where , and are the relative translations following the camera axes.
3.5. Computing the Rotation and Translation Using the Singular Value Decomposition Approach
| Algorithm 1: Rotation and Translation Computation Algorithm. |
| Input : and Output: and // initialization // iterate to the total number of feature points  // compute the covariance matrix , and = matrices with and as their columns // determine the SVD of // compute the rotation // compute the translation return: , |
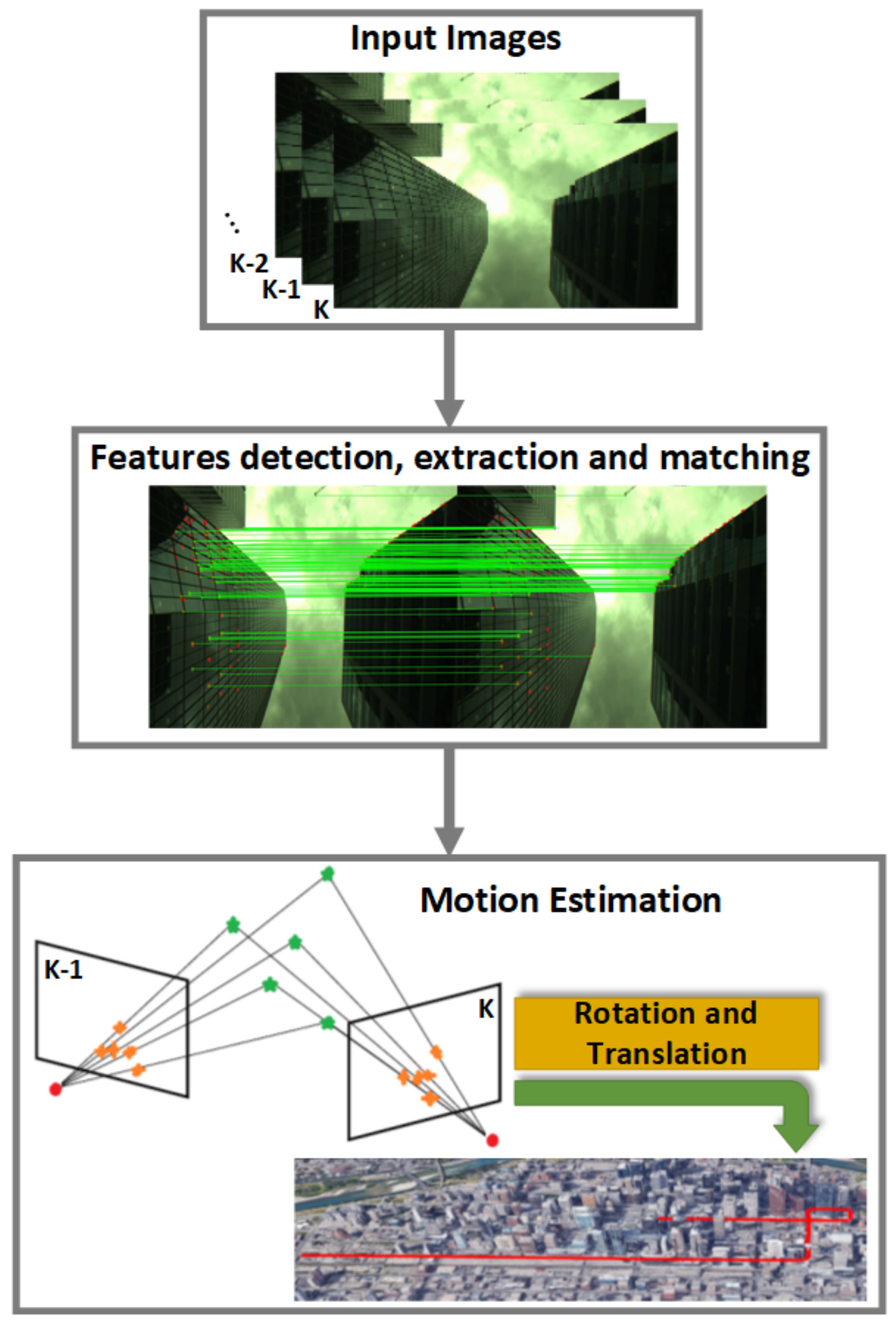
4. Camera-Based Non-Line-Of-Sight Effect Mitigation
4.1. Image Segmentation-Based NLOS Mitigation Algorithm
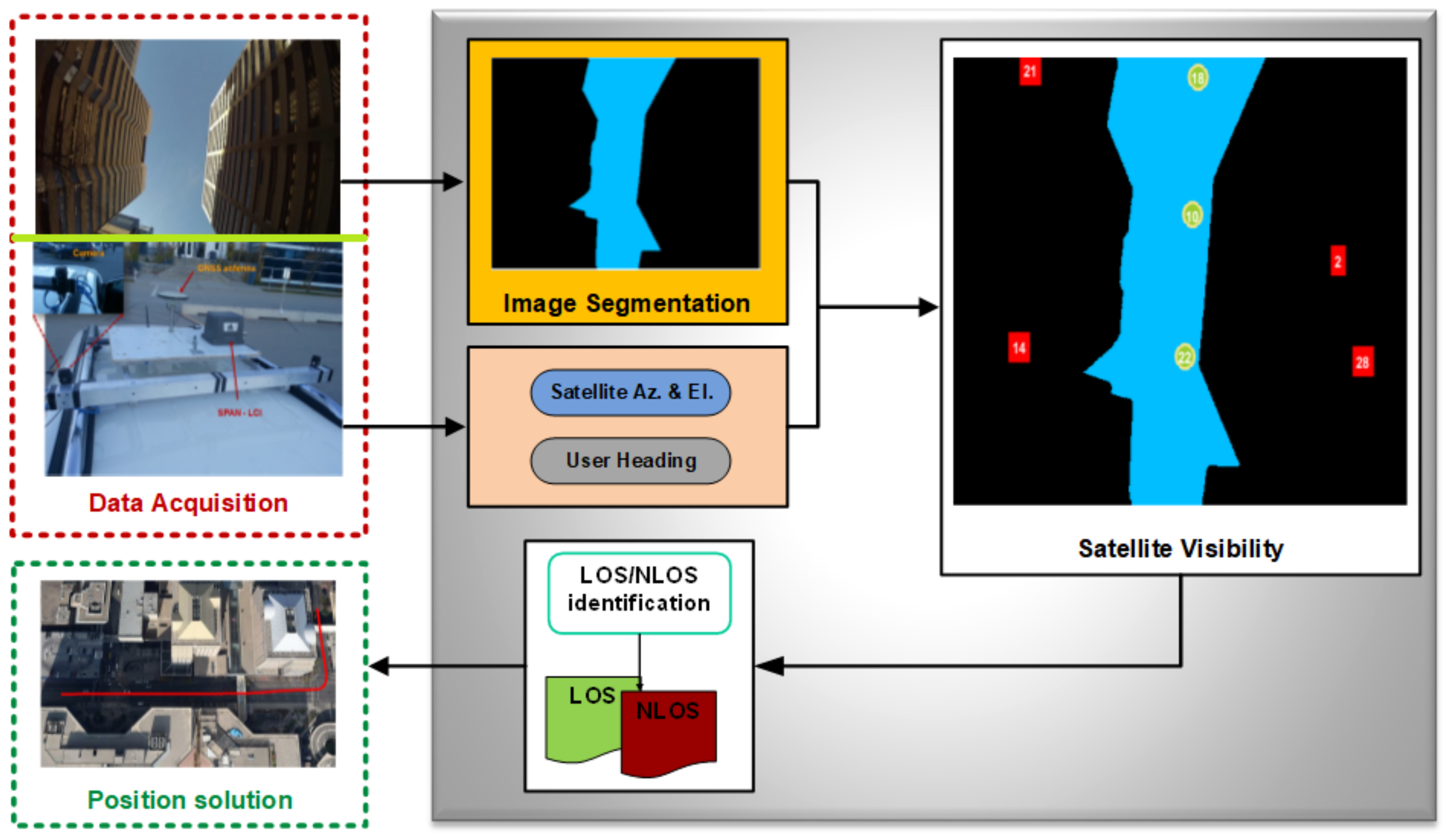
- Image filtering: Given that the images captured using a sky-pointing camera are highly corrupted by bright (e.g., sun light) and dark (e.g., buildings or clouds) objects/structures, we adopted a sequential application of open-close filters denoted Alternate Sequential Filter (ASF) [60]. Indeed, we observed that when the noise is wide-spread over an image, using a single open-close filter with a large structuring element leads to segmentation errors (bright objects tend to be lost and the difference between the sky segment and the other structures in the image becomes hard to observe). ASF provides efficient results since it alternates openings and closings proceeding in an incremental way from small to a given size of the structuring element m, [60]. Consider and the morphological opening and closing of size m, respectively. The ASF is a sequential combination of and such as is a morphological filter. Thus, we have:For illustration, if , we have , where I is the image to filter. The result obtained by using the filter defined in Equation (8) is a less noisy image than the original image. The different portions of the image are more obvious after this step. However, the output of the ASF still provide edges within the sky areas. Since our approach uses edges to categorize sky and non-sky, it is important to remove such edges. For this reason, the levelling algorithm [61] is used along with ASF to find a good trade-off between good identification of edges between sky and buildings and suppression of edges within the same structures (sky and other objects in the image).
- Colour space conversion: once the image is filtered, we determine that the perceptual brightness (luminance) of the image is enough to accurately distinguish the main partitions contained in the image since it depicts sharp details. For this reason, the RGB (Red, Green and Blue) image is converted to the Luv colour space. The luminance channel L is then extracted for further processing.
- Edge detection: the luminance channel extracted from the filtered image is smooth and suitable for edge detection with limited errors. The edge detection here consists of finding discontinuity in the luminance of the pixels within the image. The well-known canny edge detector [59], which consists of smoothing the image with a Gaussian filter, computing horizontal and vertical gradients, computing the magnitude of the gradient, performing non-maximal suppression and performing hysteresis thresholding, is used in this paper.
- Flood-fill algorithm application: At this point, the decision should be made on which edges mark the limit between sky and non-sky areas. The flood-fill step is initialized by assuming the pixel at the centre of the image as belonging to the sky category. Then, the pixels from the centre of the image are filled until we reach an edge. In other words, we used the output of the edge detector algorithm as a mask to stop filling at edges. This process is illustrated in Figure 6.
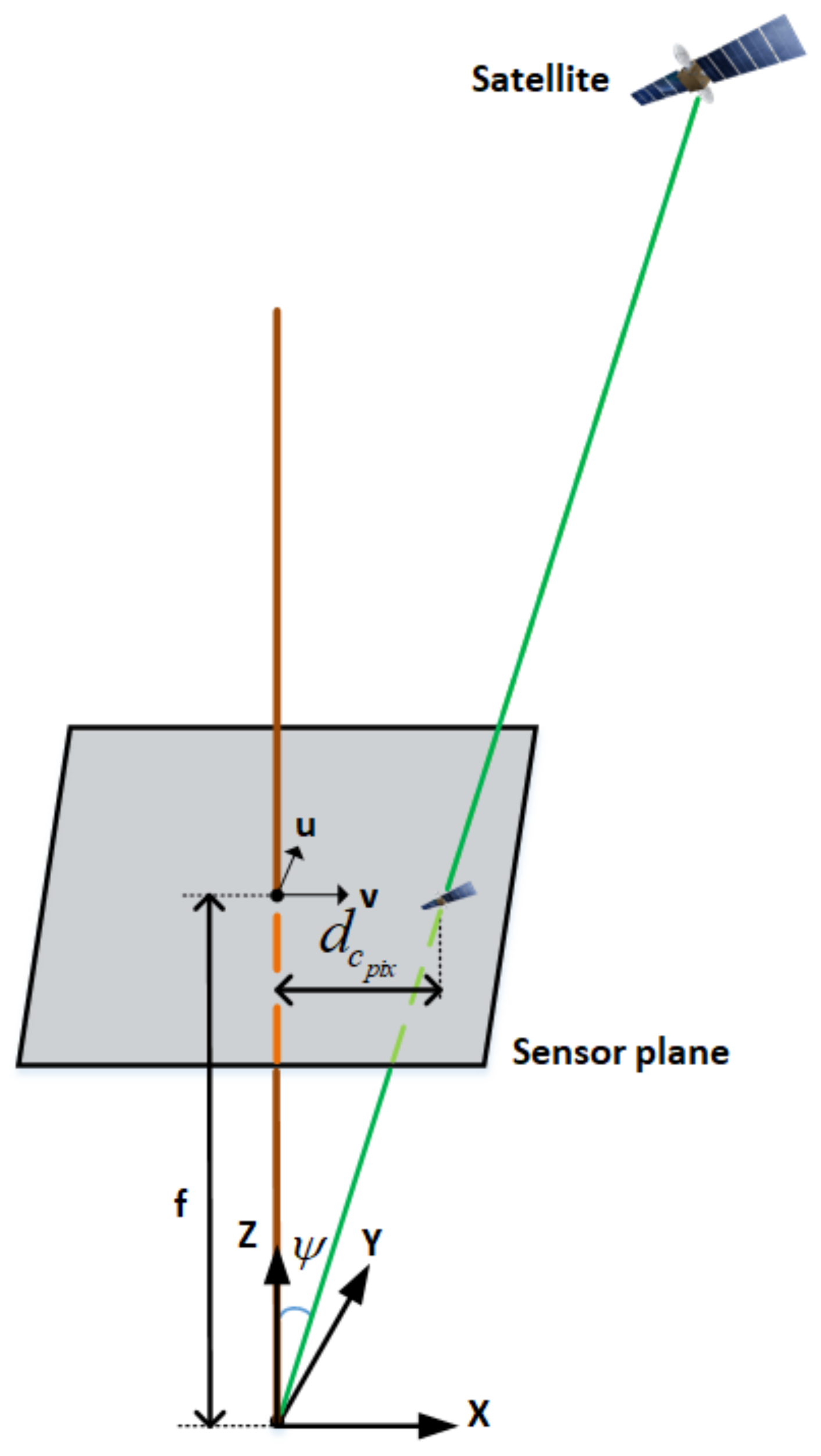
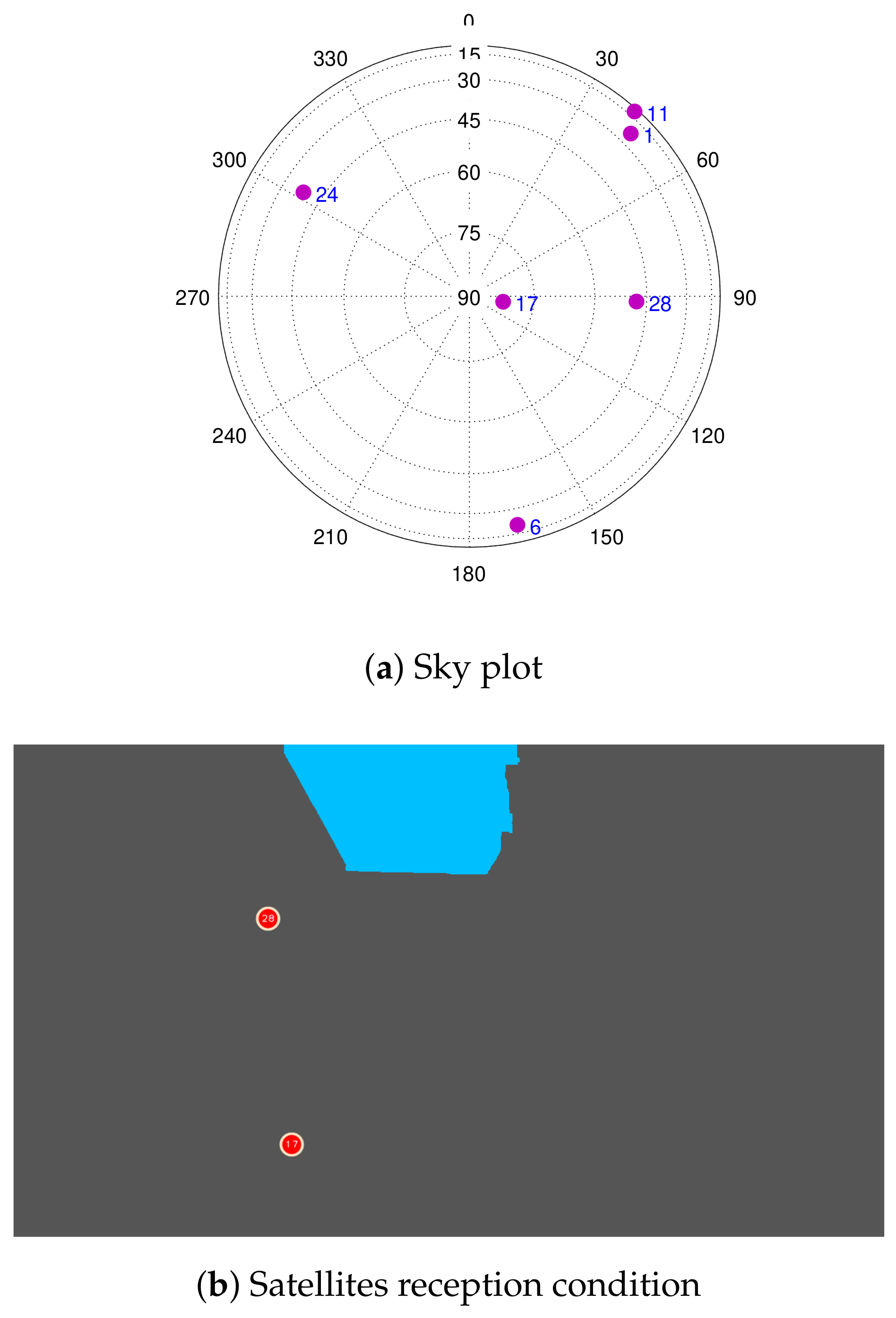
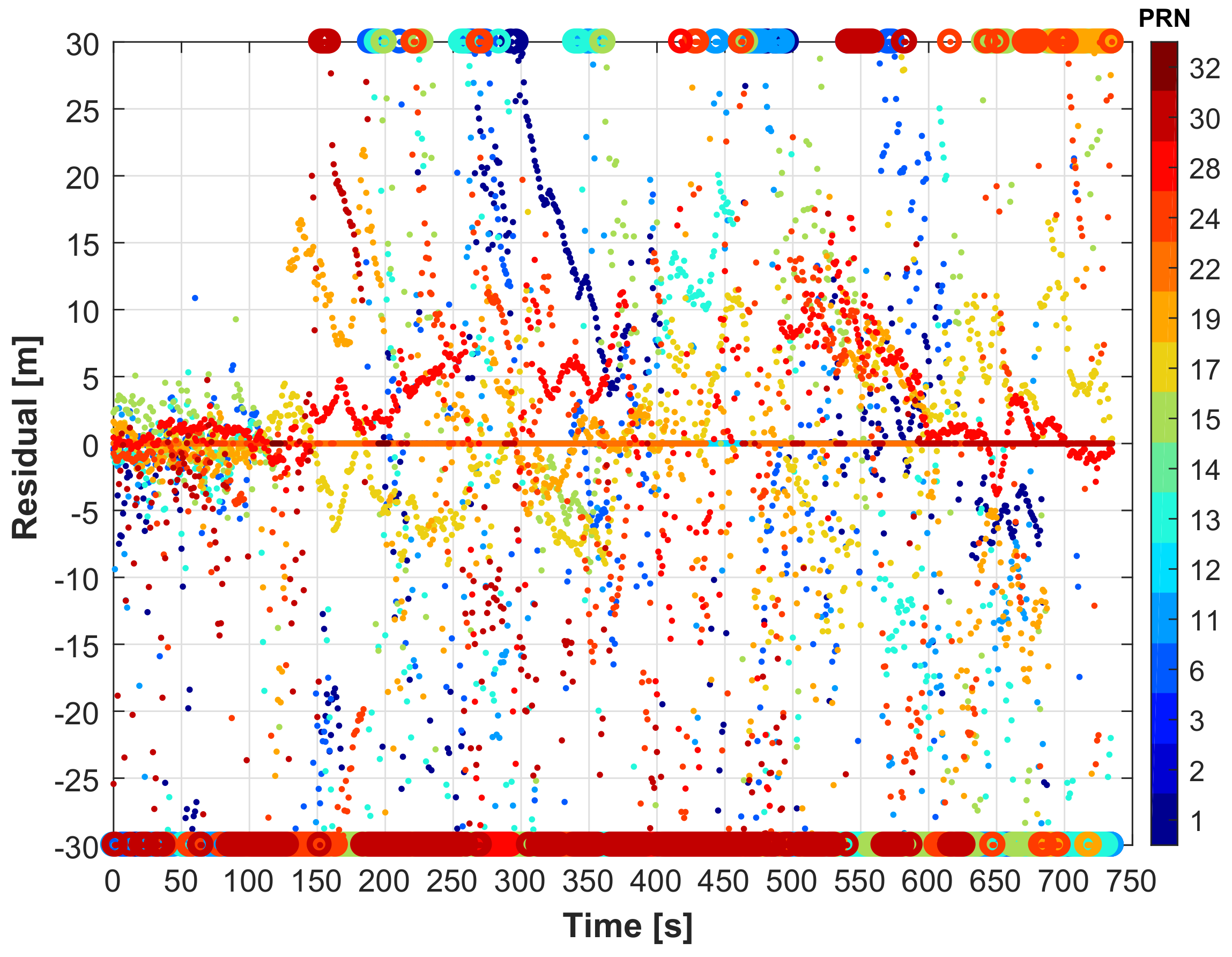
4.2. Satellite Projection and Rejection
- The distance from the centre of the image in pixels (): this corresponds to the elevation angle of the satellite (),
- The azimuth within an image: for this, the heading of the platform is required.
- are the projected satellite coordinates on the image plane;
- is the heading of the platform;
- is the satellite azimuth.
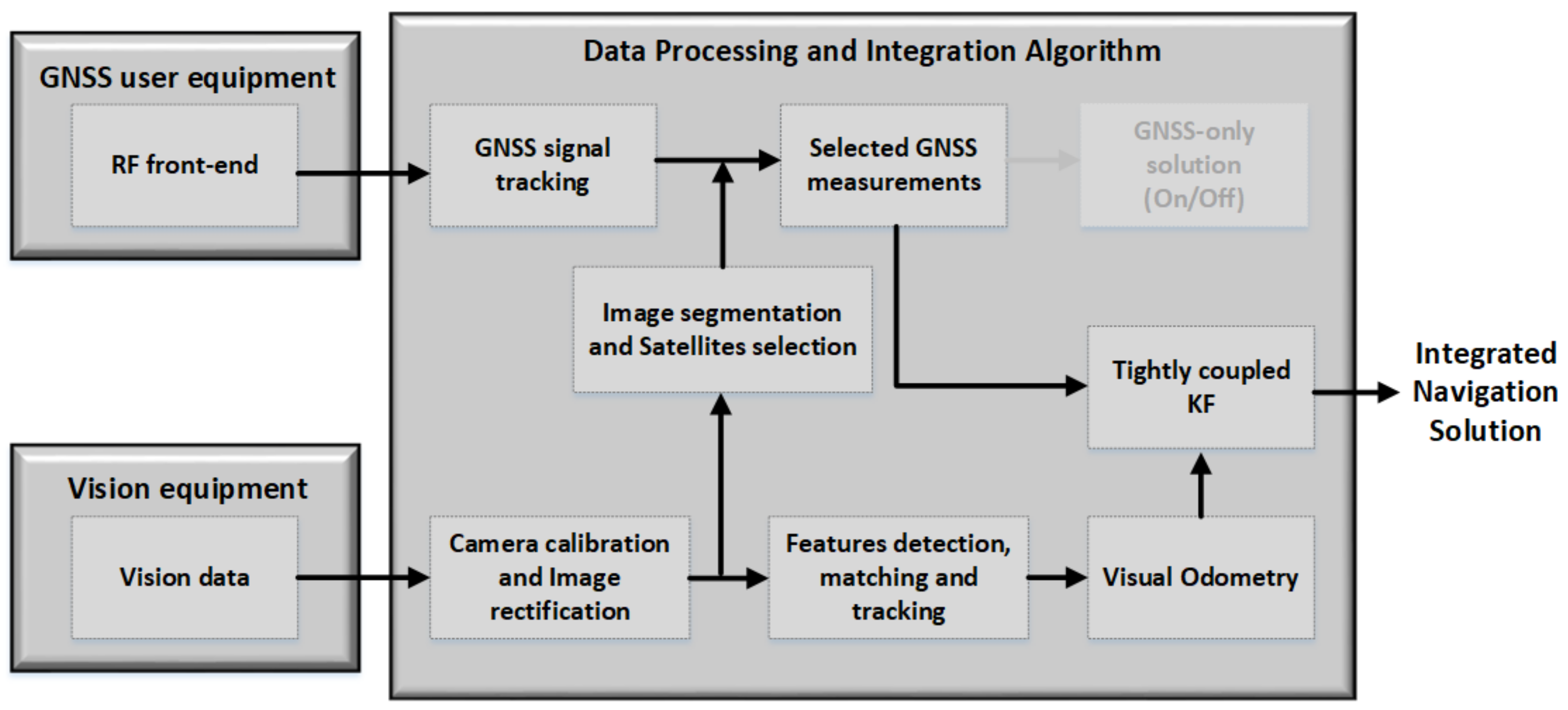
5. Algorithm Development: GNSS/Vision Integration
5.1. Global Navigation Satellite Systems
5.2. Pseudorange Observation
- is the pseudorange of the satellite;
- denotes the satellite’s position at the transmission time;
- represents the user position at the reception time;
- is the receiver clock bias;
- denotes the sum of all errors on the measurement;
- denotes the magnitude of a vector.
- and are the satellite and user velocities, respectively, expressed in the Earth-Centred Earth-Fixed (ECEF) coordinate frame;
- d is the receiver clock drift in m/s;
- represents the ensemble of errors in the measurement in m/s;
- (•) denotes the dot product.
5.3. Visual Odometry
5.4. Tightly-Coupled GNSS/Vision
- and are the state vector and the dynamics matrix, respectively;
- represents the shaping matrix;
- w is a vector of zero-mean, unit variance white noise.
- , and h represent the position components;
- v and a stand for speed and acceleration, respectively;
- A, p and r are the azimuth, pitch and roll respectively;
- represents their corresponding rates.
- denotes the design matrix, which is the derivative of the measurements with respect to the states;
- represents the Kalman gain.
5.4.1. GNSS Observables
5.4.2. Vision Observables
5.5. State Estimation and Data Integration
- denotes a vector of zeros;
- , with M the total number for features;
- is the matrix defining the homogeneous coordinates of the feature points from consecutive image frames;
- is the position change vector between consecutive frames;
- denotes the unknown range.
- represent the estimated platform’s position.
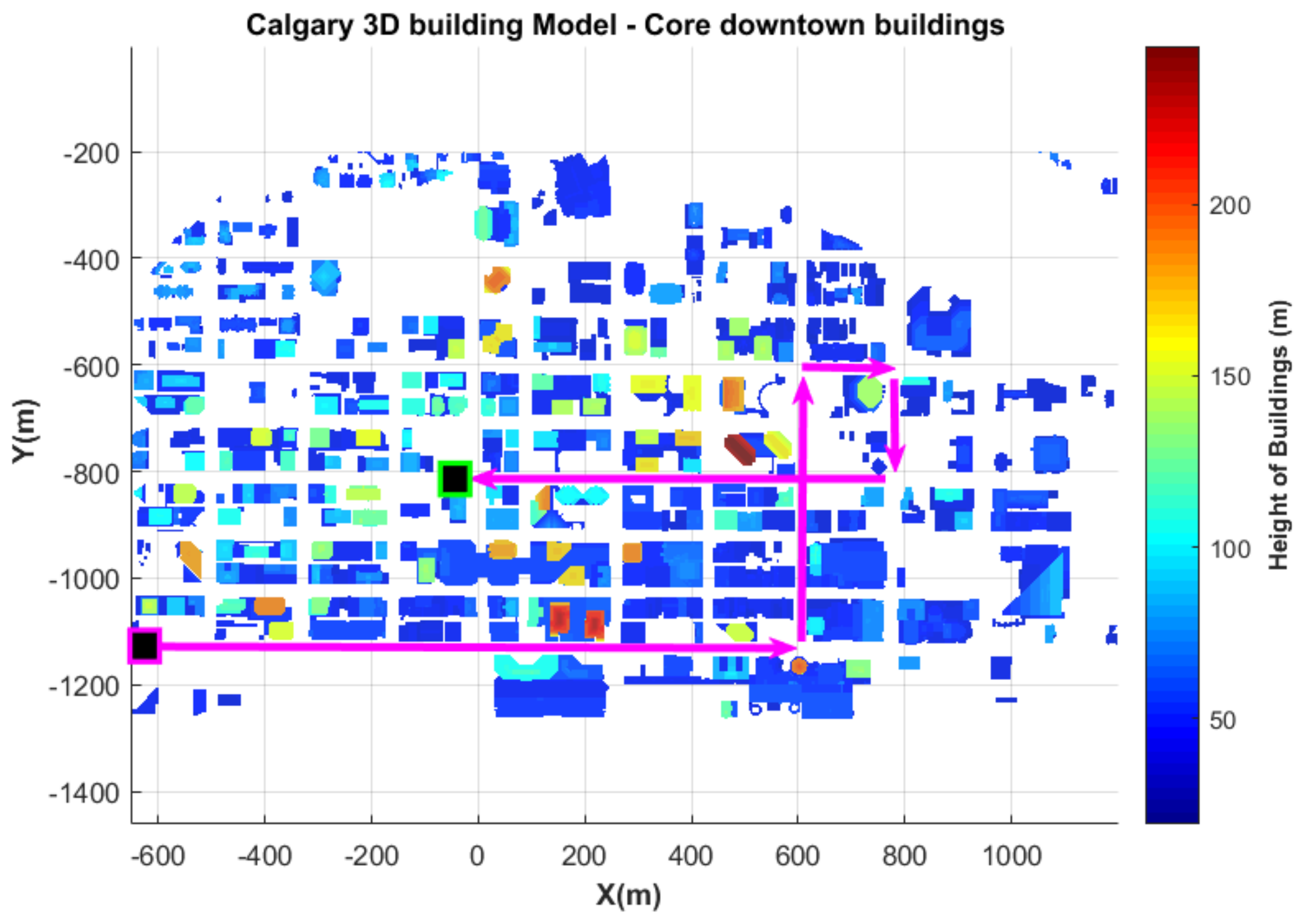
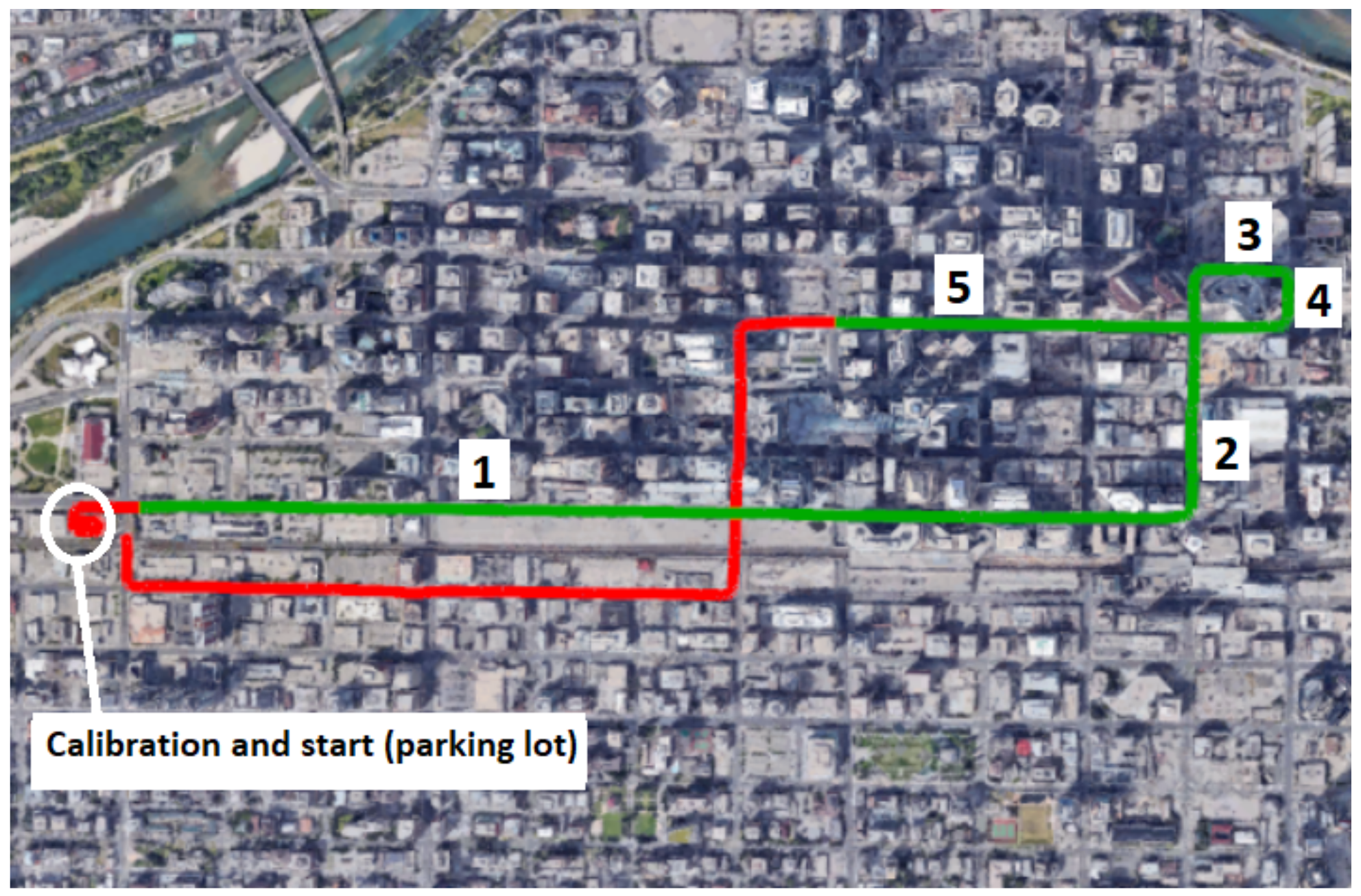
6. Experiment and Results
6.1. Hardware
- VFOV stands for Vertical Field of View;
- and are the radial lens and the tangential distortions obtained from the calibration matrix as defined in Section 3.1.
6.2. Results and Interpretations
- The GNSS-only navigation solution: For this, the PLAN-nav (University of Calgary’s module of the GSNRx™ software receiver) was used. As with most consumer-grade receivers, it uses local level position and velocity states for its GPS-only Kalman filter. In the results, this solution is referred to as GNSS-KF;
- The tightly-coupled GNSS/vision solution: The Line Of Sight (LOS) satellites are first selected. Then, this solution tightly couples the vision-based relative motion estimate to the GNSS. In the results, this is referred to as Tightly-Coupled (TC) GNSS/vision;
- The loosely-coupled GNSS/vision solution integrates measurements from the vision system with the GNSS least squares PVTsolution obtained by using range and range rate observations. Both systems independently compute the navigation solutions, and they are integrated in a loosely-coupled way. This means that if one of the system is unable to provide the solution (e.g., GNSS), then no update from that system is provided to the integration filter. This solution will help to clearly see how beneficial the proposed integration method is, especially when there are fewer than four (LOS) satellites. We refer to this as Loosely-Coupled (LC) GNSS/vision in the text. More details on integration strategies can be found in [10,65].
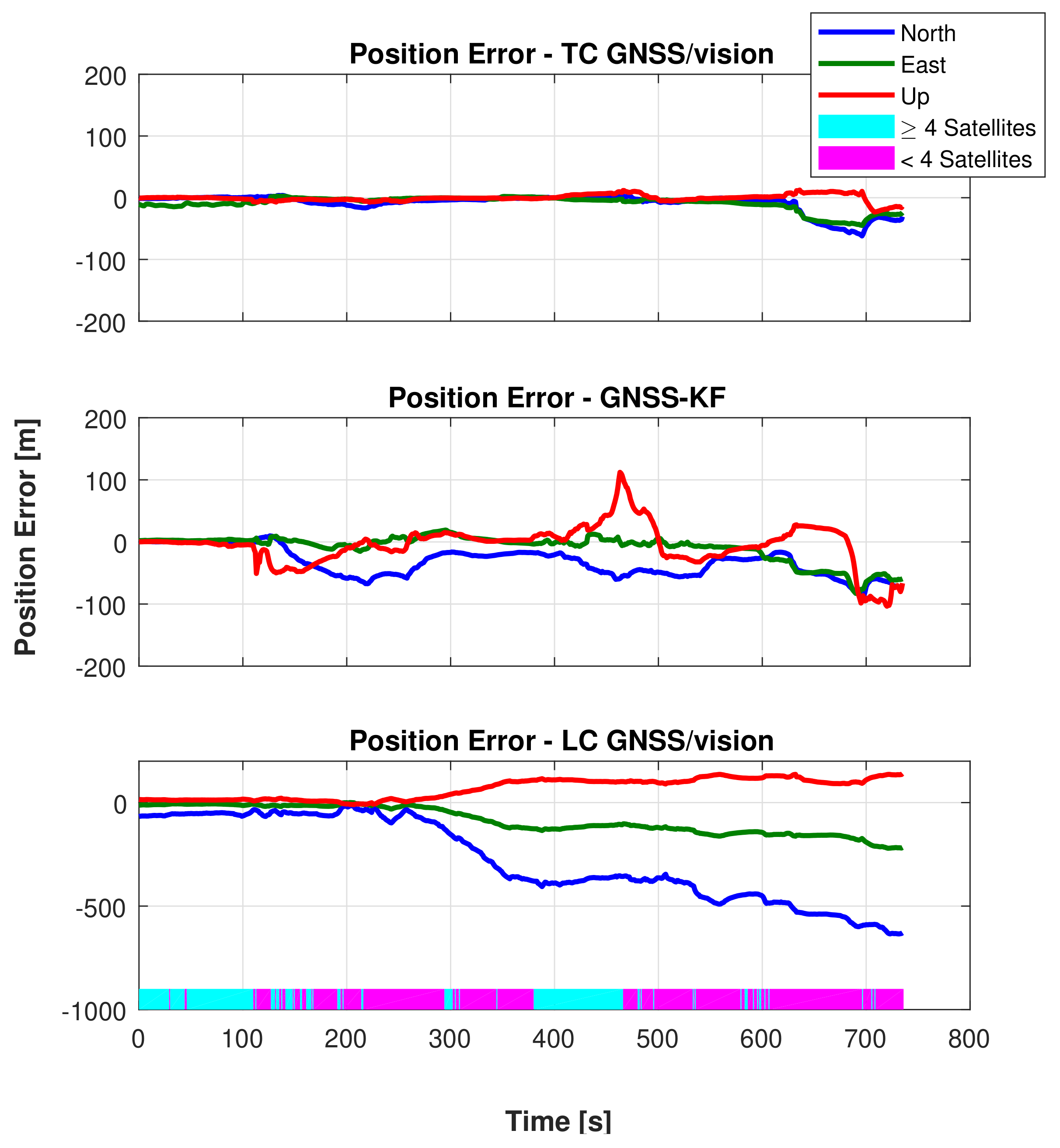
 , to the end of the travelled path, there are less than four satellites (after NLOS exclusion) 75.8% of the time. For this reason, the LC GNSS/vision integration, which in this situation relies on the vision system only, performs poorly, while the proposed TC GNSS/vision closely follows the reference solution.
, to the end of the travelled path, there are less than four satellites (after NLOS exclusion) 75.8% of the time. For this reason, the LC GNSS/vision integration, which in this situation relies on the vision system only, performs poorly, while the proposed TC GNSS/vision closely follows the reference solution. and
and 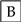 , we can observe that the proposed method does not drift too much while the GNSS-KF provides poor solutions. From Figure 18, it is seen that the solution obtained from the LC GNSS/vision outputs larger error compared to the two other approaches. In Zone
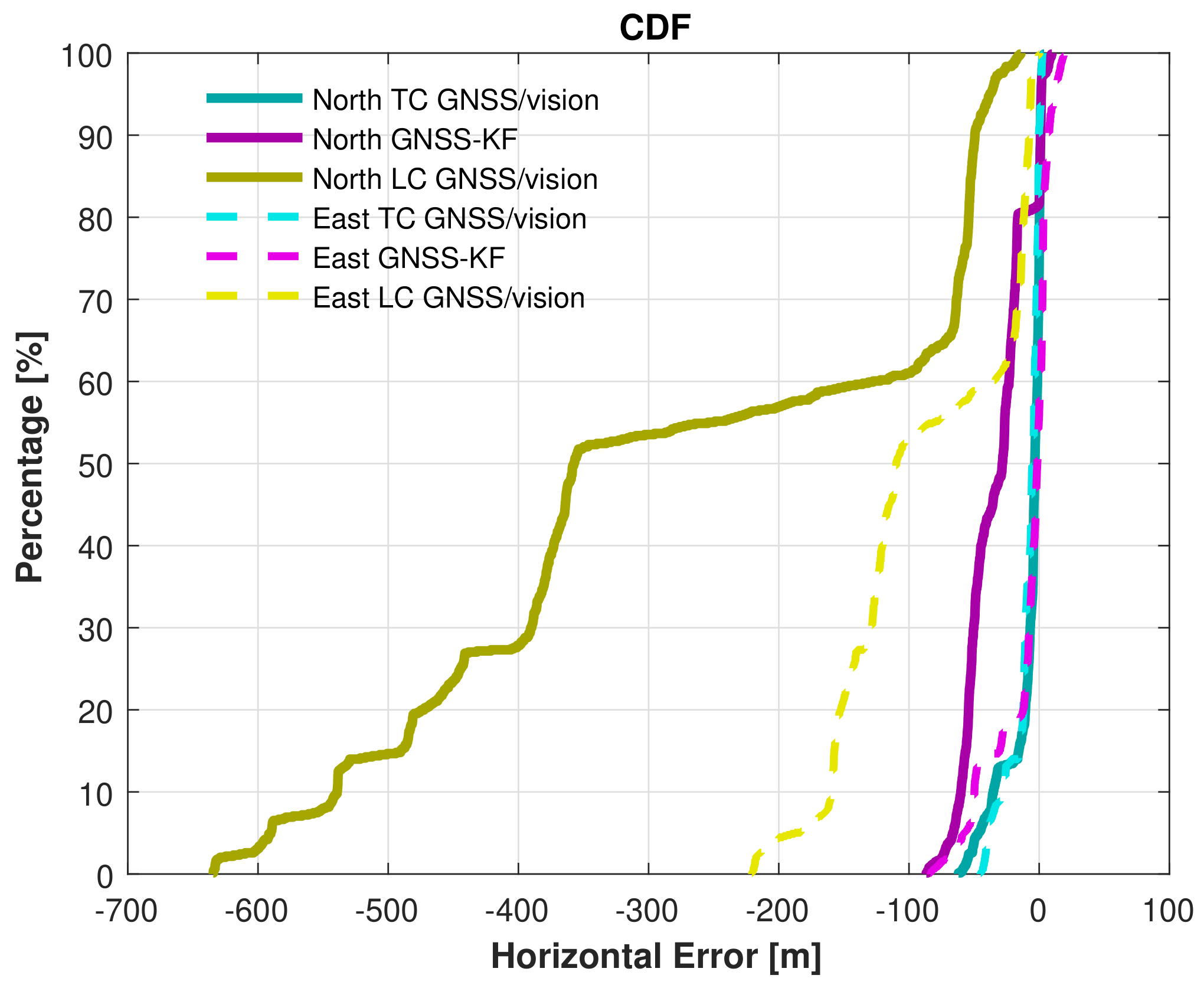
, we can observe that the proposed method does not drift too much while the GNSS-KF provides poor solutions. From Figure 18, it is seen that the solution obtained from the LC GNSS/vision outputs larger error compared to the two other approaches. In Zone  (Figure 16), after NLOS satellites exclusion, there are constantly less than four satellites (Figure 16). As a result, GNSS-aiding is not available, and the obtained navigation solution is poor. The Cumulative Distribution Functions (CDF) of the horizontal errors are provided in Figure 19.
(Figure 16), after NLOS satellites exclusion, there are constantly less than four satellites (Figure 16). As a result, GNSS-aiding is not available, and the obtained navigation solution is poor. The Cumulative Distribution Functions (CDF) of the horizontal errors are provided in Figure 19. depicts a straight moving zone where both TC GNSS/vision and GNSS-KF provide a poor position estimation. This case, although not alarming for the proposed method, requires further investigation. The two reasons mentioned previously that cause poor integrated solutions occur at this location. Due to a traffic jam, the vehicle stopped under a bridge where LOS satellites were not observed, and the visual odometry was very poor, caused by the fact that very few feature points were detected (the very dark captured images are shown in Figure 20b).
depicts a straight moving zone where both TC GNSS/vision and GNSS-KF provide a poor position estimation. This case, although not alarming for the proposed method, requires further investigation. The two reasons mentioned previously that cause poor integrated solutions occur at this location. Due to a traffic jam, the vehicle stopped under a bridge where LOS satellites were not observed, and the visual odometry was very poor, caused by the fact that very few feature points were detected (the very dark captured images are shown in Figure 20b).7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| 3DBM | 3D Building Mode |
| 6-DOF | Six Degrees of Freedom |
| ASF | Alternate Sequential Filter |
| CDF | Cumulative Distribution Function |
| DGPS | Differential Global Positioning System |
| ECEF | Earth-Centred, Earth-Fixed |
| EKF | Extended Kalman Filter |
| FOV | Field of View |
| GNSS | Global Navigation Satellite Systems |
| GPS | Global Positioning System |
| GRD | Geodesic Reconstruction by Dilatation |
| IMU | Inertial Measurement Unit |
| KF | Kalman Filter |
| LOS | Line Of Sight |
| MMPL | Multiple Model Particle Filter |
| NLOS | Non-Line of Sight |
| PnP | Perspective-n-Point |
| PR | Pseudorange |
| RGB | Red, Green, Blue (colour space) |
| SLAM | Simultaneous Localization and Mapping |
| SVD | Singular Value Decomposition |
| UAV | Unmanned Aerial Vehicle |
| UWB | Ultra-Wideband |
| V2I | Vehicle to Infrastructure |
| VO | Visual Odometry |
References
- Petovello, M. Real-Time Integration of a Tactical-Grade IMU and GPS for High-Accuracy Positioning and Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2003. [Google Scholar]
- Won, D.H.; Lee, E.; Heo, M.; Sung, S.; Lee, J.; Lee, Y.J. GNSS integration with vision-based navigation for low GNSS visibility conditions. GPS Solut. 2014, 18, 177–187. [Google Scholar] [CrossRef]
- Ben Afia, A.; Escher, A.C.; Macabiau, C. A Low-cost GNSS/IMU/Visual monoSLAM/WSS Integration Based on Federated Kalman Filtering for Navigation in Urban Environments. In ION GNSS+ 2015, Proceedings of the 28th International Technical Meeting of The Satellite Division of the Institute of Navigation, Tampa, FL, USA, 14–18 September 2015; ION, Institute of Navigation: Tampa, FL, USA, 2015; pp. 618–628. [Google Scholar]
- Gao, Y.; Liu, S.; Atia, M.M.; Noureldin, A. INS/GPS/LiDAR Integrated Navigation System for Urban and Indoor Environments Using Hybrid Scan Matching Algorithm. Sensors 2015, 15, 23286–23302. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.B.; Bazin, J.C.; Lee, H.K.; Choi, K.H.; Park, S.Y. Ground vehicle navigation in harsh urban conditions by integrating inertial navigation system, global positioning system, odometer and vision data. IET Radar Sonar Navig. 2011, 5, 814–823. [Google Scholar] [CrossRef]
- Levinson, J.; Thrun, S. Robust vehicle localization in urban environments using probabilistic maps. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4372–4378. [Google Scholar] [CrossRef]
- Braasch, M.S. Multipath Effects. In Global Positioning System: Theory and Applications; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1996; Volume I, pp. 547–568. [Google Scholar]
- Brown, A.; Gerein, N. Test Results from a Digital P(Y) Code Beamsteering Receiver for Multipath Minimization. In Proceedings of the ION 57th Annual Meeting, Albuquerque, NM, USA, 11–13 June 2001; pp. 872–878. [Google Scholar]
- Keshvadi, M.H.; Broumandan, A. Analysis of GNSS Beamforming and Angle of Arrival estimation in Multipath Environments. In Proceedings of the 2011 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 24–26 January 2011; pp. 427–435. [Google Scholar]
- Groves, P.D. Principles of GNSS, inertial, and multisensor integrated navigation systems, 2nd edition [Book review]. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 26–27. [Google Scholar] [CrossRef]
- Groves, P.D.; Jiang, Z. Height Aiding, C/N0 Weighting and Consistency Checking for GNSS NLOS and Multipath Mitigation in Urban Areas. J. Navig. 2013, 66, 653–669. [Google Scholar] [CrossRef]
- Attia, D.; Meurie, C.; Ruichek, Y.; Marais, J. Counting of Satellite with Direct GNSS Signals using Fisheye camera: A Comparison of Clustering Algorithms. In Proceedings of the ITSC 2011, Washington, DC, USA, 5–7 October 2011. [Google Scholar] [CrossRef]
- Suzuki, T.; Kubo, N. N-LOS GNSS Signal Detection Using Fish-Eye Camera for Vehicle Navigation in Urban Environments. In Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2014), Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- Gakne, P.V.; Petovello, M. Assessing Image Segmentation Algorithms for Sky Identification in GNSS. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Calgary, AB, Canada, 13–16 October 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Obst, M.; Bauer, S.; Wanielik, G. Urban multipath detection and mitigation with dynamic 3D maps for reliable land vehicle localization. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 685–691. [Google Scholar] [CrossRef]
- Peyraud, S.; Bétaille, D.; Renault, S.; Ortiz, M.; Mougel, F.; Meizel, D.; Peyret, F. About Non-Line-Of-Sight Satellite Detection and Exclusion in a 3D Map-Aided Localization Algorithm. Sensors 2013, 13, 829–847. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Petovello, M.G. 3D building model-assisted snapshot positioning algorithm. GPS Solut. 2017, 21, 1923–1935. [Google Scholar] [CrossRef]
- Ulrich, V.; Alois, B.; Herbert, L.; Christian, P.; Bernhard, W. Multi-Base RTK Positioning Using Virtual Reference Stations. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000; pp. 123–131. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Valiente, D.; Gil, A.; Reinoso, S.; Juliá, M.; Holloway, M. Improved Omnidirectional Odometry for a View-Based Mapping Approach. Sensors 2017, 17, 325. [Google Scholar] [CrossRef] [PubMed]
- Valiente, D.; Gil, A.; Payá, L.; Sebastián, J.M.; Reinoso, S. Robust Visual Localization with Dynamic Uncertainty Management in Omnidirectional SLAM. Appl. Sci. 2017, 7, 1294. [Google Scholar] [CrossRef]
- Gakne, P.V.; O’Keefe, K. Skyline-based Positioning in Urban Canyons Using a Narrow FOV Upward-Facing Camera. In Proceedings of the 30th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 2574–2586. [Google Scholar]
- Petovello, M.; He, Z. Skyline positioning in urban areas using a low-cost infrared camera. In Proceedings of the 2016 European Navigation Conference (ENC), Helsinki, Finland, 30 May–2 June 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Alatise, M.B.; Hancke, G.P. Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter. Sensors 2017, 17, 2164. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gao, Y.; Li, Z.; Meng, X.; Hancock, C.M. A Tightly-Coupled GPS/INS/UWB Cooperative Positioning Sensors System Supported by V2I Communication. Sensors 2016, 16, 944. [Google Scholar] [CrossRef] [PubMed]
- Soloviev, A.; Venable, D. Integration of GPS and Vision Measurements for Navigation in GPS Challenged Environments. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 826–833. [Google Scholar] [CrossRef]
- Chu, T.; Guo, N.; Backén, S.; Akos, D. Monocular camera/IMU/GNSS integration for ground vehicle navigation in challenging GNSS environments. Sensors 2012, 12, 3162–3185. [Google Scholar] [CrossRef] [PubMed]
- Vetrella, A.R.; Fasano, G.; Accardo, D.; Moccia, A. Differential GNSS and Vision-Based Tracking to Improve Navigation Performance in Cooperative Multi-UAV Systems. Sensors 2016, 16, 2164. [Google Scholar] [CrossRef] [PubMed]
- Aumayer, B. Ultra-Tightly Coupled Vision/GNSS for Automotive Applications. Ph.D. Thesis, Department of Geomatics Engineering, The University of Calgary, Calgary, AB, Canada, 2016. [Google Scholar]
- Meguro, J.I.; Murata, T.; Takiguchi, J.I.; Amano, Y.; Hashizume, T. GPS Multipath Mitigation for Urban Area Using Omnidirectional Infrared Camera. IEEE Trans. Intell. Transp. Syst. 2009, 10, 22–30. [Google Scholar] [CrossRef]
- Marais, J.; Ambellouis, S.; Flancquart, A.; Lefebvre, S.; Meurie, C.; Ruichek, Y. Accurate Localisation Based on GNSS and Propagation Knowledge for Safe Applications in Guided Transport. Procedia Soc. Behav. Sci. 2012, 48, 796–805. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Fraundorfer, F. Visual Odometry [Tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Deretey, E.; Ahmed, M.T.; Marshall, J.A.; Greenspan, M. Visual indoor positioning with a single camera using PnP. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 834–849. [Google Scholar]
- Engel, J.; Stückler, J.; Cremers, D. Large-scale direct SLAM with stereo cameras. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1935–1942. [Google Scholar] [CrossRef]
- Caruso, D.; Engel, J.; Cremers, D. Large-scale direct SLAM for omnidirectional cameras. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 141–148. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance; Ganga-Jamuna Press: Lincoln, MA, USA, 2011. [Google Scholar]
- Peng, X. Improving High Sensitivity GNSS Receiver Performance in Multipath Environments for Vehicular Applications. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2013. [Google Scholar]
- He, Z.; Petovello, M.; Lachapelle, G. Indoor Doppler error characterization for High Sensitivity GNSS receivers. IEEE Trans. Aerosp. Electron. Syst. 2014, 50. [Google Scholar] [CrossRef]
- Xie, P.; Petovello, M.G. Improved Correlator Peak Selection for GNSS Receivers in Urban Canyons. J. Navig. 2015, 68, 869–886. [Google Scholar] [CrossRef]
- Ren, T.; Petovello, M. Collective bit synchronization for weak GNSS signals using multiple satellites. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 547–555. [Google Scholar] [CrossRef]
- Aumayer, B.M.; Petovello, M.G.; Lachapelle, G. Development of a Tightly Coupled Vision/GNSS System. In Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2014), Tampa, FL, USA, 8–12 September 2014; pp. 2202–2211. [Google Scholar]
- Schreiber, M.; Königshof, H.; Hellmund, A.M.; Stiller, C. Vehicle localization with tightly coupled GNSS and visual odometry. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 858–863. [Google Scholar] [CrossRef]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Bradski, G. The OpenCV Library. Dr. Dobb’s Journal of Software Tools, 1 November 2000. [Google Scholar]
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer Vision with the OpenCV Library; O’Reilly: Cambridge, MA, USA, 2008. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An Efficient Alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision (ICCV’11), Barcelona, Spain, 6–13 November 2011; IEEE Computer Society: Washington, DC, USA, 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Rosten, E.; Drummond, T. Fusing Points and Lines for High Performance Tracking. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 2, pp. 1508–1515. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features. In European Conference on Computer Vision: Part IV; Springer: Berlin/Heidelberg, Germany, 2010; pp. 778–792. [Google Scholar]
- Hamming, R. Error Detecting and Error Correcting Codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Nister, D. An Efficient Solution to the Five-point Relative Pose Problem. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 756–770. [Google Scholar] [CrossRef] [PubMed]
- Hartley, R.I.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; ISBN 0521540518. [Google Scholar]
- Gakne, P.V.; O’Keefe, K. Monocular-based pose estimation using vanishing points for indoor image correction. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Horn, A. Doubly Stochastic Matrices and the Diagonal of a Rotation Matrix. Am. J. Math. 1954, 76, 620–630. [Google Scholar] [CrossRef]
- Ruotsalainen, L. Vision-Aided Pedestrian Navigation for Challenging GNSS Environments, vol. 151. Ph.D. Thesis, Publications of the Finnish Geodetic Institute, Masala, Finland, November 2013. [Google Scholar]
- Meguro, J.; Murata, T.; Takiguchi, J.; Amano, Y.; Hashizume, T. GPS Accuracy Improvement by Satellite Selection using Omnidirectional Infrared Camera. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 Septemebr 2008; pp. 1804–1810. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis: Principles and Applications; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Meyer, F. Levelings, Image Simplification Filters for Segmentation. J. Math. Imaging Vis. 2004, 20, 59–72. [Google Scholar] [CrossRef]
- Datta, B.N. Linear state-space models and solutions of the state equations. In Numerical Methods for Linear Control Systems; Datta, B.N., Ed.; Academic Press: San Diego, CA, USA, 2004; Chapter 5; pp. 107–157. [Google Scholar] [CrossRef]
- Koch, K.R. Parameter Estimation and Hypothesis Testing in Linear Models; Springer Inc.: New York, NY, USA, 1988. [Google Scholar]
- Petovello, M.G.; Zhe, H. Assessment of Skyline Variability for Positioning in Urban Canyons. In Proceedings of the ION 2015 Pacific PNT Meeting, Honolulu, HI, USA, 20–23 April 2015; pp. 1059–1068. [Google Scholar]
- Noureldin, A.; Tashfeen, B.K.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration; Springer: New York, NY, USA, 2013. [Google Scholar]
- Toledo-Moreo, R.; Colodro-Conde, C.; Toledo-Moreo, J. A Multiple-Model Particle Filter Fusion Algorithm for GNSS/DR Slide Error Detection and Compensation. Appl. Sci. 2018, 8, 445. [Google Scholar] [CrossRef]
- Giremus, A.; Tourneret, J.Y.; Calmettes, V. A Particle Filtering Approach for Joint Detection/Estimation of Multipath Effects on GPS Measurements. IEEE Trans. Signal Process. 2007, 55, 1275–1285. [Google Scholar] [CrossRef]
- Gakne, P.V.; O’Keefe, K. Replication Data for: Tightly-Coupled GNSS/Vision using a Sky-pointing Camera for Vehicle Navigation in Urban Area. Scholars Portal Dataverse. 2018. [Google Scholar] [CrossRef]








 ; (d) zoomed challenging Zone
; (d) zoomed challenging Zone  ; (e) zoomed challenging Zone
; (e) zoomed challenging Zone  . TC, Tightly-Coupled; LC, Loosely-Coupled.
. TC, Tightly-Coupled; LC, Loosely-Coupled.
 ; (d) zoomed challenging Zone
; (d) zoomed challenging Zone 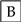 ; (e) zoomed challenging Zone
; (e) zoomed challenging Zone  . TC, Tightly-Coupled; LC, Loosely-Coupled.
. TC, Tightly-Coupled; LC, Loosely-Coupled.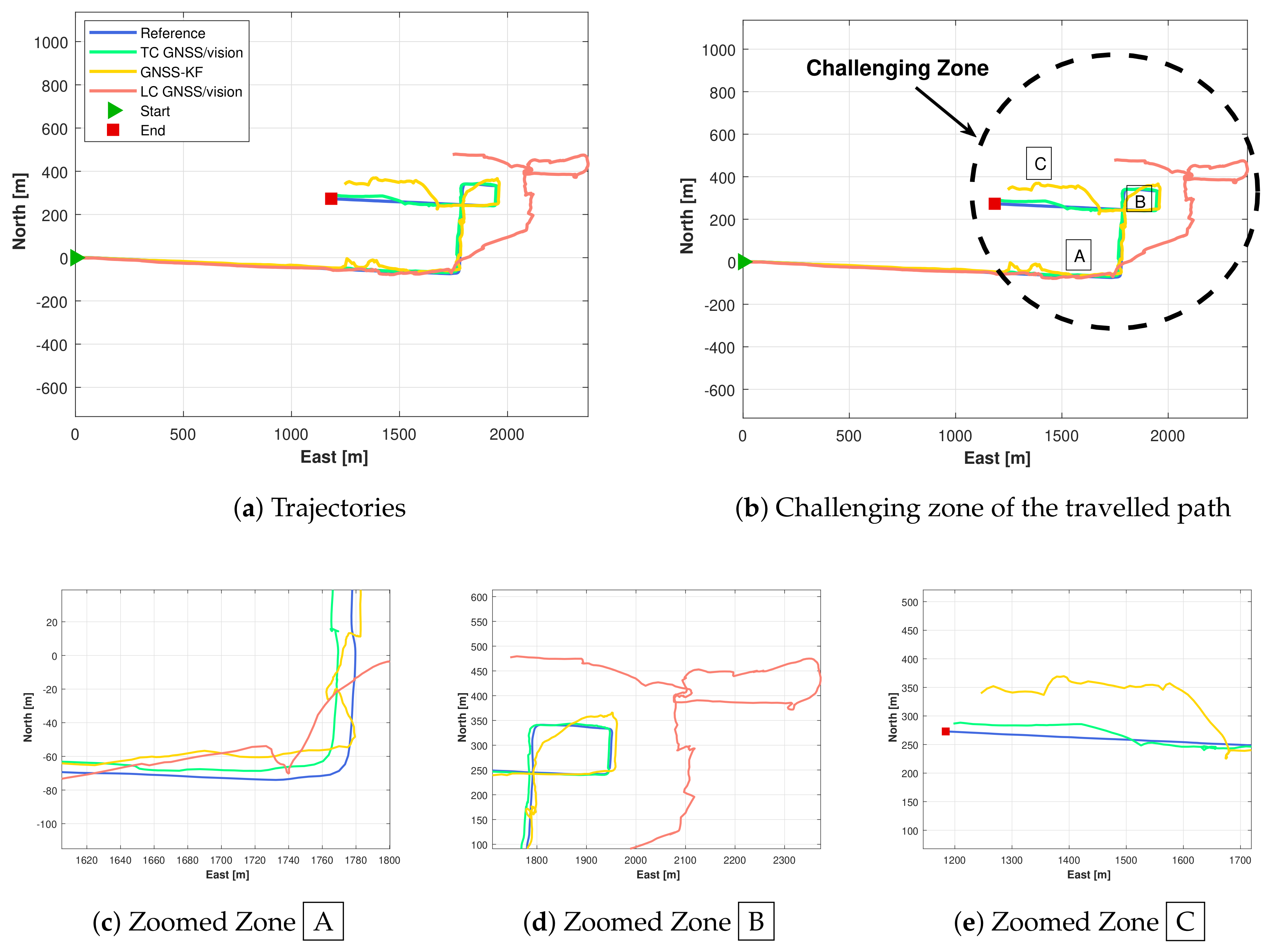

| Reference and GNSS | |
| SPAN-SE | dual-frequency L1/L2 GPS + GLONASS |
| Combination | GPS + GLONASS combined with UIMU-LCI |
| Camera (Lens Specification, Intrinsic Parameters) and Images | |
| Aperture | f/1.2—closed |
| Focal length | mm |
| VFOV (1/3”) | 90% |
| Image resolution | |
| Image frame rate | 10 fps |
| Image centre | (643.5, 363.5) |
| 0 | |
| 0 | |
| Estimator | 2D rms Error (m) | 2D Maximum Error (m) |
|---|---|---|
| GNSS-KF | 39.8 | 113.2 |
| LC GNSS/vision | 56.3 | 402.7 |
| TC GNSS/vision | 14.5 | 61.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gakne, P.V.; O’Keefe, K. Tightly-Coupled GNSS/Vision Using a Sky-Pointing Camera for Vehicle Navigation in Urban Areas. Sensors 2018, 18, 1244. https://doi.org/10.3390/s18041244
Gakne PV, O’Keefe K. Tightly-Coupled GNSS/Vision Using a Sky-Pointing Camera for Vehicle Navigation in Urban Areas. Sensors. 2018; 18(4):1244. https://doi.org/10.3390/s18041244
Chicago/Turabian StyleGakne, Paul Verlaine, and Kyle O’Keefe. 2018. "Tightly-Coupled GNSS/Vision Using a Sky-Pointing Camera for Vehicle Navigation in Urban Areas" Sensors 18, no. 4: 1244. https://doi.org/10.3390/s18041244
APA StyleGakne, P. V., & O’Keefe, K. (2018). Tightly-Coupled GNSS/Vision Using a Sky-Pointing Camera for Vehicle Navigation in Urban Areas. Sensors, 18(4), 1244. https://doi.org/10.3390/s18041244





