DCT-Based Preprocessing Approach for ICA in Hyperspectral Data Analysis
Abstract
1. Introduction
2. ICA
3. DCT
4. The Proposed Preprocessing Procedure Description
5. Data and Evaluation Process
5.1. Data
5.1.1. The Indian Pines Dataset
5.1.2. The Kennedy Space Center (KSC) Dataset
5.2. Evaluation Process
6. Results and Discussion
6.1. Intrinsic Dimension Criterion
6.2. ClassificationofIndian Pines and Kennedy Space Centerdatasets
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Feng, F.; Li, W.; Du, Q.; Zhang, B. Dimensionality reduction of hyperspectral image with graph-based discriminant analysis considering spectral similarity. Remote Sens. 2017, 9, 323. [Google Scholar] [CrossRef]
- Hughes, G.F. On the Mean Accuracy of Statistical Pattern Recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Pan, L.; Li, H.-C.; Deng, Y.-J.; Zhang, F.; Chen, X.-D.; Du, Q. Hyperspectral dimensionality reduction by tensor sparse and low-rank graph-based discriminant analysis. Remote Sens. 2017, 9, 452. [Google Scholar] [CrossRef]
- Li, J.; Marpu, P.R.; Antonio, P.; Bioucas-Dias, J.M.; Benediktsson, J.A. Generalized Composite Kernel Framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 32, 29–43. [Google Scholar] [CrossRef]
- Du, Q.; Yang, H. Similarity-based unsupervised band selection for hyperspectral image analysis. IEEE Geosci. Remote Sens. Lett. 2008, 5, 564–568. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, B.; Jia, X.; Liao, W.; Zhang, B. Optimized kernel minimum noise fraction transformation for hyperspectral image classification. Remote Sens. 2017, 9, 548. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; Haykin, S., Ed.; John Wiley: Hoboken, NJ, USA, 2001; ISBN 9780471405405. [Google Scholar]
- Villa, A.; Chanussot, J.; Jutten, C.; Benediktsson, J.; Moussaoui, S. On the Use of ICA for Hyperspectral Image Analysis. Int. Geosci. Remote Sens. Symp. 2009, 4, 97–100. [Google Scholar]
- Wang, J.; Chang, C.I. Independent component analysis-based dimensionality reduction with applications in hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1586–1600. [Google Scholar] [CrossRef]
- Du, Q.; Kopriva, I.; Szu, H. Independent-component analysis for hyperspectral remote sensing imagery classification. Opt. Eng. 2006, 45, 17008. [Google Scholar]
- Wang, J.; Wu, Z.; Jeon, G.; Jeong, J. An efficient spatial deblocking of images with DCT compression. Digit. Signal Process. A Rev. J. 2015, 42, 80–88. [Google Scholar] [CrossRef]
- Oktem, R.; Ponomarenko, N.N. Image filtering based on discrete cosine transform. Telecommun. Radio Eng. 2007, 66, 1685–1701. [Google Scholar]
- Gao, L.R.; Zhang, B.; Zhang, X.; Zhang, W.J.; Tong, Q.X. A New Operational Method for Estimating Noise in Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 83–87. [Google Scholar] [CrossRef]
- Martin-Herrero, J. A New Operational Method for Estimating Noise in Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 705–709. [Google Scholar] [CrossRef]
- Chen, G.; Qian, S.-E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2011, 49, 973–980. [Google Scholar] [CrossRef]
- Karray, E.; Loghmari, M.A.; Naceur, M.S. Second-Order Separation by Frequency-Decomposition of Hyperspectral Data. Am. J. Signal Process. 2012, 2, 122–133. [Google Scholar] [CrossRef][Green Version]
- Jing, L.; Yi, L. Hyperspectral remote sensing images terrain classification in DCT SRDA subspace. J. China Univ. Posts Telecommun. 2015, 22, 65–71. [Google Scholar] [CrossRef]
- Fakiris, E.; Papatheodorou, G.; Geraga, M.; Ferentinos, G. An automatic target detection algorithm for swath sonar backscatter imagery, using image texture and independent component analysis. Remote Sens. 2016, 8, 373. [Google Scholar] [CrossRef]
- Tu, T. Unsupervised signature extraction and separation in hyperspectral images: a noise-adjusted fast independent component analysis approach. Opt. Eng. 2000, 39, 897–906. [Google Scholar] [CrossRef]
- Chang, C.-I. I.; Chiang, S.-S. S.; Smith, J.A.; Ginsberg, I.W. Linear spectral random mixture analysis for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 375–392. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, C.H. New independent component analysis method using higher order statistics with application to remote sensing images. Opt. Eng. 2002, 41, 12–41. [Google Scholar] [CrossRef]
- Yusuf, B.L.; He, Y. Application of hyperspectral imaging sensor to differentiate between the moisture and reflectance of healthy and infected tobacco leaves. African J. Agric. Res. 2011, 6, 6267–6280. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 1991; ISBN 0-471-06259-6. [Google Scholar]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Pearson: Hoboken, NJ, USA, 2009; ISBN 978-0-13-147139-9. [Google Scholar]
- Amari, S.; Cichocki, A.; Yang, H.H. A new learning algorithm for blind signal separation. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1996; pp. 757–763. [Google Scholar]
- Bell, A.J.; Sejnowski, T.J. A non-linear information maximisation algorithm that performs blind separation. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1995; pp. 467–474. [Google Scholar]
- Cardoso, J.-F. Infomax and maximum likelihood for blind source separation. IEEE Signal Process. Lett. 1997, 4, 112–114. [Google Scholar] [CrossRef]
- Pham, D.; Garrat, P.; Jutten, C. Separation of a mixture of independent sources through a maximum likelihood approach. In Proceedings of the EUSIPCO-92, VI European Signal Processing Conference, Brussels, Belgium, 24–27 August 1992; pp. 771–774. [Google Scholar]
- Langlois, D.; Chartier, S.; Gosselin, D. An introduction to independent component analysis: InfoMax and FastICA algorithms. Tutor. Quant. Methods Psychol. 2010, 6, 31–38. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. One-unit learning rules for independent component analysis. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 480–486. [Google Scholar]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [PubMed]
- Saalbach, A.; Lange, O.; Nattkemper, T.; Meyer-Baese, A. On the application of (topographic) independent and tree-dependent component analysis for the examination of DCE-MRI data. Biomed. Signal Process. Control 2009, 4, 247–253. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Du, W.; Ma, S.; Fu, G.S.; Calhoun, V.D.; Adali, T. A novel approach for assessing reliability of ICA for FMRI analysis. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 2084–2088. [Google Scholar]
- International Organization for Standardization. ISO/IEC JTC1 CD 11172, Coding of Moving Pictures and Associated Audio for Digital Storage Media up to 1.5 Mbits/s; ISO: Geneva, Switzerland, 1992. [Google Scholar]
- Ahmed, N.; Natarajan, T.; Rao, K.R. Discrete Cosine Transform. Comput. IEEE Trans. 1974, C-23, 90–93. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M.P. Estimation of signal subspace on hyperspectral data. Proc. SPIE 2005, 5982, 59820L. [Google Scholar]
- Ghamary Asl, M.; Mojaradi, B. Virtual dimensionality estimation in hyperspectral imagery based on unsupervised feature selection. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-7, 17–23. [Google Scholar] [CrossRef]
- Story, M.; Congalton, R.G. Accuracy assessment: a user’s perspective. Photogramm. Eng. Remote Sens. 1986, 52, 397–399. [Google Scholar] [CrossRef]
- Li, J.; Xi, B.; Li, Y.; Du, Q.; Wang, K. Hyperspectral Classification Based on Texture Feature Enhancement and Deep Belief Networks. Remote Sens. 2018, 10, 396. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Du, Q. Diverse Region-Based CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Tramel, E.W.; Prasad, S.; Fowler, J.E. Nearest regularized subspace for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 477–489. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
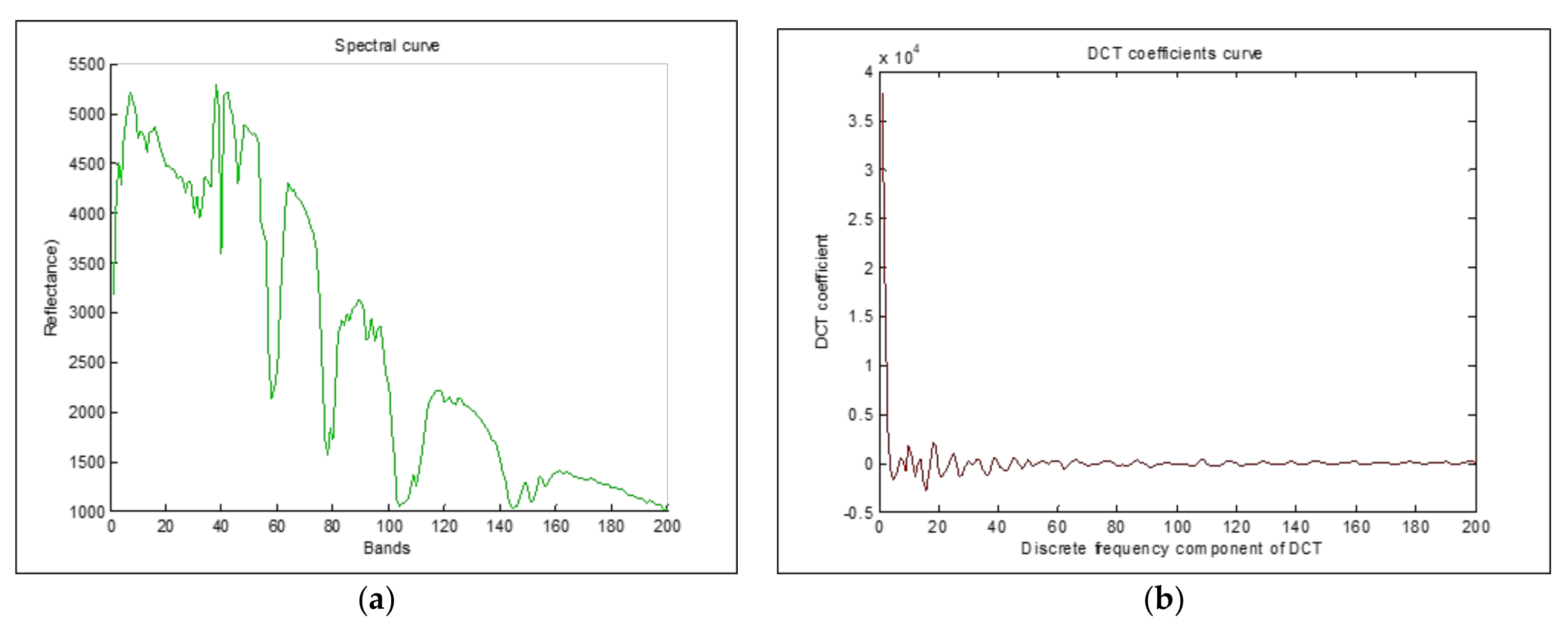


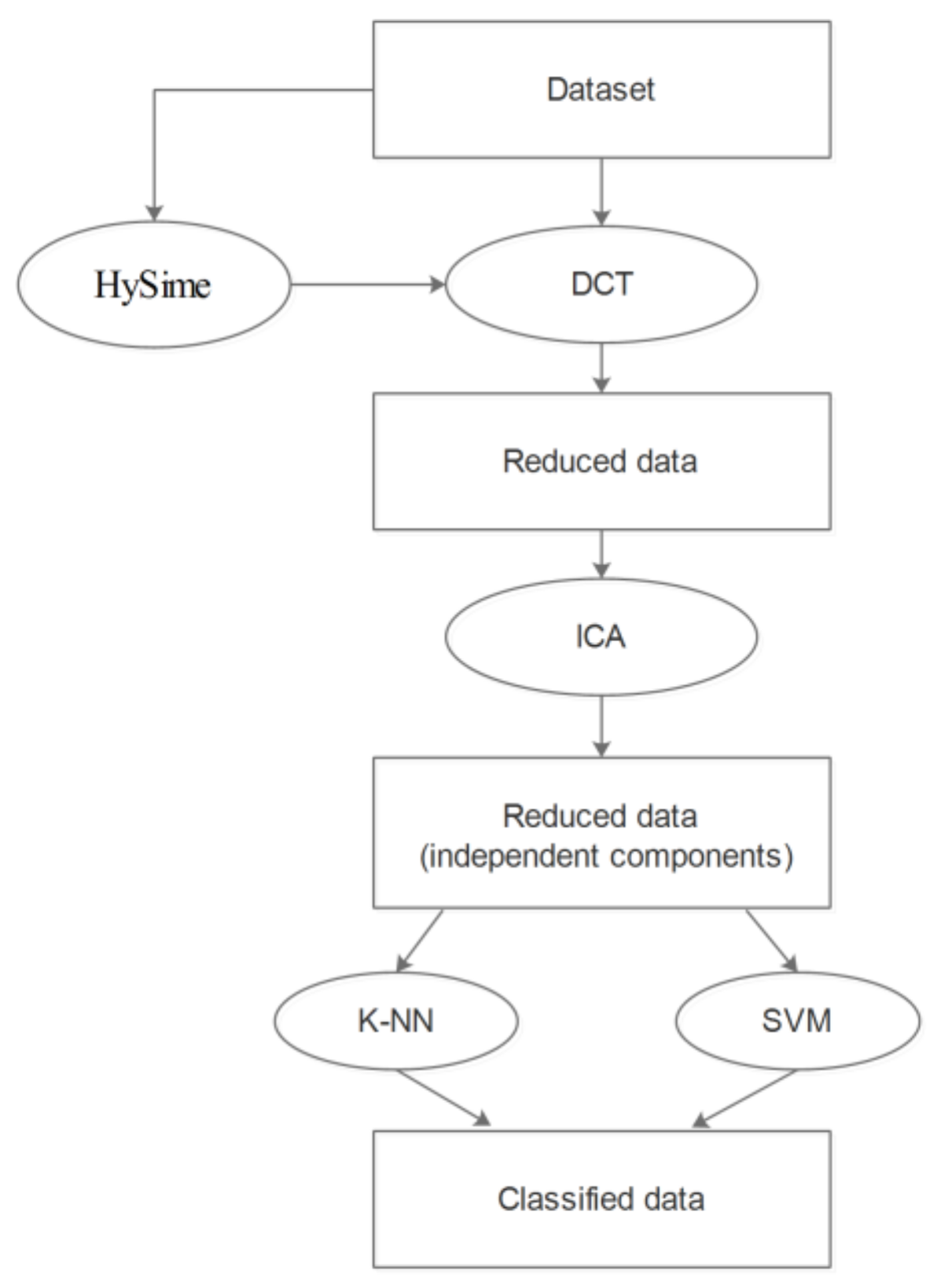
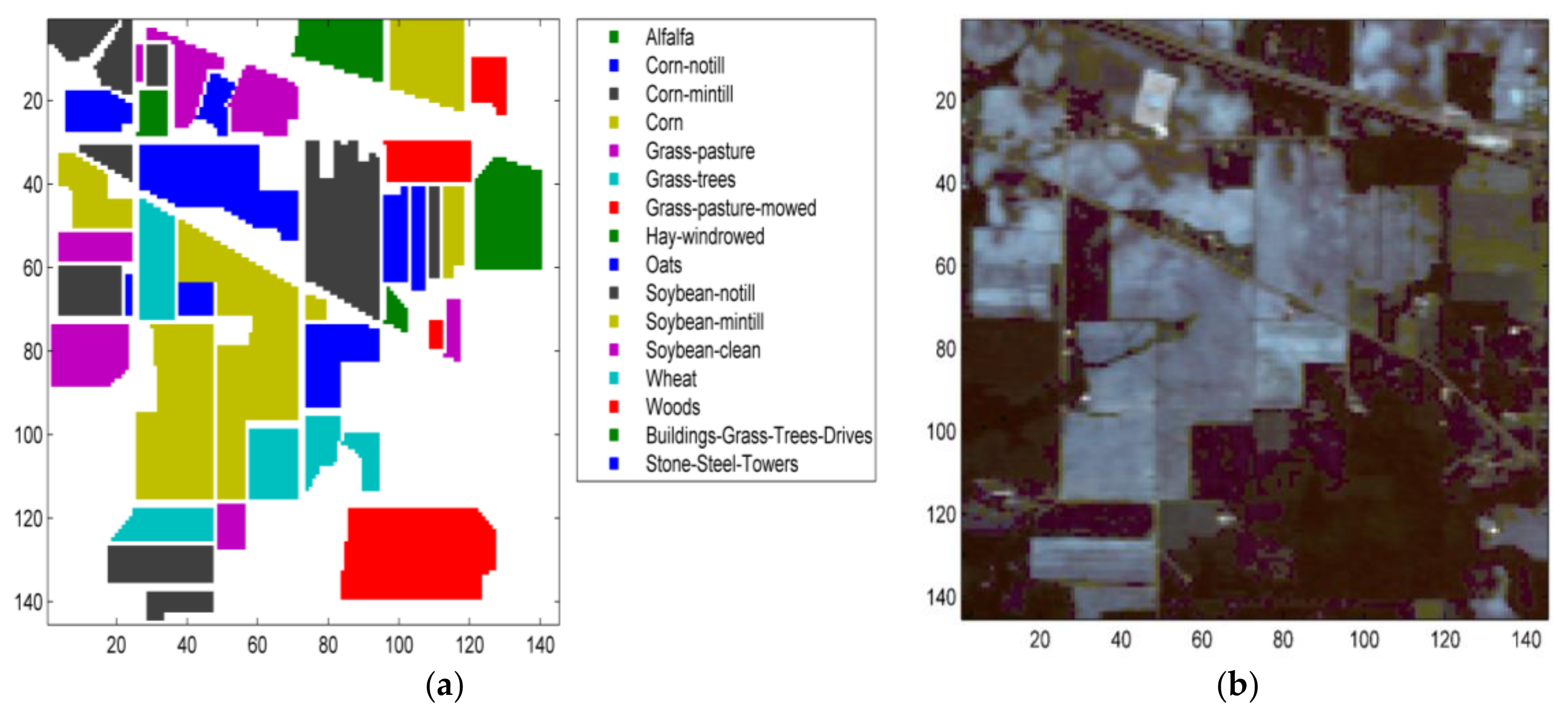
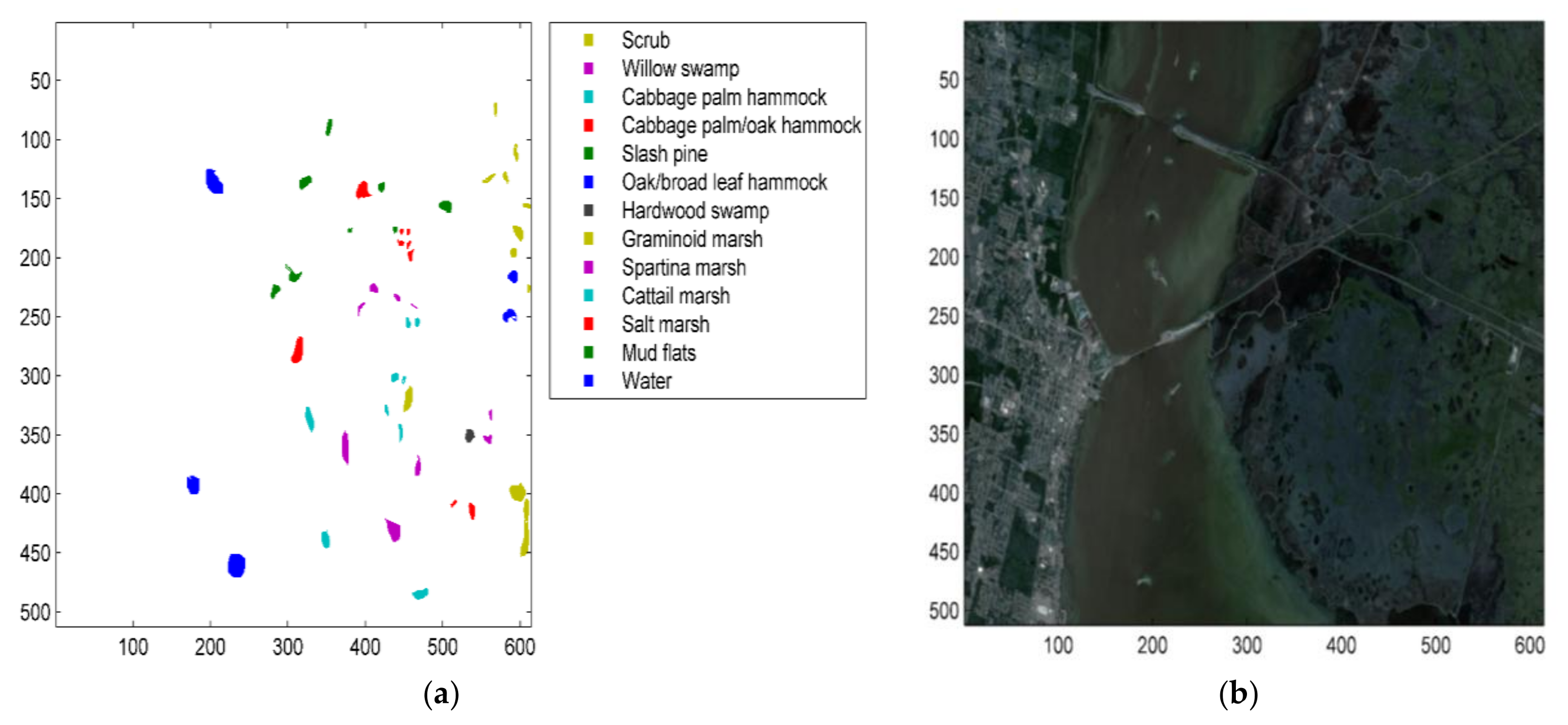


| Class | Type | Samples | Training | Testing |
|---|---|---|---|---|
| 1 | Alfalfa | 46 | 36 | 10 |
| 2 | Corn-notill | 1428 | 1142 | 286 |
| 3 | Corn-mintill | 830 | 664 | 166 |
| 4 | Corn | 237 | 189 | 48 |
| 5 | Grass-pasture | 483 | 386 | 97 |
| 6 | Grass-trees | 730 | 584 | 146 |
| 7 | Grass-pasture-mowed | 28 | 22 | 6 |
| 8 | Hay-windrowed | 478 | 382 | 96 |
| 9 | Oats | 20 | 16 | 4 |
| 10 | Soybean-notill | 972 | 777 | 195 |
| 11 | Soybean-mintill | 2455 | 1964 | 491 |
| 12 | Soybean-clean | 593 | 474 | 119 |
| 13 | Wheat | 205 | 164 | 41 |
| 14 | Woods | 1265 | 1012 | 253 |
| 15 | Buildings-Grass-Trees-Drives | 386 | 308 | 78 |
| 16 | Stone-Steel-Towers | 93 | 74 | 19 |
| Class | Type | Samples | Training | Testing |
|---|---|---|---|---|
| 1 | Scrub | 875 | 700 | 175 |
| 2 | Willow swamp | 279 | 223 | 56 |
| 3 | Cabbage palm hammock | 294 | 235 | 59 |
| 4 | Cabbage palm/oak hammock | 290 | 232 | 58 |
| 5 | Slash pine | 185 | 148 | 37 |
| 6 | Oak/broad leaf hammock | 263 | 210 | 53 |
| 7 | Hardwood swamp | 121 | 96 | 25 |
| 8 | Graminoid marsh | 496 | 396 | 100 |
| 9 | Spartina marsh | 598 | 478 | 120 |
| 10 | Cattail marsh | 465 | 372 | 93 |
| 11 | Salt marsh | 482 | 385 | 97 |
| 12 | Mud flats | 578 | 462 | 116 |
| 13 | Water | 1066 | 852 | 214 |
| Criterion | Indian Pines | KSC |
|---|---|---|
| Hysime | 18 | 32 |
| Classes | K-NN | SVM | ||||
|---|---|---|---|---|---|---|
| ICA | DCT-ICA | PCA-ICA | ICA | DCT-ICA | PCA-ICA | |
| 1 | 58.89 | 78.44 | 76.00 | 80.22 | 86.67 | 72.00 |
| 2 | 66.45 | 74.93 | 69.54 | 61.84 | 82.71 | 61.63 |
| 3 | 47.35 | 65.18 | 63.01 | 25.18 | 64.46 | 44.58 |
| 4 | 46.84 | 50.59 | 50.25 | 42.65 | 78.42 | 52.33 |
| 5 | 88.20 | 94.20 | 90.46 | 91.09 | 93.17 | 93.37 |
| 6 | 96.99 | 97.81 | 97.40 | 94.79 | 96.03 | 96.30 |
| 7 | 76.00 | 83.33 | 82.67 | 69.33 | 92.67 | 82.67 |
| 8 | 98.53 | 98.95 | 98.13 | 98.11 | 99.58 | 97.48 |
| 9 | 35.00 | 60.00 | 35.00 | 25.00 | 90.00 | 65.00 |
| 10 | 69.13 | 80.45 | 76.54 | 30.66 | 69.55 | 53.60 |
| 11 | 73.32 | 81.47 | 77.52 | 75.40 | 75.15 | 74.01 |
| 12 | 39.12 | 59.86 | 50.77 | 9.27 | 72.35 | 26.63 |
| 13 | 93.66 | 99.02 | 95.61 | 95.12 | 96.59 | 93.66 |
| 14 | 93.60 | 94.86 | 93.91 | 96.28 | 96.52 | 95.81 |
| 15 | 43.52 | 49.21 | 44.32 | 54.16 | 66.54 | 54.66 |
| 16 | 92.40 | 94.56 | 93.39 | 94.56 | 97.84 | 95.67 |
| Kappa (%) | 68.74 | 77.86% | 73.90 | 60.50 | 78.61 | 66.47 |
| OA (%) | 72.66 | 80.61% | 77.15 | 66.06 | 81.28 | 70.87 |
| AA (%) | 69.94 | 78.93% | 74.66 | 65.23 | 84.89 | 72.46 |
| Time (s) | 4.1755 | 0.44037 | 0.77588 | 140.8222 | 93.5459 | 128.1354 |
| Classes | K-NN | SVM | ||||
|---|---|---|---|---|---|---|
| ICA | DCT-ICA | PCA-ICA | ICA | DCT-ICA | PCA-ICA | |
| 1 | 89.23 | 94.22 | 91.59 | 92.12 | 96.58 | 91.59 |
| 2 | 74.49 | 87.24 | 82.30 | 78.62 | 97.53 | 76.99 |
| 3 | 59.75 | 91.00 | 77.35 | 78.88 | 92.16 | 80.46 |
| 4 | 37.32 | 66.26 | 41.35 | 53.15 | 87.72 | 44.39 |
| 5 | 47.90 | 55.34 | 49.20 | 52.18 | 82.61 | 47.23 |
| 6 | 22.26 | 45.45 | 27.93 | 48.93 | 84.27 | 43.59 |
| 7 | 62.86 | 88.57 | 56.19 | 64.76 | 93.33 | 63.81 |
| 8 | 71.00 | 87.00 | 71.25 | 76.81 | 95.37 | 61.46 |
| 9 | 86.15 | 95.00 | 86.92 | 90.19 | 98.85 | 86.54 |
| 10 | 48.74 | 92.81 | 69.04 | 77.74 | 98.52 | 78.96 |
| 11 | 95.23 | 97.38 | 95.46 | 96.18 | 99.52 | 97.85 |
| 12 | 63.63 | 90.05 | 70.20 | 75.77 | 96.81 | 79.72 |
| 13 | 98.92 | 99.35 | 99.35 | 99.57 | 99.89 | 99.68 |
| Kappa (%) | 71.63 | 87.80 | 76.47 | 80.81 | 95.62 | 78.68 |
| OA (%) | 74.61 | 89.06 | 78.93 | 82.77 | 96.07 | 80.86 |
| AA (%) | 65.96 | 83.82 | 70.63 | 75.76 | 94.09 | 73.25 |
| Time (s) | 0.9565 | 0.2033 | 0.4924 | 60.962 | 9.8957 | 53.9262 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boukhechba, K.; Wu, H.; Bazine, R. DCT-Based Preprocessing Approach for ICA in Hyperspectral Data Analysis. Sensors 2018, 18, 1138. https://doi.org/10.3390/s18041138
Boukhechba K, Wu H, Bazine R. DCT-Based Preprocessing Approach for ICA in Hyperspectral Data Analysis. Sensors. 2018; 18(4):1138. https://doi.org/10.3390/s18041138
Chicago/Turabian StyleBoukhechba, Kamel, Huayi Wu, and Razika Bazine. 2018. "DCT-Based Preprocessing Approach for ICA in Hyperspectral Data Analysis" Sensors 18, no. 4: 1138. https://doi.org/10.3390/s18041138
APA StyleBoukhechba, K., Wu, H., & Bazine, R. (2018). DCT-Based Preprocessing Approach for ICA in Hyperspectral Data Analysis. Sensors, 18(4), 1138. https://doi.org/10.3390/s18041138






