Positioning Locality Using Cognitive Directions Based on Indoor Landmark Reference System
Abstract
:1. Introduction
- (1)
- On the basis of the complexity of locality description, we propose that people tend to select near landmarks in ILRS when describing locality with the directions of locality description.
- (2)
- We develop a novel membership function for polygon landmarks to model qualitative distance relations, such as near relations.
- (3)
- We propose the calculation of relative direction for polygon landmarks from the perspectives of algorithm and cognition.
- (4)
- We provide the method of positioning locality based on a joint probability function that consists of qualitative distance and relative direction membership functions. Cognitive experiments are conducted to evaluate the positioning accuracy. Test results demonstrate that a positioning accuracy of 3.55 m can be achieved in a 45 m visual space.
2. Related Work
2.1. Locality Description
2.2. Landmarks
2.3. Spatial Relations: Distance and Direction Relationship
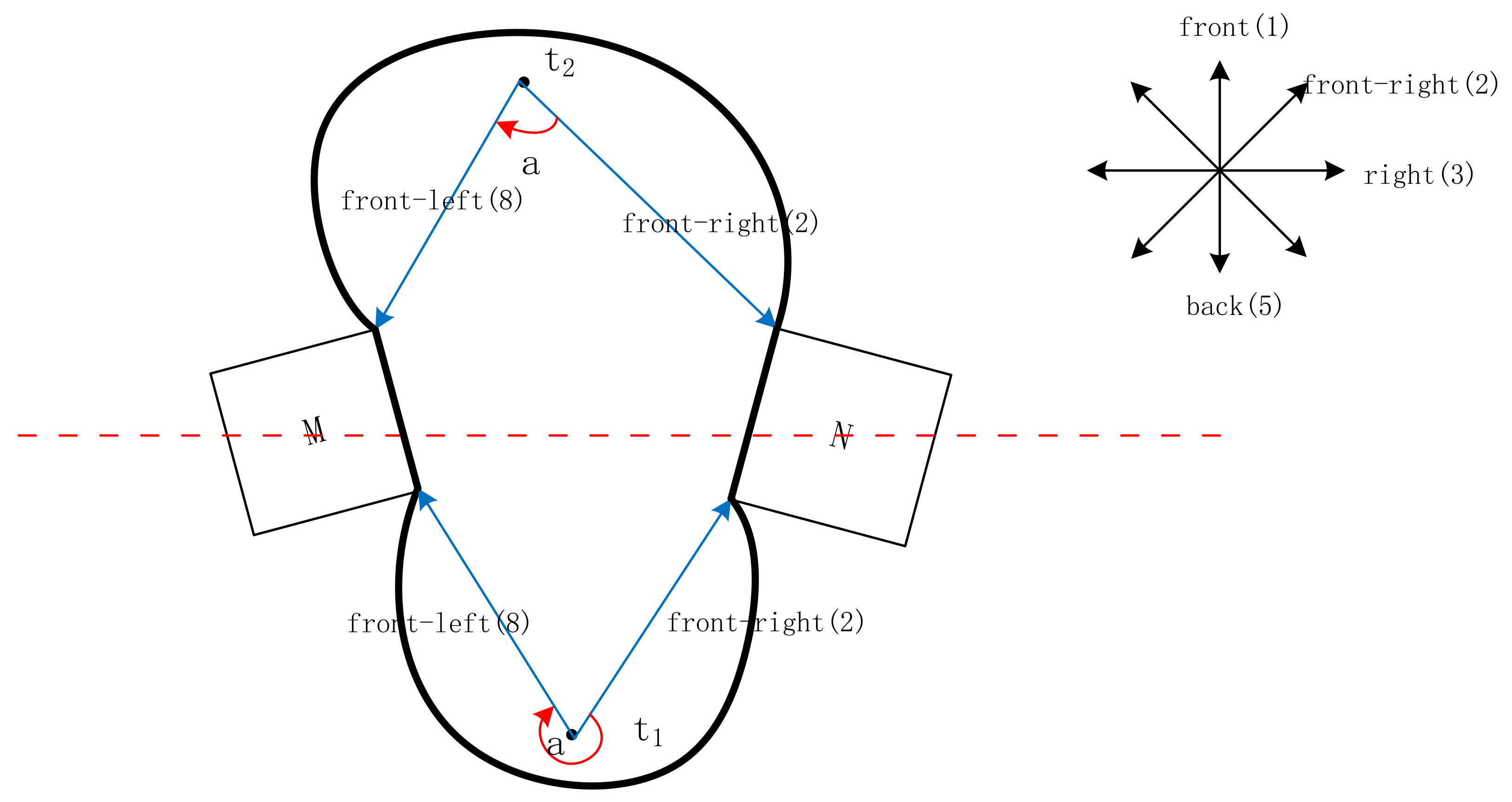
3. Membership Functions Based on Fuzzy Set: Near and Relative Direction
3.1. Membership Function for Near Relation
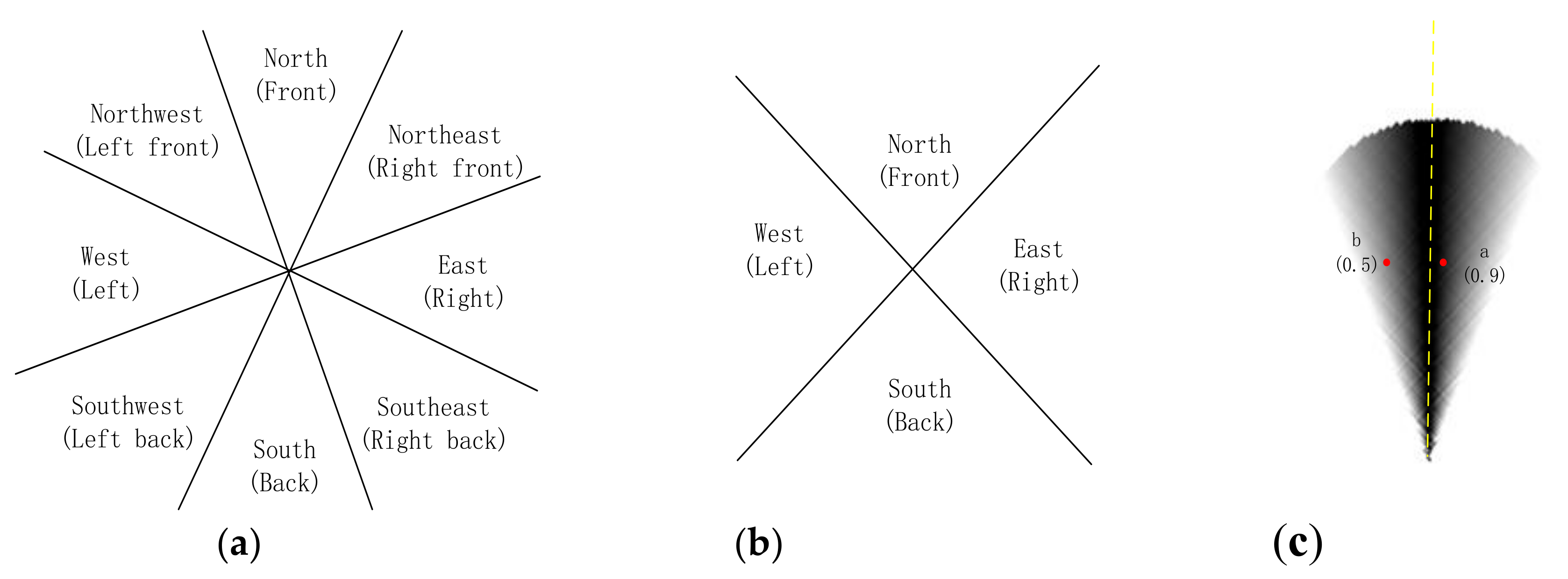
3.2. Relative Direction Membership Function
4. Method
| Algorithm 1: Algorithm for positioning with direction and near relations |
| Obtain the domain where the positioning localities may be located. (Section 4.1) Calculate the probability of relative direction in the domain, i.e., Preldir. (Section 4.2) Calculate the probability of qualitative distance (“near”) in the domain, i.e., Pqdis. (Section 4.3) Calculate the locality using a joint probability function which consist of qualitative distance and relative direction function. (Section 4.3) End for |
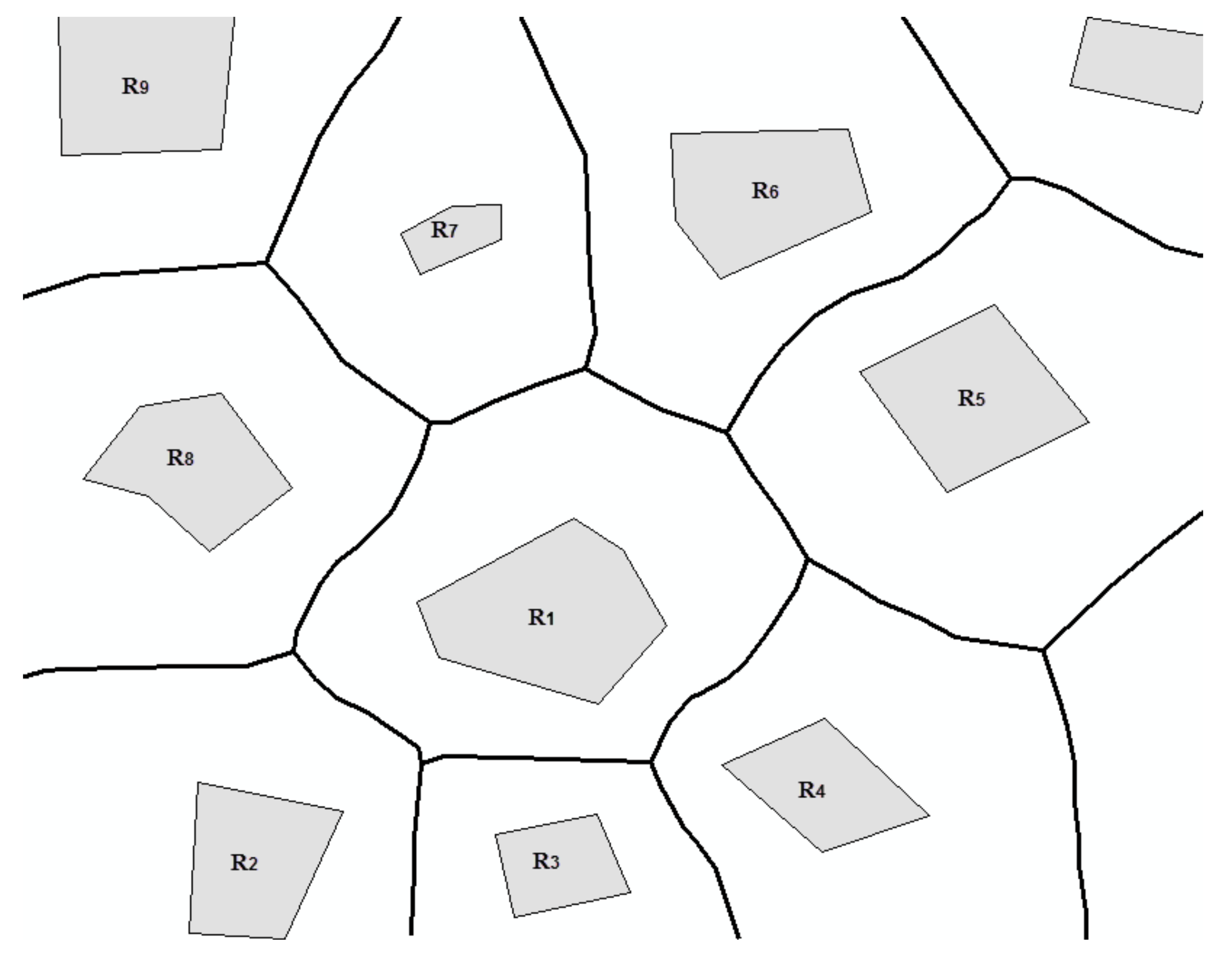
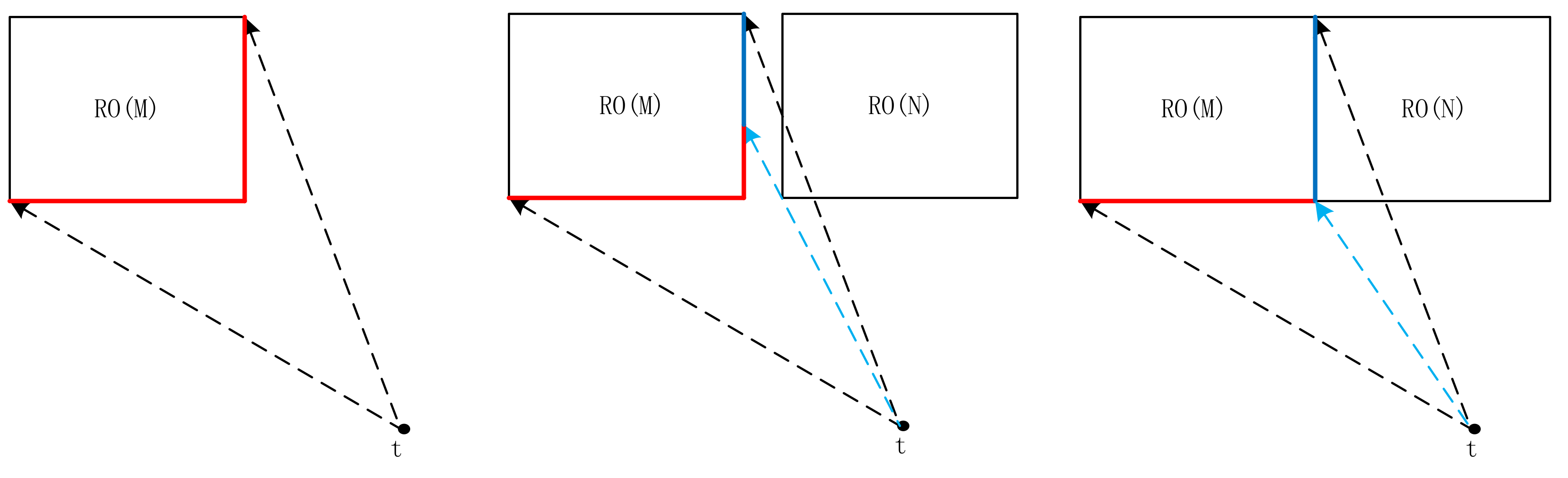
4.1. Domain of Positioning Localities
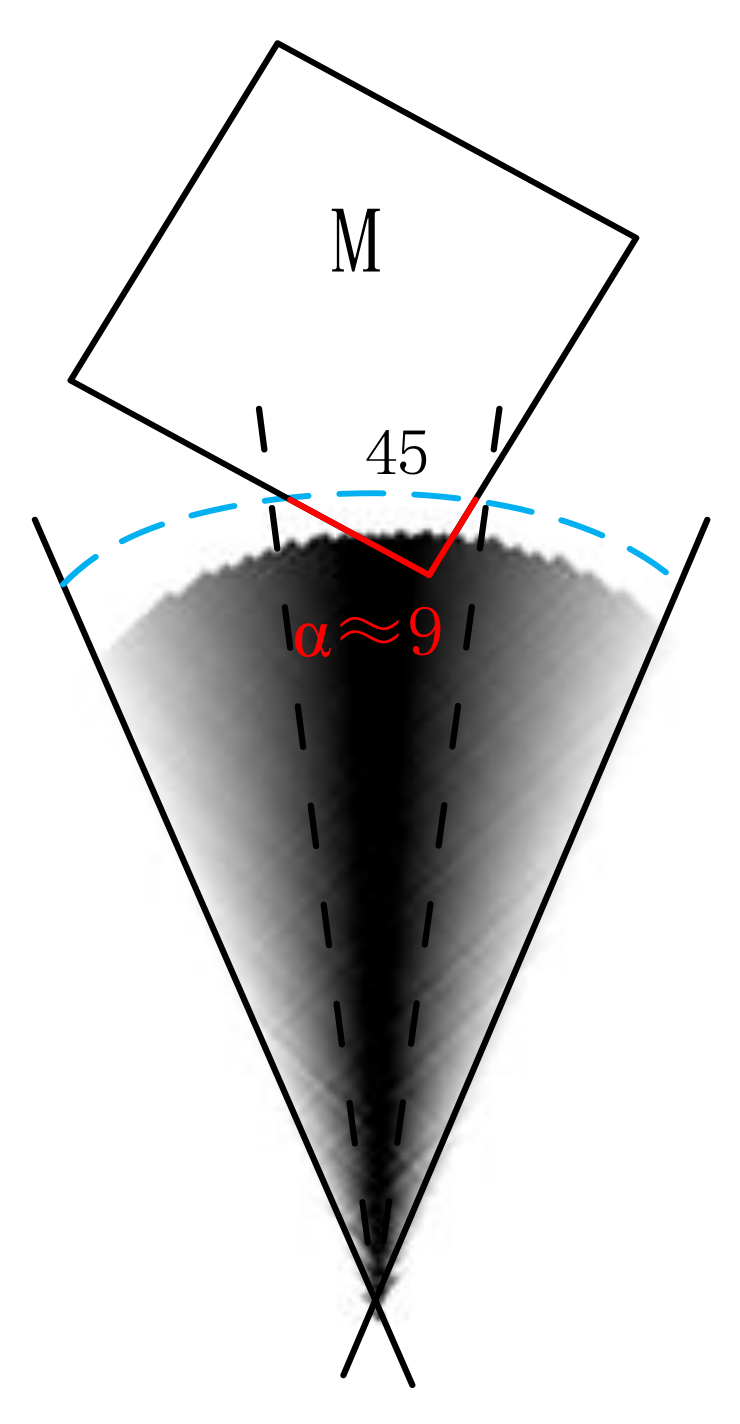
4.2. Probability of Relative Direction in Domain
4.3. Probability of Qualitative Distance in Domain
4.4. Positioning Localities
5. Case Study
6. Discussion
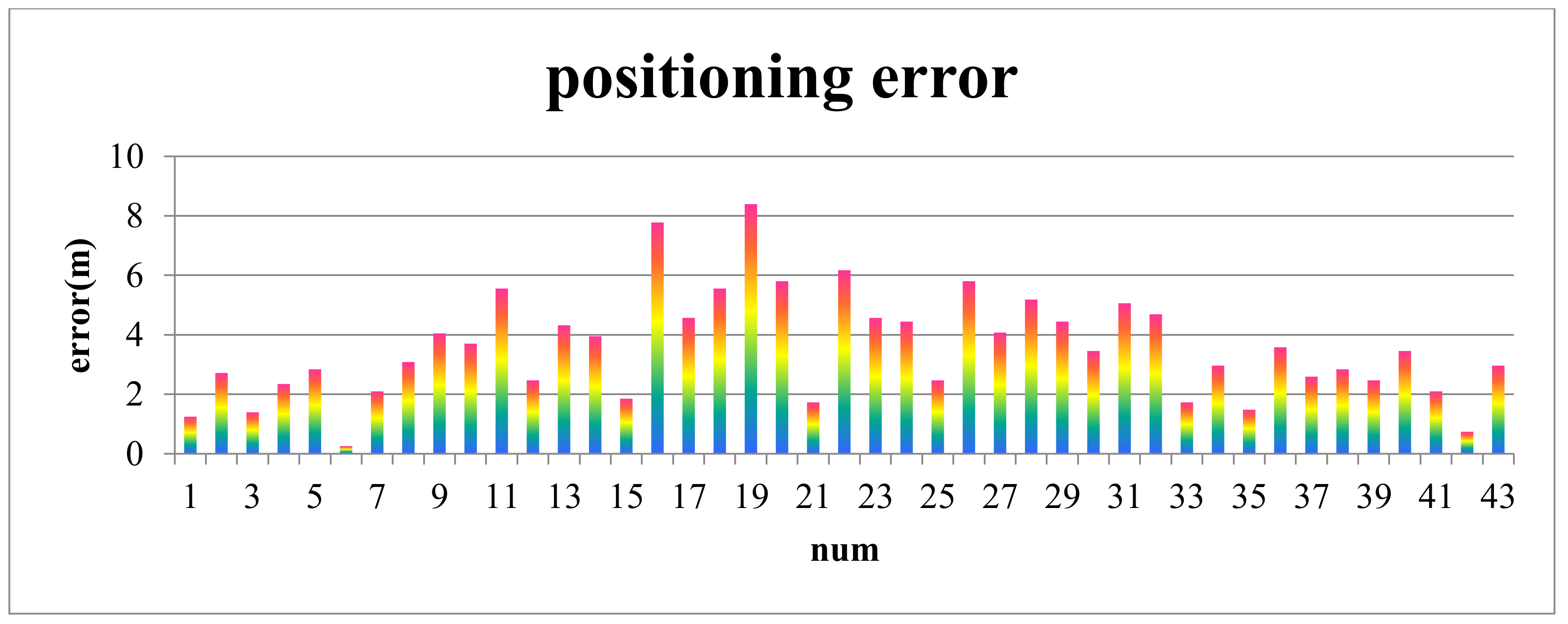
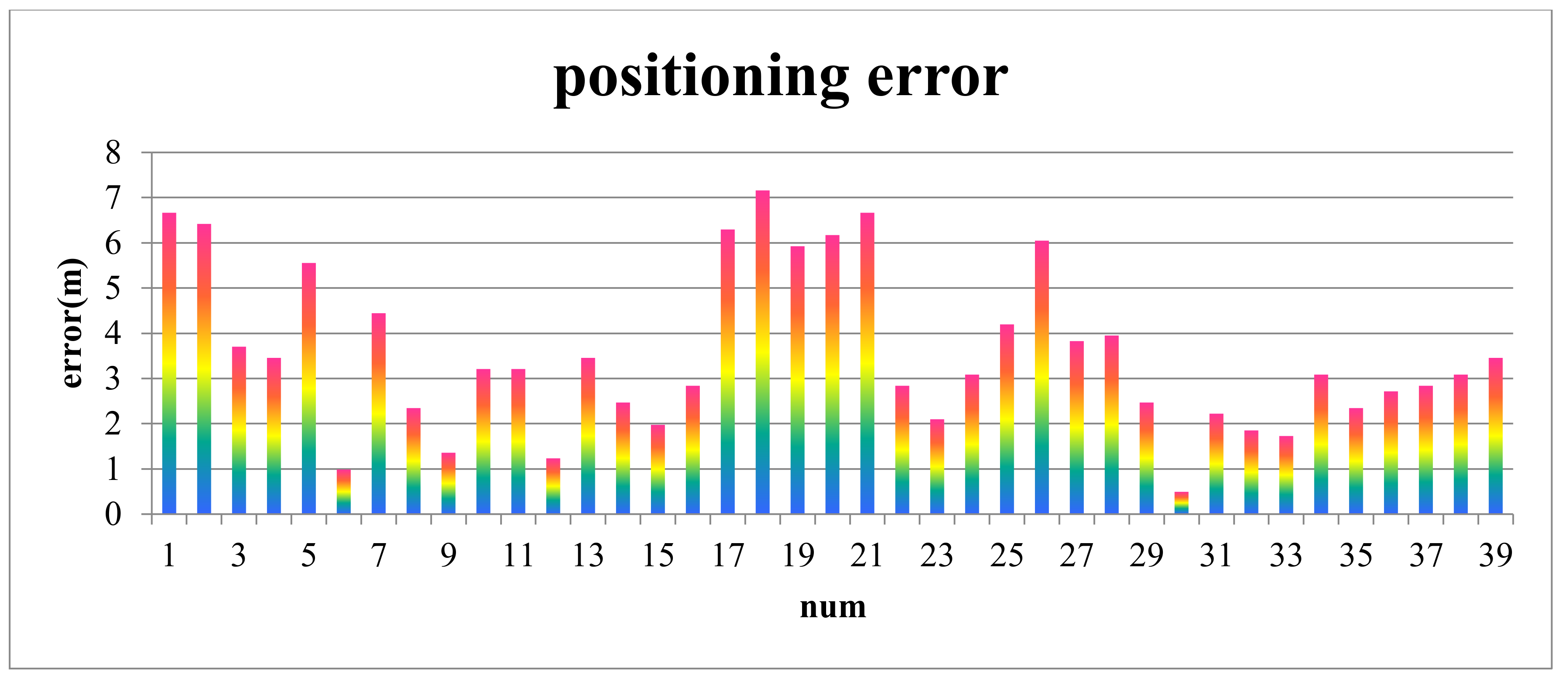
6.1. Positioning Errors
6.2. Analysis of Near Relation
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bentley, R.A.; O’Brien, M.J.; Brock, W.A. Mapping collective behavior in the big-data era. Behav. Brain Sci. 2014, 37, 63–76. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Yao, X. Location-based services and GIS in perspective. Comput. Environ. Urban Syst. 2006, 30, 712–725. [Google Scholar] [CrossRef]
- Nesi, P.; Pantaleo, G.; Tenti, M. Geographical localization of web domains and organization addresses recognition by employing natural language processing, Pattern Matching and clustering. Eng. Appl. Artif. Intell. 2016, 51, 202–211. [Google Scholar] [CrossRef]
- Melo, F.; Martins, B. Automated geocoding of textual documents: A survey of current approaches. Trans. GIS 2017, 21, 3–38. [Google Scholar] [CrossRef]
- Zhang, W.; Gelernter, J. Geocoding location expressions in Twitter messages: A preference learning method. J. Spat. Inf. Sci. 2014, 9, 37–70. [Google Scholar]
- Kim, J.; Vasardani, M.; Winter, S. Similarity matching for integrating spatial information extracted from place descriptions. Int. J. Geogr. Inf. Sci. 2017, 31, 56–80. [Google Scholar] [CrossRef]
- Liu, F.; Vasardani, M.; Baldwin, T. Automatic identification of locative expressions from social media text: A comparative analysis. In Proceedings of the 4th International Workshop on Location and the Web, Shanghai, China, 3–7 November 2014; ACM: New York, NY, USA, 2014; pp. 1–30. [Google Scholar]
- Khan, A.; Vasardani, M.; Winter, S. Extracting spatial information from place descriptions. In Proceedings of the First ACM SIGSPATIAL International Workshop on Computational Models of Place, Orlando, FL, USA, 5-8 November 2013; ACM: New York, NY, USA, 2013; pp. 62–69. [Google Scholar]
- Yao, X.; Thill, J.C. Spatial queries with qualitative locations in spatial information systems. Comput. Environ. Urban Syst. 2006, 30, 485–502. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, Q.H.; Wieczorek, J.; Goodchild, M.F. Positioning localities based on spatial assertions. Int. J. Geogr. Inf. Sci. 2009, 23, 1471–1501. [Google Scholar] [CrossRef]
- Richter, D.; Winter, S.; Richter, K.F.; Stirling, L. Granularity of locations referred to by place descriptions. Comput. Environ. Urban Syst. 2013, 41, 88–99. [Google Scholar] [CrossRef]
- Gong, Y.X.; Li, G.C.; Liu, Y.; Yang, J. Positioning localities from spatial assertions based on Voronoi neighboring. Sci. China Technol. Sci. 2010, 53, 143–149. [Google Scholar] [CrossRef]
- Brennan, J.; Martin, E. Foundations for a formalism of nearness. In Proceedings of the Australian Joint Conference on Artificial Intelligence, Canberra, Australia, 2–6 December 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 71–82. [Google Scholar]
- Gong, Y.; Wu, L.; Lin, Y.; Liu, Y. Probability issues in locality descriptions based on Voronoi neighbor relationship. J. Vis. Lang. Comput. 2012, 23, 213–222. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Keller, J.M.; Ma, Y. Quantitative analysis of properties and spatial relations of fuzzy image regions. IEEE Trans. Fuzzy Syst. 1993, 1, 222–233. [Google Scholar] [CrossRef]
- Bloch, I.; Ralescu, A. Directional relative position between objects in image processing: A comparison between fuzzy approaches. Pattern Recognit. 2003, 36, 1563–1582. [Google Scholar] [CrossRef]
- Richter, D.; Winter, S.; Richter, K.F.; Stirling, L. How people describe their place: Identifying predominant types of place descriptions. In Proceedings of the 1st ACM SIGSPATIAL International Workshop on Crowdsourced and Volunteered Geographic Information, Redondo Beach, CA, USA, 7–9 November 2012; ACM: New York, NY, USA, 2012; pp. 30–37. [Google Scholar]
- Guo, Q.; Liu, Y.; Wieczorek, J. Georeferencing locality descriptions and computing associated uncertainty using a probabilistic approach. Int. J. Geogr. Inf. Sci. 2008, 22, 1067–1090. [Google Scholar] [CrossRef]
- Wieczorek, J.; Guo, Q.; Hijmans, R. The point-radius method for georeferencing locality descriptions and calculating associated uncertainty. Int. J. Geogr. Inf. Sci. 2004, 18, 745–767. [Google Scholar] [CrossRef]
- Zhou, S.; Winter, S.; Vasardani, M.; Shunping, Z. Place descriptions by landmarks. J. Spat. Sci. 2017, 62, 47–67. [Google Scholar] [CrossRef]
- Caduff, D.; Timpf, S. On the assessment of landmark salience for human navigation. Cognit. Proc. 2008, 9, 249–267. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, Y.; Gao, Z.; Lun, W. Landmark-based qualitative reference system. In Proceedings of the International Conference on Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 932–935. [Google Scholar]
- Sorrows, M.; Hirtle, S. The nature of landmarks for real and electronic spaces. In Proceedings of the International Conference on Spatial Information Theory, Stade, Germany, 25–29 August 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 37–50. [Google Scholar]
- Winter, S.; Tomko, M.; Elias, B.; Sester, M. Landmark hierarchies in context. Environ. Plan. B 2008, 35, 381–398. [Google Scholar] [CrossRef]
- Tezuka, T.; Tanaka, K. Landmark extraction: A web mining approach. In Proceedings of the International Conference on Spatial Information Theory, Ellicottville, NY, USA, 14–18 September 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 379–396. [Google Scholar]
- Lyu, H.; Yu, Z.; Meng, L. A Computational Method for Indoor Landmark Extraction. In Progress in Location-Based Services 2014; Springer: Cham, Switzerland, 2015; pp. 45–59. [Google Scholar]
- Haihong, Z.; Ya, W.; Kai, M.; Lin, L.; Guozhong, L.; Yuqi, L. A Quantitative POI Salience Model for Indoor Landmark Extraction. Geomat. Inf. Sci. Wuhan Univ. 2015, 5, 1–7. [Google Scholar]
- Worboys, M.F. Nearness relations in environmental space. Int. J. Geogr. Inf. Sci. 2001, 15, 633–651. [Google Scholar] [CrossRef]
- Yao, X.; Thill, J.C. How Far Is Too Far? A Statistical Approach to Context-contingent Proximity Modeling. Trans. GIS 2005, 9, 157–178. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Jin, X.; Wu, L. On internal cardinal direction relations. In Proceedings of the International Conference on Spatial Information Theory, Ellicottville, NY, USA, 19–23 September 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 283–299. [Google Scholar]
- Bloch, I.; Colliot, O.; Cesar, R.M. On the ternary spatial relation “between”. IEEE Trans. Syst. Man Cybern. Part B 2006, 36, 312–327. [Google Scholar] [CrossRef]
- Clementini, E. Directional relations and frames of reference. GeoInformatica 2013, 17, 235–255. [Google Scholar] [CrossRef]
- Vanegas, M.C.; Bloch, I.; Inglada, J. A fuzzy definition of the spatial relation “surround”-Application to complex shapes. In Proceedings of the 7th Conference of the European Society for Fuzzy Logic and Technology, Amsterdam, Holland, 22 July 2011; pp. 844–851. [Google Scholar]
- Takemura, C.M.; Cesar, R.M.; Bloch, I. Modeling and measuring the spatial relation “along”: Regions, contours and fuzzy sets. Pattern Recognit. 2012, 45, 757–766. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, H.; Chen, R. Indoors Locality Positioning Using Cognitive Distances and Directions. Sensors 2017, 17, 2828. [Google Scholar] [CrossRef] [PubMed]
- Dong, P. Generating and updating multiplicatively weighted Voronoi diagrams for point, line and polygon features in GIS. Comput. Geosci. 2008, 34, 411–421. [Google Scholar] [CrossRef]
- Gong, Y.; Li, G.; Tian, Y.; Lin, Y.; Liu, Y. A vector-based algorithm to generate and update multiplicatively weighted Voronoi diagrams for points, polylines, and polygons. Comput. Geosci. 2012, 42, 118–125. [Google Scholar] [CrossRef]






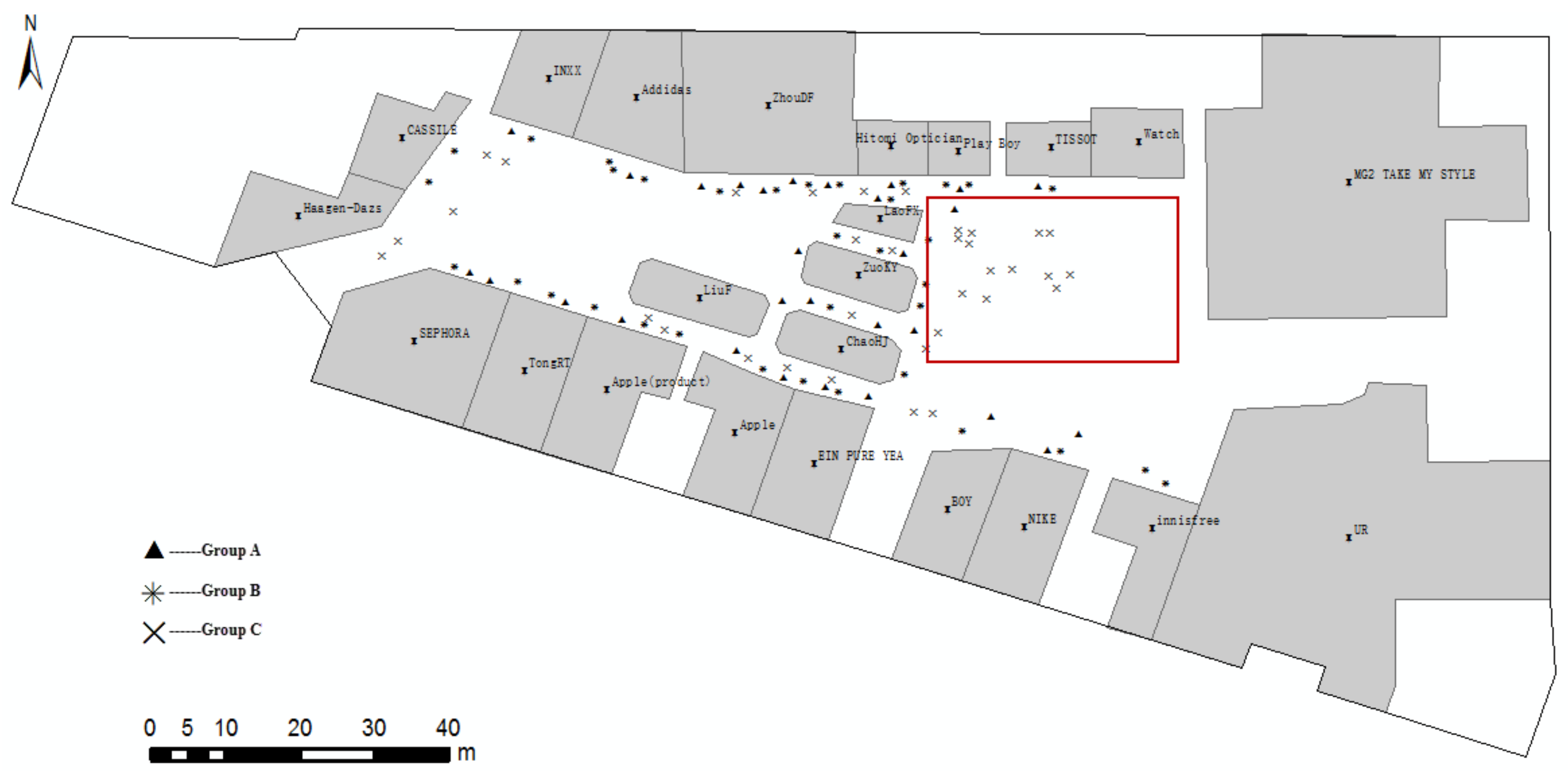
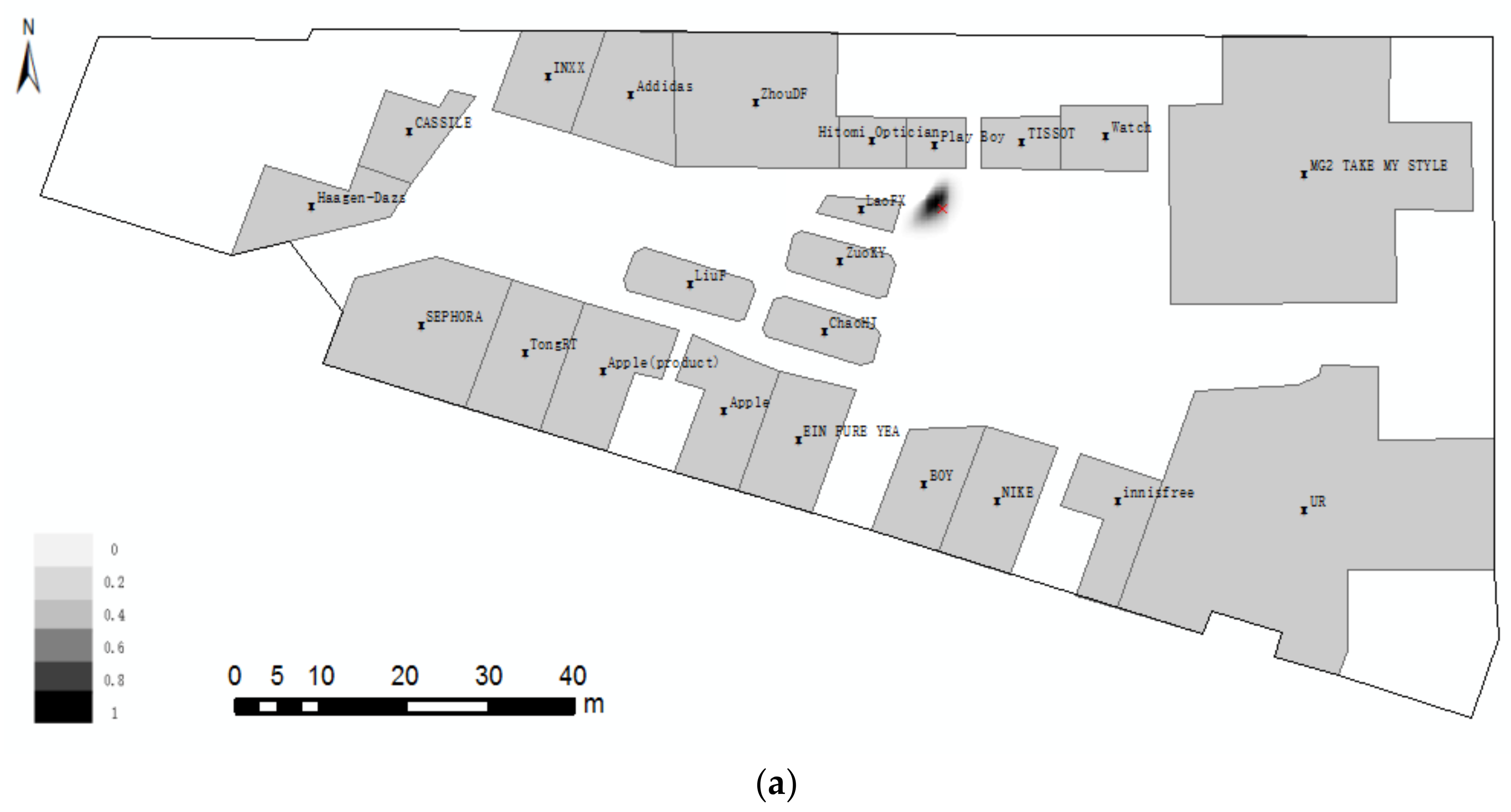

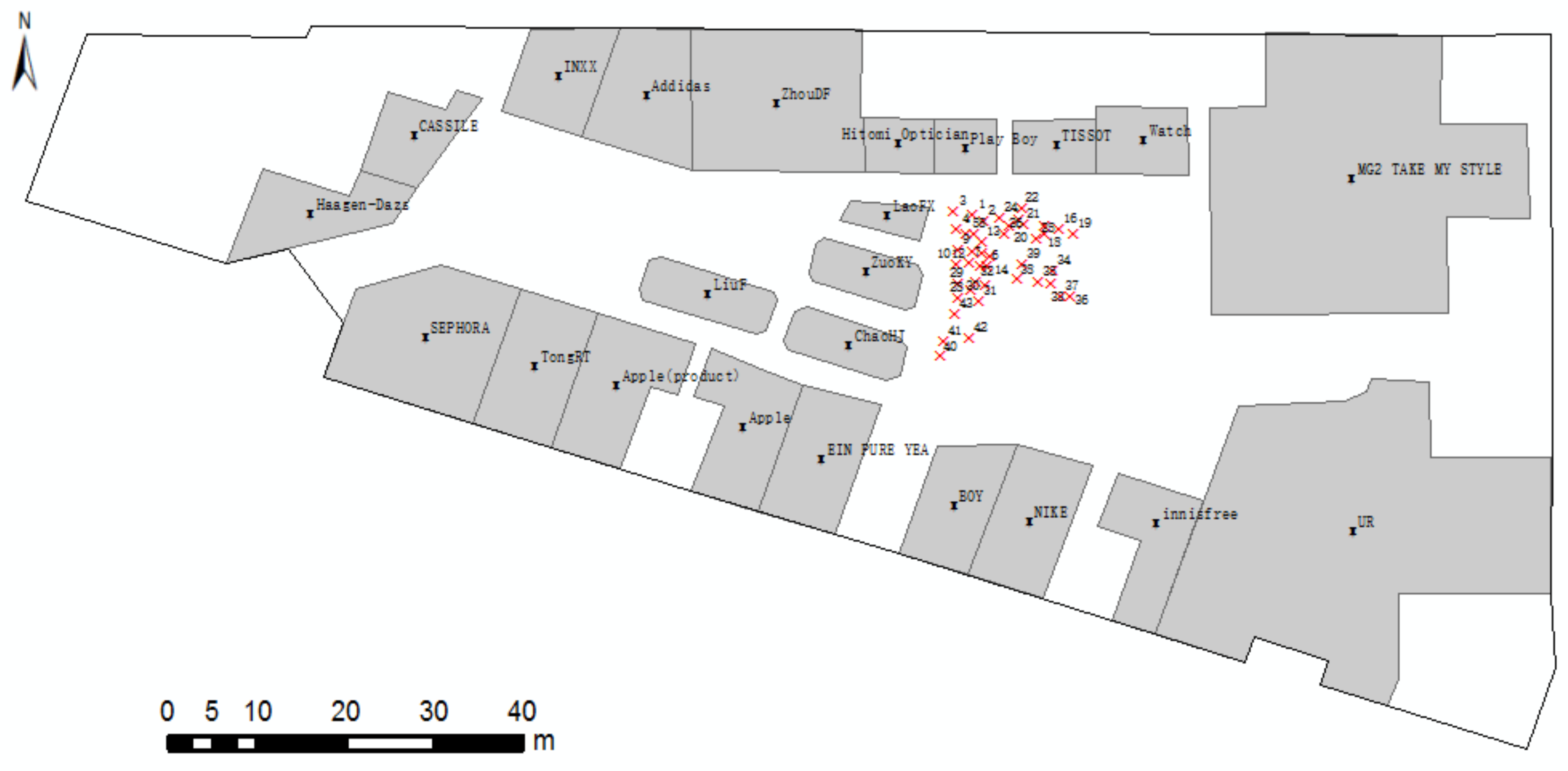

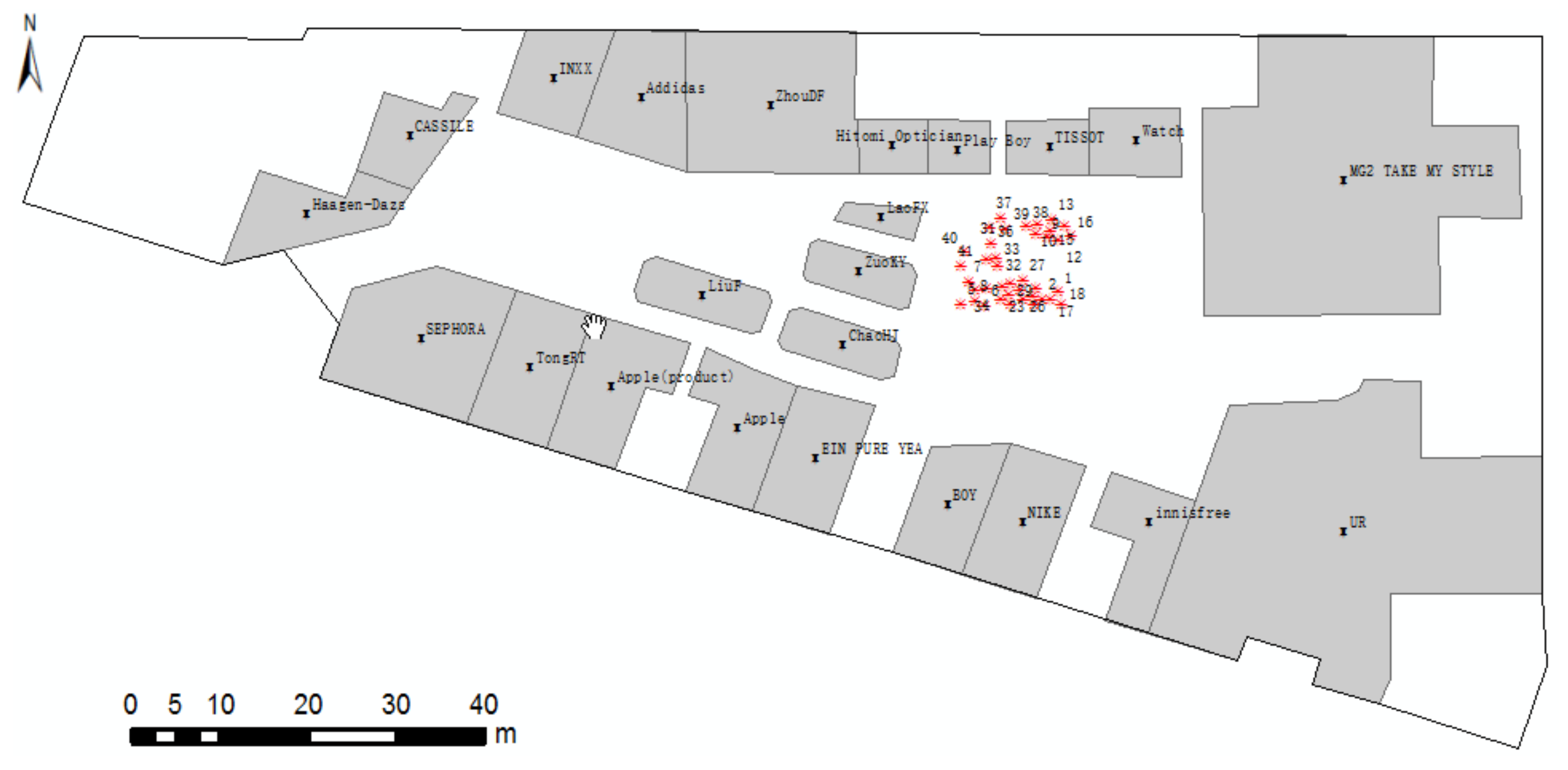
| Num | RO1 | RO2 | ||
|---|---|---|---|---|
| Name | Direction | Name | Direction | |
| 1 | PlayBoy | front | LaoFX | left |
| 2 | LaoFX | front-left | PlayBoy | front-right |
| 3 | PlayBoy | front | LaoFX | left |
| 4 | LaoFX | front | PlayBoy | right |
| 5 | LaoFX | front | PlayBoy | right |
| 6 | ZuoKY | front-left | LaoFX | front-right |
| 7 | ZuoKY | front-left | LaoFX | front-right |
| 8 | PlayBoy | front | LaoFX | left |
| 9 | LaoFX | front | ZuoKY | left |
| 10 | ZuoKY | front-left | LaoFX | front-right |
| 11 | LaoFX | front-left | PlayBoy | front-right |
| 12 | LaoFX | front-right | ZuoKY | front-left |
| 13 | PlayBoy | front-right | LaoFX | front-left |
| 14 | LaoFX | front-left | PlayBoy | front |
| 15 | ZuoKY | front-left | LaoFX | front-right |
| 16 | LaoFX | left | TISSOT | front |
| 17 | PlayBoy | front-left | TISSOT | front |
| 18 | LaoFX | left | TISSOT | front |
| 19 | LaoFX | left | TISSOT | front |
| 20 | PlayBoy | front-right | LaoFX | front-left |
| 21 | PlayBoy | front | TISSOT | left |
| 22 | TISSOT | front | PlayBoy | front-left |
| 23 | PlayBoy | front-left | TISSOT | front |
| 24 | LaoFX | front-left | PlayBoy | front-right |
| 25 | PlayBoy | front-left | TISSOT | front |
| 26 | LaoFX | front-left | PlayBoy | front-right |
| 27 | ZuoKY | front | LaoFX | front-right |
| 28 | LaoFX | front-right | ZuoKY | front |
| 29 | ZuoKY | front | LaoFX | front-right |
| 30 | ZuoKY | front | LaoFX | front-right |
| 31 | LaoFX | front-right | ZuoKY | front |
| 32 | ZuoKY | left | LaoFX | front |
| 33 | TISSOT | left | ZuoKY | front |
| 34 | ZuoKY | front | TISSOT | left |
| 35 | ZuoKY | front | TISSOT | left |
| 36 | ZuoKY | left | TISSOT | front |
| 37 | TISSOT | front | ZuoKY | left |
| 38 | TISSOT | front-right | LaoFX | front-left |
| 39 | LaoFX | left | TISSOT | front |
| 40 | CHJ | front | ZuoKY | front-left |
| 41 | ZuoKY | front-left | CHJ | front |
| 42 | CHJ | front-right | ZuoKY | front-left |
| 43 | ZuoKY | front-left | CHJ | front-right |
| Num | RO1 | RO2 | RO3 | |||
|---|---|---|---|---|---|---|
| Name | Direction | Name | Direction | Name | Direction | |
| 1 | LaoFX | front-left | TISSOT | front | ZuoKY | left |
| 2 | ZuoKY | front | LaoFX | front-left | TISSOT | left |
| 3 | PlayBoy | front | LaoFX | front-left | ZuoKY | left |
| 4 | LaoFX | front | PlayBoy | front-right | ZuoKY | front-left |
| 5 | PlayBoy | front | LaoFX | front-left | ZuoKY | left |
| 6 | ZuoKY | front | LaoFX | front-right | CHJ | front-left |
| 7 | CHJ | front-left | LaoFX | front-right | ZuoKY | front |
| 8 | LaoFX | front-right | ZuoKY | front | CHJ | front-left |
| 9 | PlayBoy | front-left | TISSOT | front | Watch | front-right |
| 10 | TISSOT | front | PlayBoy | front-left | Watch | front-right |
| 11 | PlayBoy | front-left | Watch | front-right | TISSOT | front |
| 12 | TISSOT | front | PlayBoy | front-left | Watch | front-right |
| 13 | Watch | front-right | TISSOT | front | PlayBoy | front-left |
| 14 | PlayBoy | front-left | TISSOT | front | Watch | front-right |
| 15 | Watch | front-right | TISSOT | front | PlayBoy | front-left |
| 16 | Watch | front-right | TISSOT | front | PlayBoy | front-left |
| 17 | TISSOT | front | ZuoKY | left | LaoFX | front-left |
| 18 | LaoFX | front-left | TISSOT | front | ZuoKY | left |
| 19 | LaoFX | front-left | ZuoKY | left | TISSOT | front |
| 20 | TISSOT | front | LaoFX | front-left | ZuoKY | left |
| 21 | LaoFX | front-left | TISSOT | front | ZuoKY | left |
| 22 | ZuoKY | front | LaoFX | front-right | CHJ | front-left |
| 23 | LaoFX | front-right | ZuoKY | front | CHJ | front-left |
| 24 | ZuoKY | front | LaoFX | front-right | CHJ | front-left |
| 25 | ZuoKY | front | CHJ | front-left | LaoFX | front-right |
| 26 | LaoFX | front-left | TISSOT | front | ZuoKY | left |
| 27 | LaoFX | front-left | TISSOT | front | ZuoKY | left |
| 28 | ZuoKY | front | CHJ | front-left | LaoFX | front-right |
| 29 | ZuoKY | front | LaoFX | front-right | CHJ | front-left |
| 30 | LaoFX | front | PlayBoy | front-right | ZuoKY | front-left |
| 31 | PlayBoy | front | TISSOT | right | ZuoKY | left |
| 32 | LaoFX | front | ZuoKY | front-left | PlayBoy | front-right |
| 33 | PlayBoy | front-right | ZuoKY | front-left | LaoFX | front |
| 34 | LaoFX | left | TISSOT | front-right | PlayBoy | front-left |
| 35 | LaoFX | left | TISSOT | front-right | PlayBoy | front-left |
| 36 | Watch | front-right | TISSOT | front | PlayBoy | front-left |
| 37 | LaoFX | front-left | TISSOT | front-right | PlayBoy | front |
| 38 | LaoFX | front | PlayBoy | front-right | ZuoKY | front-left |
| 39 | PlayBoy | front-right | ZuoKY | front-left | LaoFX | front |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Fan, H.; Chen, R.; Li, H.; Wang, L.; Zhao, K.; Du, W. Positioning Locality Using Cognitive Directions Based on Indoor Landmark Reference System. Sensors 2018, 18, 1049. https://doi.org/10.3390/s18041049
Wang Y, Fan H, Chen R, Li H, Wang L, Zhao K, Du W. Positioning Locality Using Cognitive Directions Based on Indoor Landmark Reference System. Sensors. 2018; 18(4):1049. https://doi.org/10.3390/s18041049
Chicago/Turabian StyleWang, Yankun, Hong Fan, Ruizhi Chen, Huan Li, Luyao Wang, Kang Zhao, and Wu Du. 2018. "Positioning Locality Using Cognitive Directions Based on Indoor Landmark Reference System" Sensors 18, no. 4: 1049. https://doi.org/10.3390/s18041049
APA StyleWang, Y., Fan, H., Chen, R., Li, H., Wang, L., Zhao, K., & Du, W. (2018). Positioning Locality Using Cognitive Directions Based on Indoor Landmark Reference System. Sensors, 18(4), 1049. https://doi.org/10.3390/s18041049





