A Sparsity-Promoted Method Based on Majorization-Minimization for Weak Fault Feature Enhancement
Abstract
:1. Introduction
2. Basic Theory
2.1. Basis Pursuit Algorithm
2.2. Majorzation-Minimization Algorithm
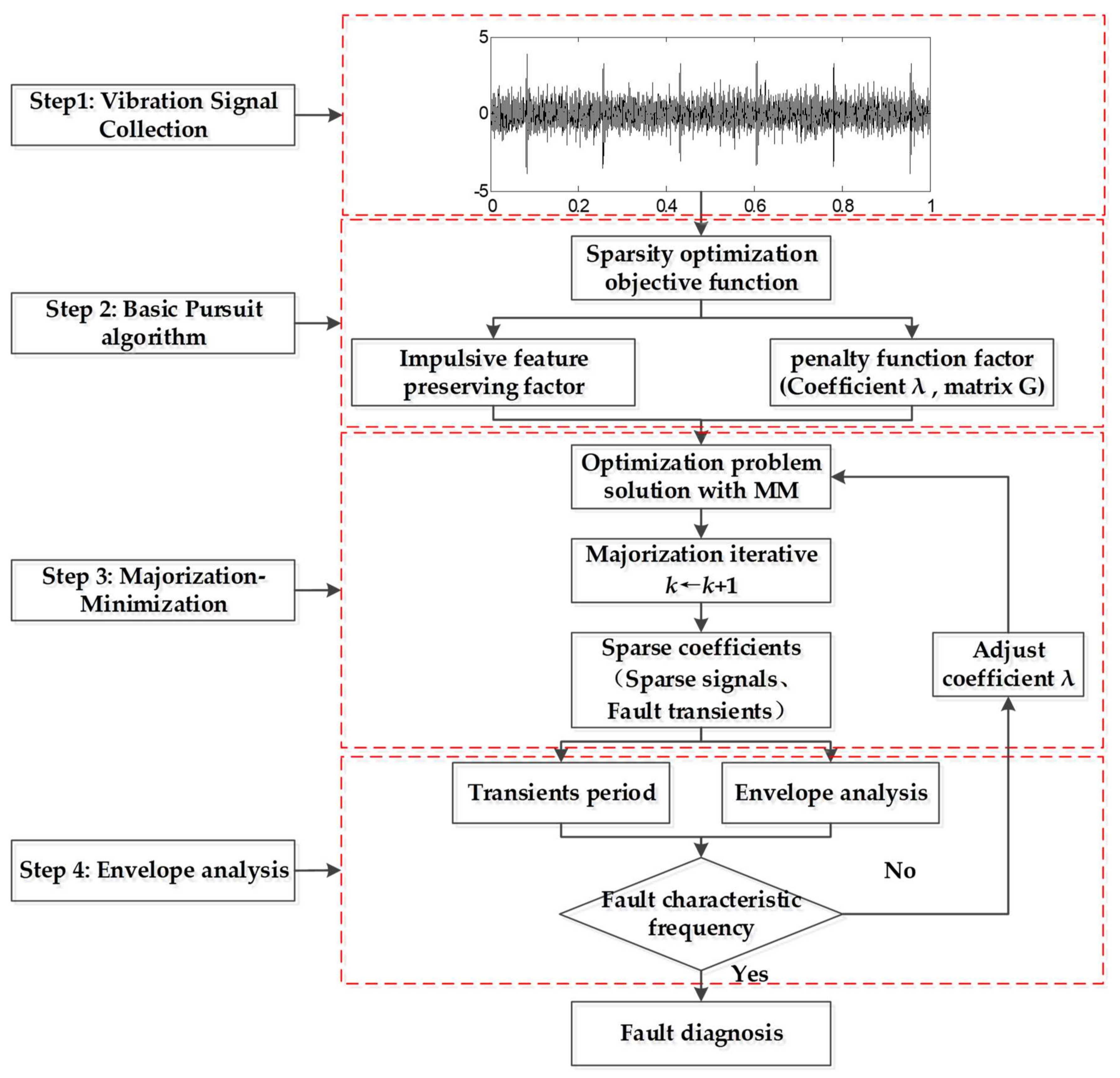
3. Weak Fault Feature Enhancing Strategy Using Sparsity-Promoted Method
- (1)
- Collect the vibration signals y using acceleration sensors,
- (2)
- Construct the Majorization iterative function and initialize k = 1, sparse matrix D, penalty factor , and ,
- (3)
- According to Equation (18), carry out the Majorization iterative steps and update the iterative number k←k + 1.
- (4)
- Obtain sparse signal xk+1, which only contains the transient components.
- (5)
- Perform envelope analysis and extract the fault characteristic frequency.
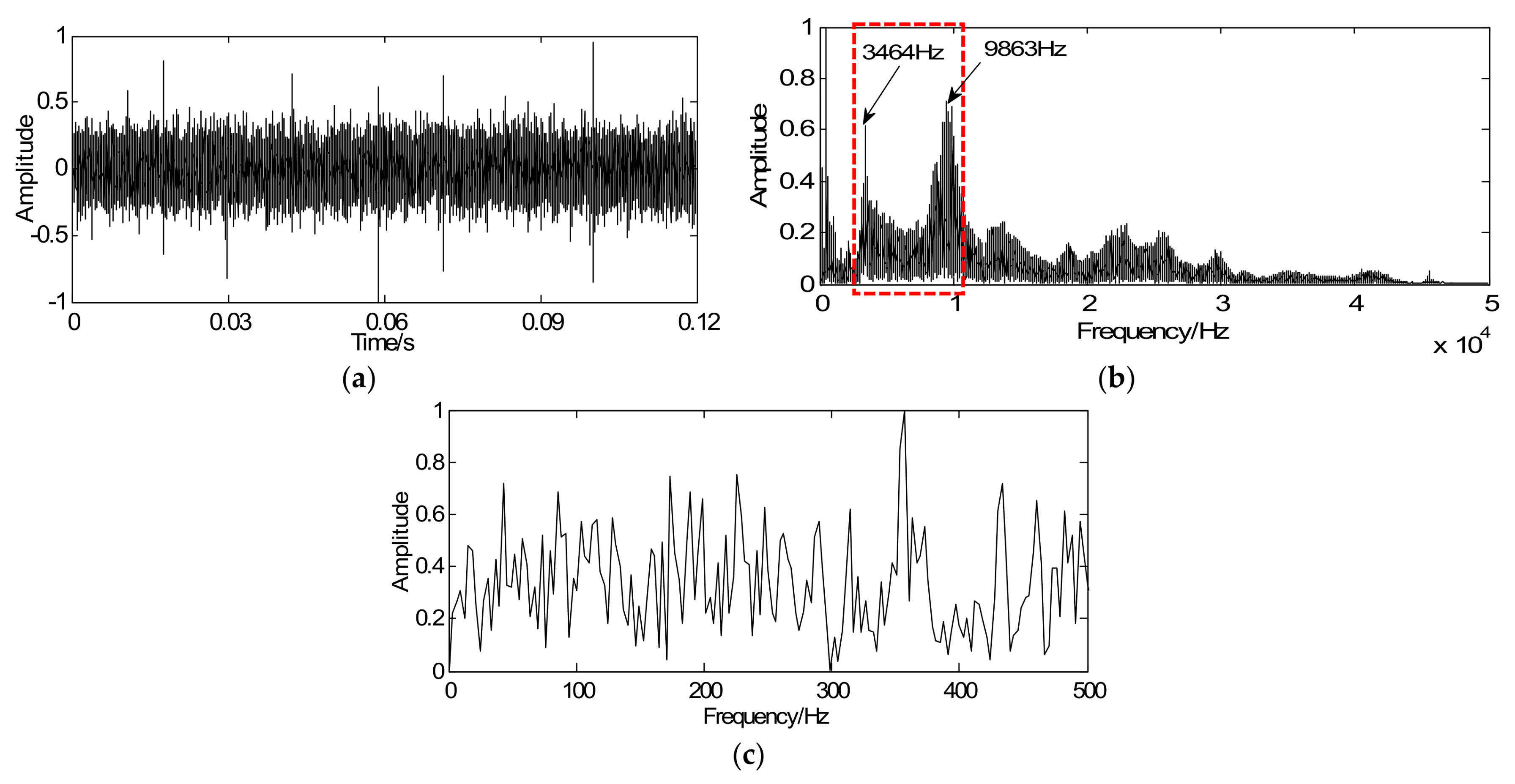
4. Application Cases
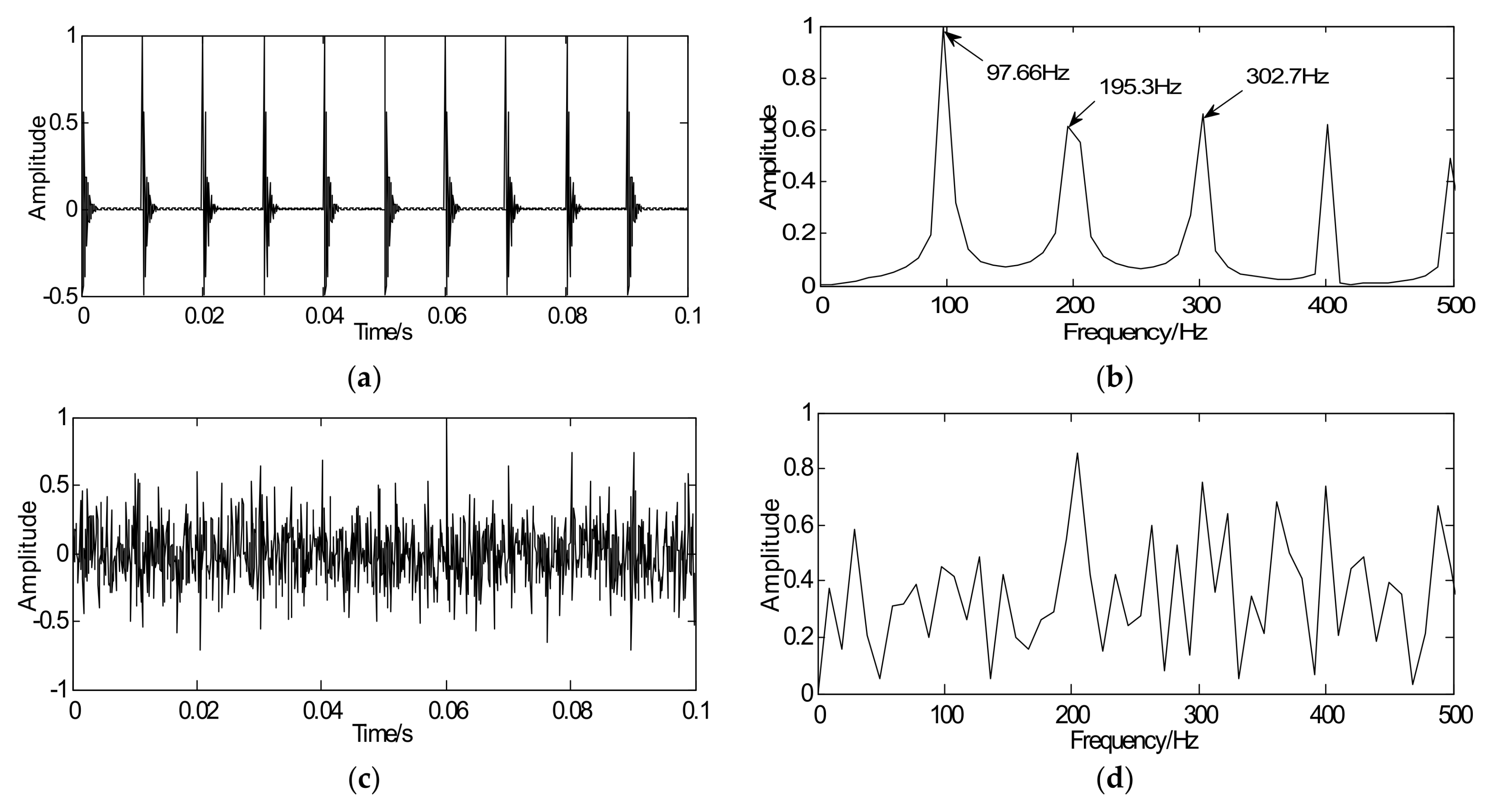
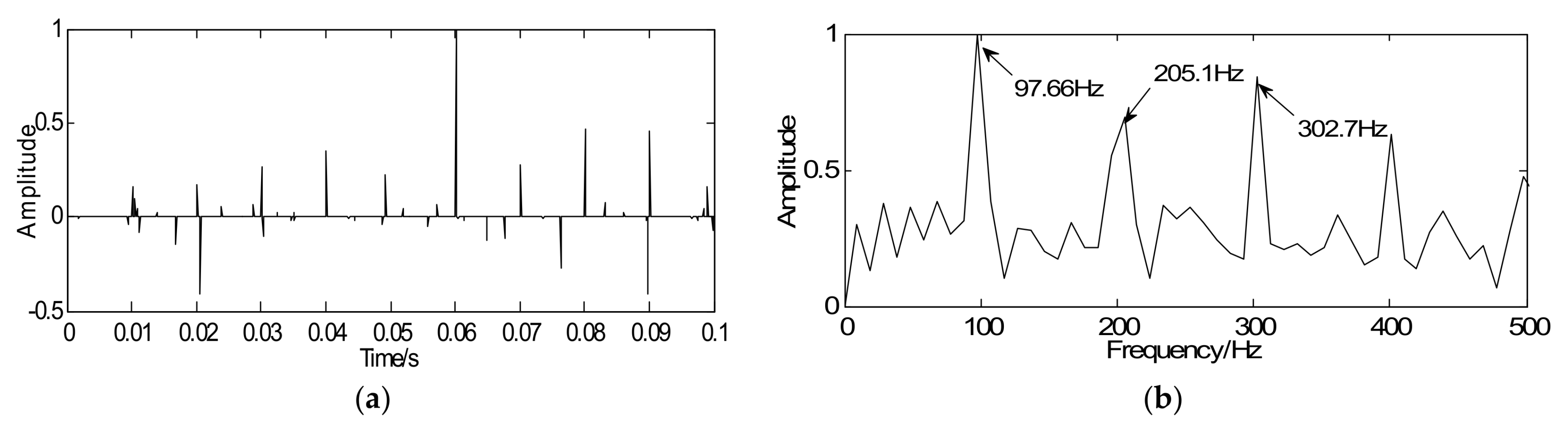
4.1. Simulation Analysis
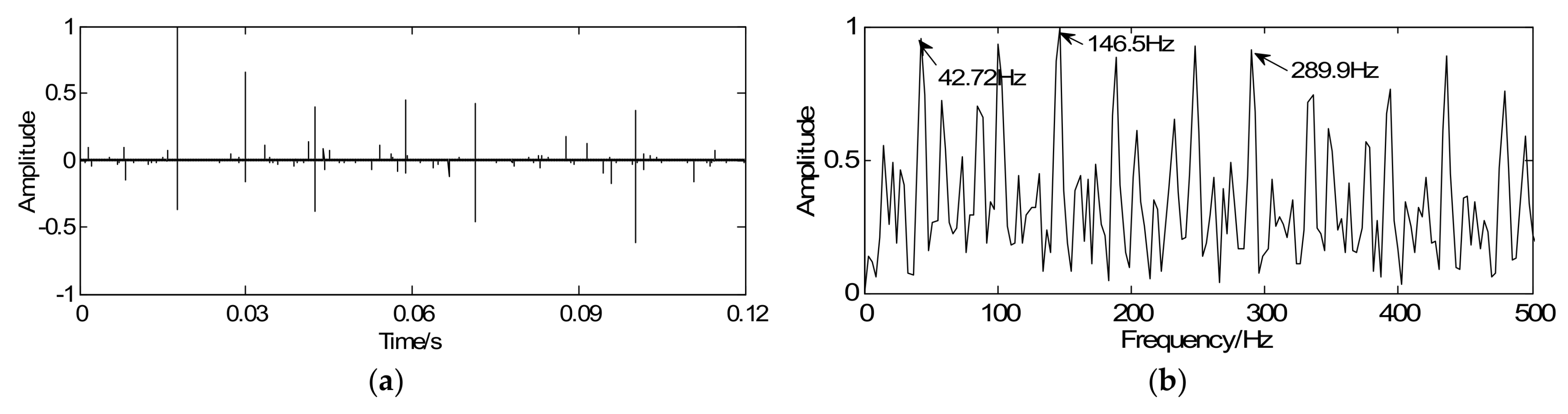
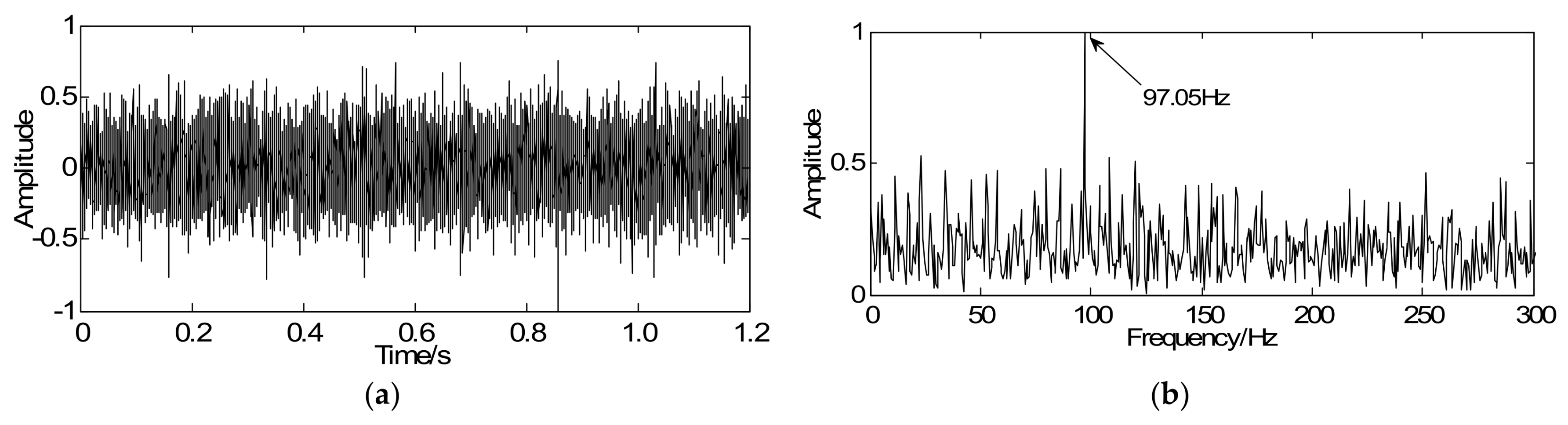
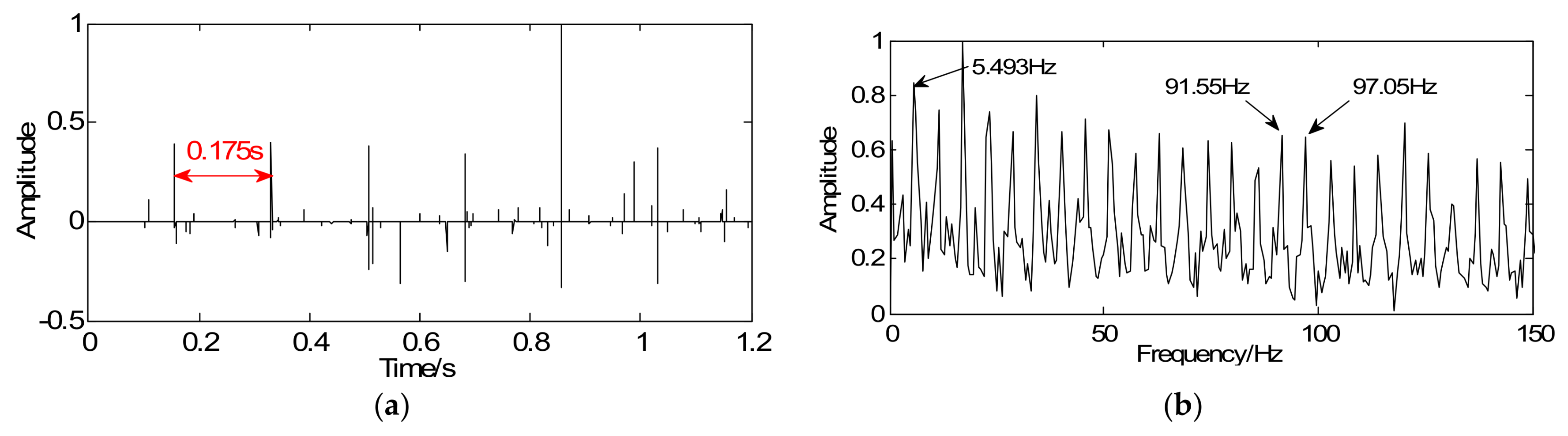
4.2. Experimental Verification and Discussion
4.2.1. Test Rig
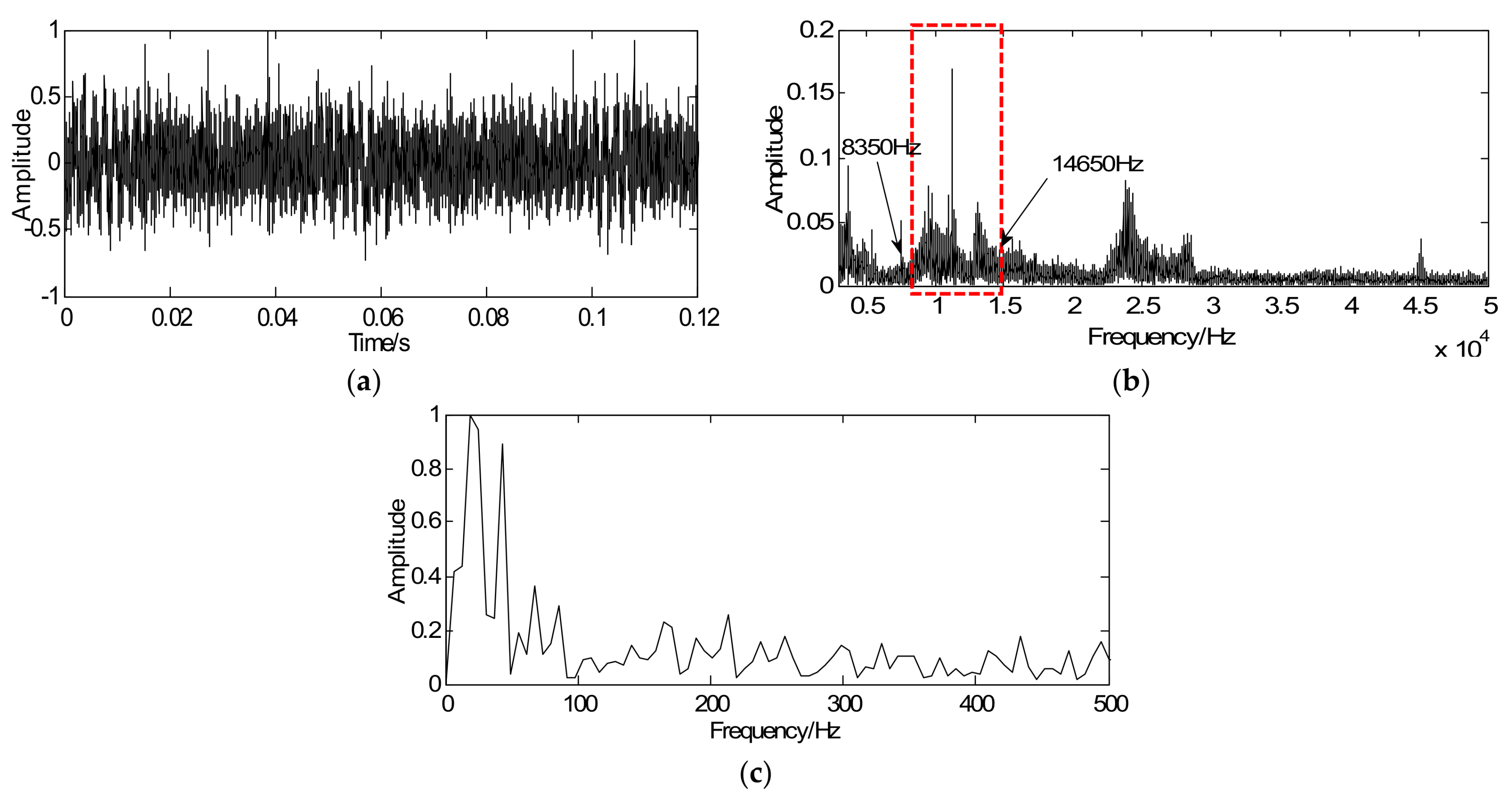
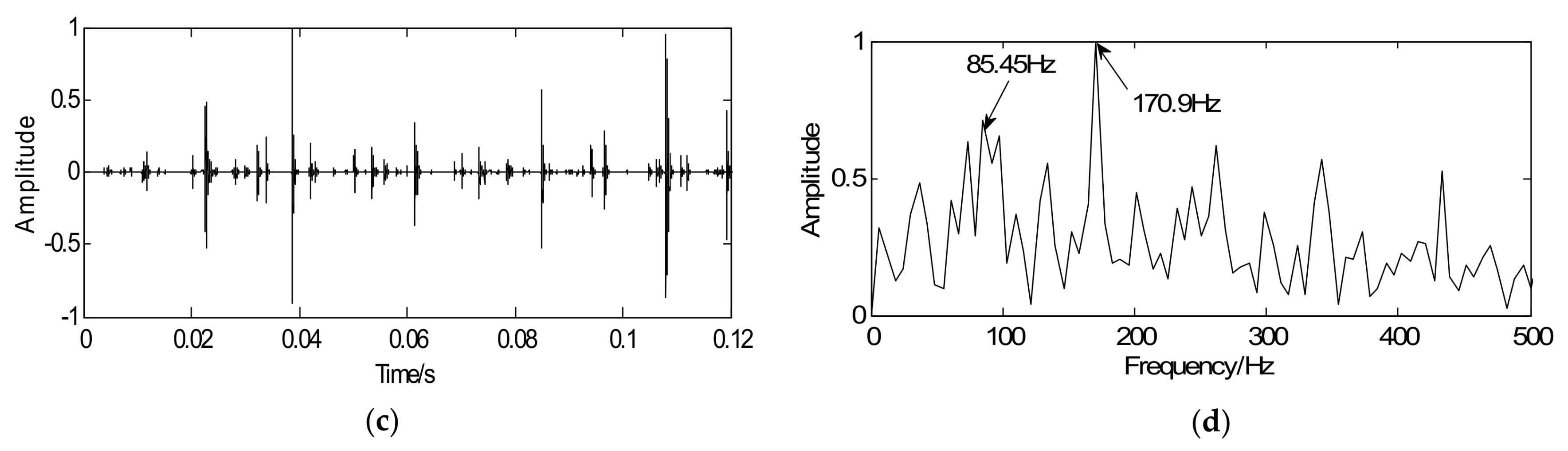
4.2.2. Detection of the Bearing Fault in the Outer Race
4.2.3. Detection of the Bearing Fault in the Inner Race
4.2.4. Detection of the Gearbox Fault with Broken-Tooth
4.3. Comparison with the Traditional MM Algorithm
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Han, T.; Jiang, D.; Zhang, X.; Sun, Y. Intelligent Diagnosis Method for Rotating Machinery Using Dictionary Learning and Singular Value Decomposition. Sensors 2017, 17, 689. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, R.; Tang, G.; Cao, X. A compound fault diagnosis for rolling bearings method based on blind source separation and ensemble empirical mode decomposition. PLoS ONE 2014, 9, e109166. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ke, Y.; Luo, G.; Li, L.; Tang, G. A Two-Stage Compression Method for the Fault Detection of Roller Bearings. Shock Vib. 2016, 4, 1–11. [Google Scholar] [CrossRef]
- Tang, H.; Chen, J.; Dong, G. Sparse representation based latent components analysis for machinery weak fault detection. Mech. Syst. Signal Process. 2014, 46, 373–388. [Google Scholar] [CrossRef]
- Wang, D.; Guo, W.; Wang, X. A joint sparse wavelet coefficient extraction and adaptive noise reduction method in recovery of weak bearing fault features from a multi-component signal mixture. Appl. Soft Comput. 2013, 13, 4097–4104. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Z.; Sun, C.; Li, B.; Zi, Y.; He, Z. Fault feature extraction of gearbox by using overcomplete rational dilation discrete wavelet transform on signals measured from vibration sensors. Mech. Syst. Signal Process. 2012, 33, 275–298. [Google Scholar] [CrossRef]
- Tian, X.; Gu, J.; Rehab, I.; Abdalla, G.; Gu, F. A robust detector for rolling element bearing condition monitoring based on the modulation signal bispectrum and its performance evaluation against the Kurtogram. Mech. Syst. Signal Process. 2016, 100, 167–187. [Google Scholar] [CrossRef]
- Zhang, W.; Bai, K.; Song, P.; Yang, W.; Zhao, H. Wang, Z. Wind Turbine Rolling Bearing Fault Feature Extraction Method Based on VMD and Singular Value Energy Difference Spectrum. N. C. Electr. Power 2017, 3, 59–64. [Google Scholar]
- Tang, G.; Yang, Q.; Wang, H.; Luo, G.; Ma, J. Sparse classification of rotating machinery faults based on compressive sensing strategy. Mechatronics 2015, 31, 60–67. [Google Scholar] [CrossRef]
- Figueiredo, M.; Nowak, R.; Wright, S. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Li, S.; Yin, H.; Fang, L. Group-sparse representation with dictionary learning for medical image denoising and fusion. IEEE Trans. Biomed. Eng. 2012, 59, 3450–3459. [Google Scholar] [CrossRef] [PubMed]
- He, G.; Ding, K.; Lin, H. Fault feature extraction of rolling element bearings using sparse representation. J. Sound Vib. 2016, 366, 514–527. [Google Scholar] [CrossRef]
- Huang, K.; Aviyente, S. Sparse representation for signal classification. Adv. Neural Inf. Process. Syst. 2007, 19, 609–616. [Google Scholar]
- Guo, L.; Gao, H.; Li, J.; Huang, H.; Zhang, X. Machinery vibration signal denoising based on learned dictionary and sparse representation. J. Phys. Conf. Ser. 2015, 628, 012124. [Google Scholar] [CrossRef]
- Zayyani, H.; Babaie-Zadeh, M.; Jutten, C. Bayesian pursuit algorithm for sparse representation. Acoust. Speech Signal Process. 2009, 11, 1549–1552. [Google Scholar]
- Fan, W.; Cai, G.; Huang, W.; Shang, L.; Zhu, Z. Sparse Representation of Transients Based on Wavelet Basis and Majorization-Minimization Algorithm for Machinery Fault Diagnosis. Math. Probl. Eng. 2014, 1–11. [Google Scholar] [CrossRef]
- Wang, H.; Ke, Y.; Song, L.; Tang, G.; Chen, P. A sparsity-promoted decomposition for compressed fault diagnosis of roller bearings. Sensors 2016, 16, 1524. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.; Moussaoui, S.; Idier, J.; Collewet, G.; Xu, M. Majorization-Minimization Algorithms for Maximum Likelihood Estimation of Magnetic Resonance Images. In Proceedings of the Seventh IEEE International Conference on Image Processing Theory, Tools and Applications (IPTA’2017), Montreal, QC, Canada, 28 November–1 December 2017. [Google Scholar]
- Sun, Y.; Babu, P.; Palomar, D.P. Majorization-Minimization Algorithms in Signal Processing, Communica-tions, and Machine Learning. IEEE Trans. Signal Process. 2016, 65, 794–816. [Google Scholar] [CrossRef]
- Sriperumbudur, B.K.; Torres, D.A.; Lanckriet, G.R.G. A majorization- minimization approach to the sparse generalized eigenvalue problem. Mach. Learn. 2011, 85, 3–39. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, G.; Shan, X.; Hu, X.; Guo, Q.; Hou, G. Research of weak fault feature information extraction of planetary gear based on ensemble empirical mode decomposition and adaptive stochastic resonance. Measurement 2015, 73, 55–67. [Google Scholar] [CrossRef]
- Chen, S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 1998, 20, 33–61. [Google Scholar] [CrossRef]
- Yaghoobi, M.; Blumensath, T.; Davies, M.E. Dictionary learning for sparse approximations with the majorization method. IEEE Trans. Signal Process. 2009, 57, 2178–2191. [Google Scholar] [CrossRef]
- Yin, W.; Osher, S.; Goldfarb, D.; Darbon, J. Bregman iterative algorithms for l1-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 2008, 1, 143–168. [Google Scholar] [CrossRef]
- Šorel, M.; Šroubek, F. Fast convolutional sparse coding using matrix inversion lemma. Digit. Signal Process. 2016, 55, 44–51. [Google Scholar] [CrossRef]
- He, W.P.; Zi, Y.Y.; Chen, B.Q. Majorization Minimization Oriented Sparse Optimization Method for Feature Extration Technique in Machinery Fault Diagnosis. J. Xi’an Jiaotong Univ. 2016, 50, 94–99. [Google Scholar]
- Wang, H.; Hou, W.; Tang, G.; Yuan, H.; Zhao, Q.; Cao, X. Fault Detection Enhancement in Rolling Element Bearings via Peak-Based Multiscale Decomposition and Envelope Demodulation. Math. Probl. Eng. 2014, 1, 135–142. [Google Scholar] [CrossRef]
- Hao, Y.; Song, L.; Ke, Y.; Wang, H.; Chen, P. Diagnosis of Compound Fault Using Sparsity Promoted-Based Sparse Component Analysis. Sensors 2017, 17, 1307. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Wang, H.; Tang, G.; Yuan, H.; Yang, Y. An improved method based on CEEMD for fault diagnosis of rolling bearing. Adv. Mech. Eng. 2014, 1–10. [Google Scholar] [CrossRef]
- Feng, Z.; Zhao, L.; Chu, F. Vibration Spectral Characteristics of Localized Gear Fault of Planetary Gearboxes. Proc. CSEE 2013, 33, 119–127. [Google Scholar]








| Number of Rollers | External Diameter (mm) | Inner Diameter (mm) | Width (mm) |
|---|---|---|---|
| 11 | 47 | 20 | 14 |
| Research Object | Number of Teeth | Rotating Period (s) | Rotating Frequency (Hz) | Meshing Frequency (Hz) |
|---|---|---|---|---|
| Driving Gear I | 80 | 3.448 | 0.29 | 23.15 |
| Driven Gear II | 19 | 0.824 | 1.214 | |
| Driving Gear II | 80 | 0.824 | 1.214 | 97.13 |
| Driven Gear III | 17 | 0.175 | 5.714 |
| Fault Category | Outer Race | Inner Race | Broken-Tooth |
|---|---|---|---|
| Fault characteristic frequency (Hz) | 86.32 | 145.84 | 5.714 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, B.; Hao, Y.; Wang, H.; Song, L.; Tang, G.; Yuan, H. A Sparsity-Promoted Method Based on Majorization-Minimization for Weak Fault Feature Enhancement. Sensors 2018, 18, 1003. https://doi.org/10.3390/s18041003
Ren B, Hao Y, Wang H, Song L, Tang G, Yuan H. A Sparsity-Promoted Method Based on Majorization-Minimization for Weak Fault Feature Enhancement. Sensors. 2018; 18(4):1003. https://doi.org/10.3390/s18041003
Chicago/Turabian StyleRen, Bangyue, Yansong Hao, Huaqing Wang, Liuyang Song, Gang Tang, and Hongfang Yuan. 2018. "A Sparsity-Promoted Method Based on Majorization-Minimization for Weak Fault Feature Enhancement" Sensors 18, no. 4: 1003. https://doi.org/10.3390/s18041003
APA StyleRen, B., Hao, Y., Wang, H., Song, L., Tang, G., & Yuan, H. (2018). A Sparsity-Promoted Method Based on Majorization-Minimization for Weak Fault Feature Enhancement. Sensors, 18(4), 1003. https://doi.org/10.3390/s18041003





