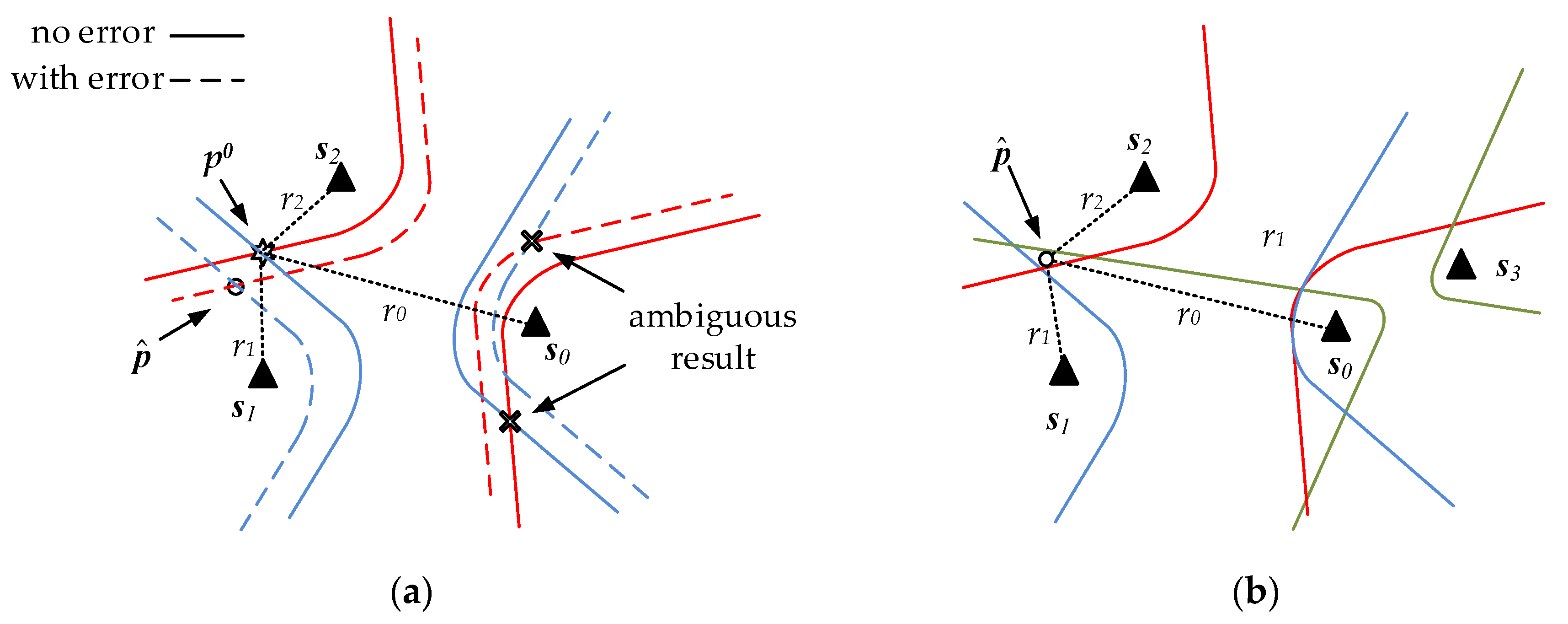
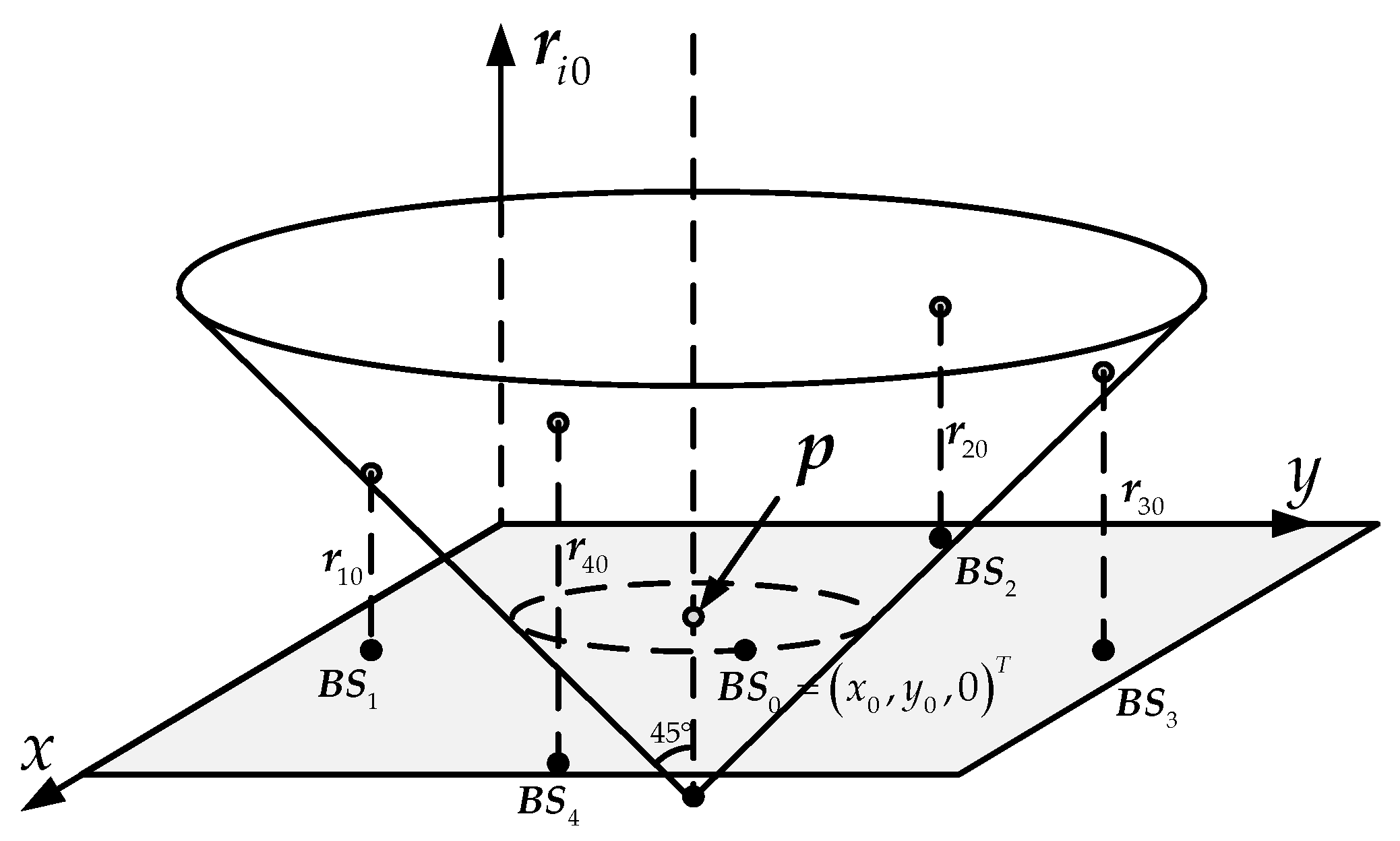
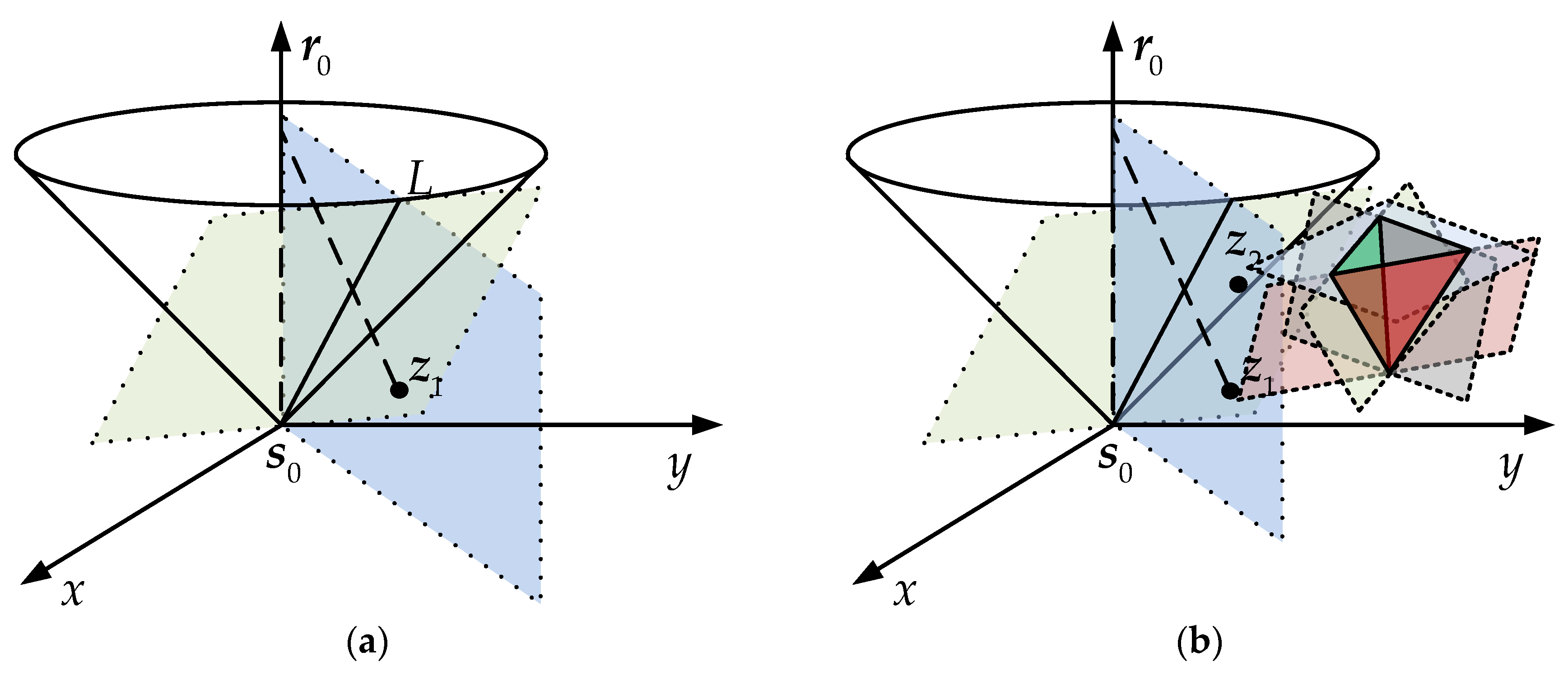
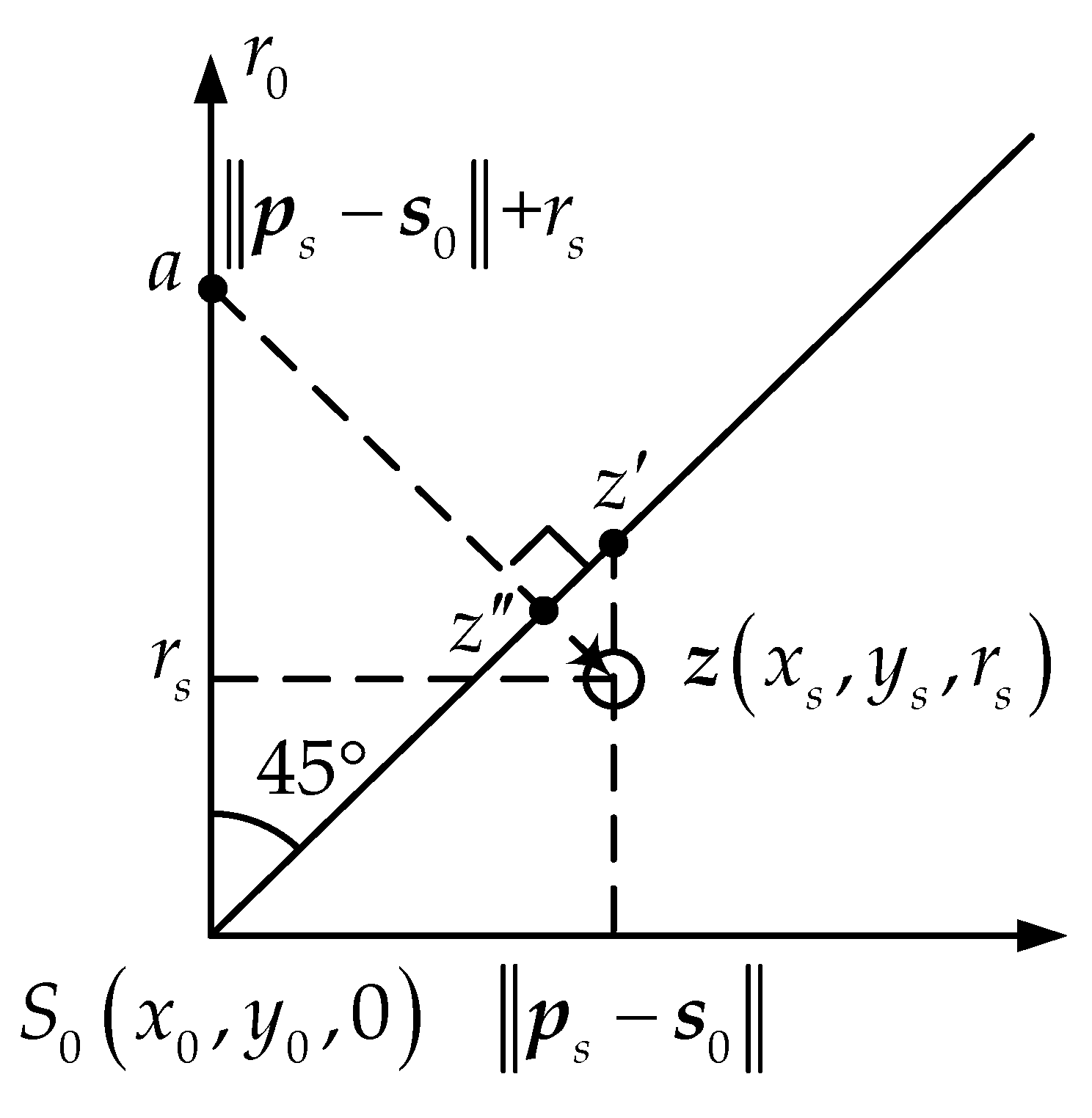1. Introduction
Location technology based on time of arrival is an important branch of passive location and crucial in radar searching, underwater positioning, indoor positioning and other similar applications. As an object-detection system, radar determines the range, angle, or velocity of objects by radio waves. Radio waves (pulsed or continuous) from the transmitter reflect off the object and return to the receiver, give information about the object’s location and speed [
1]. It thus can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations and terrain. When an autonomous-underwater-vehicle (AUV) is executing a task in deep sea without GPS or other radio signals, Long-base-line (LBL) acoustic positioning system is effective in AUV navigation. LBL gathers distance information between the underwater objective and the seabed array element to solve the target position. It can provide accurate positioning of an underwater vehicle within a local area [
2]. Indoor positioning also needs the support of this technology. Reference [
3] presents an ultrasonic-based indoor positioning (ICKON) system for indoor environments. It uses only ultrasonic signals and calculates the position of the mobile platform at centimeter-level accuracy. Reference [
4] considers the use of seismic sensors for footstep localization in indoor environments based on TDOA. The position estimation error is only some tens of centimeters. In addition, the strategies of smartphone localization and speaker localization are analogous to indoor positioning [
5,
6]. The technology is also widely applied in radio navigation, such as the famous LORAN system and Gee system. When the earthquake occurs, earthquake waves inside of radio signal and provides the TDOA measurements in seismic source finding.
TDOA is one of the means of passive location. Two basic sensors (BSs) serves as the focus. The difference between the distances of the two BSs to a source serves as the focal length, which makes up a hyperbola. The intersection of two hyperbolas provides the source position. Compared to time-of-arrival (TOA), TDOA localization does not need synchronization between the source and receivers and are easy to implement [
7,
8]. It eliminates system errors to a certain extent, improves location precision and performs with high accuracy in non-line-of-sight (NLOS) environments [
9]. Solving nonlinear equations is a Gordian knot in TDOA localization due to a sum of squares of coordinates and the range. Numerous methods have been introduced, validated and published in the literature. The most used TDOA-based source-localization algorithms when LOS between receivers and sources exist are summarized in [
10].
Common closed-form solution includes Fang, SI, SX and Chan [
11,
12,
13]. Fang uses an elimination method to multivariate nonlinear equation into a quadratic equation and then solves unknowns one by one. However, there may be no root or multiple roots in the quadratic equation. The problems of computation and root are more serious in 3-D. In addition, the number of equations must equal to the number of unknowns. Therefore, precision cannot be improving by comprehensively analyzing the redundant information from more BSs. SI assumes the source’s coordinates
x,
y and the range
r0 between the source and the reference sensor are independent of each other and then eliminates
r0. It does not consider the geometrical relationship of the source coordinates and range. So, SI performs well in distant but dissatisfactory in close. SX assumes known
r0 and solves
x,
y in terms of
r0. And then it uses
r0 to find
x,
y. Since
r0 is assumed constant in the first step, the degree of freedom to minimize the second norm of
ϕ is reduced. The solution obtained is, therefore, non-optimum [
14]. Chan is widely used with two features. One assumes
x,
y and
r0 are independent and obtains the optimal estimate by WLS. The other is a correction with increment square. However, there are some flaws in the process. The first feature will lead to a contradiction among
x,
y and
r0 especially in distant, which affects the other relative values later. The second feature gets multi results after being square rooted. The correction is uncorrelated with geometric equations, so it is hard to find a balance between the result of correction and geometric solution. In addition, Chan proposes two approaches to solve the problem in the different range. Nevertheless, the critical point is not specific.
The iterative method tends to be more accurate than the closed-form solution. It requires an initial value to begin the process. The result is challenged by the initial value quality and the final convergence effect. The Taylor estimator is such an effective method [
15] but it suffers from local convergence [
16]. Reference [
17] offers a new and unifying perspective that includes the adoption of a multidimensional reference frame obtained by adding the range difference coordinate to the spatial coordinates of the source. Reference [
18] proposed a localization approach through the fitting of propagation cones (FoPC). It also constructed a space-range reference frame with range as the third axis. All of the sensors in the array correspond to the points on the cone in this frame. The apex of the cone is the source position. It transforms the hyperbolic localization into finding the optimal cone based on the sensors for the source position. The optimal cone is from iterative updating using maximum likelihood estimation. Reference [
19] has done more research based on this idea.
Inspired by these perspectives, this study adds the range as a new coordinate to construct a multidimensional reference frame, which consequently facilitates linearization of the surface problem from the perspective of spatial geometry. Unlike [
18], the reference sensor is set to be the cone’s apex in this method. So, the apex and the cone are fixed, the source to be known is on the cone surface. We use WLS to find the optimal source position. WLS is an optimal estimation of linear problems. In this paper, besides the measurement planes in the basic mathematical model, WLS includes a vertical plane constraint and a cone tangent plane constraint. The cone tangent plane constraints the range-coordinates relationship instead of the cone in local approximation. The vertical constraint and the cone tangent constraint are derived from the initial value and updated again after each iteration. The result is close to the optimal solution on the cone by multiple WLS.
In the following sections, we will introduce the algorithm in detail and compared with Taylor algorithm and FoPC proposed in [
18] under different conditions. In some locations, Taylor and FoPC may be divergent. The simulations section shows the characteristics comparisons of these methods. It illustrates that the approach in this paper performs better than the state-of-the-art algorithms do.
3. Performance Analysis
In this section, some simulations were run for the performance of the cone constraint algorithm. Notice that the huge performance advantage of the iterative approaches over the closed-form algorithms such as Chan and SI. Therefore, the proposed algorithm is compared with Taylor and FoPC. In the FoPC, two methods,
Jεa and
Jεe, are proposed based on different cost functions [
18]. Their differences are defined in Equations (18) to (21).
where
and the subscript
k is replaced by
a or
e according to which error definition is adopted.
We start introducing the metrics adopted for accuracy evaluation and then we describe the simulation setup. The comparison of robustness is analyzed in the second section. Some of the factors, which affect positioning performance, were simulated then. The first is the accuracy analysis when the source at different locations. Another is TDOA errors, we tested the impact of different degrees of noise on TDOA localization.
3.1. Setup and Evaluation Metrics
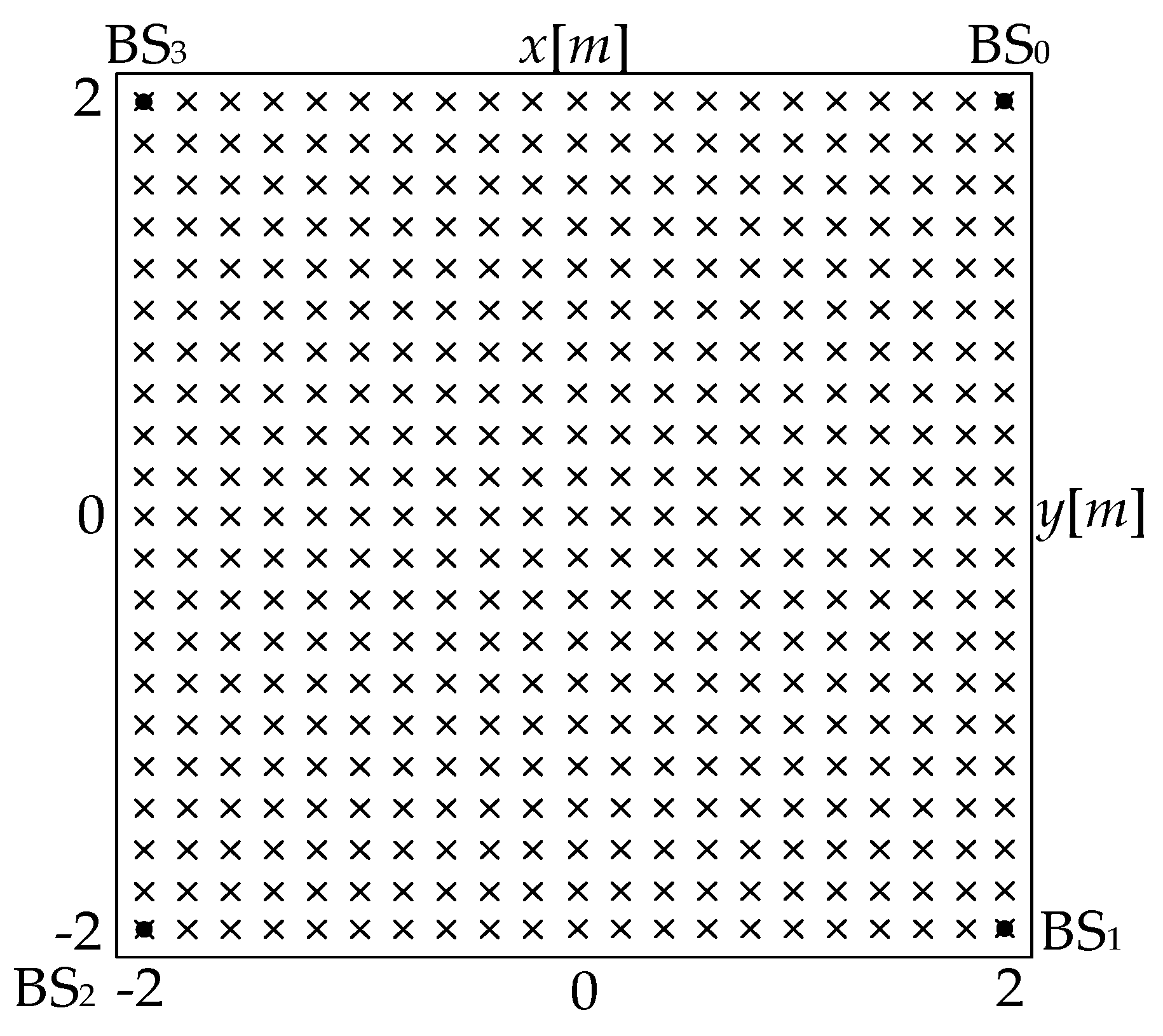
As
Figure 8, the setup used for simulations and experiments is as same as that of the single array simulation in [
18]. The filled circles denote BSs, while crosses mark possible positions of the source. In particular, the area covered by BSs in the simulations is a square of 4 m × 4 m. We assume that BS locations are calibrated, i.e. their positions are not affected by errors.
The time difference was simulated as truth added with Gaussian white noise. Considering that a single test is contingent, the Monte Carlo method was performed with various inputs. The statistical results of 200 tests in each input condition (location or noise) were illustrated the performance. The accuracy of the localization algorithm is evaluated using the following metrics, they are also used in [
18] and we improve some definitions.
Average bias of the localized source is
where
n is the number of noisy measurements tested for each source location,
x and
y are the coordinates of the source,
and
are their estimations based on the
ith realization. This is the measure of the average coordinates distance between the estimated source and the real one.
Root-mean-square-error (RMSE) on the distance is
where
n is the number of noisy measurements tested for each source location.
All the geometries in
Figure 8 are symmetrical. The reference sensor is located at (2, 2). CRLB provides the theoretical lower bound on the variance of any unbiased estimator [
21]. It is also used in the comparisons.
3.2. The Robustness
The drawback of iterative algorithm is that the result may not converge or fall into the local minima. The main factor is the poor quality of the noisy measurements. In the following sections, it will be found that in some cases the Jεa-based-FoPC and Taylor algorithms converge incorrectly, which affects the statistical results of the test.
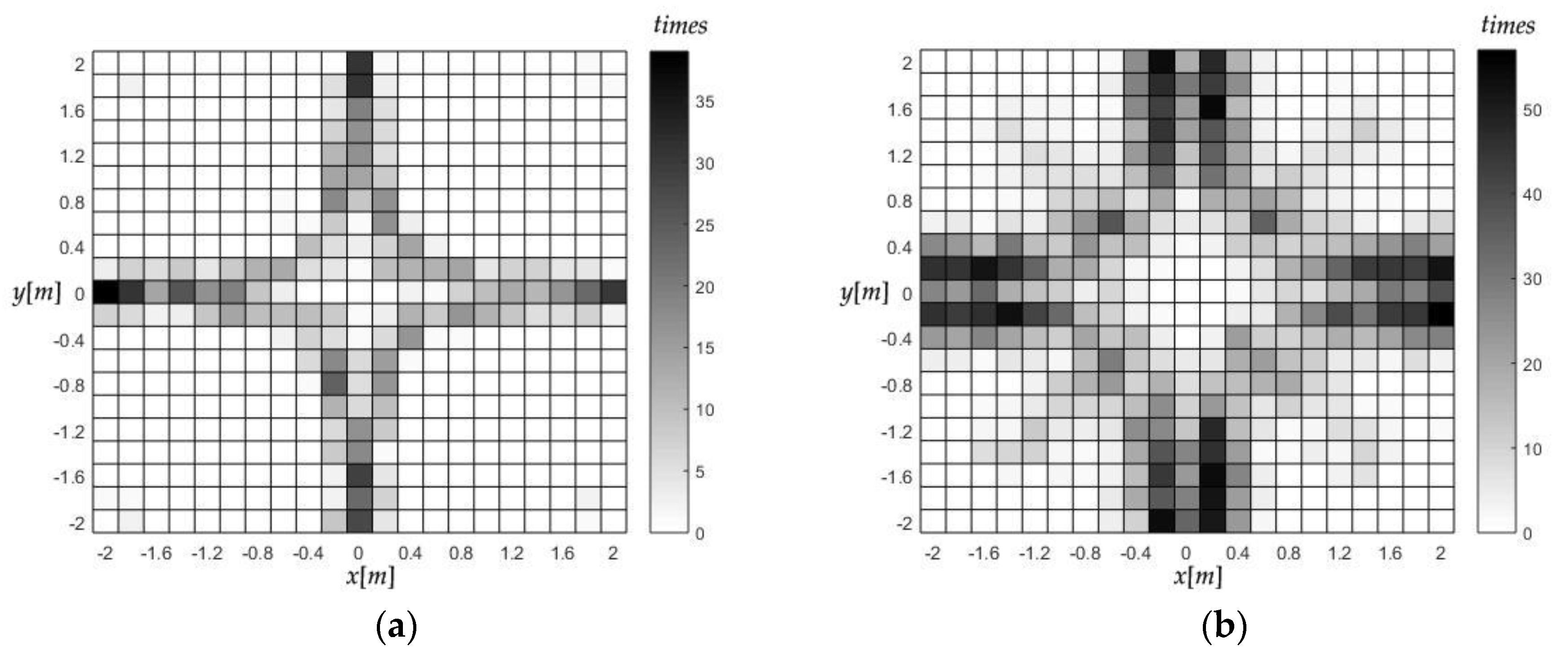
Figure 9 is the divergence times distribution of the four algorithms. The divergence of Taylor and
Jεa-based-FoPC were concurrent, while the
Jεe-based-FoPC and this algorithm both converged well in all the tests. Notice that most of the divergence occurs near the crosshairs in the array, as
Figure 9a. One of the TDOA measurements on these places is close to 0, which is more sensitive to errors and makes some matrix singular. So, it may be related to the dissatisfactory robustness of the two algorithms. When the measurement error becomes larger, as shown in
Figure 9b, the divergence becomes more serious.
The input conditions were recorded when the wrong convergence happened and we take a part of these anomalies to observe in this section, as
Table 1.
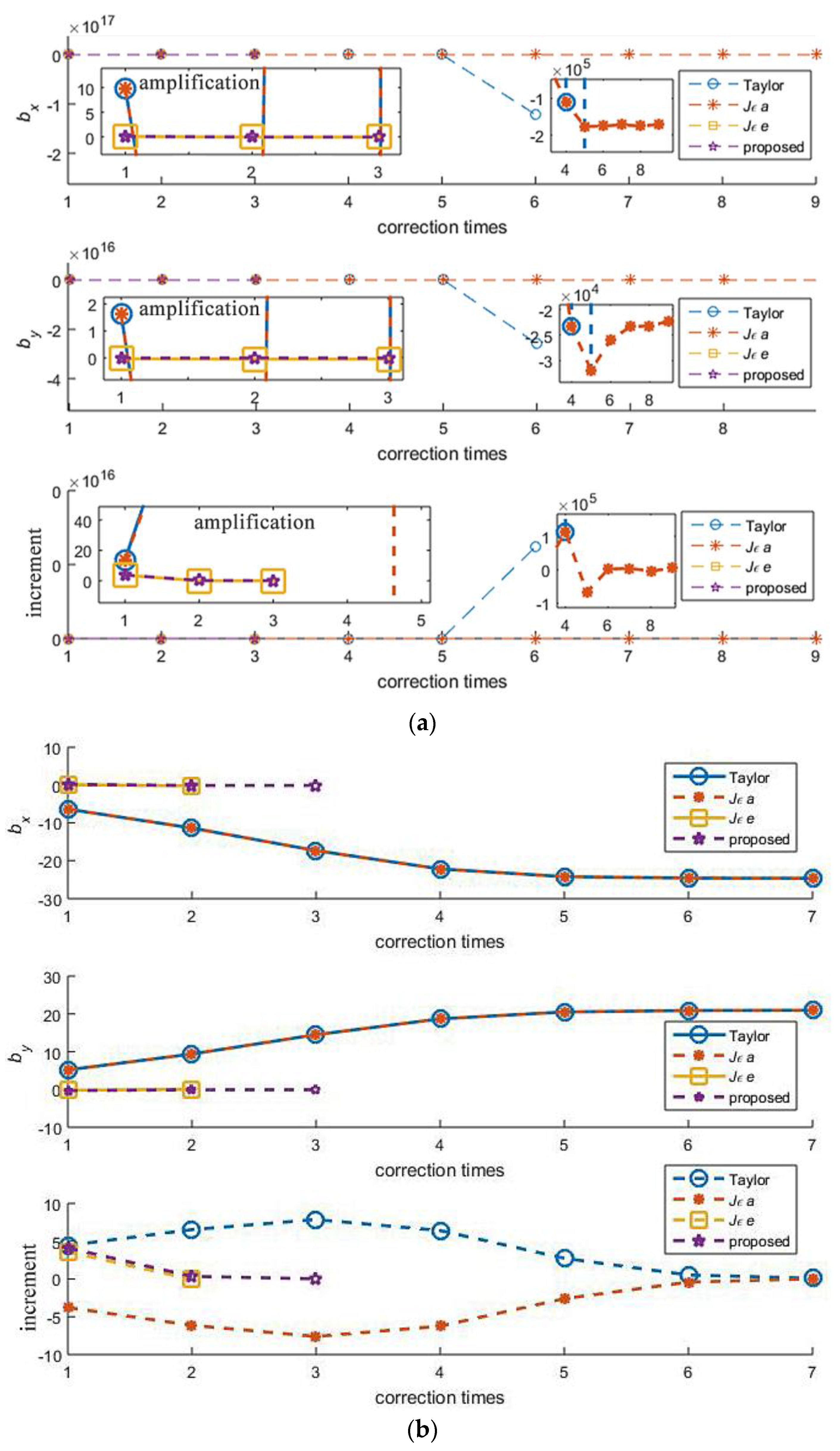
Under the input condition of the first line in
Table 1, the iteration experience of these algorithms is shown in
Figure 10a. The proposed approach and
Jεe-based-FoPC have converged and stopped correcting after three times. While Taylor and
Jεa-based-FoPC were of divergence from the correction beginning, the former was out of control and the latter was correcting in a wrong way.
Under the input condition of the sixth line in
Table 1, the iteration experience of these algorithms is shown in
Figure 10b. The proposed approach finished the correction after three times,
Jεe-based-FoPC cost two times. Taylor and
Jεa-based-FoPC seem to be converged, however, they failed into wrong results.
3.3. The Impact of the Source Position on Localization Accuracy
As above, the accuracy of TDOA localization is different when the localized source is in different places inside the array. If we exclude these singular results in statistics, the better features of Taylor and
Jεa-based-FoPC arise, as shown in
Table 2.
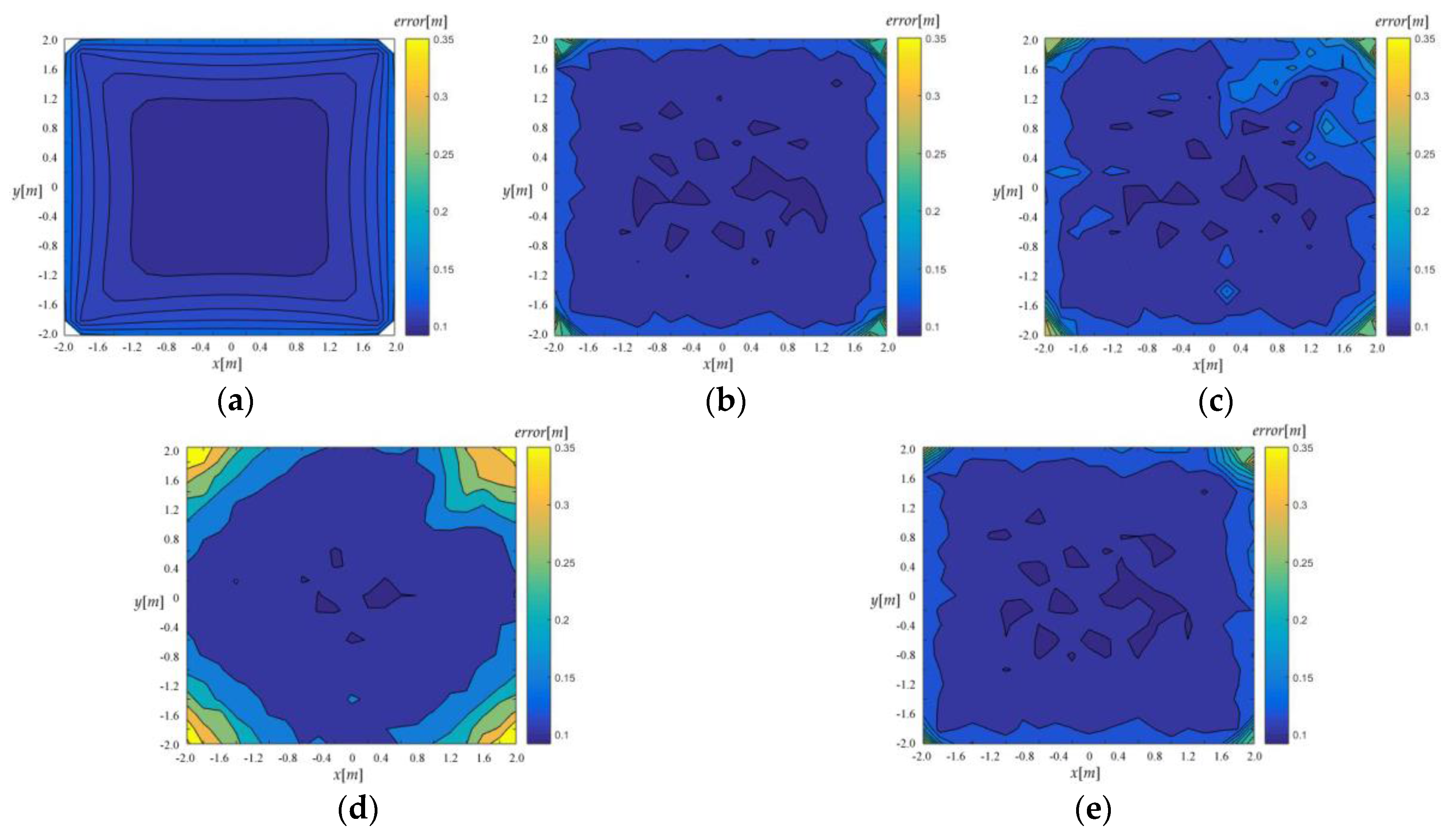
In general, the localization accuracy is higher near the center of the array while it rapidly decreases near the BSs, which is illustrated in the CRLB distribution and the simulation results consistently. See in
Figure 11.
Three trajectory lines are drawn through the array along
y = 0,
y = −0.8,
y = −1.8 and the source localization performance on these lines are analyzed using the four algorithms. At the corresponding positions in
Figure 9, the phenomenon of multiple divergences was expectedly presented and those locations are marked with gray areas below. The statistical results excluding the singular value are shown in
Figure 12.
If converge completely, Taylor approximates to CRLB. The
Jεa-based-FoPC is similar to Taylor ideally. In
Figure 12, some local minimum convergences have not been completely eliminated in statistics, which affected the results on some locations. The
Jεe-based-FoPC and our method are robust and correctly converged inside the array. However, the
Jεe-based-FoPC accuracy somewhat less than the others. In addition to robustness, the proposed algorithm is also close to CRLB as Taylor on accuracy.
3.4. The Impact of Measurement Noise on Localization Accuracy
Measurement noise are the other factors of the precision effect in TDOA localization. We conducted 2000 statistical tests at location (0, 0) with TDOA errors, ranging from 0.002 m to 0.4 m. The performance at location (0, 0) is best inside the array. The results are listed in
Table 3. The RMSE of these algorithms are almost at the same and is proportional to
σ. Notice that the statistical divergence times of Taylor and
Jεa-based-FoPC also increase with TDOA errors, while the divergence never happens on
Jεe-based-FoPC and the proposed algorithm at all.
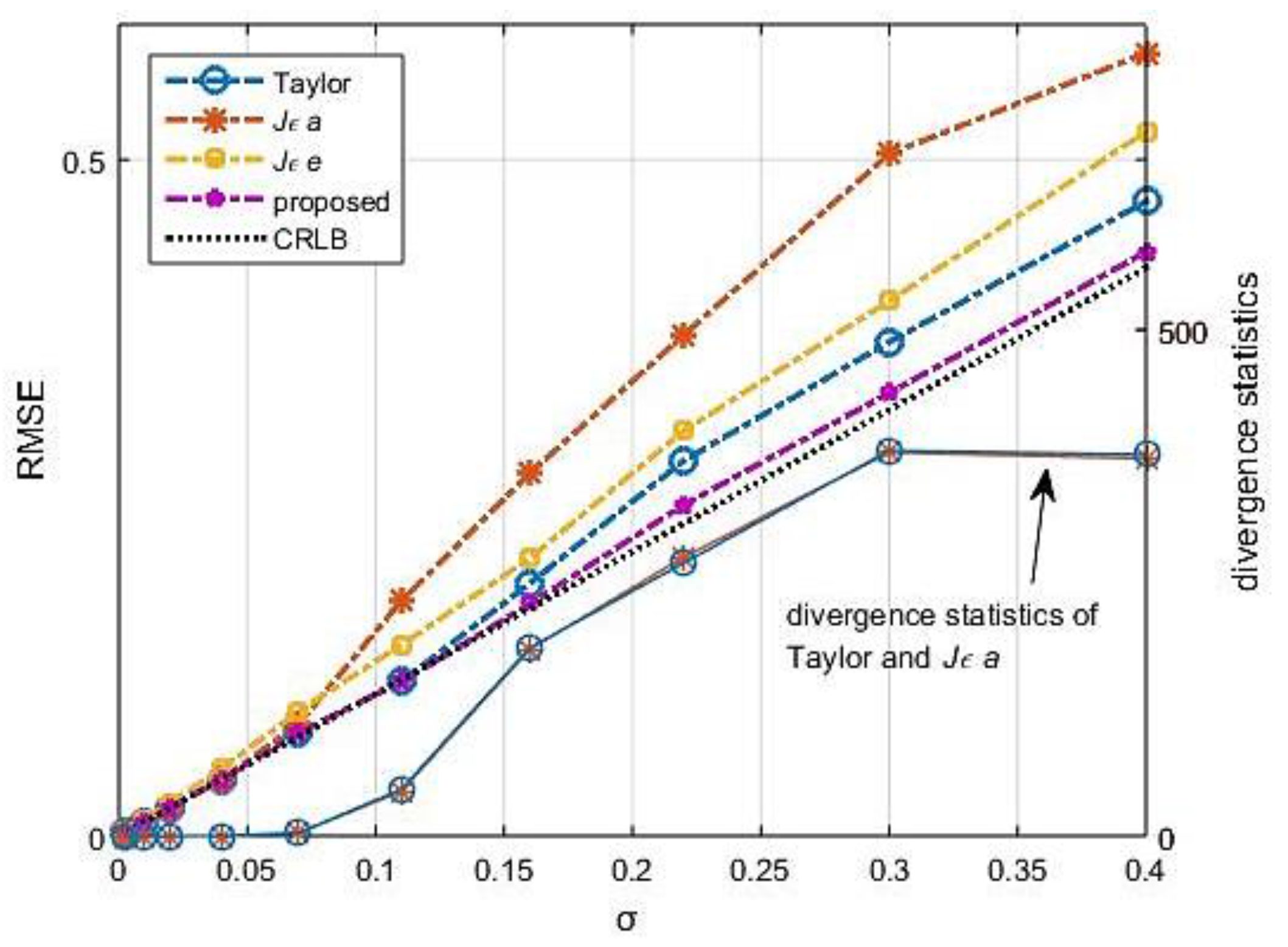
Figure 13 shows the simulation results under the same conditions at location (1.2, 0.8). Although it can be concluded from
Figure 9 that the convergence at location (1.2, 0.8) is better than others nearby, the divergence of Taylor and
Jεa-based-FoPC is up to 380 times at most. Moreover, the differences in the anti-noise characteristics of the algorithms are evident in these cases. As we can see in
Figure 13, the algorithm we proposed is always close to CRLB without divergence, it is robust distinctly.
4. Conclusions
In this paper, we have proposed a weighted least squares method solving the hyperbolic passive localization under the space-range frame. Unlike currently available cone-related ideas, this method uses cone tangent plane instead of cone surface locally and converts the nonlinear model into a linear model. In this way, the optimal solution can be obtained by WLS. In order to be robust, we add a vertical plane to constrain the estimations on the tangent without deviating from the cone. As same as some state-of-the-art algorithms, the correction process may be repeated until convergence to an optimal result. In theory, we resolve the weight value expressions of the two constrained planes, which effectively controls the convergence as we expect. The problem with the existing iterative algorithms is that they cannot achieve both precision and robustness at the same time. The cone tangent plane constraint algorithm provided a solution to this trouble in the paper.
We tested the performance of this algorithm and other analogs with a series of experiments. In the experiment, we found that classical Taylor algorithm and Jεa-based-FoPC algorithm often fail to converge under some conditions. High accuracy of these algorithms was observed through the data post-processing, which masked the real performance of the algorithms. These defects do not exist in this algorithm. Two cost functions proposed in FoPC have quite different properties. Jεa-based-FoPC is accurate but poor robustness, while Jεe-based-FoPC is the opposite. Tests in different locations illustrated the regional distribution of TDOA positioning accuracy; with the highest accuracy at the center while the poorer accuracy at the corners. Finally, in the noise increasing simulations, we observed the impact on positioning when the measurement error was great. Under these conditions, Taylor and Jεa-based-FoPC might converge abnormally even in the center. This impact is evident elsewhere and the differences in the performance of the algorithms are highlighted under loud noises. Notice that the proposed algorithm is always close to CRLB. In these experiments, the proposed algorithm has no risk of divergence and always guarantees the convergence and accuracy. It is also the significance of the newly designed algorithm with cone tangent plane constraint.