A Liquid-Surface-Based Three-Axis Inclination Sensor for Measurement of Stage Tilt Motions
Abstract
:1. Introduction
2. Principle of the Proposed Three-Axis Inclination Sensor
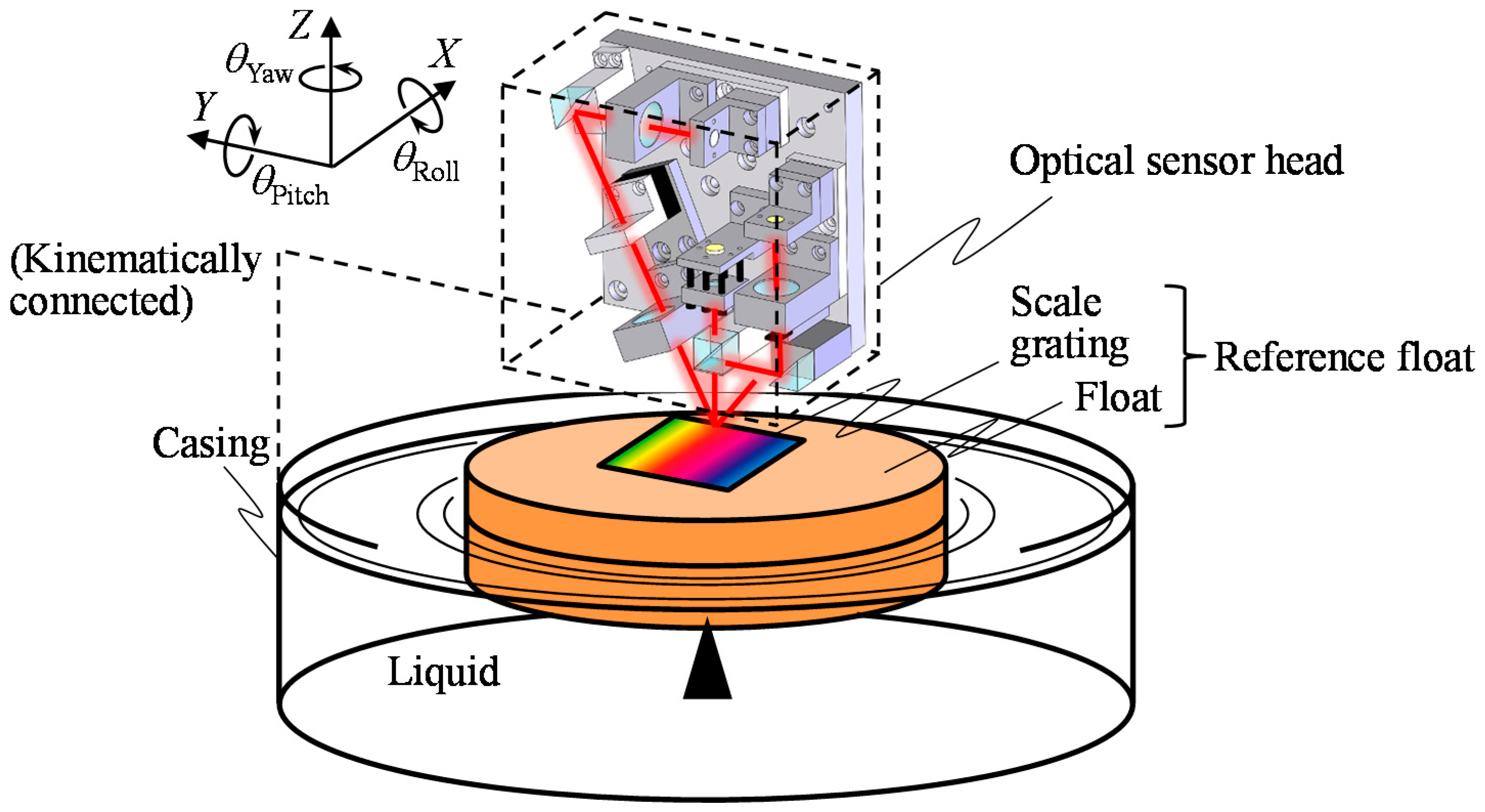
2.1. A Concept of the Proposed Three-Axis Inclination Sensor
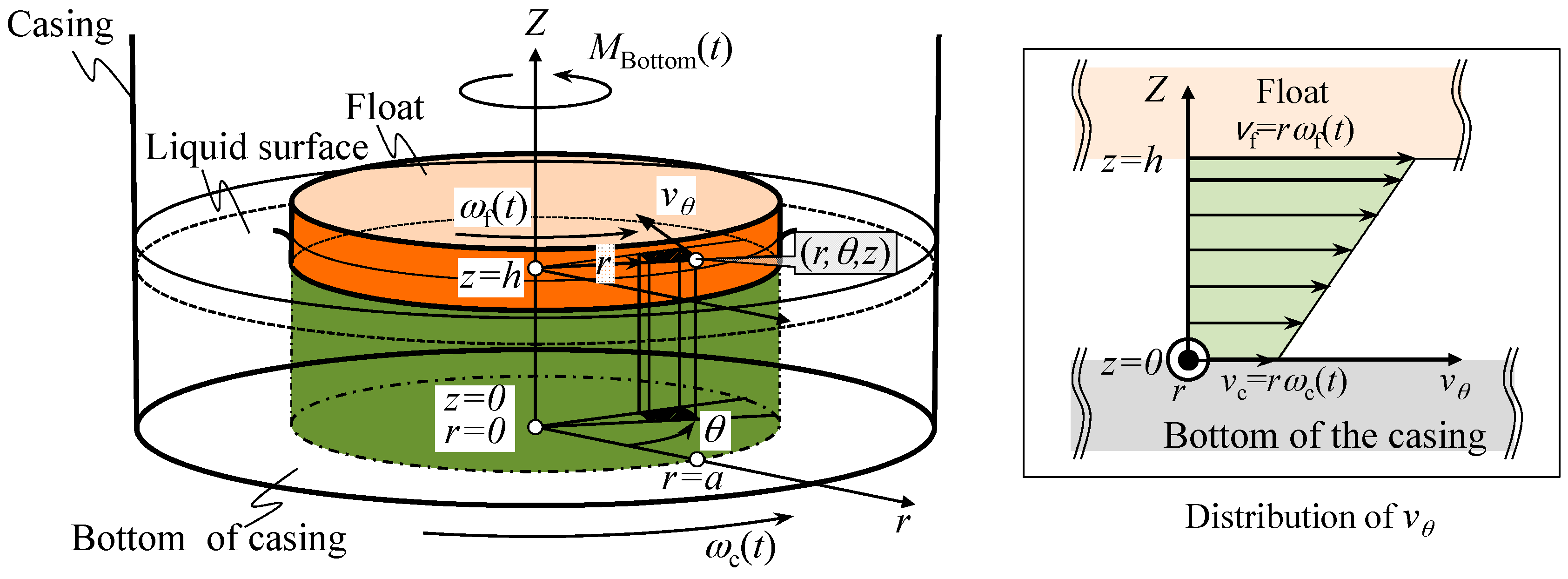
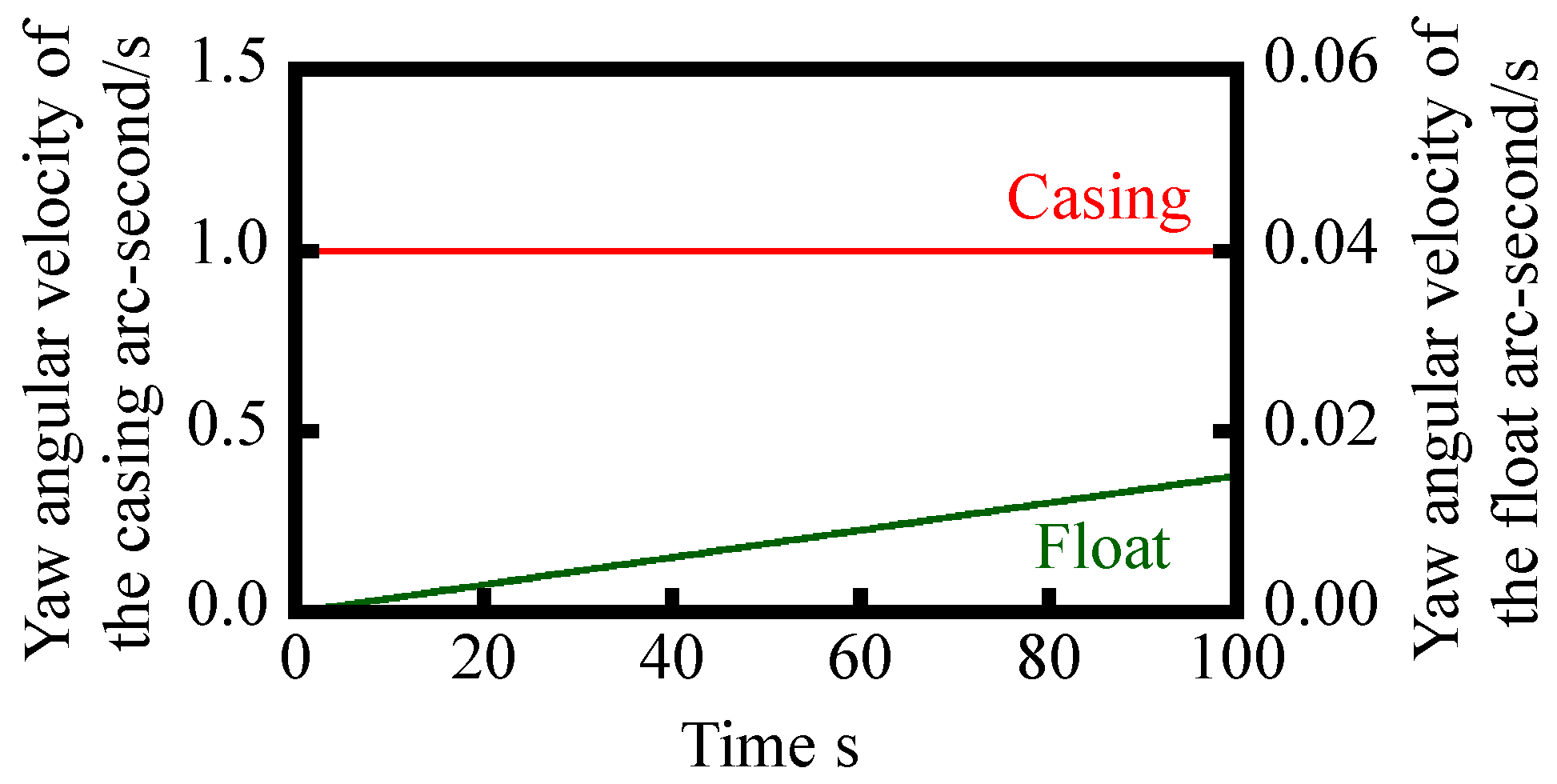
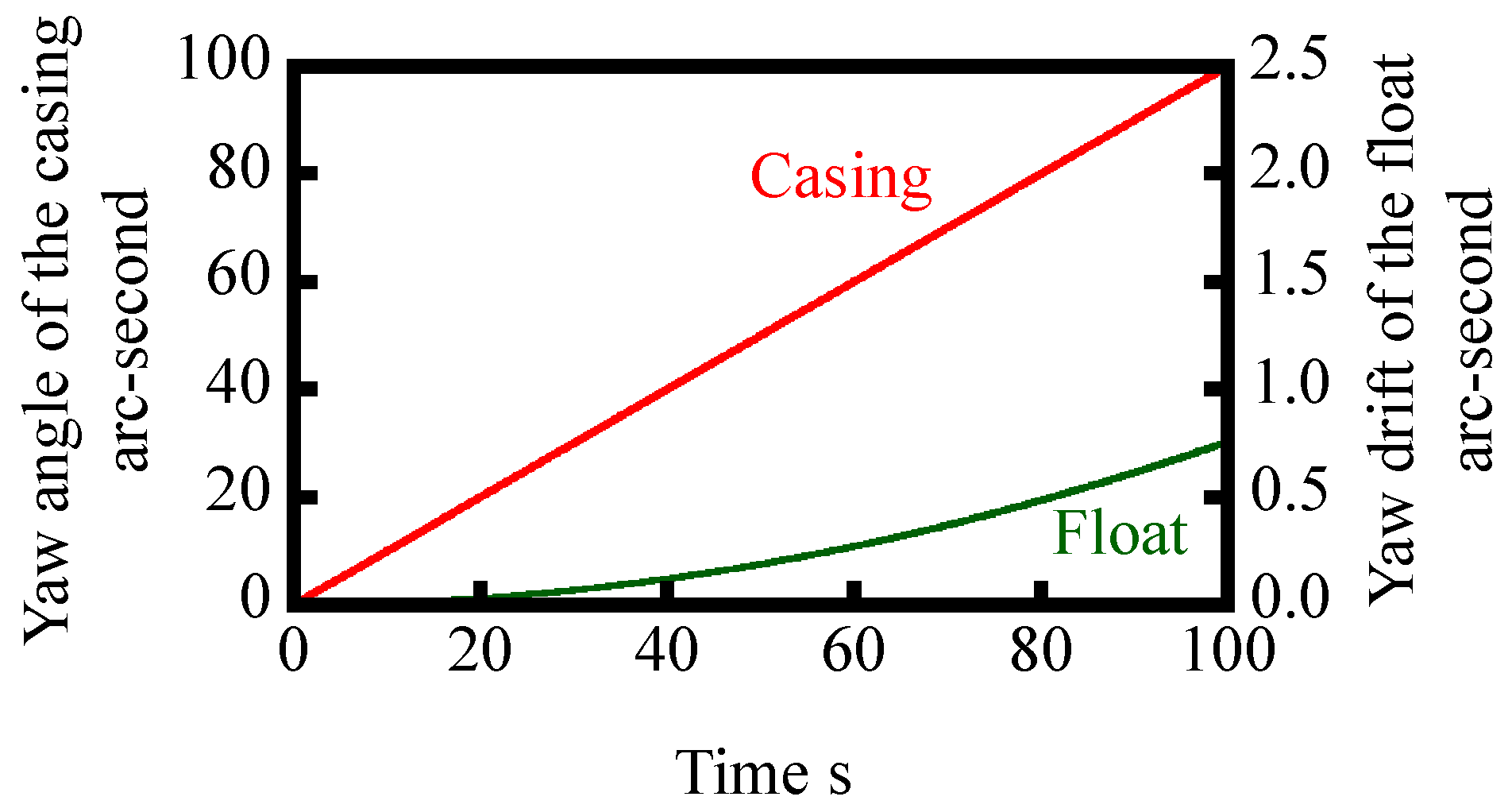
2.2. Modeling of the Yaw Motion of Inclination Angle Reference Float
- (a)
- The flow is not a function of time (steady flow: ∂/∂t = 0).
- (b)
- The flow is incompressible (ρ = const.)
- (c)
- The radial and the Z-directional velocity components of the flow are zero (vr = 0, vz = 0)
- (d)
- The circumferential velocity component of the flow is uniform along the Z-direction ()
- (e)
- The pressure distribution is uniform along the circumferential direction ()
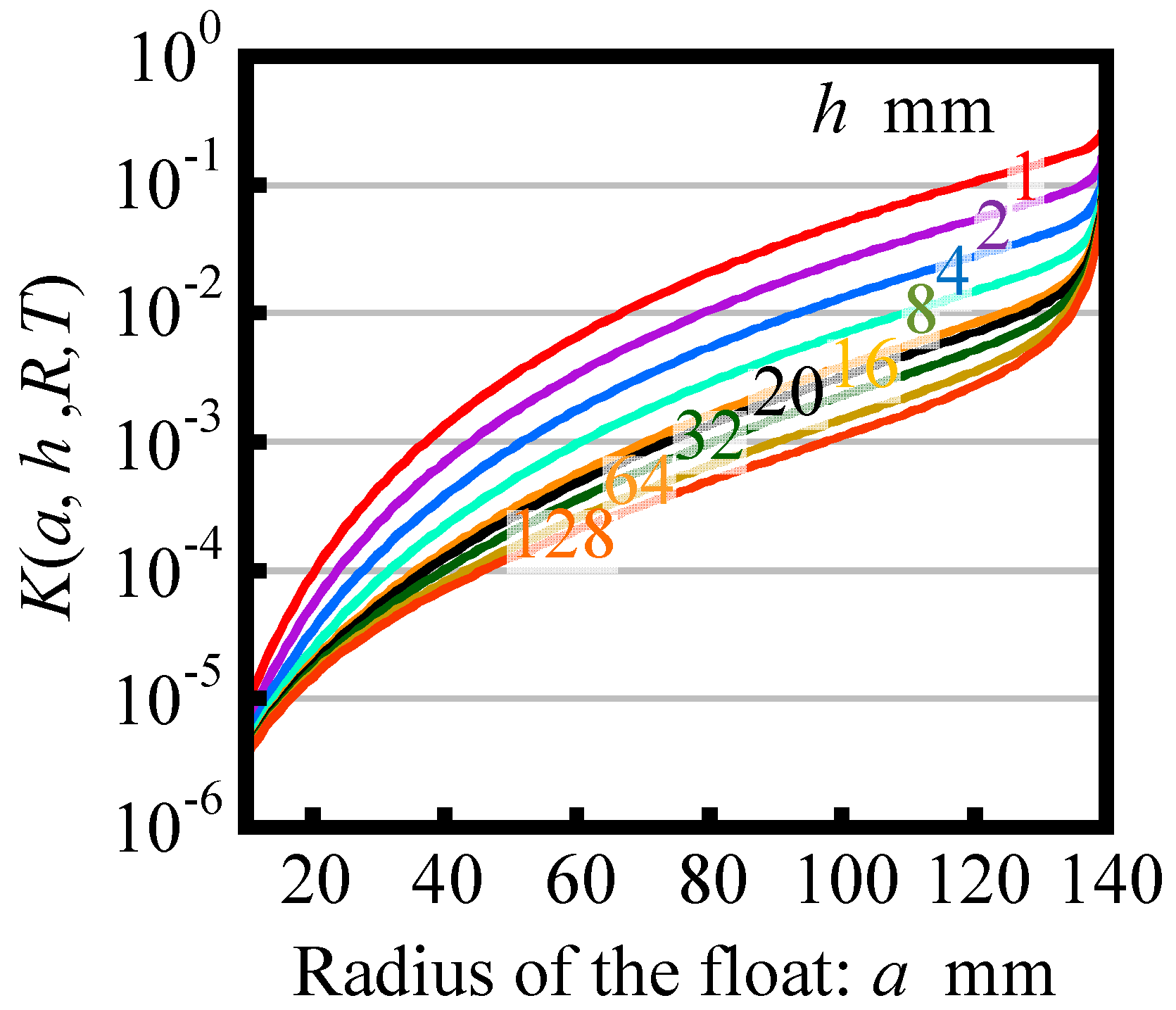
- (1)
- Set the radius of casing R as large as possible with respect to the radius of reference float a.
- (2)
- Design the radius of float a as small as possible.
- (3)
- Set the distance h between the bottom surface of the float and that of the casing as large as possible.
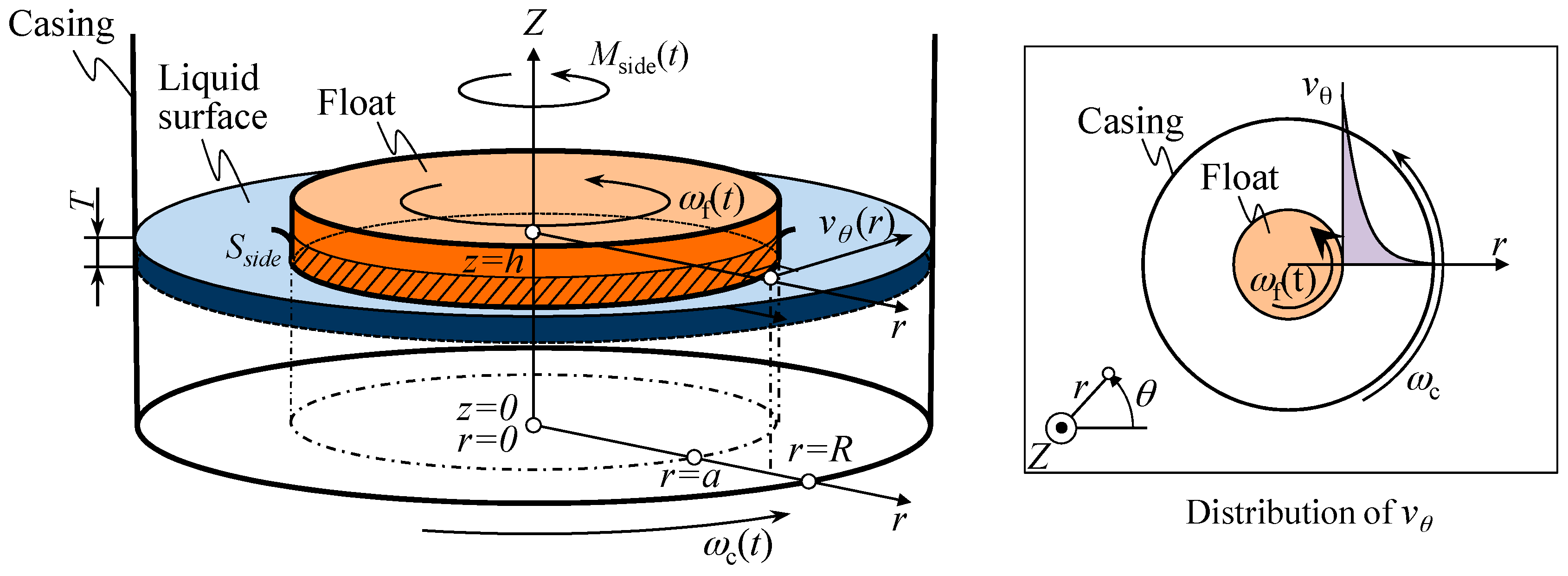
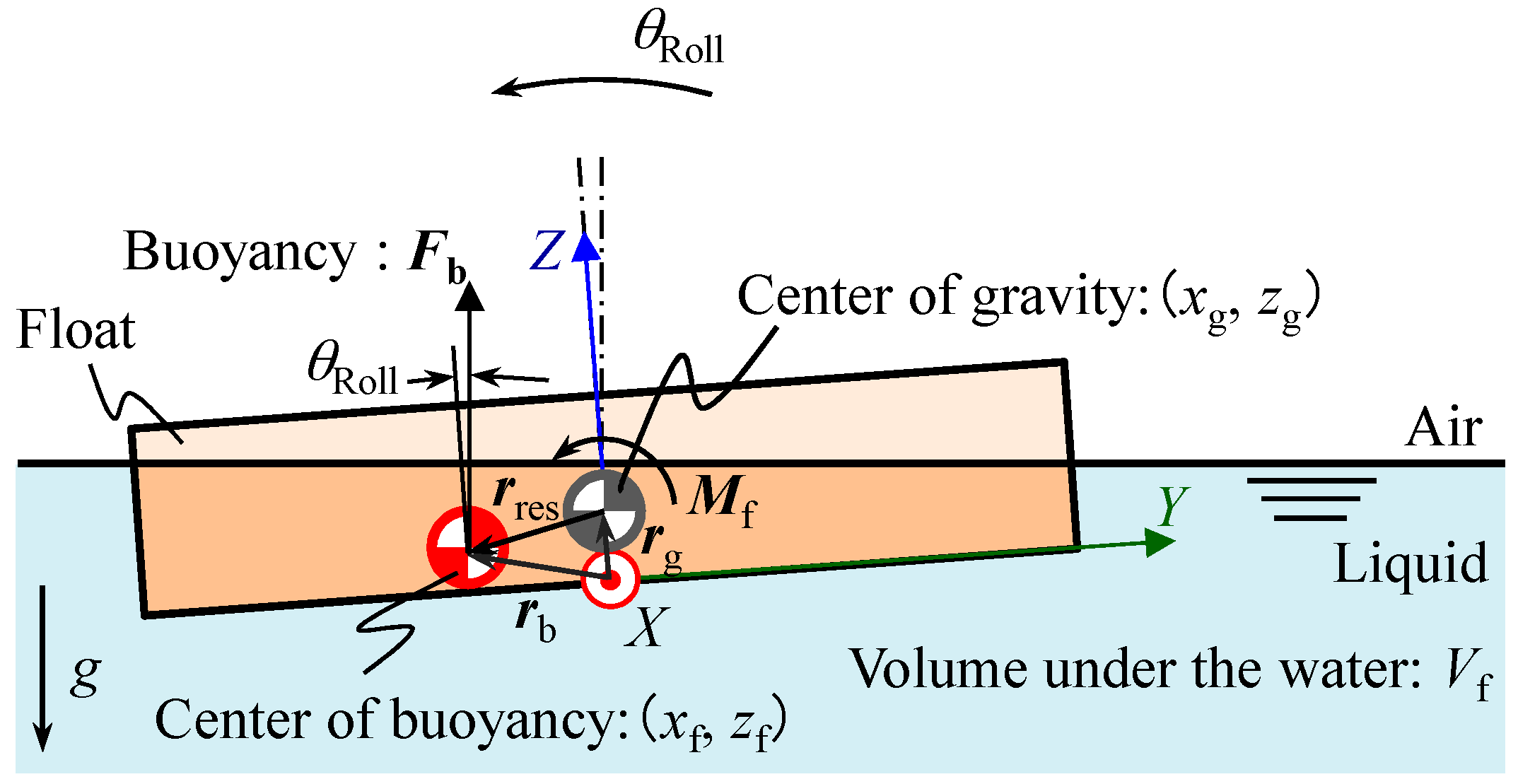
2.3. Modeling of the Pitch and Roll Motions of Inclination Angle Reference Float
3. Design of the Three-Axis Inclination Sensor
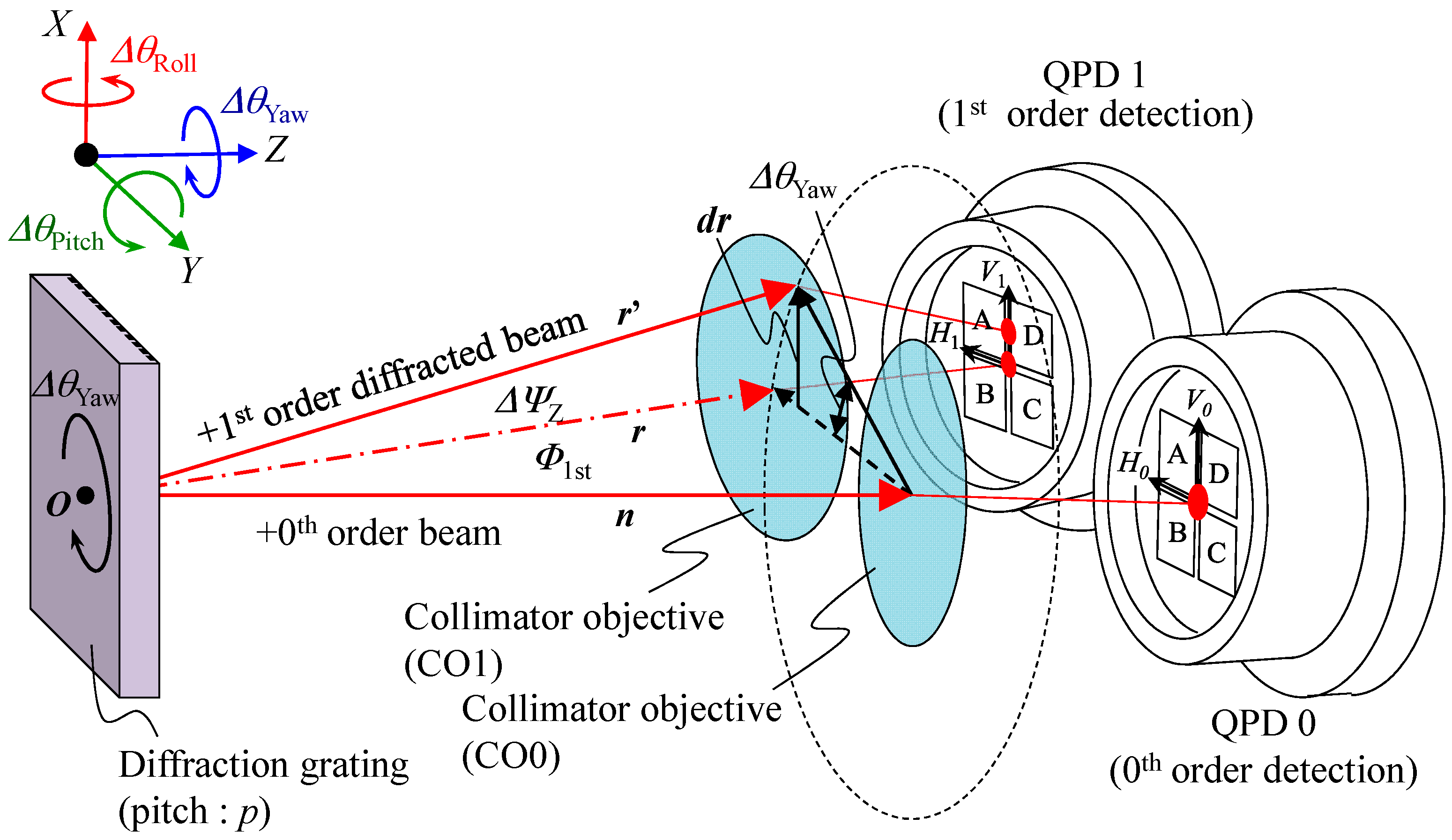
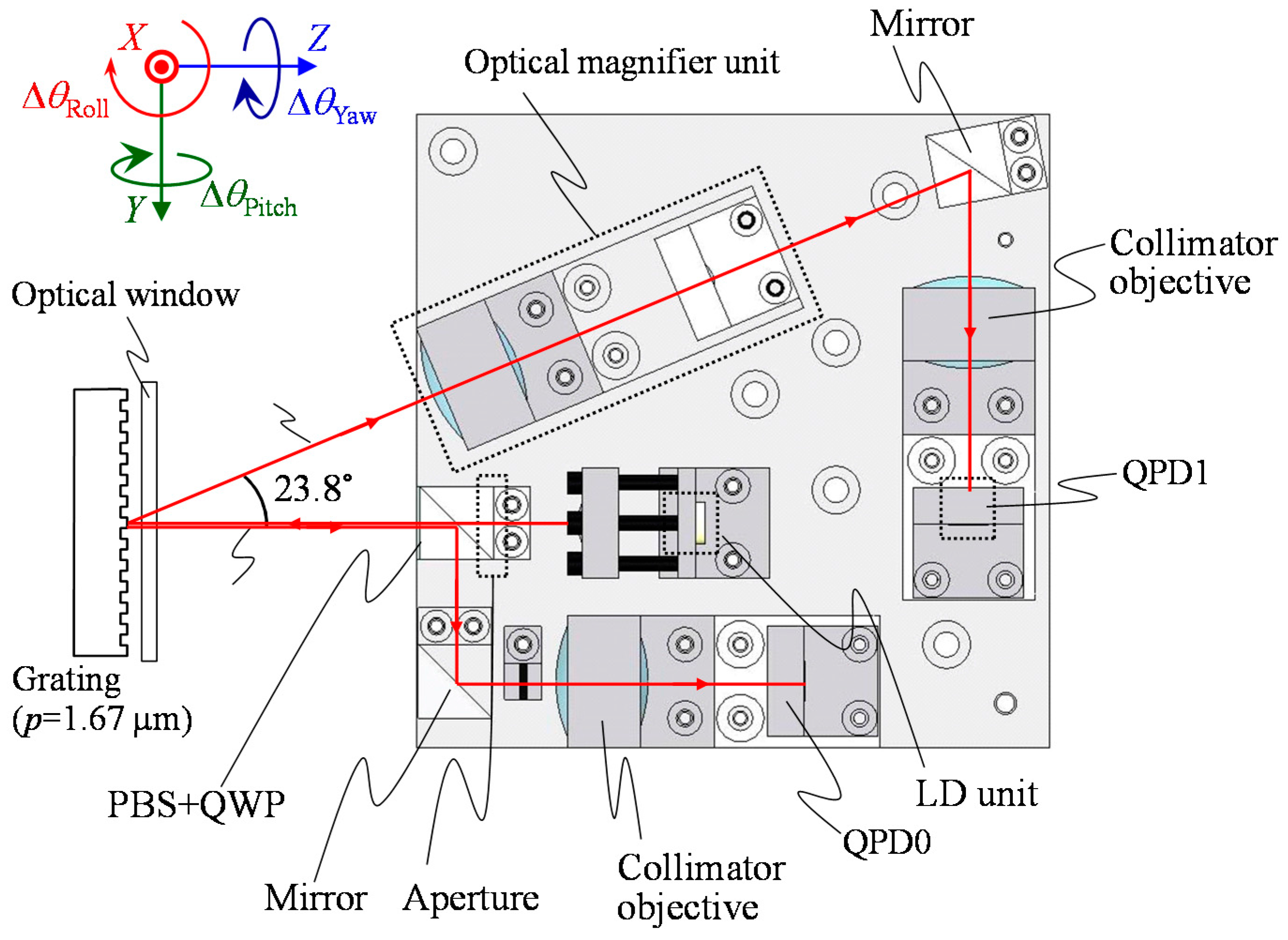
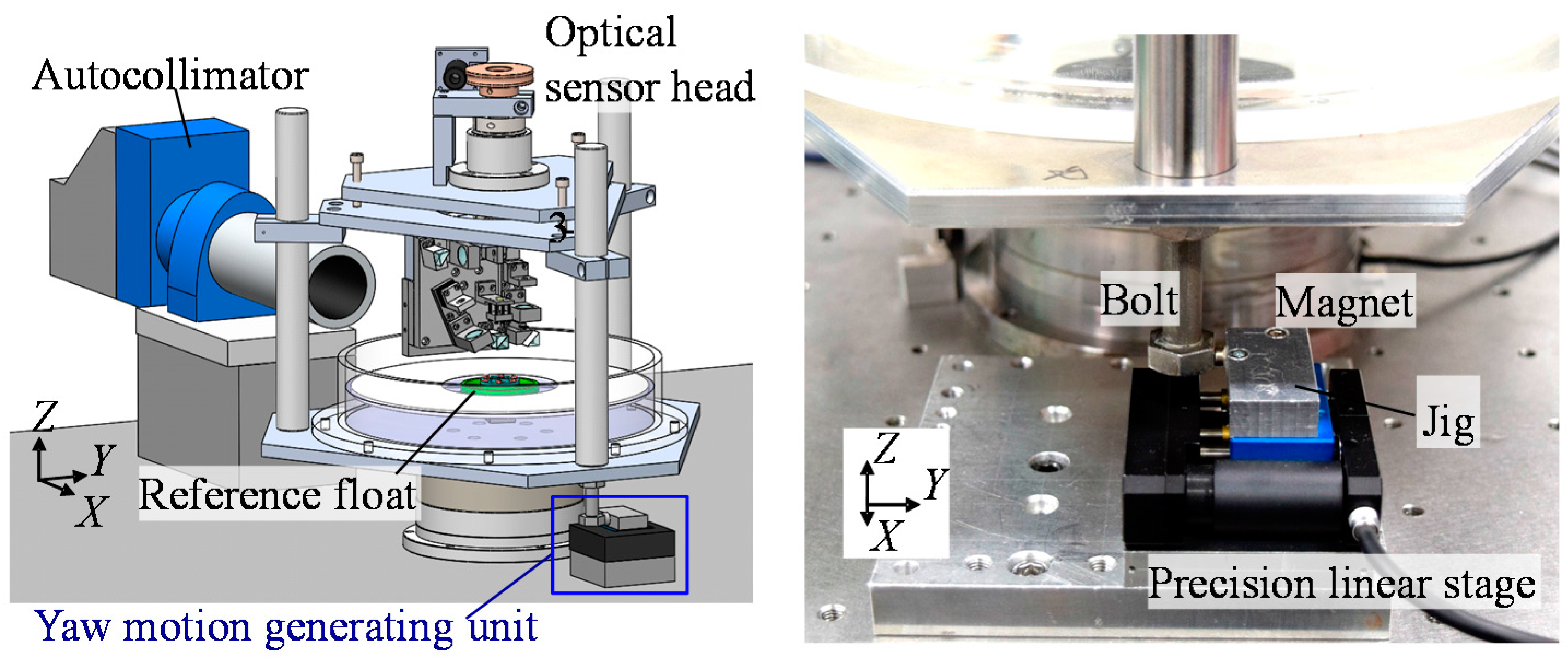
3.1. An Optical Sensor Head
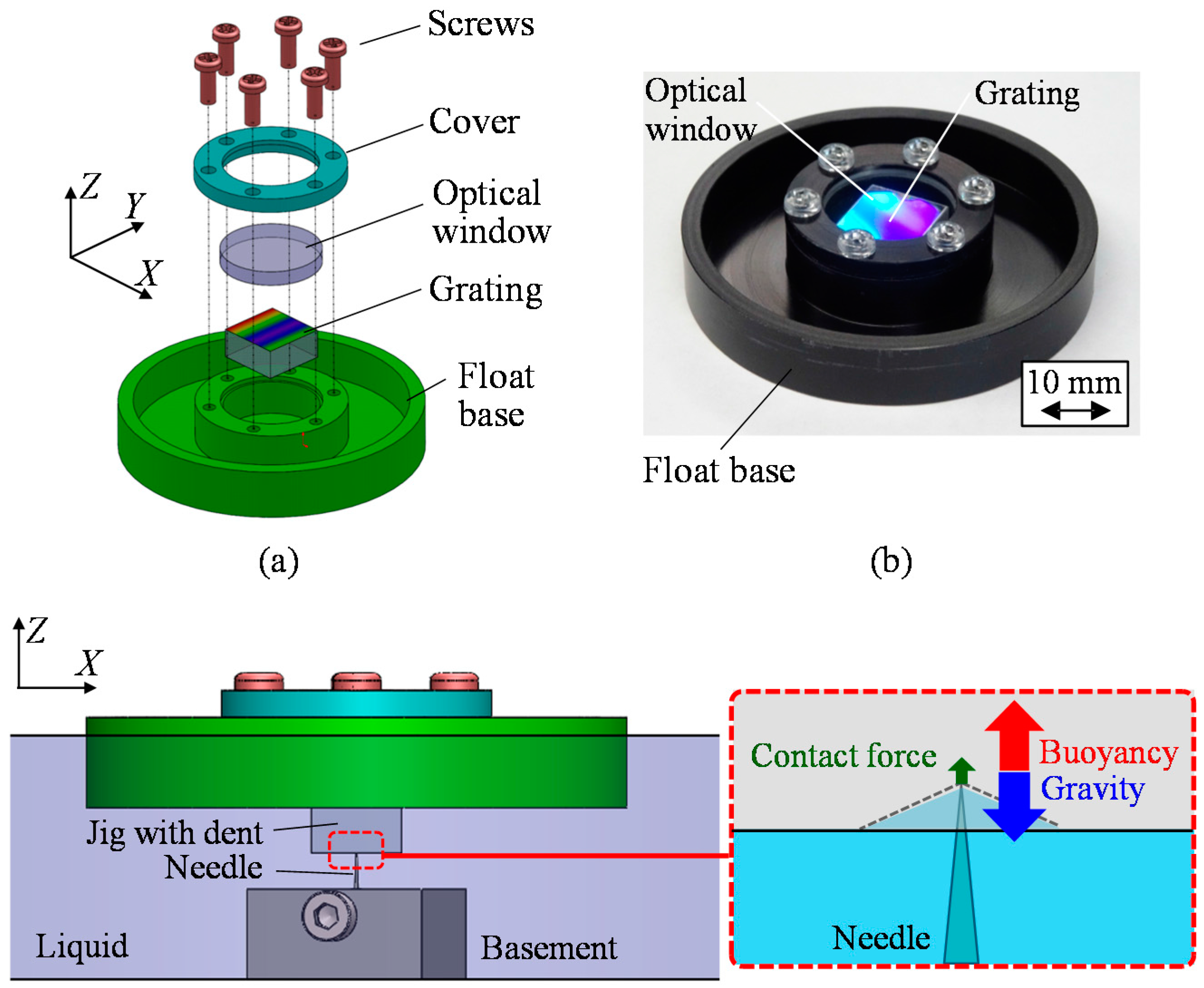
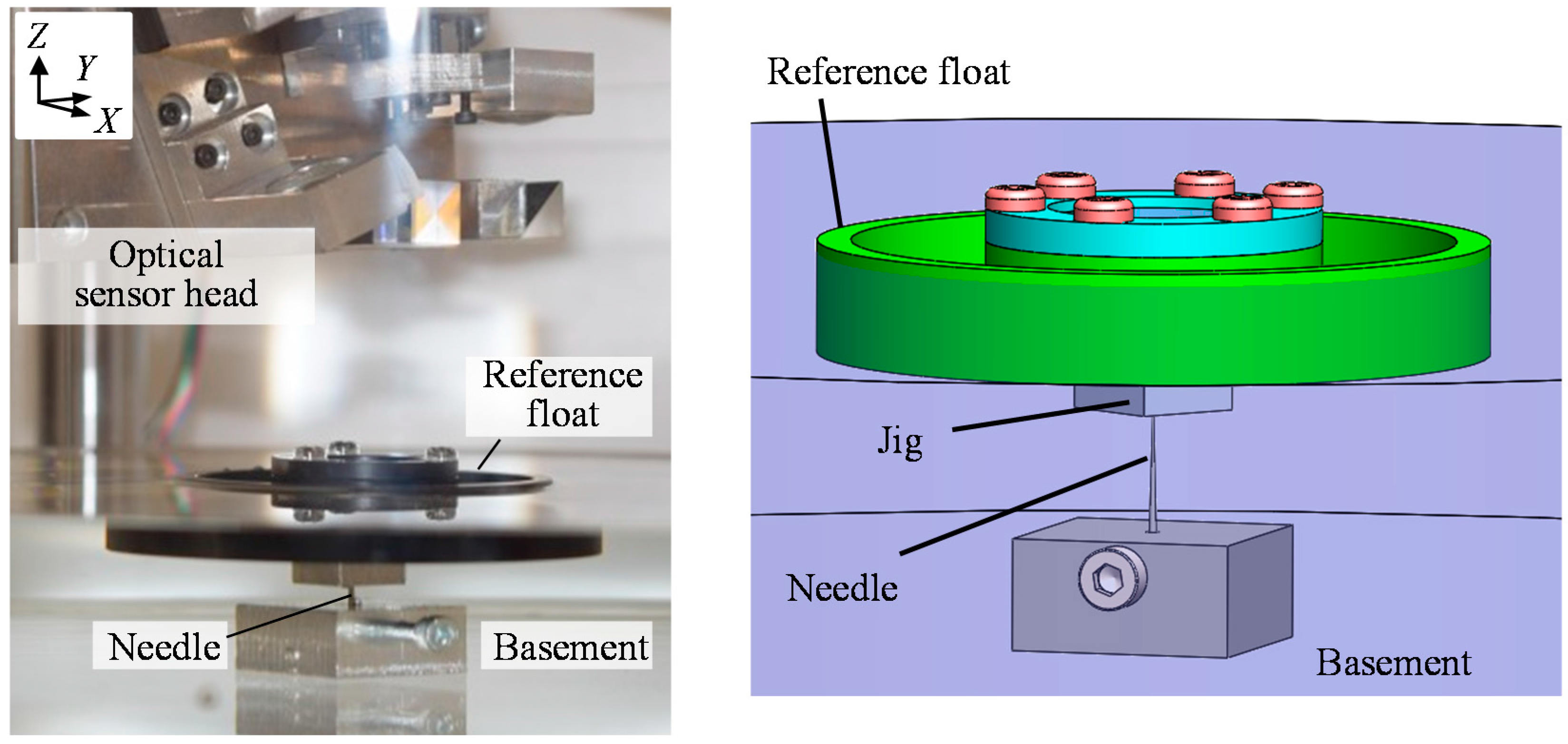
3.2. Reference Float
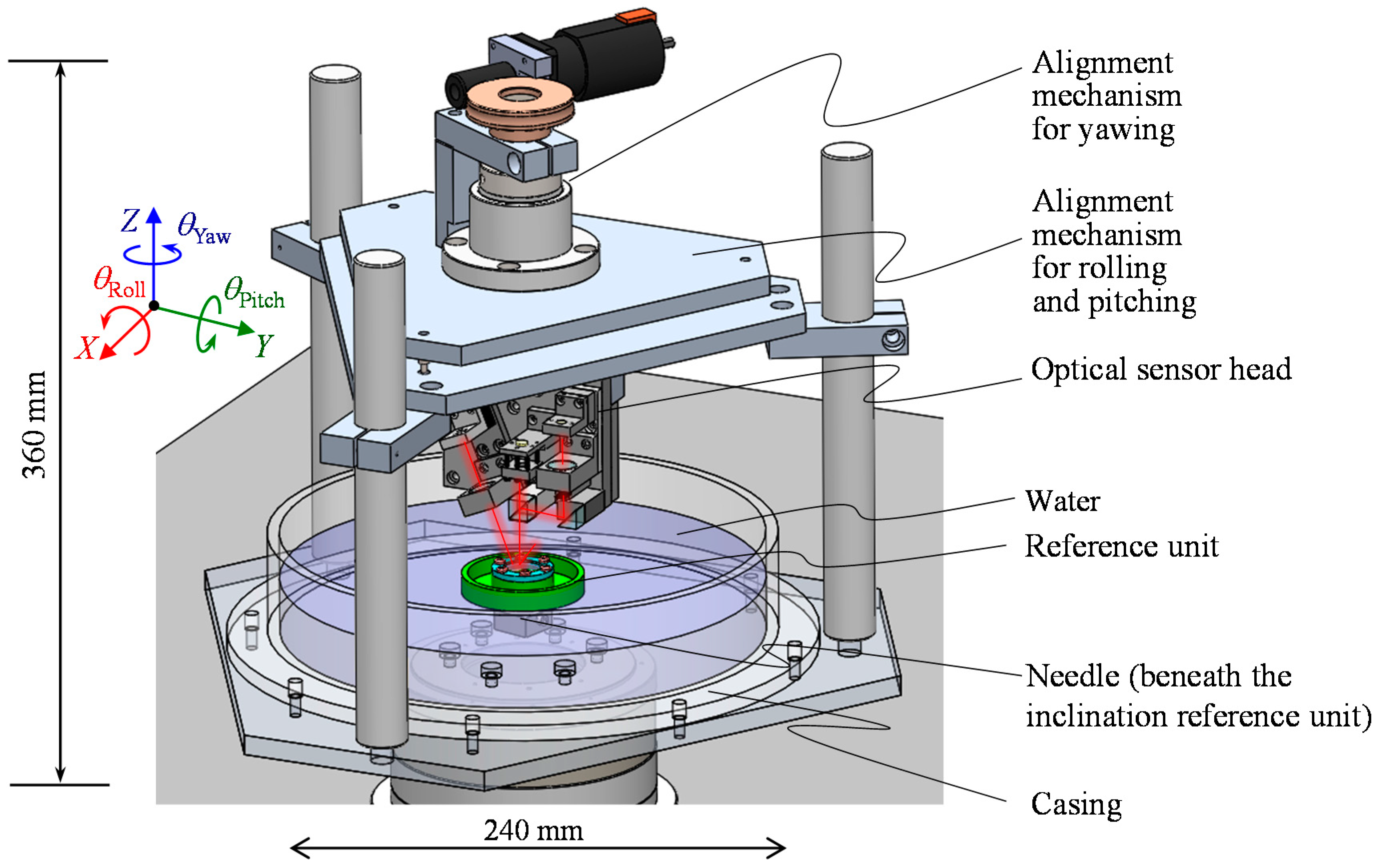
3.3. System Integration
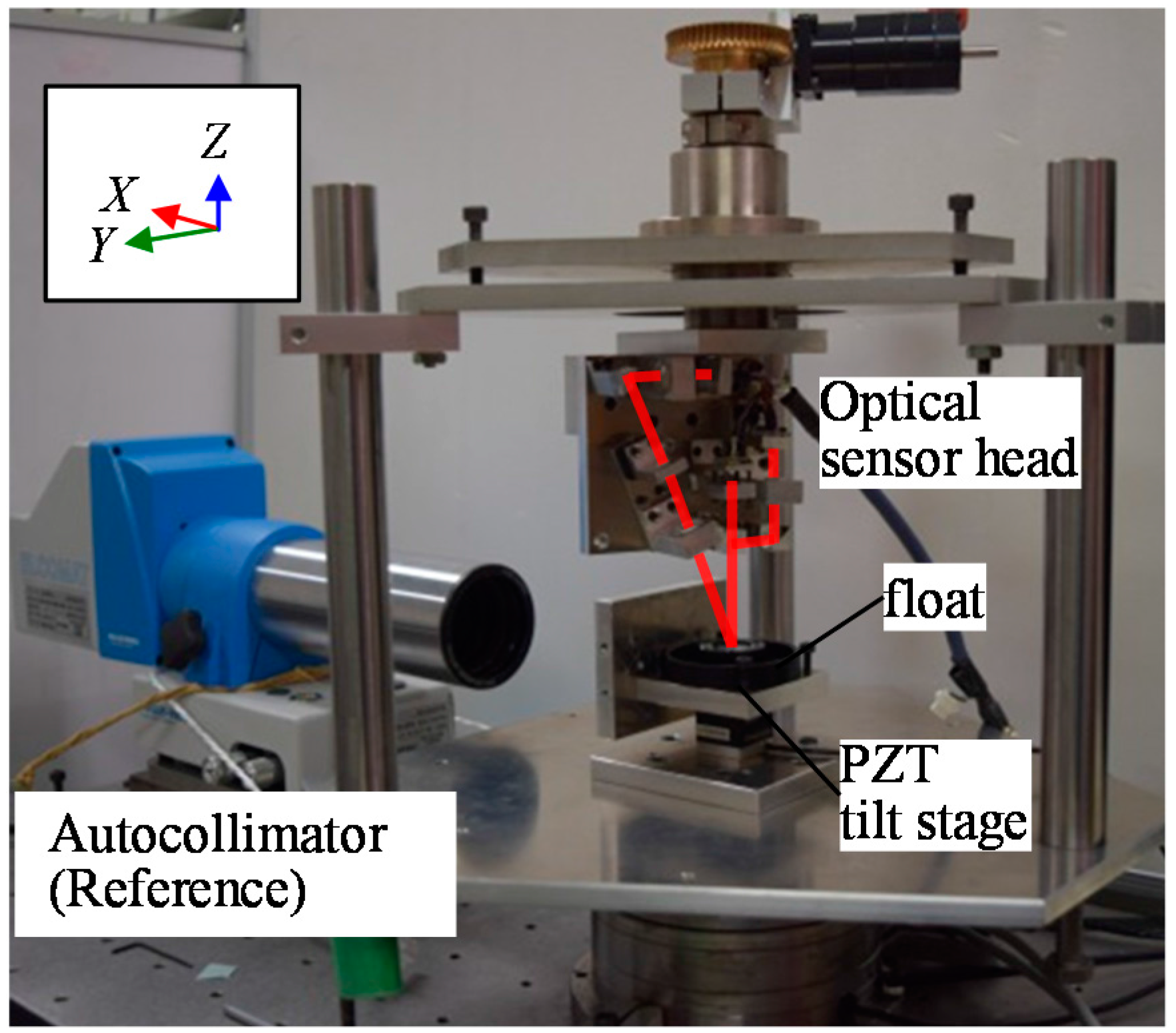
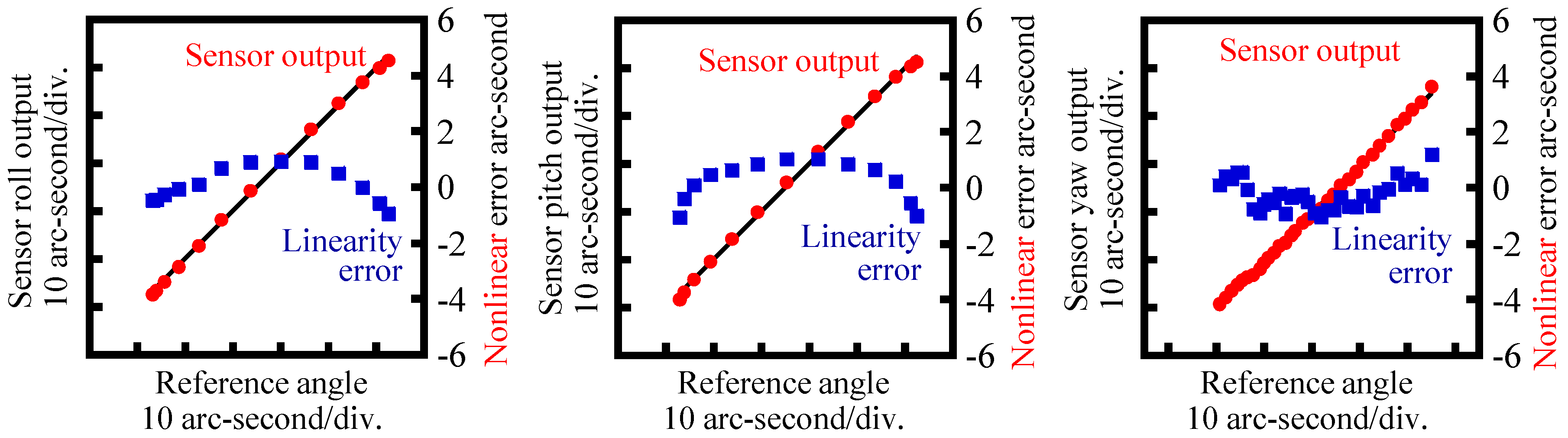
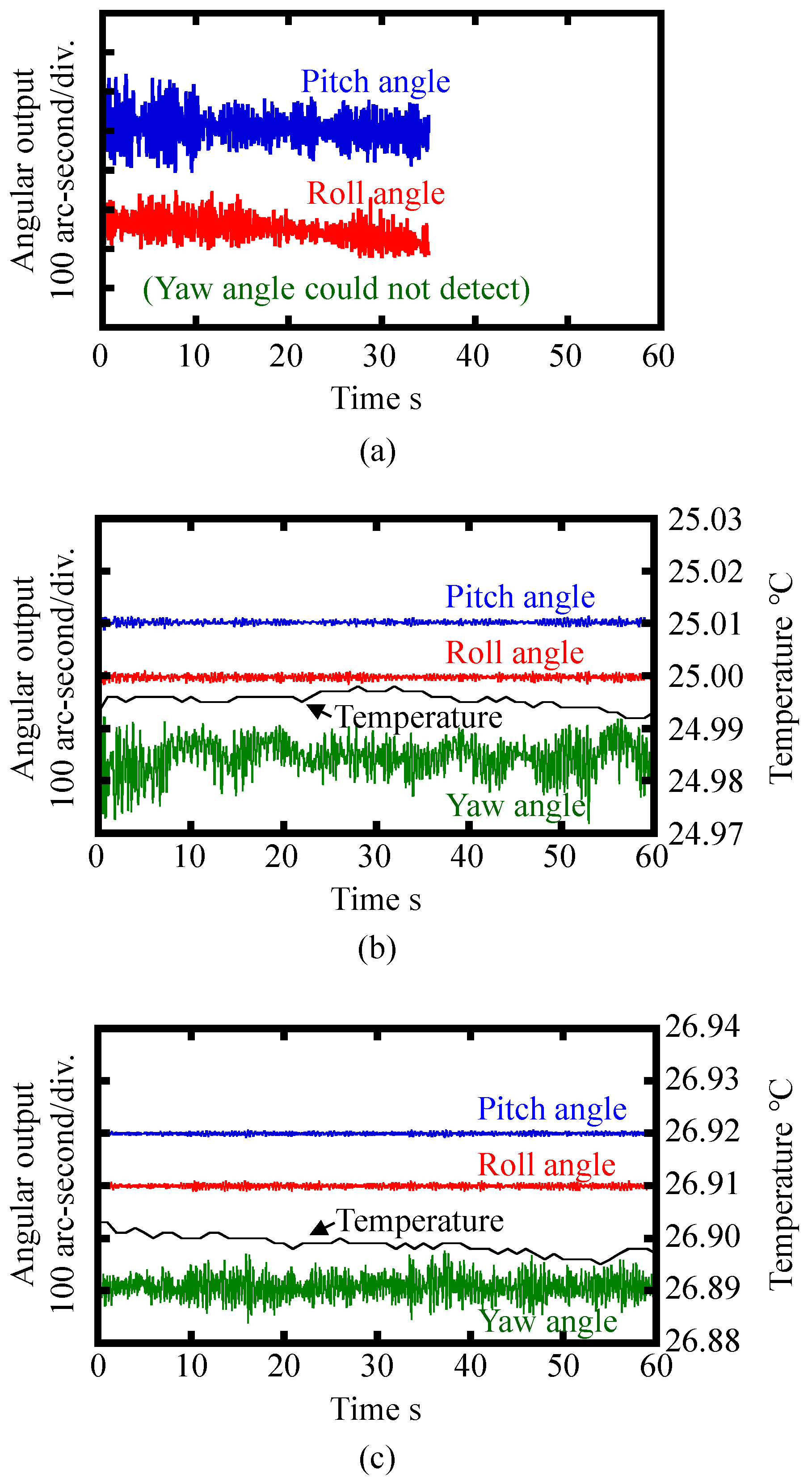
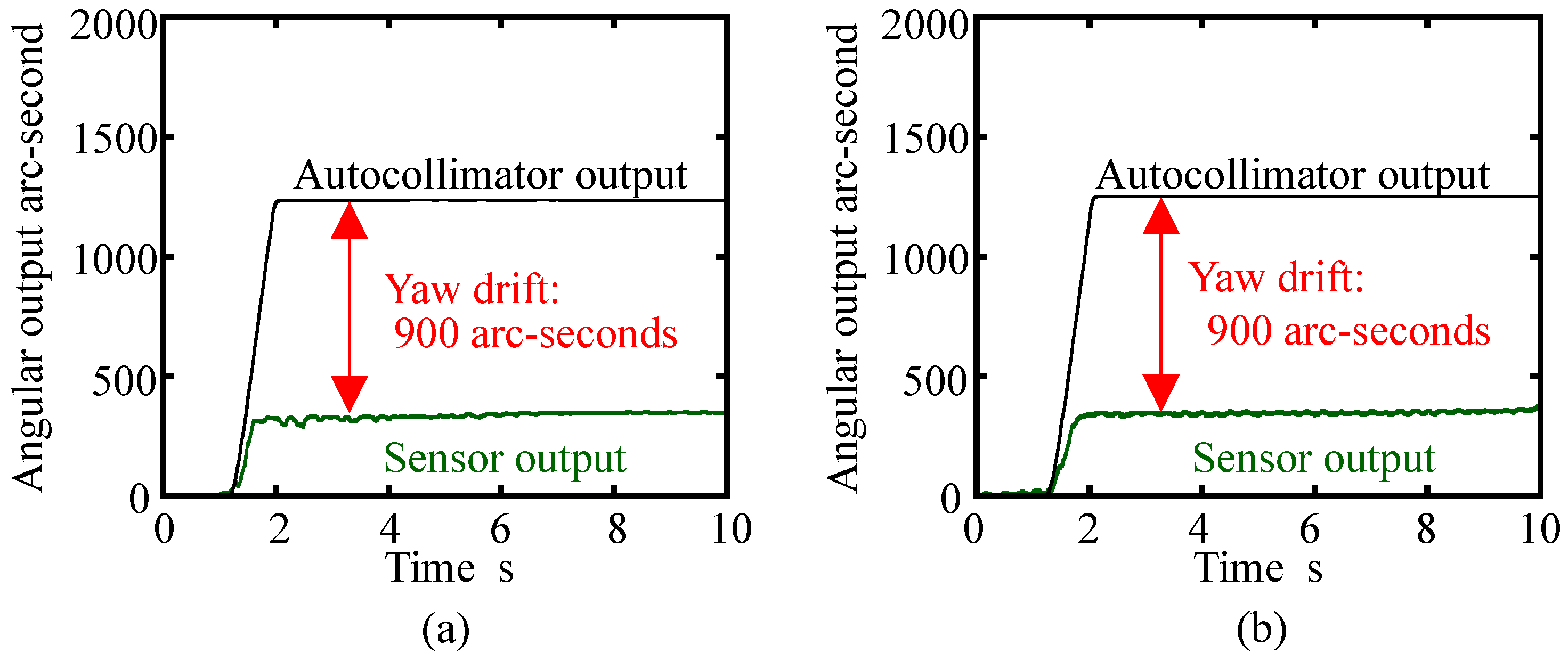
4. Evaluation of the Basic Characteristics of the Developed Three-Axis Inclination Sensor
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schwenke, H.; Knapp, W.; Haitjema, H.; Weckenmann, A.; Schmitt, R.; Delbressine, F. Geometric error measurement and compensation of machines—An update. CIRP Ann. Manuf. Technol. 2008, 57, 660–675. [Google Scholar] [CrossRef]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.L.; Lu, X.D.; Knapp, W.; Weckenmann, A.; Estler, W.T.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. Manuf. Technol. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Gao, W. Precision Nanometrology—Sensors and Measuring Systems for Nanomanufacturing; Springer: London, UK, 2010. [Google Scholar]
- Bryan, J.B. The Abbe Principle Revisited: An Updated Interpretation. Precis. Eng. 1979, 1, 129–132. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 230–1:2012 Test Code for Machine Tools—Part 1: Geometric Accuracy of Machines Operating under No-Load or Quasi-Static Conditions; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Möller-Werdel Optical GmbH “Electric Autocollimators” Data Sheet. Available online: http://www.moeller- wedel-optical.com (accessed on 8 December 2017).
- Gao, W.; Ohnuma, H.; Shimizu, H.; Kiyono, S. A Precision Angle Sensor Using a Multi-Cell Photodiode Array. CIRP Ann. Manuf. Technol. 2004, 53, 425–428. [Google Scholar] [CrossRef]
- Zhang, J.H.; Menq, C.H. A Linear/Angular Interferometer Capable of Measuring Large Angular Motion. Meas. Sci. Technol. 1999, 10, 1247–1253. [Google Scholar] [CrossRef]
- Gao, W.; Arai, Y.; Shibuya, A.; Kiyono, S.; Park, C.H. Measurement of multi-degree-of-freedom error motions of a precision linear air-bearing stage. Precis. Eng. 2006, 30, 96–103. [Google Scholar] [CrossRef]
- Tan, S.L.; Shimizu, Y.; Meguro, T.; Ito, S.; Gao, W. Design of a Laser Autocollimator-based Optical Sensor with a Rangefinder for Error Correction of Precision Slide Guideways. Int. J. Precis. Eng. Manuf. 2015, 16, 423–431. [Google Scholar] [CrossRef]
- Chow, W.W.; Gea-Banacloche, J.; Pedrotti, L.M.; Sanders, V.E.; Schleich, W.; Scully, M.O. The ring laser gyro. Rev. Mod. Phys. 1985, 57, 61–104. [Google Scholar] [CrossRef]
- Vali, V.; Shorthill, R.W. Fiber Ring Interferometer. Appl. Opt. 1976, 15, 1099–1100. [Google Scholar] [CrossRef] [PubMed]
- Yazdi, N.; Ayazi, F.; Najafi, K. Micromachined Inertial Sensors. Proc. IEEE 1998, 86, 1640–1659. [Google Scholar] [CrossRef]
- Titterton, D.; Weston, J. Strapdown Inertial Navigation Technology; Institution of Engineering and Technology (IET): Stevenage, UK, 2004. [Google Scholar]
- Barbour, N.M. Inertial Navigation Sensors. NATO RTO 2011, 116, 1–28. [Google Scholar]
- Gao, W.; Saito, Y.; Muto, H.; Arai, Y.; Shimizu, Y. A three-axis autocollimator for detection of angular error motions of a precision stage. CIRP Ann. 2011, 60, 515–518. [Google Scholar] [CrossRef]
- Ennos, A.E.; Virdee, M.S. High accuracy profile measurement of quasi-conical mirror surfaces by laser autocollimation. Precis. Eng. 1982, 4, 5–8. [Google Scholar] [CrossRef]
- Shimizu, Y.; Kataoka, S.; Gao, W. High resolution clinometers for measurement of roll error motion of a precision linear slide. Chin. J. Mech. Eng. 2017. accepted. [Google Scholar]
- LSOC/LSOP Inclinometer, Sherborne Sensors. Available online: http://www.sherbornesensors.com (accessed on 1 July 2016).
- Ueda, H.; Ueno, H.; Itoigawa, K.; Hattori, T. Development of micro capacitive inclination sensor. IEEJ Transa. Sens. Micromach. 2006, 126, 637–642. [Google Scholar] [CrossRef]
- Yotter, R.A.; Baxter, R.R.; Ohno, S.; Hawley, S.D.; Wilson, D.M. On a micromachined fluidic inclinometer. In Proceedings of the 12th International Conference on Solid-State Sensors, Actuators and Microsystems, Boston, MA, USA, 8–12 June 2003; Volume 2, pp. 1279–1282. [Google Scholar]
- Debenham, M.; Dew, G.D. Determining gravitationl deformation of an optical flat by liquid surface interferometry. Precis. Eng. 1980, 2, 93–97. [Google Scholar] [CrossRef]
- Talyvel 6 Electronic Levels, Taylor Hobson. Available online: http://www.taylor-hobson.com/products/alignment-level/electronic-levels-and-clinometers/ (accessed on 17 January 2018).
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge Mathematical Library: Cambridge, UK, 2000. [Google Scholar]
- Temam, R. Navier-Stokes Equations: Theory and Numerical Analysis; AMS-Chelsea Publishing: Providence, RI, USA, 1977. [Google Scholar]
- Atkinson, K.E. An Introduction to Numerical Analysis, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Saito, Y.; Arai, Y.; Gao, W. Investigation of an optical sensor for small tilt angle detection of a precision linear stage. Meas. Sci. Technol. 2010, 21, 054006. [Google Scholar] [CrossRef]
- Hecht, E. Optics; Addison-Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Haitjema, H.; Meijer, J. Evaluation of surface plate flatness measurements. Eur. J. Mech. Environ. Eng. 1993, 38, 165–172. [Google Scholar]

| Component | Parameters | Symbol | Value |
|---|---|---|---|
| Float | Radius | a | 30 mm |
| Draft | T | 8 mm | |
| Moment of inertia about the Z-axis | Iz | 9.02 × 10−4 kg m2 | |
| Casing | Radius | R | 120 mm |
| Water level | h | 80 mm | |
| Fluid | Type | - | Water |
| Viscosity | μ | 0.89 × 10−3 Pa s | |
| Density | ρ | 1.00 × 103 kg/m3 |
| Parameters | Symbol | Value |
|---|---|---|
| Moment of inertia of the float about the X-axis | IX | 5.17 × 10−4 kg m2 |
| Sensitivity coefficient | α | −0.0281 m/rad |
| Gravity | g | 9.80 m/s2 |
| Parameters | Value |
|---|---|
| Light wavelength | 685 nm |
| Aperture diameter | 2 mm |
| Grating period | 1.67 μm |
| Focal length of the collimator objective | 25.4 mm |
| Parameters | Symbol | Value |
|---|---|---|
| Radius | a | 30 mm |
| Thickness | 10 mm | |
| Draft | T | 8.8 mm |
| mass | 24.4 × 10−3 kg | |
| Moment of inertia about the Z-axis | Iz | 9.02 × 10−4 kg m2 |
| Moment of inertia about the X/Y-axis | IX/IY | 5.17 × 10−4 kg m2 |
| Material | - | Polyoxymethylene |
| Density | ρ | 1390 kg/m3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimizu, Y.; Kataoka, S.; Ishikawa, T.; Chen, Y.-L.; Chen, X.; Matsukuma, H.; Gao, W. A Liquid-Surface-Based Three-Axis Inclination Sensor for Measurement of Stage Tilt Motions. Sensors 2018, 18, 398. https://doi.org/10.3390/s18020398
Shimizu Y, Kataoka S, Ishikawa T, Chen Y-L, Chen X, Matsukuma H, Gao W. A Liquid-Surface-Based Three-Axis Inclination Sensor for Measurement of Stage Tilt Motions. Sensors. 2018; 18(2):398. https://doi.org/10.3390/s18020398
Chicago/Turabian StyleShimizu, Yuki, Satoshi Kataoka, Tatsuya Ishikawa, Yuan-Liu Chen, Xiuguo Chen, Hiraku Matsukuma, and Wei Gao. 2018. "A Liquid-Surface-Based Three-Axis Inclination Sensor for Measurement of Stage Tilt Motions" Sensors 18, no. 2: 398. https://doi.org/10.3390/s18020398
APA StyleShimizu, Y., Kataoka, S., Ishikawa, T., Chen, Y.-L., Chen, X., Matsukuma, H., & Gao, W. (2018). A Liquid-Surface-Based Three-Axis Inclination Sensor for Measurement of Stage Tilt Motions. Sensors, 18(2), 398. https://doi.org/10.3390/s18020398







