Single-Photon Tracking for High-Speed Vision †
Abstract
:1. Introduction
2. Materials and Methods
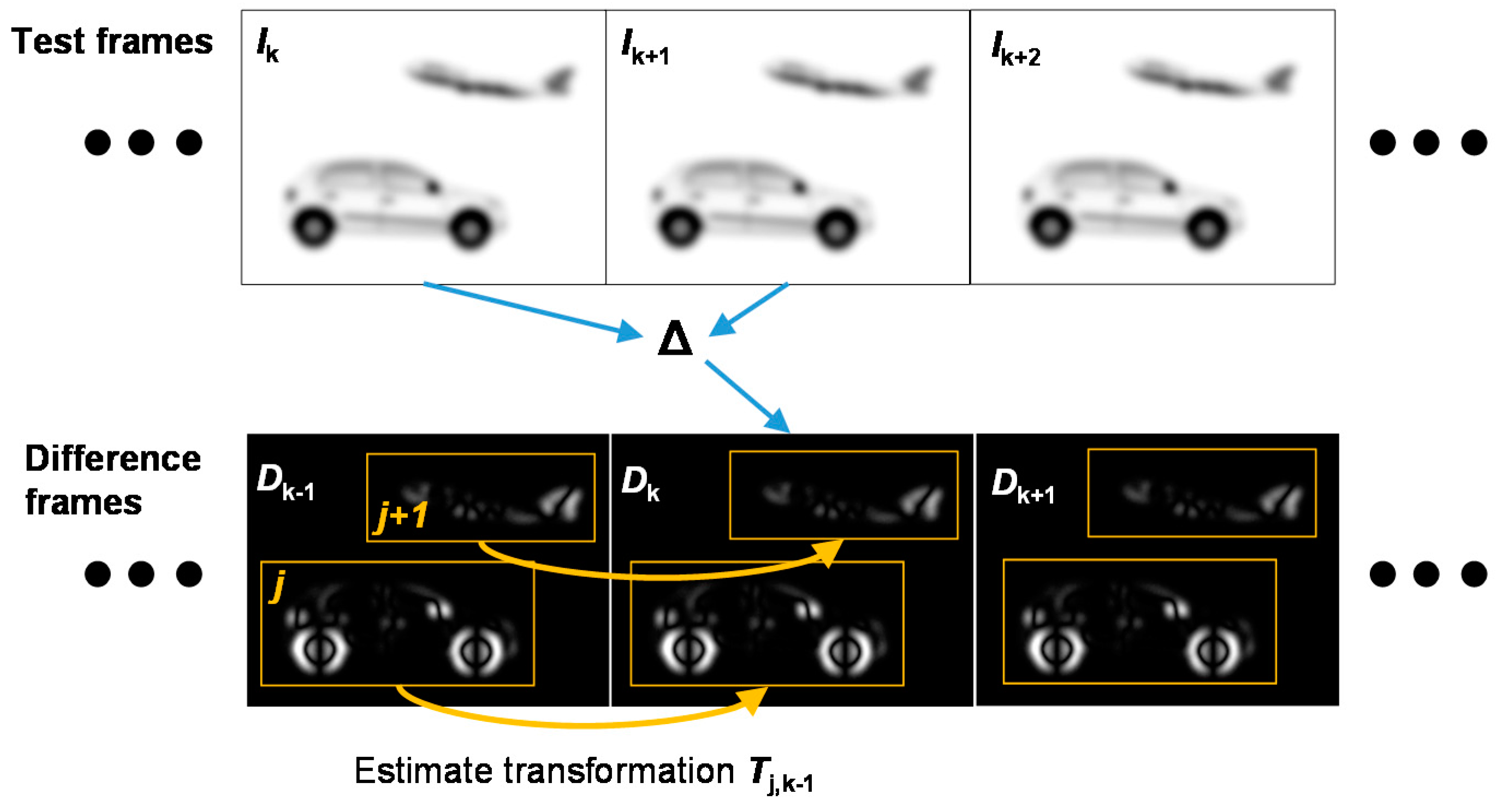
2.1. Motion Detection
2.2. Clustering and Object Tracking
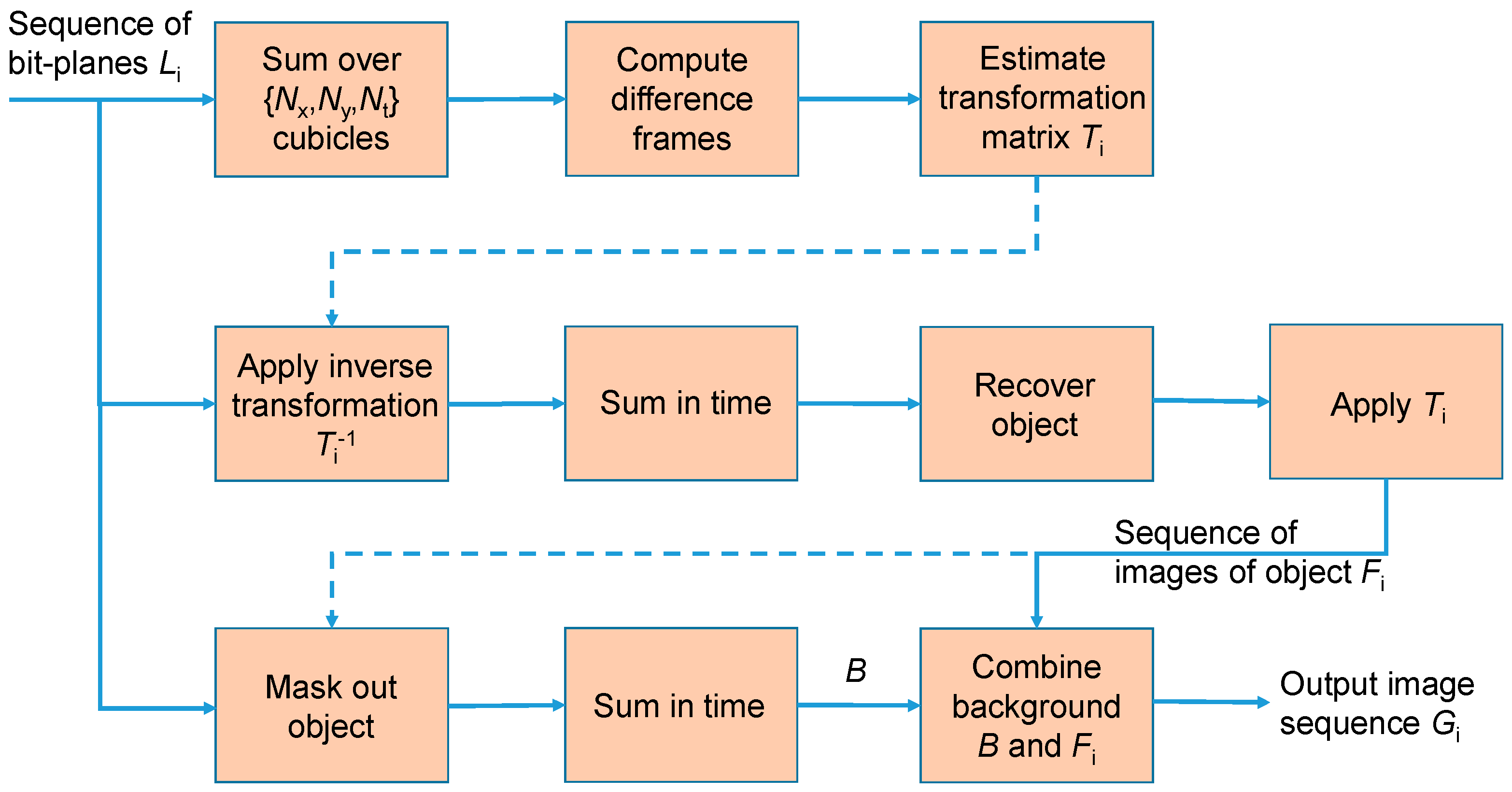
2.3. Reconstruction of Objects and Background
2.4. Practical Implications
3. Results
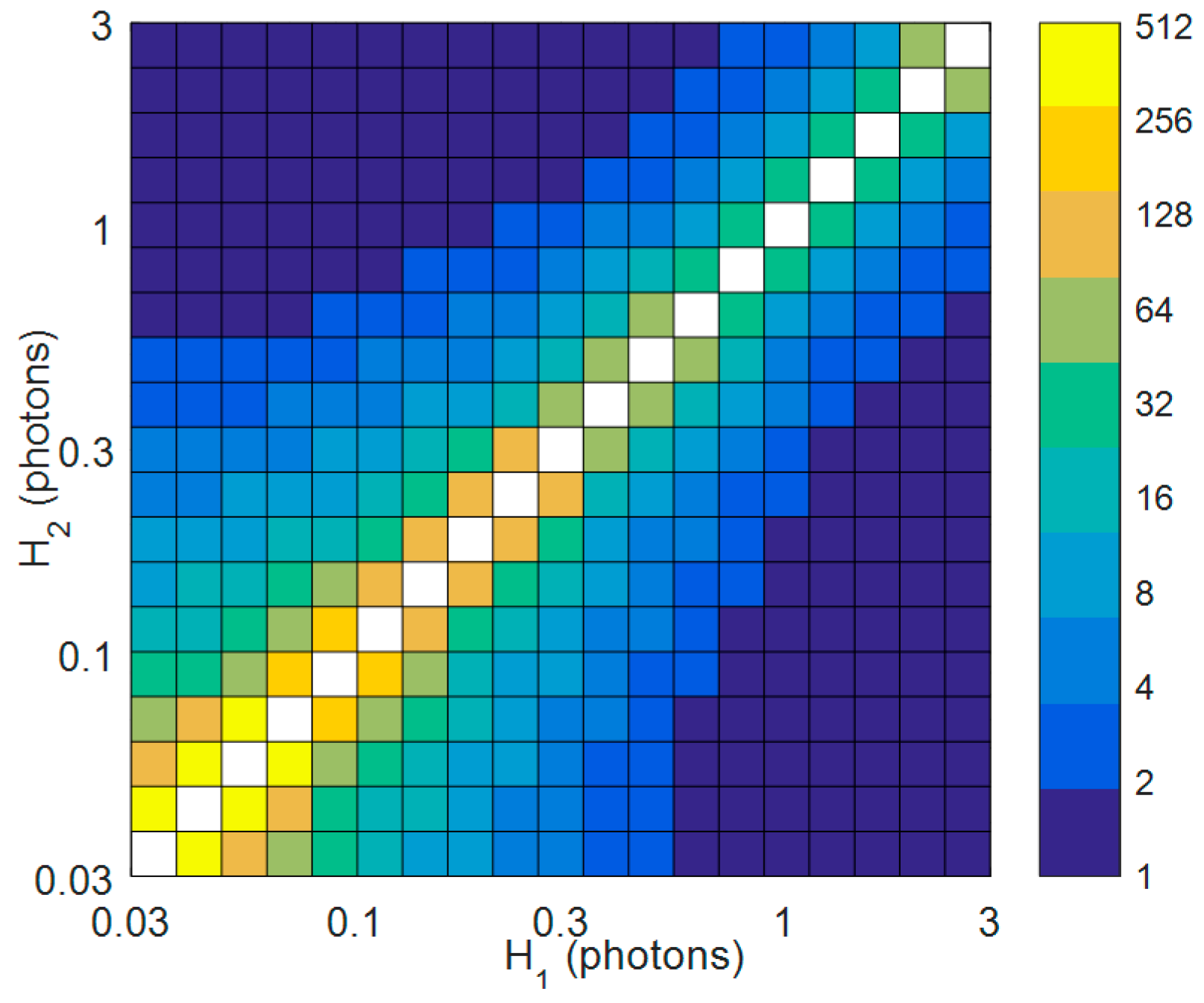
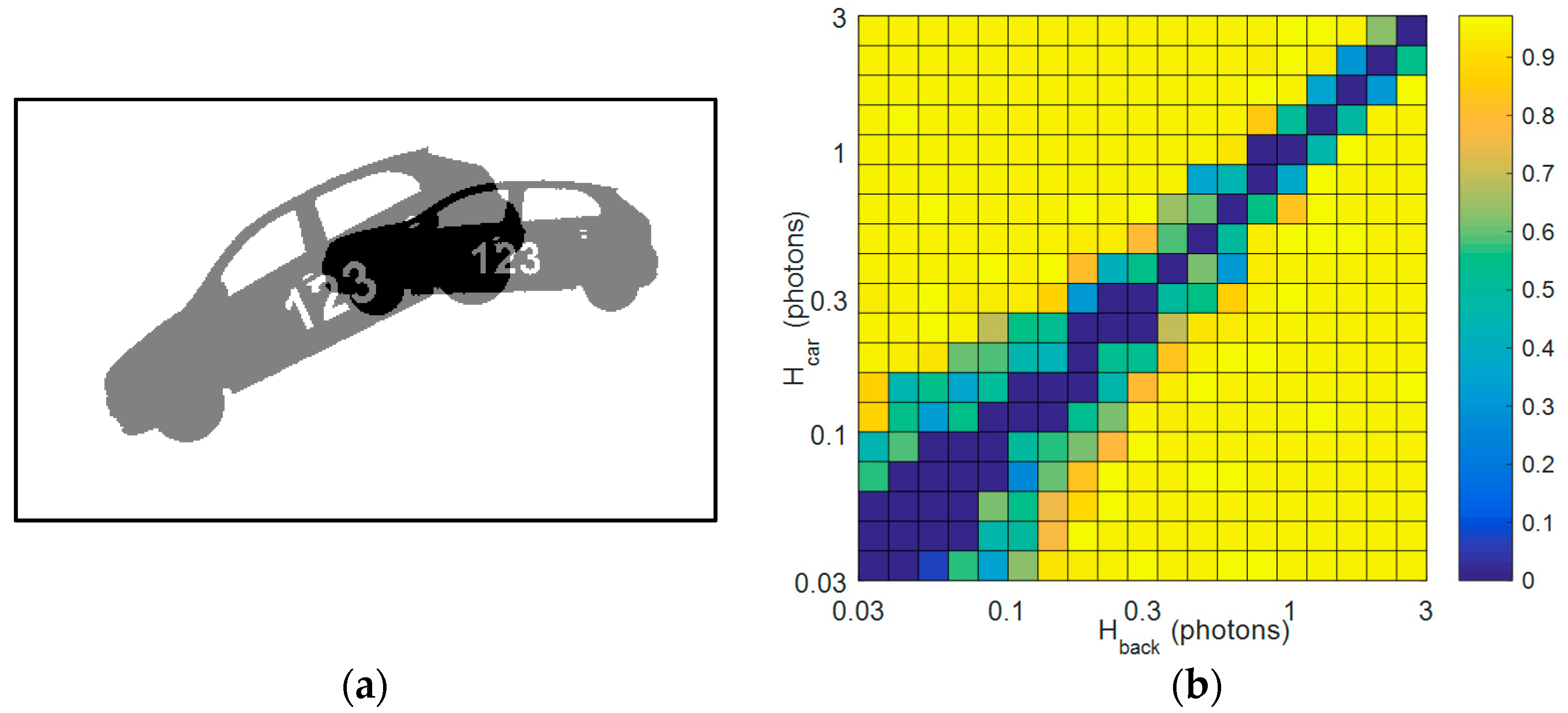
3.1. Simulated Data
3.2. Fan and Car Sequence
3.3. Table Tennis Ball
3.4. Camera Shake Compensation
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A

References
- Fossum, E.R.; Ma, J.; Masoodian, S.; Anzagira, L.; Zizza, R. The quanta image sensor: Every photon counts. Sensors 2016, 16, 1260. [Google Scholar] [CrossRef] [PubMed]
- Masoodian, S.; Ma, J.; Starkey, D.; Wang, T.J.; Yamashita, Y.; Fossum, E.R. Room temperature 1040fps, 1 megapixel photon-counting image sensor with 1.1 um pixel pitch. Proc. SPIE 2017, 10212, 102120H. [Google Scholar]
- Chen, B.; Perona, P. Vision without the Image. Sensors 2016, 16, 484. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.H.; Elgendy, O.A.; Wang, X. Images from Bits: Non-Iterative Image Reconstruction for Quanta Image Sensors. Sensors 2016, 16, 1961. [Google Scholar] [CrossRef] [PubMed]
- Gyongy, I.; Dutton, N.; Parmesan, L.; Davies, A.; Saleeb, R.; Duncan, R.; Rickman, C.; Dalgarno, P.; Henderson, R.K. Bit-plane processing techniques for low-light, high speed imaging with a SPAD-based QIS. In Proceedings of the 2015 International Image Sensor Workshop, Vaals, The Netherlands, 8–11 June 2015. [Google Scholar]
- Gyongy, I.; Davies, A.; Dutton, N.A.; Duncan, R.R.; Rickman, C.; Henderson, R.K.; Dalgarno, P.A. Smart-aggregation imaging for single molecule localisation with SPAD cameras. Sci. Rep. 2016, 6, 37349. [Google Scholar] [CrossRef] [PubMed]
- Fossum, E.R. Modeling the performance of single-bit and multi-bit quanta image sensors. IEEE J. Electron Devices Soc. 2013, 1, 166–174. [Google Scholar] [CrossRef]
- Elgendy, O.A.; Chan, S.H. Optimal Threshold Design for Quanta Image Sensor. arXiv 2017, arXiv:10.1109/TCI.2017.2781185. [Google Scholar]
- Bascle, B.; Blake, A.; Zisserman, A. Motion deblurring and super-resolution from an image sequence. In Proceedings of the 4th ECCV ’96 European Conference on Computer Vision, Cambridge, UK, 15–18 April 1996; pp. 571–582. [Google Scholar]
- Nayar, S.K.; Ben-Ezra, M. Motion-based motion deblurring. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 689–698. [Google Scholar] [CrossRef] [PubMed]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 1981 DARPA Image Understanding Workshop, Washington, DC, USA, 23 April 1981; pp. 121–130. [Google Scholar]
- Barron, J.L.; Fleet, D.J.; Beauchemin, S.S. Performance of optical flow techniques. Int. J. Comput. Vis. 1994, 12, 43–77. [Google Scholar] [CrossRef]
- Aull, B. Geiger-Mode Avalanche Photodiode Arrays Integrated to All-Digital CMOS Circuits. Sensors 2016, 16, 495. [Google Scholar] [CrossRef] [PubMed]
- La Rosa, F.; Virzì, M.C.; Bonaccorso, F.; Branciforte, M. Optical Image Stabilization (OIS). Available online: www.st.com/resource/en/white_paper/ois_white_paper.pdf (accessed on 31 October 2017).
- Gyongy, I.; Al Abbas, T.; Dutton, N.A.; Henderson, R.K. Object Tracking and Reconstruction with a Quanta Image Sensor. In Proceedings of the 2017 International Image Sensor Workshop, Hiroshima, Japan, 30 May–2 June 2017; pp. 242–245. [Google Scholar]
- Agresti, A.; Coull, B.A. Approximate is better than “exact” for interval estimation of binomial proportions. Am. Stat. 1998, 52, 119–126. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Imregtform—Mathworks. Available online: https://uk.mathworks.com/help/images/ref/imregtform.html (accessed on 31 October 2017).
- Myler, H.R. Fundamentals of Machine Vision; SPIE Press: Bellingham, WA, USA, 1999; p. 87. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Dutton, N.A.; Parmesan, L.; Holmes, A.J.; Grant, L.A.; Henderson, R.K. 320 × 240 oversampled digital single photon counting image sensor. In Proceedings of the 2014 Symposium on VLSI Circuits Digest of Technical Papers, Honolulu, HI, USA, 10–13 June 2014. [Google Scholar]
- DBSCAN Algorithm-Yarpiz. Available online: http://yarpiz.com/255/ypml110-dbscan-clustering (accessed on 31 October 2017).
- Hseih, B.C.; Khawam, S.; Ioannis, N.; Muir, M.; Le, K.; Siddiqui, H.; Goma, S.; Lin, R.J.; Chang, C.H.; Liu, C.; et al. A 3D Stacked Programmable Image Processing Engine in a 40 nm Logic Process with a Detector Array in a 45nm CMOS Image Sensor Technologies. In Proceedings of the 2017 International Image Sensor Workshop, Hiroshima, Japan, 30 May–2 June 2017; pp. 4–7. [Google Scholar]
- Nose, A.; Yamazaki, T.; Katayama, H.; Uehara, S.; Kobayashi, M.; Shida, S.; Odahara, M.; Takamiya, K.; Hisamatsu, Y.; Matsumoto, S.; et al. A 1ms High-Speed Vision Chip with 3D-Stacked 140GOPS Column-Parallel PEs for Diverse Sensing Applications. In Proceedings of the 2017 International Image Sensor Workshop, Hiroshima, Japan, 30 May–2 June 2017; pp. 360–363. [Google Scholar]
- Takahashi, T.; Kaji, Y.; Tsukuda, Y.; Futami, S.; Hanzawa, K.; Yamauchi, T.; Wong, P.W.; Brady, F.; Holden, P.; Ayers, T.; et al. A 4.1 Mpix 280fps stacked CMOS image sensor with array-parallel ADC architecture for region control. In Proceedings of the 2017 Symposium on VLSI Circuits, Kyoto, Japan, 5–8 June 2017; pp. C244–C245. [Google Scholar]
- Masoodian, S.; Ma, J.; Starkey, D.; Yamashita, Y.; Fossum, E.R. A 1Mjot 1040fps 0.22 e-rms Stacked BSI Quanta Image Sensor with Cluster-Parallel Readout. In Proceedings of the 2017 International Image Sensor Workshop, Hiroshima, Japan, 30 May–2 June 2017; pp. 230–233. [Google Scholar]
- Inside iPhone 8: Apple’s A11 Bionic Introduces 5 New Custom Silicon Engines. Available online: http://appleinsider.com/articles/17/09/23/inside-iphone-8-apples-a11-bionic-introduces-5-new-custom-silicon-engines (accessed on 31 October 2017).







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gyongy, I.; Dutton, N.A.W.; Henderson, R.K. Single-Photon Tracking for High-Speed Vision. Sensors 2018, 18, 323. https://doi.org/10.3390/s18020323
Gyongy I, Dutton NAW, Henderson RK. Single-Photon Tracking for High-Speed Vision. Sensors. 2018; 18(2):323. https://doi.org/10.3390/s18020323
Chicago/Turabian StyleGyongy, Istvan, Neale A.W. Dutton, and Robert K. Henderson. 2018. "Single-Photon Tracking for High-Speed Vision" Sensors 18, no. 2: 323. https://doi.org/10.3390/s18020323
APA StyleGyongy, I., Dutton, N. A. W., & Henderson, R. K. (2018). Single-Photon Tracking for High-Speed Vision. Sensors, 18(2), 323. https://doi.org/10.3390/s18020323




