Abstract
Despite the importance of computing soil pore water electrical conductivity (σp) from soil bulk electrical conductivity (σb) in ecological and hydrological applications, a good method of doing so remains elusive. The Hilhorst concept offers a theoretical model describing a linear relationship between σb, and relative dielectric permittivity (εb) in moist soil. The reciprocal of pore water electrical conductivity (1/σp) appears as a slope of the Hilhorst model and the ordinary least squares (OLS) of this linear relationship yields a single estimate () of the regression parameter vector (σp) for the entire data. This study was carried out on a sandy soil under laboratory conditions. We used a time-varying dynamic linear model (DLM) and the Kalman filter (Kf) to estimate the evolution of σp over time. A time series of the relative dielectric permittivity (εb) and σb of the soil were measured using time domain reflectometry (TDR) at different depths in a soil column to transform the deterministic Hilhorst model into a stochastic model and evaluate the linear relationship between εb and σb in order to capture deterministic changes to (1/σp). Applying the Hilhorst model, strong positive autocorrelations between the residuals could be found. By using and modifying them to DLM, the observed and modeled data of εb obtain a much better match and the estimated evolution of σp converged to its true value. Moreover, the offset of this linear relation varies for each soil depth.
1. Introduction
Salinization reduces crop productivity, decreases profitability, and causes land scarcity [1]. Thus, it decreases the world’s agricultural productivity and causes a global income loss of US$ 12 billion per year [2]. Extracting soil solution by suction or using saturated paste conductivity measurements are the common methods to determine the electrical conductivity of soil pore water (σp) as an indicator of the soil salinity; however, they are labour- and cost intensive. There is no evidence that all ions are collected in the sample extract [3]. For soil salinity assessment, it is important to look for practical methods that evaluate the soil salinity state temporally and spatially. These methods help to correctly evaluate soil salinity evolution and reasonably predict its values [4,5,6,7,8,9]. In recent times, soil electromagnetic sensors have been used to estimate bulk electrical conductivity (σb). Then, methods are required to transform σb to σp [3,6,10].
According to Wyllie and Southwick [11], three conductance pathways, see Figure 1, contribute to the σb of a soil: (i) solid phase pathway through soil particles that are continuous contact with one another, (ii) liquid phase pathway through dissolved ions in the soil water inhabiting the large pores, and (iii) a liquid–solid interphase pathway through exchangeable cations like surfaces of clay minerals. Electrical conductivity (EC) in the liquid phase (σp) is used to estimate the soil salinity, a high EC refers to a high concentration of soluble salts, and vice versa. The σp could be estimated if the relationship between σp, σb, and water content (θ) is fixed [12,13,14]. The discovered linear correlation between the soil relative dielectric permittivity (εb) and σb values [15] enabled Hilhorst [3] to convert σb to σp by using a theoretical model. According to Hilhorst, σp can be determined from the equation:
where σp is the pore water electrical conductivity (dS/m); εp is the relative dielectric permittivity of the soil pore water (dimensionless), εb is the relative dielectric permittivity of the bulk soil (dimensionless, relative dielectric permittivity is dimensionless since it is a ratio of permittivity of medium to the permittivity of free space), σb is the bulk electrical conductivity (dS/m), εσb=0 is the relative dielectric permittivity of the soil when the bulk electrical conductivity is 0 (dimensionless). However, εσb=0 appears as an offset of the linear relationship between εb and σb. The Hilhorst model [3] concluded that his method could be validated for water contents between 0.10 and saturation and for a conductivity of the pore water up to 0.3 S m−1. He found that εσb=0 depends on soil type and varies between 1.9 and 7.6. He recommended using 4.1 as a generic offset. Many studies applied the deterministic Hilhorst model [3] in their experiments to convert σb into σp but they did not use the same offset to achieve their study objective. For example, some studies concluded their work by using different offsets (within the range of 3.67 to 6.38) according to the soil type [10]. The producer of capacitance soil moisture sensors 5TE [16] recommends the use of an offset εσb=0 of 6 while another study found that an offset εσb=0 = 6 does not present a good linear relationship between εb and σb [17]. The WET sensor (Delta-T Device Ltd., Cambridge, UK) is a frequency domain dielectric sensor. It has been designed to estimate the σp based on the Hilhorst model [3] and incorporate the standard offset εσb=0 = 4.1 of the model in the software of the device. By applying the Hilhorst model [3] in a saline gypsum-influenced soil, the accuracy of the WET sensor in predicting σp was very poor when using the offset model =4.1 [18]. Another study used a WET sensor for experimental measurements in the laboratory using four different soils (sand, sandy loam, loam, and clay) [9] and found that the offset depends on both soil type and σp, where it becomes larger for larger σp. Moreover, oscillator frequency and sensor circuitry could affect the estimation of εb and water content () [19].
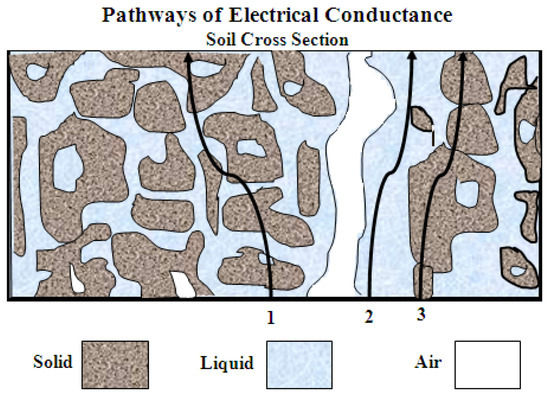
Figure 1.
Three conductance pathways for the σb measurements, inspired by Wyllie and Southwick [11].
There are three elementary causes responsible for why the deterministic system and control theories do not produce a totally sufficient means of performing this analysis and design:
- (i)
- many effects are left unknown since the objective of the model is to represent the main modes of system response,
- (ii)
- deterministic models are driven not by only our own control inputs but also disturbances which we can neither control nor model deterministically, and
- (iii)
- sensors do not offer exact readings of chosen quantities but present their own system dynamics and distortions as well and these devices are noise corrupted [20]. Despite the importance of computing σp from σb, a good method for doing so remains elusive (Campbell [16], personal communication).
Solute transport and water flow in the unsaturated zone are normally derived from the classical Richards equation and the convection–dispersion equations. Deterministic explanations of these equations are important aspects of research; due to soil heterogeneity at a variety of spatial scales, these equations for predicting actual field-scale processes are being increasingly questioned [21]. Therefore, some researchers working on soil heterogeneity concluded that for the evolution of soil water and solutes, it is more desirable to use stochastic models rather than constant values, where the parameters of stochastic transport models are treated as random variables with discrete values assigned according to a given probability distribution [21,22,23,24,25,26]. Among stochastic models, many studies used Kalman filtering in hydrological applications. A Kalman filter is an optimal recursive data processing algorithm that recursively couples the most recent measurements into the linear model to update the model state output [27]. Under the assumption that the linear system is a stochastic process with Gaussian noises, it produces the best estimation with minimum mean square error and it has been widely used in hydrological models to optimally merge information from the model simulations and the independent observations with appropriate modeling [28,29,30,31,32].
In previous work, we installed frequency domain reflectometry (FDR) sensors (5 TE), which are commercially available from METER Group, Inc. USA, in field conditions at different depths where the soil is heterogeneous to estimate σp [22]. We used εb and σb observations to modify the Hilhorst deterministic model [3] to a stochastic model using a time-varying dynamic linear model and Klaman filter before studying the linear relationship between them.
In this study, we used Time Domain Reflectometry (TDR) sensors (FP/mts), which are commercially available from Easy Test, Poland, to measure εb and σb in laboratory conditions where the soil is homogeneous. Then, we tried to use the Hilhorst model [3] to convert σb to σp. Later, we could show the weakness of applying the deterministic Hilhorst model [3] even in homogeneous soils. Thus, we are aiming to adapt this approach to a stochastic model under laboratory conditions. Thus, we used one homogeneous soil type to accurately estimate the changes in σp over time and to conclude whether the model offset is constant or if it changes in one soil profile.
2. Material and Methods
2.1. The Column Experiment
To achieve the objective of this study, we used two soil columns with a height of 55 cm provided by a sprinkler, see Figure 2. The lower boundary was controlled using a vacuum pump at a constant pressure head of −30 hPa. The columns were packed with a density of 1.4 g/cm3. The substrate was sand, 80% of which was fine sand. The water content during packing was approximately 4 m3/m3. The TDR and soil temperatures sensors were installed in four depths: 7, 21, 35, and 48 cm. Since the soil is sand, the soil relative dielectric permittivity (εb), bulk electrical conductivity (σb), and temperature were measured every 5 min to obtain enough observations for modeling.
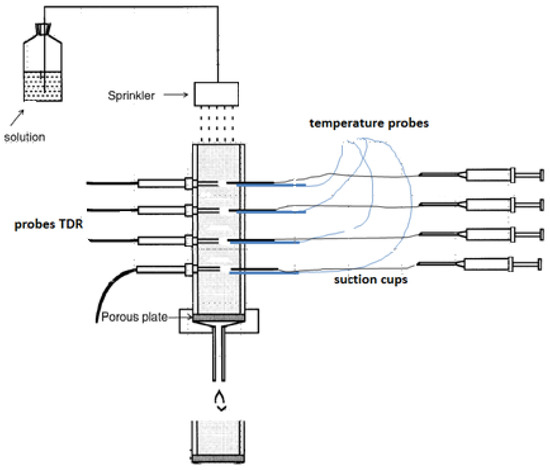
Figure 2.
Measurement set.
Additionally, porous suction cups for taking soil solution samples were installed at each depth to validate the results of our model. The lower boundary of the column uses a membrane to let the water drain. Drainage water was collected in a bottle under −30 hPa vacuum, which is supplied in the range from −20 to −30 hPa. The sprinkler is 5 cm above the soil surface and allows water to drop through small nozzles. Five irrigation events using KCl solution with different electrical conductivities were applied. The first three events were irrigated with 20 dS/m of KCl, then the fourth, and fifth events with 30 dS/m of KCl. The flux was approximately 1 l/h. The columns were free of salt at the beginning and before the irrigations events started. The TDR probes are FP/mts commercially available from Easy Test, Poland, and have been calibrated in air and deionized water. The temperature probes are Thermistors of the type 2k252 (type Fenwal UUA 32J3) with a range of −20 up to 60 °C. Soil temperature data (Tsoil) were used to estimate the relative dielectric permittivity of the soil pore water directly (εp):
To apply the dynamic linear model and the Kalman filter, a time series of the variable of interest is needed [27]. In our study, time series of εb, σb, and εp are required to estimate σp. Therefore, we used five irrigation events with two levels of KCL solution to obtain the variation of these variables over time for each depth. In total, 289 observations were made of σb, εp, and εb for each soil depth and these were used to estimate both the offset εσb=0 of the modified Hilhorst model [3] and the evolution of σp at its corresponding depth, of which 144 observations were used to validate their forecasts.
2.2. Time-Varying Dynamic Linear Model
In general, the state space model is identified by two assumptions, (i) there is a hidden or latent process xt called the state process. The state process is assumed to be a Markov process, where past and future values of xt are independent, conditional on the present xt, ({xs, S > t}, and {xs, S< t} are independent on the xt), (ii) the observations, yt are independent given the states xt. This means that the dependence among the observations is generated by states. The dynamic linear model (DLM) or linear Gaussian state space model, in its simple form, employs a first-order, p-dimensional vector autoregression as the state equation:
We do not observe the state vector xt directly, but only a linear transformed version of them with noise added, say:
yt is an m-dimensional vector, representing the observation at time t, is a q × p measurement or observation matrix. Equation (4) is called the observation equation, in which , are the Gaussian white-noise errors. The evolution variances are , and can be estimated from available data using maximum likelihood or Bayesian techniques.
In this study, we modified the deterministic Hihlorst model (1) to a stochastic one. The model (1) has the variables σb, εp, σp, εb, and εσb = 0. The σp and εσb = 0 are unobserved and they need to be estimated by the state Equation (3) as xt, while σb, εp, and εb are observed by the sensors (εp is calculated from Equation (2) using soil temperature sensor data) and represented by observation Equation (4) as yt.
The R [33] package, dlm [34], provides an integrated environment for Bayesian inference using DLM, and the package includes functions for Kalman filtering and smoothing, as well as for maximum likelihood estimation.
3. Results and Discussion
3.1. Deterministic Model
The offset of the Hilhorst model [3] can be calculated from Equation (1):
We derived the offset (εσb = 0) from this linear model after using measurements of εb and σb. For example, applying the ordinary least squares (OLS) on measurements of εb and σb obtained from soil column 2 data during the third irrigation at a depth of 21 cm, Table 1 shows that the offset of the linear relationship between εb–σb is 9.41. Further, the single estimate of the slope () of the regression parameter vector (1/σp) for the entire data set is very small. Thus, the estimated soil pore water electrical conductivity (σp ) is too high compared with the EC meter value, see Table 2. Afterward, we applied the Durbin–Watson test in order to test if there was any autocorrelation between the residuals of the regression. Table 3 shows that there is an extremely strong and positive autocorrelation, meaning that the result of that regression is not valid.

Table 1.
Estimated parameters gained from the linear regression analysis.

Table 2.
Electrical conductivity of the soil solution (dS/m) according to soil column number, irrigation event, and depth (cm); it is collected by porous suction cups and measured by an electrical conductivity (EC) meter device.

Table 3.
Durbin–Watson test for linear regression εb-σb.
For each irrigation event, we obtained one solution sample at each depth by using porous suction cups. Unfortunately, some samples did not have enough solution to measure their electrical conductivity using the EC meter device. Table 2 shows the values of EC measured by the EC meter device. The table shows eight EC values from the EC meter according to the depth and irrigation event number for each soil column. Due to the variability in the water flow in unsaturated soil, we observed in our experiment a variation in the time needed to collect the solution sample. More time was required to collect enough solution for the EC meter device when a greater number of ions gathered in the sample resulting in a high EC value of the sample. Therefore, there is a difference in the EC values between the soil columns at the same depth, see Table 2. We applied a modified Hilhorst model on the eight time-series data corresponding to Table 2 (depth, irrigation event, and soil column) to compare our finding of σp obtained from our modified model to the values of σp obtained by the EC meter device, see Table 2.
The reason for choosing 1 l/h for the irrigation rate and 5 min for the irrigation interval is visualized in Figure 3. At each depth, we could see how the bulk electrical conductivity responds to the irrigation event.
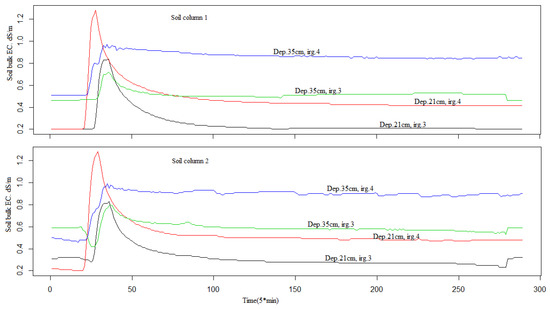
Figure 3.
Bulk electrical conductivity (σb) in the two soil columns for two irrigation events (N°.3 and N° 4) at two depths (21 cm and 35 cm). Series peaks are related to time irrigation.
3.2. Time-Varying Linear Dynamic Model (LDM)
The deterministic Equation (5) can be modified into the time-varying DLM for observation and unobservable (state) models. In this case, the observation data are the soil relative dielectric permittivity (εb), bulk electrical conductivity (σb), and the relative dielectric permittivity (εp), while the unobservable data are the offset (εσb=0) and pore water electrical conductivity (σp). Equation (4) can be modified to the time-varying DLM as follows:
- The observation equation can be obtained by modifying the Hilhorst model [3] (written in Equation (5)) into a stochastic equation, in accordance with Equation (4) as follows:
- The state equation (unobservable data) in Equation (3) is εσb = 0, and the slope, 1/σp. They can be converted to the unobservable state equation of the time-varying DLM according to Equation (3). The unobservable state equation can be arranged as follows:
Here, we consider εσb = 0 as a constant. The actual value is related only to its past value. The slope 1/σp changes over time and its actual value is related to its past value plus the Gaussian white-noise errors (). We applied the equation in reverse order to estimate the state variables (εσb = 0 and σp) at all time points from a complete series of the soil relative dielectric permittivity (εb). This process is known as smoothing.
An example of the evolution of εb, εp, and σb data needed for the Hilhorst model [3] is shown in Figure 4. By applying the Equations (6) and (7) using DLM and the Kalman filter on the eight time-series data, we see in Figure 5 the observed and predicted time series of the soil relative dielectric permittivity (εb). The predicted and observed values of εb agree reasonably well. The mean absolute prediction error (MAPE) for the time series never exceeded 0.02.
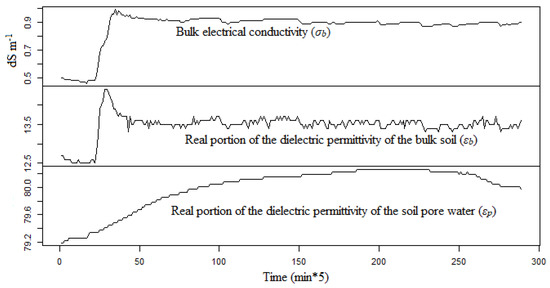
Figure 4.
Known variables for the Hilhorst model (σb, εb, and εp); data from soil column 2, depth 35 cm and irrigation event N°4.
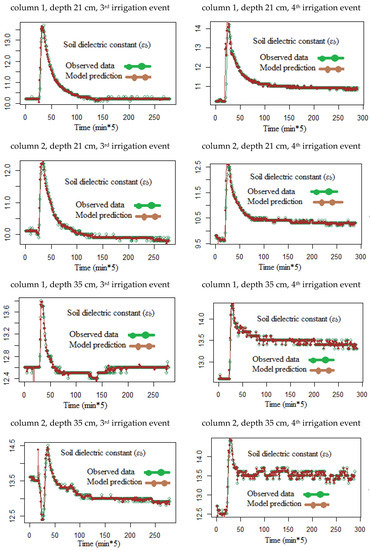
Figure 5.
Observed and predicted soil relative dielectric permittivities according to the soil column number, depth, and irrigation event.
Since the prediction of the soil relative dielectric permittivity (εb) is valid, the estimation of the electrical conductivity of pore water (σp) and the offset εσb = 0, see Equation (7), are also valid because they are used in the prediction of the soil relative dielectric permittivity (εb) and have converged to their true values. The evolution of σp over time obtained by DLM is presented in Figure 6; it shows the importance of using DLM because it obtained all the changes of σp over time and not a single value of σp for the entire data set. Another interesting aspect is that Figure 6 shows the changes in the model offset for each irrigation event at each depth. This finding is very important since it shows that the offset does not depend on the soil type [10,14,15,16] nor on the soil type and salinity [17] when two columns with the same type soil are used, as in this study. Moreover, in Figure 6 we put the corresponding value of σp measured by the EC meter device for each depth according the irrigation event and soil column number.
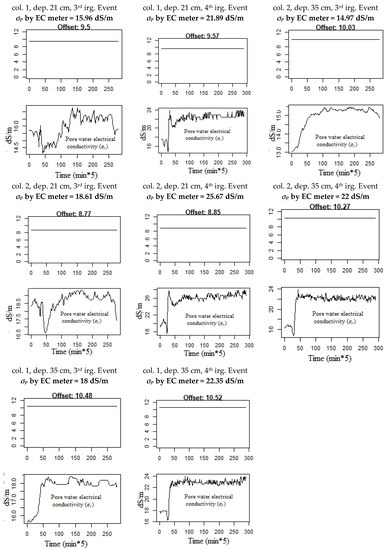
Figure 6.
Estimation of the unobservable data (εσb = 0 and σp) by applying the time-varying dynamic linear model (DLM) and the Kalman filter on the data according to the soil column number (col.), depth (dep.), and irrigation event (irg. Event), the corresponding of σp by EC meter device is given for each estimated σp.
Comparing the mean evolution of σp values obtained from our modified Hilhorst model, see Figure 6, with the single corresponding EC value obtained from porous suction cups and measured by the EC meter device, see Table 2, we found that they agree very well (R2 = 72%).
From these results, three advantages are evident when using DLM and a Kalman filter to estimate σp in two homogenous soil columns; first, we observed that the offset value of the Hilhorst model does not depend on the soil type and σp and it changes in the same soil profile. Secondly, we obtained the changes in the estimated σp over time and not just a single value as a coefficient for the entire data set. Third, the estimated changes in σp occur instantly and save time and labor costs.
4. Conclusions
In this study, we applied the εb-σb linear relationship to homogeneous soil column data obtained from TDR sensors. We found an extremely strong positive autocorrelation between the residuals of the regression analysis. When residuals are correlated, the least squares method is not the most efficient model coefficient estimator. By modifying the regression by a time-varying dynamic linear model (DLM), the match between the observed and modeled data of εb is significantly improved and the estimated evolution of σp converges to its true value. Moreover, in this study, we used two homogeneous soil columns with the same condition to show that the offset of the Hilhorst model [3] is not constant, as suggested for all moist soil or, as others suggested, that it is soil-type-dependent [10,14,15,16] or soil-type- and salinity-dependent [17]. We repeated the experiment to show that the offset changes even in the same soil type and the same conditions. A dynamic linear model enables the capture of the offset changes and it shows the importance of calculating it simultaneously when estimating σp using the Hilhorst model. The next promising step would be programming and inserting these models into the TDR software in order to estimate the soil pore water electrical conductivity (σp) from senor records directly.
Author Contributions
Investigation, B.A. and J.A.S.-E.; Methodology, J.A.S.-E.; Software, J.A.S.-E. and B.A; Validation, B.A.; Writing—original draft, B.A.; Writing—review & editing, B.A. and G.W.
Funding
By Open Access Publication Funds of TU Berlin.
Acknowledgments
The authors express their thank to the German Research Foundation DFG (GRK 2032) for funding project of Basem Aljoumani as part of the research training group ‘Urban Water Interfaces’. Also they owe gratitude to Steffen Trinks and Andre Peters for their technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thiruchelvam, S.; Pathmarajah, S. An Economic Analysis of Salinity Problems in the Mahaweli River System H Irrigation Scheme in Sri Lanka; EEPSEA: Ho Chi Minh, Vietnam, 1999; p. 47. [Google Scholar]
- Ghassemi, F.; Jakeman, A.J.; Nix, H.A. Salinisation of Land and Water Resources: Human Causes, Extent, Management and Case Studies; CAB International: Wallingford, CT, USA, 1995. [Google Scholar]
- Hilhorst, M.A. A Pore Water Conductivity Sensor. Soil Sci. Soc. Am. J. 2000, 64, 1922–1925. [Google Scholar] [CrossRef]
- Hajrasuliha, S.; Baniabbassi, N.; Metthey, J.; Nielsen, D.R. Spatial Variability of Soil Sampling for Salinity Studies in Southwest Iran. Irrig. Sci. 1980, 1, 197–208. [Google Scholar] [CrossRef]
- Cetin, M.; Kirda, C. Spatial and Temporal Changes of Soil Salinity in a Cotton Field Irrigated with Low-Quality Water. J. Hydrol. 2003, 272, 238–249. [Google Scholar] [CrossRef]
- Rhoades, J.D.; Shouse, P.J.; Alves, W.J.; Manteghi, N.A.; Lesch, S.M. Determining Soil Salinity from Soil Electrical Conductivity Using Different Models and Estimates. Soil Sci. Soc. Am. J. 1990, 54, 46–54. [Google Scholar] [CrossRef]
- Shouse, P.J.; Goldberg, S.; Skaggs, T.H.; Soppe, R.W.O.; Ayars, J.E. Changes in Spatial and Temporal Variability of SAR Affected by Shallow Groundwater Management of an Irrigated Field, California. Agric. Water Manag. 2010, 97, 673–680. [Google Scholar] [CrossRef]
- Li, X.; Yang, J.; Liu, M.; Liu, G.; Yu, M. Spatio-Temporal Changes of Soil Salinity in Arid Areas of South Xinjiang Using Electromagnetic Induction. J. Integr. Agric. 2012, 11, 1365–1376. [Google Scholar] [CrossRef]
- Kargas, G.; Persson, M.; Kanelis, G.; Markopoulou, I.; Kerkides, P. Prediction of Soil Solution Electrical Conductivity by the Permittivity Corrected Linear Model Using a Dielectric Sensor. J. Irrig. Drain. Eng. 2017, 143, 04017030. [Google Scholar] [CrossRef]
- Persson, M. Evaluating the Linear Dielectric Constant-Electrical Conductivity Model Using Time-Domain Reflectometry. Hydrol. Sci. J. 2002, 47, 269–277. [Google Scholar] [CrossRef]
- Wyllie, M.R.J.; Southwick, P.F. An Experimental Investigation of the S.P. and Resistivity Phenomena in Dirty Sands. J. Pet. Technol. 1954, 6, 44–57. [Google Scholar] [CrossRef]
- Rhoades, J.D.; Raats, P.A.C.; Prather, R.J. Effects of Liquid-Phase Electrical Conductivity, Water Content, and Surface Conductivity on Bulk Soil Electrical Conductivity1. Soil Sci. Soc. Am. J. 1976, 40, 651–655. [Google Scholar] [CrossRef]
- Mualem, Y.; Friedman, S.P. Theoretical Prediction of Electrical Conductivity in Saturated and Unsaturated Soil. Water Res. Res. 1991, 27, 2771–2777. [Google Scholar] [CrossRef]
- Malicki, M.A.; Walczak, R.T. Evaluating Soil Salinity Status from Bulk Electrical Conductivity and Permittivity. Eur. J. Soil Sci. 1999, 50, 505–514. [Google Scholar] [CrossRef]
- Malicki, M.A.; Walczak, R.; Koch, S.; Fluhler, H. Determining Soil Salinity from Simultaneous Readings of Its Electrical Conductivity and Permittivity Using TDR. In Proceedings of the Symposium and Workshop on Time Domain Reflectometry in Environmental, Infrastructure, and Mining Applications, Evanston, IL, USA, 7–9 September 1994; Volume 101, pp. 7–9. [Google Scholar]
- Decagon Devices. 5TE Water Content, EC, and Temperature Sensors Operator’s Manual; Decagon Devices: Pullman, WA, USA, 2008. [Google Scholar]
- Rodriguez, A.; Ruben, F. Calibrating Capacitance Sensors to Estimate Water Content, Matric Potential, and Electrical Conductivity in Soilless Substrates. Master’s Thesis, University of Maryland, College Park, MD, USA, 2009. [Google Scholar]
- Bouksila, F.; Persson, M.; Berndtsson, R.; Bahri, A. Soil Water Content and Salinity Determination Using Different Dielectric Methods in Saline Gypsiferous Soil/Détermination de La Teneur En Eau et de La Salinité de Sols Salins Gypseux à l’aide de Différentes Méthodes Diélectriques. Hydrol. Sci. J. 2008, 53, 253–265. [Google Scholar] [CrossRef]
- Visconti, F.; Martínez, D.; Molina, M.J.; Ingelmo, F.; Miguel de Paz, J. A Combined Equation to Estimate the Soil Pore-Water Electrical Conductivity: Calibration with the WET and 5TE Sensors. Soil Res. 2014, 52, 419–430. [Google Scholar] [CrossRef]
- Maybeck, P.S. Stochastic Models, Estimation, and Control; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Genuchten, M.V. Recent Progress in Modelling Water Flow and Chemical Transport in the Unsaturated Zone. In Proceedings of the 20th General Assembly of the International Union of Geodesy and Geophysics, Vienna, Austria, 11–24 August 1991; pp. 169–183. [Google Scholar]
- Aljoumani, B.; Sànchez-Espigares, J.A.; Cañameras, N.; Wessolek, G.; Josa, R. Transfer Function and Time Series Outlier Analysis: Modelling Soil Salinity in Loamy Sand Soil by Including the Influences of Irrigation Management and Soil Temperature. Irrig. Drain. 2018, 67, 282–294. [Google Scholar] [CrossRef]
- Aljoumani, B.; Sànchez-Espigares, J.A.; Cañameras, N.; Josa, R. An Advanced Process for Evaluating a Linear Dielectric Constant–Bulk Electrical Conductivity Model Using a Capacitance Sensor in Field Conditions. Hydrol. Sci. J. 2015, 60, 1828–1839. [Google Scholar] [CrossRef]
- Aljoumani, B.; Sànchez-Espigares, J.A.; Cañameras, N.; Josa, R.; Monserrat, J. Time Series Outlier and Intervention Analysis: Irrigation Management Influences on Soil Water Content in Silty Loam Soil. Agric. Water Manag. 2012, 111, 105–114. [Google Scholar] [CrossRef]
- Beven, K.; Germann, P. Macropores and Water Flow in Soils. Water Res. Res. 1982, 18, 1311–1325. [Google Scholar] [CrossRef]
- White, R.E. The Influence of Macropores on the Transport of Dissolved and Suspended Matter Through Soil. In Advances in Soil Science; Stewart, B.A., Ed.; Springer: New York, NY, USA, 1985; pp. 95–120. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Wendroth, O.; Rogasik, H.; Koszinski, S.; Ritsema, C.J.; Dekker, L.W.; Nielsen, D.R. State-space Prediction of field-scale Soil Water Content Time Series in a Sandy Loam. Soil Tillage Res. 1999, 9, 85–93. [Google Scholar] [CrossRef]
- Hoeben, R.; Troch, P.A. Assimilation of Active Microwave Observation Data for Soil Moisture Profile Estimation. Water Resour. Res. 2000, 36, 2805–2819. [Google Scholar] [CrossRef]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual State–Parameter Estimation of Hydrological Models Using Ensemble Kalman Filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef]
- Anderson, J.L. An Ensemble Adjustment Kalman Filter for Data Assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar] [CrossRef]
- Liu, Y.; Weerts, A.H.; Clark, M.; Hendricks Franssen, H.-J.; Kumar, S.; Moradkhani, H.; Seo, D.-J.; Schwanenberg, D.; Smith, P.; van Dijk, A.I.J.M.; et al. Advancing Data Assimilation in Operational Hydrologic Forecasting: Progresses, Challenges, and Emerging Opportunities. Hydrol. Earth Syst. Sci. 2012, 16, 3863–3887. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Petris, G. An R Package for Dynamic Linear Models. J. Stat. Softw. 2010, 36. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).