Novel Simulation Technique of Electromagnetic Wave Propagation in the Ultra High Frequency Range within Power Transformers
Abstract
:1. Introduction
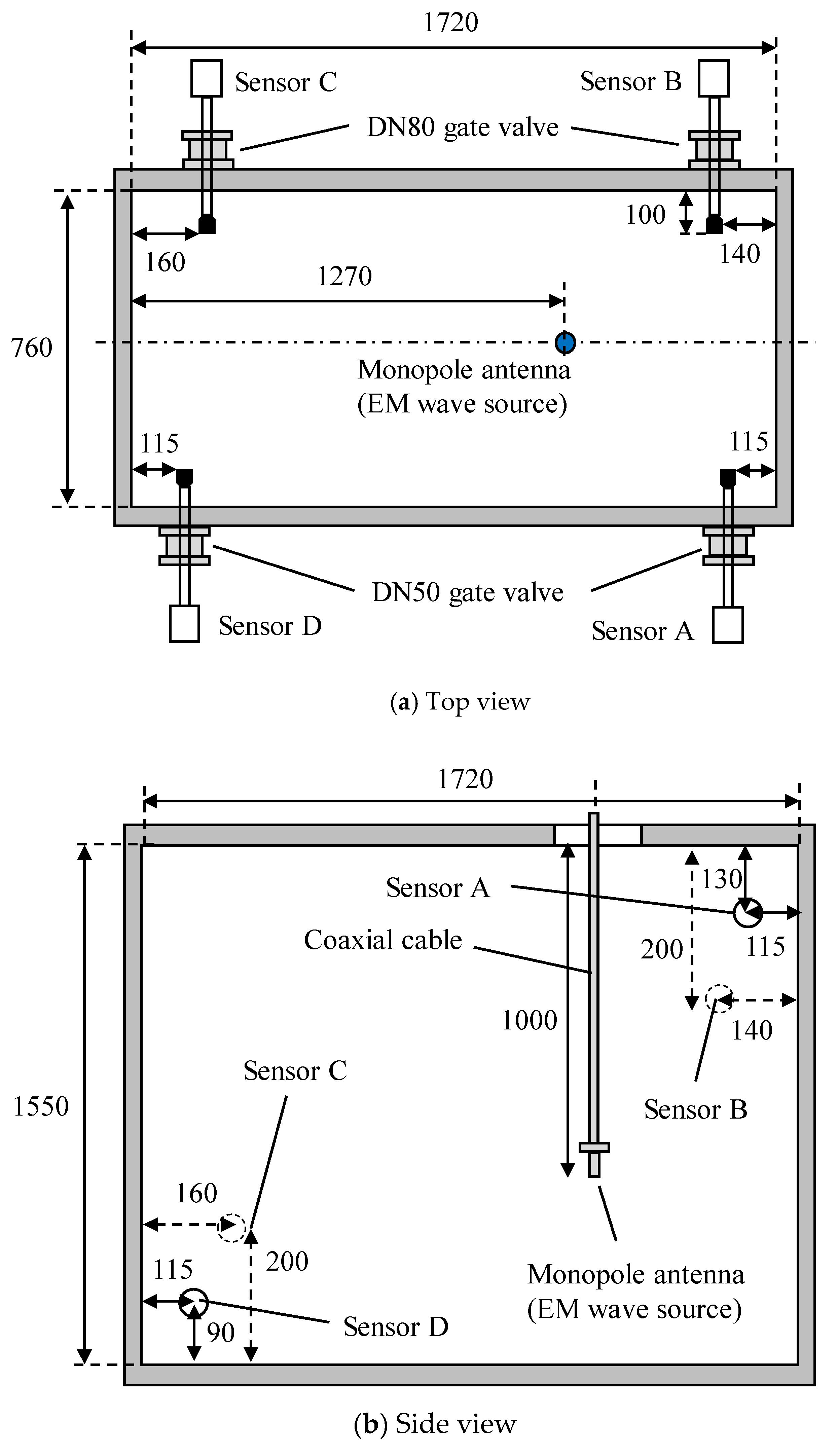
2. Experimental Method
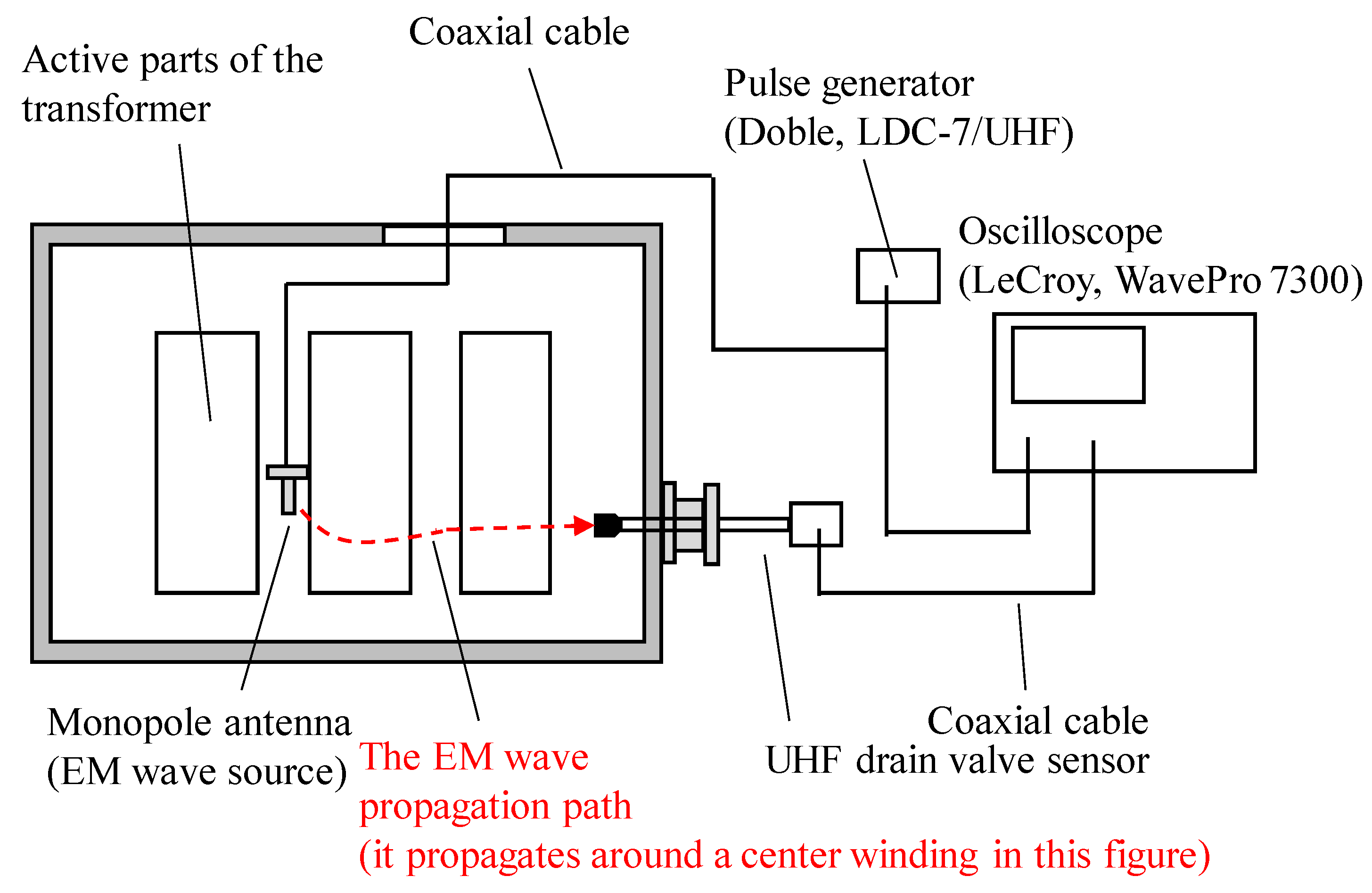
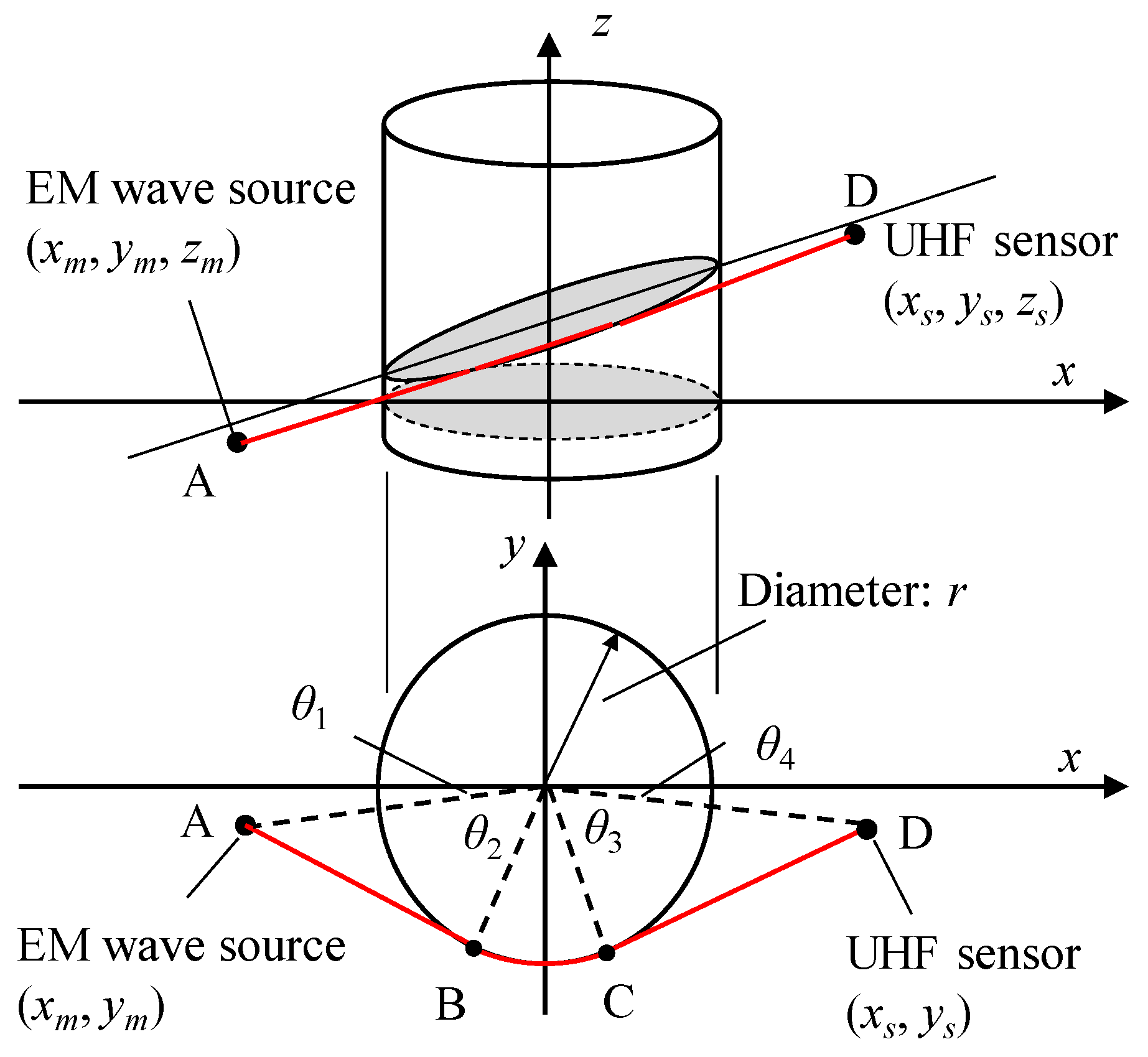
2.1. UHF Sensors and EM Wave Source
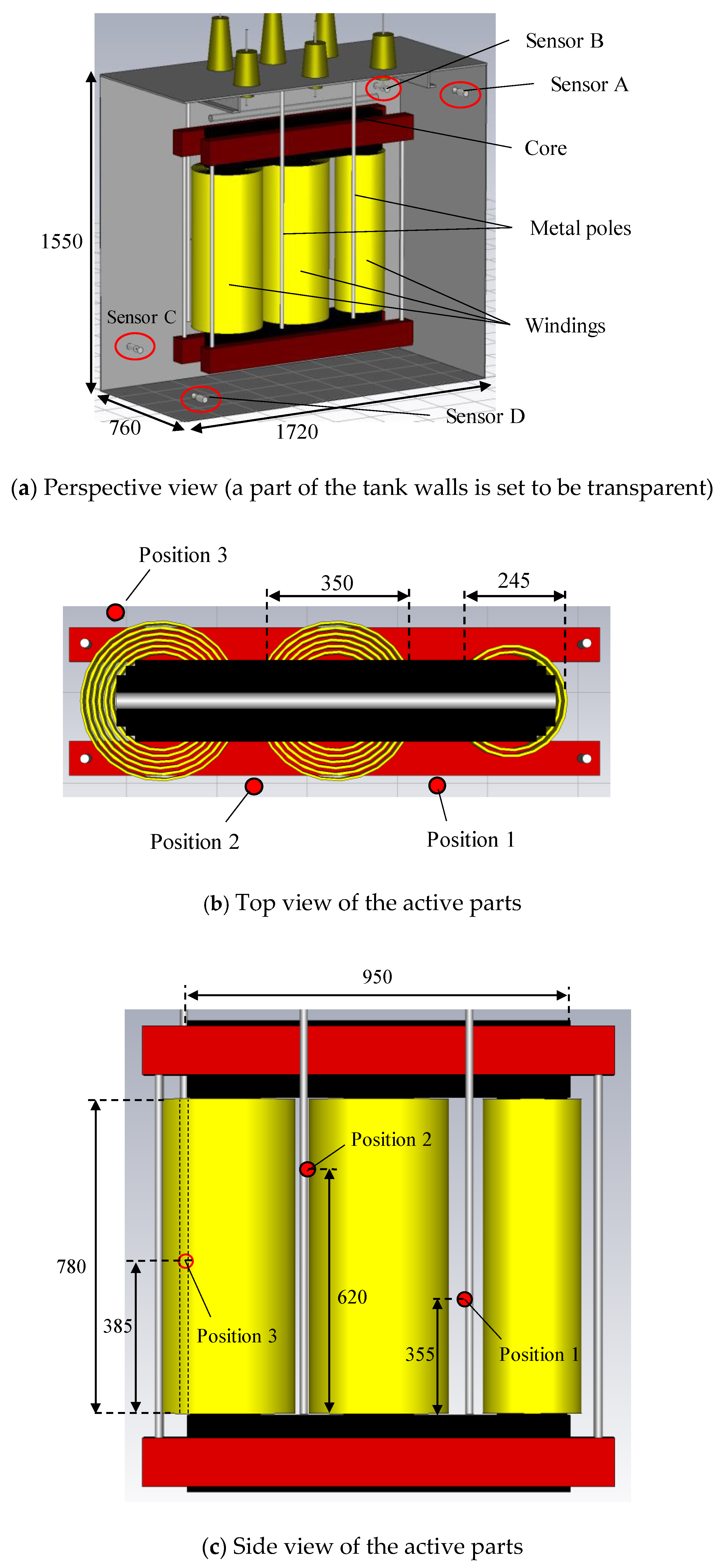
2.2. Active Part of the Transformer
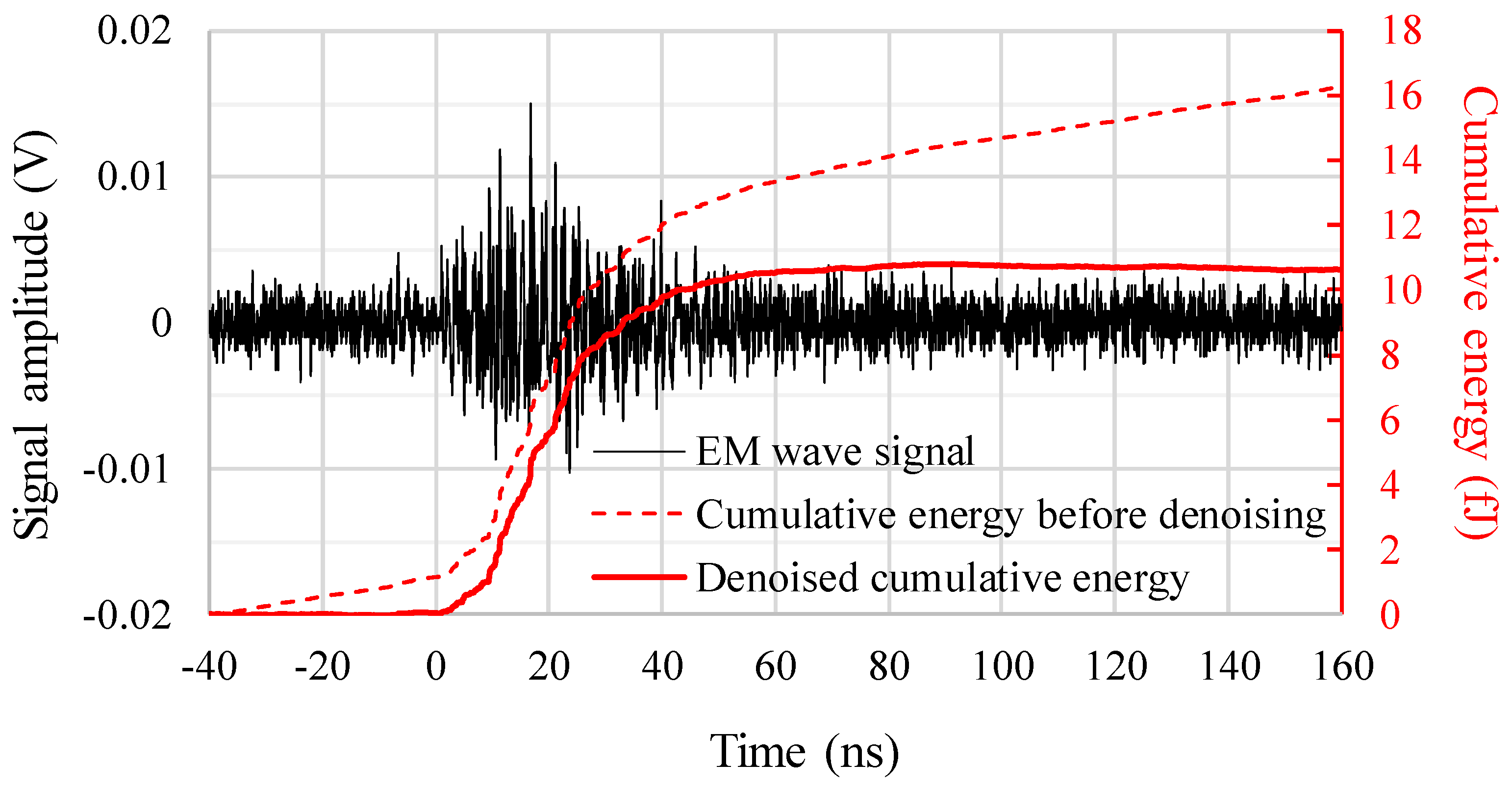
2.3. Denoising of the Cumulative Energies
3. Simulation Technique of the EM Wave Propagation
3.1. 3-D Modeling of the Transformer
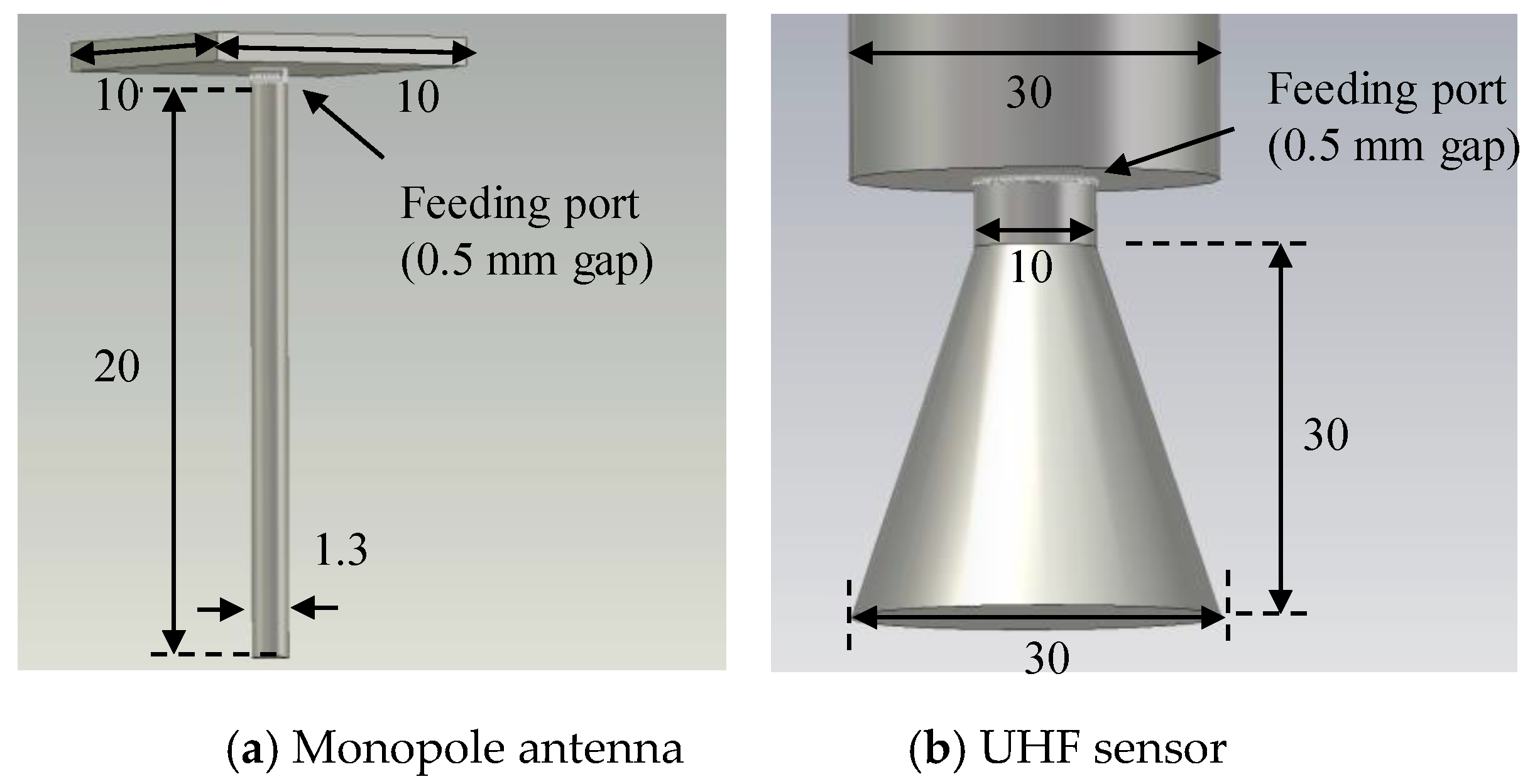
3.2. Antenna Modeling
3.3. Other Computational Conditions
4. Evaluations of the Simulated Results and Discussions
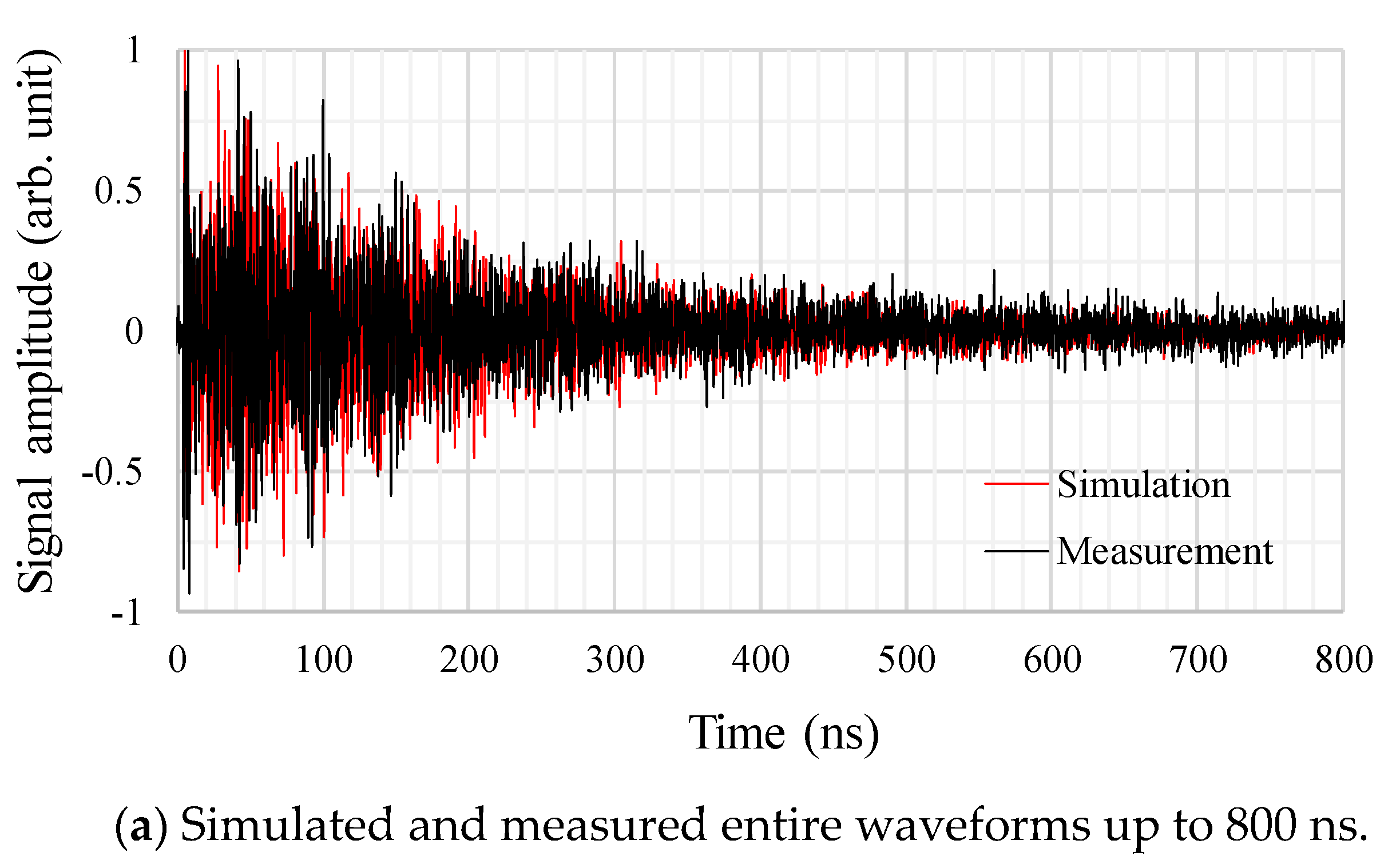
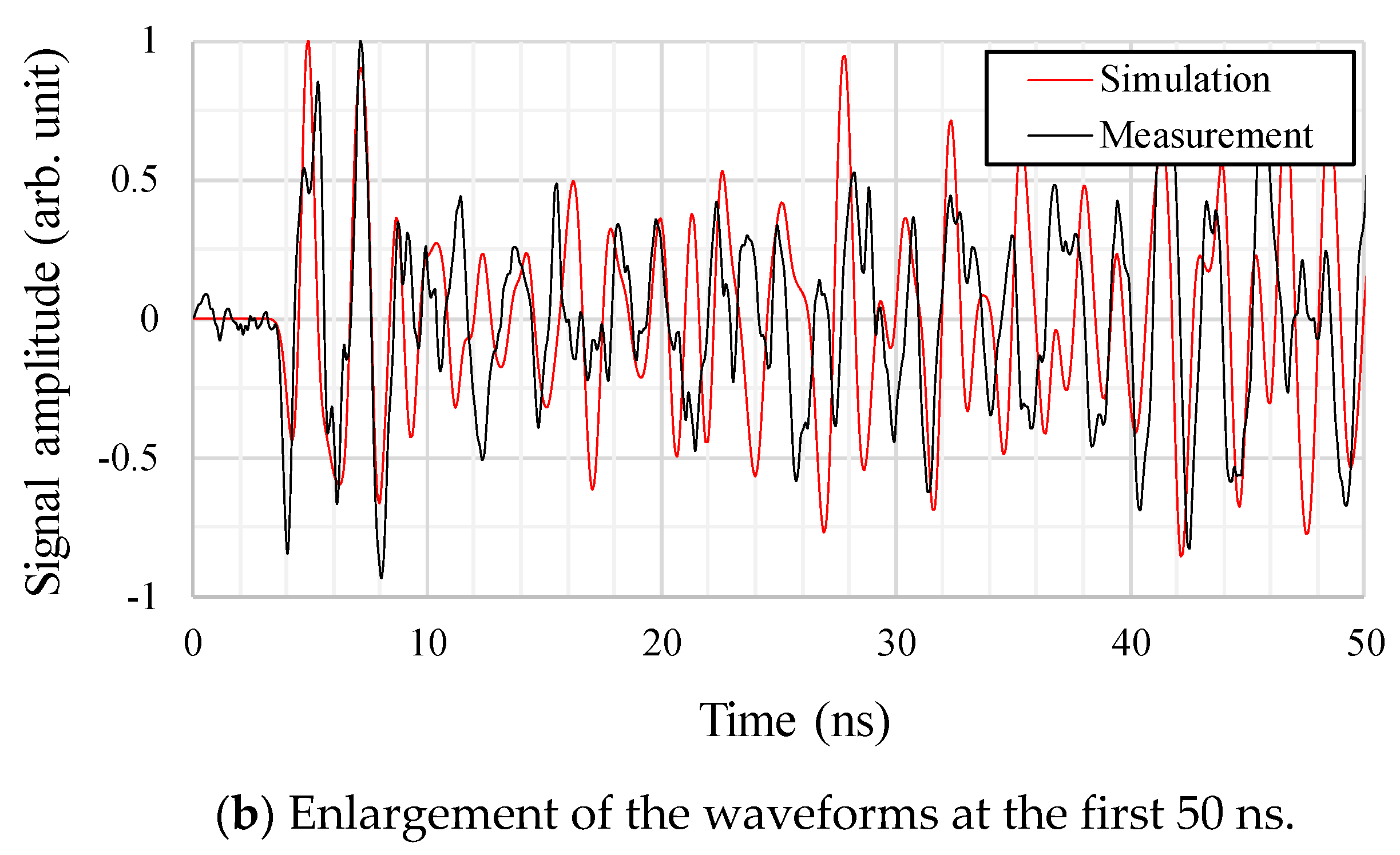
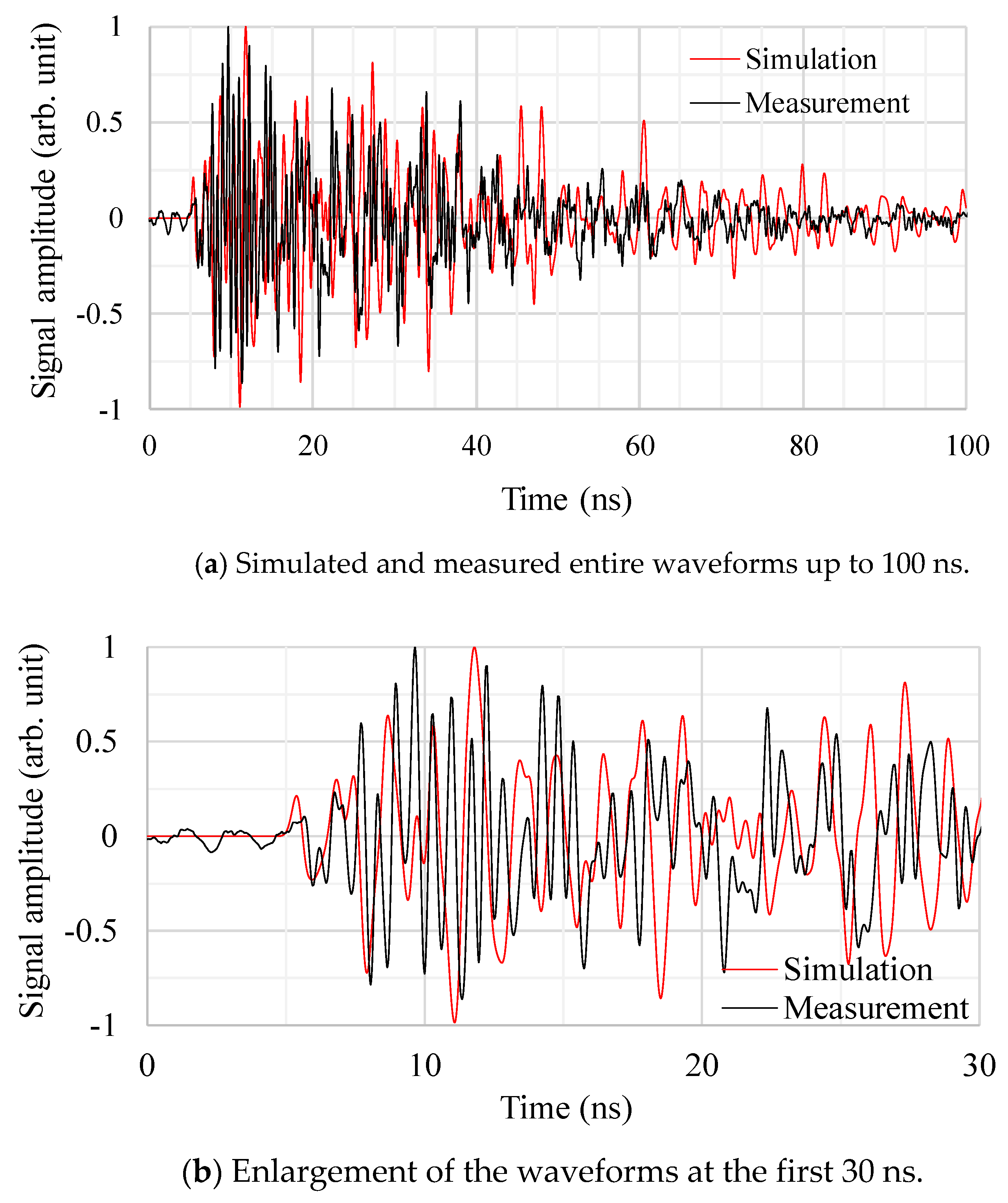
4.1. Validations of the Antenna and Transformer Tank Modeling
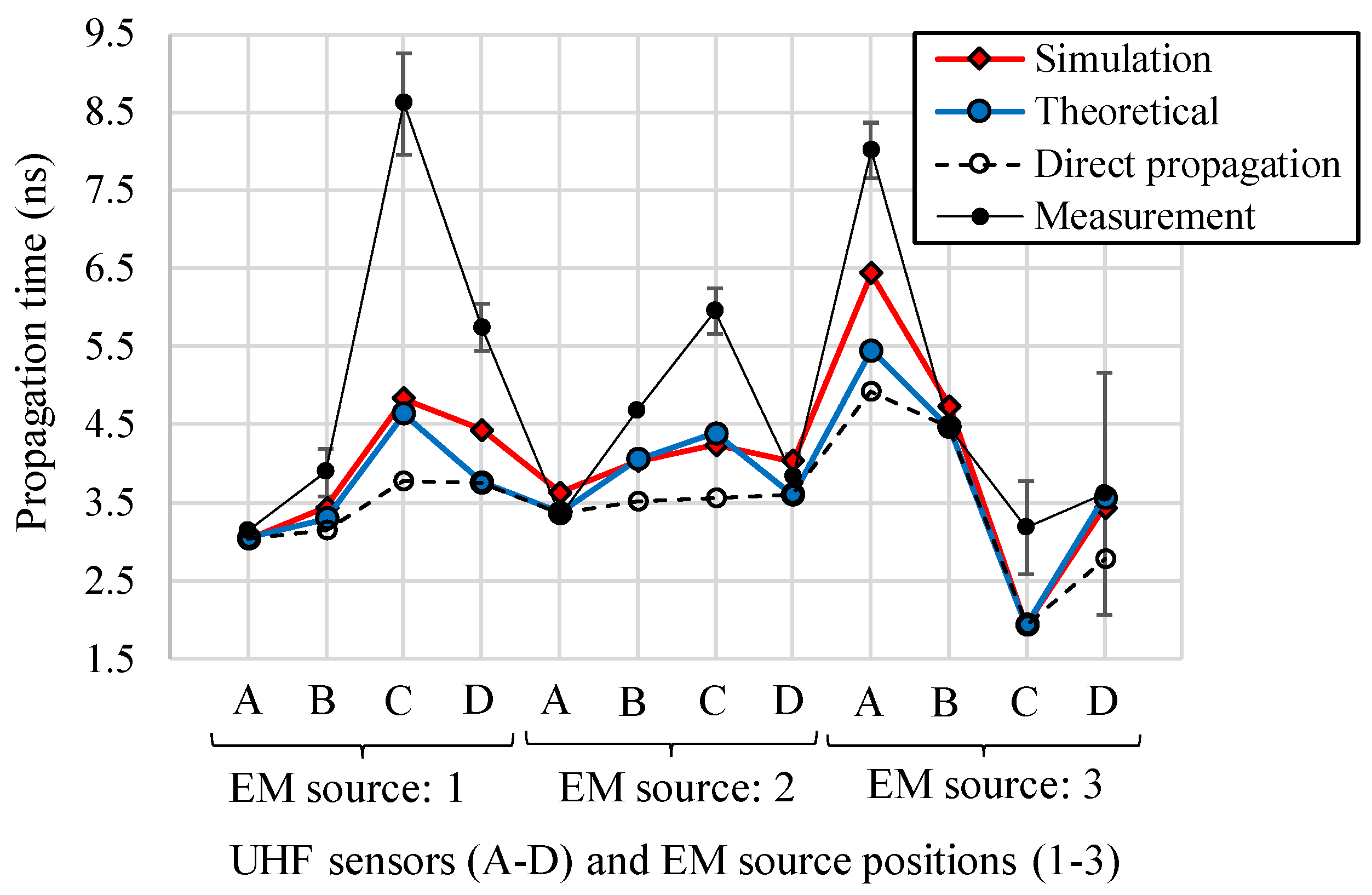
4.2. Propagation Times of the EM Waves within a Transformer
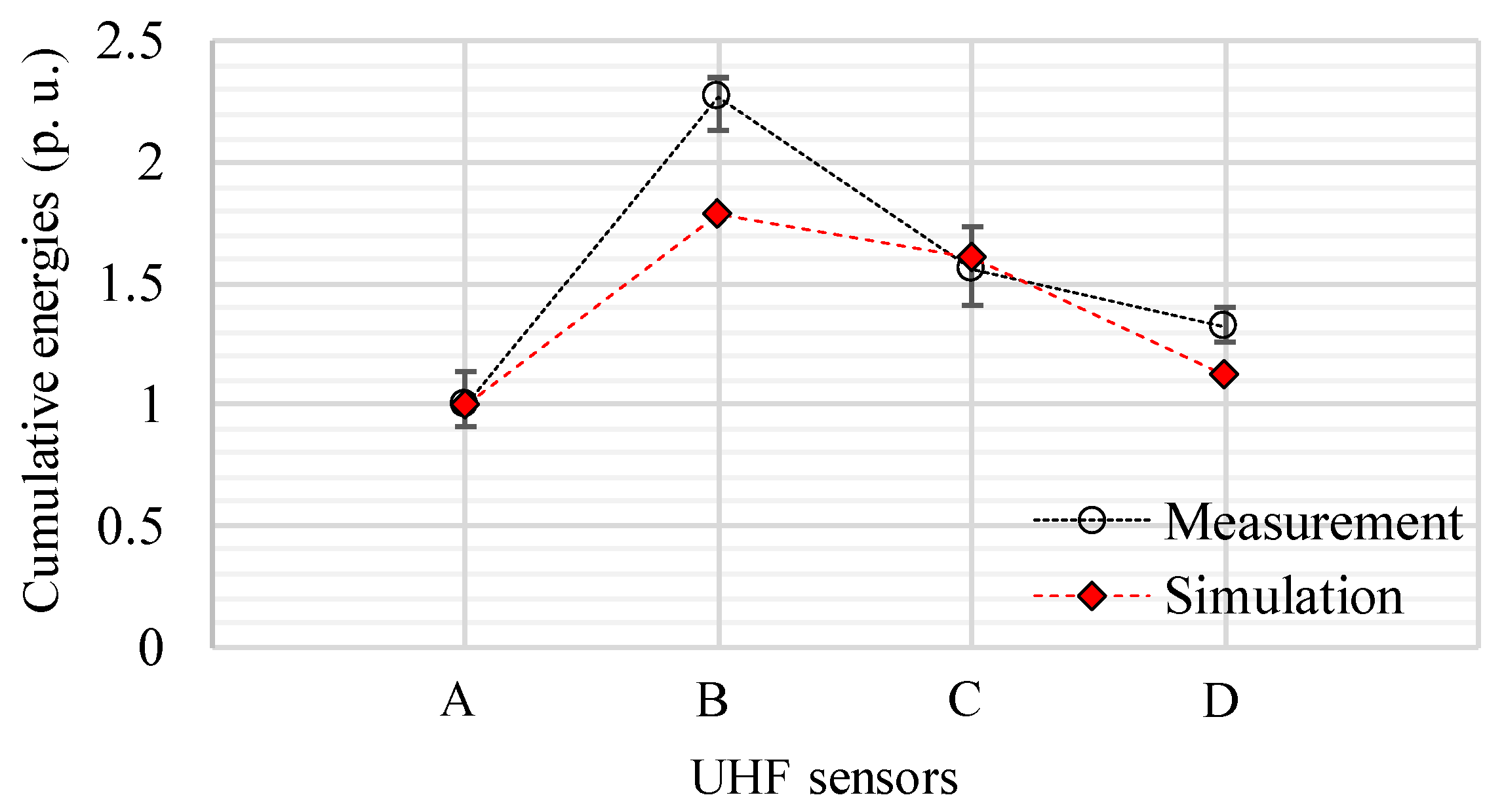
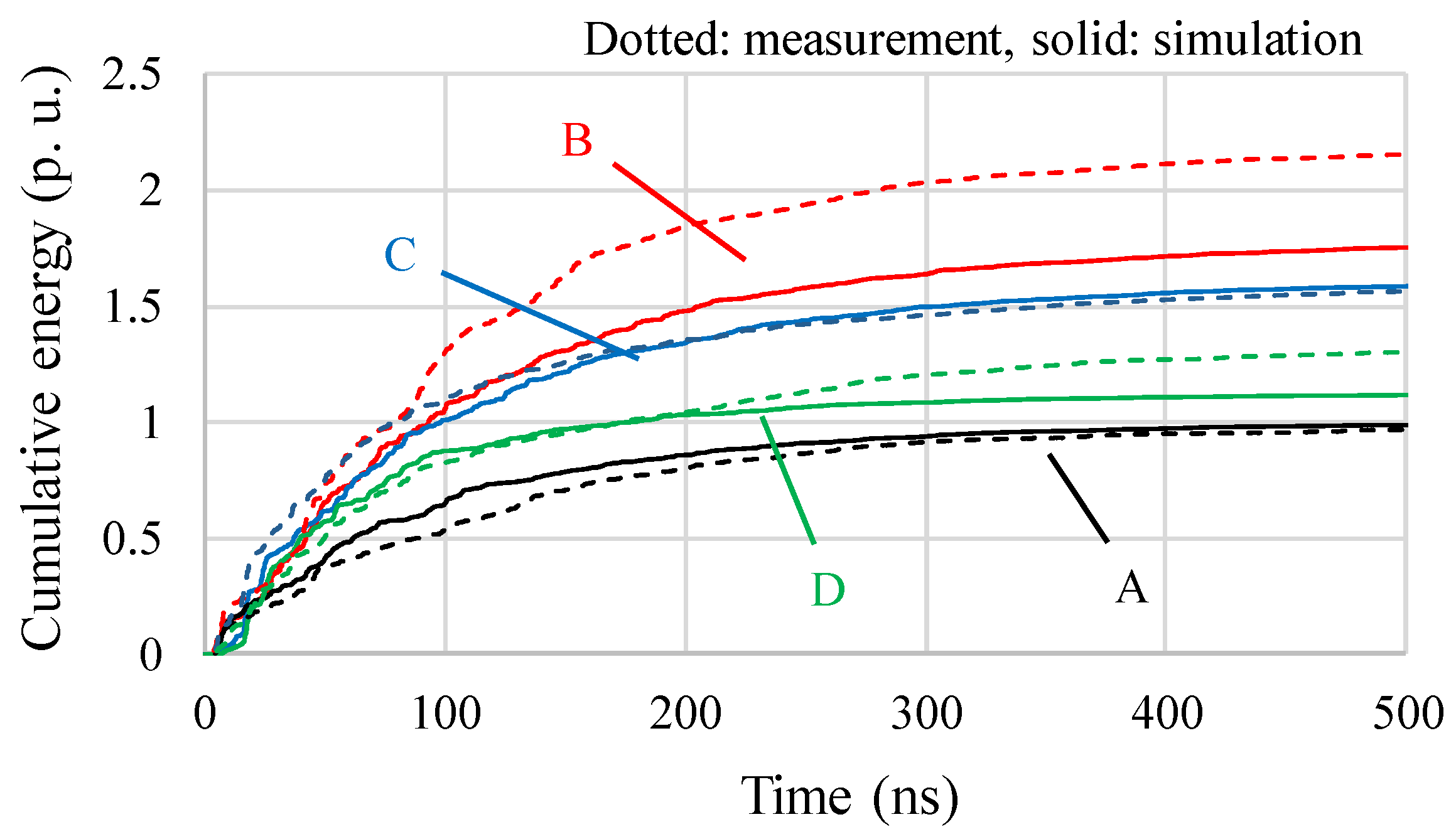
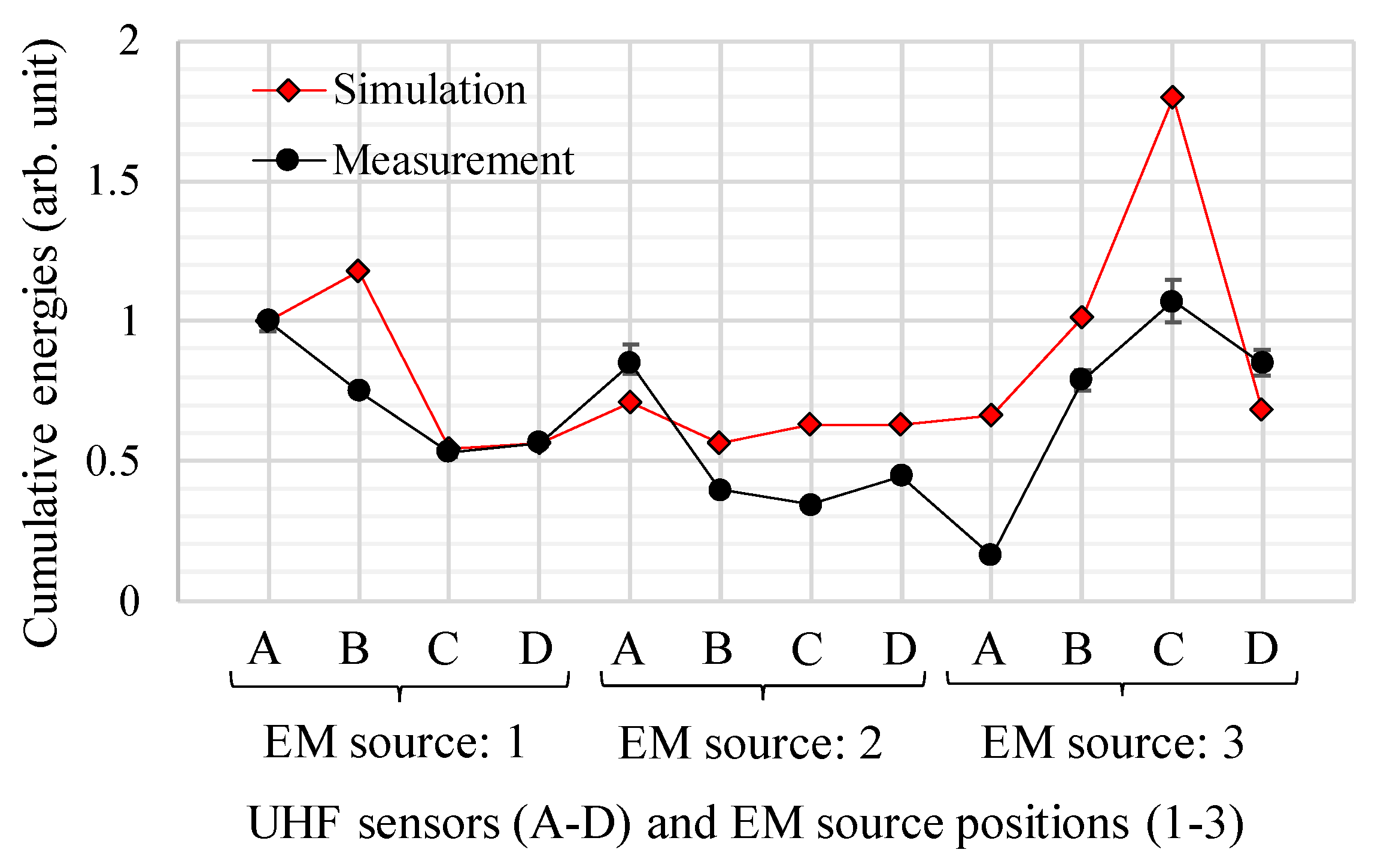
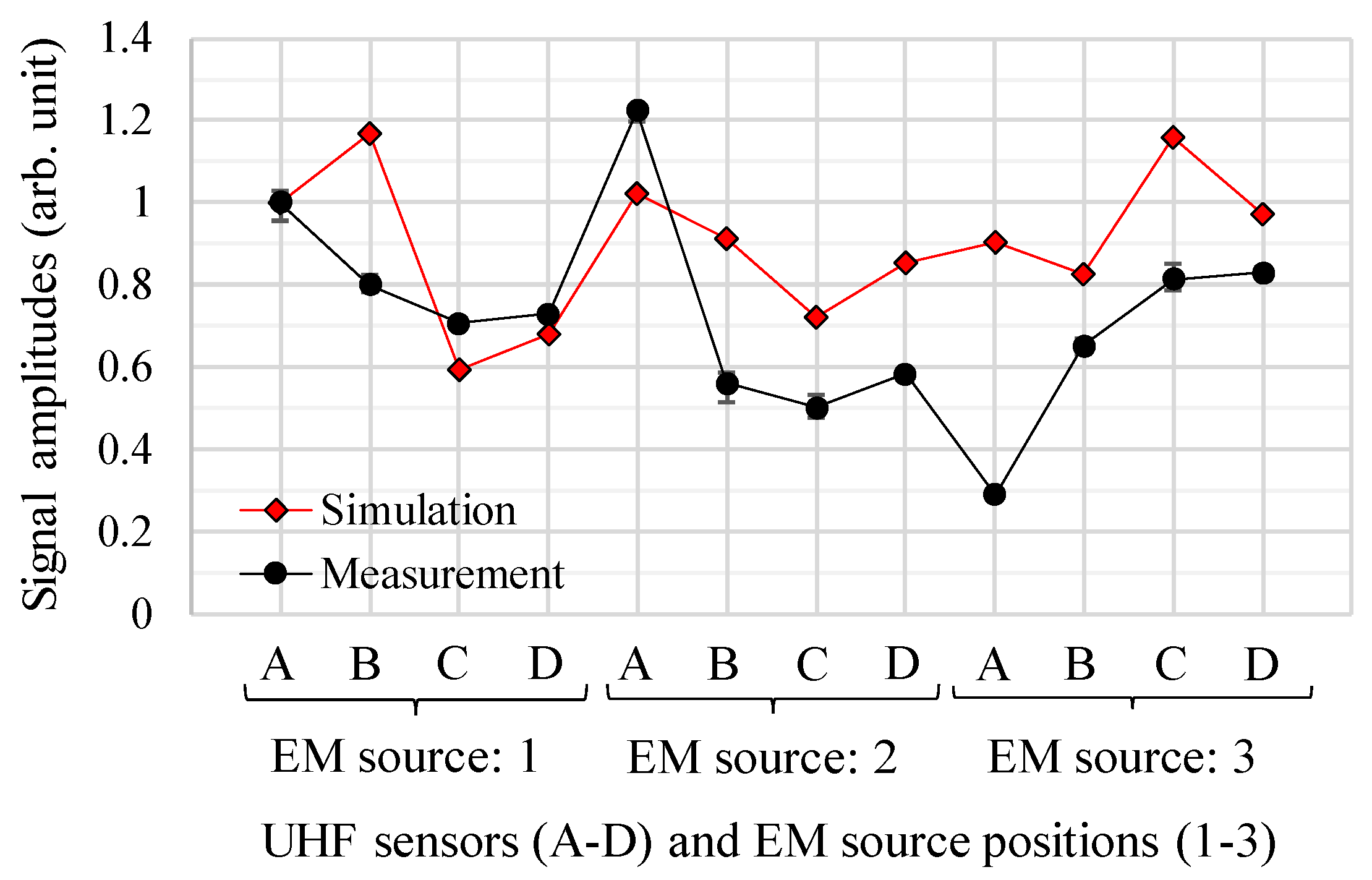
4.3. Cumulative Energies and Signal Amplitudes as a Function of Sensor Positions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Godina, R.; Rodrigues, E.M.G.; Matias, J.C.O.; Catalao, J.P.S. Effect of loads and other key factors on oil-transformer aging: Sustainability benefits and challenges. Energies 2015, 8, 12147–12186. [Google Scholar] [CrossRef]
- Yang, Q.; Su, P.; Chen, Y. Comparison of impulse wave and sweep frequency response analysis methods for diagnosis of transformer winding faults. Energies 2017, 10, 431. [Google Scholar] [CrossRef]
- Cennamo, N.; Maria, L.D.; D’Agostino, G.; Zeni, L.; Pesavento, M. Monitoring of low levels of furfural in power transformer oil witih a sensor system based on a POF-MIP platform. Sensors 2015, 15, 8499–8511. [Google Scholar] [CrossRef] [PubMed]
- Tenbohlen, S.; Denissov, D.; Hoek, S.M.; Markalous, S.M. Partial discharge measurement in the ultra-high frequency (UHF) range. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1544–1552. [Google Scholar] [CrossRef]
- International Electrotechnical Commission (IEC). IEC 60270, High Voltage Test Techniques—Partial Discharge Measurements; IEC: Geneva, Switzerland, 2000. [Google Scholar]
- Li, S.; Gao, G.; Hu, G.; Gao, B.; Yin, H.; Wei, W.; Wu, G. Influences of traction load shock on artificial partial discharge faults within traction transformer—Experimental test for pattern recognition. Energies 2017, 10, 1556. [Google Scholar]
- Duval, M. A review of faults detectable by gas-in-oil analysis in transformers. IEEE Electr. Insul. Mag. 2002, 18, 8–17. [Google Scholar] [CrossRef]
- Markalous, S.; Tenbohlen, S.; Feser, K. Detection and location of partial discharges in power transformers using acoustic and electromagnetic signals. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1576–1583. [Google Scholar] [CrossRef]
- Albarracin, R.; Ardila-Rey, J.A.; Mas’ud, A.A. On the use of monopole antennas for determining the effect of the enclosure of a power transformer tank in partial discharges electromagnetic propagation. Sensors 2016, 16, 148. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G.; Li, Y.; Zhang, J.; Huang, R. On the feasibility of gap detection of power transformer partial discharge UHF signals: Gap propagation characteristics of electromagnetic waves. Energies 2017, 10, 1531. [Google Scholar] [CrossRef]
- Siegel, M.; Beltle, M.; Tenbohlen, S.; Coenen, S. Application of UHF sensors for PD measurement at power transformers. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 331–339. [Google Scholar] [CrossRef]
- Siegel, M.; Beltle, M.; Tenbohlen, S. Characteristics of UHF PD sensors for power transformers using an oil-filled GTEM cell. IEEE Trans. Dielectr. Electr. Insul. 2017, 23, 1580–1588. [Google Scholar] [CrossRef]
- Mirzaei, H.; Akbari, A.; Gockenbach, E.; Miralikhani, K. Advancing new techniques for UHF PD detection and localization in the power transformers in the factory tests. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 448–455. [Google Scholar] [CrossRef]
- Tang, Z.; Li, C.; Cheng, X.; Wang, W.; Ji, J.; Li, J. Partial discharge location in power transformers using wideband RF detection. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 1193–1199. [Google Scholar] [CrossRef]
- Judd, M.; Yang, L.; Hunter, I. Partial discharge monitoring for power transformers using UHF sensors part 1: Sensors and signal interpretation. IEEE Electr. Insul. Mag. 2005, 21, 5–14. [Google Scholar] [CrossRef]
- Tang, Z.; Li, C.; Wang, W.; Wang, H.; Wang, L.; Ding, Y. The propagation characteristics of electromagnetic wave generated from partial discharges in power transformer by FDTD simulation. In Proceedings of the Electrical Insulation and Dielectric Phenomena, Vancouver, BC, Canada, 17–20 October 2007; pp. 200–203. [Google Scholar]
- Wang, P.; Li, J.; Zhao, L.; Jiang, T.; He, Z. Investigation on the propagation characteristic of electromagnetic waves in converter transformers. In Proceedings of the IEEE International Conference on High Voltage Engineering and Application, Shanghai, China, 17–20 September 2012; pp. 353–357. [Google Scholar]
- Okabe, S.; Yuasa, S.; Kaneko, S.; Yoshimura, M.; Muto, H.; Yoshiyasu, H.; Nishida, C.; Kamei, M. Simulation of propagation characteristics of higher order mode electromagnetic waves in GIS. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 855–861. [Google Scholar] [CrossRef]
- Yoshimura, M.; Muto, H.; Nishida, C.; Kamei, M.; Okabe, S.; Kaneko, S. Propagation properties of electromagnetic wave through T-branch in GIS. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 328–333. [Google Scholar] [CrossRef]
- Behrmann, G.; Smajic, J. RF PD signal propagation in GIS: Comparing S-parameter measurements with an RF transmission model for a short section of GIS. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1331–1337. [Google Scholar] [CrossRef]
- Mirzaei, H.R.; Akbari, A.; Gockenbach, E.; Zanjani, M.; Miralikhani, K. A novel method for ultra-high-frequency partial discharge localization in power transformers using the particle swarm optimization algorithm. IEEE Electr. Insul. Mag. 2013, 29, 26–39. [Google Scholar] [CrossRef]
- Choi, W.; Hwangbo, S.; Park, C.; Park, J. Denoising of UHF Signals Based on RBPF and the Localization of PD Sources Using FDTD Method in Power Transformer; No. A2-105; Cigre2016: Paris, France, 2016. [Google Scholar]
- Du, J.; Chen, W.; Xie, B. Simulation analysis on the propagation characteristics of electromagnetic wave generated by partial discharges in power transformer. In Proceedings of the 2016 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Toronto, ON, Canada, 16–19 October 2016; pp. 179–182. [Google Scholar]
- Sinaga, H.H.; Phung, B.T.; Blackburn, T.R. Partial discharge localization in transformers using UHF detection method. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1891–1900. [Google Scholar] [CrossRef]
- Judd, M.D.; Hampton, B.F.; Farish, O. Modeling partial discharge excitation of UHF signals in waveguide structures using Green’s functions. IEE Proc. Sci. Meas. Technol. 1996, 143, 63–70. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1996, AP-14, 302–307. [Google Scholar]
- Weiland, T. Time domain electromagnetic field computation with finite difference methods. Int. J. Numer. Modell. Electr. Netw. Devices Fields 1996, 9, 295–319. [Google Scholar] [CrossRef]
- Homsup, N.; Jariyanorawiss, T. An improved FDTD model for the feeding gap of a dipole antenna. In Proceedings of the IEEE SoutheastCon 2010, Concord, NC, USA, 18–21 March 2010; pp. 475–478. [Google Scholar]
- Viola, F.; Romano, P. Building Partial Discharge Signal Wireless Probes; Progress in Compact Antennas; Laure Huitema, Intech: London, UK, 2014; pp. 177–203. [Google Scholar]
- Liu, T.; Zhao, Y.; Zheng, Y.; Jia, M. Accurate computation of input admittance of the antennas on the platform using the advanced delta-gap source model. In Proceedings of the Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, Taipei, Taiwan, 23–27 July 2012; pp. 30–34. [Google Scholar]
- Liu, L.; Weng, Y.; Cheung, S.; Yuk, T.; Foged, L. Modeling of cable for measurements of small monopole antennas. In Proceedings of the Antennas and Propagation Conference, Loughborough, UK, 14–15 November 2011. [Google Scholar]
- Hyun, S.; Kim, S.; Kim, Y. Finite-difference time-domain model for the feeding gap of coaxial probe driven antennas. IET Microw. Propag. 2009, 3, 501–506. [Google Scholar] [CrossRef]
- Hertel, T.; Smith, G. On the convergence of common FDTD feed models for antennas. IEEE Trans. Antennas Propag. 2003, 51, 1771–1779. [Google Scholar] [CrossRef]
- Akbazadeh, A.R.; Shen, Z. On the gap source model for monopole antenna. IEEE Antennas Wirel. Propag. Lett. 2008, 7, 115–118. [Google Scholar] [CrossRef]
- Schmitt, H.J.; Harrison, C.W., Jr.; Williams, C.S., Jr. Calculated and experimental response of thin cylindrical antennas to pulse excitation. IEEE Trans. Antennas Propag. 1966, 14, 120–127. [Google Scholar] [CrossRef]
- Yang, L.; Judd, M.D. Propagation characteristics of UHF signals in transformers for locating partial discharge sources. In Proceedings of the 13rd International Symposium on High Voltage Engineering, Delft, The Netherlands, 25–29 August 2003. [Google Scholar]


| Material (Model Component) | Conductivity (S/m) | Relative Permittivity | Relative Permeability |
|---|---|---|---|
| Air | 0 | 1 | 1 |
| Copper (winding model) | 6.0 × 107 | ∞ | 1 |
| Paper (layer-insulation) | 1.0 × 10−14 | 3.9 | 1 |
| Silicon steel (core) | 1.0 × 105 | ∞ | 6000 |
| Steel (tank) | 5.0 × 105 | ∞ | 500 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umemoto, T.; Tenbohlen, S. Novel Simulation Technique of Electromagnetic Wave Propagation in the Ultra High Frequency Range within Power Transformers. Sensors 2018, 18, 4236. https://doi.org/10.3390/s18124236
Umemoto T, Tenbohlen S. Novel Simulation Technique of Electromagnetic Wave Propagation in the Ultra High Frequency Range within Power Transformers. Sensors. 2018; 18(12):4236. https://doi.org/10.3390/s18124236
Chicago/Turabian StyleUmemoto, Takahiro, and Stefan Tenbohlen. 2018. "Novel Simulation Technique of Electromagnetic Wave Propagation in the Ultra High Frequency Range within Power Transformers" Sensors 18, no. 12: 4236. https://doi.org/10.3390/s18124236
APA StyleUmemoto, T., & Tenbohlen, S. (2018). Novel Simulation Technique of Electromagnetic Wave Propagation in the Ultra High Frequency Range within Power Transformers. Sensors, 18(12), 4236. https://doi.org/10.3390/s18124236





