Decentralized 3D Collision Avoidance for Multiple UAVs in Outdoor Environments
Abstract
1. Introduction
- First, we propose 3D-SWAP, a novel algorithm for 3D collision avoidance with multiple UAVs. The algorithm extends ideas from our previous work on ground robots that swap their positions in a traffic roundabout fashion. Here, a similar strategy on a horizontal plane is combined with a control of the UAVs’ altitude to navigate safely in 3D environments. Thus, UAVs that are far enough in altitude can ignore each other, making the swapping of the rest more efficient. Moreover, our approach requires low computational load, is decentralized and works with noisy sensors and restricted communication.
- Second, we detail our system architecture and the implementation of our method in a real team of UAVs. We tested our algorithm in realistic simulations to assess its performance. Later, we also run tests in outdoor field experiments, coping with noisy communication, inaccurate positioning systems, wind gusts, etc. We explain our procedures for the development and integration of the algorithm in these field experiments.
2. Related Work
3. Problem Description
- Holonomic vehicles. We model UAVs as holonomic vehicles (e.g., multirotors). They can move in any direction independently from their yaw orientation. We assume that their acceleration and speed constraints allow them to stop horizontally within a planar breaking distance , and stop their vertical movement within a vertical distance .
- Noisy localization. UAVs can localize themselves by means of noisy sensors. In outdoor scenarios, UAVs could carry GPS receivers and altimeters, for instance. Each UAV has access to its own noisy localization , such that and . and are the maximum localization errors on the xy-plane and altitude, respectively. We differentiate them, as altitude is usually more precise due to the use of altimeters or lasers.
- Local communication. If two UAVs i and j are within communication range, i.e., , they can exchange their noisy localizations and . Thus, UAVs share with their neighbors their position, but not their goals, velocities nor orientations. We do not assume a perfect communication. When communication links fail, other UAVs could still be detected with the onboard sensors.
- Obstacle detection. UAVs have onboard sensors to detect obstacles within a 3D distance . In particular, we assume that each UAV has a 3D sensor generating poincloud-based measurements from the obstacles around (e.g., a Lidar). Each pointcloud consists of M points, where each point m, without losing generality, can be expressed in cylindrical coordinates relative to the UAV . Again, we assume those measurements to be noisy.
4. 3D-SWAP
4.1. Overview and Preliminaries
| Algorithm 1 3D-SWAP for each UAV i |
Input: Pointcloud from local sensors, current position , goal position
|
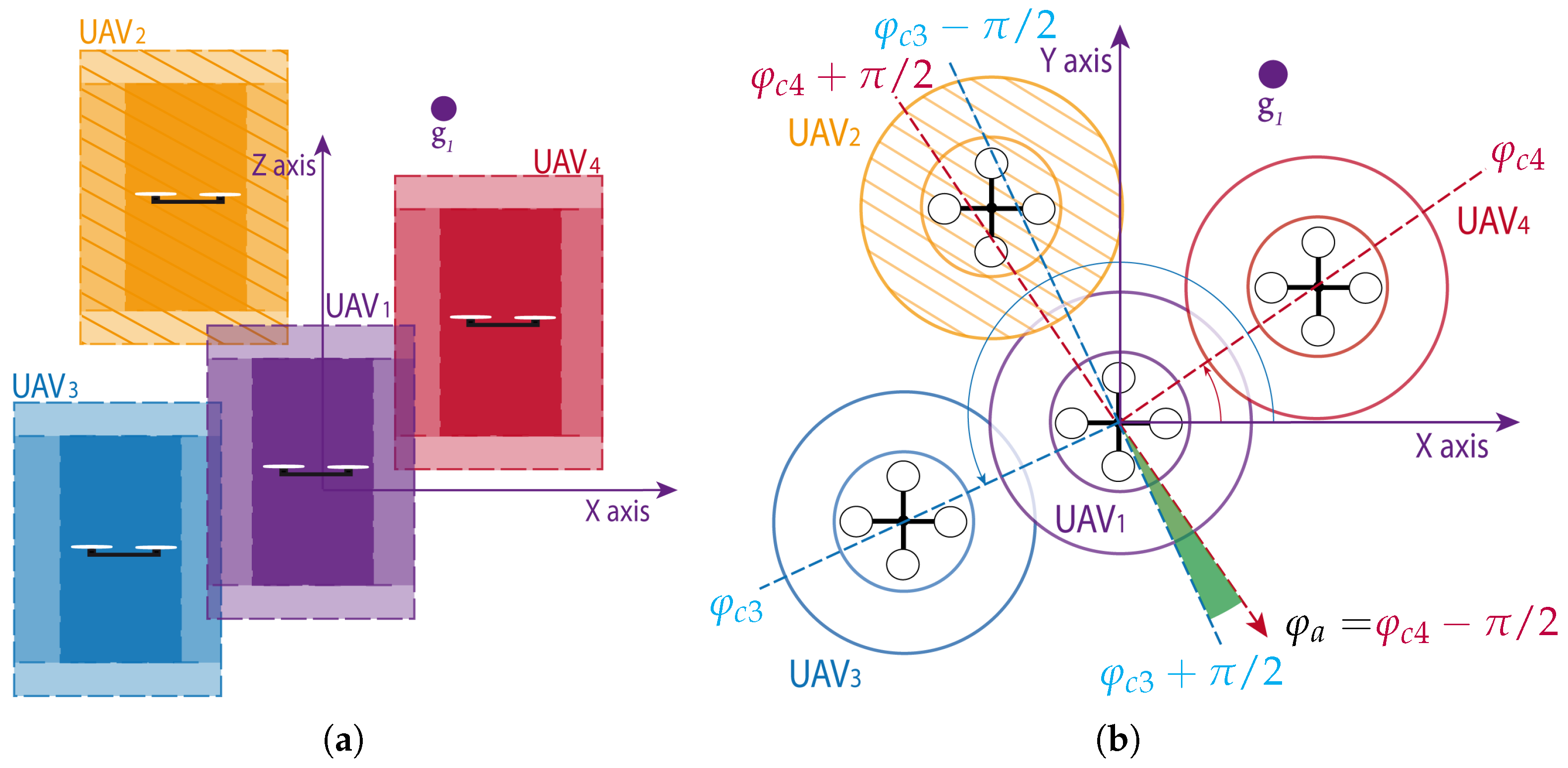
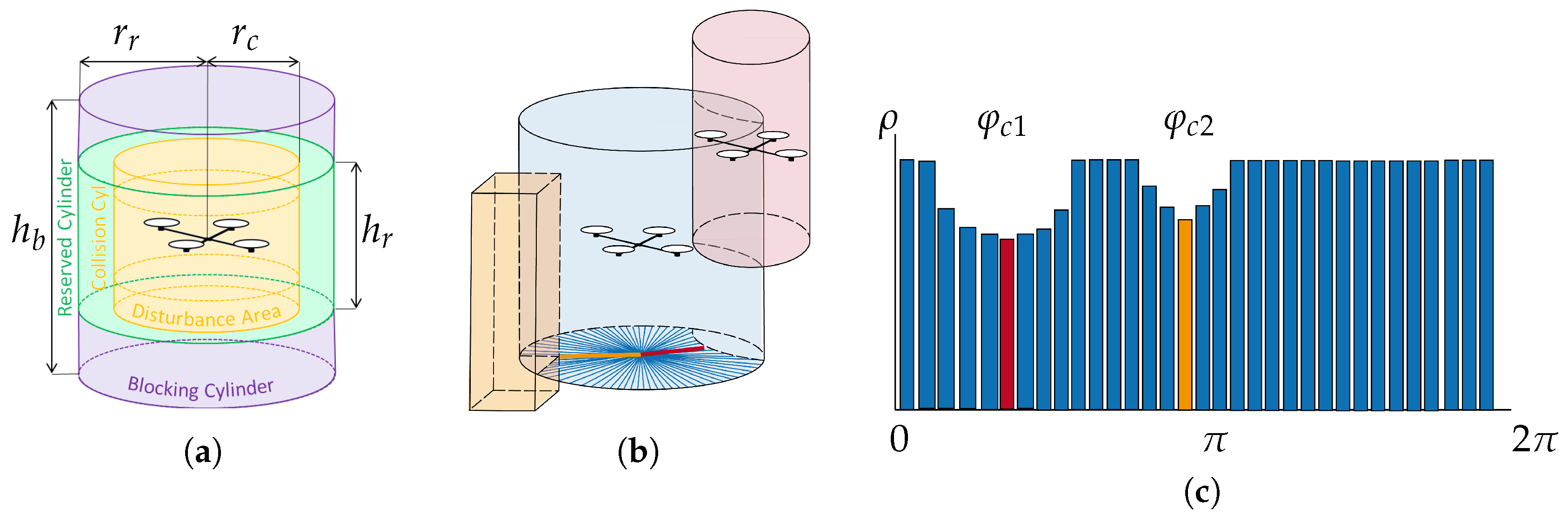
4.2. The Cylindrical Obstacle Diagram
4.3. Avoidance Maneuvers
5. Discussion
5.1. Convergence
5.2. Optimality and Robustness
5.3. Scalability
6. System Integration and Experiments
6.1. Aerial Platforms
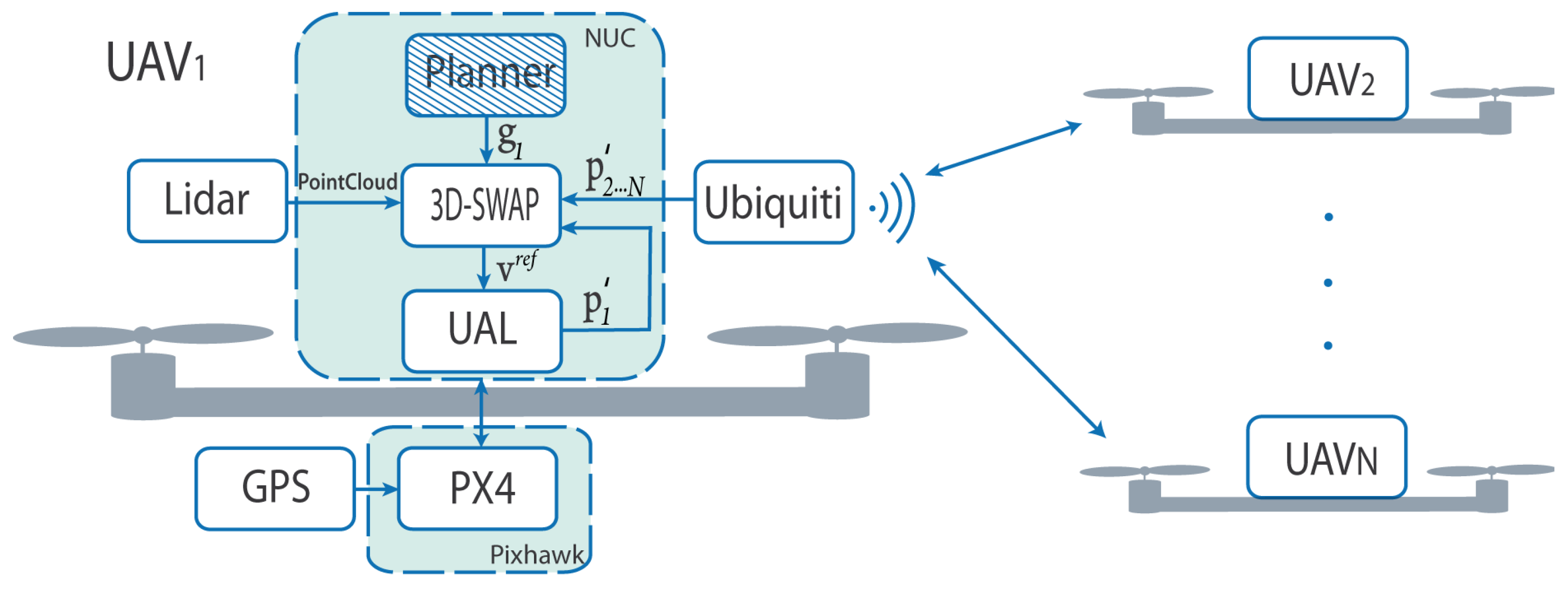
6.2. System Integration
6.3. Simulations
6.4. Field Experiments
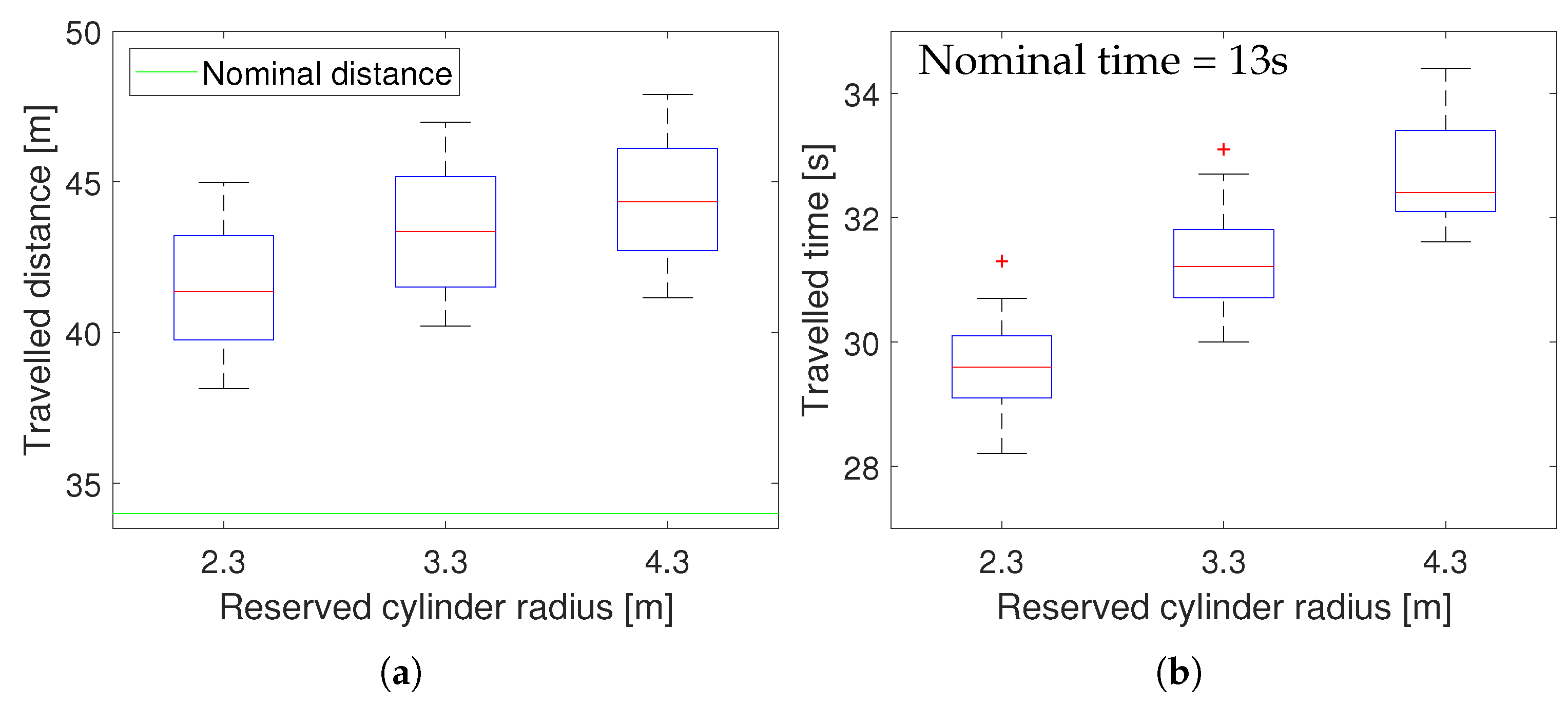
6.4.1. Tuning Parameters
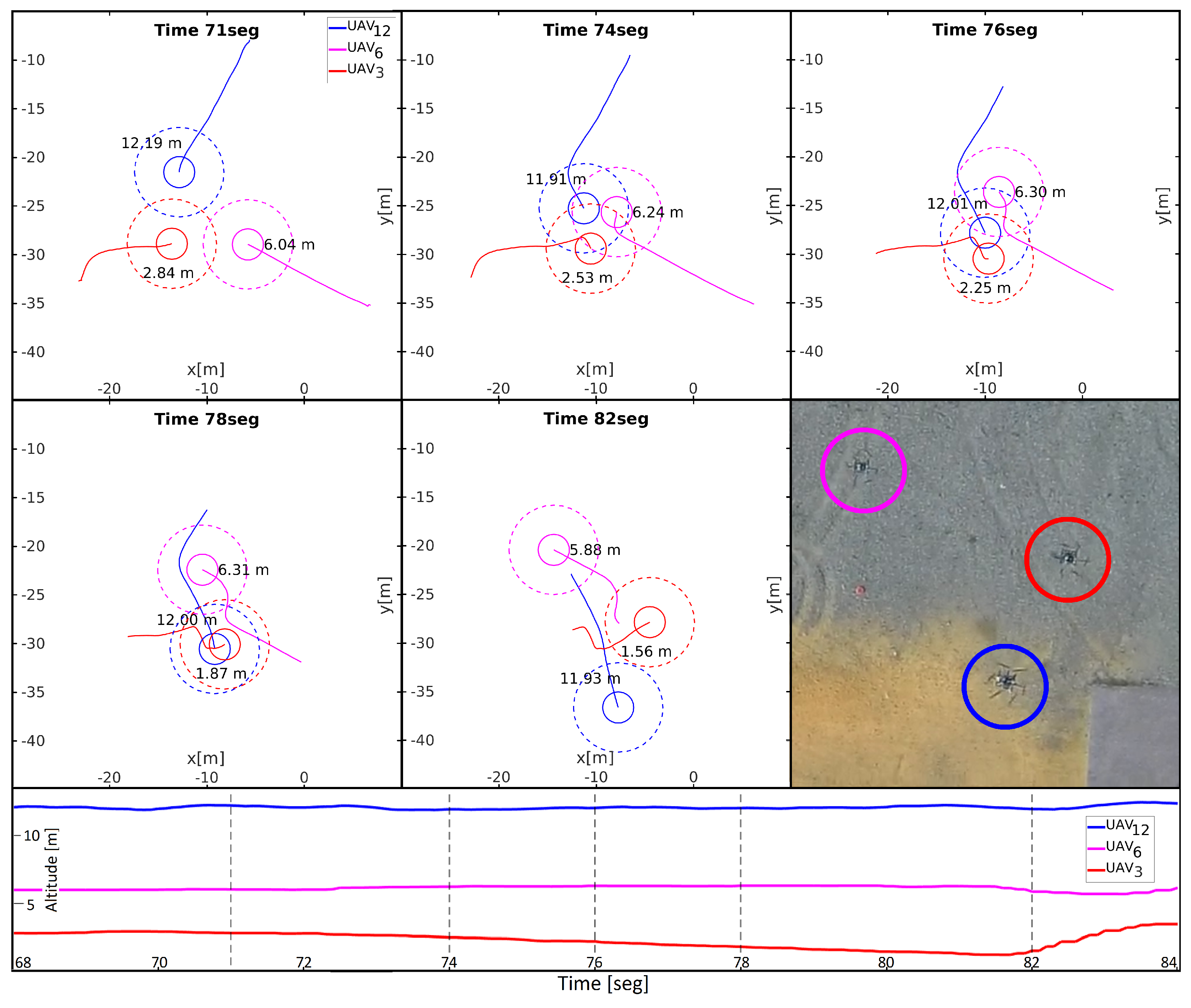
6.4.2. Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mellinger, D.; Shomin, M.; Michael, N.; Kumar, V. Cooperative Grasping and Transport Using Multiple Quadrotors. In Distributed Autonomous Robotic Systems: The 10th International Symposium; Martinoli, A., Mondada, F., Correll, N., Mermoud, G., Egerstedt, M., Hsieh, M.A., Parker, L.E., Støy, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 545–558. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef]
- Nägeli, T.; Meier, L.; Domahidi, A.; Alonso-Mora, J.; Hilliges, O. Real-time Planning for Automated Multi-view Drone Cinematography. ACM Trans. Graph. 2017, 36, 132:1–132:10. [Google Scholar] [CrossRef]
- Ferrera, E.; Capitán, J.; Castaño, A.R.; Marrón, P.J. Decentralized safe conflict resolution for multiple robots in dense scenarios. Robot. Auton. Syst. 2017, 91, 179–193. [Google Scholar] [CrossRef]
- Goerzen, C.; Kong, Z.; Mettler, B. A Survey of Motion Planning Algorithms from the Perspective of Autonomous UAV Guidance. J. Intell. Robot. Syst. 2009, 57, 65. [Google Scholar] [CrossRef]
- Mellinger, D.; Kushleyev, A.; Kumar, V. Mixed-integer quadratic program trajectory generation for heterogeneous quadrotor teams. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 477–483. [Google Scholar] [CrossRef]
- Yu, J.; LaValle, S.M. Optimal Multirobot Path Planning on Graphs: Complete Algorithms and Effective Heuristics. IEEE Trans. Robot. 2016, 32, 1163–1177. [Google Scholar] [CrossRef]
- Chen, Y.; Cutler, M.; How, J.P. Decoupled multiagent path planning via incremental sequential convex programming. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5954–5961. [Google Scholar] [CrossRef]
- Turpin, M.; Mohta, K.; Michael, N.; Kumar, V. Goal assignment and trajectory planning for large teams of interchangeable robots. Auton. Robot. 2014, 37, 401–415. [Google Scholar] [CrossRef]
- Turpin, M.; Michael, N.; Kumar, V. CAPT: Concurrent assignment and planning of trajectories for multiple robots. Int. J. Robot. Res. 2014, 33, 98–112. [Google Scholar] [CrossRef]
- Liu, Y.; Bucknall, R. A survey of formation control and motion planning of multiple unmanned vehicles. Robotica 2018, 36, 1019–1047. [Google Scholar] [CrossRef]
- Karamouzas, I.; Guy, S.J. Prioritized group navigation with Formation Velocity Obstacles. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5983–5989. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Montijano, E.; Schwager, M.; Rus, D. Distributed multi-robot formation control among obstacles: A geometric and optimization approach with consensus. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 5356–5363. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Naegeli, T.; Siegwart, R.; Beardsley, P. Collision avoidance for aerial vehicles in multi-agent scenarios. Auton. Robot. 2015, 39, 101–121. [Google Scholar] [CrossRef]
- Kamel, M.; Alonso-Mora, J.; Siegwart, R.; Nieto, J. Robust collision avoidance for multiple micro aerial vehicles using nonlinear model predictive control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 236–243. [Google Scholar] [CrossRef]
- Lalish, E.; Morgansen, K.A. Distributed reactive collision avoidance. Auton. Robot. 2012, 32, 207–226. [Google Scholar] [CrossRef]
- Vásárhelyi, G.; Virágh, C.; Somorjai, G.; Tarcai, N.; Szörényi, T.; Nepusz, T.; Vicsek, T. Outdoor flocking and formation flight with autonomous aerial robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3866–3873. [Google Scholar] [CrossRef]
- Price, E.; Lawless, G.; Ludwig, R.; Martinovic, I.; Buelthoff, H.H.; Black, M.J.; Ahmad, A. Deep Neural Network-based Cooperative Visual Tracking through Multiple Micro Aerial Vehicles. IEEE Robot. Autom. Lett. 2018, 3, 3193–3200. [Google Scholar] [CrossRef]
- Droeschel, D.; Nieuwenhuisen, M.; Beul, M.; Holz, D.; Stückler, J.; Behnke, S. Multilayered Mapping and Navigation for Autonomous Micro Aerial Vehicles. J. Field Robot. 2016, 33, 451–475. [Google Scholar] [CrossRef]
- Nuske, S.; Choudhury, S.; Jain, S.; Chambers, A.; Yoder, L.; Scherer, S.; Chamberlain, L.; Cover, H.; Singh, S. Autonomous Exploration and Motion Planning for an Unmanned Aerial Vehicle Navigating Rivers. J. Field Robot. 2015, 32, 1141–1162. [Google Scholar] [CrossRef]
- Mcfadyen, A.; Mejias, L. A survey of autonomous vision-based See and Avoid for Unmanned Aircraft Systems. Prog. Aerosp. Sci. 2016, 80, 1–17. [Google Scholar] [CrossRef]
- Mcfadyen, A.; Mejias, L.; Corke, P.; Pradalier, C. Aircraft collision avoidance using spherical visual predictive control and single point features. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 50–56. [Google Scholar] [CrossRef]
- Furrer, F.; Burri, M.; Achtelik, M.; Siegwart, R. RotorS—A modular Gazebo MAV simulator framework. In Robot Operating System (ROS): The Complete Reference; Koubaa, A., Ed.; Springer International Publishing: Berlin, Germany, 2016; Volume 1, pp. 595–625. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrera, E.; Alcántara, A.; Capitán, J.; Castaño, A.R.; Marrón, P.J.; Ollero, A. Decentralized 3D Collision Avoidance for Multiple UAVs in Outdoor Environments. Sensors 2018, 18, 4101. https://doi.org/10.3390/s18124101
Ferrera E, Alcántara A, Capitán J, Castaño AR, Marrón PJ, Ollero A. Decentralized 3D Collision Avoidance for Multiple UAVs in Outdoor Environments. Sensors. 2018; 18(12):4101. https://doi.org/10.3390/s18124101
Chicago/Turabian StyleFerrera, Eduardo, Alfonso Alcántara, Jesús Capitán, Angel R. Castaño, Pedro J. Marrón, and Aníbal Ollero. 2018. "Decentralized 3D Collision Avoidance for Multiple UAVs in Outdoor Environments" Sensors 18, no. 12: 4101. https://doi.org/10.3390/s18124101
APA StyleFerrera, E., Alcántara, A., Capitán, J., Castaño, A. R., Marrón, P. J., & Ollero, A. (2018). Decentralized 3D Collision Avoidance for Multiple UAVs in Outdoor Environments. Sensors, 18(12), 4101. https://doi.org/10.3390/s18124101




