1. Introduction
Internet of Things (IoT) is a network that aims to connect all the devices in the world and makes the information exchange between them easily. With the rapid development of wireless communication technologies, the IoT has been realized step by step in recent years. Over 60% of the IoT application scenarios are massive narrowband IoT (NB-IoT), whose characteristics include massive access devices, transmission delay tolerance and low cost, such as smart meters, eHealth, and so on [
1,
2,
3,
4,
5]. The low-cost requirement means that cheap/inaccurate crystal oscillators are used, which leads to a large frequency offset between the transmitter and the receiver. It poses challenges to the design of the downlink synchronization signal which is used to obtain the downlink timing. In a traditional Long Term Evolution (LTE) system, the primary synchronization signal (PSS) and the secondary synchronization signal (SSS) are used to achieve the downlink timing [
6,
7]. PSS detection, as the very first process, usually suffers from the large frequency offset. The frequency offset will destroy the ‘perfect’ correlation of the Zadoff–Chu (ZC) sequence used by the PSS, which could lead to a timing error even if there is no noise [
7]. Then, the differential correlator or partial correlator is usually used to remove or diminish the effects of the frequency offset on timing detection [
8].
In this paper, we firstly proposed a new general synchronization signal structure with two PSS sequences in an adjacent period which are conjugated to remove the potential timing error caused by the frequency offset. Then, we analyze the suitable sequence for our proposed structure and analyze a special ZC sequence as an example. Finally, simulation results are given to verify our proposed design.
2. System Model
Assume that the synchronization signal in time domain is
at the transmitter, where
is the length of the synchronization sequence. Assuming there is one receiving antenna, the received signal at the device can be written as follows:
where
is the channel gain, unknown but assumed to be constant over the PSS transmission duration,
is the number of samples corresponding to the signal propagation time between the transmitter and the receiver, and
is the white Gaussian noise.
When considering the frequency offset, the received signal at the device can be rewritten as follows:
where
is the Nyquist sampling rate without a consideration of the sampling offset and
is the frequency offset between the transmitter (base station) and the receiver (device).
At the receiver, a local sequence which is a copy of the transmitter synchronization sequence is used to detect the right receiving start time by calculating the correlation between the received signal and the local sequence. The output of the direct correlator can be written as follows [
9]:
When the phase change caused by the frequency offset is large in the signal duration, e.g.,
, the M-part correlator or differential correlator will be used to replace the direct correlator [
8]. Just as the name implies, the purpose of the M-part correlator is to divide the sequence into M parts while doing correlation operations. M is decided by the maximum phase shift, and the relationship can be written as follows:
where
is the threshold to limit the phase change in each part; its value depends on its specific applied environment. Then, we can work out the number of segments:
is the integer-valued function. Obviously, the maximum phase in each part will decrease as the number of segments increase, which means stronger frequency offset tolerance. The output of the M-part correlator can be written as follows:
Obviously, the processing gain will decrease approximately dB for the M-part correlator due to the non-coherent combination among the different parts compared to the direct correlator.
The output of the differential correlator can be expressed as follows [
10]:
Although the differentiation operation can remove the frequency offset perfectly, there will be at least a 3 dB loss in the signal-to-noise ratio (SNR) due to the fact that the noise is amplified by the multiplication between two received samples [
5]. Therefore, these two methods are usually used when the frequency offset is large.
Then, a maximum likelihood estimate (MLE) is used to estimate the right timing, and it can be expressed as follows [
9]:
3. Conjugated-Sequences-Based Timing Structure
Our proposed synchronization signal consists of a couple of sequences which are conjugated. When we ignore the noise and the channel gain (constant in one detection process), the output of the direct correlator in (3) can be rewritten as follows:
where
,
is the index of the direct correlator output with local sequence
.
The other synchronization sequence in our design is
. The corresponding correlator output can be expressed as follows:
where
,
is the index of the direct correlator output with local sequence
.
Obviously, when
without considering the data adjacent to the synchronization sequence, that is
It means if the timing estimated from the correlator with local sequence
is
the timing estimated from the correlator with local sequence
must happen at
where
and
are the timing estimation errors which are the same according to (11).
Therefore, the right timing can be estimated according to
which can remove the potential reducible timing error caused by the large frequency offset which is difficult to avoid [
11].
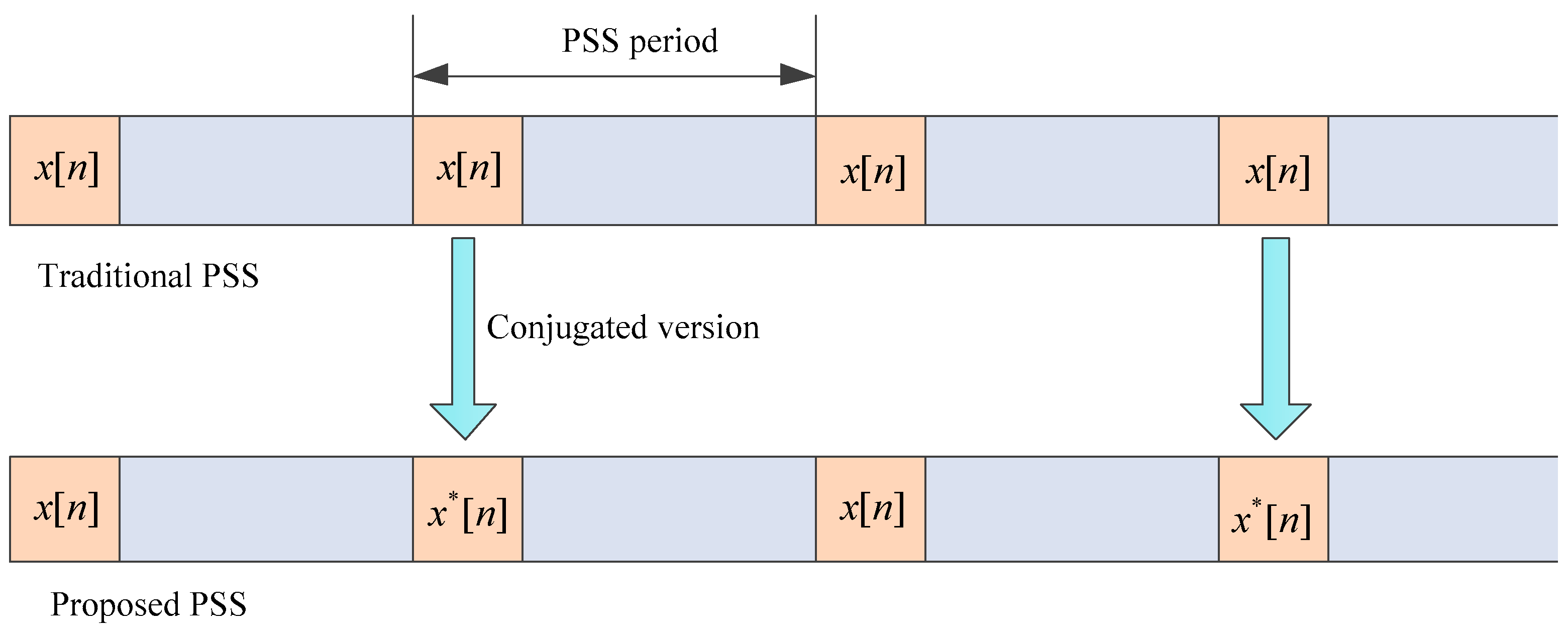
In the current LTE system, the synchronization signal is periodic, so we let the two PSS sequences in the adjacent period utilize the
and
, respectively, as shown in
Figure 1. When the timing error caused by the frequency offset is small (for the device with an expensive crystal oscillator), it needs to search just one of the PSS signals rather than two for the purpose of a quick search, low complexity, and compatibility. In addition, it can maintain the peak-to-average power ratio (PAPR) property of the original sequence
without the need of PAPR reduction techniques [
12,
13,
14,
15].
Obviously, the key of our proposed design is to find a sequence whose maximum correlator output is insensitive to the frequency offset.
4. Frequency Offset Tolerant Signal Selection
Accord to the Cauchy–Schwartz inequality [
16], the output of the direct correlator from Equation (9) satisfies
where
is the energy of the synchronization signal. The Equation (16) holds if and only if
where
is constant.
For the consideration of good PAPR, the amplitude of
should be constant (
). We assume
Substituting (8) into (17) yields
By comparing the coefficient of
on both sides of the equation, we can obtain
Then, substituting (20) into (19) yields
where
is the frequency offset normalized to the subcarrier spacing
. According to the property of the sine function, (21) can be rewritten as
where
,
is the integer-valued function. It means the correlator output only depends on the fractional part of coefficient
that corresponds to the sequence. For ease of discussion, we can only consider the value of
.
From the previous analysis, we know that the ZC sequence is one of the sequences that satisfies the constraints and is suitable for our proposed PSS design. It can be expressed as [
17]
where
is the length of the ZC sequence,
is the root of the ZC sequence and
.
Apparently, the correlator outputs of the ZC sequences with different roots are different. In addition, the low reduction of maximum output of the correlator under large frequency offsets is beneficial to our proposed method.
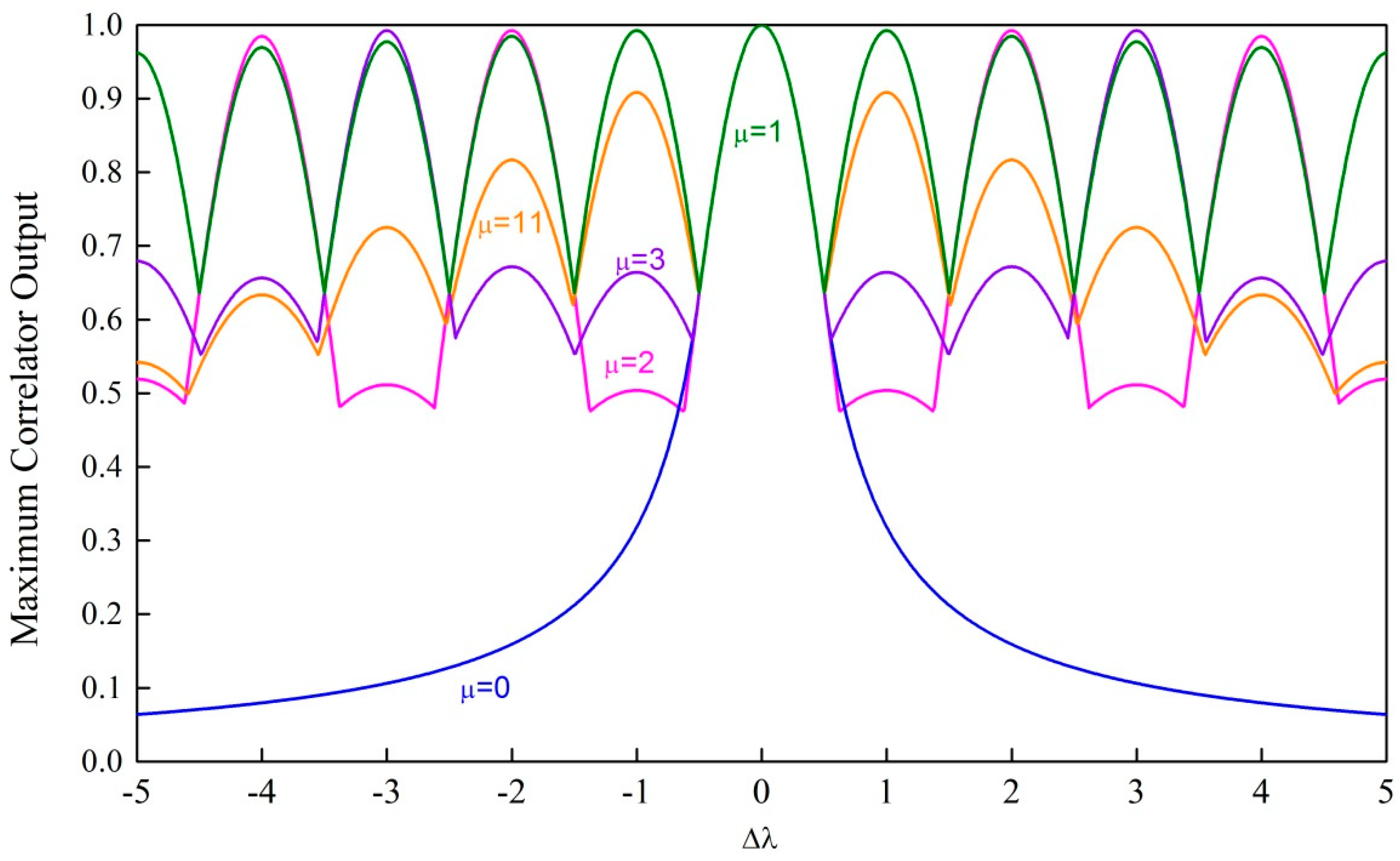
Figure 2 shows an example of the maximum correlator output of different ZC sequences (e.g.,
) under different frequency offsets, where different colors represent ZC sequences with different roots. The maximum output of the correlator is defined as
From
Figure 2, we can see that the ZC sequence with root
is most insensitive to the frequency offset. When
, (22) can be rewritten as
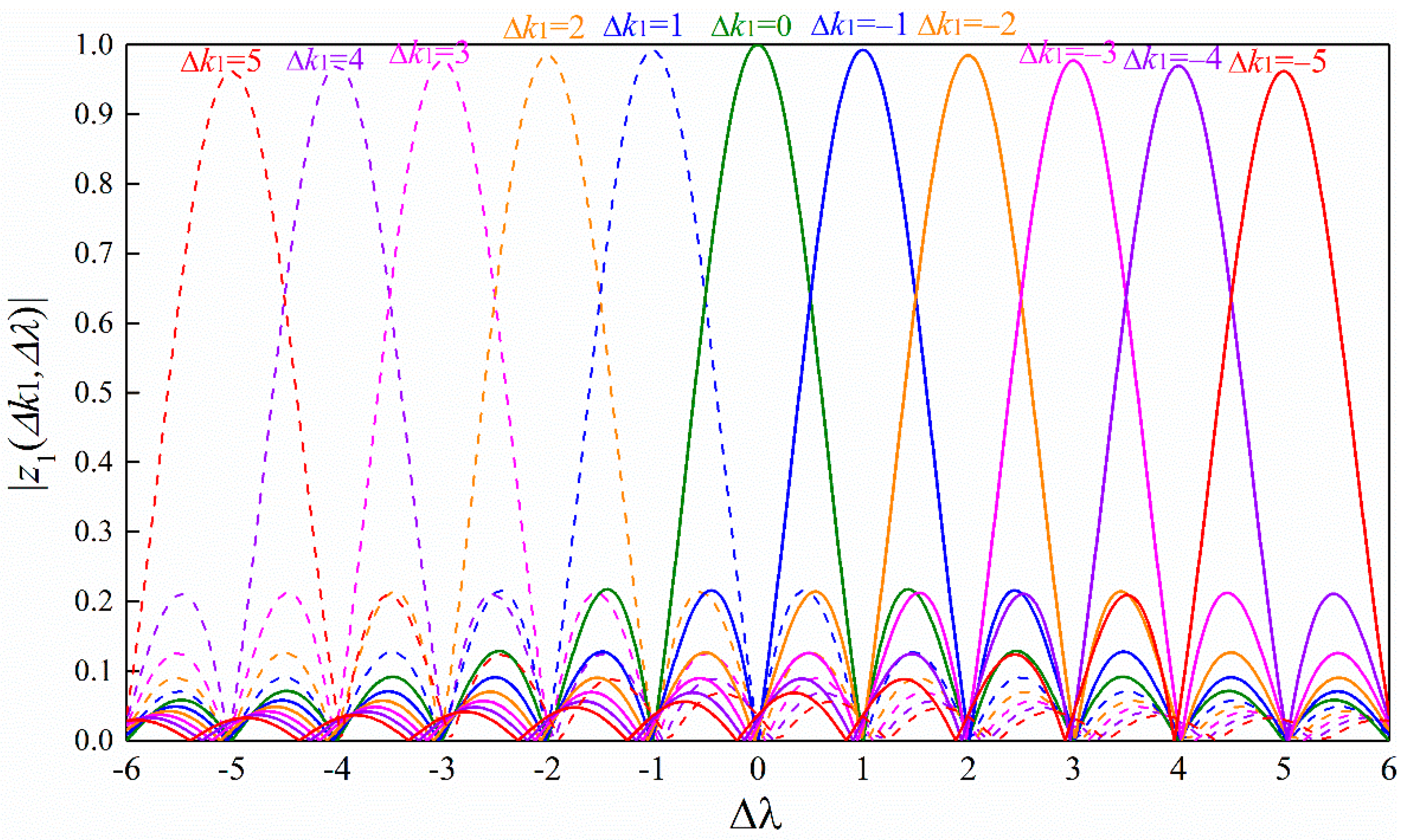
Figure 3 shows the correlator output in (25) under different frequency offsets and different timing offsets with
. We can see that there is no timing error when the frequency offset is small (e.g.,
). However, when the frequency offset increases, the timing error is present according to the criterion defined in (8). However, the timing error can be removed easily by our proposed design. In addition, by comparing
Figure 2 and
Figure 3, we can see that the minimum of the maximum correlator output decreases slowly when the frequency offset
increases step by 1. This is because the gap of the timing offset
corresponding to the adjacent peaks is one which is always true with
for arbitrary
. Therefore, the ZC sequence with
is suitable for our proposed conjugated-sequences-based timing structure.
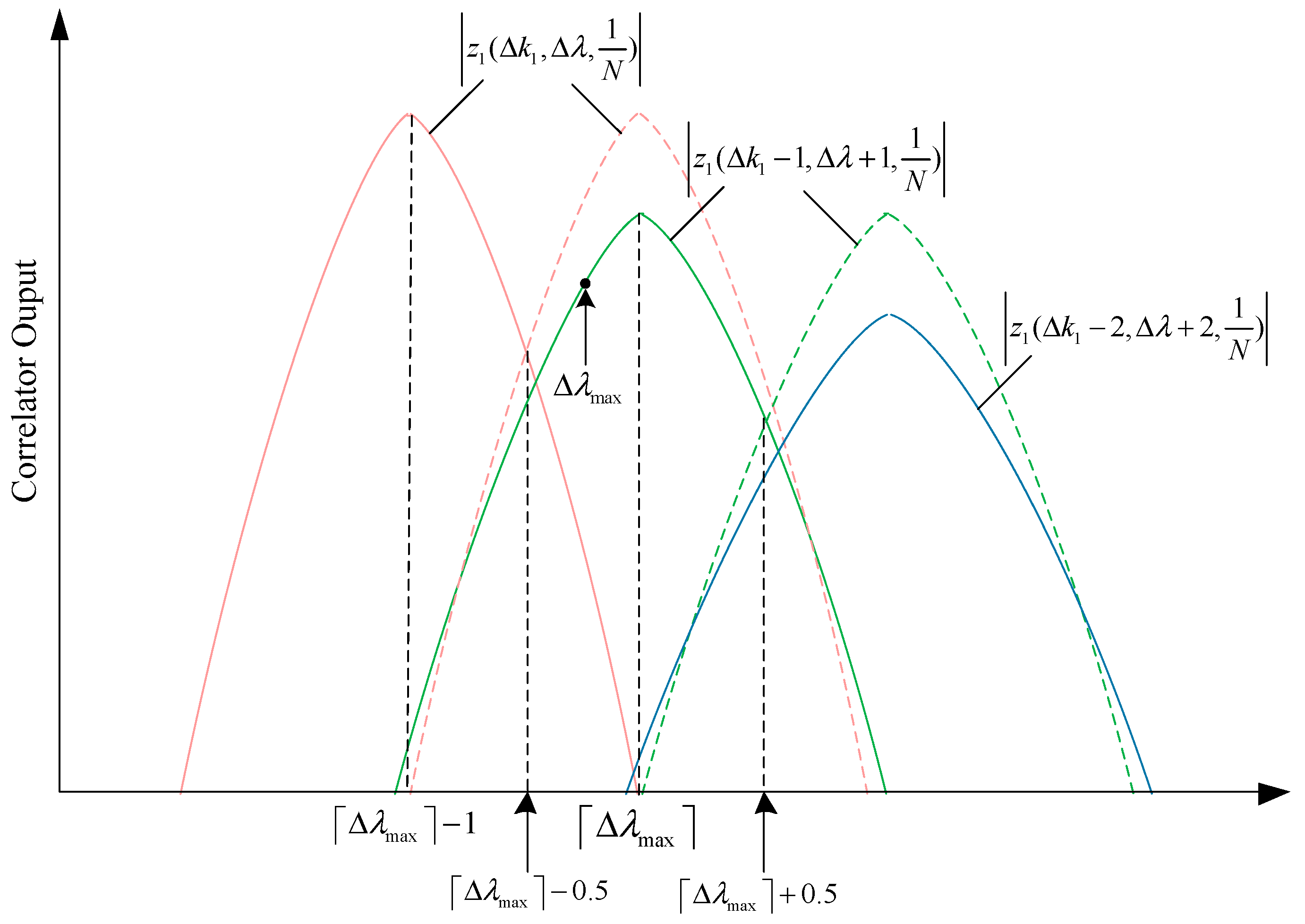
According to (25) and
Figure 3, we can know that the minimum of the maximum correlator output happens at the cross point corresponding to the adjacent timing offset. When
,
, it is easy to show that
according to (25). When
,
, it is also easy to show that
According to (26), (27) and
Figure 4, we can get that at the given maximum frequency offset
, the minimum of the maximum correlator output satisfies
The current narrowband PSS (NPSS) in NB-IoT is about 0.8 ms in time domain [
18], so the subcarrier spacing in our proposed PSS is
and
for the justice comparison. When the maximum frequency offset is 40 kHz, which is equal to 20 ppm at the carrier frequency 2 GHz, the maximum detection energy loss is approximately
which is smaller than the energy loss in the differential correlator and M-part correlator.
Therefore, the ZC sequence with root is very suitable for our proposed conjugated-sequences-based PSS structure whose correlator output is insensitive to frequency offset.
5. Simulation Results
In this section, simulation results are given to verify the performance of our proposed PSS signal with a couple of ZC sequences which are conjugated. The system parameters are set as follows: the proposed PSS is generated in a time domain in the orthogonal frequency division multiplexing (OFDM) system, the subcarrier spacing is
kHz, the length of ZC sequence is
, the root of ZC sequence is
, and the synchronization signal period is 10 ms (the same as the NPSS in NB-IoT [
18]). In the simulation, the frequency offset is randomly and uniformly selected and added. The additive white Gaussian noise (AWGN) channel is used in the simulations. When the timing error is larger than 1 us, we regard it as detection error.
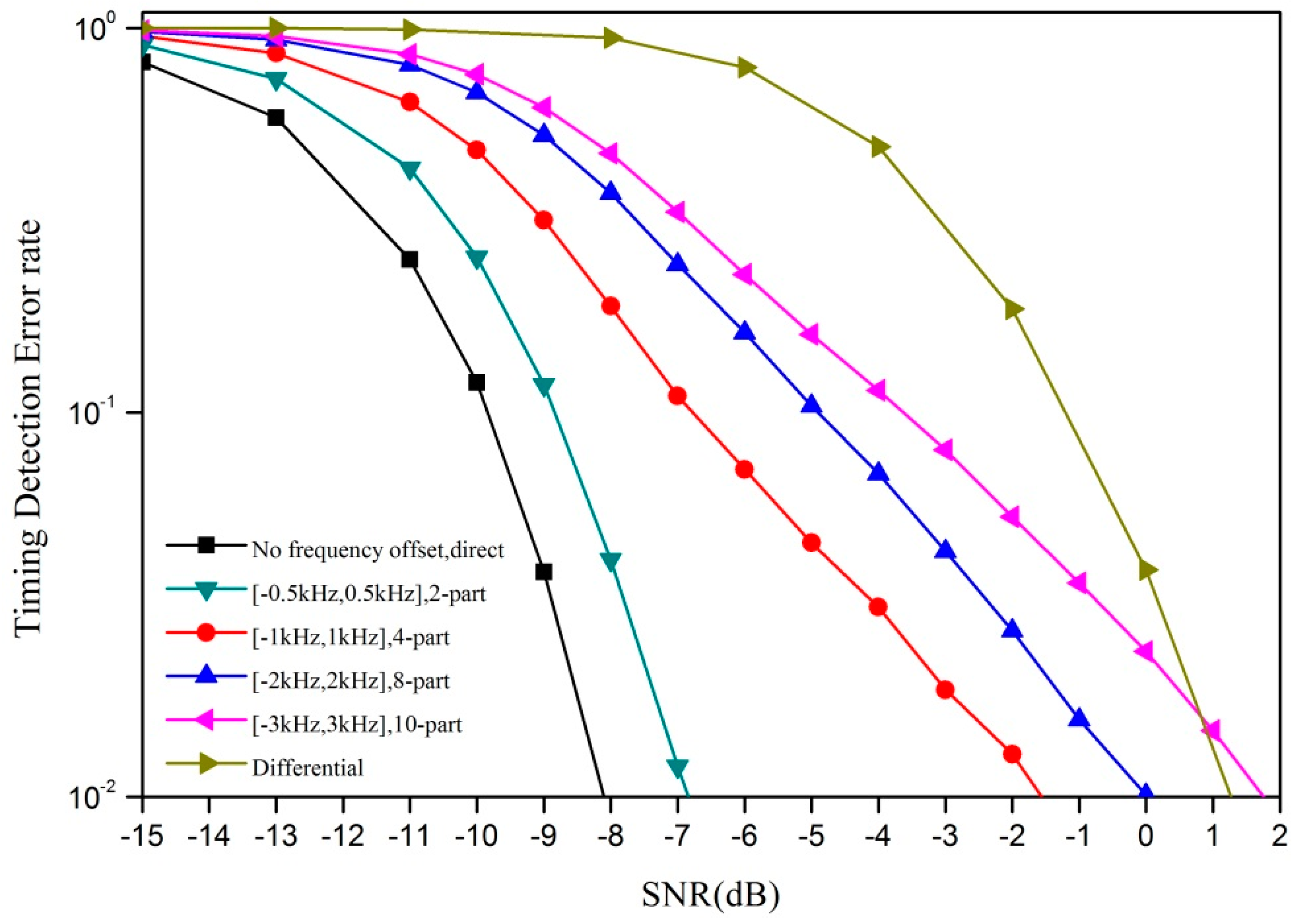
Figure 5 shows a contrast of the timing detection error rate between the M-part correlator and the differential correlator. We can see that 3 kHz is a cut-off point between the M-part correlator and the differential correlator. In low frequency offset scenarios, thanks to the reduction of phase change in each segment, the M-part correlator works better than the differential correlator. However, when the frequency offset is larger than 3 kHz or more, the M-part correlator has to enlarge M in order to ensure that each part’s phase change is small enough. A larger M means a lower correlation peak, so its performance largely depends on noise. In this scenario, differential correlator is evidently a better choice.
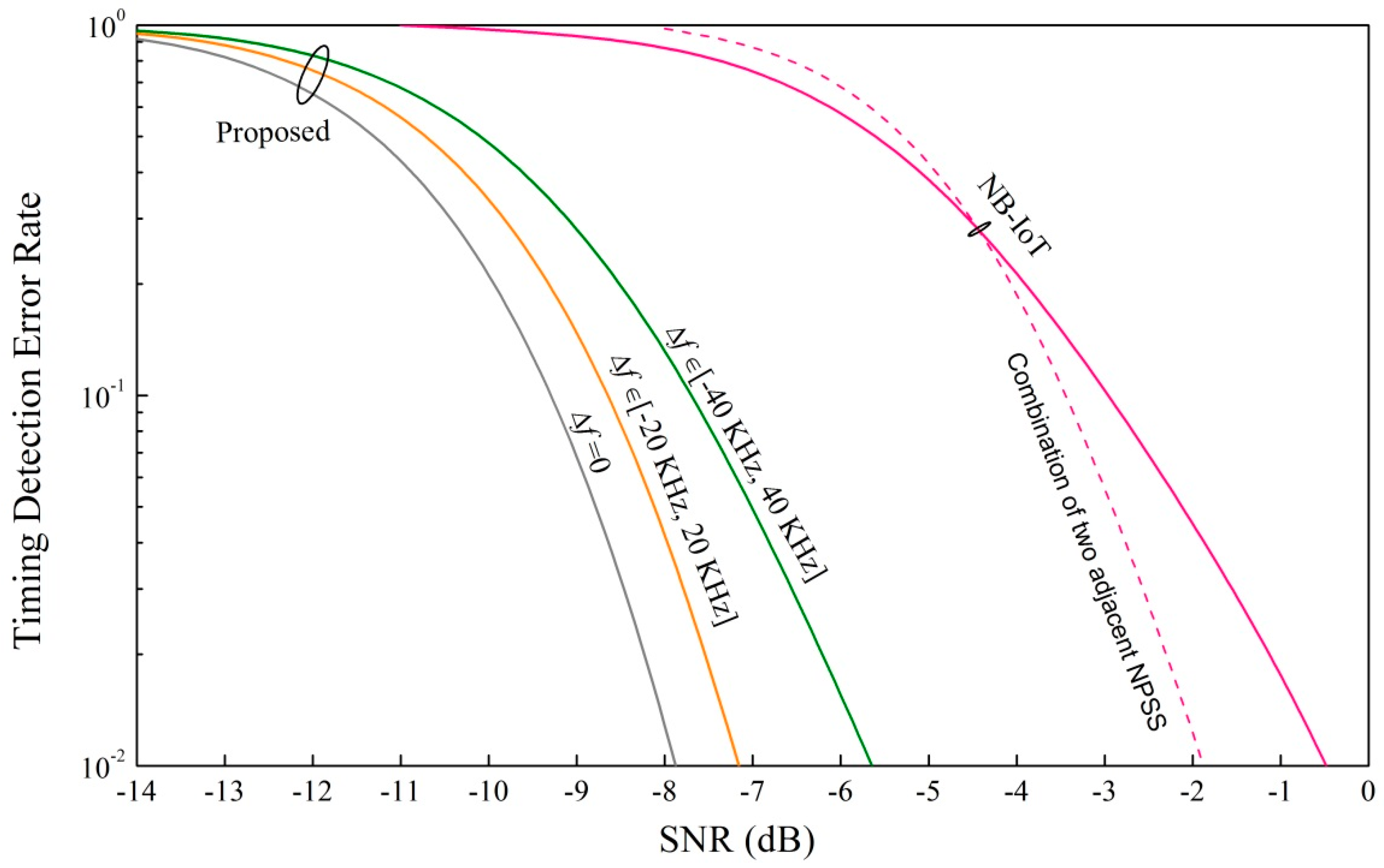
Figure 6 shows the timing detection error rate of our proposed PSS at different SNRs. We also add the NB-IoT NPSS detection performance as a reference where the differential correlator is used [
19]. For a fair comparison, we also simulated the timing performance of the combination of two adjacent NPSS that the estimated timing is the average of the timing estimated from the two adjacent NPSS. We can see that the deterioration of the timing performance caused by the frequency offset is small because the correlator output of the ZC sequence with root 1 is insensitive to the frequency offset. We can see that our proposed synchronization signal can work better than the NPSS with a differential correlator even under the maximum frequency offset 40 kHz. It is true that the detection performance of our proposed synchronization signal will be worse than the NB-IoT PSS with the increment of frequency offset due to the fact that the differentiation operation can remove the frequency offset effect on detection. However, our proposed PSS design is good enough to cover the potential frequency offset range in NB-IoT scenarios (less than 40 kHz [
20]).