On Consensus-Based Distributed Blind Calibration of Sensor Networks
Abstract
1. Introduction
2. Related Work
3. Problem Definition and the Basic Algorithm
4. Convergence Analysis
5. Extensions of the Basic Algorithm
5.1. Communication Errors
5.2. Measurement Noise
5.3. Asynchronous Broadcast Gossip Communication
- ,
- is the step size given by , where is the number of parameter updates of node i up to the iteration k, with ( denotes the indicator function),
- , whereare the corrected outputs of node and node i.
- ,
- ,
- , with and for all , , otherwise,
- ,
- , where and , for all , , otherwise.
6. Discussion
6.1. Rate of Convergence
6.2. Stationarity of the Measured Signal
6.3. Network Weights Design
- By reducing the values of all the elements in the i-th row of , or
- By increasing the values , , from the i-th column (keeping in mind that must be row stochastic).
6.4. Macro Calibration for Networks with Reference Nodes
6.5. Autonomous Gain Correction and Relationship with Time Synchronization
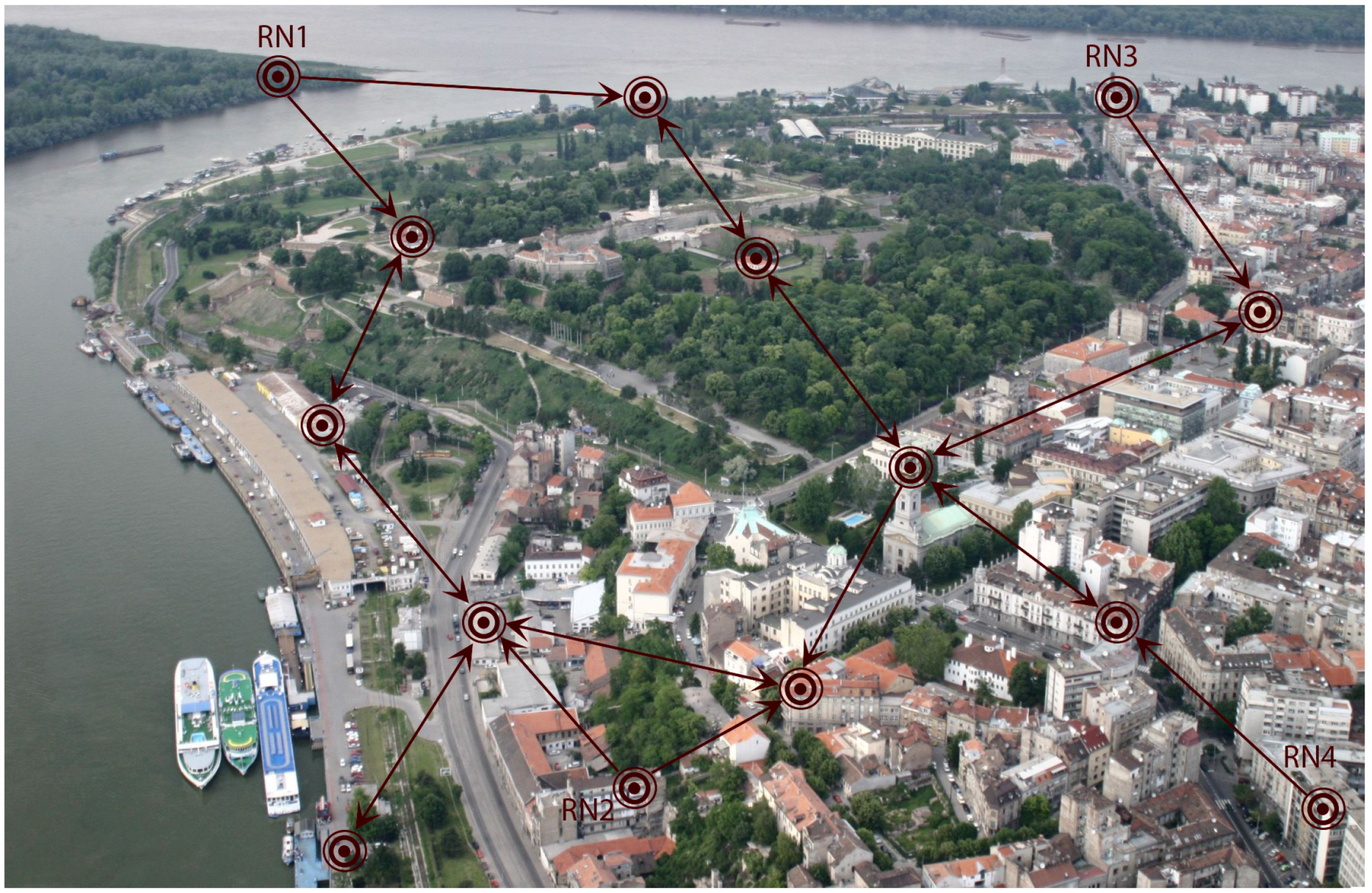
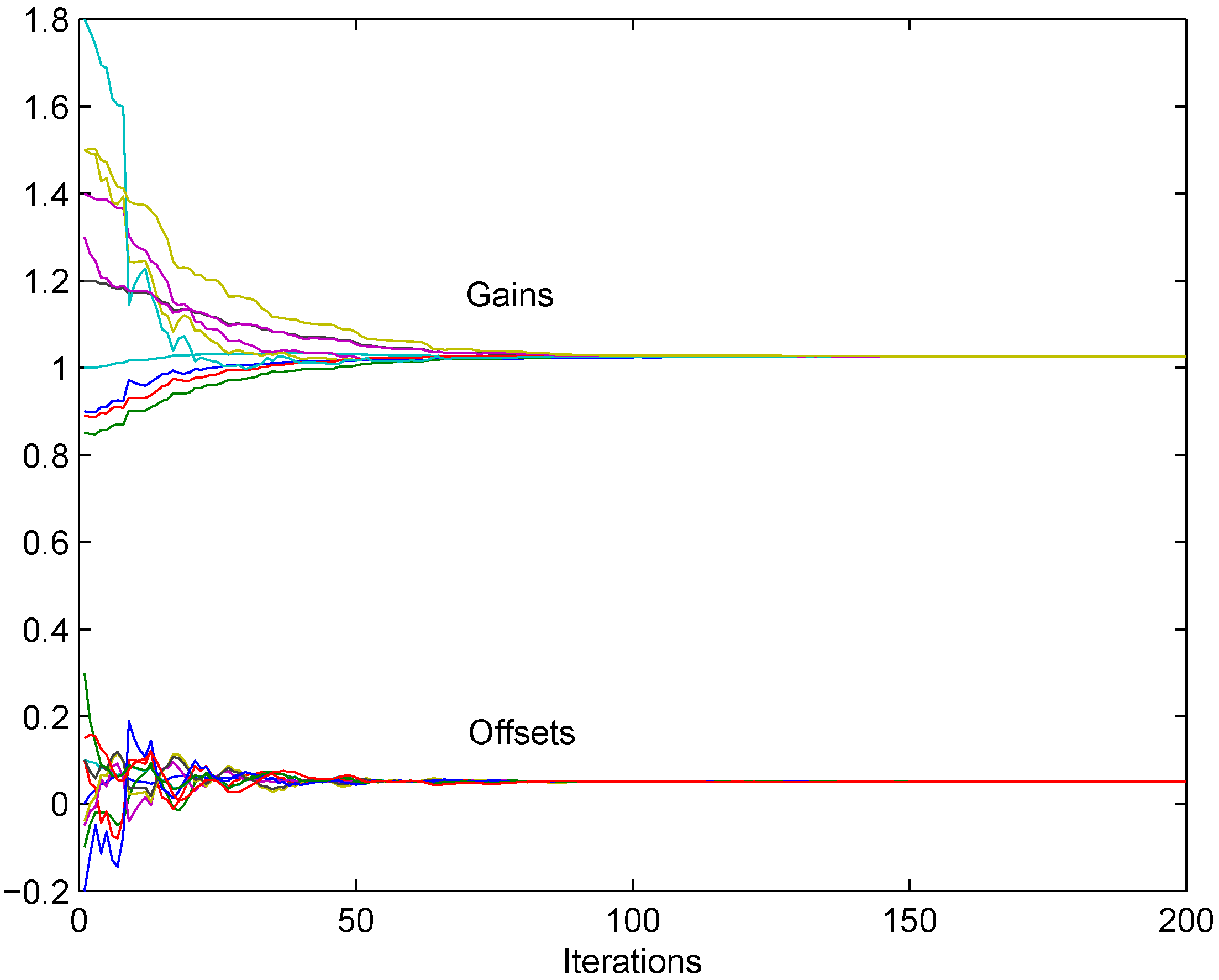
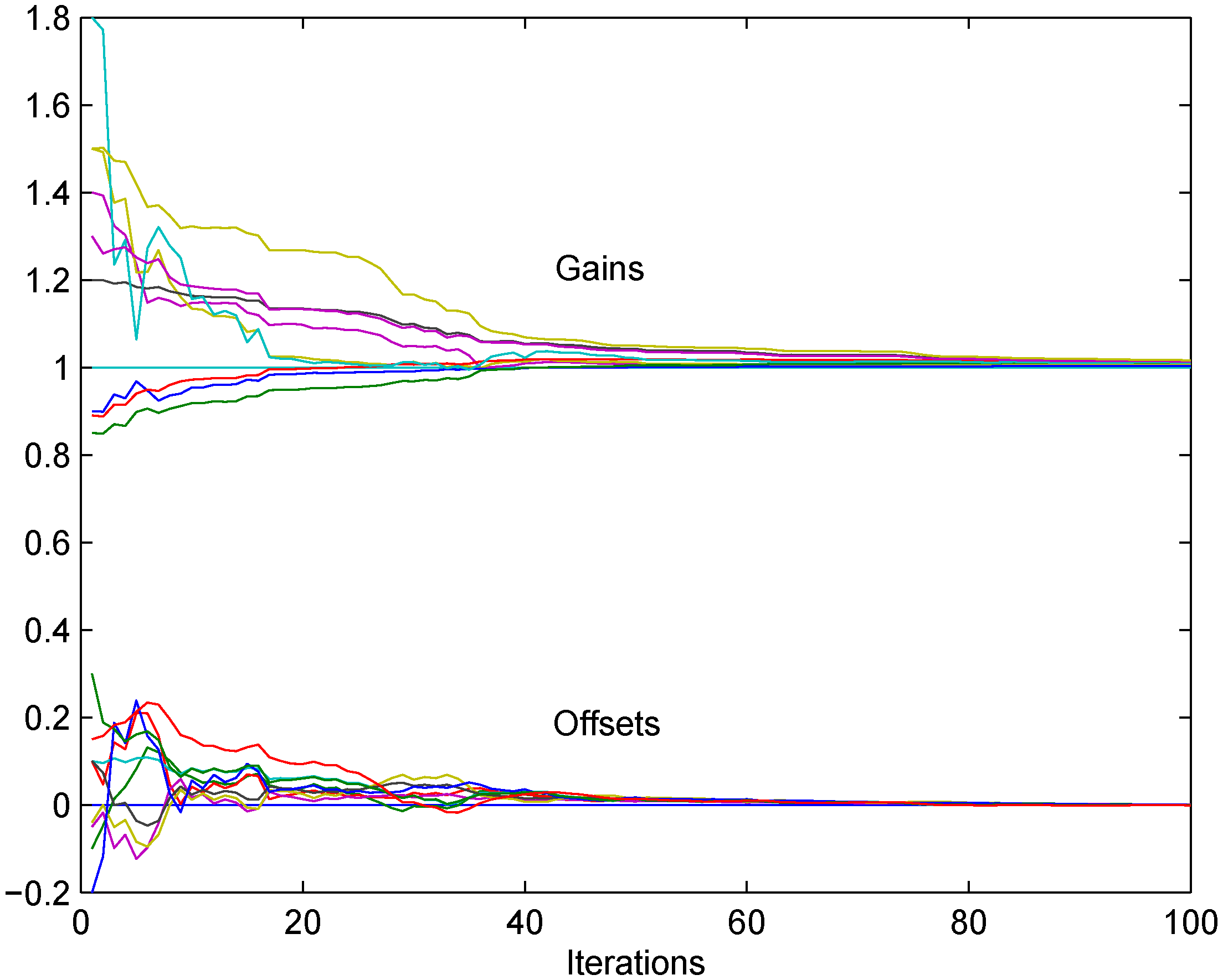
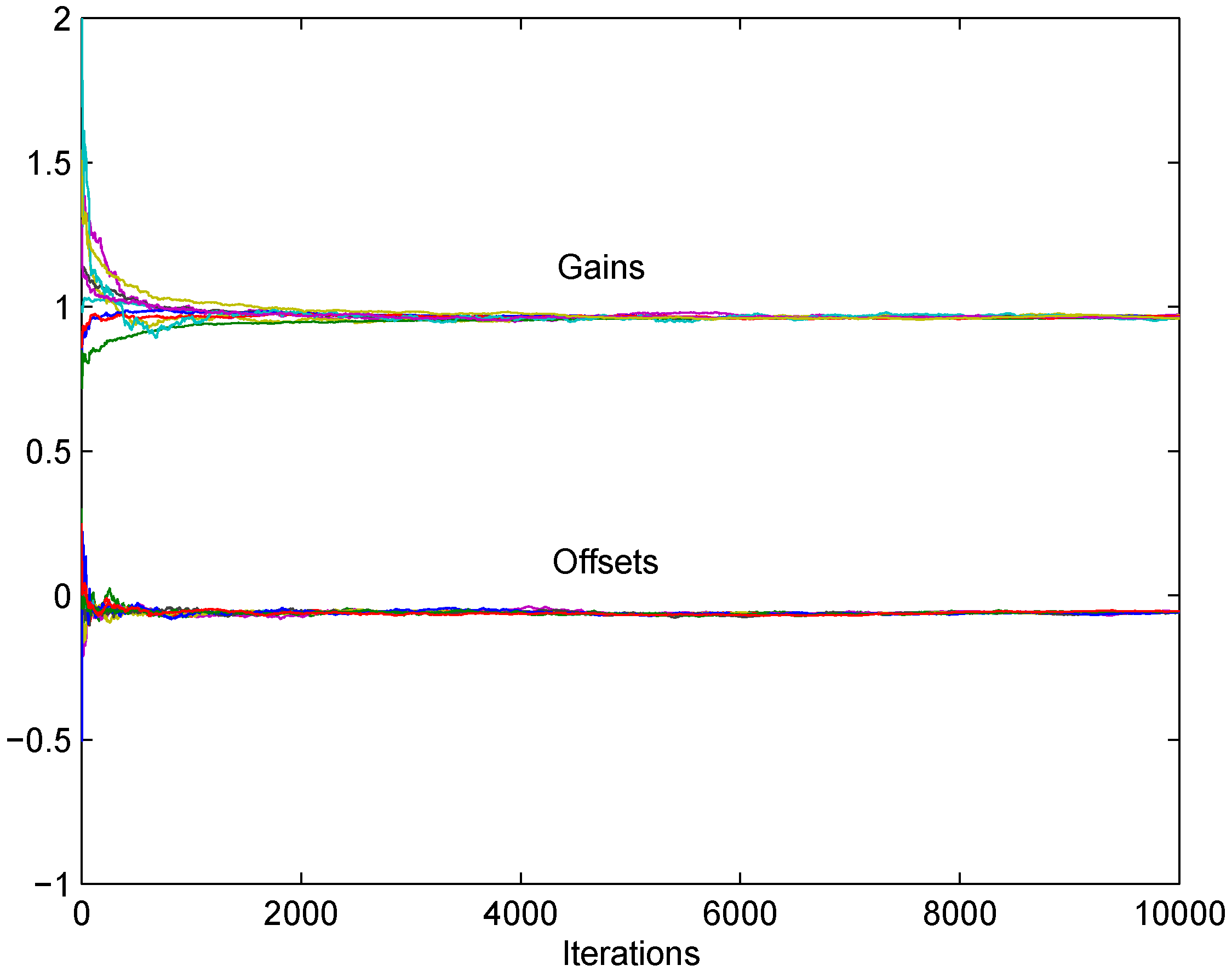
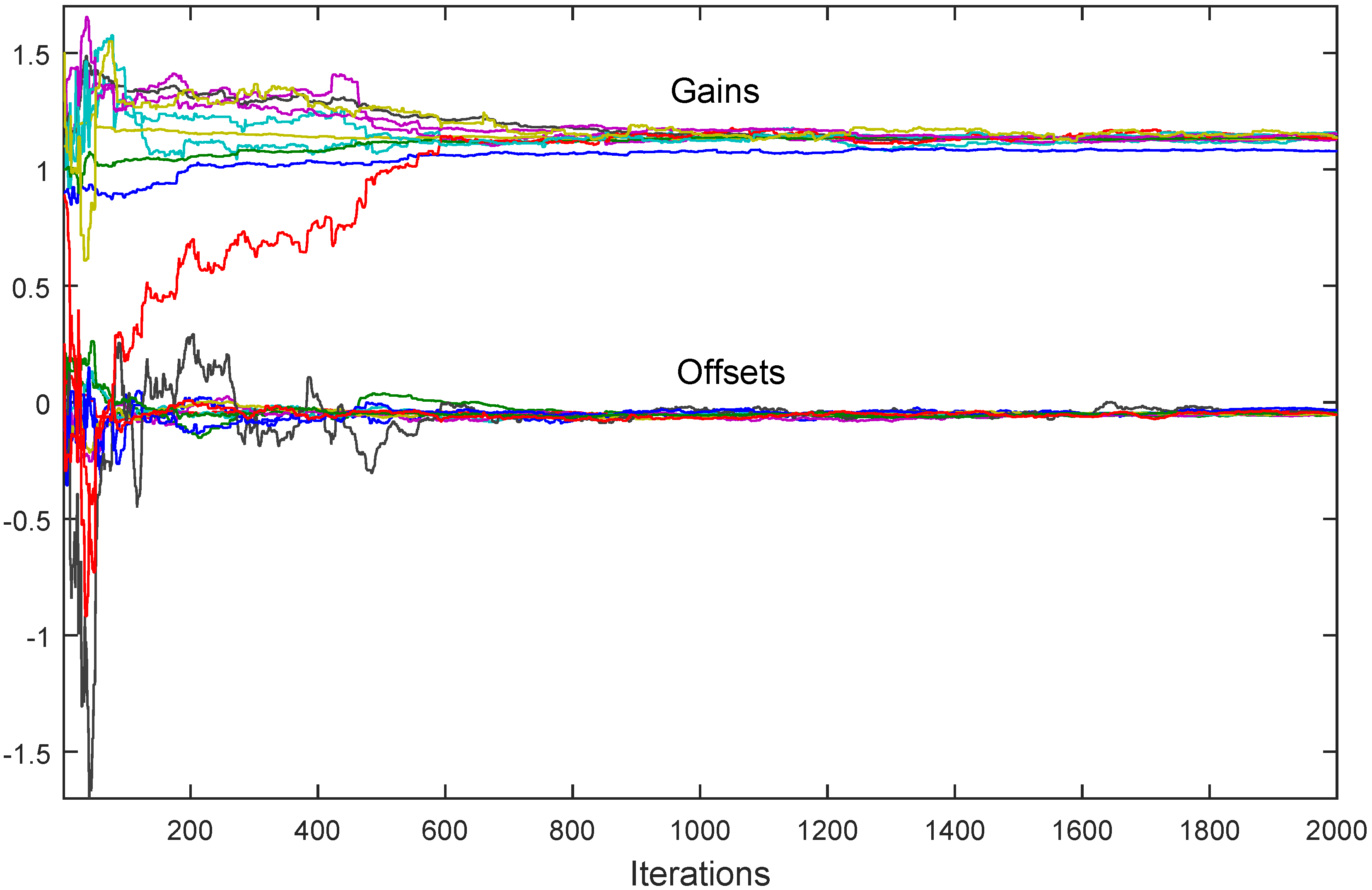
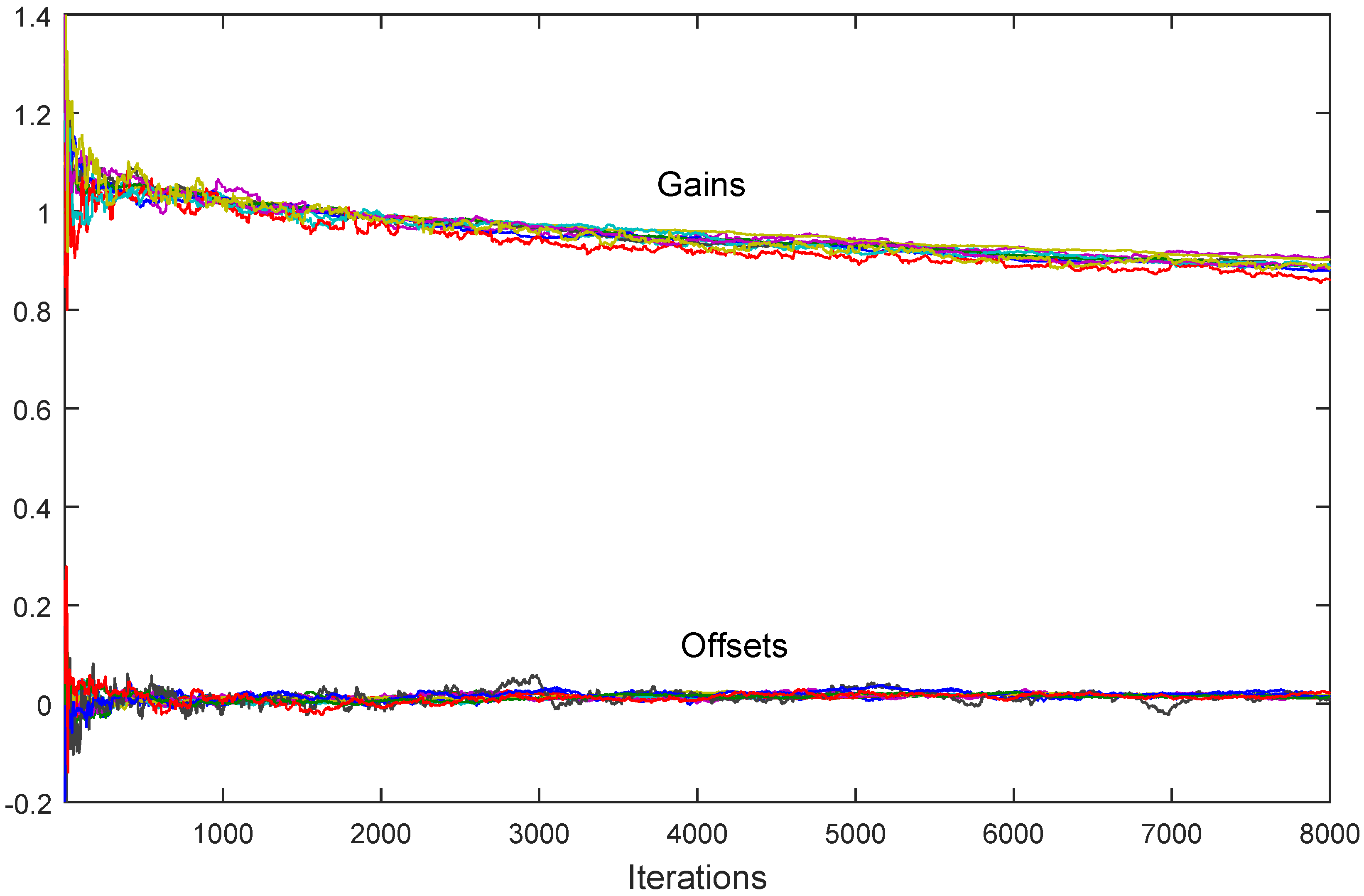
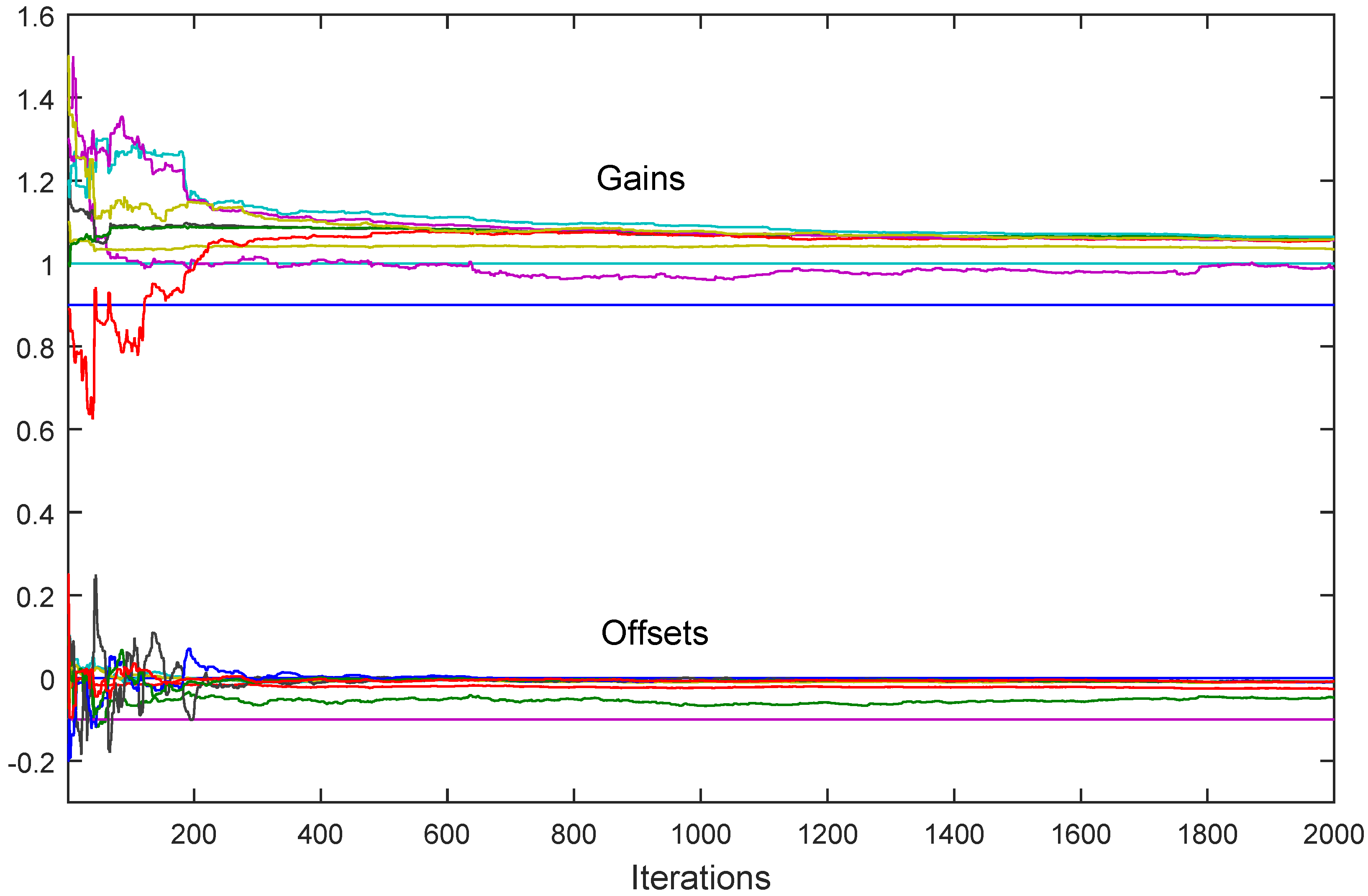
7. Simulation Results
8. Conclusions
Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Kim, K.D.; Kumar, P.R. Cyber–physical systems: A perspective at the centennial. Proc. IEEE 2012, 100, 1287–1308. [Google Scholar]
- Holler, J.; Tsiatsis, V.; Mulligan, C.; Avesand, S.; Karnouskos, S.; Boyle, D. From Machine-to-Machine to the Internet of Things: Introduction to a New Age of Intelligence; Academic Press: Cambridg, MA, USA, 2014. [Google Scholar]
- Akyildiz, I.F.; Vuran, M.C. Wireless Sensor Networks; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Gharavi, H.; Kumar, S.P. Special issue on sensor networks and applications. Proc. IEEE 2003, 91, 1151–1256. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Speranzon, A.; Fischione, C.; Johansson, K.H. Distributed and collaborative estimation over wireless sensor networks. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 1025–1030. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R. Distributed RSS-AoA Based Localization with Unknown Transmit Powers. IEEE Wirel. Commun. Lett. 2016, 5, 392–395. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. Distributed algorithm for target localization in wireless sensor networks using RSS and AoA measurements. Pervasive Mob. Comput. 2017, 37, 63–77. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. Distributed RSS-Based Localization in Wireless Sensor Networks Based on Second-Order Cone Programming. Sensors 2014, 14, 18410–18432. [Google Scholar] [CrossRef] [PubMed]
- Whitehouse, K.; Culler, D. Calibration as parameter estimation in sensor networks. In Proceedings of the 1st ACM International Workshop on Wireless sensor networks and applications, Atlanta, GA, USA, 28 September 2002; pp. 59–67. [Google Scholar]
- Whitehouse, K.; Culler, D. Macro-calibration in sensor/actuator networks. Mob. Netw. Appl. 2003, 8, 463–472. [Google Scholar] [CrossRef]
- Balzano, L.; Nowak, R. Blind calibration of sensor networks. In Proceedings of the 6th International Conference on Information Processing in Sensor Networks, Cambridge, MA, USA, 25–27 April 2007; pp. 79–88. [Google Scholar]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. Distributed Blind Calibration in Lossy Sensor Networks via Output Synchronization. IEEE Trans. Autom. Control 2015, 60, 3257–3262. [Google Scholar] [CrossRef]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. Asynchronous Distributed Blind Calibration of Sensor Networks under Noisy Measurements. IEEE Trans. Control Netw. Syst. 2018, 5, 571–582. [Google Scholar] [CrossRef]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. Distributed Macro Calibration in Sensor Networks. In Proceedings of the 20th Mediterranean Conference on Control & Automation (MED), Barcelona, Spain, 3–6 July 2012; pp. 1049–1054. [Google Scholar]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. Distributed Calibration for Sensor Networks under Communication Errors and Measurement Noise. In Proceedings of the IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 1380–1385. [Google Scholar]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. A consensus-based distributed calibration algorithm for sensor networks. Serb. J. Electr. Eng. 2016, 13, 111–132. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, A.; Murray, R. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Ohta, Y.; Siljak, D. Overlapping block diagonal dominance and existence of Lyapunov functions. J. Math. Anal. Appl. 1985, 112, 396–410. [Google Scholar] [CrossRef]
- Šiljak, D.D. Decentralized Control of Complex Systems; Academic Press: New York, NY, USA, 1991. [Google Scholar]
- Pierce, I.F. Matrices with dominating diagonal blocks. J. Econ. Theory 1974, 9, 159–170. [Google Scholar] [CrossRef]
- Levin, A.; Weiss, Y.; Durand, F.; Freeman, W. Understanding and evaluating blind deconvolution algorithms. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1964–1971. [Google Scholar]
- Yu, C.; Xie, L. On Recursive Blind Equalization in Sensor Networks. IEEE Trans. Signal Process. 2015, 63, 662–672. [Google Scholar] [CrossRef]
- Nandi, A. Blind Estimation Using Higher-Order Statistics; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
- Balzano, L.; Nowak, R. Blind Calibration; Technical Report TR-UCLA-NESL-200702-01; Networked and Embedded Systems Laboratory, UCLA: Los Angeles, CA, USA, 2007. [Google Scholar]
- Lipor, J.; Balzano, L. Robust blind calibration via total least squares. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 4244–4248. [Google Scholar]
- Bilen, C.; Puy, G.; Gribonval, R.; Daudet, L. Convex Optimization Approaches for Blind Sensor Calibration Using Sparsity. IEEE Trans. Signal Process. 2014, 62, 4847–4856. [Google Scholar] [CrossRef]
- Bychkovskiy, V.; Megerian, S.; Estrin, D.; Potkonjak, M. A Collaborative Approach to In-Place Sensor Calibration. In Proceedings of the International Conference on Information Processing in Sensor Networks, Palo Alto, CA, USA, 22–23 April 2003; pp. 301–316. [Google Scholar]
- Wang, C.; Ramanathan, P.; Saluja, K.K. Moments Based Blind Calibration in Mobile Sensor Networks. In Proceedings of the 2008 IEEE International Conference on Communications, Beijing, China, 19–23 May 2008; pp. 896–900. [Google Scholar]
- Takruri, M.; Challa, S.; Yunis, R. Data Fusion Techniques for Auto Calibration in Wireless Sensor Networks. In Proceedings of the International Conference on Information Fusion, Seattle, WA, USA, 6–9 July 2009; pp. 132–139. [Google Scholar]
- Wang, Y.; Yang, A.; Li, Z.; Wang, P.; Yang, H. Blind drift calibration of sensor networks using signal space projection and Kalman filter. In Proceedings of the 2015 IEEE Tenth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Singapore, 7–9 April 2015; pp. 1–6. [Google Scholar]
- Wang, Y.; Yang, A.; Li, Z.; Chen, X.; Wang, P.; Yang, H. Blind Drift Calibration of Sensor Networks Using Sparse Bayesian Learning. IEEE Sens. J. 2016, 16, 6249–6260. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, A.; Chen, X.; Wang, P.; Wang, Y.; Yang, H. A Deep Learning Approach for Blind Drift Calibration of Sensor Networks. IEEE Sens. J. 2017, 17, 4158–4171. [Google Scholar] [CrossRef]
- Yang, J.; Tay, W.P.; Zhong, X. A dynamic Bayesian nonparametric model for blind calibration of sensor networks. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 4207–4211. [Google Scholar]
- Lee, B.; Son, S.; Kang, K. A Blind Calibration Scheme Exploiting Mutual Calibration Relationships for a Dense Mobile Sensor Network. IEEE Sens. J. 2014, 14, 1518–1526. [Google Scholar] [CrossRef]
- Dorffer, C.; Puigt, M.; Delmaire, G.; Roussel, G. Blind Calibration of Mobile Sensors Using Informed Nonnegative Matrix Factorization. In Latent Variable Analysis and Signal Separation; Vincent, E., Yeredor, A., Koldovský, Z., Tichavský, P., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 497–505. [Google Scholar]
- Dorffer, C.; Puigt, M.; Delmaire, G.; Roussel, G. Blind mobile sensor calibration using an informed nonnegative matrix factorization with a relaxed rendezvous model. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2941–2945. [Google Scholar]
- Schulke, C.; Caltagirone, F.; Zdeborova, L. Blind sensor calibration using approximate message passing. J. Stat. Mech. Theory Exp. 2015, 2015. [Google Scholar] [CrossRef]
- Kumar, D.; Rajasegarar, S.; Palaniswami, M. Geospatial Estimation-Based Auto Drift Correction in Wireless Sensor Networks. ACM Trans. Sens. Netw. 2015, 11, 50. [Google Scholar] [CrossRef]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. Distributed drift estimation for time synchronization in lossy networks. In Proceedings of the 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; pp. 779–784. [Google Scholar]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. Distributed time synchronization for networks with random delays and measurement noise. Automatica 2018, 93, 126–137. [Google Scholar] [CrossRef]
- Giridhar, D.; Kumar, P.R. Distributed clock synchronization over wireless networks: Algorithms and analysis. In Proceedings of the IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 263–270. [Google Scholar]
- Sommer, P.; Wattenhofer, R. Gradient clock synchronization in wireless sensor networks. In Proceedings of the 2009 International Conference on Information Processing in Sensor Networks, San Francisco, CA, USA, 13–16 April 2009; pp. 37–48. [Google Scholar]
- Schenato, L.; Fiorentin, F. Average TimeSynch: A consensus-based protocol for time synchronization in wireless sensor networks. Automatica 2011, 47, 1878–1886. [Google Scholar] [CrossRef]
- Carli, R.; Chiuso, A.; Schenato, L.; Zampieri, S. Optimal Synchronization for Networks of Noisy Double Integrators. IEEE Trans. Autom. Control 2008, 56, 1146–1152. [Google Scholar] [CrossRef]
- Liao, C.; Barooah, P. Distributed clock skew and offset estimation from relative measurements in mobile networks with Markovian switching topologies. Automatica 2013, 49, 3015–3022. [Google Scholar] [CrossRef]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. Distributed time synchronization in lossy wireless sensor networks. In Proceedings of the 3rd IFAC Workshop on Distributed Estimation and Control in Networked Systems, Santa Barbara, CA, USA, 13–14 September 2012; pp. 25–30. [Google Scholar]
- Ravazzi, C.; Frasca, P.; Tempo, R.; Ishii, H. Ergodic randomized algorithms and dynamics over networks. IEEE Trans. Control Netw. Syst. 2015, 2, 78–87. [Google Scholar] [CrossRef]
- Carron, A.; Todescato, M.; Carli, R.; Schenato, L. An asynchrnous consensus-based algorithm for estimation from noisy relative measurements. IEEE Trans. Control Netw. Syst. 2014, 1, 283–295. [Google Scholar] [CrossRef]
- Bolognani, S.; Favero, S.D.; Schenato, L.; Varagnolo, D. Consensus-based distributed sensor calibration and least-square parameter identification in WSNs. Int. J. Robust Nonlinear Control 2010, 20, 176–193. [Google Scholar] [CrossRef]
- Miluzzo, E.; Lane, N.D.; Campbell, A.T.; Olfati-Saber, R. CaliBree: A Self-calibration System for Mobile Sensor Networks. In Proceedings of the 4th IEEE International Conference on Distributed Computing in Sensor Systems, Santorini Island, Greece, 11–14 June 2008; pp. 314–331. [Google Scholar]
- Ramakrishnan, N.; Ertin, E.; Moses, R.L. Gossip-Based Algorithm for Joint Signature Estimation and Node Calibration in Sensor Networks. IEEE J. Sel. Top. Signal Process. 2011, 5, 665–673. [Google Scholar] [CrossRef]
- Buadhachain, S.O.; Provan, G. A model-based control method for decentralized calibration of wireless sensor networks. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 6571–6576. [Google Scholar]
- Ren, W.; Beard, R. Consensus seeking in multi-agent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Ljung, L.; Söderström, T. Theory and Pracice of Recursive Identification; MIT Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Xiao, Y.; Xiong, Z.; Niyato, D.; Han, Z. Distortion minimization via adaptive digital and analog transmission for energy harvesting-based wireless sensor networks. In Proceedings of the IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; pp. 518–521. [Google Scholar]
- Chen, H.F. Stochastic Approximation and Its Applications; Kluwer Academic: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Li, T.; Zhang, J.F. Consensus conditions of multi agent systems with time varying topologies. IEEE Trans. Autom. Control 2010, 55, 2043–2056. [Google Scholar] [CrossRef]
- Huang, M.; Manton, J.H. Stochastic consensus seeking with noisy and directed inter-agent communications: Fixed and randomly varying topologies. IEEE Trans. Autom. Control 2010, 55, 235–241. [Google Scholar] [CrossRef]
- Ljung, L. System Identification—Theory for the User; Prentice Hall International: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Söderström, T.; Stoica, P. System Identification; Prentice Hall International: Hemel Hempstaed, UK, 1989. [Google Scholar]
- Aysal, T.C.; Yildriz, M.E.; Sarwate, A.D.; Scaglione, A. Broadcast gossip algorithms for consensus. IEEE Trans. Signal Process. 2009, 57, 2748–2761. [Google Scholar] [CrossRef]
- Nedić, A. Asynchronous broadcast-based convex optimization over a network. IEEE Trans. Autom. Control 2011, 56, 1337–1351. [Google Scholar] [CrossRef]
- Bradley, R.C. Basic Properties of Strong Mixing Conditions a Survey and Some Open Questions. Probab. Surv. 2005, 2, 107–144. [Google Scholar] [CrossRef]
- Ibragimov, I. Some limit theorems for stochastic processes stationary in the strict sense. Dokl. Akad. Nauk SSSR 1959, 125, 711–714. [Google Scholar]
- Rosenblatt, M. A central limit theorem and a strong mixing condition. Proc. Natl. acad. Sci. USA 1956, 42, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Godsil, C.; Royle, G. Algebraic Graph Theory; Springer: New York, NY, USA, 2001. [Google Scholar]
- Borkar, V.; Meyn, S.P. The ODE method for convergence of stochastic approximation and reinforcement learning. SIAM J. Control Optim. 2000, 38, 447–469. [Google Scholar] [CrossRef]
- Stanković, M.S.; Stanković, S.S.; Johansson, K.H. Distributed Offset Correction for Time Synchronization in Networks with Random Delays. In Proceedings of the European Control Conference, Limassol, Cyprus, 12–15 June 2018. [Google Scholar]
- Tian, Y.P.; Zong, S.; Cao, Q. Structural modeling and convergence analysis of consensus-based time synchronization algorithms over networks: Non-topological conditions. Automatica 2016, 65, 64–75. [Google Scholar] [CrossRef]
- Chen, J.; Yu, Q.; Zhang, Y.; Chen, H.H.; Sun, Y. Feedback-Based Clock Synchronization in Wireless Sensor Networks: A Control Theoretic Approach. IEEE Trans. Veh. Technol. 2010, 59, 2963–2973. [Google Scholar] [CrossRef]
- Stanković, M. Distributed Asynchronous Consensus-based Algorithm for Blind Calibration of Sensor Networks with Autonomous Gain Correction. IET Control Theory Appl. 2018, 12, 2287–2293. [Google Scholar] [CrossRef]
- Stanković, S.S.; Stanković, M.S.; Stipanović, D.M. Consensus based overlapping decentralized estimator. IEEE Trans. Autom. Control 2009, 54, 410–415. [Google Scholar] [CrossRef]
- Stanković, S.S.; Stanković, M.S.; Stipanović, D.M. Consensus Based Overlapping Decentralized Estimation with Missing Observations and Communication Faults. Automatica 2009, 45, 1397–1406. [Google Scholar] [CrossRef]
- Stanković, M.S.; Stanković, S.S.; Stipanović, D.M. Consensus-based decentralized real-time identification of large-scale systems. Automatica 2015, 60, 219–226. [Google Scholar] [CrossRef]
- Stanković, S.S.; Šiljak, D.D. Model abstraction and inclusion principle: A comparison. IEEE Trans. Autom. Control 2001, 8, 816–832. [Google Scholar] [CrossRef]
- Seyboth, G.; Schmidt, G.; Allgöwer, F. Output synchronization of linear parameter-varying systems via dynamic couplings. In Proceedings of the IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 5128–5133. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanković, M.S.; Stanković, S.S.; Johansson, K.H.; Beko, M.; Camarinha-Matos, L.M. On Consensus-Based Distributed Blind Calibration of Sensor Networks. Sensors 2018, 18, 4027. https://doi.org/10.3390/s18114027
Stanković MS, Stanković SS, Johansson KH, Beko M, Camarinha-Matos LM. On Consensus-Based Distributed Blind Calibration of Sensor Networks. Sensors. 2018; 18(11):4027. https://doi.org/10.3390/s18114027
Chicago/Turabian StyleStanković, Miloš S., Srdjan S. Stanković, Karl Henrik Johansson, Marko Beko, and Luis M. Camarinha-Matos. 2018. "On Consensus-Based Distributed Blind Calibration of Sensor Networks" Sensors 18, no. 11: 4027. https://doi.org/10.3390/s18114027
APA StyleStanković, M. S., Stanković, S. S., Johansson, K. H., Beko, M., & Camarinha-Matos, L. M. (2018). On Consensus-Based Distributed Blind Calibration of Sensor Networks. Sensors, 18(11), 4027. https://doi.org/10.3390/s18114027






