Quantitative Evaluation of Broadband Photoacoustic Spectroscopy in the Infrared with an Optical Parametric Oscillator
Abstract
1. Introduction
2. Materials and Methods
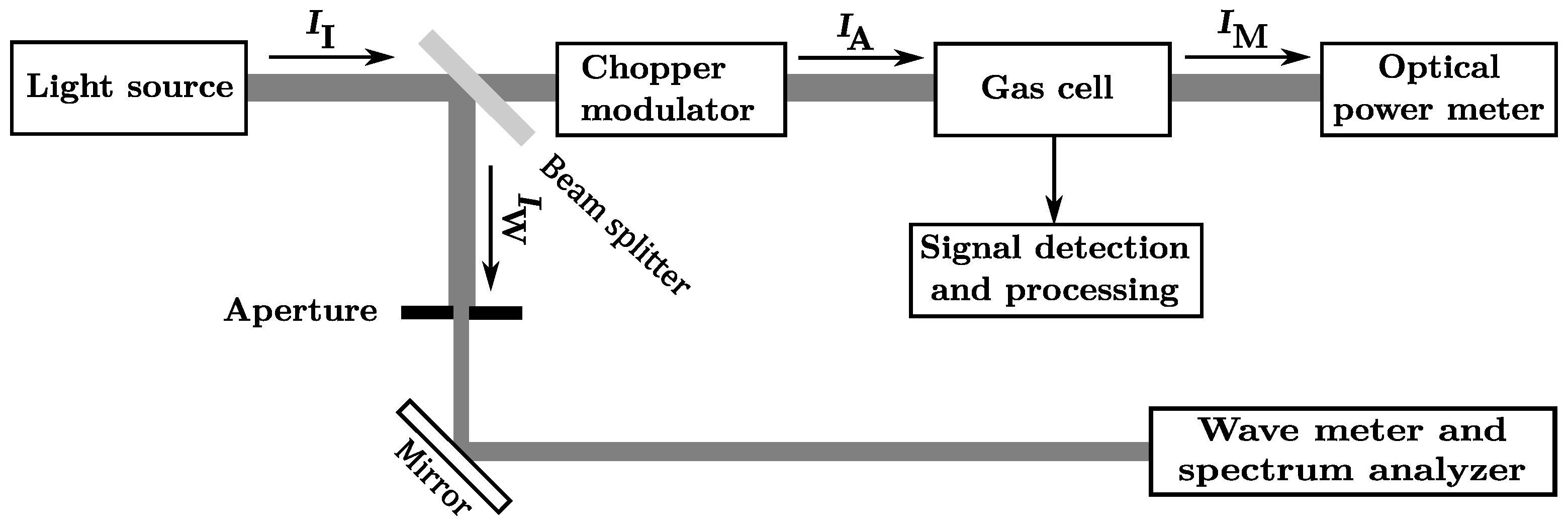
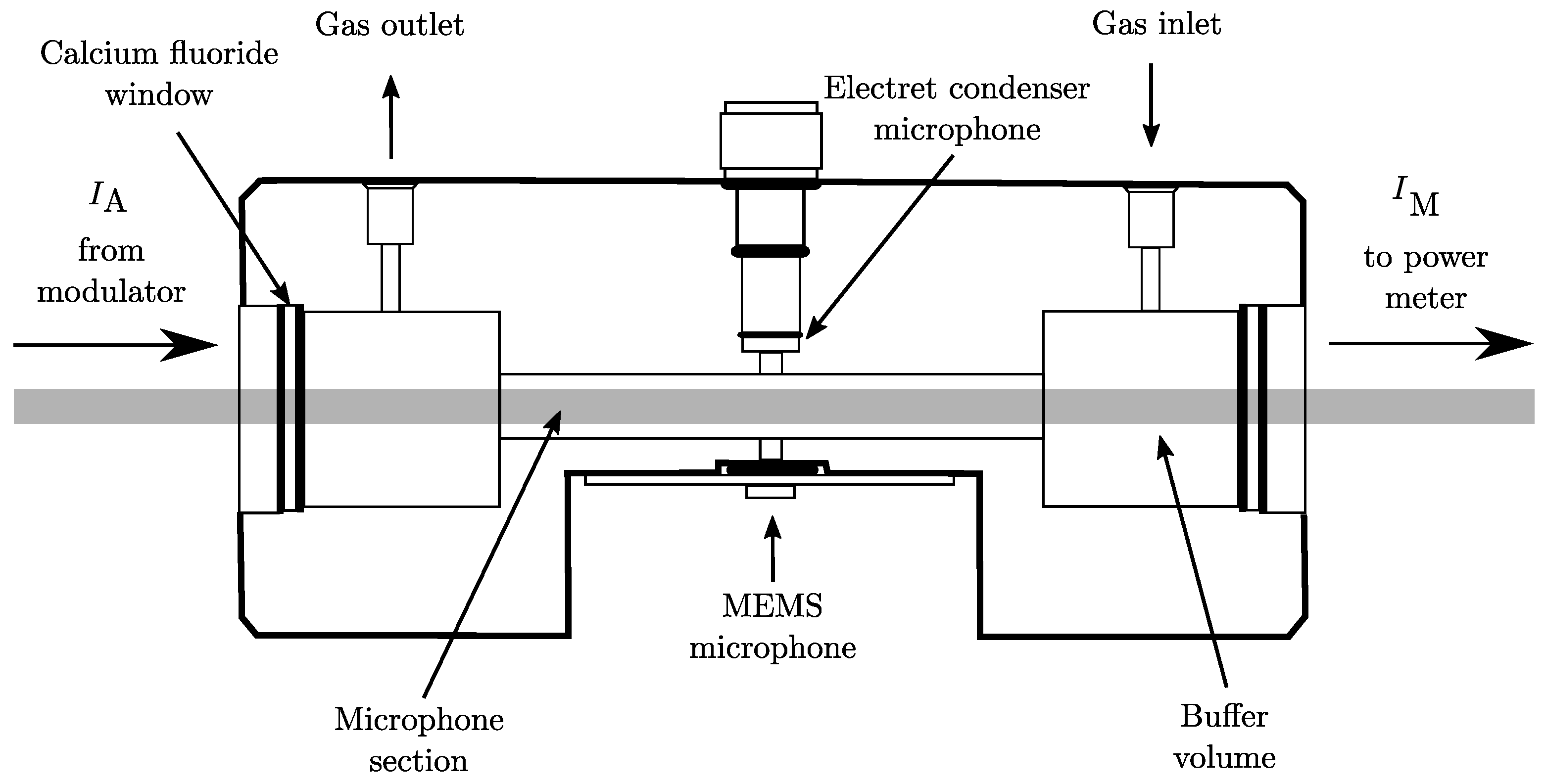
2.1. Experimental Setup
2.2. Measurements
3. Results and Interpretation
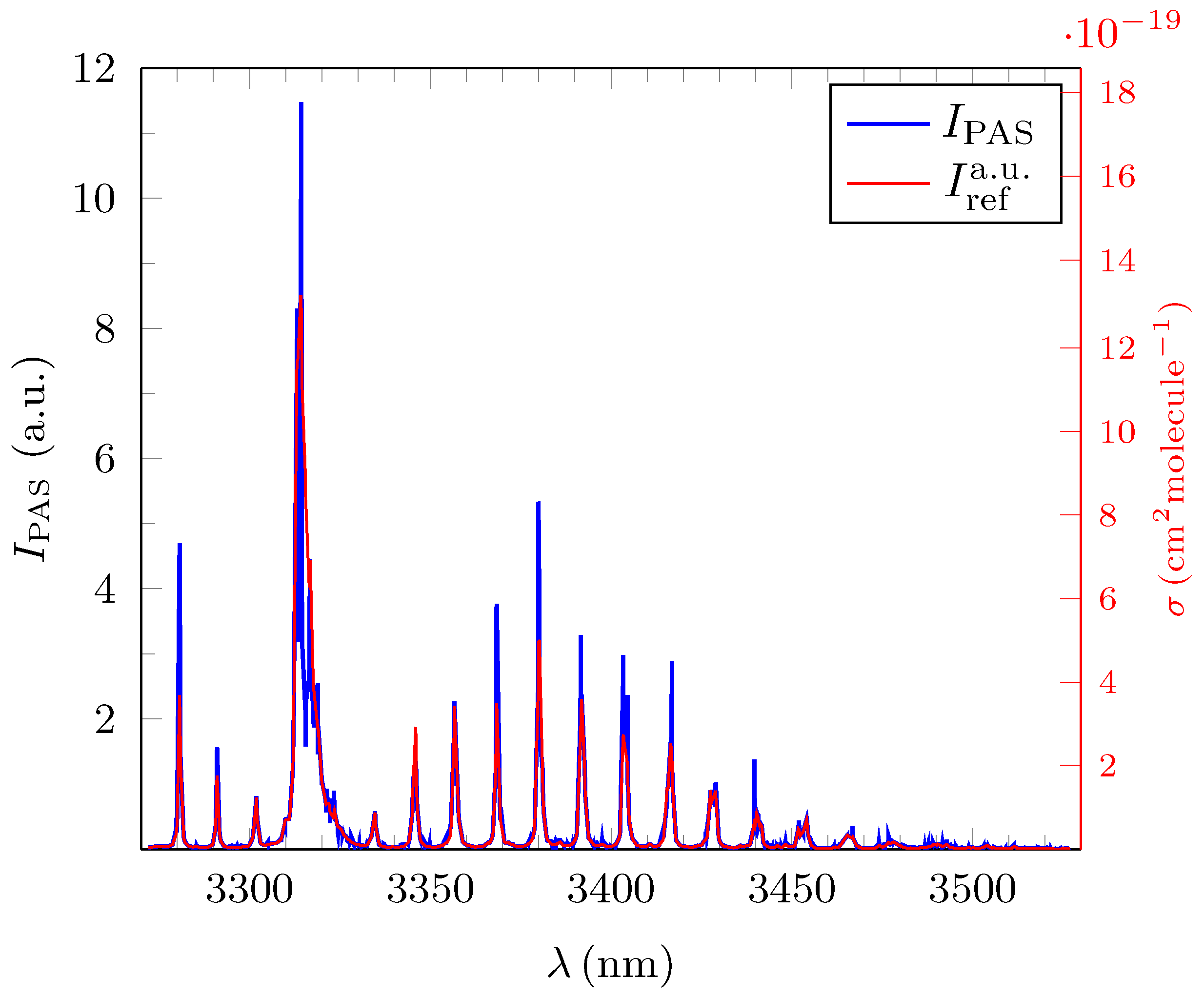
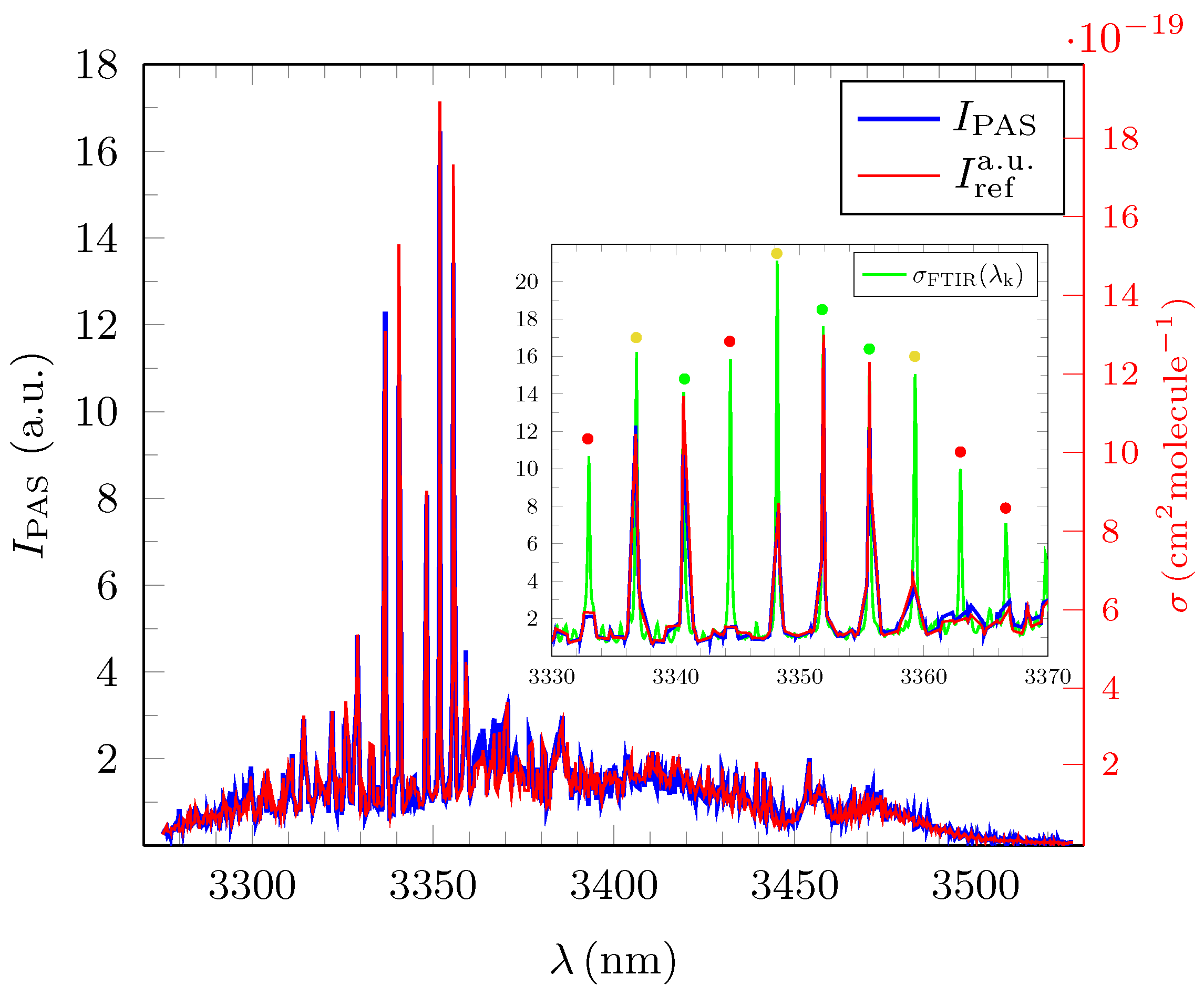
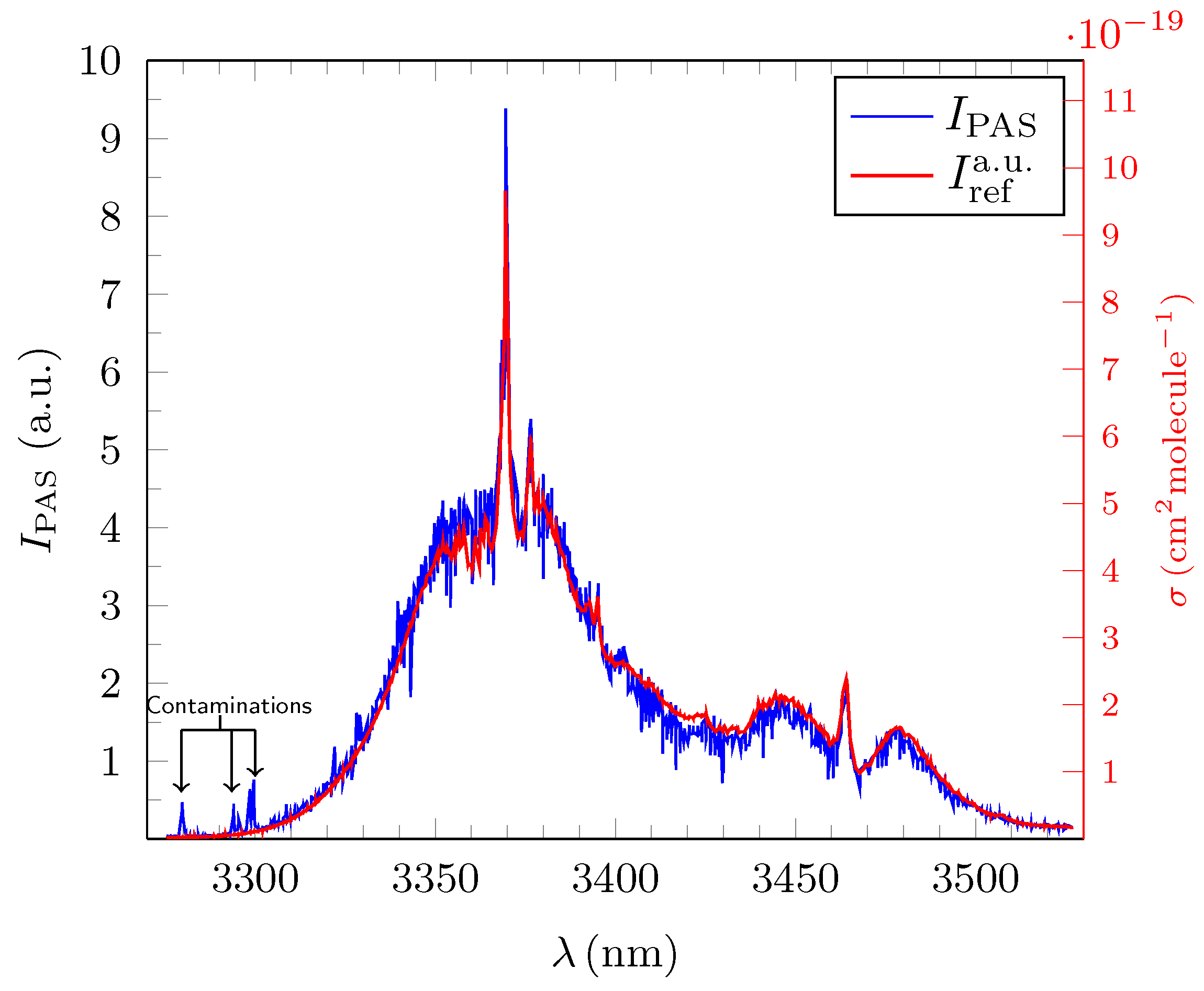
3.1. Quantitative Evaluation of the Obtained Broadband PAS Spectra for Methane, Ethane and Propane
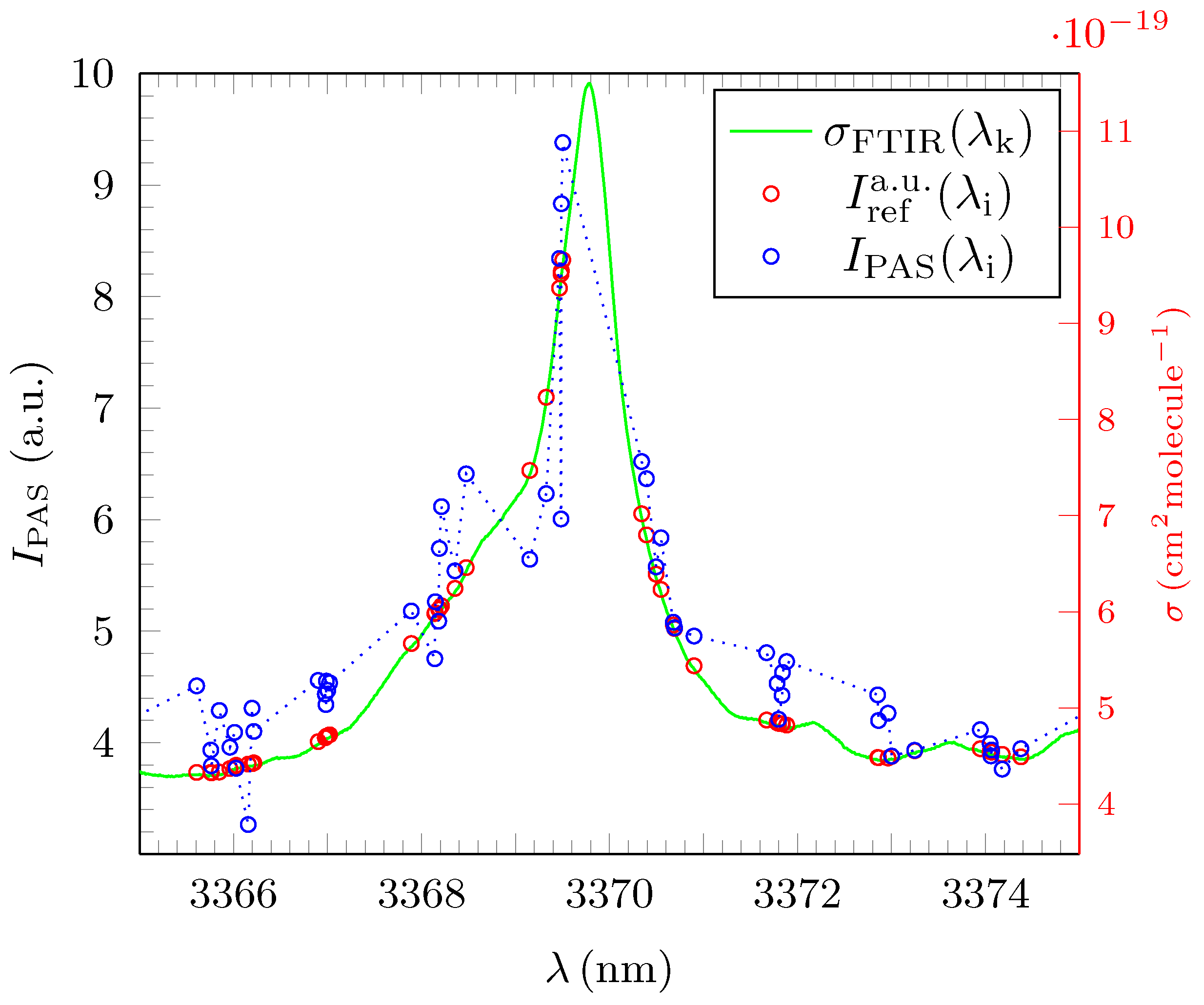
3.2. Analysis and Quantitative Evaluation of Prominent Absorption Lines
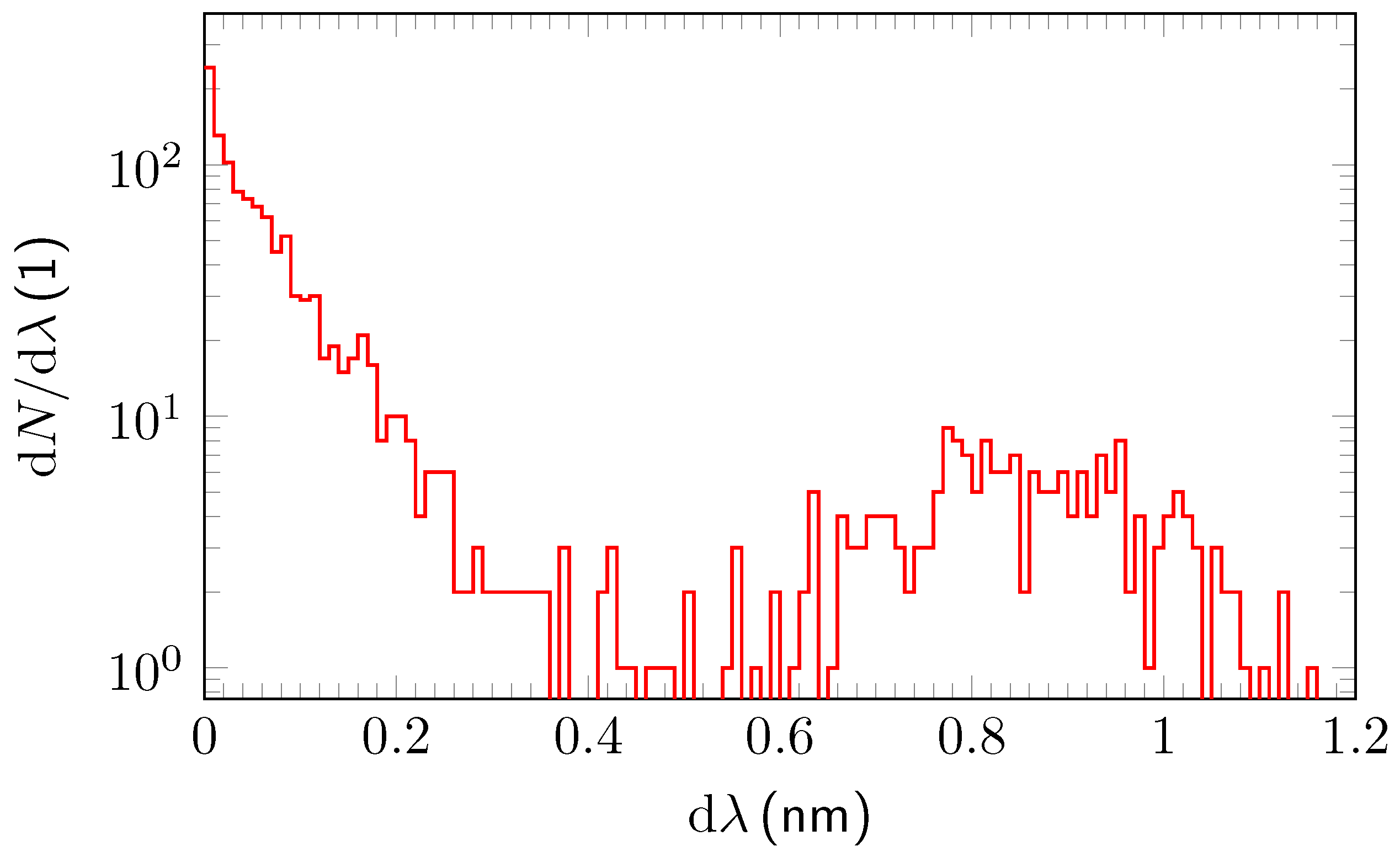
3.3. Estimation of the Signal-to-Noise Ratio (SNR) and the Limit of Detection (LOD)
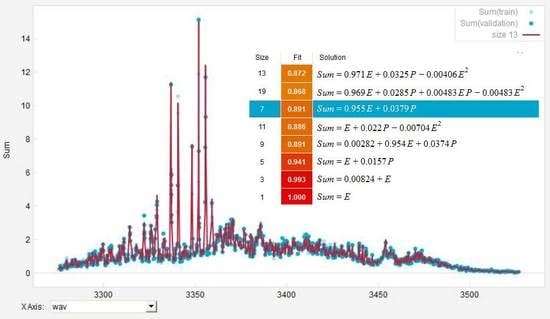
4. Simulation of Deconvolution of Photoacoustic Spectra of Gas Mixtures
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| FTIR | Fast Fourier transformation in the infrared |
| FWHM | Full-width-half-maximum |
| IR | Infrared |
| LOD | Limit of detection |
| MEMS | Microelectromechanical systems microphone |
| NA | Natural abundance |
| OPO | Optical-parametric oscillator |
| PAS | Photoacoustic spectroscopy |
| PPLN | Periodically poled lithium niobate |
| SNR | Signal-to-noise ratio |
References
- Phillips, M.; Gleeson, K.; Hughes, J.M.B.; Greenberg, J.; Cataneo, R.N.; Baker, L.; McVay, W.P. Volatile organic compounds in breath as markers of lung cancer: A cross-sectional study. Lancet 1999, 353, 1930–1933. [Google Scholar] [CrossRef]
- Boots, A.; van Berkel, J.; Dallinga, J.; Smolinska, A.; Wouters, E.; van Schooten, F. The versatile use of exhaled volatile organic compounds in human health and disease. J. Breath Res. 2012, 6, 027108. [Google Scholar] [CrossRef] [PubMed]
- Dent, A.G.; Sutedja, T.G.; Zimmerman, P.V. Exhaled breath analysis for lung cancer. J. Thoratic Dis. 2013, 5, S540–S550. [Google Scholar]
- Krilaviciute, A.; Heiss, J.A.; Leja, M.; Kupcinskas, J.; Haick, H.; Brenner, H. Detection of cancer through exhaled breath: A systematic review. Oncotarget 2015, 6, 38643–38657. [Google Scholar] [CrossRef] [PubMed]
- Saalberg, Y.; Wolff, M. VOC breath biomarkers in lung cancer. Clin. Chim. Acta 2016, 459, 5–9. [Google Scholar] [CrossRef] [PubMed]
- Michaelian, K. Photoacoustic IR Spectroscopy; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Vainio, M.; Halonen, L. Mid-infrared optical parametric oscillators and frequency combs for molecular spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 4266–4294. [Google Scholar] [CrossRef] [PubMed]
- Dumitras, D.C.; Dutu, D.C.; Matei, C.; Magureanu, A.M.; Petrus, M.; Popa, C.; Patachia, M. Measurements of ethylene concentration by laser photoacoustic techniques with applications at breath analysis. Rom. Rep. Phys. 2008, 60, 593–602. [Google Scholar]
- Popa, C.; Bratu, A.M.; Matei, C.; Cernat, R.; Popescu, A.; Dumitras, D.C. Qualitative and quantitative determination of human biomarkers by laser photoacoustic spectroscopy methods. Laser Phys. 2011, 21, 1336–1342. [Google Scholar] [CrossRef]
- Navas, M.; Jiménez, A.; Asuero, A. Human biomarkers in breath by photoacoustic spectroscopy. Clin. Chim. Acta 2012, 413, 1171–1178. [Google Scholar] [CrossRef] [PubMed]
- Saalberg, Y.; Bruhns, H.; Wolff, M. Photoacoustic Spectroscopy for the Determination of Lung Cancer Biomarkers—A Preliminary Investigation. Sensors 2017, 17, 210. [Google Scholar] [CrossRef] [PubMed]
- Bell, A. Upon the Production of Sound by Radiant Energy. Science 1881, 28, 242–253. [Google Scholar] [CrossRef] [PubMed]
- Röntgen, W. On tones produced by the intermittent irradiation of a gas. Philos. Mag. 1881, 11, 308–311. [Google Scholar] [CrossRef]
- Goddard, W.; Tang, Y.; Wu, S.; Deev, A.; Ma, Q.; Li, G. Novel Gas Isotope Interpretation Tools to Optimize Gas Shale Production; Technical Report; California Institute of Technology: Pasadena, CA, USA, 2013. [Google Scholar]
- Schallschmidt, K.; Becker, R.; Jung, C.; Bremser, W.; Walles, T.; Neudecker, J.; Leschber, G.; Frese, S.; Nehls, I. Comparison of volatile organic compounds from lung cancer patients and healthy controls—Challenges and limitations of an observational study. J. Breath Res. 2016, 10, 046007. [Google Scholar] [CrossRef] [PubMed]
- NIST Chemistry WebBook, SRD 69. Available online: http://webbook.nist.gov/chemistry/vib-ser.html (accessed on 28 July 2017).
- Bruhns, H.; Saalberg, Y.; Wolff, M. Photoacoustic Hydrocarbon Spectroscopy Using a Mach-Zehnder Modulated cw OPO. Sens. Transd. J. 2015, 188, 40–47. [Google Scholar]
- Bruhns, H.; Marianovich, A.; Wolff, M. Photoacoustic Spectroscopy Using a MEMS Microphone with Inter-IC Sound Digital Output. Int. J. Thermophys. 2014, 35, 2292–2301. [Google Scholar] [CrossRef]
- Goertzel, G. An algorithm for the evaluation of finite trigonometric series. Am. Math. Mon. 1958, 65. [Google Scholar] [CrossRef]
- Bruhns, H.; Marianovich, A.; Rhein, S.; Wolff, M. Digital MEMS microphone with Inter-IC Sound Interface for photoacoustic spectroscopy. In Proceedings of the 14th International Meeting on Chemical Sensors–IMCS 2012, Nuremberg, Germany, 20–23 May 2012. [Google Scholar]
- Lassen, M.; Lamard, L.; Balslev-Harder, D.; Peremans, A.; Petersen, J.C. Photoacoustic spectroscopy of NO_2 using a mid-infrared pulsed optical parametric oscillator as light source. arXiv, 2017; arXiv:1712.04547. [Google Scholar]
- HITRAN 2012, Infrared cross Sections. Available online: ftp://cfa-ftp.harvard.edu/pub/HITRAN2012/IR-XSect/Supplemental/ (accessed on 23 September 2015).
- Harrison, J.; Bernath, P. Infrared absorption cross sections for propane C3H8 in the 3 μm region. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1282–1288. [Google Scholar] [CrossRef]
- Loh, A.; Wolff, M. Absorption cross sections of 13C ethane and propane isotopologues in the 3 μm region. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 517–521. [Google Scholar] [CrossRef]
- Rothman, L. The HITRAN 2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 3–69. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling Free-Form Natural Laws from Experimental Data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Olivero, J.; Longbothum, R. Empirical fits to the Voigt line width: A brief review. J. Quant. Spectrosc. Radiat. Transf. 1977, 17, 233–236. [Google Scholar] [CrossRef]
- Bruhns, H. Hydrocarbon Detection Based on Mid Infrared Photoacoustic Spectroscopy with an OPO. Ph.D. Thesis, University of the West of Scotland, Paisley, UK, 2015. [Google Scholar]
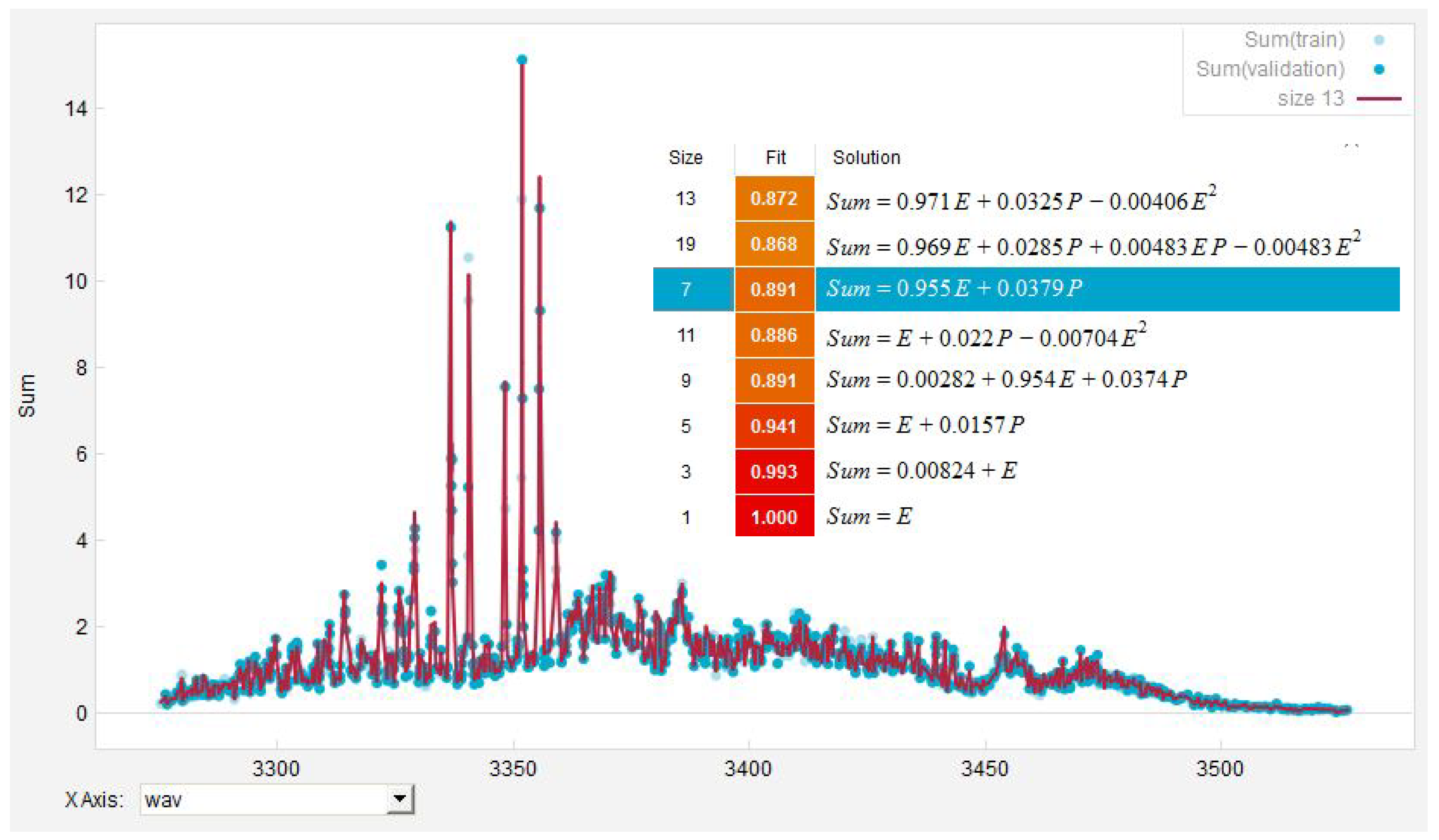
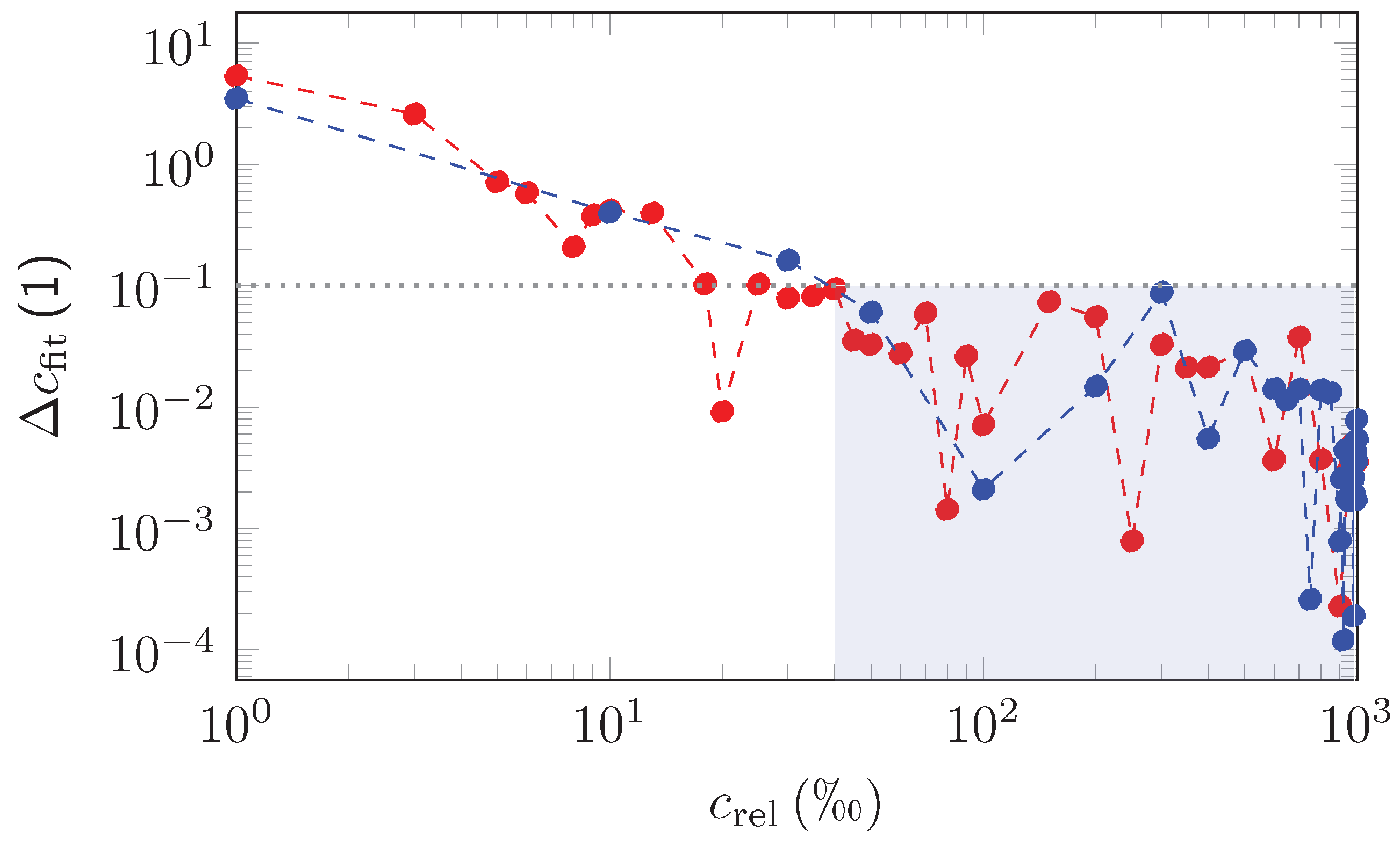
| Measurement | EUREQA-Fit | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| /ppm | /nm | /nm | /nm | /a.u. | /% | ||||
| Methane | 99.1 | 3272.0361 | 3526.8055 | 1350 | 0.1887(3025) | 464.1 | 15.0(14) | 1.0288 | 0.8260 |
| Ethane | 95.5 | 3275.2941 | 3526.8729 | 1345 | 0.1870(2926) | 1593.9 | 8.7(11) | 0.9959 | 0.9759 |
| Propane | 99.5 | 3275.3858 | 3526.9183 | 1351 | 0.1865(2931) | 2170.7 | 7.1(6) | 0.9996 | 0.9760 |
| /nm | / | FWHM/nm | /% | EUREQA-Fit | ||||
|---|---|---|---|---|---|---|---|---|
| PAS | FTIR | PAS | FTIR | |||||
| Methane | 3280.5219 | 3280.6543 | −4.036 | 0.568 | 0.641 | −11.50 | 0.5313 | 0.9354 |
| 3291.1426 | 3291.0667 | 2.306 | 0.599 | 0.738 | −18.84 | 0.6196 | 0.9976 | |
| 3368.6480 | 3368.5638 | 2.500 | 0.745 | 0.996 | −25.16 | 0.6205 | 0.9231 | |
| 3391.9170 | 3392.0495 | −3.906 | 1.636 | 1.376 | 18.85 | 0.1047 | 0.7012 | |
| 3428.1770 | 3428.1805 | −0.102 | 2.321 | 2.361 | −1.69 | 0.0005 | 0.8692 | |
| 3465.8520 | 3465.7252 | 3.659 | 3.317 | 2.823 | 17.49 | 0.2794 | 0.6394 | |
| Ethane | 3336.7143 | 3336.8223 | −3.237 | 0.275 | 0.178 | 54.46 | 1.0000 | 0.9416 |
| 3340.5772 | 3340.6186 | −1.389 | 0.158 | 0.197 | −19.83 | 0.9999 | 0.9981 | |
| 3348.2759 | 3348.1813 | 2.825 | 0.176 | 0.181 | −3.14 | 0.9995 | 0.9990 | |
| 3351.9117 | 3351.8977 | 0.418 | 0.139 | 0.179 | −22.06 | 0.5437 | 0.9954 | |
| 3355.6083 | 3355.9151 | −0.203 | 0.231 | 0.198 | 18.17 | 0.9994 | 0.9999 | |
| Propane | 3369.8481 | 3369.7503 | 2.902 | 0.653 | 0.792 | −17.62 | 0.5056 | 0.8014 |
| 3463.6431 | 3463.7889 | −4.209 | 2.268 | 2.072 | 9.44 | 0.5533 | 0.8147 | |
| Experiment | Hypothetical | ||||
|---|---|---|---|---|---|
| /a.u. | /ppb | /ppb | |||
| Methane | 11.4747 | 13.6 | 143.4 | 3.0 | 227.9 |
| Ethane | 16.4530 | 7.1 | 205.7 | 2.4 | 270.3 |
| Propane | 9.3811 | 13.2 | 117.3 | 4.9 | 137.3 |
| Nitrogen | 0.0800 | 1.0 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruhns, H.; Wolff, M.; Saalberg, Y.; Spohr, K.M. Quantitative Evaluation of Broadband Photoacoustic Spectroscopy in the Infrared with an Optical Parametric Oscillator. Sensors 2018, 18, 3971. https://doi.org/10.3390/s18113971
Bruhns H, Wolff M, Saalberg Y, Spohr KM. Quantitative Evaluation of Broadband Photoacoustic Spectroscopy in the Infrared with an Optical Parametric Oscillator. Sensors. 2018; 18(11):3971. https://doi.org/10.3390/s18113971
Chicago/Turabian StyleBruhns, Henry, Marcus Wolff, Yannick Saalberg, and Klaus Michael Spohr. 2018. "Quantitative Evaluation of Broadband Photoacoustic Spectroscopy in the Infrared with an Optical Parametric Oscillator" Sensors 18, no. 11: 3971. https://doi.org/10.3390/s18113971
APA StyleBruhns, H., Wolff, M., Saalberg, Y., & Spohr, K. M. (2018). Quantitative Evaluation of Broadband Photoacoustic Spectroscopy in the Infrared with an Optical Parametric Oscillator. Sensors, 18(11), 3971. https://doi.org/10.3390/s18113971