Performance Evaluation of a Quality of Service Control Scheme in Multi-Hop WBAN Based on IEEE 802.15.6
Abstract
1. Introduction
- The performance of our previously proposed QoS control scheme is improved by appropriately determining the coding rate using channel estimation. With this improvement, data packets can be relayed to the hub with a small number of transmissions even when the maximum number of retransmissions is limited by a two-hop extension.
- Novel performance evaluations are conducted as a function of the distance between transmitter and receiver assuming a real environment, which were not considered in our previous work [20,21,22]. Through these evaluations, we confirm that our proposed QoS control method is effective even assuming a real environment. It is also clear that it is better to perform two-hop expansion than one-hop case by setting the distance between transmitter and receiver in each hop appropriately. In addition, this paper contributes to theoretically clarifying the relevant optimum setting.
2. Related State of the Art Research
3. Related Description of IEEE Std. 802.15.6
3.1. UWB PHY
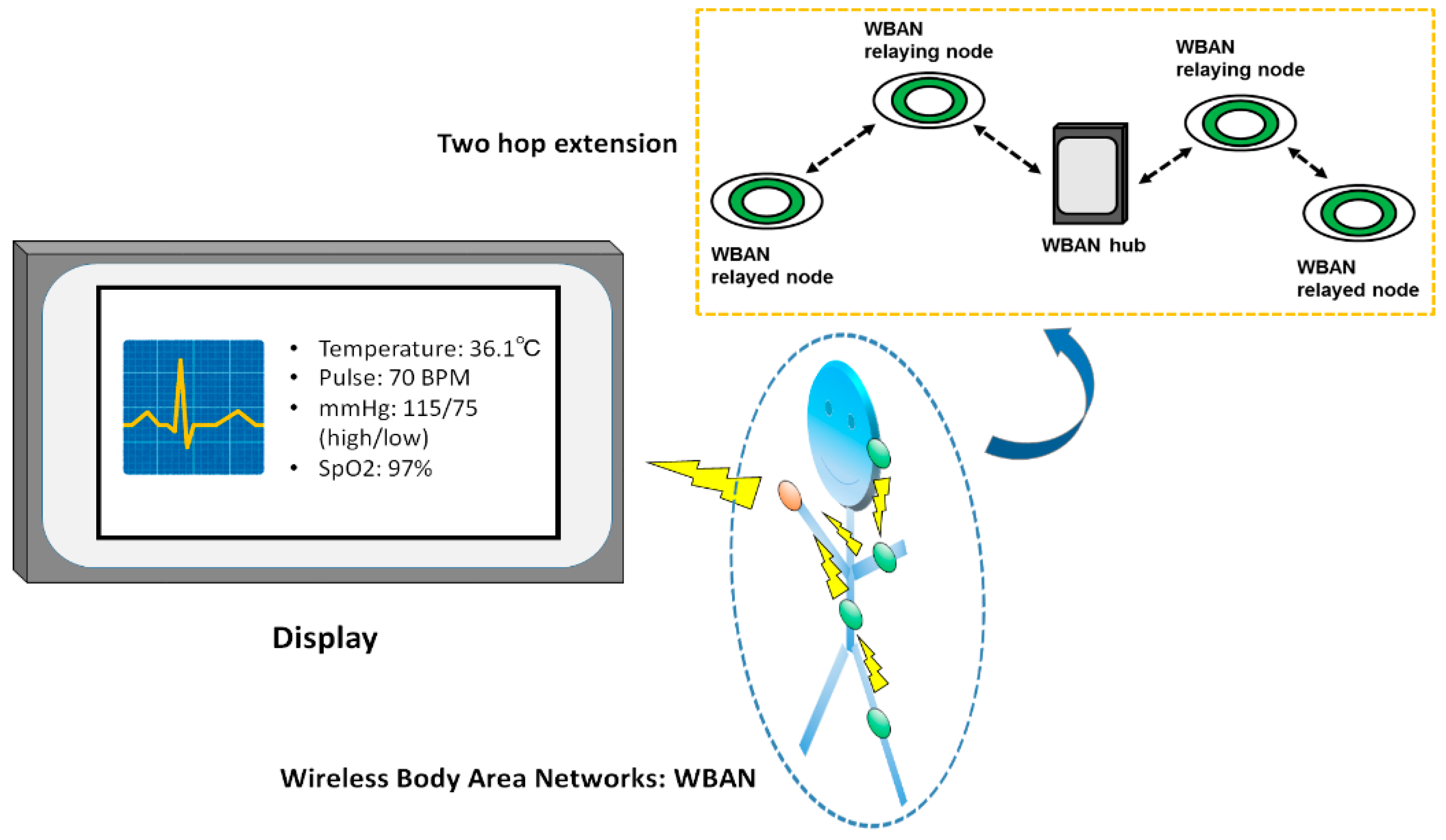
3.2. Two-Hop Extension
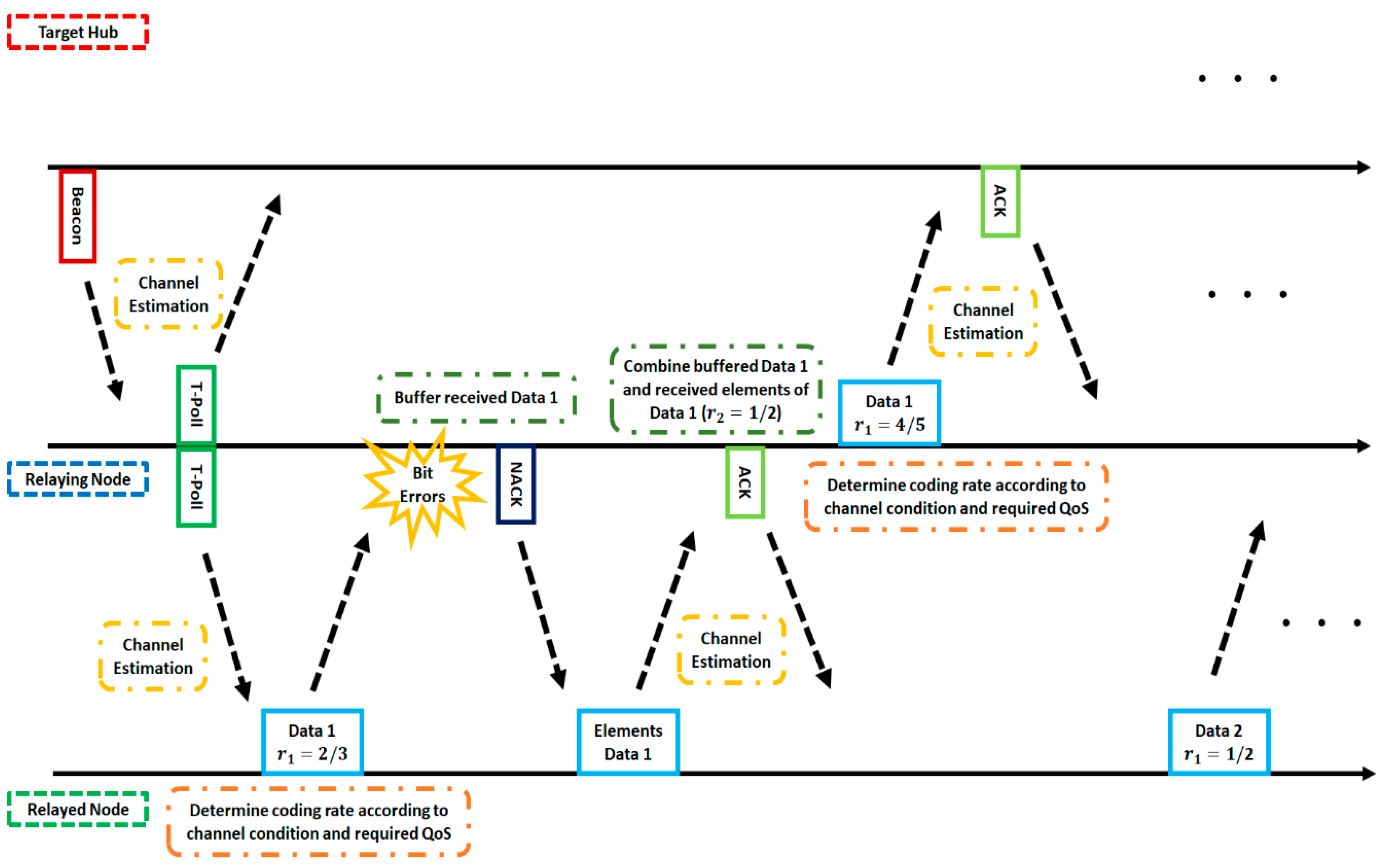
4. Previously Proposed Error Control Method
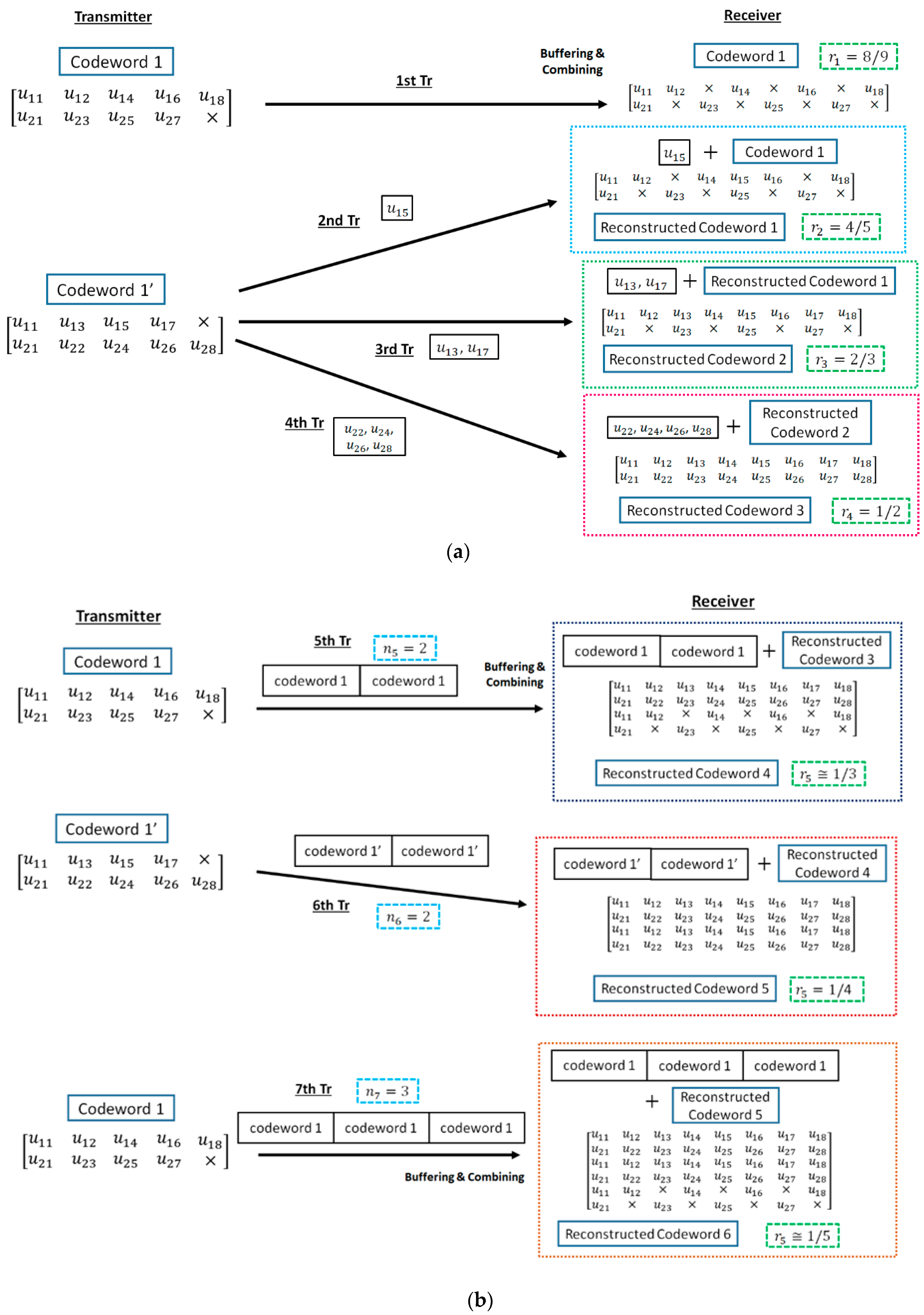
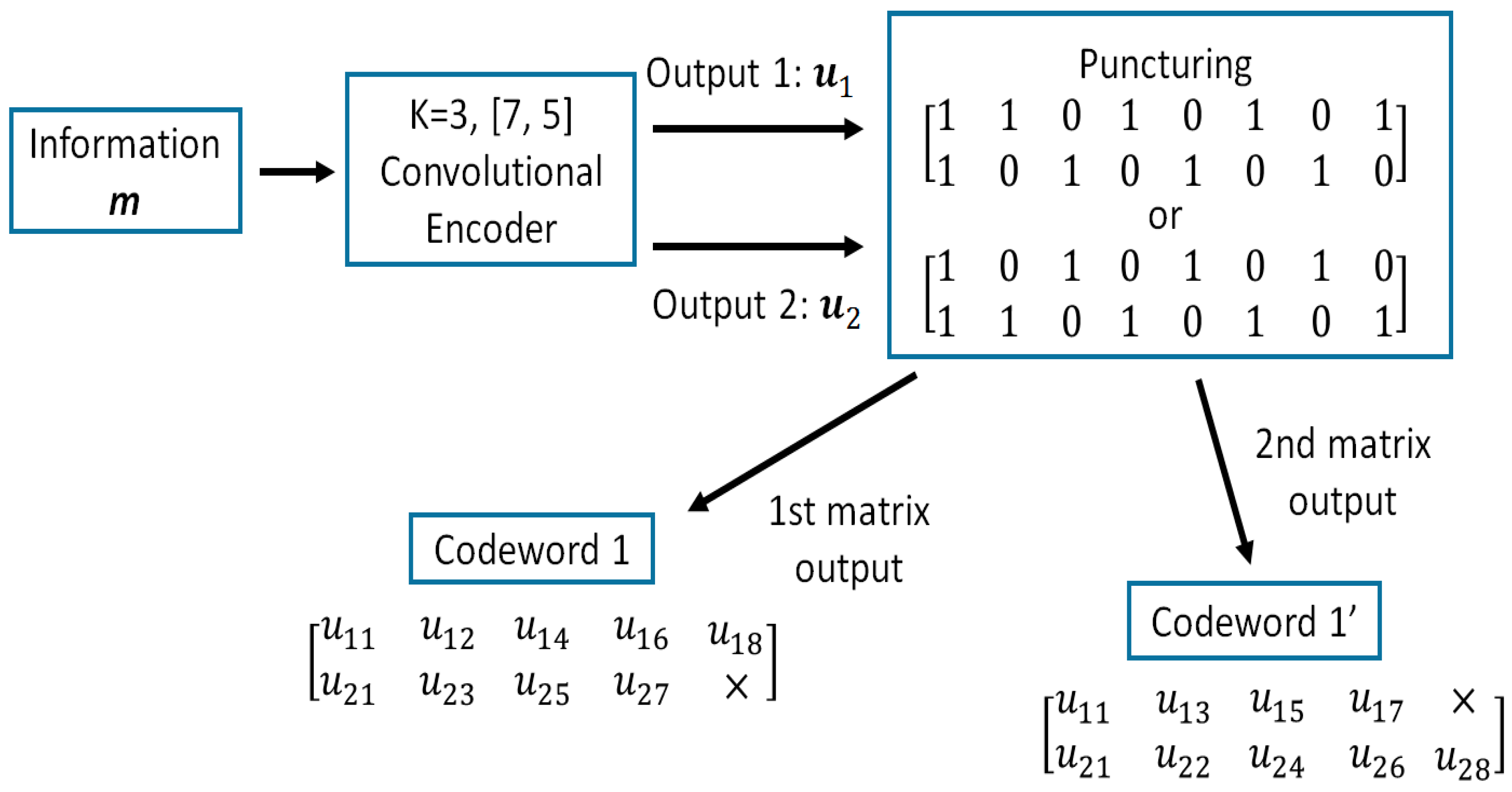
- Firstly, the information bit sequence is encoded via the punctured convolutional code, and codeword 1 is transmitted.
- If bit errors are detected after decoding codeword 1, the receiver stores the transmitted codeword 1, and the transmitter re-sends the sub-codeword of codeword 1′ times if . At the receiver, the received sub-codeword and stored codeword are combined, and the reconstructed codeword is decoded.
- After the third retransmission, codeword 1 is sent times and combined with a buffered codeword at the receiver. If bit errors are detected after decoding reconstructed codeword, the codeword 1 is buffered in the receiver, and codeword 1′ is transmitted times and combined with a stored codeword.
- After that, codeword 1 and 1′ are sent alternately times and stored. Then, a receiver reconstructs and decodes low-rate decomposable codes by changing the number of data copies in Weldon’s ARQ protocol. At this time, a buffered old codeword is updated to a transmitted new codeword.
- This operation continues until no bit errors are detected or the maximum number of transmissions is achieved.
5. System Model in Two-Hop Case
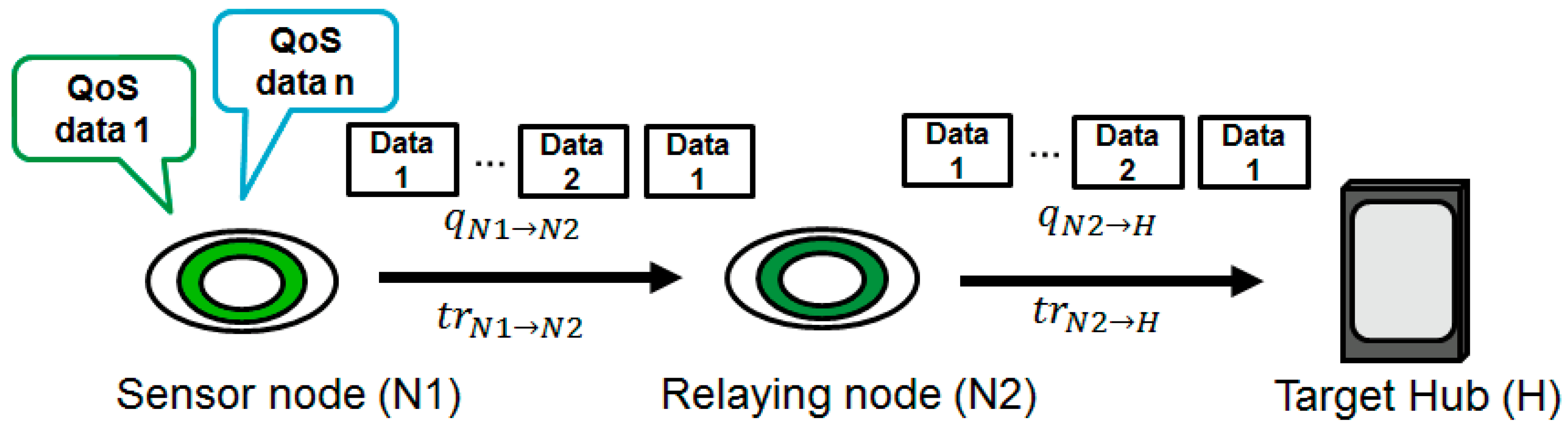
5.1. System Model and QoS Requirement
5.2. Two Proposed Schemes
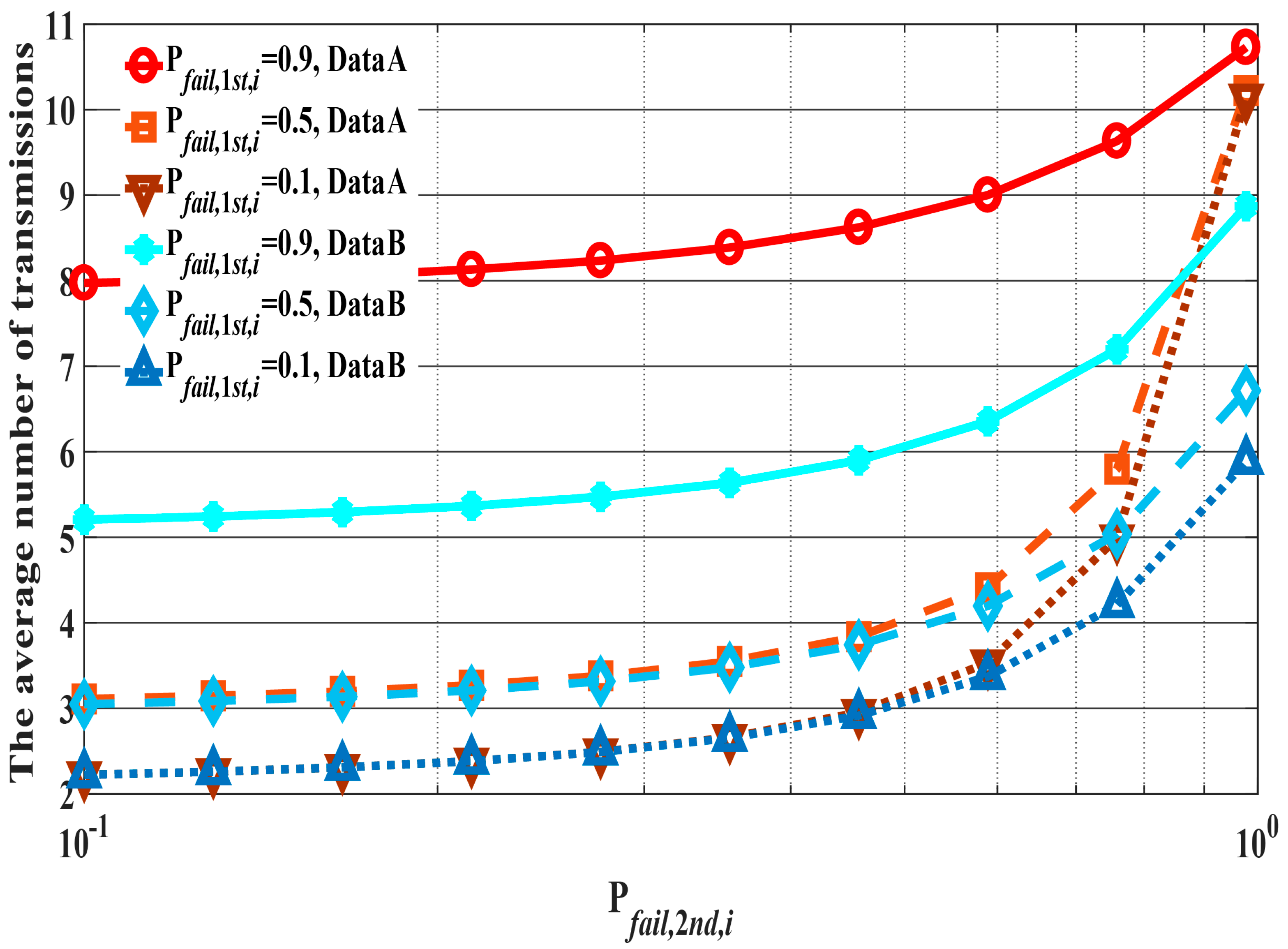
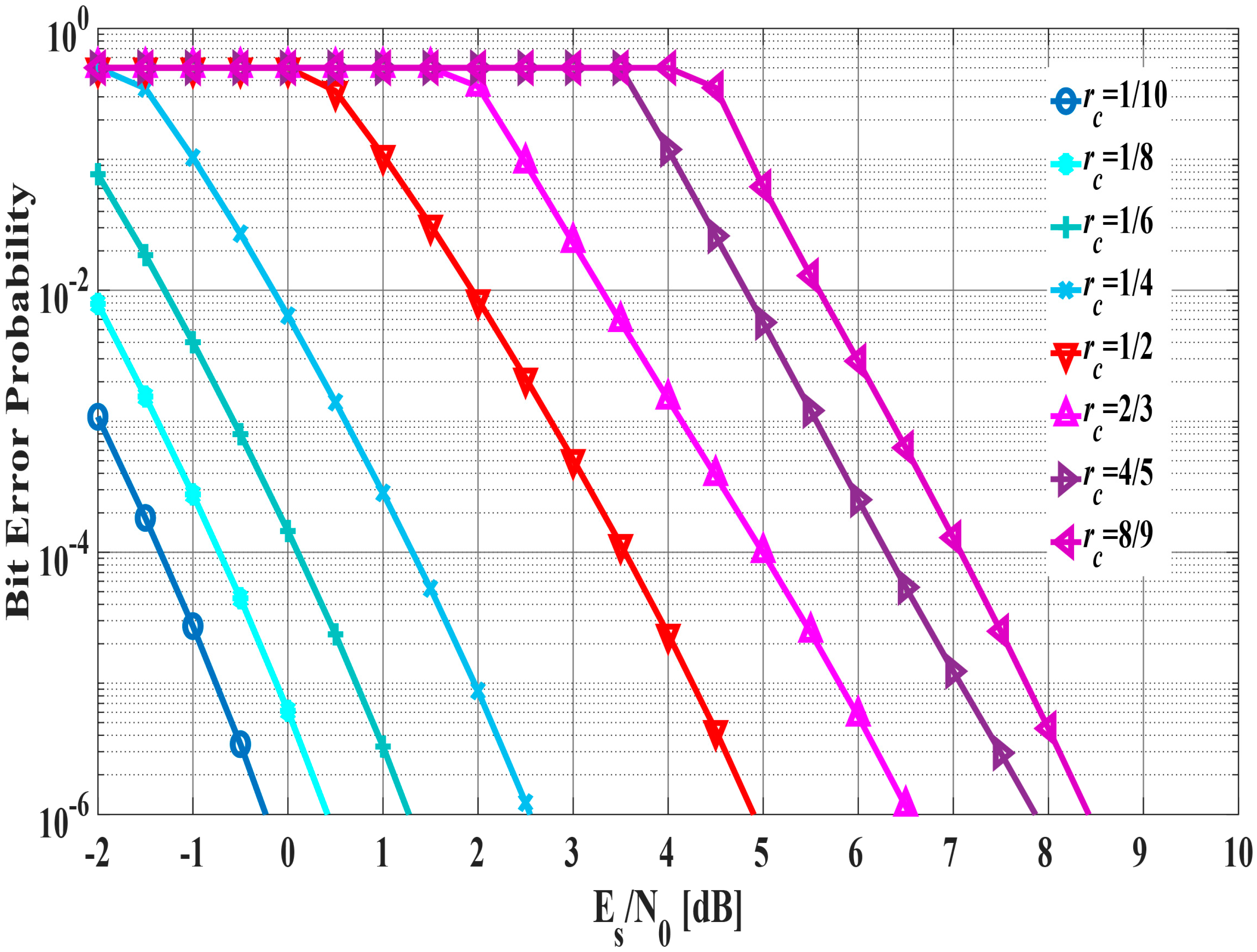
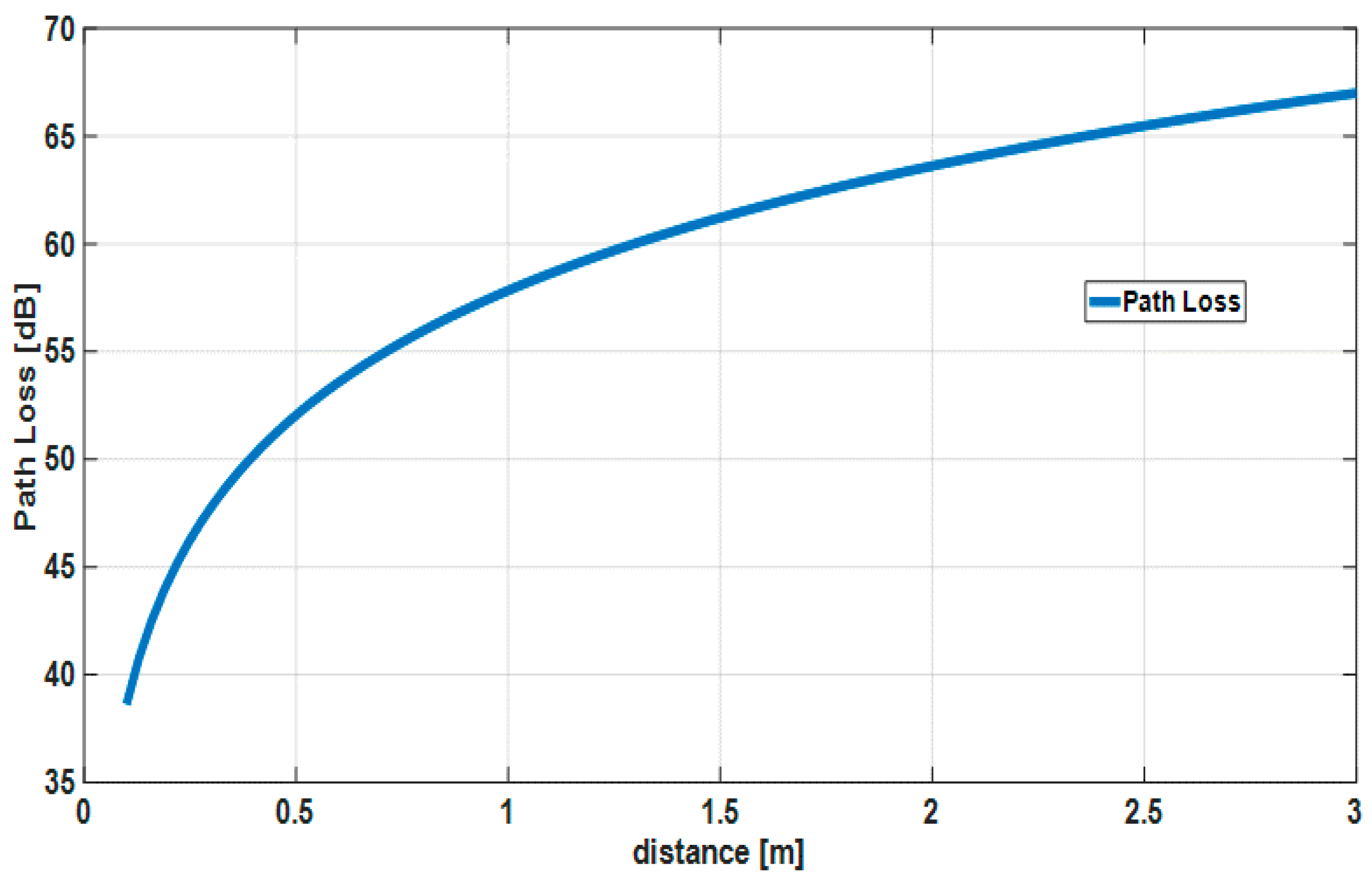
6. Results and Discussion
6.1. Performance Evaluation by Computer Simulation
6.2. Theoretical Analysis of Constant
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, M.; Gonzalez, S.; Vasilakos, A.V.; Cao, H. VCM Leung, Body Area Networks: A Survey. Mob. Netw. Appl. 2010, 16, 171–193. [Google Scholar] [CrossRef]
- Acampora, G.; Cook, D.J.; Rashidi, P.; Vasilakos, A.V. A Survey on Ambient Intelligence in Healthcare. Proc. IEEE 2013, 101, 2470–2494. [Google Scholar] [CrossRef] [PubMed]
- Hayajneh, T.; Almashaqbeh, G.; Ullah, S.; Vasilakos, A.V. A survey of wireless technologies coexistence in WBAN: Analysis and open research issues. Wirel. Netw. 2014, 20, 2165–2199. [Google Scholar] [CrossRef]
- Fortino, G.; Fatta, G.D.; Pathan, M.; Vasilakos, A.V. Cloud-assisted body area networks: State-of-the-art and future challenges. Wirel. Netw. 2014, 20, 1925–1938. [Google Scholar] [CrossRef]
- Zhou, J.; Cao, Z.; Dong, X.; Lin, X.; Vasilakos, A.V. Securing m-healthcare social networks: Challenges, countermeasures and future directions. IEEE Wirel. Commun. 2013, 20, 12–21. [Google Scholar] [CrossRef]
- Zhou, J.; Cao, Z.; Dong, X.; Xiong, N.; Vasilakos, A.V. 4S: A secure and privacy-preserving key management scheme for cloud-assisted wireless body area network in m-healthcare social networks. Inf. Sci. 2014, 314, 255–276. [Google Scholar] [CrossRef]
- Cao, H.; Leung, V.; Chow, C.; Chan, H. Enabling technologies for wireless body area networks: A survey and outlook. IEEE Commun. Mag. 2009, 47, 84–93. [Google Scholar] [CrossRef]
- Viswanathan, H.; Chen, B.; Pompili, D. Research challenges in computation, communication, and context awareness for ubiquitous healthcare. IEEE Commun. Mag. 2012, 50, 92–99. [Google Scholar] [CrossRef]
- Bachmann, C.; Ashouei, M.; Pop, V.; Vidojkovic, M.; Groot, H.D.; Gyselinckx, B. Low-power wireless sensor nodes for ubiquitous long-term biomedical signal monitoring. IEEE Commun. Mag. 2012, 50, 20–27. [Google Scholar] [CrossRef]
- Caldeira, J.M.L.P.; Rodrigues, J.J.P.C.; Lorenz, P. Toward ubiquitous mobility solutions for body sensor networks on healthcare. IEEE Commun. Mag. 2012, 50, 108–115. [Google Scholar] [CrossRef]
- Boulis, A.; Smith, D.; Miniutti, D.; Libman, L.; Tselishchev, Y. Challenges in body area networks for healthcare: The MAC. IEEE Commun. Mag. 2012, 50, 100–106. [Google Scholar] [CrossRef]
- Suzuki, T.; Tanaka, H.; Minami, S.; Yamada, H.; Miyata, T. Wearable Wireless Vital Monitoring Technology for Smart Health Care. In Proceedings of the 7th International Symposium on Medical Information and Communication Technology (ISMICT), Tokyo, Japan, 6–8 March 2013. [Google Scholar]
- Cavallari, R.; Martelli, F.; Rosini, R.; Buratti, C.; Verdone, R. A Survey on Wireless Body Area Networks: Technologies and Design Challenges. IEEE Commun. Surv. Tutor. 2014, 16, 1635–1657. [Google Scholar] [CrossRef]
- Movassaghi, S.; Abolhasan, M.; Lipman, J.; Smith, D.; Jamalipour, A. Wireless Body Area Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 1658–1686. [Google Scholar] [CrossRef]
- Patel, M.; Wang, J. Applications, challenges, and prospective in emerging body area networking technologies. IEEE Wirel. Commun. 2010, 17, 80–88. [Google Scholar] [CrossRef]
- Rodrigues, J.J.P.C. Digital Advances in Medicine, E-Health, and Communication Technologies; IGI Global: Hershey, PA, USA, 2013; ISBN 978-1-466-62794-9. [Google Scholar]
- IEEE Standard for Information Technology—Telecommunications and Information Exchange between Systems-Local and Metropolitan Area Networks-Specific Requirements: Part 15.6: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Wireless Personal Area Networks (WPANs) Used in or 12 around a Body. IEEE, 2012. Available online: https://ieeexplore.ieee.org/document/6161600 (accessed on 28 September 2018).
- Smart Body Area Network (SmartBAN); Low Complexity Medium Access Control (MAC) for SmartBAN, ETSI TC Smart BAN TS 103 325 V1.1.1. 2015. Available online: http://www.etsi.org/deliver/etsi_ts/103300_103399/103325/01.01.01_60/ts_103325v010101p.pdf (accessed on 28 September 2018).
- IEEE Std 802.15.4-2011 (Revision of IEEE Std 802.15.4-2006)-IEEE Standard for Local and Metropolitan Area Networks—Part 15.4: Low-Rate Wireless Personal Area Networks (LR-WPANs). IEEE, 2011. Available online: https://ieeexplore.ieee.org/document/6012487 (accessed on 28 September 2018).
- Takabayashi, K.; Tanaka, H.; Sugimoto, C.; Kohno, R. Multiplexing and Error Control Scheme for Body Area Network employing IEEE 802.15.6. IEICE Trans. Commun. 2014, 97, 564–570. [Google Scholar] [CrossRef]
- Takabayashi, K.; Tanaka, H.; Sugimoto, C.; Kohno, R. Performance Analysis of Multiplexing and Error Control Scheme for Body Area Networks. EURASIP J. Wirel. Commun. Netw. 2016, 2016, 1–16. [Google Scholar] [CrossRef]
- Takabayashi, K.; Karvonen, H.; Paso, T.; Tanaka, H.; Sugimoto, C.; Kohno, R. Performance Evaluation of a QoS-aware Error Control Scheme for Multiple-WBAN Environment. IEEJ Trans. Electr. Electron. Eng. TEEE C 2017, 12, S146–S157. [Google Scholar] [CrossRef]
- Latre, B.; Braem, B.; Moerman, I.; Blondia, C.; Reusens, E.; Joseph, W.; Demeester, P. A Low-delay Protocol for Multihop Wireless Body Area Networks. In Proceedings of the 2007 Fourth Annual International Conference on Mobile and Ubiquitous Systems: Networking & Services (MobiQuitous), Philadelphia, PA, USA, 6–10 August 2007. [Google Scholar]
- Ivanov, S.; Botvich, D.; Balasubramaniam, S. Cooperative wireless sensor environments supporting body area networks. IEEE Trans. Consum. Electron. 2012, 58, 284–292. [Google Scholar] [CrossRef]
- Torabi, N.; Leung, V.C.M. Cross-Layer Design for Prompt and Reliable Transmissions over Body Area Networks. IEEE J. Biomed. Health Inf. 2014, 18, 1303–1316. [Google Scholar] [CrossRef] [PubMed]
- Moosavi, H.; Bui, F.M. Optimal Relay Selection and Power Control with Quality-of-Service Provisioning in Wireless Body Area Networks. IEEE Trans. Wirel. Commun. 2016, 15, 5497–5510. [Google Scholar] [CrossRef]
- Liang, L.; Ge, Y.; Feng, G.; Ni, W.; Wai, A.A.P. Experimental study on adaptive power control based routing in multi-hop Wireless Body Area Networks. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012. [Google Scholar]
- Reusens, E.; Joseph, W.; Latré, B.; Braem, B.; Vermeeren, G.; Tanghe, E.; Martens, L.; Moerman, I.; Blondia, C. Characterization of On-Body Communication Channel and Energy Efficient Topology Design for Wireless Body Area Networks. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 933–945. [Google Scholar] [CrossRef] [PubMed]
- Moosavi, H.; Bui, F.M. Delay-Aware Optimization of Physical Layer Security in Multi-Hop Wireless Body Area Networks. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1928–1939. [Google Scholar] [CrossRef]
- Shi, L.; Yuan, J.; Yu, S.; Li, M. MASK-BAN: Movement-Aided Authenticated Secret Key Extraction Utilizing Channel Characteristics in Body Area Networks. IEEE Int. Things J. 2015, 2, 52–62. [Google Scholar] [CrossRef]
- Waheed, M.; Ahmad, R.; Ahmed, W.; Drieberg, M.; Alam, M.M. Towards Efficient Wireless Body Area Network Using Two-Way Relay Cooperation. Sensors 2018, 18, 565. [Google Scholar] [CrossRef] [PubMed]
- Kamiya, Y. Digital Wireless Communication Technologies with MATLAB, 1st ed.; Corona Publishing Co., Ltd.: Tokyo, Japan, 2008; pp. 168–169. ISBN 978-4-339-00800-5. (In Japanese) [Google Scholar]
- Yazdandoost, K.Y.; Sayrafian-Pour, K. Channel Model for Body Area Network (BAN). IEEE P802.15 Working Group for Wireless Personal Area Networks (WPANs), IEEE P802.15-08-0780-10-0006. 2009. Available online: https://mentor.ieee.org/802.15/file/08/15-08-0780-10-0006-tg6-channel-model.pdf (accessed on 28 September 2018).
- Karvonen, H.; Iinatti, J.; Hämäläinen, M. A cross-layer energy efficiency optimization model for WBAN using IR-UWB transceivers. Telecommun. Syst. 2015, 58, 165–177. [Google Scholar] [CrossRef]
- Abughalieh, N.; Steenhaut, K.; Nowé, A.; Anpalagan, A. Turbo codes for multihop wireless sensor networks with decode-and-forward mechanism. EURASIP J. Wirel. Commun. Netw. 2014, 204, 1–13. [Google Scholar]
- Ryckaert, J.; Desset, C.; Fort, A.; Badaroglu, M.; De Heyn, V.; Wambacq, P.; Van der Plas, G.; Donnay, S.; Van Poucke, B.; Gyselinckx, B. Ultra-wide-band transmitter for low-power wireless body area networks: Design and evaluation. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 2515–2525. [Google Scholar] [CrossRef]
- Zou, Z.; Mendoza, D.S.; Wang, P.; Zhou, Q.; Mao, J.; Jonsson, F.; Tenhunen, H.; Zheng, L.R. A Low-Power and Flexible Energy Detection IR-UWB Receiver for RFID and Wireless Sensor Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1470–1482. [Google Scholar] [CrossRef]


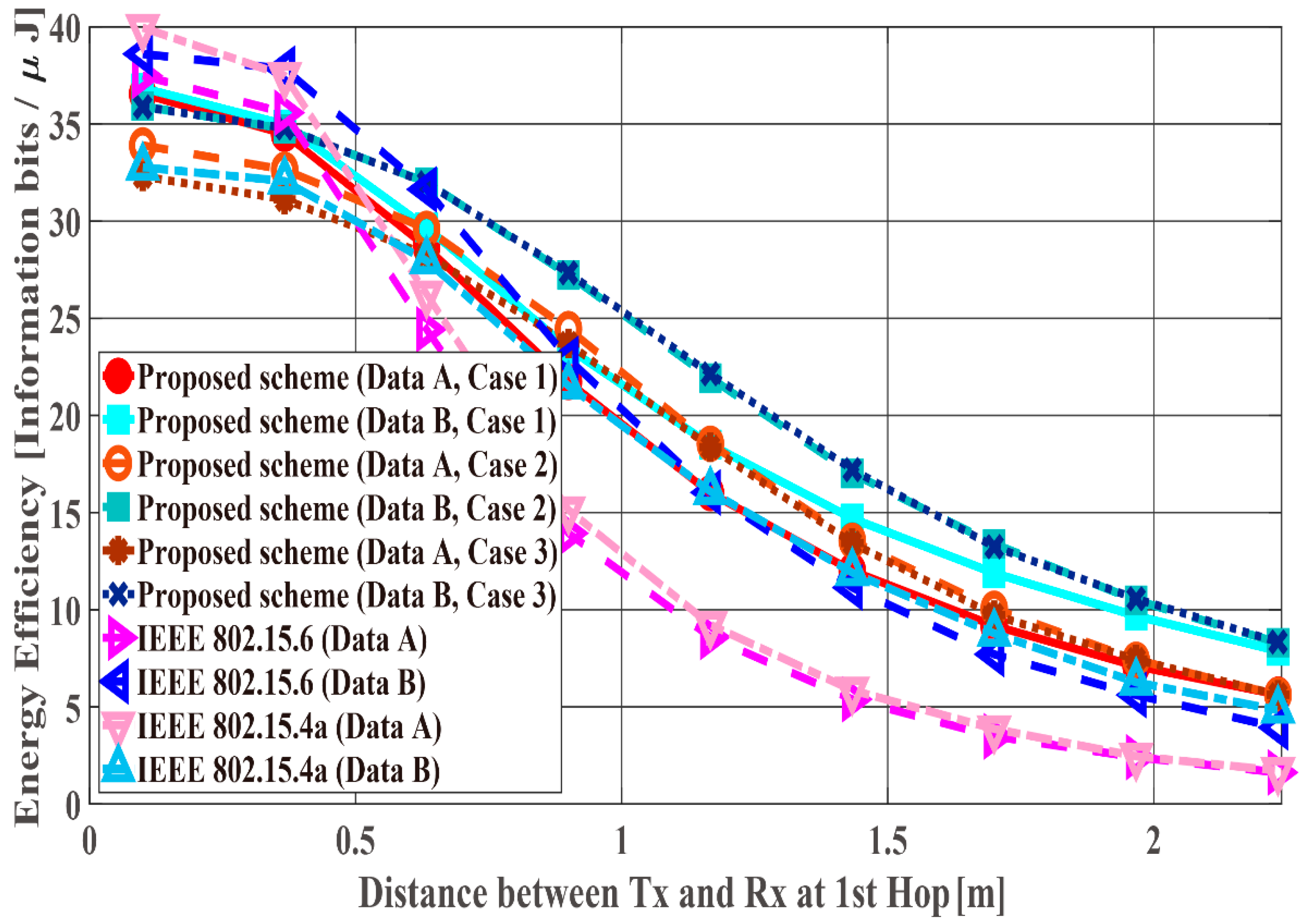
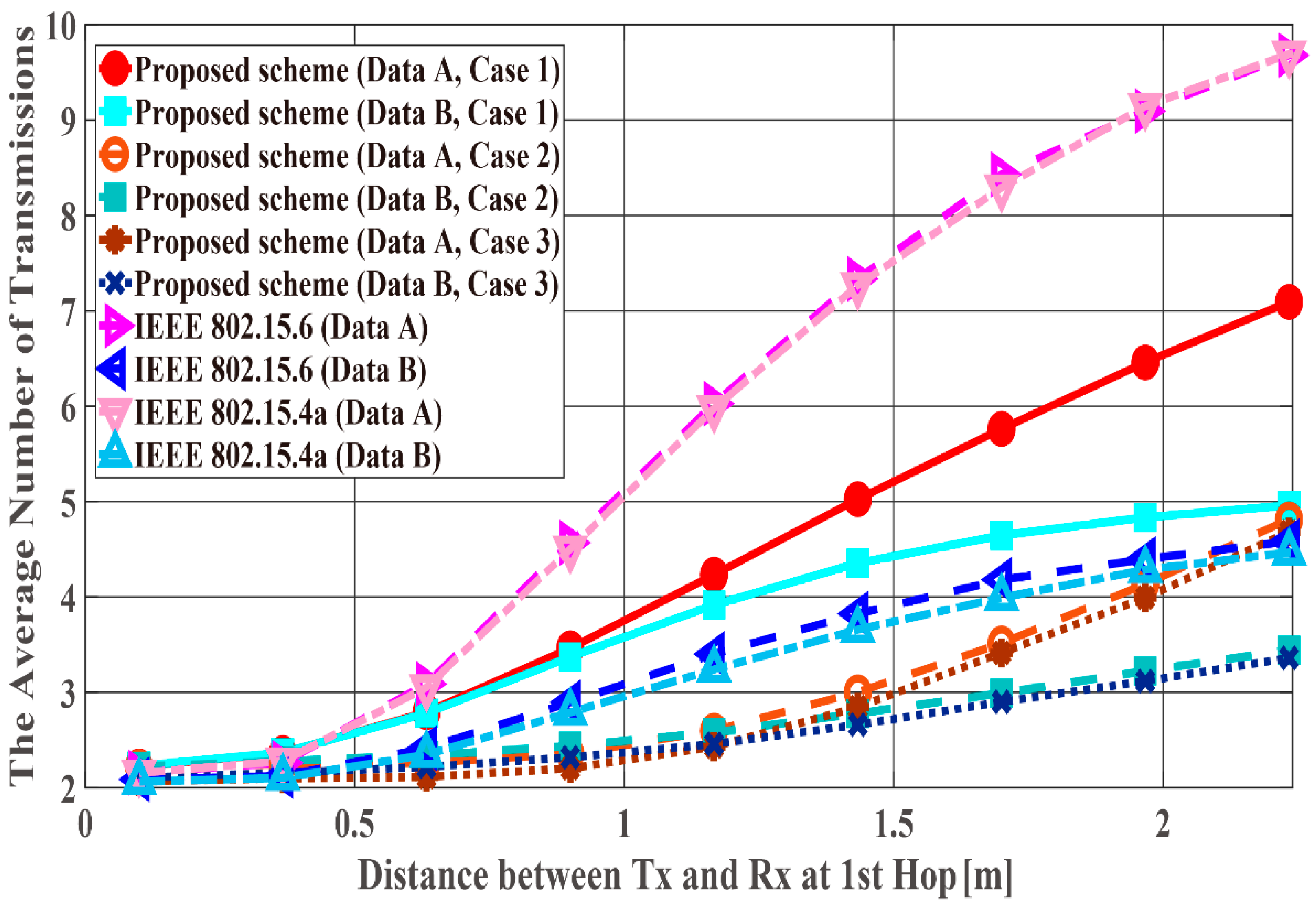
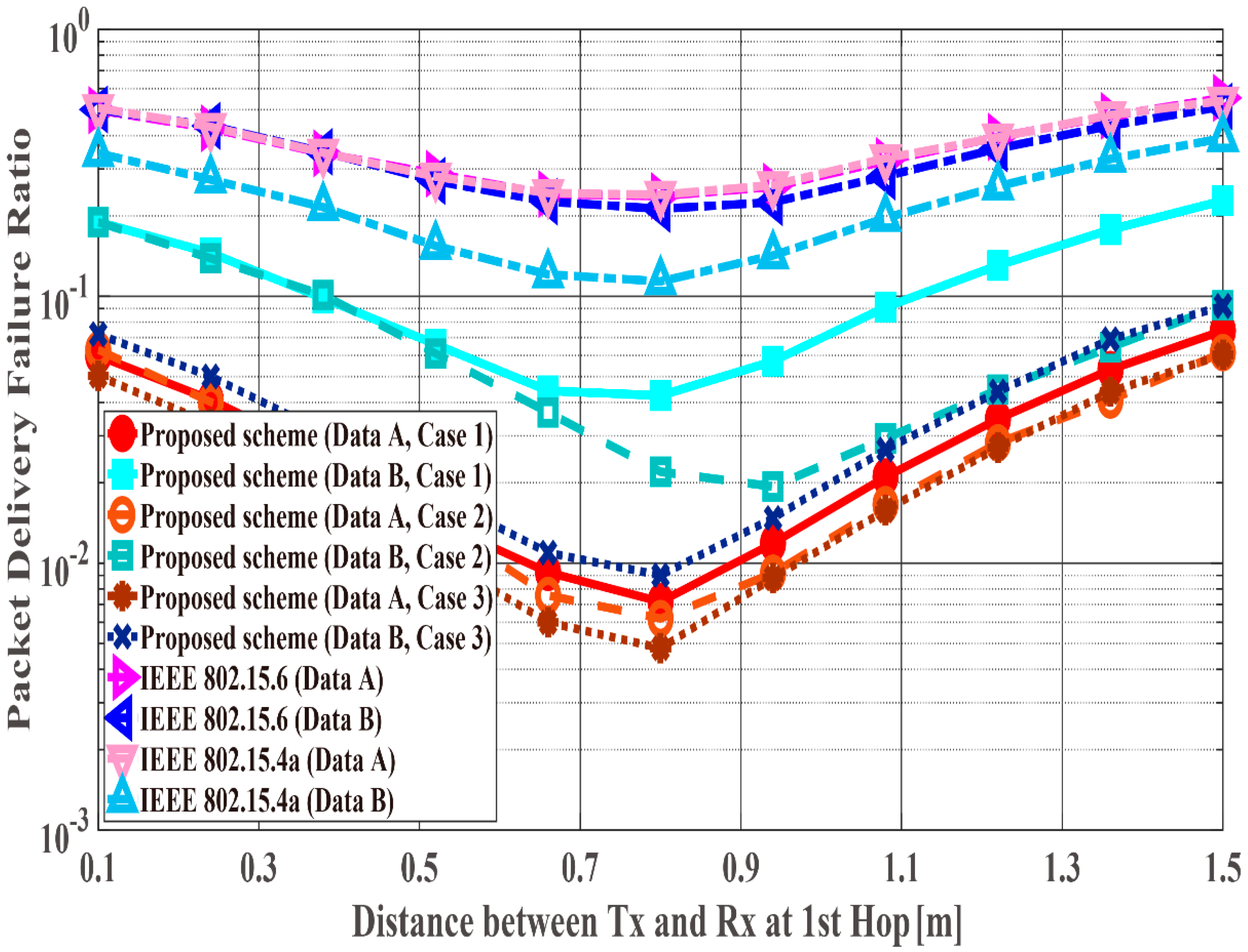
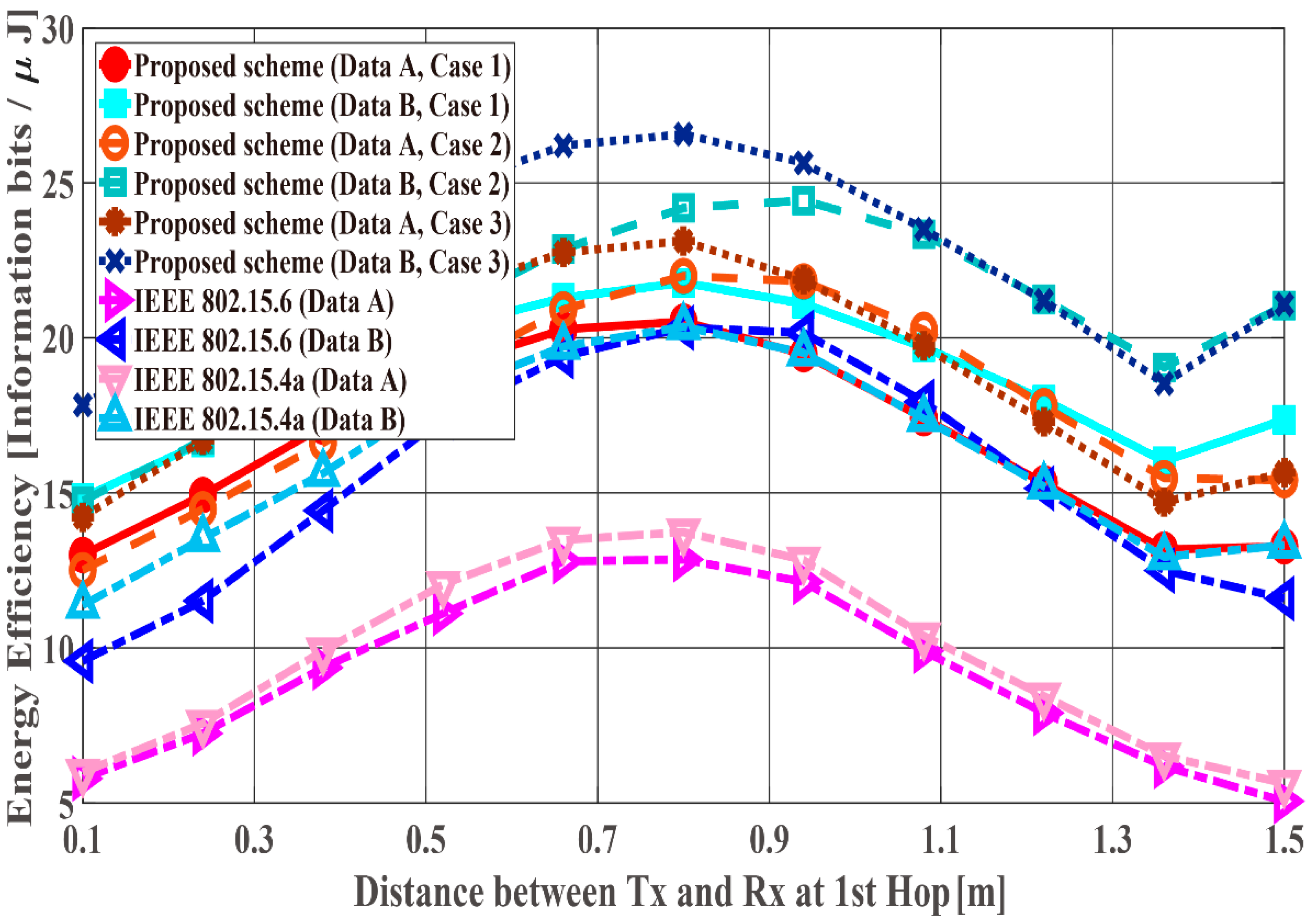

| Data Types | Data A | Data B |
|---|---|---|
| User priority | 5 | 6 |
| PER | ||
| Energy efficiency | low | high |
| Data A | 11 | 11 | |
| Data B | 5 | 5 | 10 |
| Parameter | Detail |
|---|---|
| Channel model | IEEE model CM3 |
| Path loss model | IEEE model CM3 |
| Bandwidth (BW) | 499.2 MHz |
| Central frequency () | 3993.6 MHz |
| Pulse shape | Gaussian mono pulse |
| Pulse duration () | 2.003 ns |
| Modulation | DBPSK |
| FEC | 8/9 to 1/16, Convolutional codes |
| Decoding | Soft decision Viterbi decoding |
| ARQ protocol | Weldon’s ARQ |
| Power spectral density () | −41.3 dBm/MHz |
| Thermal noise density () | −174 dBm/Hz |
| Implementation losses () | 3 dB |
| Receiver noise figure (NF) | 5 dB |
| Tx RF power consumption () | 37 μW |
| Tx circ. power consumption () | 2 mW |
| Rx power consumption () | 20 mW |
| Number of pulses per bit () | 2 |
| Integer number of pulse waveform positions () | 32 |
| Uncoded data rate (R) | 7.8 Mbps |
| Synch. header duration () | 40.32 μs |
| PHY header durations () | 82.052 μs |
| Information bit length () | 306 bits |
| ACK length () | 7 bytes |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data A | 1 | 4 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 |
| Data B | 1 | 1 | 2 | 3 | 4 | - | - | - | - | - | - |
| Case 1 | Scheme 1 | Scheme 1 |
| Case 2 | Scheme 1 | Scheme 2 |
| Case 3 | Scheme 2 | Scheme 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takabayashi, K.; Tanaka, H.; Sugimoto, C.; Sakakibara, K.; Kohno, R. Performance Evaluation of a Quality of Service Control Scheme in Multi-Hop WBAN Based on IEEE 802.15.6. Sensors 2018, 18, 3969. https://doi.org/10.3390/s18113969
Takabayashi K, Tanaka H, Sugimoto C, Sakakibara K, Kohno R. Performance Evaluation of a Quality of Service Control Scheme in Multi-Hop WBAN Based on IEEE 802.15.6. Sensors. 2018; 18(11):3969. https://doi.org/10.3390/s18113969
Chicago/Turabian StyleTakabayashi, Kento, Hirokazu Tanaka, Chika Sugimoto, Katsumi Sakakibara, and Ryuji Kohno. 2018. "Performance Evaluation of a Quality of Service Control Scheme in Multi-Hop WBAN Based on IEEE 802.15.6" Sensors 18, no. 11: 3969. https://doi.org/10.3390/s18113969
APA StyleTakabayashi, K., Tanaka, H., Sugimoto, C., Sakakibara, K., & Kohno, R. (2018). Performance Evaluation of a Quality of Service Control Scheme in Multi-Hop WBAN Based on IEEE 802.15.6. Sensors, 18(11), 3969. https://doi.org/10.3390/s18113969