A Noninvasive TDR Sensor to Measure the Moisture Content of Rigid Porous Materials
Abstract
1. Introduction
2. Concept of the Surface TDR Sensor
- construction of TDR probes of significant size, consisting of steel rods of the required diameter and durable head [4];
- construction of the TDR surface sensor.
3. Materials and Methods
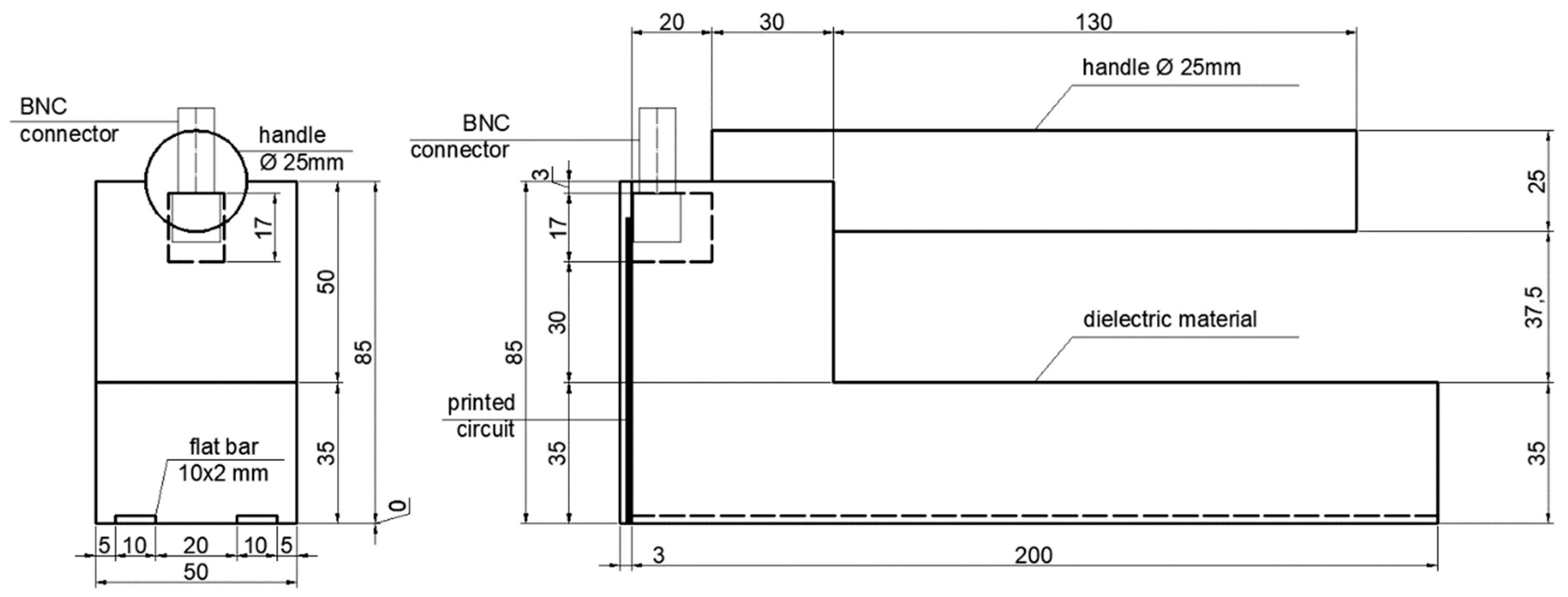
3.1. Details of the Developed Sensor
3.2. Measuring Setup
- Aerated concrete, dry apparent density 600 kg/m3;
- Laboratory oven VO-500 (Memmert, Schwabach, Germany);
- Bitumen isolation;
- Laboratory scale WPT 6C/1 (RADWAG, Radom, Poland);
- Multifunctional scale WPW 30/H3/K (RADWAG, Radom, Poland),
- Water reservoir equipped with necessary equipment to sustain the constant water level;
- TDR equipment including laboratory multimeter LOM (ETest, Lublin, Poland);
- TDR sensor presented in this article, concentric cable;
- Personal Computer for meter control and data management;
- Capacitive moisture meter LB-796, (LABEL, Reguły, Poland);
- Atomizer (for calibration procedure).
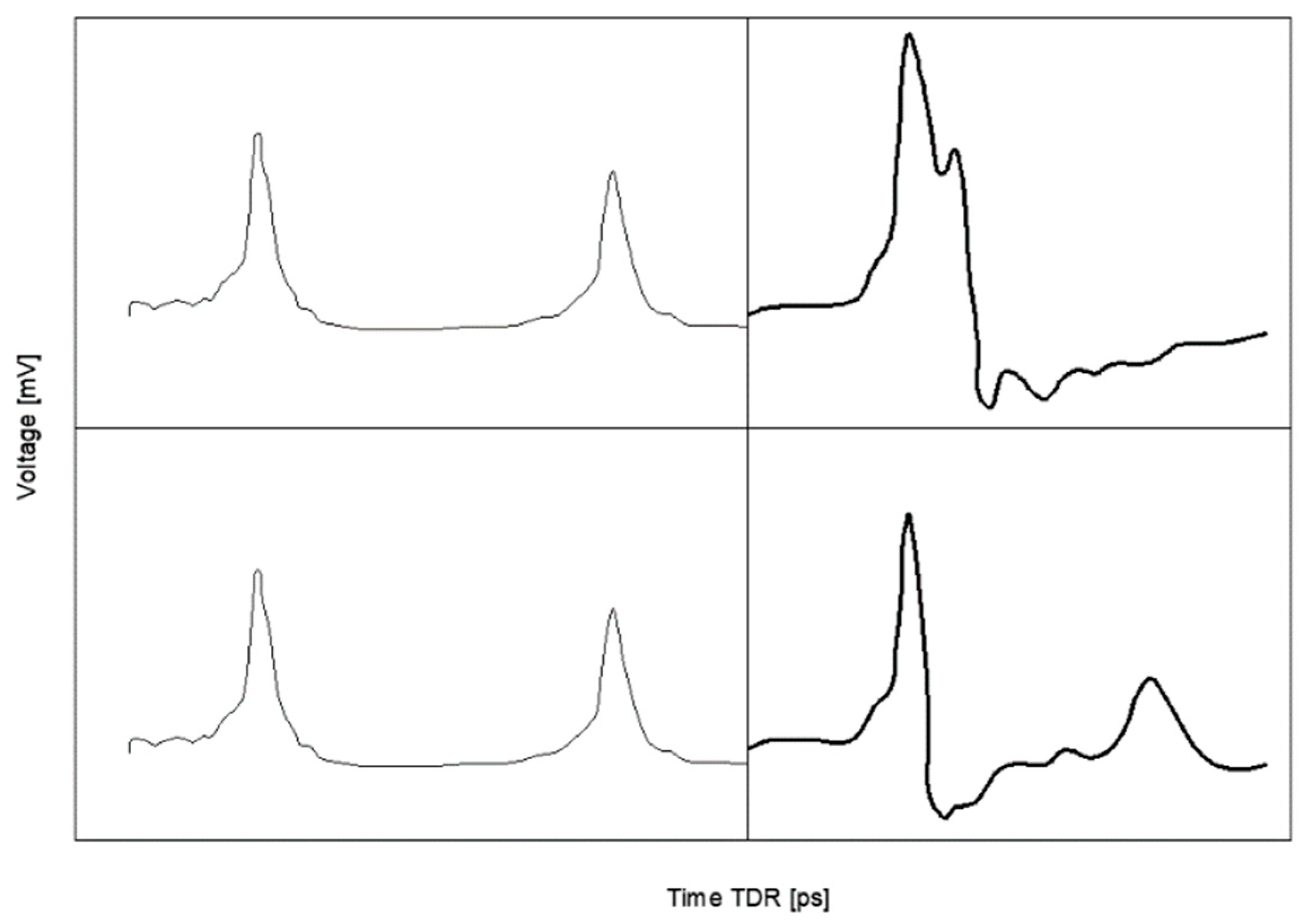
3.3. Preliminary Research
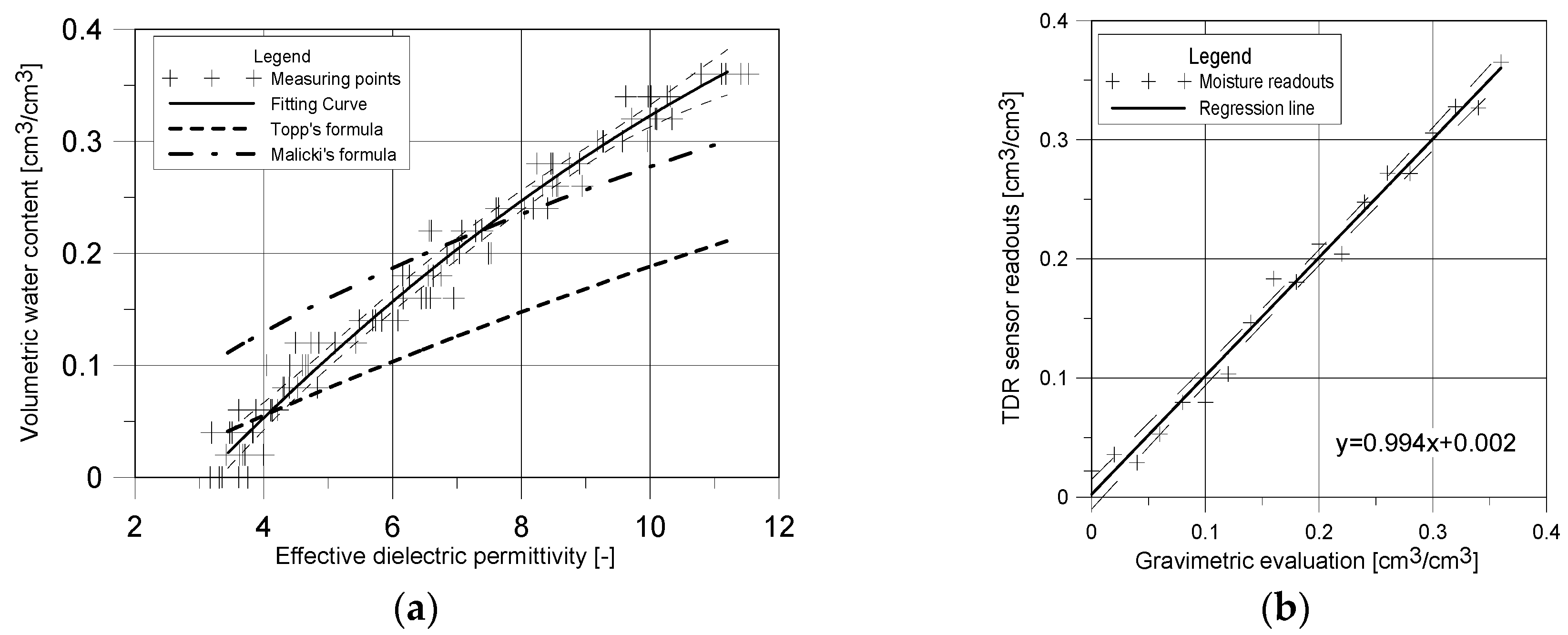
3.4. Calibration the Sensor
3.5. Model of Regression
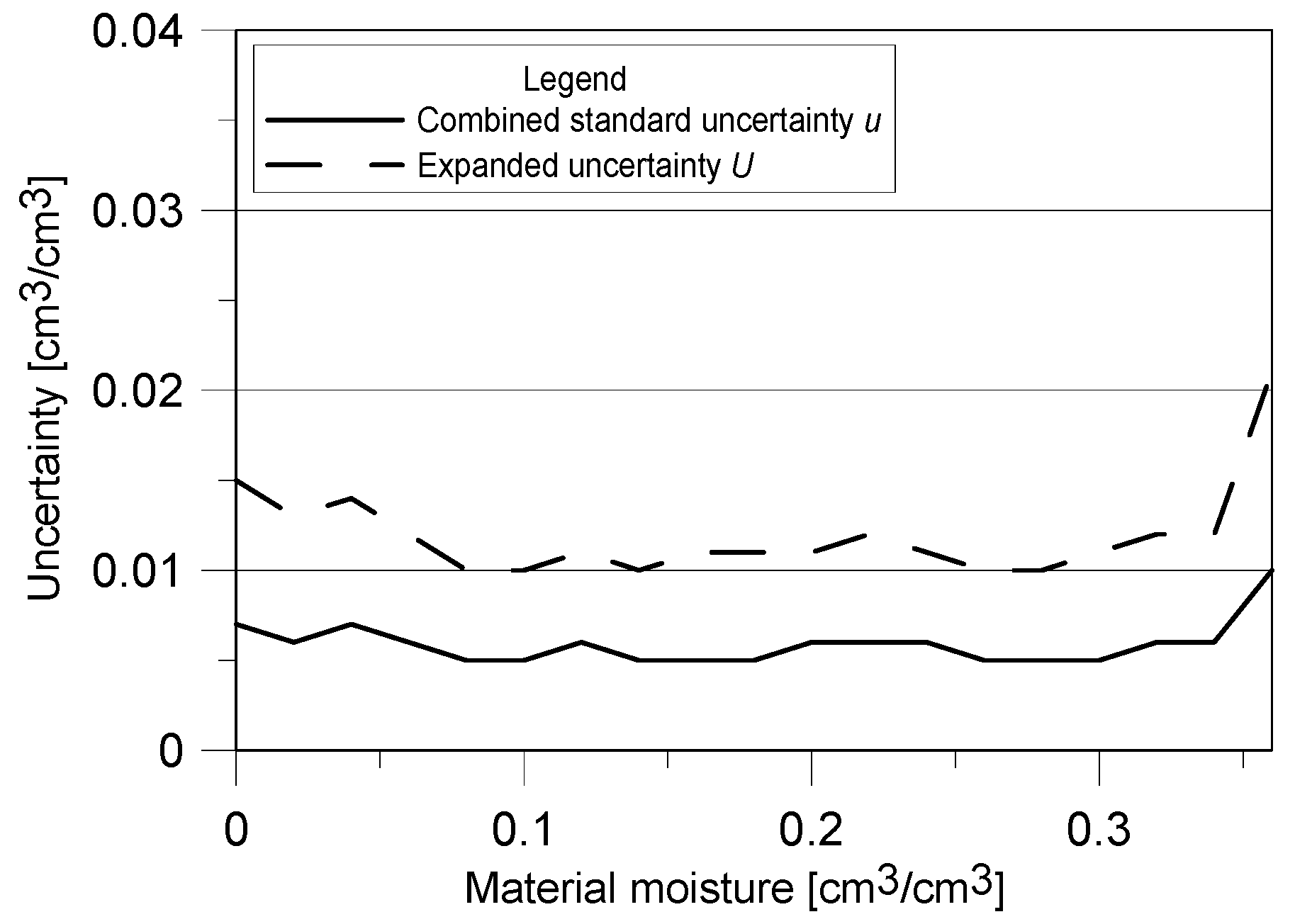
3.6. Calculation of Uncertainty
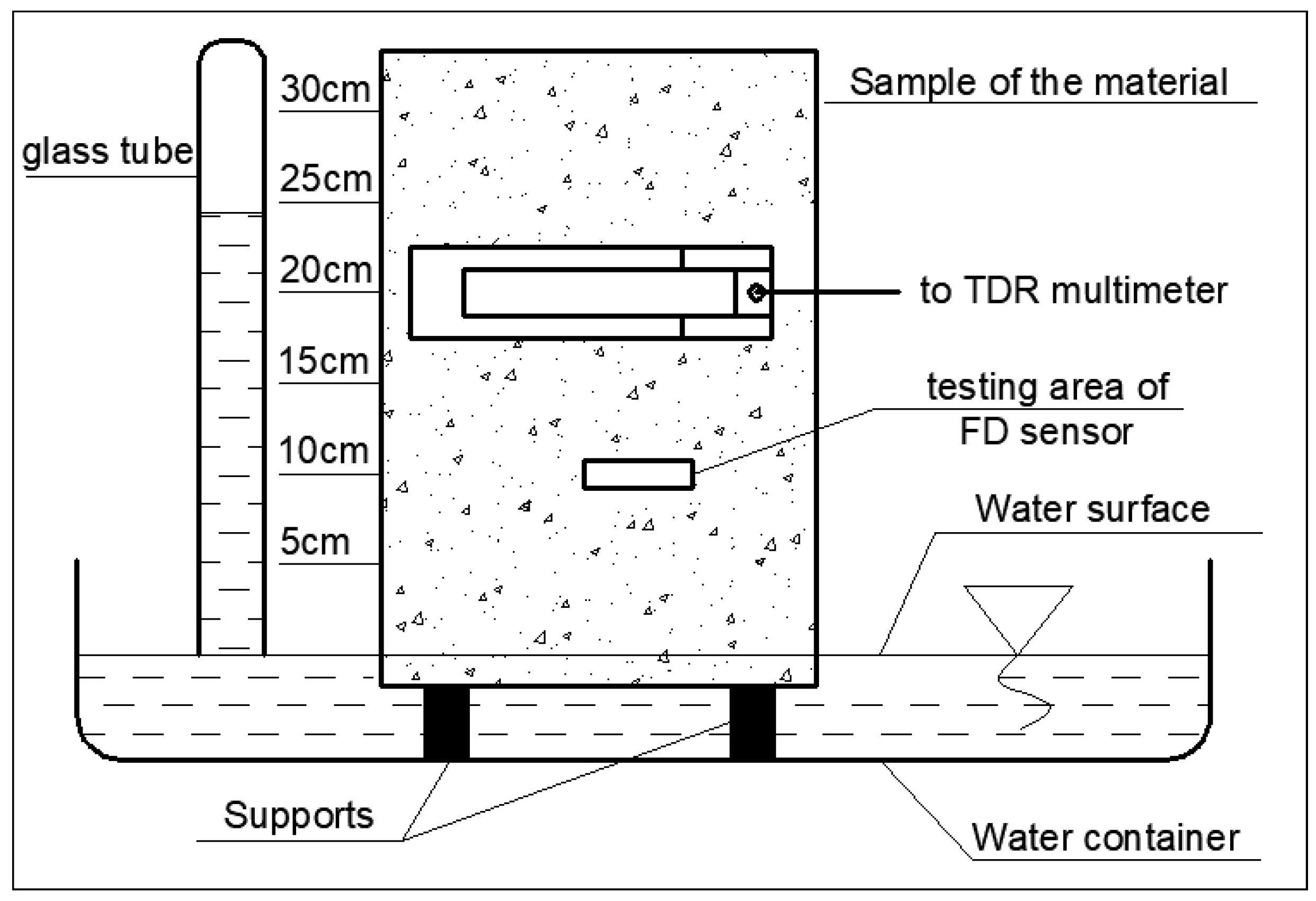
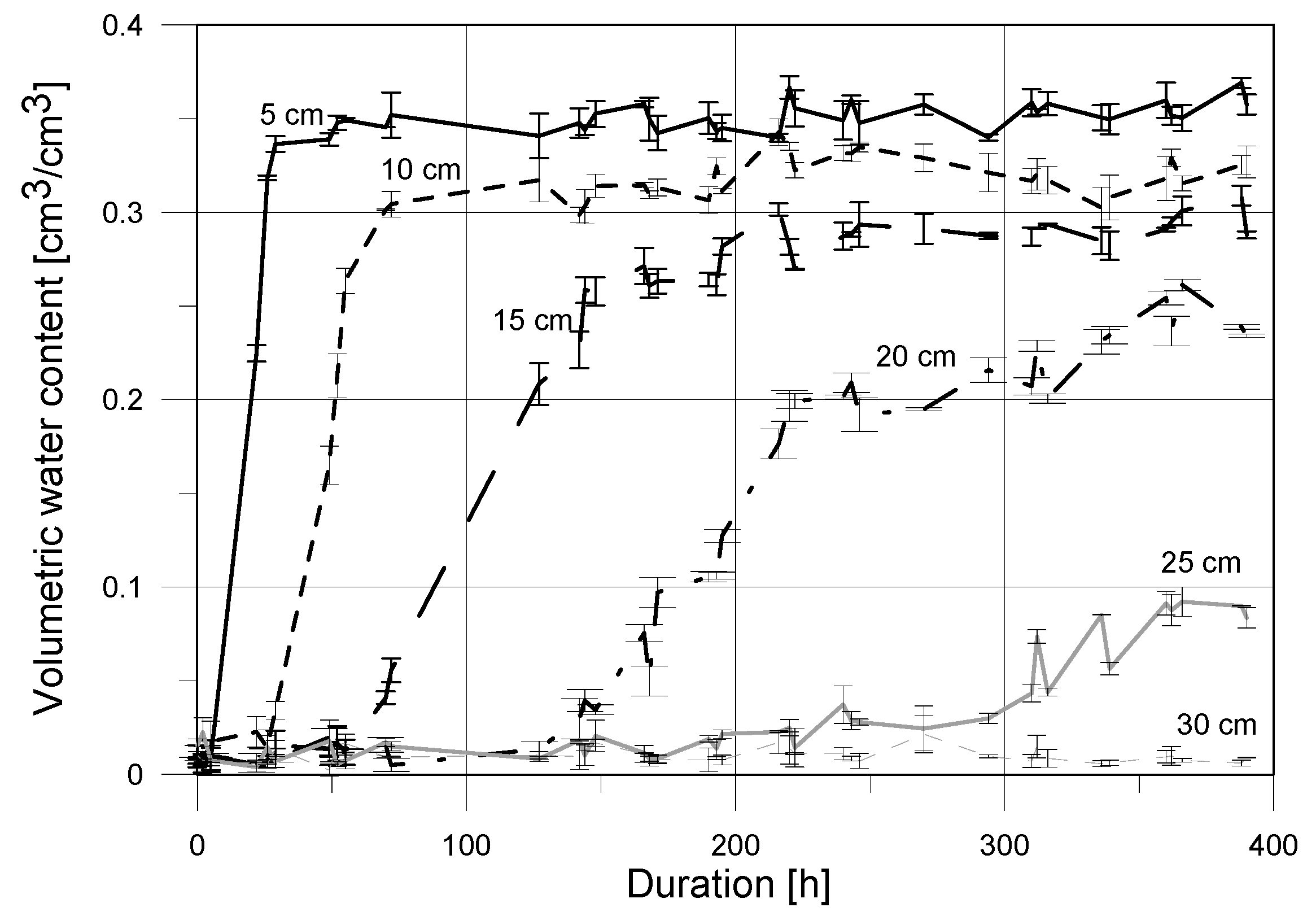
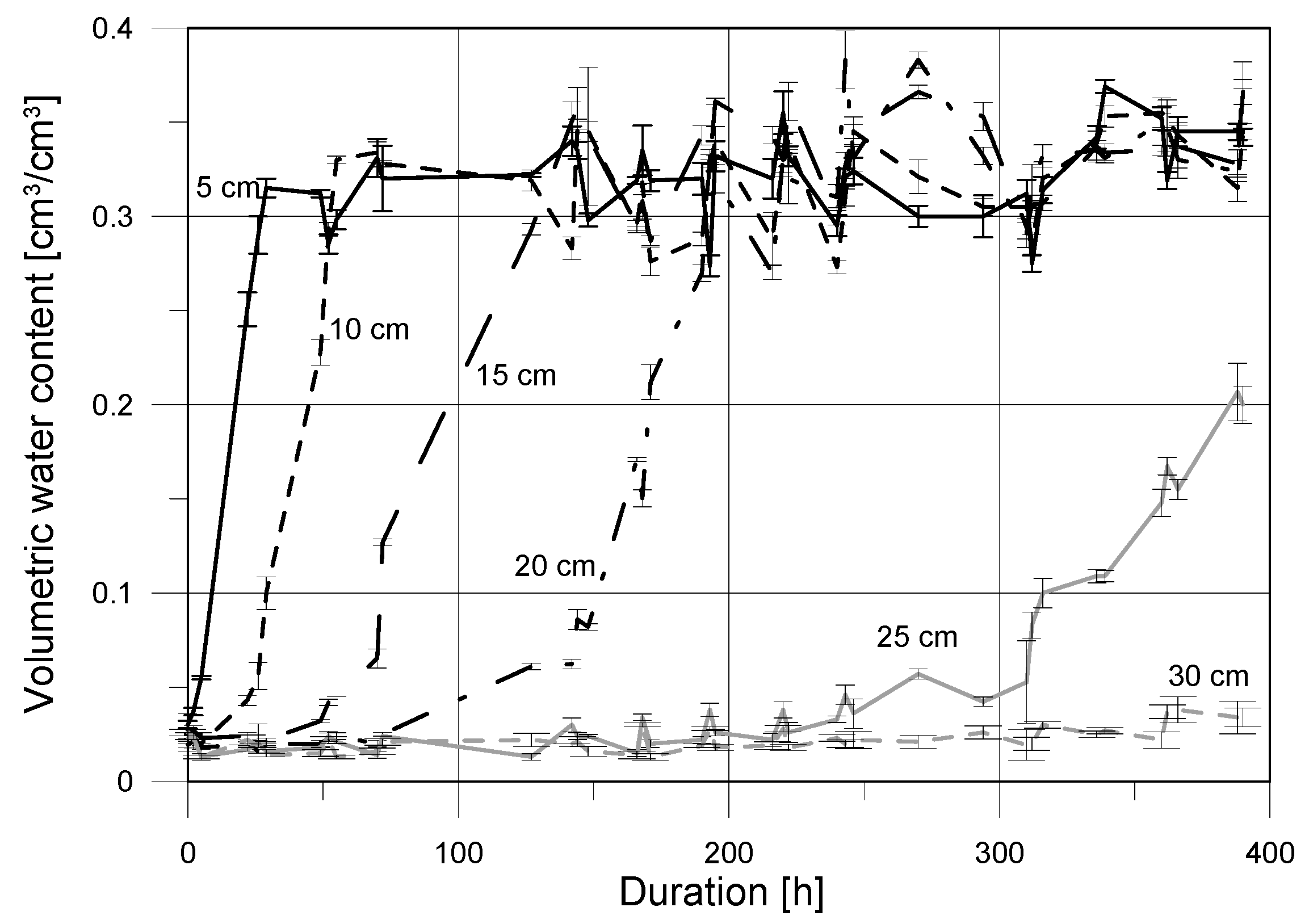
3.7. Capillary Suction Test
4. Results
4.1. Preliminary Test Results
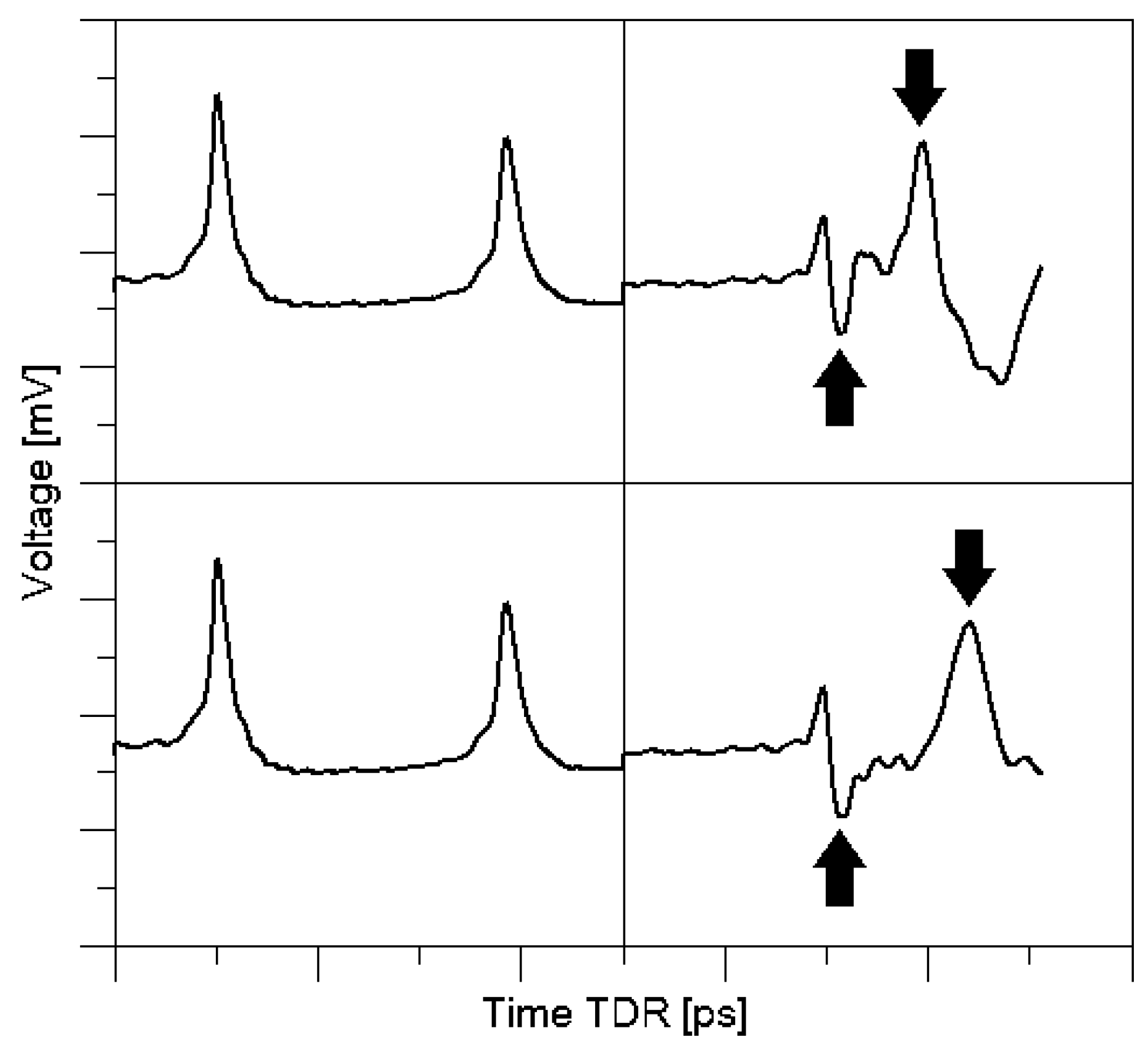
4.2. Calibration of the TDR Sensor
4.3. Combined Standard and Expanded Measurement Uncertainty
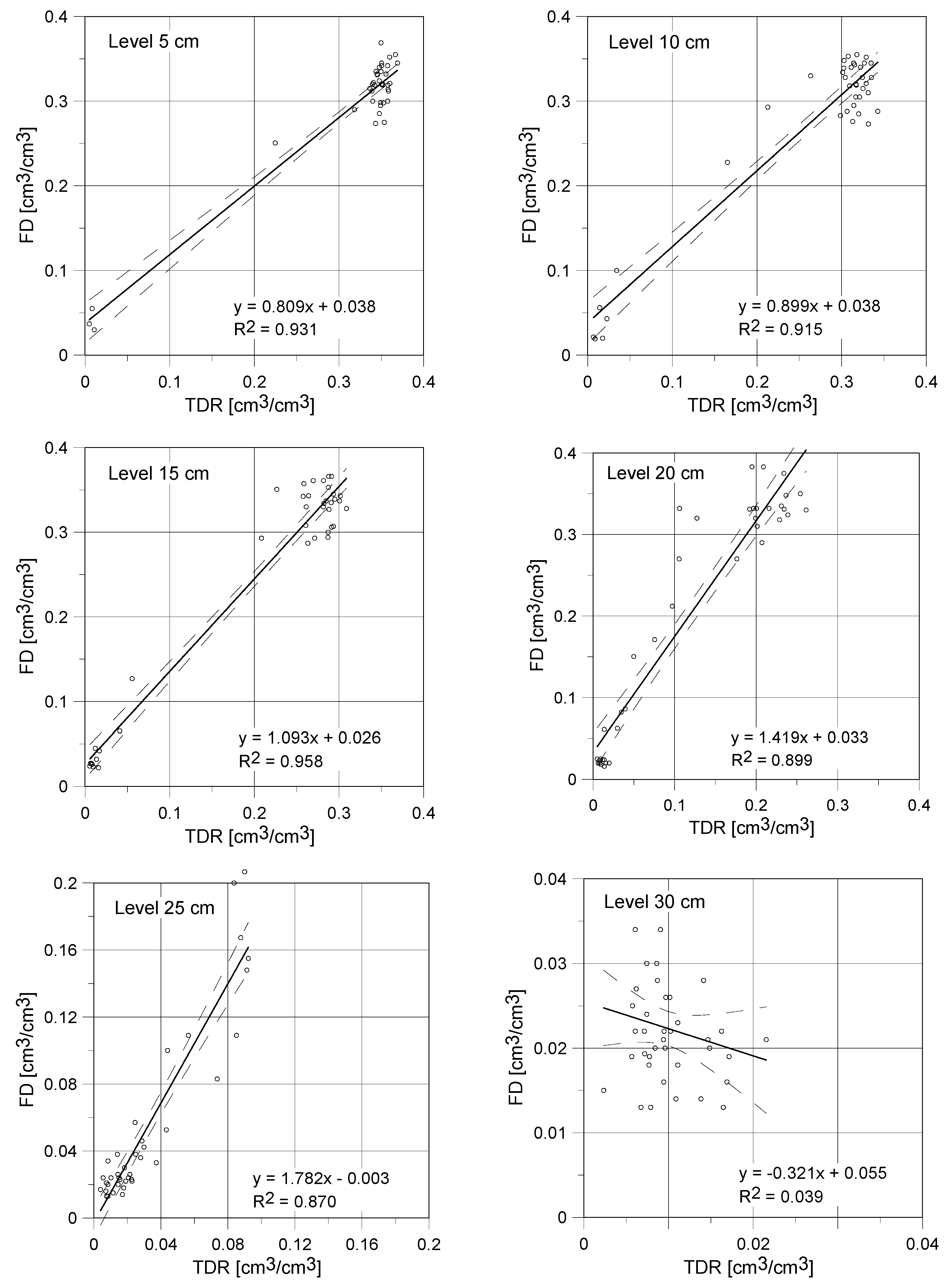
4.4. Capilary Suction Results
5. Discussion
5.1. Discussion on the Calibration Results and Uncertainty Calculations
- model of regression is individual;
- most of the cited models were developed for soil media, less homogenous in comparison to the tested building material (autoclaved aerated concrete).
5.2. Discussion on Capillary Uptake Experiment Results
- moisture readouts at points located at low height about the water table (5 and 10 cm) were higher for the TDR noninvasive sensor;
- at the height of 15 cm moisture content determined by capacitive probe was slightly higher that one indicated by the TDR sensor which is confirmed by the slope of regression higher than 1 and positive value of the y-intercept;
- for low saturation conditions the FD probe showed higher moisture readouts than the TDR surface sensor;
- both of the tested probes showed high measurement instability for low saturation (close to dry), which is visible in Figure 10 for the reference level at 30 cm, with the negative coefficient of regression;
- the maximal noted standard deviation for the TDR sensor was equal to 0.012 cm3/cm3 with the maximal standard deviation for the FD probe was higher, reaching 0.037 cm3/cm3.
6. Conclusions
- (1)
- For proper recalculation of reflectometric moisture readouts, the noninvasive, surface TDR sensors require individual calibration.
- (2)
- Due to influence of polyoxymethylene cover of the sensor, apparent permittivity read by the noninvasive sensor is lower than one read by the traditional probe in relation to the same moisture level. These differences can be abolished by application of the individual calibration.
- (3)
- Residual mean squared error (RMSE) for the calibration formula developed for the discussed sensor and material equals 0.013 cm3/cm3 and is smaller than found in the literature for the traditional invasive probes utilizing the standard empirical calibration formulas.
- (4)
- Expanded uncertainty of the discussed sensor equals 0.01 cm3/cm3 in the most of the range of material moisture which is lower value than found in the literature for the invasive sensors utilizing the traditional empirical calibration formulas.
- (5)
- Expanded uncertainty of the tested sensor is higher at nearly dry and nearly saturated states of the measured material.
- (6)
- In the range of high moisture values, water content readouts by the TDR surface sensor were higher than those acquired by the capacitive sensor.
- (7)
- In the range of average and low moisture values, water content readouts by the TDR surface sensor were lower than those acquired by the capacitive sensor.
- (8)
- During the comparison of the indirect, electric estimation of moisture using noninvasive TDR and FD sensors with the gravimetric evaluation it was noticed that the TDR readouts were underestimated for 4.4% and the FD readouts were overestimated for 12.6%.
- (9)
- Comparing the maximal standard deviations in both tests using electric techniques of moisture detection it was noted, that capacitive sensors are characterized by greater values of this parameter.
Author Contributions
Funding
Conflicts of Interest
References
- Topp, G.C.; Ferré, T.P.A. Time-Domain Reflectometry. In Encyclopedia of Soils in the Environment; Hillel, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 174–181. ISBN 978-0-12-348530-4. [Google Scholar]
- Rubio-Celorio, M.; Garcia-Gil, N.; Gou, P.; Arnau, J.; Fulladosa, E. Effect of temperature, high pressure and freezing/thawing of dry-cured ham slices on dielectric time domain reflectometry response. Meat Sci. 2015, 100, 91–96. [Google Scholar] [CrossRef] [PubMed]
- Nasraoui, M.; Nowik, W.; Lubelli, B. A comparative study of hygroscopic moisture content, electrical conductivity and ion chromatography for salt assessment in plasters of historical buildings. Constr. Build. Mater. 2009, 23, 1731–1735. [Google Scholar] [CrossRef]
- Sobczuk, H.; Plagge, R. Time Domain Reflectometry Method in Environmental Measurements; Polska Akademia Nauk. Komitet Inzynierii Srodowiska: Lublin, Poland, 2007; Volume 39, pp. 1–114. ISBN 83-89293-51-X. [Google Scholar]
- Malicki, M.A.; Campbell, E.C.; Hanks, R.J. Investigations on power factor of the soil electrical impedance as related to moisture, salinity and bulk density. Irrig. Sci. 1989, 10, 55–62. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Skierucha, W.; Wilczek, A.; Alokhina, O. Calibration of a TDR probe for low soil water content measurements. Sens. Actuators A Phys. 2008, 147, 544–552. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, P. Electromagnetic determination of soil water content using TDR: I. Applications to wetting fronts and steep gradients. Soil Sci. Soc. Am. J. 1982, 46, 672–678. [Google Scholar] [CrossRef]
- Malicki, M.A.; Skierucha, W.M. A manually controlled TDR soil moisture meter operating with 300 ps rise-time needle pulse. Irrig. Sci. 1989, 10, 153–163. [Google Scholar] [CrossRef]
- Zegelin, S.J.; White, I.; Jenkins, D.J. Improved field probe for soil water content and electrical conductivity measurement using time domain reflectometry. Water Resour. Res. 1989, 25, 2367–2376. [Google Scholar] [CrossRef]
- Černý, R. Time-domain reflectometry method and its application for measuring moisture content in porous materials: A review. Measurement 2009, 42, 329–336. [Google Scholar] [CrossRef]
- Blonquist, J.M.; Jones, S.B.; Robinson, D.A. A time domain transmission sensor with TDR performance characteristics. J. Hydrol. 2005, 314, 235–245. [Google Scholar] [CrossRef]
- Noborio, K. Mesurement of soil water content and electrical conductivity by time domain reflectometry: A review. Comput. Electron. Agric. 2001, 31, 213–237. [Google Scholar] [CrossRef]
- Selker, J.S.; Graff, L.; Steenhuis, T. Noninvasive time domain reflectometry moisture measurement probe. Soil Sci. Soc. Am. J. 1993, 57, 934–936. [Google Scholar] [CrossRef]
- Perrson, M.; Berndtsson, R. Noninvasive water content and electrical conductivity laboratory measurements using time domain reflectometry. Soil Sci. Soc. Am. J. 1998, 62, 1471–1476. [Google Scholar] [CrossRef]
- Malicki, M.A.; Plagge, R.; Roth, C.H. Improving the calibration of dielectric TDR soil moisture determination taking into account the solid soil. Eur. J. Soil Sci. 1996, 47, 357–366. [Google Scholar] [CrossRef]
- Sobczuk, H.; Suchorab, Z. Calibration of TDR instruments for moisture measurement of serated concrete. In Monitoring and Modelling the Properties of Soil as Porous Medium; Skierucha, W., Walczak, T., Eds.; Institute of Agrophysics, Polish Academy of Sciences: Lublin, Poland, 2005; pp. 156–165. ISBN 9788387385958. [Google Scholar]
- Lee, J.; Horton, R.; Noborio, K.; Jaynes, D.B. Characterization of preferential flow in undisturbed, structured soil columns using a vertical TDR probe. J Contam. Hydrol. 2001, 51, 131–144. [Google Scholar] [CrossRef]
- Lins, Y.; Schanz, T.; Fredlund, D.G. Modified pressure plate apparatus and column testing device for measuring SWCC of sand. Geotech. Test J. 2009, 32, 450–464. [Google Scholar] [CrossRef]
- Skierucha, W.; Wilczek, A.; Szypłowska, A.; Sławiński, C.; Lamorski, K. A TDR-based soil moisture monitoring system with simultaneous measurement of soil temperature and electrical conductivity. Sensors 2012, 12, 13545–13566. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.L.; Annan, A.P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Skierucha, W.; Malicki, M.A. TDR Method for the Measurement of Water Content and Salinity of Porous Media; Institute of Agrophysics, Polish Academy of Sciences: Lublin, Poland, 2004. [Google Scholar]
- Wilczek, A.; Szypłowska, A.; Kafarski, M.; Skierucha, W. A Time-Domain Reflectometry Method with Variable Needle Pulse Width for Measuring the Dielectric Properties of Materials. Sensors 2016, 16, 191. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.B.; Wraith, J.M.; Or, D. Time domain reflectometry measurement principles and applications. Hydrol. Proc. 2002, 16, 141–153. [Google Scholar] [CrossRef]
- De Loor, G.P. Dielectric properties of heterogeneous mixtures containing water. J. Microw. Power 1968, 3, 67–73. [Google Scholar] [CrossRef]
- Tinga, W.R.; Voss, W.A.G.; Blossey, D.F. Generalized approach to multiphase dielectric mixture theorie. J. Appl. Phys. 1973, 44, 3897–3902. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwave dielectric behavior of wet soil. Part 2: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, 23, 35–46. [Google Scholar] [CrossRef]
- Noborio, K.; Horton, R.; Tan, C.S. Time Domain Reflectometry probe for simultaneous measurement of soil matric potential and water content. Soil Sci. Soc. Am. J. 1999, 63, 1500–1505. [Google Scholar] [CrossRef]
- O’Connor, K.M.; Dowding, C.H. Geomeasurements by Pulsing TDR Cables and Probes; CRC Press: Boca Raton, FL, USA, 1999; ISBN 9780849305863. [Google Scholar]
- Moret, D.; Lopez, M.V.; Arrue, J.L. TDR application for automated water level measurement from Mariotte reservoirs in tension disc infiltrometers. J. Hydrol. 2004, 297, 229–235. [Google Scholar] [CrossRef]
- Topp, G.C.; Reynolds, W.D. Time Domain Reflectometry: A seminar technique for measuring mass and energy in soil. Soil Tillage Res. 1998, 47, 125–132. [Google Scholar] [CrossRef]
- Jones, S.B.; Or, D. Modeled effects on permittivity measurements of water content in high surface area porous media. Physica B 2003, 338, 284–290. [Google Scholar] [CrossRef]
- Skierucha, W. Accuracy of Soil Moisture Measurement by TDR Technique. Int. Agrophys. 2000, 14, 417–426. [Google Scholar]
- Rayleigh, L. On the influence of obstacles arranged in rectangular order upon the properties of the medium. Philos. Mag. 1892, 34, 481–502. [Google Scholar] [CrossRef]
- Maxwell Garnett, J.C. Colours in Metal Gases and Metal Films; Transactions of the Royal Society: London, UK, 1904; Volume 203, pp. 385–420. [Google Scholar]
- Polder, D.; van Santen, J.H. The effective permeability of mixtures of solids. Physica 1946, 12, 257–271. [Google Scholar] [CrossRef]
- Roth, K.; Schulin, R.; Flühler, H.; Attinger, W. Calibration of time domain reflectometry for water content measurement using a composite dielectric approach. Water Resour. Res. 1990, 26, 2267–2273. [Google Scholar] [CrossRef]
- Whalley, W.R. Consideration on the use of Time Domain Reflectometry (TDR) for measuring soil water content. Eur. J. Soil Sci. 1993, 44, 1–9. [Google Scholar] [CrossRef]
- Schapp, M.G.; de Lange, L.; Heimovara, T.J. TDR calibration of organic forest floor media. Soil Technol. 1996, 11, 205–217. [Google Scholar] [CrossRef]
- Skierucha, W. Wpływ Temperatury Na Pomiar Wilgotności Gleby Metodą Reflektometryczną; Acta Agrophysica, Rozprawy i Monografie, Polska Akademia Nauk: Lublin, Polska, 2005. (In Polish) [Google Scholar]
- Quinones, H.; Ruelle, P. Operative calibration methodology of a TDR sensor for soil moisture monitoring under irrigated crops. Subsurf. Sens. Technol. Appl. 2001, 2, 31–45. [Google Scholar] [CrossRef]
- Udawatta, R.P.; Anderson, S.H.; Motavalli, P.P.; Garrett, H.E. Calibration of a water content reflectometer and soil water dynamics for an agroforestry practice. Agrofor. Syst. 2011, 82, 61–75. [Google Scholar] [CrossRef]
- Mastrorilli, M.; Katerji, N.; Rana, G.; Nouna, B.B. Daily actual evapotranspiration measured with TDR technique in Mediterranean conditions. Agric. For. Meteorol. 1998, 90, 81–89. [Google Scholar] [CrossRef]
- Ren, T.; Noborio, K.; Horton, R. Measuring soil water content, electrical conductivity, and thermal properties with a thermo-time domain reflectometry probe. Soil. Sci. Soc. Am. J. 1999, 63, 450–457. [Google Scholar] [CrossRef]
- Soncela, R.; Sampaio, S.; Vilas Boas, M.A.; Tavares, M.H.F.; Smanhotto, A. Construction and calibration of TDR probes for volumetric water content estimation in a Distroferric Red Latosol. Eng. Agríc. 2013, 33, 919–928. [Google Scholar] [CrossRef]
- Ju, Z.; Liu, X.; Ren, T.; Hu, C. Measuring Soil Water Content with Time Domain Reflectometry: An Improved Calibration Considering Soil Bulk Density. Soil Sci. 2010, 175, 469–473. [Google Scholar] [CrossRef]
- Hansen, M.H. TDR measurement of moisture content in aerated concrete. In Proceedings of the 6th Symposium on Building Physics, Trondheim, Norway, 17–19 June 2002. [Google Scholar]
- Suchorab, Z.; Widomski, M.; Łagód, G.; Sobczuk, H. Capillary rise phenomenon in aerated concrete. Monitoring and simulations. Proc. ECOpole 2010, 4, 285–290. [Google Scholar]
- Suchorab, Z.; Barnat-Hunek, D.; Franus, M.; Łagód, G. Mechanical and Physical Properties of Hydrophobized Lightweight Aggregate Concrete with Sewage Sludge. Materials 2016, 9, 317. [Google Scholar] [CrossRef] [PubMed]
- Pavlík, Z.; Fiala, L.; Černý, R. Determination of Moisture Content of Hygroscopic Building Materials Using Time Domain Reflectometry. J. Appl. Sci. 2008, 8, 1732–1737. [Google Scholar] [CrossRef]
- Wraith, J.M.; Robinson, D.A.; Jones, S.B.; Long, D.S. Spatially characterizing apparent electrical conductivity and water content of surface soils with time domain reflectometry. Comput. Electron. Agric. 2005, 46, 239–261. [Google Scholar] [CrossRef]
- Ito, Y.; Chikushi, J.; Miyamoto, H. Multi-TDR probe designer for measuring soil moisture distribution near the soil surface. In Proceedings of the 19th World Congress of Soil Sciences, Brisbane, Australia: Soil Solutions for a Changing World, Brisbane, Australia, 1–6 August 2010. [Google Scholar]
- Choi, C.; Song, M.; Kim, D.; Yu, X. A New Non-Destructive TDR System Combined with a Piezoelectric Stack for Measuring Properties of Geomaterials. Materials 2016, 9, 439. [Google Scholar] [CrossRef] [PubMed]
- Sobczuk, H. Sonda Do Pomiaru Wilgotności Ośrodków Porowatych, Zwłaszcza Materiałów Budowlanych. Available online: https://rejestr.io/patenty/212837 (accessed on 13 November 2018).
- Sobczuk, H.; Suchorab, Z. Sonda Do Pomiaru Wilgotności Przegród Budowlanych, Zwłaszcza O Chropowatych Powierzchniach. Available online: https://rejestr.io/patenty/225640 (accessed on 13 November 2018).
- Sobczuk, H.; Suchorab, Z. Sonda Do Pomiaru Wilgotności, Zwłaszcza Elementów O Powierzchniach Wypukłych. Available online: https://rejestr.io/patenty/225641 (accessed on 13 November 2018).
- Sobczuk, H.; Suchorab, Z. Sonda Do Pomiaru Wilgotności, Zwłaszcza Elementów O Zakrzywionych Powierzchniach. Available online: https://rejestr.io/patenty/225639 (accessed on 13 November 2018).
- Knight, J.H. Sensitivity of time domain reflectometry measurements to lateral variations in soil water content. Water Resour. Res. 1992, 28, 2345–2352. [Google Scholar] [CrossRef]
- Suchorab, Z.; Sobczuk, H.; Cerny, R.; Pavlik, Z.; De Miguel, R.S. Sensitivity range determination of surface TDR probes. Environ. Prot. Eng. 2009, 35, 179–189. [Google Scholar]
- Majerek, D.; Widomski, M.; Garbacz, M.; Suchorab, Z. Estimation of the measurement uncertainty of humidity using a TDR probe. AIP Conf. Proc. 2018, 1988, 020027. [Google Scholar] [CrossRef]
- JCGM 100:2008, GUM 1995 with Minor Corrections, Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. Available online: http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 24 September 2018).
- Wu, S.Y.; Zhou, Q.Y.; Wang, G.; Yang, L.; Ling, C.P. The relationship between electrical capacitance-based dielectric constant and soil water content. Environ. Earth Sci. 2010, 62, 999–1011. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Bailey, W.G.; Zebchuk, W.D. The measurement of soil water content using a portable TDR hand probe. Can. J. Soil. Sci. 1984, 64, 313–321. [Google Scholar] [CrossRef]
- Amato, M.; Ritchie, J.T. Small spatial scale soi water content measurement with time-domain reflectometry. Soil Sci. Soc. Am. J. 1995, 59, 325–329. [Google Scholar] [CrossRef]

| Apparent Density [kg/m3] | Saturated Volumetric Water Content [cm3/cm3] | Saturated Gravimetric Water Content [kg/kg] |
|---|---|---|
| 612.2 ± 11.2 | 0.363 ± 0.007 | 0.593 ± 0.007 |
| Determination Coefficient R2 | Residual Standard Error RSE [cm3/cm3] | Root Mean Square Error RMSE [cm3/cm3] | F-Model Linearity Test Statistic |
|---|---|---|---|
| 0.986 | 0.014 (df = 16) | 0.013 | 580.752 *** (df = 2; 18) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suchorab, Z.; Widomski, M.K.; Łagód, G.; Barnat-Hunek, D.; Majerek, D. A Noninvasive TDR Sensor to Measure the Moisture Content of Rigid Porous Materials. Sensors 2018, 18, 3935. https://doi.org/10.3390/s18113935
Suchorab Z, Widomski MK, Łagód G, Barnat-Hunek D, Majerek D. A Noninvasive TDR Sensor to Measure the Moisture Content of Rigid Porous Materials. Sensors. 2018; 18(11):3935. https://doi.org/10.3390/s18113935
Chicago/Turabian StyleSuchorab, Zbigniew, Marcin Konrad Widomski, Grzegorz Łagód, Danuta Barnat-Hunek, and Dariusz Majerek. 2018. "A Noninvasive TDR Sensor to Measure the Moisture Content of Rigid Porous Materials" Sensors 18, no. 11: 3935. https://doi.org/10.3390/s18113935
APA StyleSuchorab, Z., Widomski, M. K., Łagód, G., Barnat-Hunek, D., & Majerek, D. (2018). A Noninvasive TDR Sensor to Measure the Moisture Content of Rigid Porous Materials. Sensors, 18(11), 3935. https://doi.org/10.3390/s18113935









