Hybrid TSR–PSR Alternate Energy Harvesting Relay Network over Rician Fading Channels: Outage Probability and SER Analysis
Abstract
1. Introduction
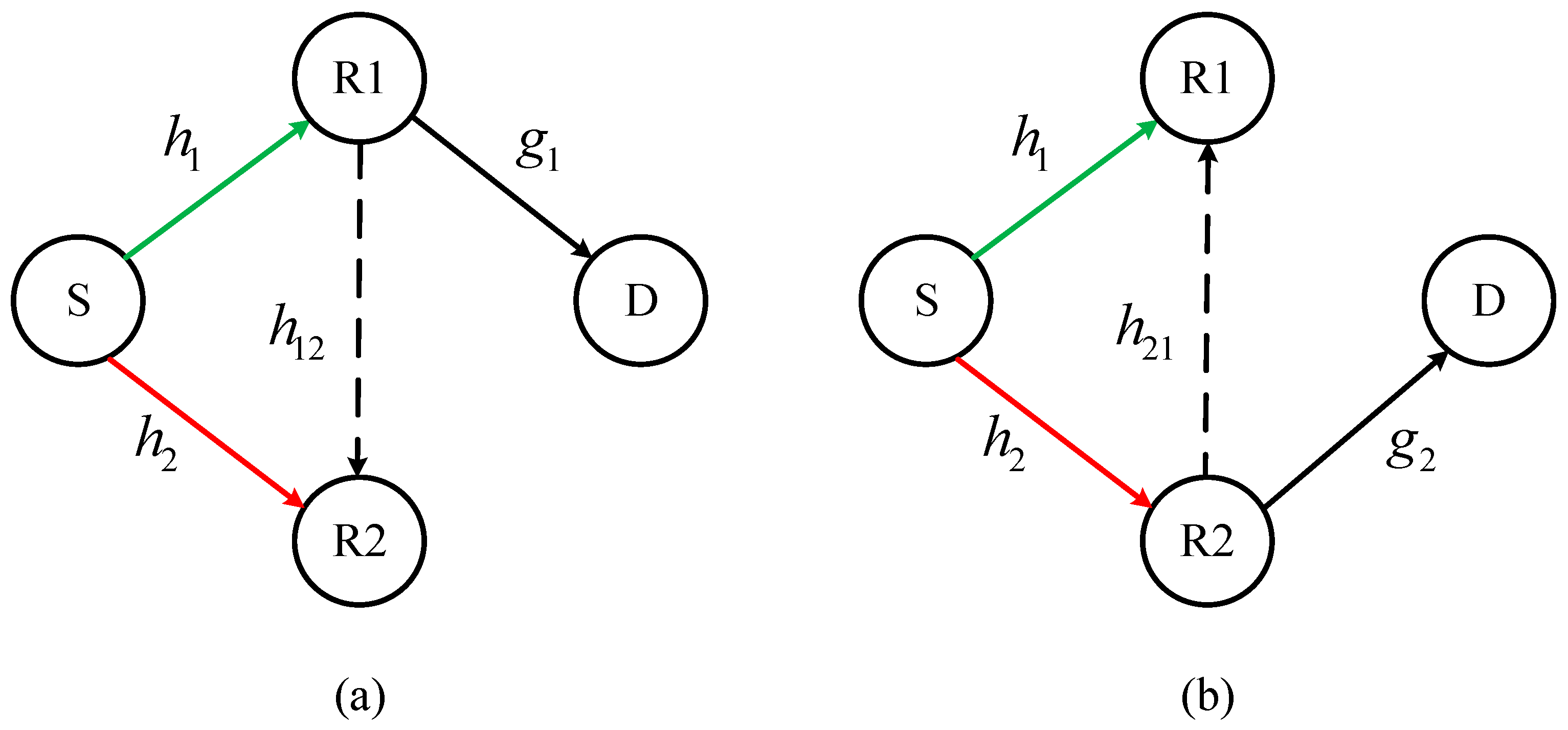
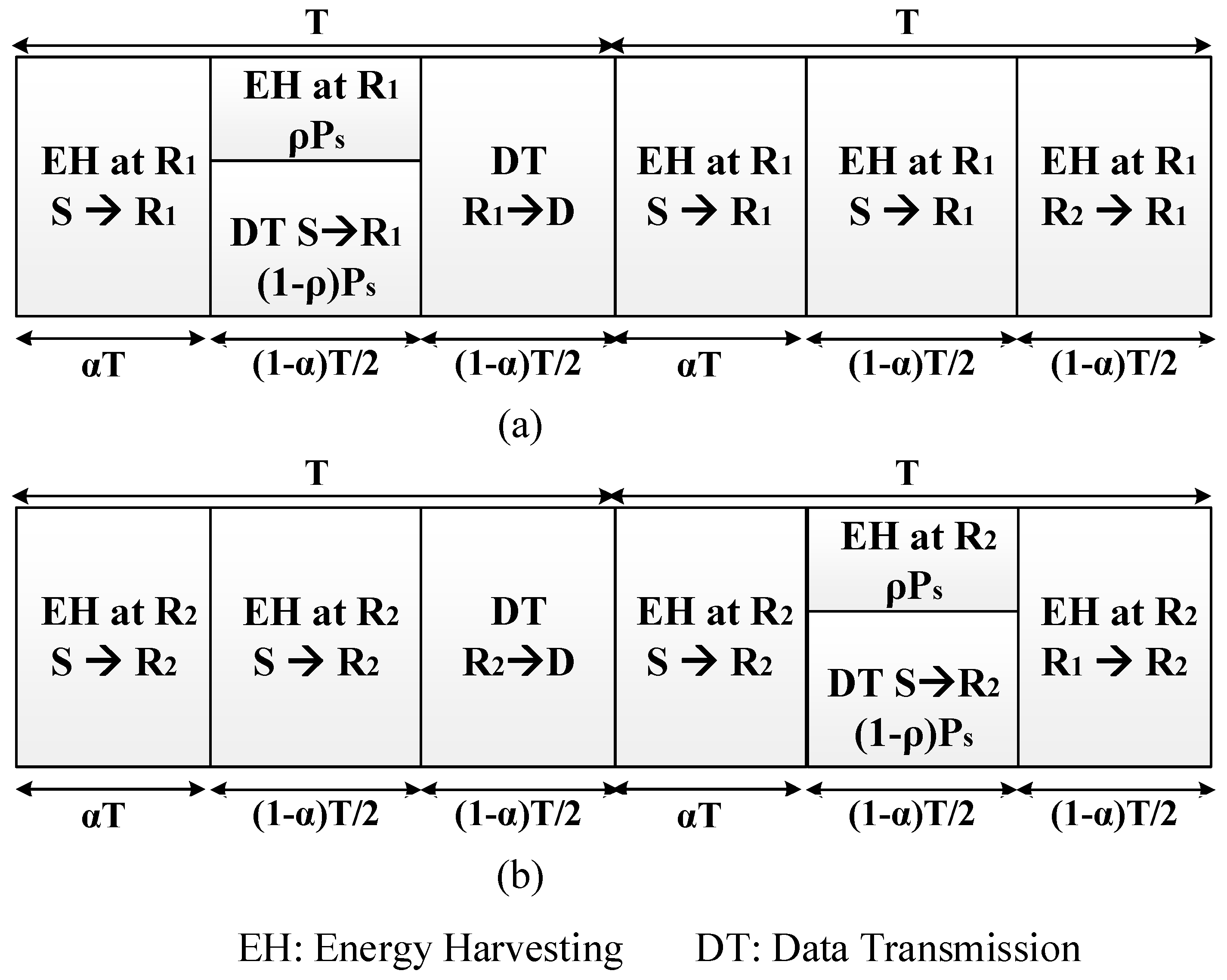
2. System Model
3. System Performance
3.1. Exact Outage Probability Analysis
3.2. Asymptotic Outage Probability Analysis
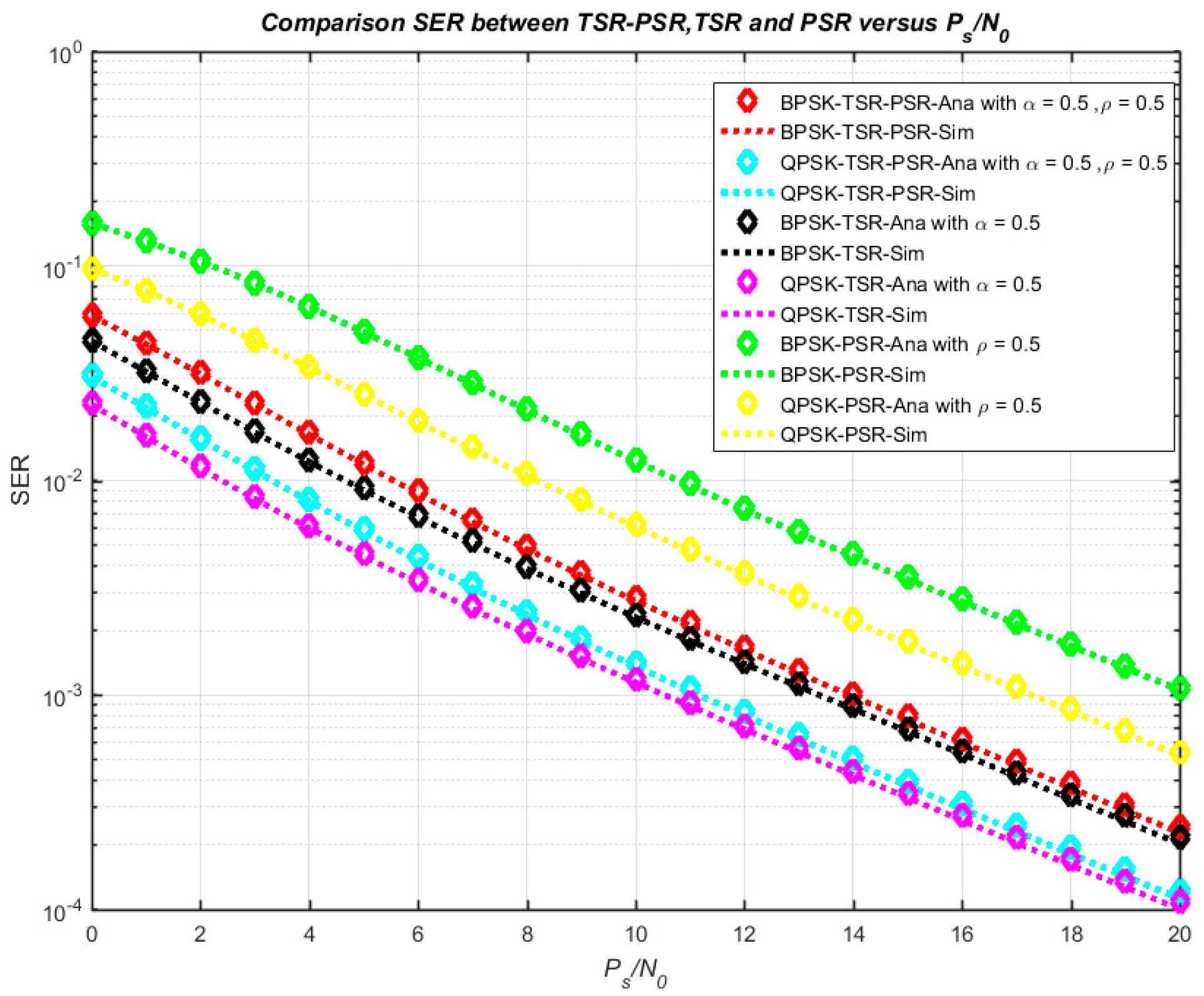
3.3. SER (Symbol Error Ratio) Analysis
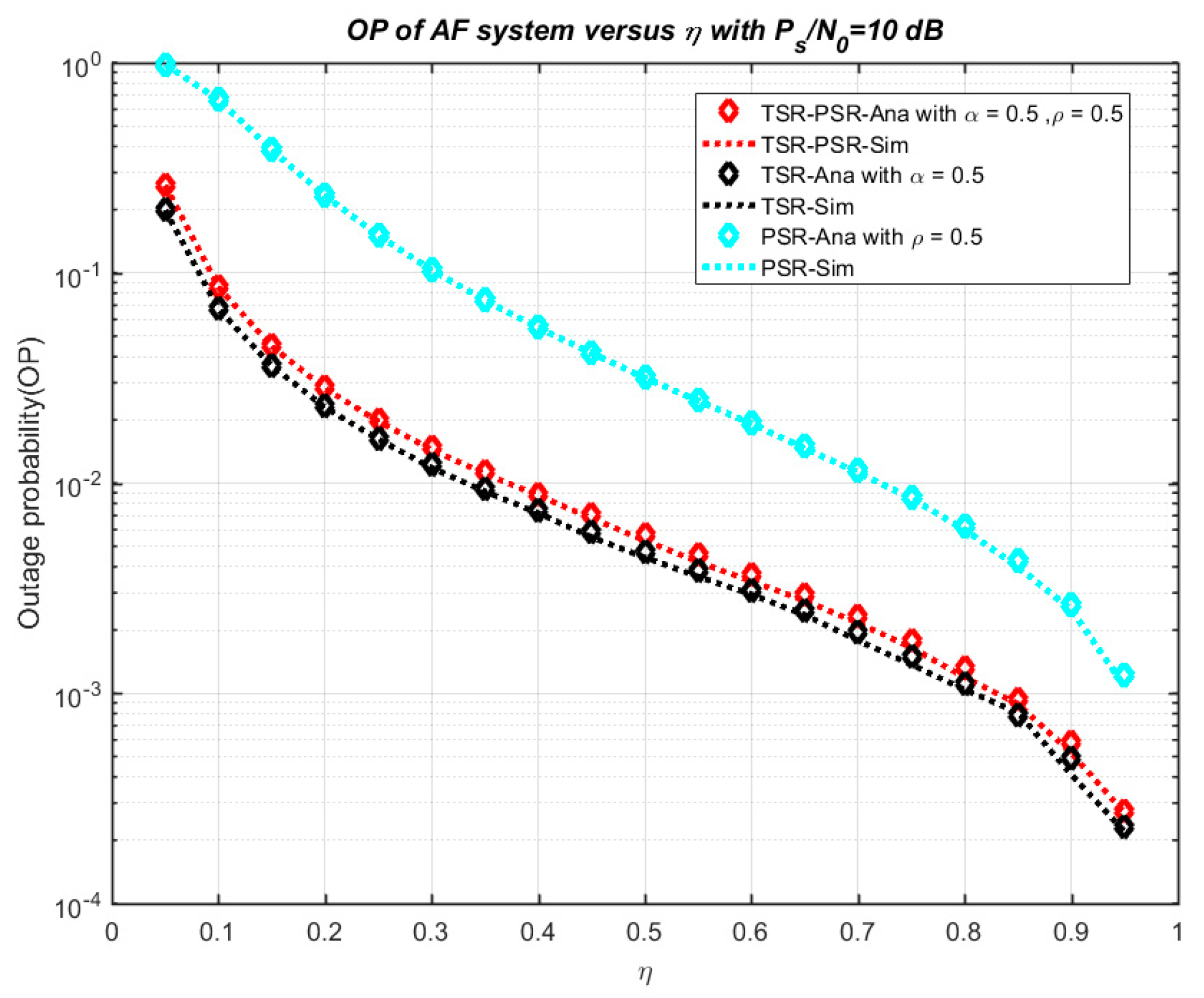
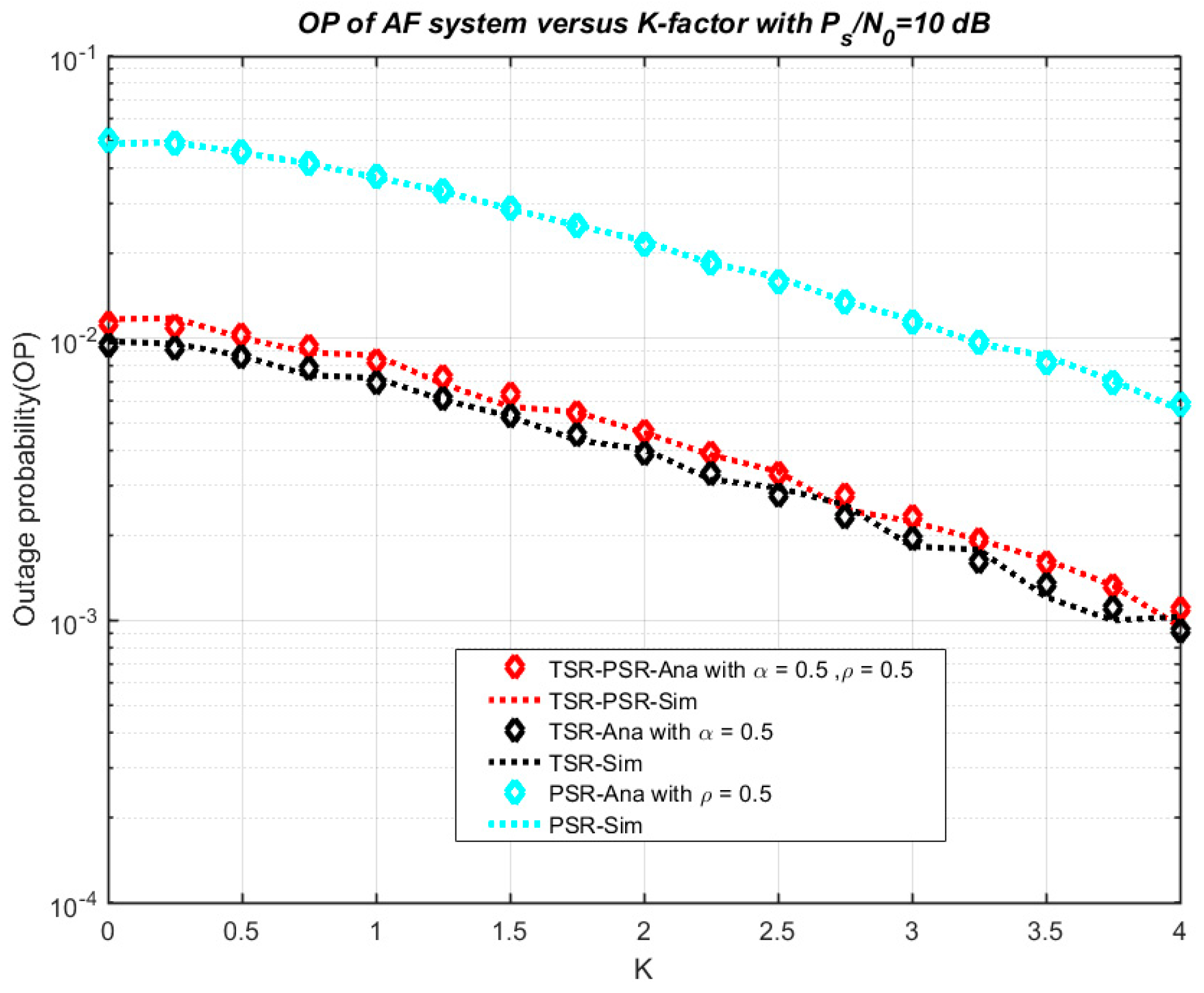
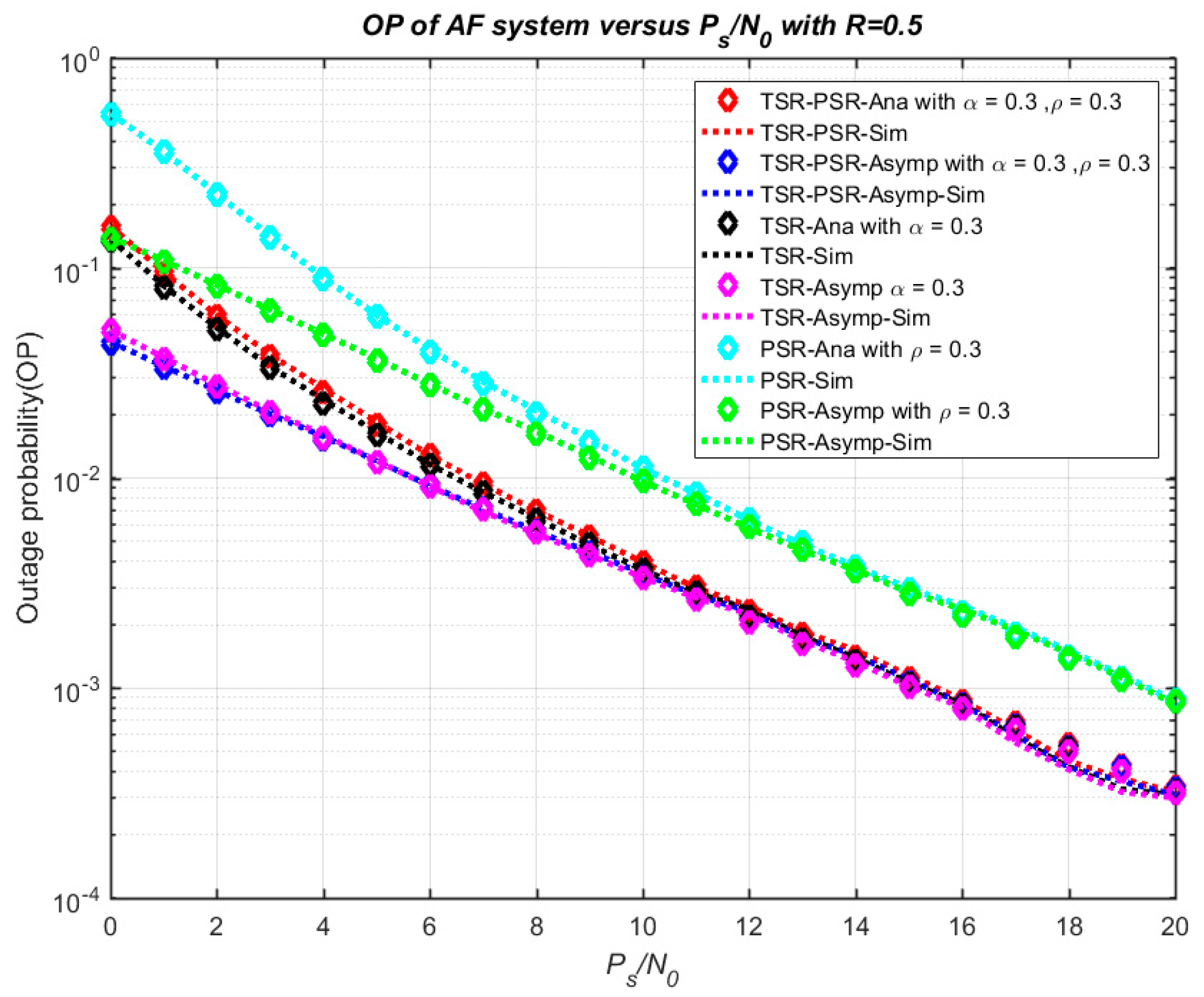
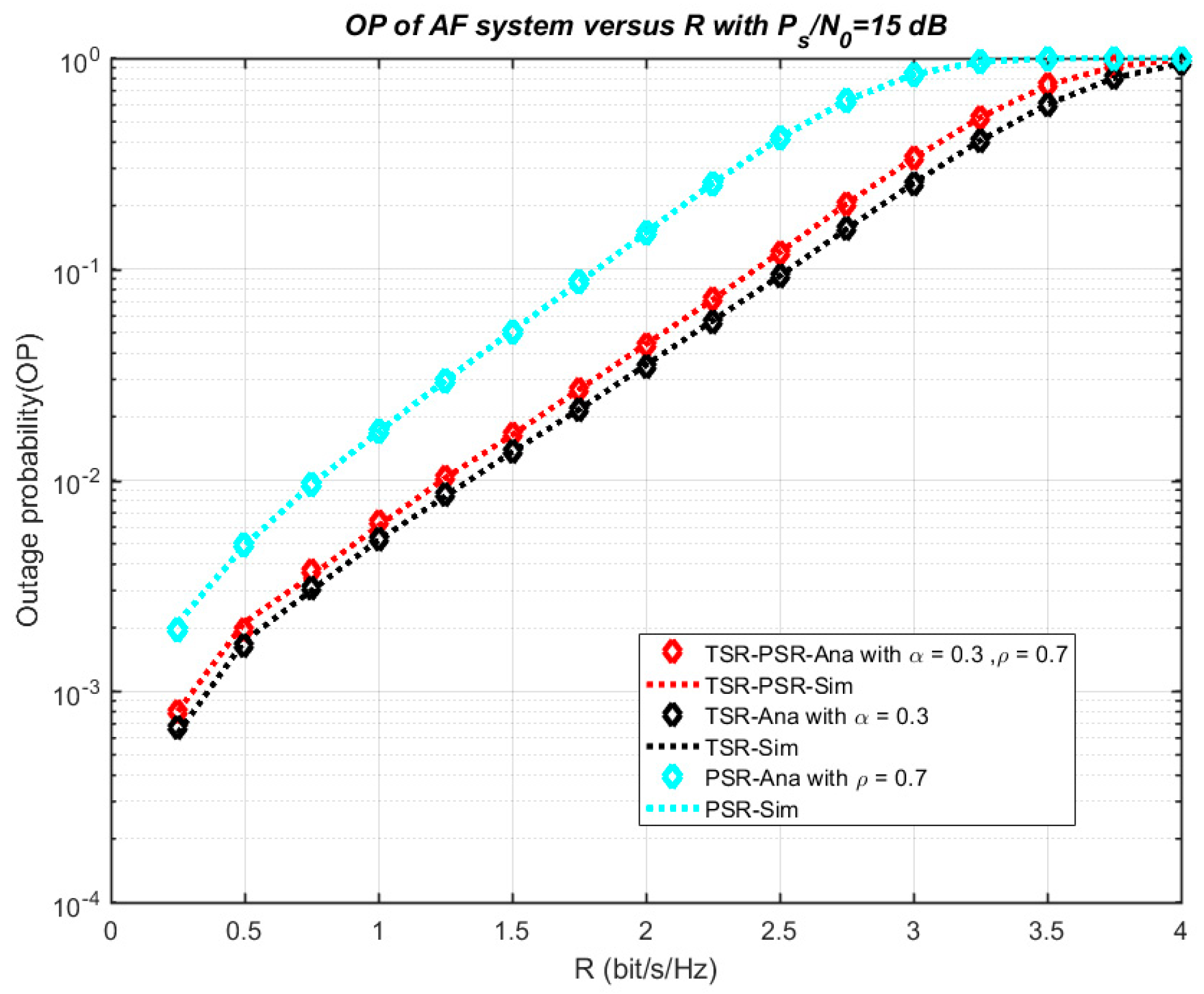
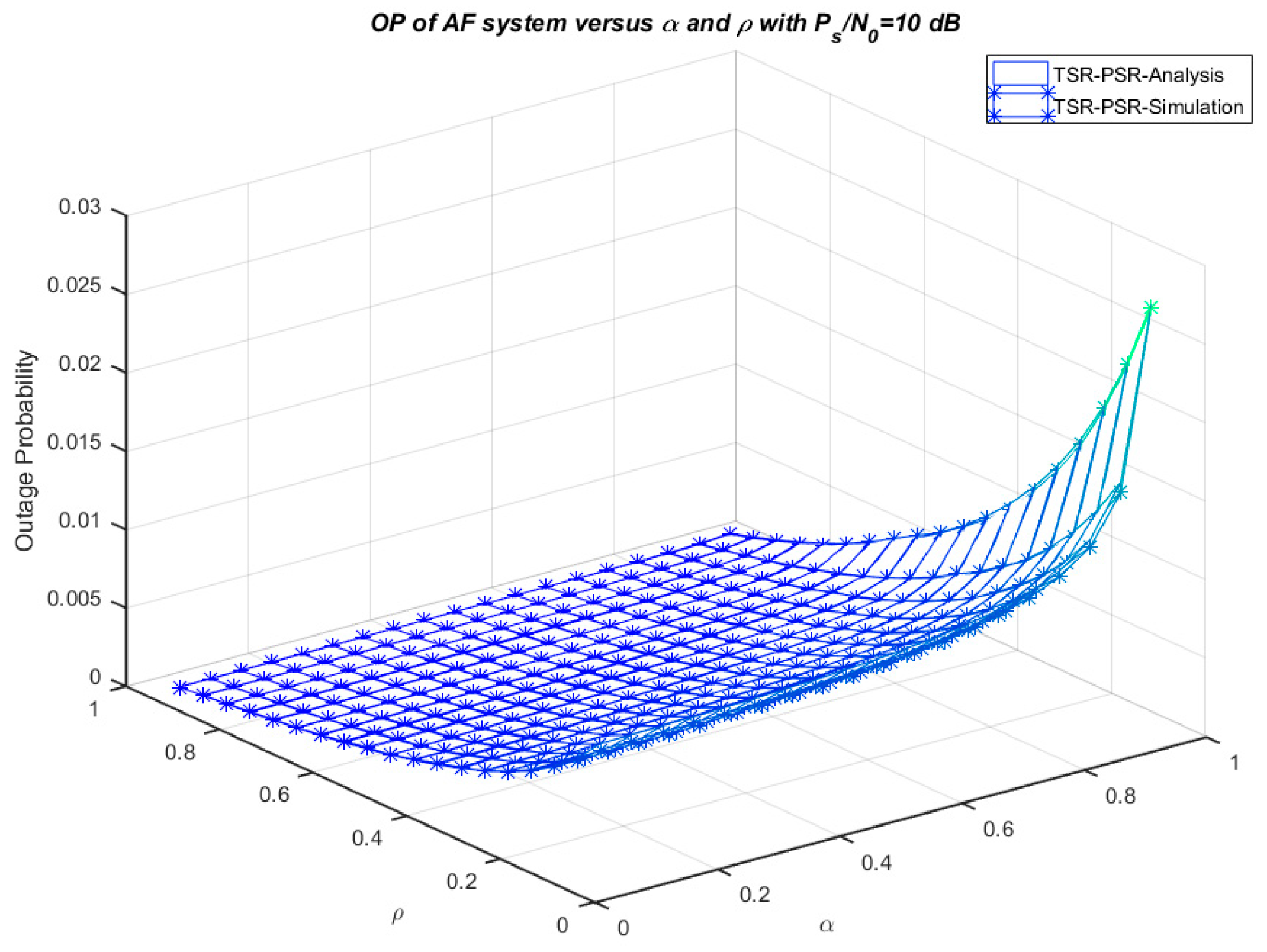
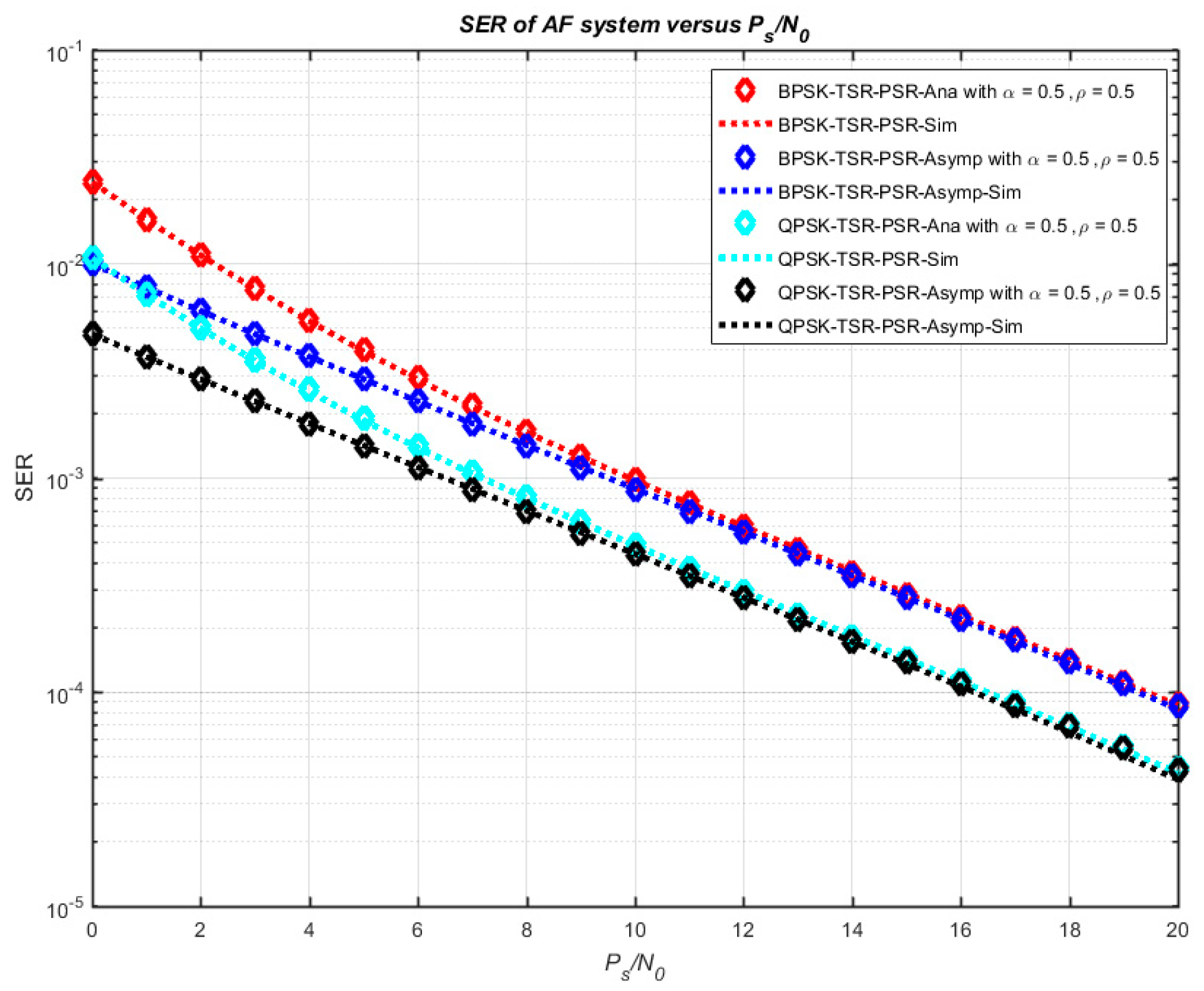
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1—Exact Outage Probability
Appendix B. Proof of Theorem 2—Exact SER Analysis
Appendix C. Proof of Theorem 3—Asymptotic SER Analysis
References
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Niyato, D.; Kim, D.I.; Maso, M.; Han, Z. Wireless Powered Communication Networks: Research Directions and Technological Approaches. IEEE Wirel. Commun. 2017, 2–11. [Google Scholar] [CrossRef]
- Yu, H.; Lee, H.; Jeon, H. What is 5G? Emerging 5G Mobile Services and Network Requirements. Sustainability 2017, 9, 1848. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless Information and Power Transfer: Architecture Design and Rate-Energy Tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Akhtar, R.; Leng, S.; Memon, I.; Ali, M.; Zhang, L. Architecture of Hybrid Mobile Social Networks for Efficient Content Delivery. Wirel. Pers. Commun. 2014, 80, 85–96. [Google Scholar] [CrossRef]
- Rango, F.D.; Gerla, M.; Marano, S. A Scalable Routing Scheme with Group Motion Support in Large and Dense Wireless Ad Hoc Networks. Comput. Electr. Eng. 2006, 32, 224–240. [Google Scholar] [CrossRef]
- Zhou, B.; Lee, Y.; Gerla, M.; de Rango, F. Geo-LANMAR: A Scalable Routing Protocol for Ad Hoc Networks with Group Motion. Wirel. Commun. Mob. Comput. 2006, 6, 989–1002. [Google Scholar] [CrossRef]
- Fazio, P.; de Rango, F.; Sottile, C.; Calafate, C. A New Channel Assignment Scheme for Interference-Aware Routing in Vehicular Networks. In Proceedings of the 2011 IEEE 73rd Vehicular Technology Conference (VTC Spring), Budapest, Hungary, 15–18 May 2011. [Google Scholar]
- Cassano, E.; Florio, F.; De Rango, F.; Marano, S. A Performance Comparison between ROC-RSSI and Trilateration Localization Techniques for WPAN Sensor Networks in a Real Outdoor Testbed. In Proceedings of the 2009 Conference on Wireless Telecommunications Symposium, Prague, Czech Republic, 22–24 April 2009. [Google Scholar]
- Chen, H.; Zhai, C.; Li, Y.; Vucetic, B. Cooperative Strategies for Wireless-Powered Communications: An Overview. IEEE Wirel. Commun. 2018, 25, 112–119. [Google Scholar] [CrossRef]
- Zhai, C.; Liu, J.; Zheng, L. Relay-Based Spectrum Sharing with Secondary Users Powered by Wireless Energy Harvesting. IEEE Trans. Commun. 2016, 64, 1875–1887. [Google Scholar] [CrossRef]
- Zhai, C.; Zheng, L.; Lan, P.; Chen, H.; Xu, H. Decode-and-forward Two-path Successive Relaying with Wireless Energy Harvesting. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017. [Google Scholar]
- Chen, Y.; Shi, R.; Feng, W.; Ge, N. AF Relaying with Energy Harvesting Source and Relay. IEEE Trans. Veh. Technol. 2016, 1. [Google Scholar] [CrossRef]
- Zheng, L.; Zhai, C.; Liu, J. Alternate Energy Harvesting and Information Relaying in Cooperative AF Networks. Telecommun. Syst. 2017, 68, 523–533. [Google Scholar] [CrossRef]
- Abbas, H.; Hamdi, K. Millimeter Wave Communications over Relay Networks. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017. [Google Scholar]
- Kong, L.; Khan, M.K.; Wu, F.; Chen, G.; Zeng, P. Millimeter-Wave Wireless Communications for IoT-Cloud Supported Autonomous Vehicles: Overview, Design, and Challenges. IEEE Commun. Mag. 2017, 55, 62–68. [Google Scholar] [CrossRef]
- Zhou, Z.; Peng, M.; Zhao, Z.; Li, Y. Joint Power Splitting and Antenna Selection in Energy Harvesting Relay Channels. IEEE Signal Process. Lett. 2015, 22, 823–827. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, K. Wireless Information and Power Transfer: A Dynamic Power Splitting Approach. IEEE Trans. Commun. 2013, 61, 3990–4001. [Google Scholar] [CrossRef]
- Zenaidi, M.R.; Rezki, Z.; Tembine, H.; Alouini, M.-S. Performance Limits of Energy Harvesting Communications under Imperfect Channel State Information. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016. [Google Scholar]
- Alexandropoulos, G.C.; Peppas, K.P. Secrecy Outage Analysis Over Correlated Composite Nakagami-m/Gamma Fading Channels. IEEE Commun. Lett. 2018, 22, 77–80. [Google Scholar] [CrossRef]
- Papadogiannis, A.; Alexandropoulos, G.C. System Level Performance Evaluation of Dynamic Relays in Cellular Networks over Nakagami-m Fading Channels. In Proceedings of the 2009 IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009. [Google Scholar]
- Papadogiannis, A.; Alexandropoulos, G.C.; Burr, A.; Grace, D. Bringing Mobile Relays for Wireless Access Networks into Practice–learning When to Relay. IET Commun. 2012, 6, 618. [Google Scholar] [CrossRef]
- Mishra, D.; George, C. Alexandropoulos. Transmit Precoding and Receive Power Splitting for Harvested Power Maximization in MIMO SWIPT Systems. IEEE Trans. Green Commun. Netw. 2018, 2, 774–786. [Google Scholar] [CrossRef]
- Mishra, D.; George, C. Alexandropoulos. Jointly Optimal Spatial Channel Assignment and Power Allocation for MIMO SWIPT Systems. IEEE Wirel. Commun. Lett. 2018, 7, 214–217. [Google Scholar] [CrossRef]
- Duy, T.T.; Son, V.N.; Tung, V.T.; Alexandropoulos, G.C.; Duong, T.Q. Outage Performance of Cognitive Cooperative Networks with Relay Selection over Double-Rayleigh Fading Channels. IET Commun. 2016, 10, 57–64. [Google Scholar] [CrossRef]
- Bhatnagar, M.R. On the Capacity of Decode-and-Forward Relaying over Rician Fading Channels. IEEE Commun. Lett. 2013, 17, 1100–1103. [Google Scholar] [CrossRef]
- Nguyen, T.; Quang Minh, T.; Tran, P.; Vozňák, M. Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments. Sensors 2018, 18, 1781. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.; Tran, P.T.; Quang Minh, T.H.; Voznak, M.; Sevcik, L. Two-Way Half Duplex Decode and Forward Relaying Network with Hardware Impairment over Rician Fading Channel: System Performance Analysis. Elektronika Ir Elektrotechnika 2018, 24. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Duy, T.T.; Luu, G.T.; Tran, P.T.; Vozňák, M. Energy Harvesting-based Spectrum Access with Incremental Cooperation, Relay Selection and Hardware Noises. Radioengineering 2017, 26, 240–250. [Google Scholar] [CrossRef]
- Mckay, M.R.; Grant, A.J.; Collings, I.B. Performance Analysis of MIMO-MRC in Double-Correlated Rayleigh Environments. IEEE Trans. Commun. 2007, 55, 497–507. [Google Scholar] [CrossRef]
- Zwillinger, D. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar] [CrossRef]
| Symbol | Definition |
|---|---|
| Energy conversion efficiency | |
| Time-switching factor | |
| Power-splitting factor | |
| Ps/N0 | Source-power-to-noise ratio |
| K | Rician K-factor |
| Mean of | |
| Mean of | |
| R | Source rate |
| Er1 | Harvested energy at relay 1 |
| Pr1 | Average transmit power of relay 1 |
| Er2 | Harvested energy at relay 2 |
| Pr2 | Average transmit power of relay 2 |
| Pout | Outage probability |
| End to end signal to noise ratio | |
| Modified Bessel function of the second kind and vth order | |
| Gamma function | |
| Hypergeometric function | |
| SER | Symbol error ratio |
| Amplifying factor | |
| Gaussian Q-function | |
| Ps | Transmit power of the source |
| T | Total time of processing |
| Symbol | Values |
|---|---|
| 0.7 | |
| 1 | |
| 1 | |
| Ps/N0 | 0:20 dB |
| K | 3 |
| R | 0.5 bps |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.N.; Tran Tin, P.; Ha, D.H.; Voznak, M.; Tran, P.T.; Tran, M.; Nguyen, T.-L. Hybrid TSR–PSR Alternate Energy Harvesting Relay Network over Rician Fading Channels: Outage Probability and SER Analysis. Sensors 2018, 18, 3839. https://doi.org/10.3390/s18113839
Nguyen TN, Tran Tin P, Ha DH, Voznak M, Tran PT, Tran M, Nguyen T-L. Hybrid TSR–PSR Alternate Energy Harvesting Relay Network over Rician Fading Channels: Outage Probability and SER Analysis. Sensors. 2018; 18(11):3839. https://doi.org/10.3390/s18113839
Chicago/Turabian StyleNguyen, Tan N., Phu Tran Tin, Duy Hung Ha, Miroslav Voznak, Phuong T. Tran, Minh Tran, and Thanh-Long Nguyen. 2018. "Hybrid TSR–PSR Alternate Energy Harvesting Relay Network over Rician Fading Channels: Outage Probability and SER Analysis" Sensors 18, no. 11: 3839. https://doi.org/10.3390/s18113839
APA StyleNguyen, T. N., Tran Tin, P., Ha, D. H., Voznak, M., Tran, P. T., Tran, M., & Nguyen, T.-L. (2018). Hybrid TSR–PSR Alternate Energy Harvesting Relay Network over Rician Fading Channels: Outage Probability and SER Analysis. Sensors, 18(11), 3839. https://doi.org/10.3390/s18113839







