A Mobile Cough Strength Evaluation Device Using Cough Sounds
Abstract
1. Introduction
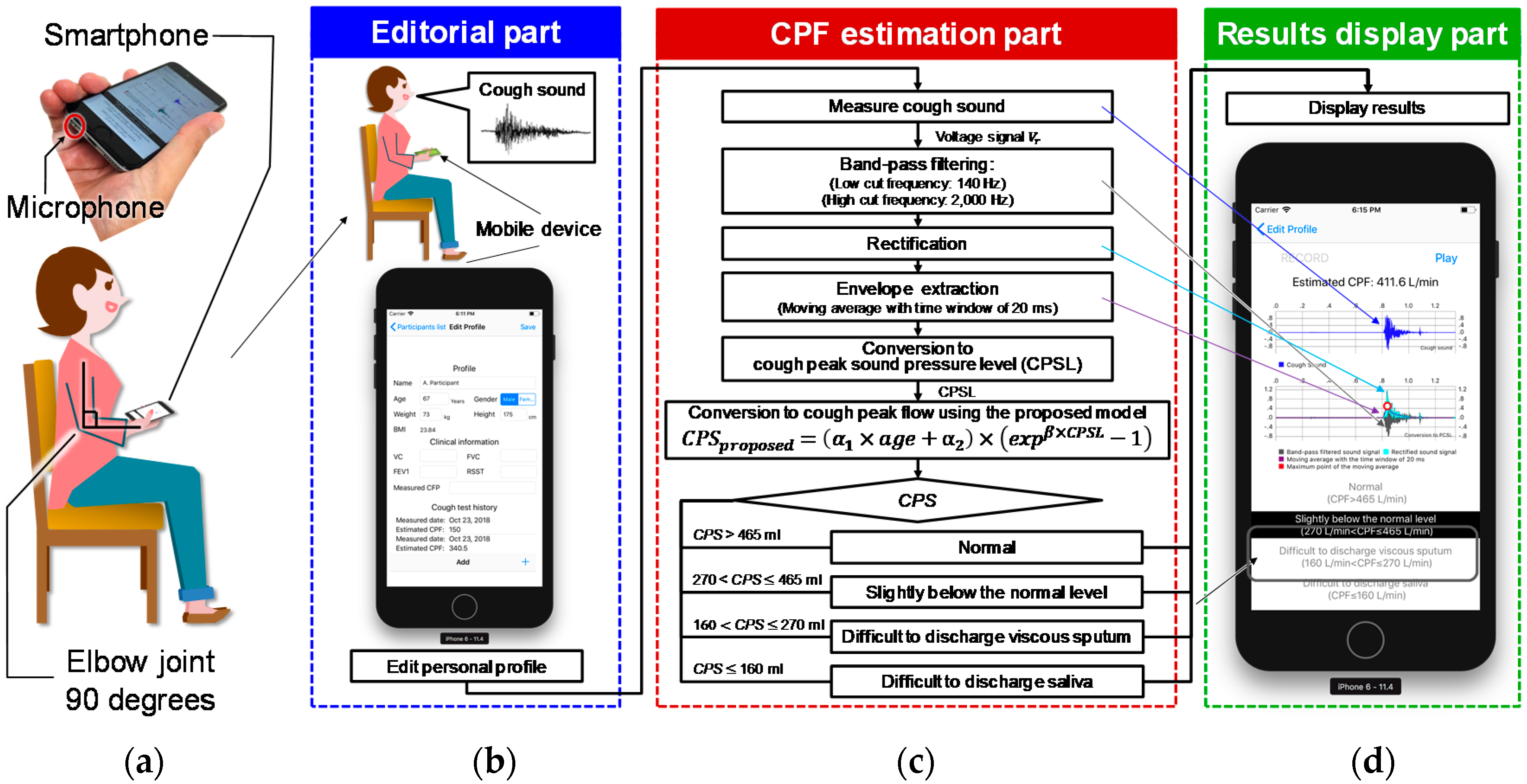
2. Proposed Device
2.1. Model
2.2. Measurement Protocol and Preprocessing for Cough Sounds
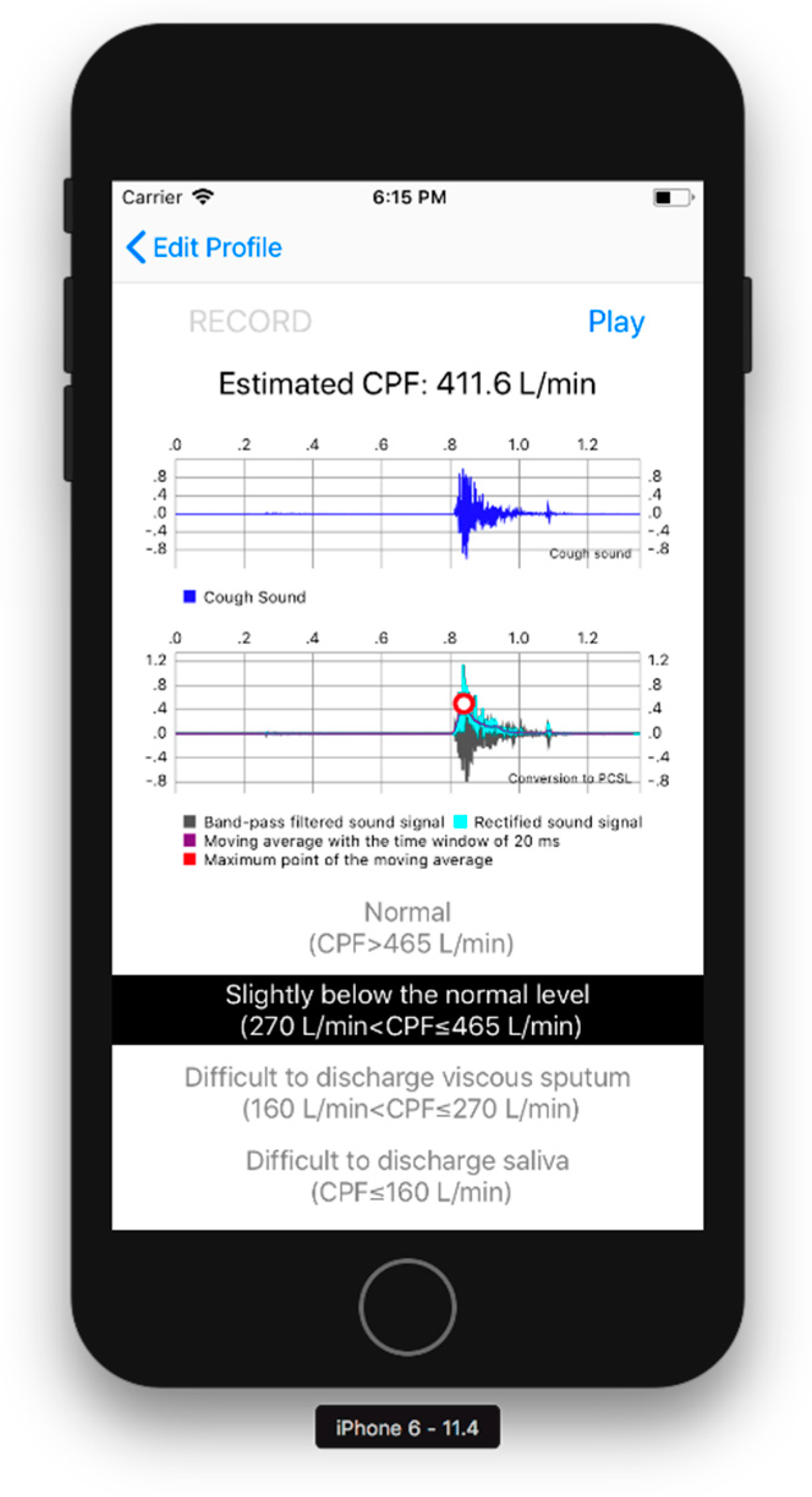
2.3. User Interface Software
3. Experiments
3.1. Participants
3.2. Methods
3.2.1. Cough Flow and Sound Measurement Methods
3.2.2. Models for Age Effect Analysis
3.2.3. Analysis of Models for Body Weight, BMI, and Height
4. Results
4.1. Parameter Determination
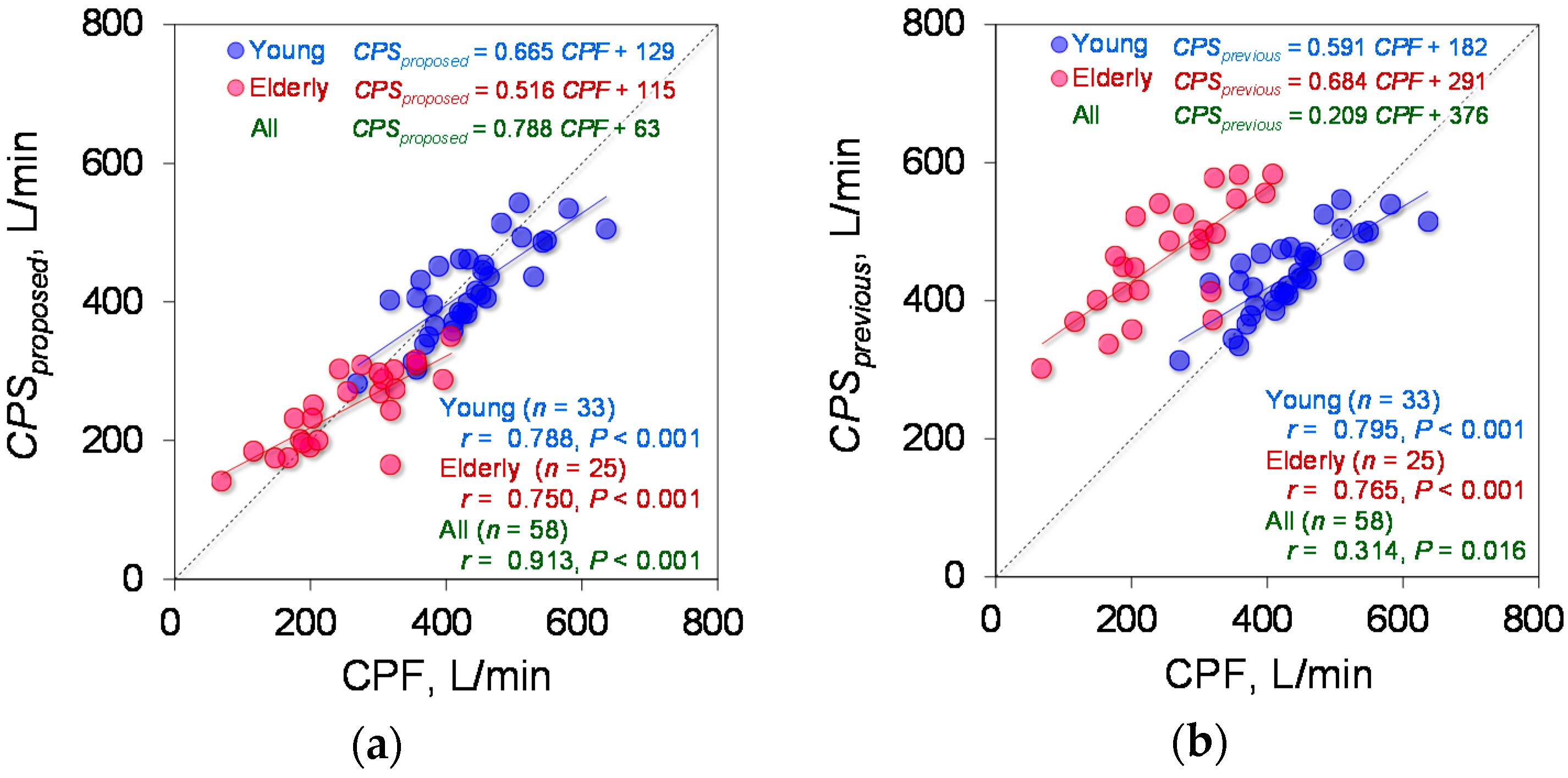
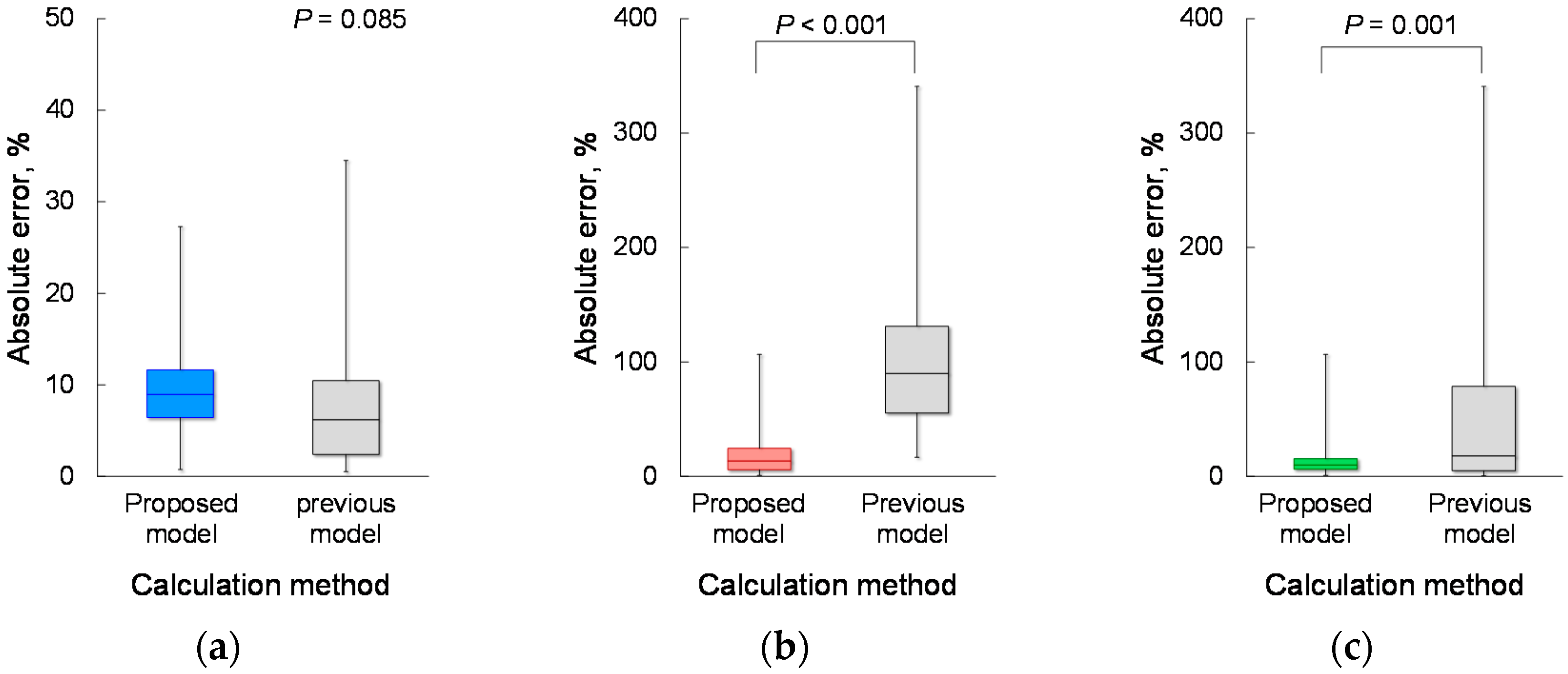
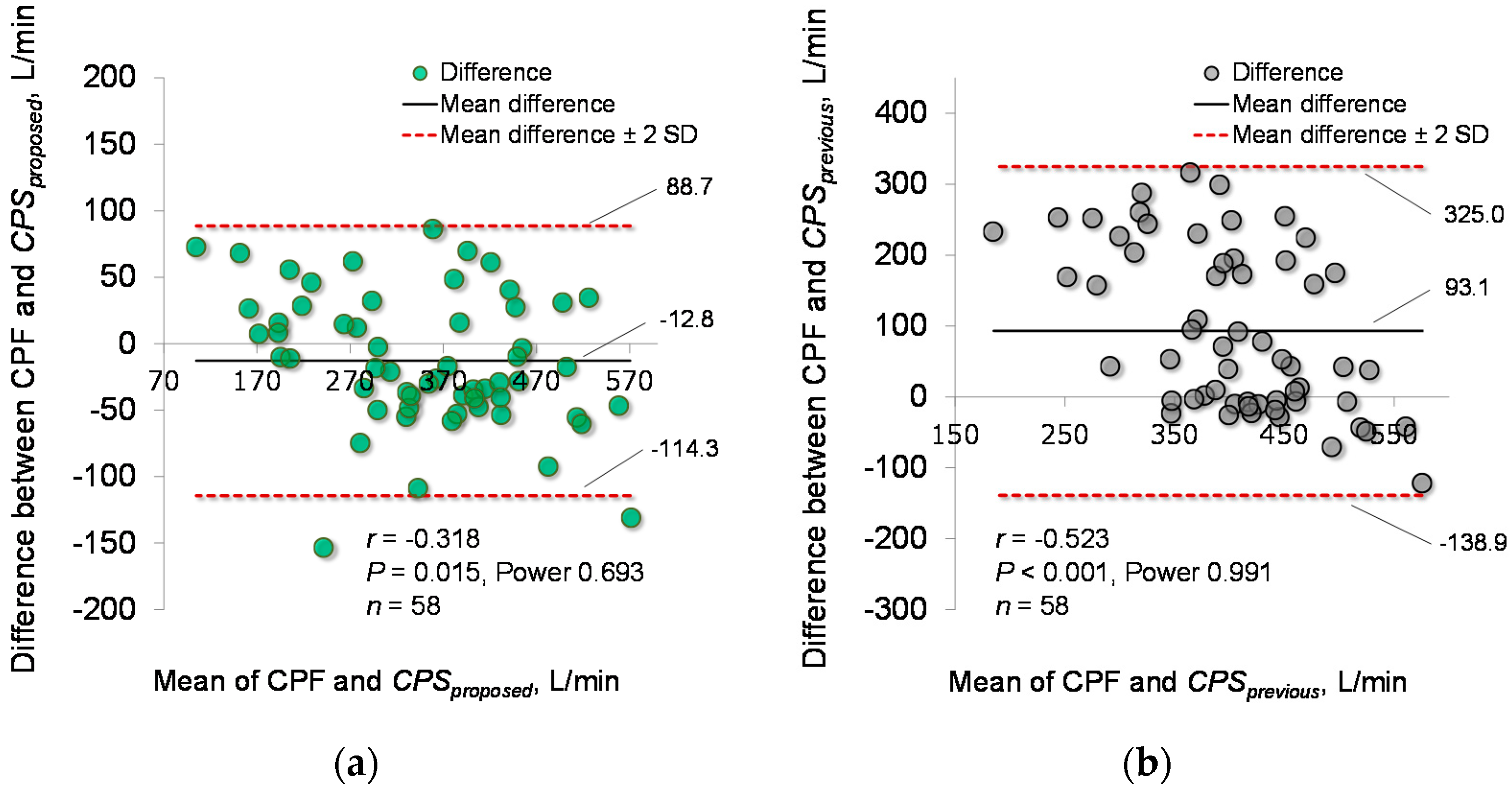
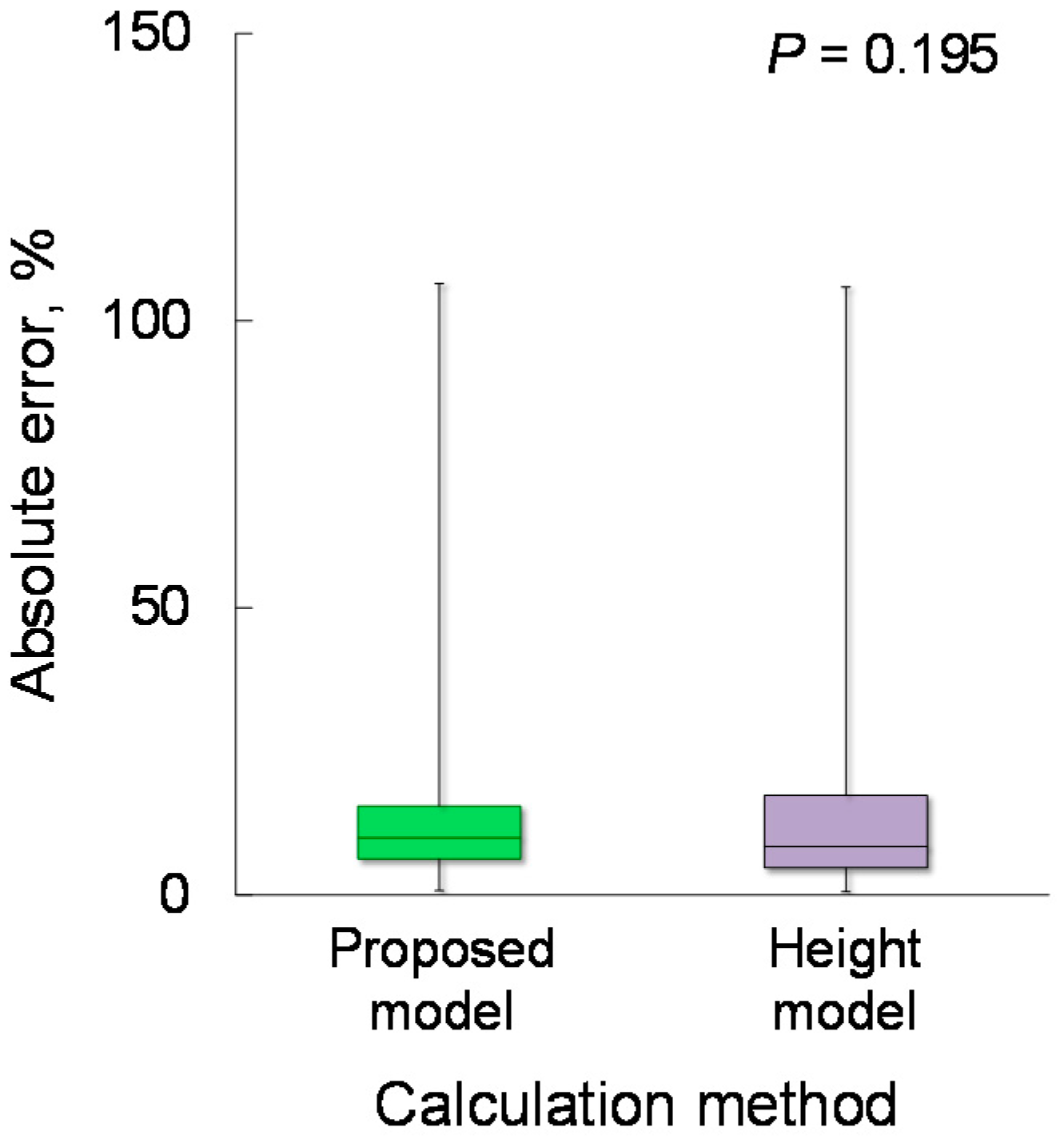
4.2. Estimation Accuracy
4.3. Effects of Body Weight and BMI on CPF Estimation Accuracy
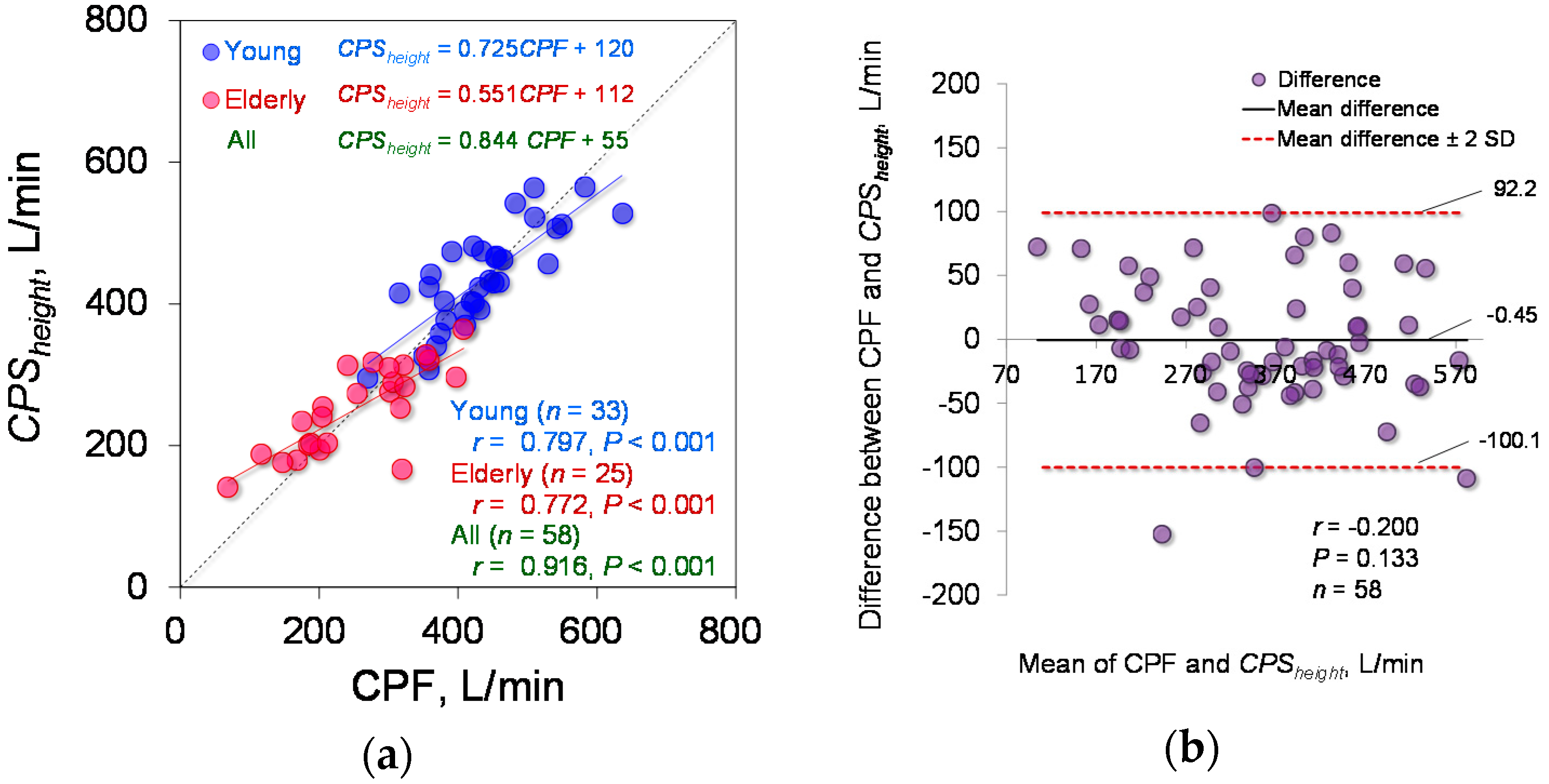
4.4. Effect of Body Height on CPF Estimation Accuracy
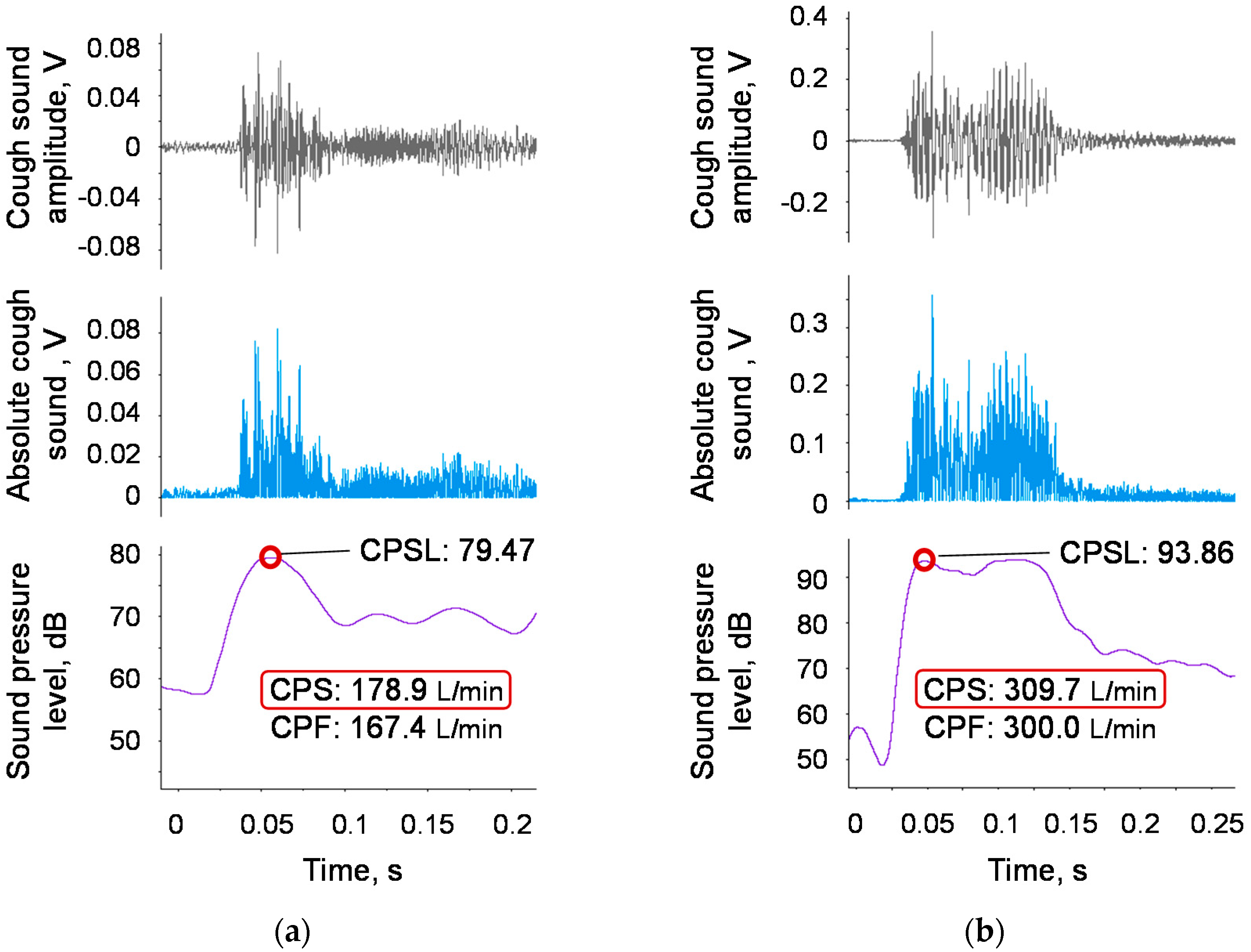
4.5. Examples of Elderly Participants
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Irwin, R.S.; Boulet, L.-P.; Cloutier, M.M.; Fuller, R.; Gold, P.M.; Hoffstein, V.; Ing, A.J.; McCool, F.D.; O’Byrne, P.; Poe, R.H.; et al. Managing cough as a defense mechanism and as a symptom. Chest 1998, 114, 133S–181S. [Google Scholar] [CrossRef] [PubMed]
- Schmit, K.M.; Coeytaux, R.R.; Goode, A.P.; McCrory, D.C.; Yancy, W.S., Jr.; Kemper, A.R.; Hasselblad, V.; Heidenfelder, B.L.; Sanders, G.D. Evaluating cough assessment tools: A systematic review. Chest 2013, 144, 1819–1826. [Google Scholar] [CrossRef] [PubMed]
- Bach, J.R.; Ishikawa, Y.; Kim, H. Prevention of pulmonary morbidity for patients with duchenne muscular dystrophy. Chest 1997, 112, 1024–1028. [Google Scholar] [CrossRef] [PubMed]
- Bach, J.R. Amyotrophic lateral sclerosis: Predictors for prolongation of life by noninvasive respiratory aids. Arch. Phys. Med. Rehabil. 1995, 76, 828–832. [Google Scholar] [CrossRef]
- Bach, J.R.; Saporito, L.R. Criteria for extubation and tracheostomy tube removal for patients with ventilatory failure: A different approach to weaning. Chest 1996, 110, 1566–1571. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, C.; Baiardi, P.; Khirani, S.; Cantarella, G. Cough peak flow as a predictor of pulmonary morbidity in patients with dysphagia. Am. J. Phys. Med. Rehabil. 2012, 91, 783–788. [Google Scholar] [CrossRef] [PubMed]
- Umayahara, Y.; Soh, Z.; Sekikawa, K.; Kawae, T.; Otsuka, A.; Tsuji, T. Estimation of cough peak flow using cough sounds. Sensors 2018, 18, 2381. [Google Scholar] [CrossRef] [PubMed]
- Umayahara, Y.; Soh, Z.; Ozaki, T.; Murakami, T.; Otsuka, A.; Tsuji, T. Ability to cough can be evaluated through cough sounds: An experimental investigation of effects of microphone type on accuracy. In Proceedings of the 2017 IEEE/SICE International Symposium on System Integration (SII), Taipei, Taiwan, 11–14 December 2017; pp. 936–941. [Google Scholar]
- Bianchi, C.; Baiardi, P. Cough peak flows: Standard values for children and adolescents. Am. J. Phys. Med. Rehabil. Assoc. Acad. Physiatr. 2008, 87, 461–467. [Google Scholar] [CrossRef] [PubMed]
- Murata, A.; Ohota, N.; Shibuya, A.; Ono, H.; Kudoh, S. New non-invasive automatic cough counting program based on 6 types of classified cough sounds. Intern. Med. 2006, 45, 391–397. [Google Scholar] [CrossRef] [PubMed]
- Sivasothy, P.; Brown, L.; Smith, I.E.; Shneerson, J.M. Effect of manually assisted cough and mechanical insufflation on cough flow of normal subjects, patients with chronic obstructive pulmonary disease (COPD), and patients with respiratory muscle weakness. Thorax 2001, 56, 438–444. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.A.; Aliverti, A.; Quaranta, M.; McGuinness, K.; Kelsall, A.; Earis, J.; Calverley, P.M. Chest wall dynamics during voluntary and induced cough in healthy volunteers. J. Physiol. 2012, 590, 563–574. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, E.D.; Cournand, A.; Richards, D.W., Jr. Pulmonary insufficiency: I. Physiological classification, clinical methods of analysis, standard values in normal subjects. Medicine 1948, 27, 243–278. [Google Scholar] [CrossRef] [PubMed]
- Berglund, E.; Birath, G.; Bjure, J.; Grimby, G.; Kjellmer, I.; Sandqvist, L.; Soderholm, B. Spirometric studies in normal subjects I: Forced expirograms in subjects between 7 and 70 years of age. Acta Med. Scand. 1963, 173, 185–192. [Google Scholar] [CrossRef] [PubMed]
- Bonilha, H.S.; Gerlach, T.T.; Sutton, L.E.; Dawson, A.E.; McGrattan, K.; Nietert, P.J.; Deliyski, D.D. Efficacy of six tasks to clear laryngeal mucus aggregation. J. Voice 2017, 31, 254.e11–254.e15. [Google Scholar] [CrossRef] [PubMed]
- Britton, D.; Benditt, J.O.; Merati, A.L.; Miller, R.M.; Stepp, C.E.; Boitano, L.; Hu, A.; Ciol, M.A.; Yorkston, K.M. Associations between laryngeal and cough dysfunction in motor neuron disease with bulbar involvement. Dysphagia 2014, 29, 637–646. [Google Scholar] [CrossRef] [PubMed]
- Makiyama, K.; Yoshihashi, H.; Park, R.; Shimazaki, N.; Nakai, M. Assessment of phonatory function by the airway interruption method: Age-related changes. Otolaryngol. Head Neck Surg. 2006, 134, 407–412. [Google Scholar] [CrossRef] [PubMed]
- Nishio, M.; Niimi, S. Changes in speaking fundamental frequency characteristics with aging. Jpn. J. Logop. Phoniatr. 2005, 46, 136–144. [Google Scholar] [CrossRef]
- Goy, H.; Fernandes, D.N.; Pichora-Fuller, M.K.; van Lieshout, P. Normative voice data for younger and older adults. J. Voice 2013, 27, 545–555. [Google Scholar] [CrossRef] [PubMed]
- Shafieian, M.; Kashani, F.H. Effect of diffusive and nondiffusive surfaces combinations on sound diffusion. Acoust. Phys. 2010, 56, 342–347. [Google Scholar] [CrossRef]
- Gross, V.; Dittmar, A.; Penzel, T.; SchÜTtler, F.; Von Wichert, P. The relationship between normal lung sounds, age, and gender. Am. J. Respir. Crit. Care Med. 2000, 162, 905–909. [Google Scholar] [CrossRef] [PubMed]
- Duffin, J.M. Puerile respiration: Laennec’s stethoscope and the physiology of breathing. Trans. Stud. Coll. Physicians Phila. 1991, 13, 125–145. [Google Scholar] [PubMed]

| Variable | Young Participants (n = 33) | Elderly Participants (n = 25) | p Value |
|---|---|---|---|
| Age, years | 21.3 ± 0.4 | 80.4 ± 6.1 | < 0.001 |
| Male sex, n | 20 | 10 | 0.209 |
| Height, cm | 164.6 ± 8.4 | 154.1 ± 8.3 | 0.093 |
| Body weight, kg (male, female) | 58.5 ± 11.6 (64.5 ± 11.3, 51.0 ± 6.2) | 55.1 ± 11.9 (58.6 ± 6.3, 53.4 ± 15.1) | 0.156 |
| BMI, kg/m2 (male, female) | 21.3 ± 0.5 (21.4 ± 0.6, 20.9 ± 0.5) | 23.3 ± 4.1 (22.5 ± 1.6, 24.0 ± 5.2) | 0.216 |
| %VC, % | 97.0 ± 8.9 | 91.5 ± 17.5 | 0.438 |
| FEV1/FVC, % | 90.4 ± 7.6 | 91.8 ± 8.2 | 0.185 |
| Model | Parameter | Determined Value | Standard Error | 95% CI | Determination Coefficient | |
|---|---|---|---|---|---|---|
| Lower | Upper | |||||
| Equation (1) | α0,(1) | 42.90 | 17.50 | 7.84 | 77.96 | 0.829 |
| α1,(1) | −0.282 | 0.113 | −0.509 | −0.055 | ||
| β(1) | 0.028 | 0.004 | 0.020 | 0.037 | ||
| Equation (3) | α0,(3) | 42.32 | 17.54 | 7.15 | 77.50 | 0.829 |
| α1,(3) | −0.212 | 0.250 | −0.713 | 0.289 | ||
| α2,(3) | −0.001 | 0.002 | −0.006 | 0.004 | ||
| β(3) | 0.028 | 0.004 | 0.020 | 0.037 | ||
| Equation (4) | α0,(4) | 6.58 | 38.34 | −70.33 | 83.49 | 0.832 |
| α1,(4) | 2.366 | 2.899 | −3.448 | 8.181 | ||
| α2,(4) | 0.000 | 0.00 | 0.00 | 0.001 | ||
| α3,(4) | −0.048 | 0.054 | −0.156 | 0.060 | ||
| β(4) | 0.028 | 0.004 | 0.020 | 0.037 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umayahara, Y.; Soh, Z.; Sekikawa, K.; Kawae, T.; Otsuka, A.; Tsuji, T. A Mobile Cough Strength Evaluation Device Using Cough Sounds. Sensors 2018, 18, 3810. https://doi.org/10.3390/s18113810
Umayahara Y, Soh Z, Sekikawa K, Kawae T, Otsuka A, Tsuji T. A Mobile Cough Strength Evaluation Device Using Cough Sounds. Sensors. 2018; 18(11):3810. https://doi.org/10.3390/s18113810
Chicago/Turabian StyleUmayahara, Yasutaka, Zu Soh, Kiyokazu Sekikawa, Toshihiro Kawae, Akira Otsuka, and Toshio Tsuji. 2018. "A Mobile Cough Strength Evaluation Device Using Cough Sounds" Sensors 18, no. 11: 3810. https://doi.org/10.3390/s18113810
APA StyleUmayahara, Y., Soh, Z., Sekikawa, K., Kawae, T., Otsuka, A., & Tsuji, T. (2018). A Mobile Cough Strength Evaluation Device Using Cough Sounds. Sensors, 18(11), 3810. https://doi.org/10.3390/s18113810





