Motion Periods of Planet Gear Fault Meshing Behavior
Abstract
1. Introduction
- The faulty tooth initially meshing with the ring gear;
- The faulty tooth initially meshing with the sun gear.
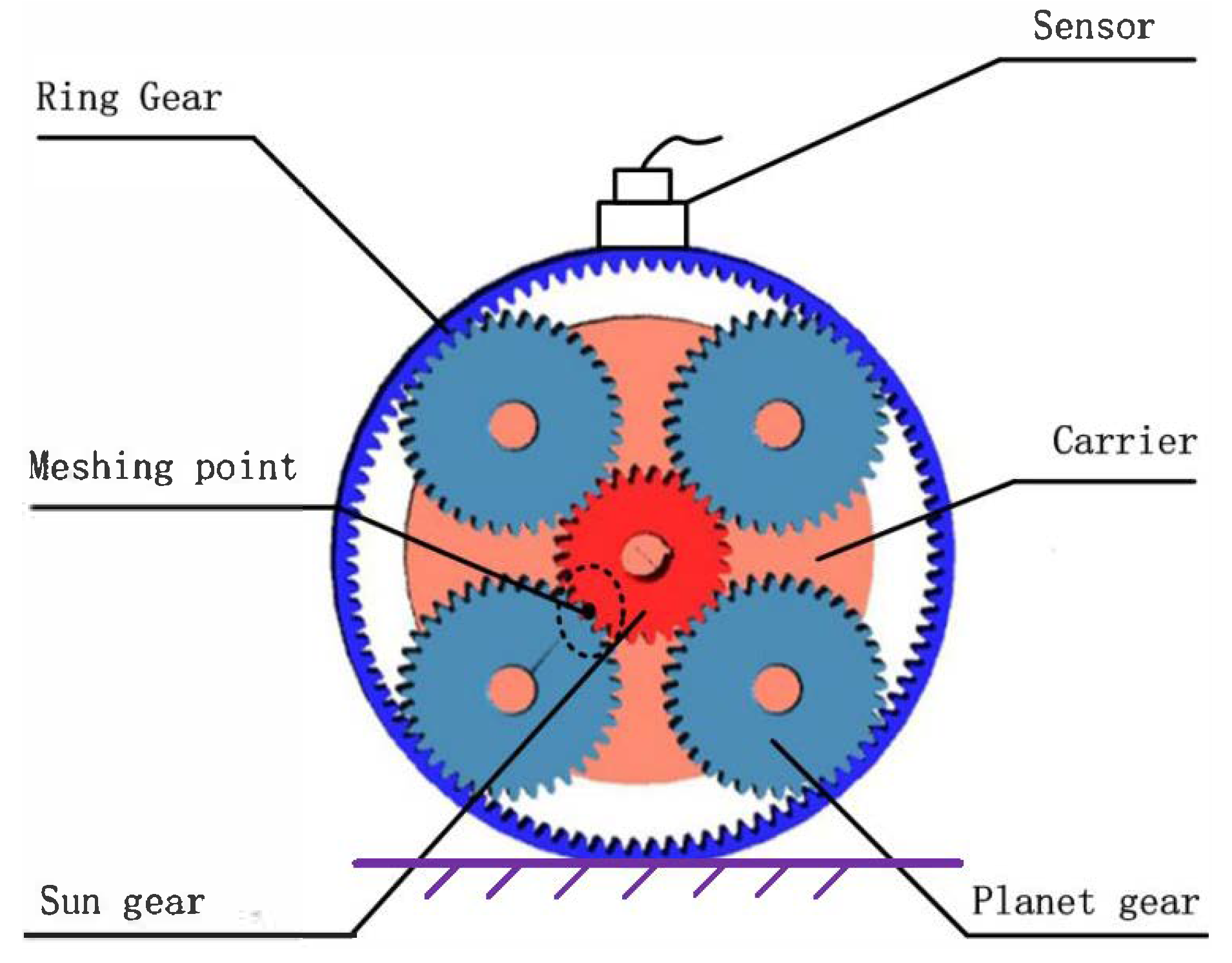
2. Motion Periods of the Planet Gear Fault-Meshing Position
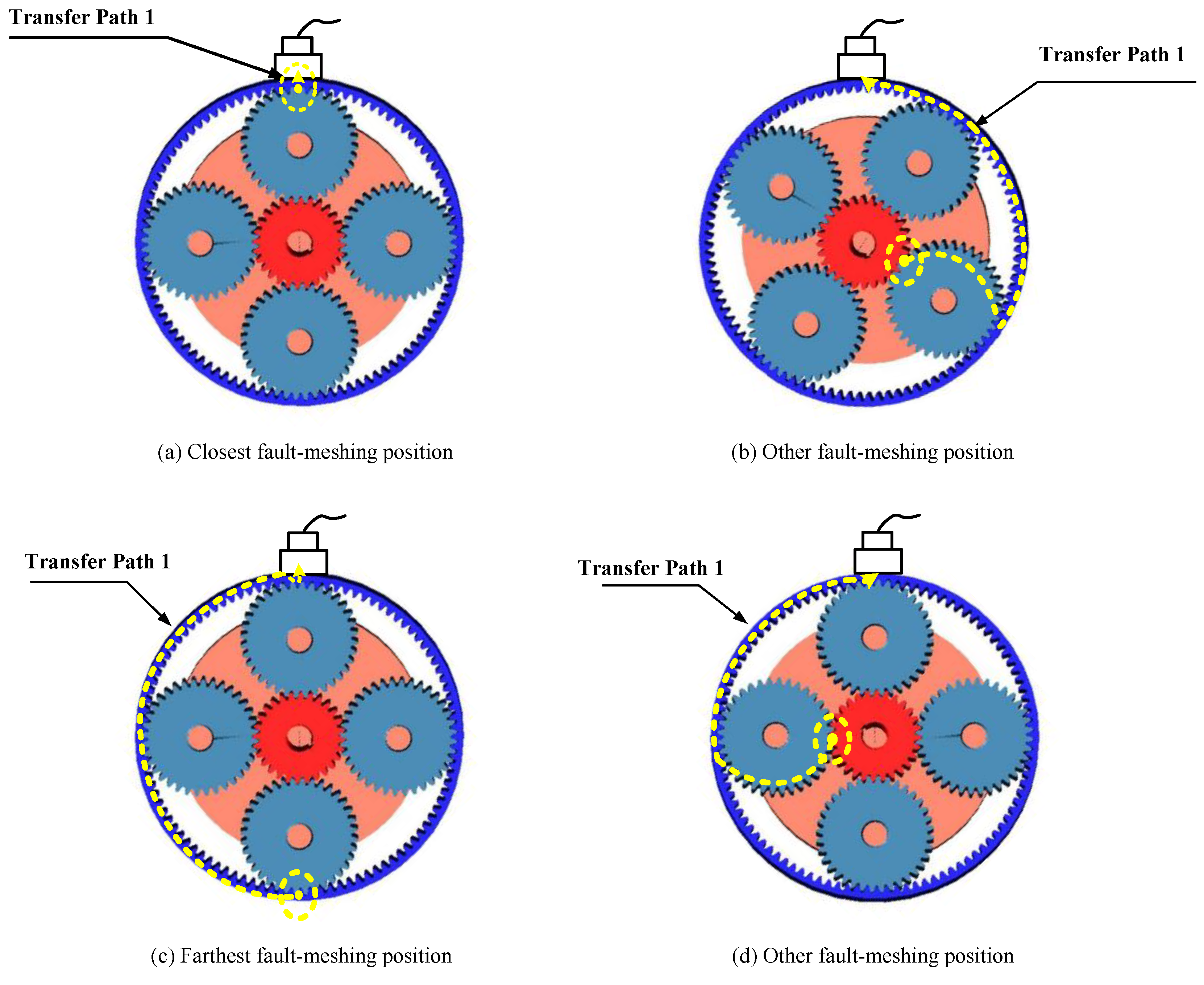
2.1. Influences of the Fault-Meshing Behavior
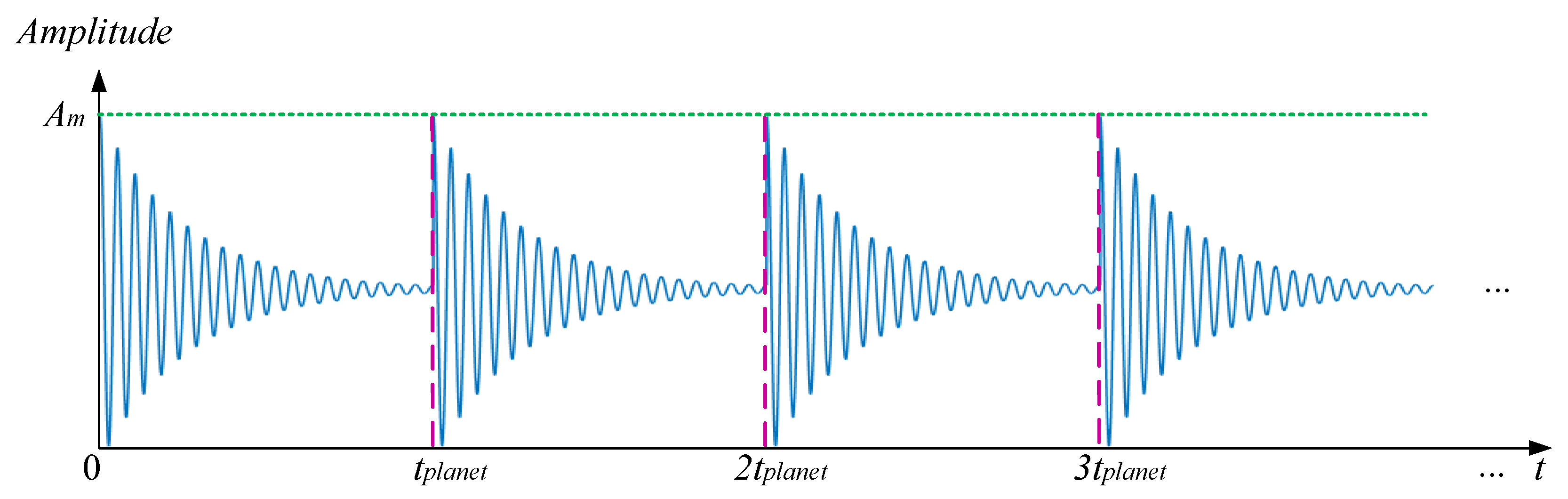
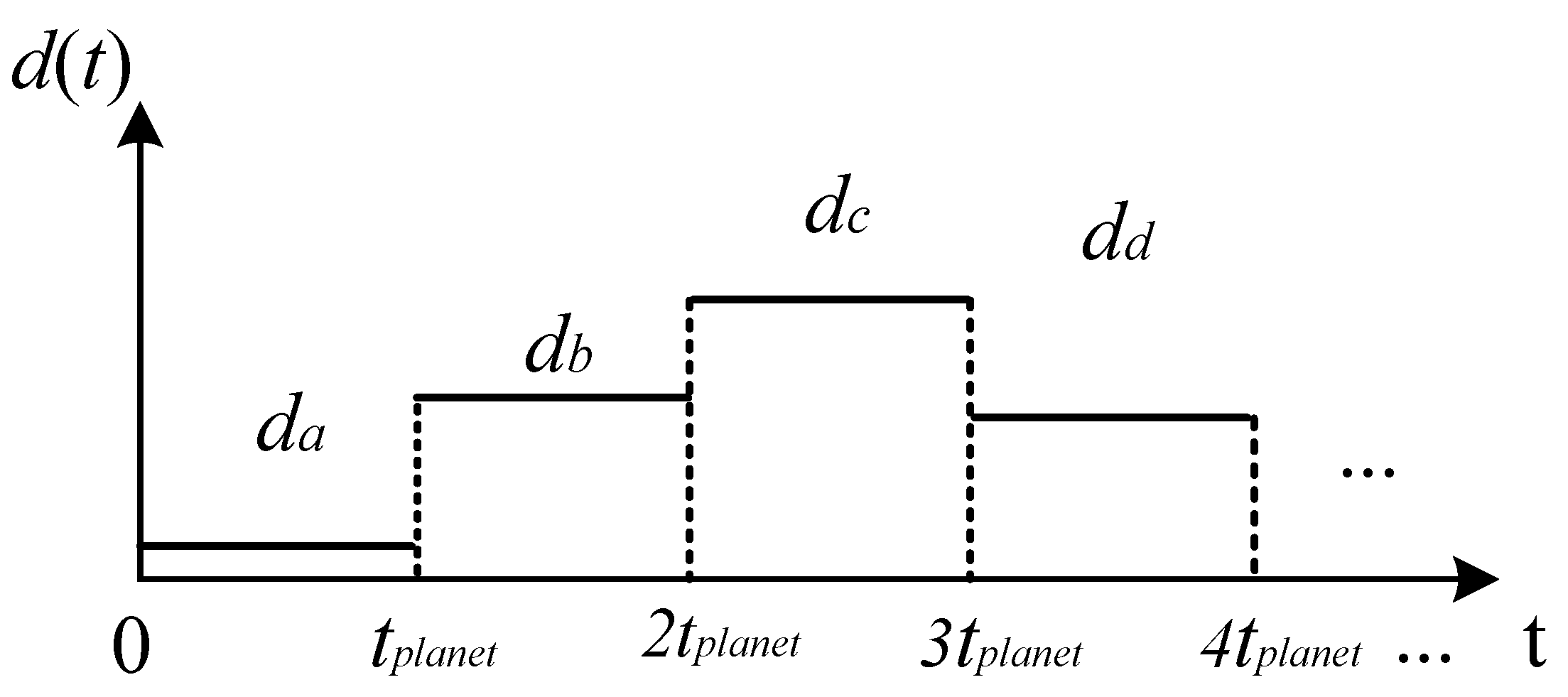
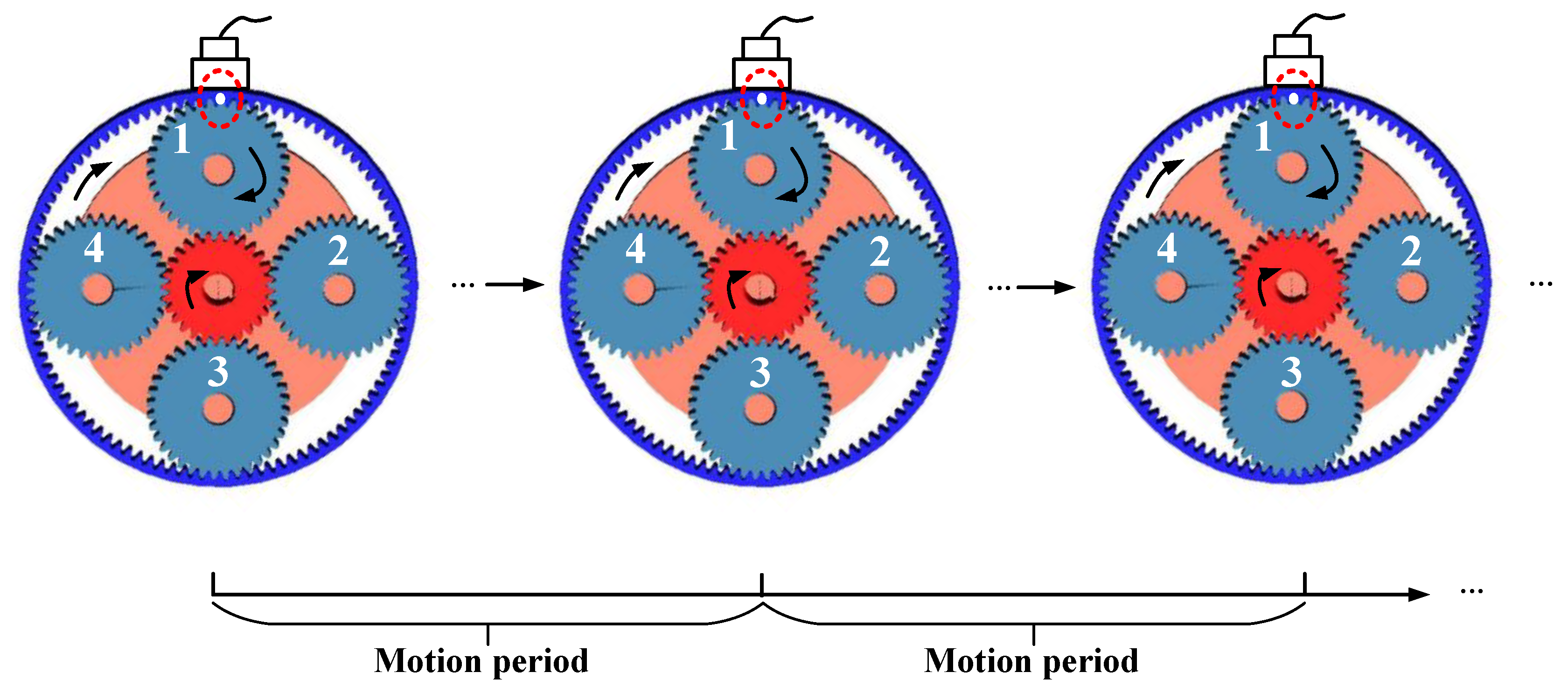
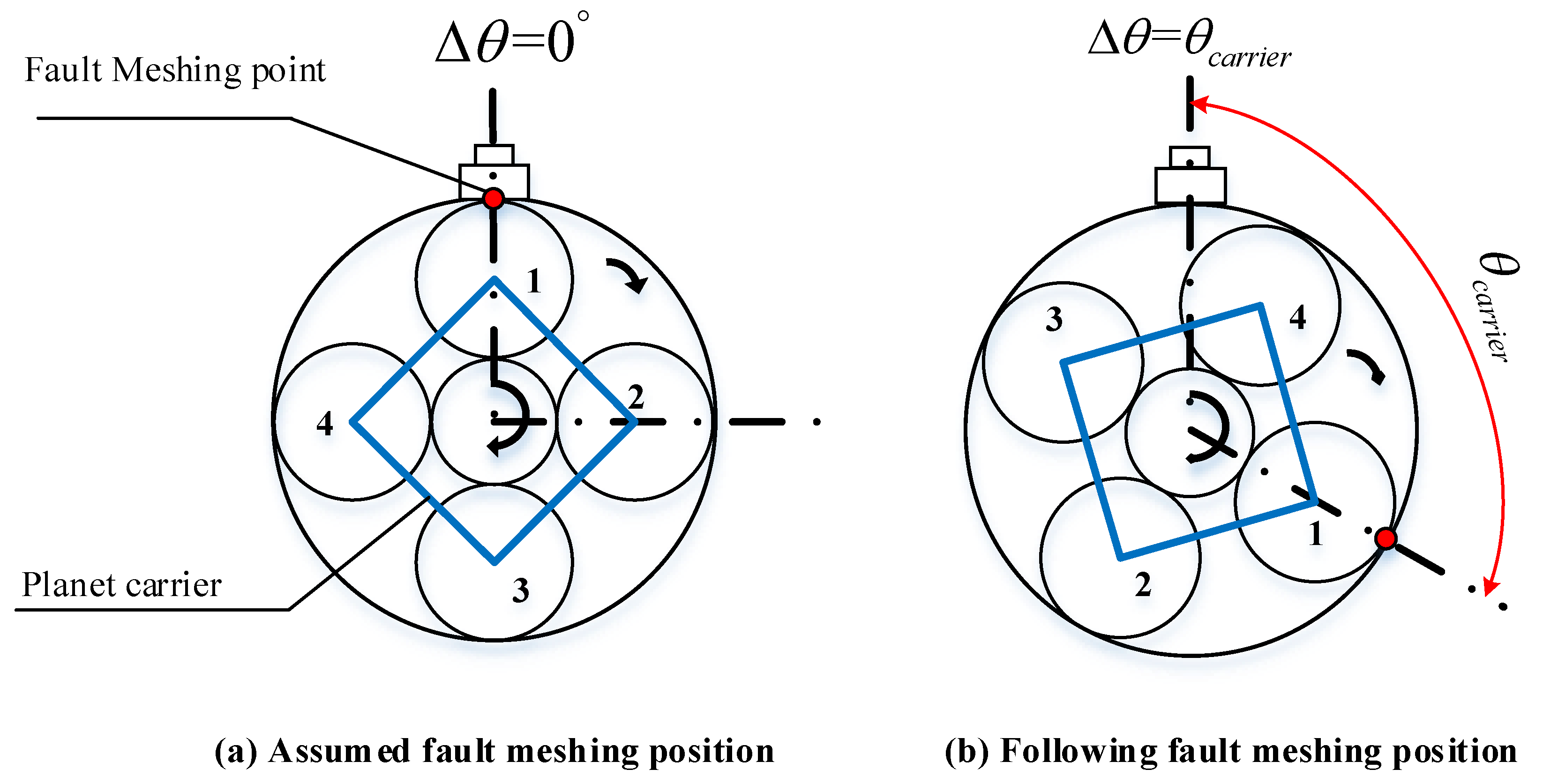
2.2. Motion Period of Planet Gear Fault-Meshing Behavior
2.2.1. Initial Fault-Meshing Position at Ring Gear
2.2.2. Initial Fault-Meshing with Sun Gear
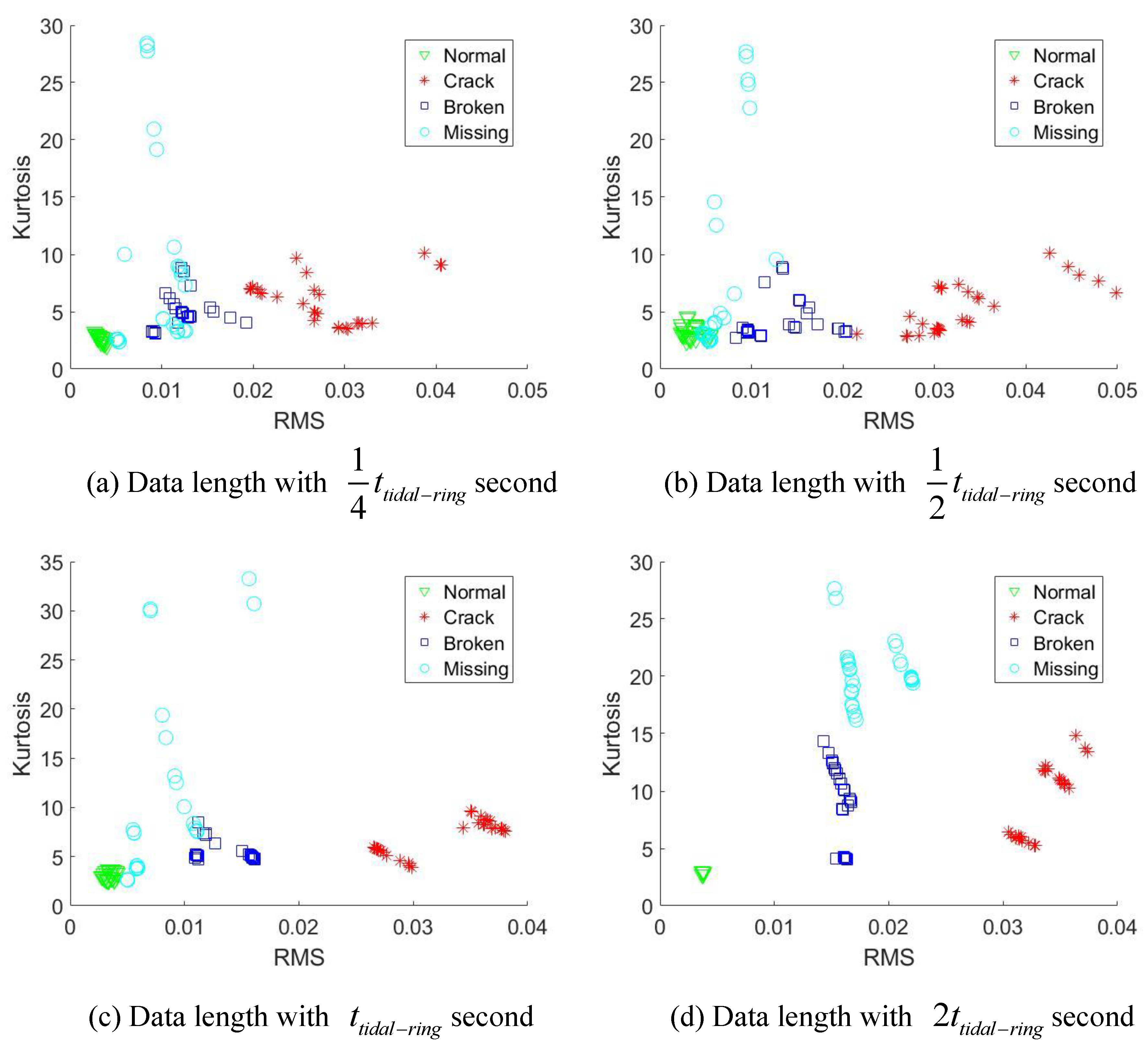
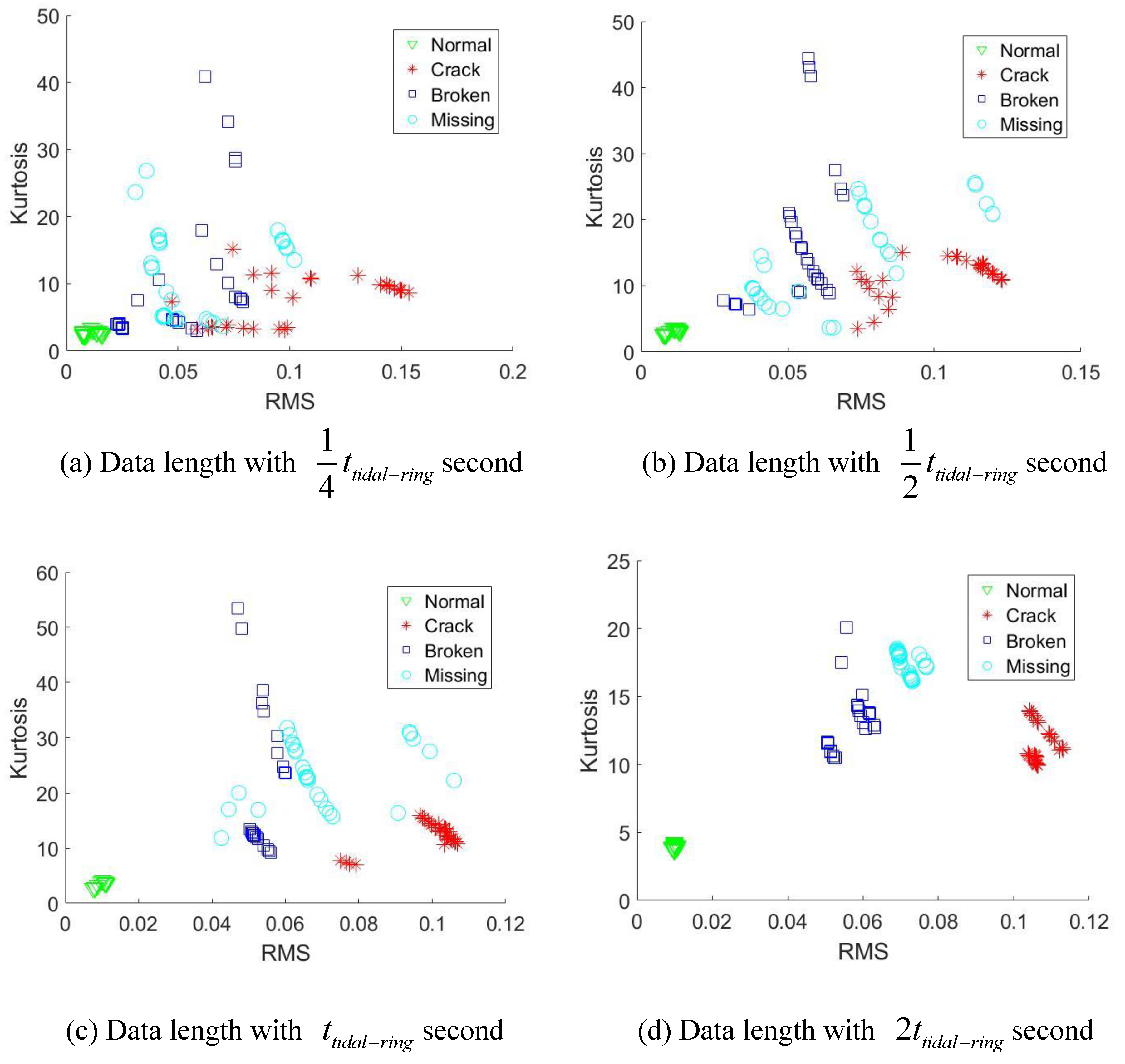
3. Experimental Study
4. Conclusions
- Condition 1: Fault meshing initially occurred on the ring gear
- Condition 2: Fault meshing initially occurred at the sun gear
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GCD | Greatest Common Divisor |
| LCM | Least Common Multiple |
Appendix A. Geometrical validation of the motion periods
| Known Parameters | Values/Unit | Description |
|---|---|---|
| Rotation angle of carrier between two times of fault-meshing | ||
| 1/cycle | Rotation angle of the faulty planet gear between two times of fault-meshing | |
| /cycle | Rotation angle of sun gear between two times of fault-meshing | |
| 576 | LCM between and | |
| 896 | LCM between and |
| Undetermined Parameters | Values/Unit | Description |
|---|---|---|
| 16/times | Total fault-meshing times of a motion period | |
| 16/cycles | Number of rotations of the faulty planet gear in a motion period | |
| 9/cycles | Number of rotations of carrier in a motion period |
| Undetermined Parameters | Values/Unit | Description |
|---|---|---|
| 112/times | Total fault-meshing times of a motion period | |
| 288/cycles | Number of rotations of the sun gear in a motion period | |
| 63/cycles | Number of rotations of carrier in a motion period | |
| 112/cycles | Number of rotations of faulty planet gear in a motion period |


References
- Zhang, M.; Wang, K.; Wei, D.; Zuo, M.J. Amplitudes of characteristic frequencies for fault diagnosis of planetary gearbox. J. Sound Vib. 2018, 432, 119–132. [Google Scholar] [CrossRef]
- Peng, D.; Smith, W.A.; Randall, R.B.; Peng, Z. Use of mesh phasing to locate faulty planet gears. Mech. Syst. Signal Process. 2019, 116, 12–24. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; Zuo, M.J.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Feng, Z. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
- Hu, Y.; Tu, X.; Li, F.; Meng, G. Joint High-Order Synchrosqueezing Transform and Multi-Taper Empirical Wavelet Transform for Fault Diagnosis of Wind Turbine Planetary Gearbox under Nonstationary Conditions. Sensors 2018, 18, 150. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liang, X.; Zuo, M.J. A dependence-based feature vector and its application on planetary gearbox fault classification. J. Sound Vib. 2018, 431, 192–211. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, K.; Wei, D. An Order Analysis Based Second-Order Cyclic Function Technique for Planetary Gear Fault Detection. In Proceedings of the International Conference on Sensing, Diagnostics, Prognostics, and Control, Shanghai, China, 16–18 August 2017; pp. 678–682. [Google Scholar]
- Sun, H.; Zi, Y.; He, Z.; Yuan, J.; Wang, X.; Chen, L. Customized Multiwavelets for Planetary Gearbox Fault Detection Based on Vibration Sensor Signals. Sensors 2013, 13, 1183–1209. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part II: Fault Diagnosis With Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Kong, D. A Method Based on Multi-Sensor Data Fusion for Fault Detection of Planetary Gearboxes. Sensors 2012, 12, 2005–2017. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Wang, K.; Zhang, M.; Zuo, M.J. Sweep excitation with order tracking: A new tactic for beam crack analysis. J. Sound Vib. 2018, 420, 129–141. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, Y.; Zuo, M.J.; Feng, Z. Time-frequency representation based on robust local mean decomposition for multicomponent AM-FM signal analysis. Mech. Syst. Signal Process. 2017, 95, 468–487. [Google Scholar] [CrossRef]
- Guo, J.; Shi, Z.; Li, H.; Zhen, D.; Gu, F.; Ball, A.D. Early Fault Diagnosis for Planetary Gearbox Based Wavelet Packet Energy and Modulation Signal Bispectrum Analysis. Sensors 2018, 18, 2908. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zuo, M.J.; Jin, Y.; Peng, D.; Qin, Y. Improved local mean decomposition for modulation information mining and its application to machinery fault diagnosis. J. Sound Vib. 2017, 397, 266–281. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J. Vibration signal models for fault diagnosis of planetary gearboxes. J. Sound Vib. 2012, 331, 4919–4939. [Google Scholar] [CrossRef]
- Halim, E.B.; Choudhury, M.S.; Shah, S.L.; Zuo, M.J. Time domain averaging across all scales: A novel method for detection of gearbox faults. Mech. Syst. Signal Process. 2008, 22, 261–278. [Google Scholar] [CrossRef]
- McFadden, P. A technique for calculating the time domain averages of the vibration of the individual planet gears and the sun gear in an epicyclic gearbox. J. Sound Vib. 1991, 144, 163–172. [Google Scholar] [CrossRef]
- Mcfadden, P.D. Window functions for the calculation of the time domain averages of the vibration of the individual planet gears and sun gear in an epicyclic gearbox. Mech. Dev. 1994, 97, 93–104. [Google Scholar] [CrossRef]
- Lewicki, D.G.; LaBerge, K.E.; Ehinger, R.T.; Fetty, J. Planetary Gearbox Fault Detection Using Vibration Separation Techniques; NASA Glenn Research Center: Cleveland, OH, USA, 2011. [Google Scholar]
- Liang, X.; Zuo, M.J.; Liu, L. A windowing and mapping strategy for gear tooth fault detection of a planetary gearbox. Mech. Syst. Signal Process. 2016, 80, 445–459. [Google Scholar] [CrossRef]
- Lewicki, D.G.; Samuel, P.D.; Conroy, J.K.; Pines, D.J. Planetary Transmission Diagnostics; NASA Glenn Research Center: Cleveland, OH, USA, 2004. [Google Scholar]
- D’Elia, G.; Mucchi, E.; Cocconcelli, M. On the identification of the angular position of gears for the diagnostics of planetary gearboxes. Mech. Syst. Signal Process. 2017, 83, 305–320. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Y.; Wu, X.; Na, J. Localized fault detection of sun gears based on windowed synchronous averaging in the angular domain. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Song, L. Vibration Signal Simulation and Localized Fault Diagnosis of Planetary Gearboxes Based on Transmission Mechanism Analysis. Master’s Thesis, UESTC, Chengdu, China, 2017. [Google Scholar]
- Wang, K.; Wang, K. A unique tidal frequency to the damage induced vibration of planetary gear system. In Proceedings of the International Conference on Artificial Intelligence: Technologies and Applications, Bangkok, Thailand, 24–25 January 2016. [Google Scholar] [CrossRef]
- Wang, K.; Wang, K.; Zuo, M.J. A fault diagnosis index based on complex movement of planetary gearbox. J. Vib. Shock 2016, 35, 216–221. [Google Scholar]
- Ha, J.M.; Youn, B.D.; Oh, H.; Han, B.; Jung, Y.; Park, J. Autocorrelation-based time synchronous averaging for condition monitoring of planetary gearboxes in wind turbines. Mech. Syst. Signal Process. 2016, 70–71, 161–175. [Google Scholar] [CrossRef]
- Ha, J.M.; Park, J.; Na, K.; Kim, Y.; Youn, B.D. Toothwise Fault Identification for a Planetary Gearbox Based on a Health Data Map. IEEE Trans. Ind. Electron. 2018, 65, 5903–5912. [Google Scholar] [CrossRef]
- Rao, S. Mechanical Vibrations. Nature 2006, 179, 504. [Google Scholar]
- Liu, L.; Liang, X.; Zuo, M.J. Vibration signal modeling of a planetary gear set with transmission path effect analysis. Measurement 2016, 85, 20–31. [Google Scholar] [CrossRef]
- Oberg, E.; Jones, F.; Horton, H.; Ryffel, H.H.; Geronimo, J.H. Machinery’s Handbook; Industrial Press: New York, NY, USA, 2016. [Google Scholar]




| N | |||
|---|---|---|---|
| 28 | 36 | 100 | 4 |
| Rotational Speed | Time Duration of |
|---|---|
| 1800 rpm | s |
| 3000 rpm | s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Wang, K.; Li, Y. Motion Periods of Planet Gear Fault Meshing Behavior. Sensors 2018, 18, 3802. https://doi.org/10.3390/s18113802
Zhang M, Wang K, Li Y. Motion Periods of Planet Gear Fault Meshing Behavior. Sensors. 2018; 18(11):3802. https://doi.org/10.3390/s18113802
Chicago/Turabian StyleZhang, Mian, Kesheng Wang, and Yaxin Li. 2018. "Motion Periods of Planet Gear Fault Meshing Behavior" Sensors 18, no. 11: 3802. https://doi.org/10.3390/s18113802
APA StyleZhang, M., Wang, K., & Li, Y. (2018). Motion Periods of Planet Gear Fault Meshing Behavior. Sensors, 18(11), 3802. https://doi.org/10.3390/s18113802





