High-Resolution Aerial Imagery Semantic Labeling with Dense Pyramid Network
Abstract
1. Introduction
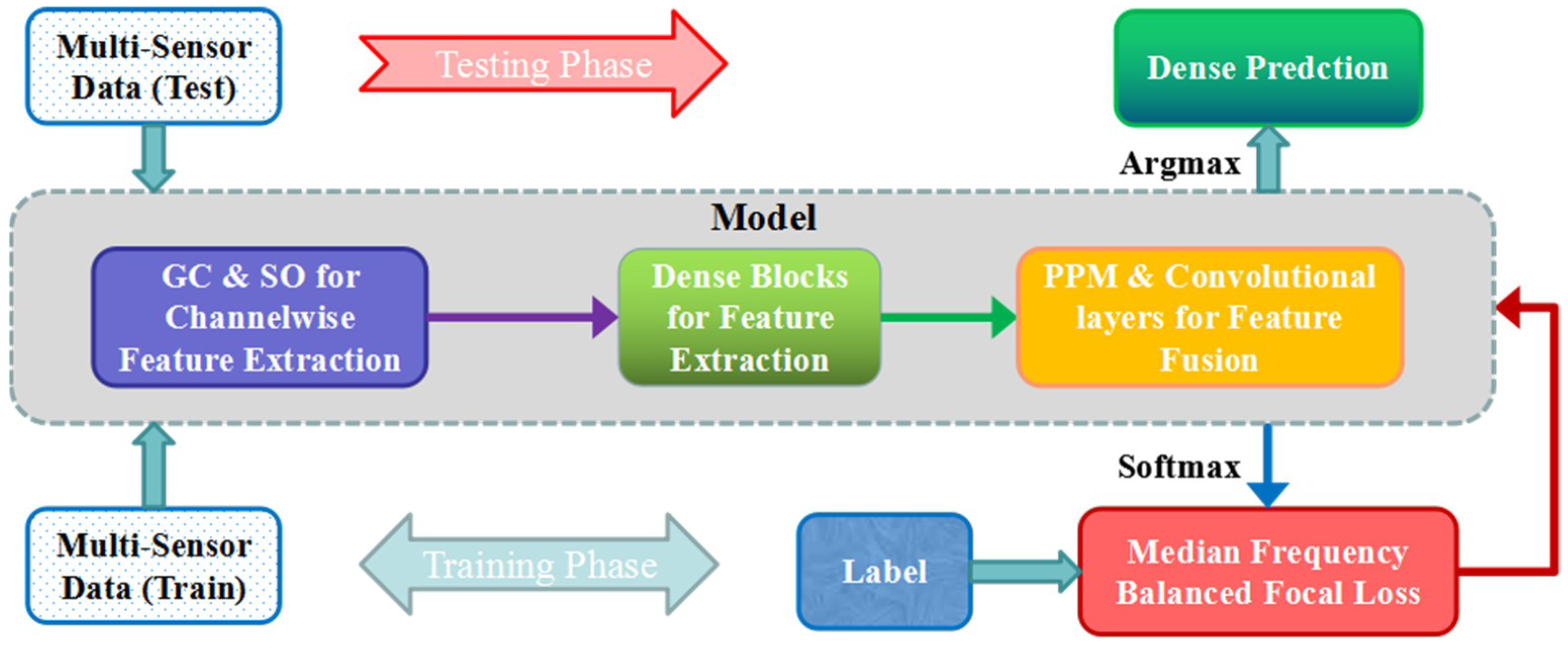
- A DPN is proposed to deal with the semantic segmentation of high-resolution aerial imagery. The architecture based on densely connected convolutions and pyramid pooling modules have wider receptive fields, and can also fuse multi-resolution features through a global contextual prior manner.
- Group convolutions and shuffling operation are set at the beginning of the network to process the multi-sensor data in channel-wise. These two operations can help the network preserve more information from multi-sensor data, while also ensuring that the information flows between channels.
- Median frequency balanced focal loss is applied to deal with class imbalance problem, as well as to reduce the relative loss for well-classified examples and to put more focus on hard, misclassified examples. In particular, we add a constraint on the median frequency weight to mitigate the overreacting problem of certain class.
2. Methods
2.1. Group Convolutions and Channel Shuffling Operation
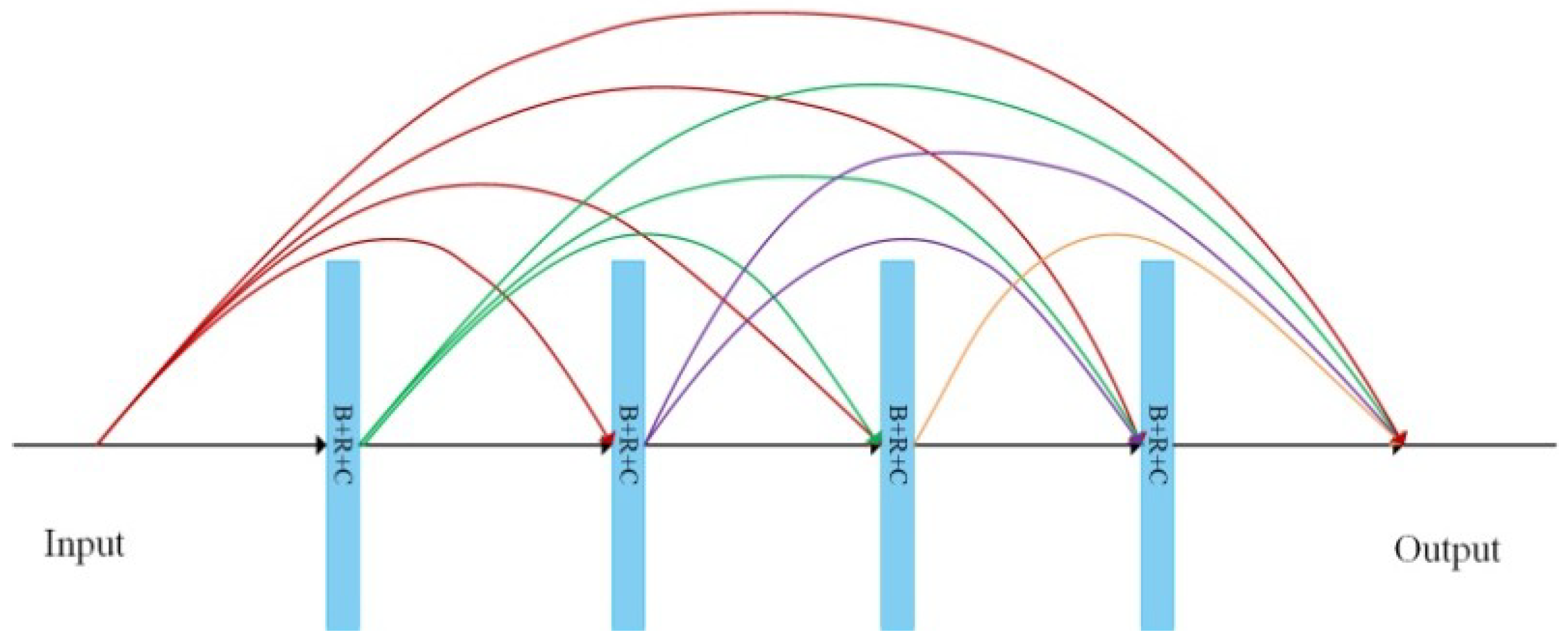
2.2. Densely Connected Convolutions
2.3. Pyramid Pooling Module
2.4. Median Frequency Balanced Focal Loss
2.5. Training and Inference Strategy of DPN
3. Results
3.1. Dataset and Evaluation Metrics
3.2. Ablation Study
3.3. Comparison with Other Methods
3.3.1. Vaihingen Dataset
- (1)
- ‘DST_2’: The method (FCN + RF + CRFs + DSMs) is proposed in Ref. [14]. The CIR images and LiDAR data are processed and combined by a hybrid FCN, of which no down-sampling FCNs are employed to preserve resolution of the output. CRFs are utilized to further improve the segmentation accuracy as a post-processing step.
- (2)
- ‘ONE_7’: The method (SegNet + DSMs/nDSMs) is proposed in Ref. [17]. Two SegNets are applied for both CIR images and synthetic data, which consist of DSMs, nDSMs, and the normalized difference vegetation index (NDVI) computed based on NIR and R channel.
- (3)
- ‘INR’: The method (CNN + MLP + DSMs) is proposed in Ref. [19]. Authors derived a CNN framework to learn features and multi-resolution features which are inputted into MLP to learn how to fuse in an effective and flexible fashion. It is worth noting that DSMs are simply added as an extra band of input data.
- (4)
- ‘CAS_Y3’: The method (PSPNet) is proposed in Ref. [25]. ResNet 101 is utilized as the feature extractor and pyramid pooling module is followed to learn global contextual information at multiple scales. No LiDAR data is used in this method, since the input of ResNet101 follows a 3-channel format.
- (5)
- ‘BKHN-5’: The method (DenseNet + DSMs/nDSMs) is proposed in Ref. [23], where 67 layers of fully convolutional DenseNet is selected as a comparison method. This is because these 67 layers of fully convolutional DenseNet achieves the best performance when compared with 46 layers (‘BKHN-9’) and 103 layers (‘BKHN-8’); the 67 layers of fully convolutional DenseNet have a similar scale with the proposed DPN, which employs 64 layers of densely connected convolutions.
- (6)
- DPN-MFFL: The method (DPN + Focal Loss + nDSMs) is proposed in this paper, where 64 layers of densely connected convolutions combined with a pyramid pooling module is employed to learn high-level features and accomplish the feature fusion through a global contextual prior manner. In addition, group convolutions and shuffling operation are adopted to preserve more information from multi-sensor data. In the training phase, the focal loss is optimized to mitigate the class imbalance problem.
3.3.2. Potsdam Dataset
- (1)
- ‘UZ_1’: The method (CNN + Deconvolution + nDSMs) is proposed in Ref. [11]. The architecture followed up-sample-then-down-sample paradigm. It learns the high-level features by convolutions, and then learns to up-sample the down-sampled features back to original size by means of deconvolutions. The nDSMs are treated as an extra band of the input data.
- (2)
- ‘RIT_L7’: The method (FCN + CRFs + nDSMs) is proposed in Ref. [12]. The authors train a FCN-8s on CIR images and a logistic regression by hand-craft features derived from nDSMs and CIR images. The results of two architectures are then fused by using a higher order CRFs to obtain the final probabilistic graphs.
- (3)
- ‘RIT_2’: The method (SegNet + nDSMs) is proposed in Ref. [33]. Two SegNets are trained on CIR images and synthetic data separately, and the features are then fused at the early stage to reduce the memory cost.
- (4)
- ‘DST_5’: The method (FCN + RF + CRFs + DSMs) is proposed in Ref. [14]. Same as ‘DST_2’ described in Section 3.3.1.
- (5)
- ‘CAS_Y3’: The method (PSPNet) is proposed in Ref. [25]. Same as ‘CAS_Y3’ described in Section 3.3.1.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Z.; Ren, J.; Zhang, D.; Sun, M.; Jiang, J. A deep learning based feature hybrid framework for spatiotemporal saliency detection inside videos. Neurocomputing 2018, 287, 68–83. [Google Scholar] [CrossRef]
- Han, J.; Zhang, D.; Cheng, G.; Zhang, D.; Cheng, G.; Guo, L.; Ren, J. Object detection in optical remote sensing images based on weakly supervised learning and high-level feature learning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3325–3337. [Google Scholar] [CrossRef]
- Han, J.; Zhang, D.; Hu, X.; Guo, L.; Ren, J.; Wu, F. Background prior-based salient object detection via deep reconstruction residual. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 1309–1321. [Google Scholar]
- Sun, J.; Yang, J.; Zhang, C.; Yun, W.; Qu, J. Automatic remotely sensed image classification in a grid environment based on the maximum likelihood method. Math. Comput. Model. 2013, 58, 573–581. [Google Scholar] [CrossRef]
- Yan, Y.; Ren, J.; Sun, G.; Zhao, H.; Han, J.; Li, X.; Marshall, S.; Zhan, J. Unsupervised image saliency detection with Gestalt-laws guided optimization and visual attention based refinement. Pattern Recognit. 2018, 79, 65–78. [Google Scholar] [CrossRef]
- Ren, J. ANN vs. SVM: Which one performs better in classification of MCCs in mammogram imaging. Knowl. Based Syst. 2012, 26, 144–153. [Google Scholar] [CrossRef]
- Cheng, G. Effective and efficient midlevel visual elements-oriented land-use classification using VHR remote sensing images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4238–4249. [Google Scholar] [CrossRef]
- Sugg, Z.P.; Finke, T.; Goodrich, D.C.; Moran, M.S.; Yool, S.R. Mapping Impervious Surfaces Using Object-Oriented Classification in a Semiarid Urban Region. Photogramm. Eng. Remote Sens. 2015, 80, 343–352. [Google Scholar] [CrossRef]
- Song, B.; Li, P.; Li, J.; Plaza, A. One-Class Classification of Remote Sensing Images Using Kernel Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1613–1623. [Google Scholar] [CrossRef]
- Paisitkriangkrai, S.; Sherrah, J.; Janney, P.; Hengel, A. Effective semantic pixel labelling with convolutional networks and conditional random fields. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 36–43. [Google Scholar]
- Volpi, M.; Tuia, D. Dense semantic labeling of subdecimeter resolution images with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 881–893. [Google Scholar] [CrossRef]
- Liu, Y.; Piramanayagam, S.; Monteiro, S.; Saber, E. Dense semantic labeling of very-high-resolution aerial imagery and lidar with fully-convolutional neural networks and higher-order CRFs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1561–1570. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Sherrah, J. Fully convolutional networks for dense semantic labelling of high-resolution aerial imagery. arXiv, 2016; arXiv:1606.02585v1. [Google Scholar]
- Li, R.; Liu, W.; Yang, L.; Sun, S.; Hu, W.; Zhang, F.; Li, W. DeepUNet: A Deep Fully Convolutional Network for Pixel-Level Sea-Land Segmentation. arXiv, 2017; arXiv:1709.00201. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Semantic segmentation of earth observation data using multimodal and multi-scale deep networks. In Proceedings of the Asian Conference on Computer Vision (ACCV), Taipei, Taiwan, 21–23 November 2016; pp. 180–196. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. High-resolution aerial image labeling with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7092–7103. [Google Scholar] [CrossRef]
- Liu, Y.; Minh Nguyen, D.; Deligiannis, N.; Ding, W.; Munteanu, A. Hourglass-shapenetwork based semantic segmentation for high resolution aerial imagery. Remote Sens. 2017, 9, 522. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Nevada, NV, USA, 3–6 December 2012; pp. 1106–1114. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. arXiv, 2017; arXiv:1707.01083. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Pan, X.; Gao, L.; Marinoni, A.; Zhang, B.; Yang, F.; Gamba, P. Semantic Labeling of High Resolution Aerial Imagery and LiDAR Data with Fine Segmentation Network. Remote Sens. 2018, 10, 743. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar]
- Lin, T.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 2999–3007. [Google Scholar] [CrossRef]
- Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Los Alamitos, CA, USA, 7–13 December 2015; pp. 2650–2658. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Sun, G.; Ma, P.; Ren, J.; Zhang, A.; Jia, X. A stability constrained adaptive alpha for gravitational search algorithm. Knowl. Based Syst. 2018, 139, 200–213. [Google Scholar] [CrossRef]
- Zhang, A.; Sun, G.; Ren, J.; Li, X.; Wang, Z.; Jia, X. A dynamic neighborhood learning-based gravitational search algorithm. IEEE Trans. Cybern. 2018, 48, 436–447. [Google Scholar] [CrossRef] [PubMed]
- ISPRS Vaihingen 2D Semantic Labeling Dataset. Available online: http://www2.isprs.org/commissions/comm3/wg4/tests.html (accessed on 1 April 2017).
- Gerke, M. Use of the Stair Vision Library within the ISPRS 2D Semantic Labeling Benchmark (Vaihingen); University of Twente: Enschede, The Netherlands, 2015. [Google Scholar]
- ISPRS Test Project on Urban Classification, 3D Building Reconstruction and Semantic Labeling. Available online: http://www2.isprs.org/commissions/comm2/wg4/potsdam-2d-semantic-labeling.html (accessed on 1 April 2017).

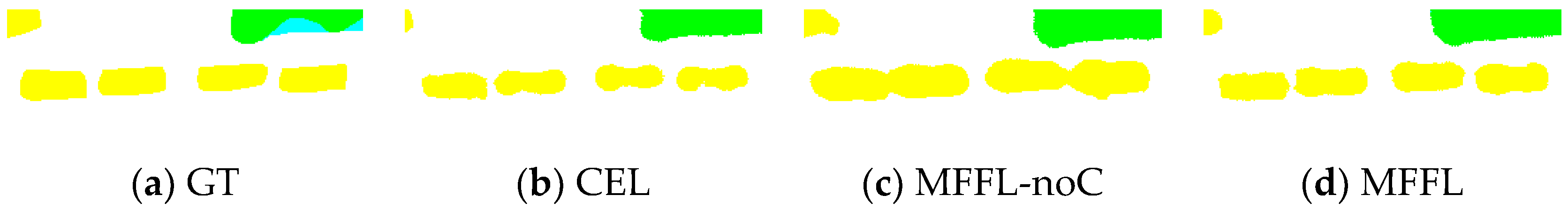





| Methods | Imp. Surf. | Build | Low Veg. | Tree | Car | Aver. F1 | OA |
|---|---|---|---|---|---|---|---|
| DPN-noGS | 90.95 | 94.68 | 79.29 | 88.46 | 82.32 | 87.14 | 88.74 |
| DPN-noPP | 90.08 | 94.95 | 79.01 | 88.16 | 83.33 | 87.11 | 88.35 |
| DPN | 91.33 | 95.53 | 80.50 | 88.49 | 83.90 | 87.95 | 89.19 |
| DPN-MFFL | 91.49 | 95.43 | 80.47 | 88.72 | 85.69 | 88.36 | 89.26 |
| Methods | Imp. Surf. | Build | Low Veg. | Tree | Car | Aver. F1 | OA |
|---|---|---|---|---|---|---|---|
| DST_2 [14] | 90.5 | 93.7 | 83.4 | 89.2 | 72.6 | 85.9 | 89.1 |
| ONE_7 [17] | 91.0 | 94.5 | 84.4 | 89.9 | 77.8 | 87.5 | 89.8 |
| INR [19] | 91.1 | 94.7 | 83.4 | 89.3 | 71.2 | 85.9 | 89.5 |
| CAS_Y3 [25] | 91.0 | 93.3 | 82.2 | 88.2 | 71.3 | 85.2 | 88.7 |
| BKHN_5 [23] | 91.4 | 94.3 | 81.9 | 88.5 | 78.4 | 86.9 | 89.1 |
| DPN+MFFL | 91.9 | 95.1 | 84.0 | 89.0 | 81.8 | 88.4 | 90.0 |
| Methods | Imp. Surf. | Build | Low Veg. | Tree | Car | Aver. F1 | OA |
|---|---|---|---|---|---|---|---|
| UZ_1 [11] | 89.3 | 95.4 | 81.8 | 80.5 | 86.5 | 86.7 | 85.8 |
| RIT_L7 [12] | 91.2 | 94.6 | 85.1 | 85.1 | 92.8 | 89.8 | 88.4 |
| RIT_2 [33] | 92.0 | 96.3 | 85.5 | 86.5 | 94.5 | 91.0 | 89.4 |
| DST_5 [14] | 92.5 | 96.4 | 86.7 | 88.0 | 94.7 | 91.7 | 90.3 |
| CAS_Y3 [25] | 92.2 | 95.7 | 87.2 | 87.6 | 95.6 | 91.7 | 90.1 |
| DPN-MFFL | 92.4 | 96.4 | 87.8 | 88.0 | 95.7 | 92.1 | 90.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, X.; Gao, L.; Zhang, B.; Yang, F.; Liao, W. High-Resolution Aerial Imagery Semantic Labeling with Dense Pyramid Network. Sensors 2018, 18, 3774. https://doi.org/10.3390/s18113774
Pan X, Gao L, Zhang B, Yang F, Liao W. High-Resolution Aerial Imagery Semantic Labeling with Dense Pyramid Network. Sensors. 2018; 18(11):3774. https://doi.org/10.3390/s18113774
Chicago/Turabian StylePan, Xuran, Lianru Gao, Bing Zhang, Fan Yang, and Wenzhi Liao. 2018. "High-Resolution Aerial Imagery Semantic Labeling with Dense Pyramid Network" Sensors 18, no. 11: 3774. https://doi.org/10.3390/s18113774
APA StylePan, X., Gao, L., Zhang, B., Yang, F., & Liao, W. (2018). High-Resolution Aerial Imagery Semantic Labeling with Dense Pyramid Network. Sensors, 18(11), 3774. https://doi.org/10.3390/s18113774






