Application of Computational Intelligence Methods for the Automated Identification of Paper-Ink Samples Based on LIBS
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
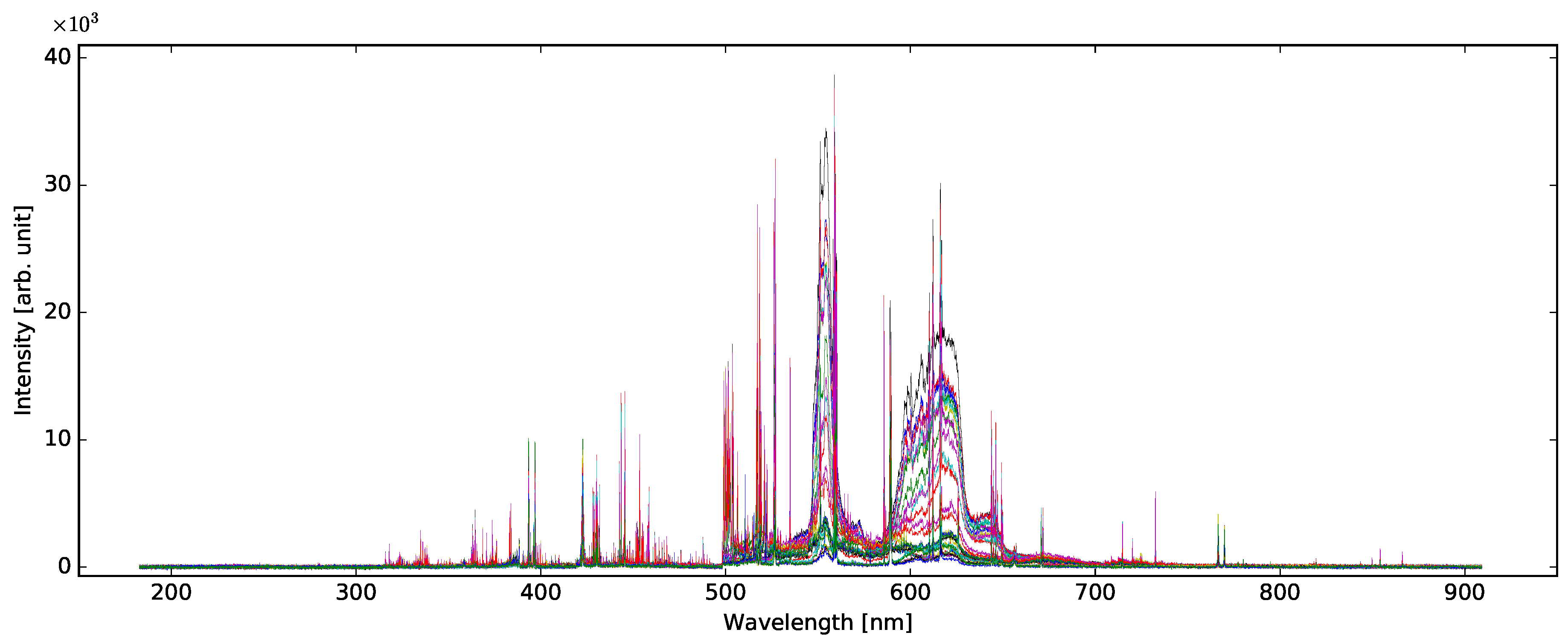
2.2. LIBS
2.3. Spectral Line Identification
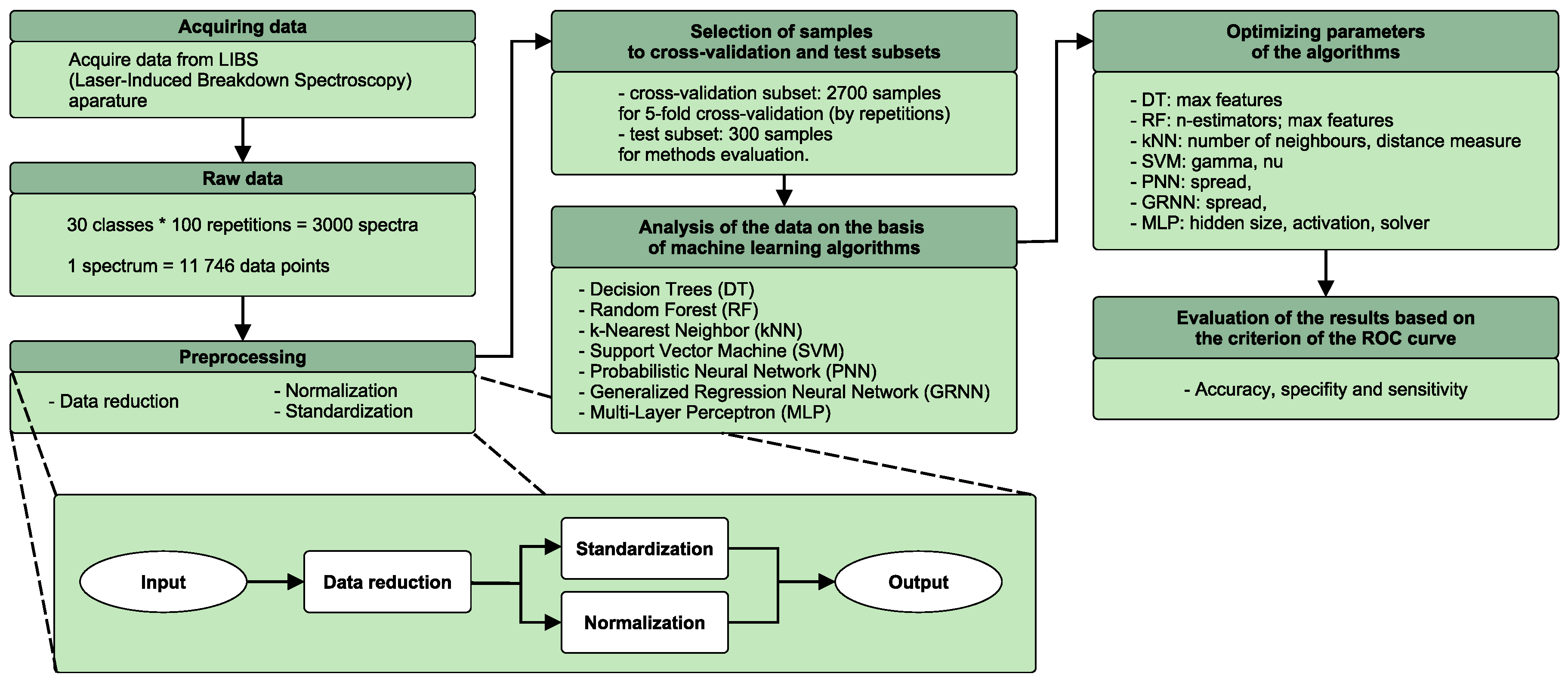
2.4. Data Analysis
- independent preprocessing of LIBS spectra;
- selection of data for the cross validation and testing sets;
- data analysis based on computational intelligence methods;
- evaluation of the results.
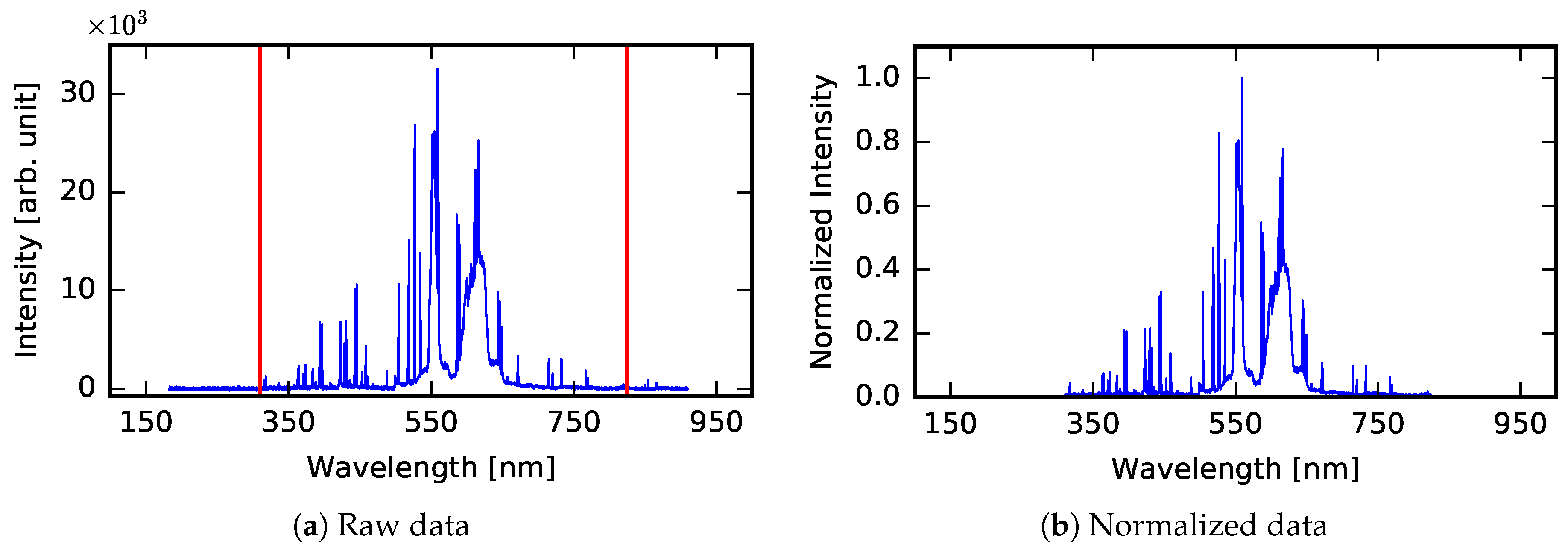
2.4.1. Signal Preprocessing
- data truncation by removing the data points from the beginning (first 3746 data points) and from the end (last 1000 data points) of the LIBS spectrum, which do not contain relevant information (7000 data points are left for further analysis);
- normalization of intensity values to the interval ;
- standardization of intensity values (therefore, the mean value becomes equal to 0 and standard deviation becomes equal to 1).
2.4.2. Cross-Validation
2.4.3. Computational Intelligence Methods
2.4.4. Evaluation Criteria
- D—the number of differentiated pairs, that is the number of pairs correctly identified as belonging to the same class or correctly identified as belonging to different classes;
- N—the number of non-differentiated pairs, ;
- T—the total number of analyzed samples (the total number of possible pairs of samples is equal to ).
3. Results
- Decision trees—the range of the number of features to consider when looking for the best split: from 100 to 7000 with a step equal to 100.
- Random forest—two parameters were optimized during preprocessing. The number of trees in the forest was optimized in range from 10 to 200 with a step of 10 and from 200 to 1000 with a step equal to 50, and the number of features to consider when looking for the best split was optimized in the same range.
- kNN—the number of neighbors was optimized in the range from 1 to 4 and exponent used to calculate the Minkowski distance was optimized from 1 to 10 with a step of 1.
- SVM—the gamma parameter of the RBF kernel function was optimized in a range from 0.01 to 1.00 with a step of 0.01 and the nu parameter of the nu-SVC algorithm, related to the error tolerance of the SVM classification, was optimized in a range from 0.01 to 1.00 with a step of 0.01.
- PNN—the radius (the spread) of the kernel function of the network (standard deviation for the probability density function of the normal distribution). This parameter was optimized in a range from 0.01 to 0.20 with a step equal to 0.01 when normalization in preprocessing was used and from 0.1 to 1.0 with a step of 0.1 when standardization was used.
- GRNN—the spread parameter with an identical meaning and range as in PNN was optimized;
- MLP—the number of neurons was optimized in a range from 10 to 200 with a step equal to 10. The activation function was selected from “identity,” “logistic,” “tanh,” “relu”. The solver for weight optimization was chosen from “lbfgs” (an optimizer in the family of quasi-Newton methods), “sgd” (a stochastic gradient descent), or “adam” (a stochastic gradient-based optimizer proposed in [55]).
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Singh, J.; Thakur, S. Laser-Induced Breakdown Spectroscopy, 1st ed.; Elsevier: London, UK, 2007. [Google Scholar]
- Anabitarte, F.; Cobo, A.; Lopez-Higuera, J.M. Laser-Induced Breakdown Spectroscopy: Fundamentals, Applications, and Challenges. Int. Sch. Res. Not. Spectrosc. 2012, 2012, 285240. [Google Scholar] [CrossRef]
- Hahn, D.W.; Omenetto, N. Laser-induced breakdown spectroscopy (LIBS), part I: Review of basic diagnostics and plasma-particle interactions: Still-challenging issues within the analytical plasma community. Appl. Spectrosc. 2010, 64, 335–366. [Google Scholar] [CrossRef] [PubMed]
- Hahn, D.W.; Omenetto, N. Laser-induced breakdown spectroscopy (LIBS), part II: Review of instrumental and methodological approaches to material analysis and applications to different fields. Appl. Spectrosc. 2012, 66, 347–419. [Google Scholar] [CrossRef] [PubMed]
- Galbács, G. A critical review of recent progress in analytical laser-induced breakdown spectroscopy. Anal. Bioanal. Chem. 2015, 407, 7537–7562. [Google Scholar] [CrossRef] [PubMed]
- Stelmaszczyk, K.; Rohwetter, P.; Méjean, G.; Yu, J.; Salmon, E.; Kasparian, J.; Ackermann, R.; Wolf, J.P.; Wöste, L. Long-distance remote laser-induced breakdown spectroscopy using filamentation in air. Appl. Phys. Lett. 2004, 85, 3977–3979. [Google Scholar] [CrossRef]
- Wiens, R.; Maurice, S. The ChemCam investigation: Compositions at the curiosity rover landing site. In Proceedings of the 2012 GSA Annual Meeting in Charlotte, Charlotte, NC, USA, 7 November 2012; Volume 44, p. 190. [Google Scholar]
- Ramirez-Cedeno, M.; Ortiz-Rivera, W.; Pacheco-Londono, L.; Hernandez-Rivera, S. Remote Detection of Hazardous Liquids Concealed in Glass and Plastic Containers. IEEE Sens. J. 2010, 10, 693–698. [Google Scholar] [CrossRef]
- Noyel, M.; Thomas, P.; Charpentier, P.; Thomas, A.; Brault, T. Implantation of an on-line quality process monitoring. In Proceedings of the 2013 International Conference on Industrial Engineering and Systems Management (IESM), Rabat, Morocco, 28–30 October 2013; pp. 1–6. [Google Scholar]
- Ortiz, R.; Ortiz, P.; Colao, F.; Fantoni, R.; Gómez-Morón, M.; Vázquez, M. Laser spectroscopy and imaging applications for the study of cultural heritage murals. Constr. Build. Mater. 2015, 98, 35–43. [Google Scholar] [CrossRef]
- Rinke-Kneapler, C.; Sigman, M. Applications of laser spectroscopy in forensic science. In Laser Spectroscopy for Sensing; Baudelet, M., Ed.; Woodhead Publishing: Sawston, UK, 2014; pp. 461–495. [Google Scholar]
- Król, M.; Kowalska, D.; Kościelniak, P. Examination of Polish Identity Documents by Laser-Induced Breakdown Spectroscopy. Anal. Lett. 2018, 51, 1592–1604. [Google Scholar] [CrossRef]
- Gaft, M.; Sapir-Sofer, I.; Modiano, H.; Stana, R. Laser induced breakdown spectroscopy for bulk minerals online analyses. Spectrochim. Acta Part B At. Spectrosc. 2007, 62, 1496–1503. [Google Scholar] [CrossRef]
- Anabitarte, F.; Mirapeix, J.; Portilla, O.M.C.; Lopez-Higuera, J.M.; Cobo, A. Sensor for the Detection of Protective Coating Traces on Boron Steel With Aluminium–Silicon Covering by Means of Laser-Induced Breakdown Spectroscopy and Support Vector Machines. IEEE Sens. J. 2012, 12, 64–70. [Google Scholar] [CrossRef]
- Bukin, O.; Proschenko, D.; Chekhlenok, A.; Golik, S.; Bukin, I.; Mayor, A.; Yurchik, V. Laser Spectroscopic Sensors for the Development of Anthropomorphic Robot Sensitivity. Sensors 2018, 18, 1680. [Google Scholar] [CrossRef] [PubMed]
- Moncayo, S.; Manzoor, S.; Navarro-Villoslada, F.; Caceres, J.O. Evaluation of supervised chemometric methods for sample classification by Laser Induced Breakdown Spectroscopy. Chemom. Intell. Lab. Syst. 2015, 146, 354–364. [Google Scholar] [CrossRef]
- Zhang, T.; Xia, D.; Tang, H.; Yang, X.; Li, H. Classification of steel samples by laser-induced breakdown spectroscopy and random forest. Chemom. Intell. Lab. Syst. 2016, 157, 196–201. [Google Scholar] [CrossRef]
- Wang, N.; Wang, X.; Chen, P.; Jia, Z.; Wang, L.; Huang, R.; Lv, Q. Metal Contamination Distribution Detection in High-Voltage Transmission Line Insulators by Laser-induced Breakdown Spectroscopy (LIBS). Sensors 2018, 18, 2623. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Shen, T.; Liu, F.; He, Y. Identification of Coffee Varieties Using Laser-Induced Breakdown Spectroscopy and Chemometrics. Sensors 2018, 18, 95. [Google Scholar] [CrossRef] [PubMed]
- El Haddad, J.; Canioni, L.; Bousquet, B. Good practices in LIBS analysis: Review and advices. Spectrochim. Acta Part B At. Spectrosc. 2014, 101, 171–182. [Google Scholar] [CrossRef]
- Tognoni, E.; Palleschi, V.; Corsi, M.; Cristoforetti, G.; Omenetto, N.; Gornushkin, I.; Smith, B.W.; Winefordner, J.D. Laser-Induced Breakdown Spectroscopy (LIBS): Fundamentals and Applications, from Sample to Signal in LIBS; Cambridge University Press: New York, NY, USA, 2006; p. 122. [Google Scholar]
- Tadeusiewicz, R. Place and Role of Intelligent Systems in Computer Science. Comput. Meth. Mater. Sci. 2010, 10, 193–206. [Google Scholar]
- Pławiak, P.; Sośnicki, T.; Niedźwiecki, M.; Tabor, Z.; Rzecki, K. Hand Body Language Gesture Recognition Based on Signals From Specialized Glove and Machine Learning Algorithms. IEEE Trans. Ind. Inform. 2016, 12, 1104–1113. [Google Scholar] [CrossRef]
- Pławiak, P. An estimation of the state of consumption of a positive displacement pump based on dynamic pressure or vibrations using neural networks. Neurocomputing 2014, 144, 471–483. [Google Scholar] [CrossRef]
- Pławiak, P.; Maziarz, W. Classification of tea specimens using novel hybrid artificial intelligence methods. Sens. Actuators B Chem. 2014, 192, 117–125. [Google Scholar] [CrossRef]
- Rzecki, K.; Pławiak, P.; Niedźwiecki, M.; Sośnicki, T.; Leśkow, J.; Ciesielski, M. Person recognition based on touch screen gestures using computational intelligence methods. Inf. Sci. 2017, 415–416, 70–84. [Google Scholar] [CrossRef]
- Pławiak, P.; Tadeusiewicz, R. Approximation of phenol concentration using novel hybrid computational intelligence methods. Int. J. Appl. Math. Comput. Sci. 2014, 24, 165–181. [Google Scholar] [CrossRef]
- Pławiak, P.; Rzecki, K. Approximation of Phenol Concentration Using Computational Intelligence Methods Based on Signals From the Metal-Oxide Sensor Array. IEEE Sens. J. 2015, 15, 1770–1783. [Google Scholar] [CrossRef]
- Pławiak, P. Novel methodology of cardiac health recognition based on ECG signals and evolutionary-neural system. Expert Syst. Appl. 2018, 92, 334–349. [Google Scholar] [CrossRef]
- Pławiak, P. Novel genetic ensembles of classifiers applied to myocardium dysfunction recognition based on ECG signals. Swarm Evol. Comput. 2018, 39, 192–208. [Google Scholar] [CrossRef]
- Abdar, M.; Zomorodi-Moghadam, M.; Das, R.; Ting, I.H. Performance analysis of classification algorithms on early detection of liver disease. Expert Syst. Appl. 2017, 67, 239–251. [Google Scholar] [CrossRef]
- Trejos, T.; Flores, A.; Almirall, J.R. Micro-spectrochemical analysis of document paper and gel inks by laser ablation inductively coupled plasma mass spectrometry and laser induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2010, 65, 884–895. [Google Scholar] [CrossRef]
- Kula, A.; Wietecha-Posłuszny, R.; Pasionek, K.; Król, M.; Woźniakiewicz, M.; Kościelniak, P. Application of laser induced breakdown spectroscopy to examination of writing inks for forensic purposes. Sci. Justice 2014, 54, 118–125. [Google Scholar] [CrossRef] [PubMed]
- Elsherbiny, N.; Nassef, O.A. Wavelength dependence of laser induced breakdown spectroscopy (LIBS) on questioned document investigation. Sci. Justice 2015, 55, 254–263. [Google Scholar] [CrossRef] [PubMed]
- Lennard, C.; El-Deftar, M.M.; Robertson, J. Forensic application of laser-induced breakdown spectroscopy for the discrimination of questioned documents. Forensic Sci. Int. 2015, 254, 68–79. [Google Scholar] [CrossRef] [PubMed]
- Hoehse, M.; Paul, A.; Gornushkin, I.; Panne, U. Multivariate classification of pigments and inks using combined Raman spectroscopy and LIBS. Anal. Bioanal. Chem. 2011, 402, 1443–1450. [Google Scholar] [CrossRef] [PubMed]
- Metzinger, A.; Rajkó, R.; Galbács, G. Discrimination of paper and print types based on their laser induced breakdown spectra. Spectrochim. Acta Part B At. Spectrosc. 2014, 94–95, 48–57. [Google Scholar] [CrossRef]
- Team of Science and Industrial Intelligent Applications. Available online: http://siia.iti.pk.edu.pl/ (accessed on 27 October 2018).
- Zieliński, T.P. Digital Signal Processing: From Theory to Applications; WK: Warsaw, Poland, 2005. [Google Scholar]
- Simple Intuitive Language for Experiment Modeling. Available online: http://silem.iti.pk.edu.pl (accessed on 27 October 2018).
- Murphy, K.P. Machine Learning: A Probabilistic Perspective, 1st ed.; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Specht, D.F. Probabilistic neural networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Hinton, G.E. Connectionist Learning Procedures. Artif. Intell. 1989, 40, 185–234. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: Berlin, Germany, 2014. [Google Scholar]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Sugeno, M. Industrial Applications of Fuzzy Control; Elsevier: London, UK, 1985. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Trejos, T.; Corzo, R.; Subedi, K.; Almirall, J. Characterization of toners and inkjets by laser ablation spectrochemical methods and Scanning Electron Microscopy-Energy Dispersive X-ray Spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2014, 92, 9–22. [Google Scholar] [CrossRef]
- Aitken, C. Statistical and the Evaluation of Evidence for Forensic Scientists; John Wiley & Sons: Chichester, UK, 1995. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Chui, C.K. An Introduction to Wavelets; Academic Press Professional, Inc.: San Diego, CA, USA, 1992. [Google Scholar]
- Pořízka, P.; Klus, J.; Képeš, E.; Prochazka, D.; Hahn, D.W.; Kaiser, J. On the utilization of principal component analysis in laser-induced breakdown spectroscopy data analysis, a review. Spectrochim. Acta 2018, 148, 65–82. [Google Scholar] [CrossRef]
Sample Availability: LIBS spectra used in this study are available on the webpage: http://libs.iti.pk.edu.pl/. |
| Pens | Papers | |||||
|---|---|---|---|---|---|---|
| Company/Model | ID | A | D | L | N | O |
| Lack | – | A | D | L | N | O |
| Bic | B | A + B | D + B | L + B | N + B | O + B |
| Rystor | R | A + R | D + R | L+R | N + R | O + R |
| Staedtler/Stick | S | A + S | D + S | L + S | N + S | O + S |
| Staedtler/Ball | SB | A + SB | D + SB | L + SB | N + SB | O + SB |
| Toma | T | A + T | D + T | L + T | N + T | O + T |
| Paper Class | Identified Elements |
|---|---|
| A | Ca, Mg, Na, K |
| D | Ca, Na, K |
| L | Ca, Ti, Al, Si, Na, K |
| N | Ca, Ti, Si, Mg, Fe, Na, K |
| O | Ca, Al, Si, Mg, Na, K |
| Ink sample | |
| B | Cr, Cu, Zn, Pb, La |
| R | Cr, Cu, Zn, Pb, Ni, Mn |
| S | Cr, Cu, Zn |
| SB | Cr, Cu, Zn, Pb |
| T | Cr |
| No. | Method | Configuration |
|---|---|---|
| 1 | Decision Trees | Criterion: gini, splitter type: best, maximum depth: none |
| 2 | Random Forest | Criterion: gini, maximum depth: none |
| 3 | kNN | Distance metric: Minkowski |
| 4 | SVM | Type: nuSVC, type of kernel function: radial basis function |
| 5 | Neural Network | Type: PNN |
| 6 | Neural Network | Type: GRNN |
| 7 | Neural Network | Type: MLP |
| Method | Parameters | ACC (%) | SEN (%) | SPE (%) | MEAN (%) | (%) | DP (%) |
|---|---|---|---|---|---|---|---|
| Decision Trees | Max features = 6100 | 98.08 | 71.13 | 99.00 | 89.40 | 70.14 | 98.40 |
| Random Forest | N estimators = 700 Max features = 950 | 99.08 | 86.27 | 99.53 | 94.96 | 85.79 | 99.08 |
| kNN | N = 1 Exponent = 1.00 | 96.72 | 50.87 | 98.31 | 81.97 | 49.17 | 96.72 |
| SVM | Nu = 0.17 Gamma = 0.03 | 98.84 | 82.53 | 99.40 | 93.59 | 81.93 | 98.85 |
| PNN | Spread = 0.2 | 96.84 | 52.60 | 98.37 | 82.60 | 50.97 | 97.80 |
| GRNN | Spread = 0.5 | 96.27 | 44.00 | 98.07 | 79.45 | 42.07 | 95.58 |
| MLP | N. of neurons = 120 | 98.22 | 73.27 | 99.08 | 90.19 | 72.34 | 98.36 |
| Standardization Decision Tree | Standardization Random Forest | Standardization kNN | Normalization SVM | Normalization PNN | Standardization GRNN | Standardization MLP | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | ACC(%) | SPE(%) | SEN(%) | ACC(%) | SPE(%) | SEN(%) | ACC(%) | SPE(%) | SEN(%) | ACC(%) | SPE(%) | SEN(%) | ACC(%) | SPE(%) | SEN(%) | ACC(%) | SPE(%) | SEN(%) | ACC(%) | SPE(%) | SEN(%) |
| A | 99.20 | 99.45 | 92.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 99.40 | 99.38 | 100.00 | 99.73 | 99.72 | 100.00 | 99.93 | 99.93 | 100.00 |
| A + B | 98.60 | 99.45 | 74.00 | 99.33 | 100.00 | 80.00 | 97.53 | 98.97 | 56.00 | 99.27 | 99.86 | 82.00 | 97.40 | 99.17 | 46.00 | 98.53 | 99.59 | 68.00 | 98.60 | 99.59 | 70.00 |
| A + R | 97.93 | 99.24 | 60.00 | 99.40 | 99.72 | 90.00 | 97.87 | 99.66 | 46.00 | 99.33 | 100.00 | 80.00 | 97.40 | 99.38 | 40.00 | 98.27 | 99.45 | 64.00 | 97.87 | 98.83 | 70.00 |
| A + S | 96.60 | 97.93 | 58.00 | 99.40 | 99.72 | 90.00 | 96.80 | 97.86 | 66.00 | 99.33 | 99.72 | 88.00 | 96.47 | 98.69 | 32.00 | 97.27 | 98.07 | 74.00 | 96.87 | 97.86 | 68.00 |
| A + SB | 96.40 | 97.93 | 52.00 | 98.67 | 98.90 | 92.00 | 97.20 | 98.14 | 70.00 | 98.60 | 98.83 | 92.00 | 95.27 | 95.93 | 76.00 | 97.47 | 98.90 | 56.00 | 96.80 | 98.69 | 42.00 |
| A + T | 98.80 | 99.72 | 72.00 | 100.00 | 100.00 | 100.00 | 99.67 | 99.72 | 98.00 | 99.60 | 99.59 | 100.00 | 98.33 | 99.31 | 70.00 | 99.27 | 99.38 | 96.00 | 99.67 | 99.72 | 98.00 |
| D | 99.80 | 99.79 | 100.00 | 100.00 | 100.00 | 100.00 | 98.60 | 98.55 | 100.00 | 99.87 | 99.93 | 98.00 | 98.47 | 98.76 | 90.00 | 99.33 | 99.31 | 100.00 | 99.87 | 99.86 | 100.00 |
| D + B | 98.07 | 99.03 | 70.00 | 99.33 | 99.72 | 88.00 | 95.80 | 98.48 | 18.00 | 98.47 | 99.59 | 66.00 | 95.67 | 98.28 | 20.00 | 96.27 | 99.31 | 8.00 | 95.73 | 98.28 | 22.00 |
| D + R | 98.40 | 99.17 | 76.00 | 99.93 | 99.93 | 100.00 | 97.80 | 99.79 | 40.00 | 99.73 | 99.72 | 100.00 | 96.67 | 98.28 | 50.00 | 98.20 | 99.31 | 66.00 | 97.93 | 99.52 | 52.00 |
| D + S | 98.53 | 99.17 | 80.00 | 99.53 | 100.00 | 86.00 | 96.40 | 97.17 | 74.00 | 99.53 | 99.86 | 90.00 | 95.40 | 97.66 | 30.00 | 97.13 | 97.66 | 82.00 | 95.60 | 97.10 | 52.00 |
| D + SB | 96.67 | 98.21 | 52.00 | 98.80 | 99.59 | 76.00 | 96.07 | 98.14 | 36.00 | 97.73 | 98.76 | 68.00 | 94.60 | 97.31 | 16.00 | 97.40 | 98.55 | 64.00 | 95.73 | 97.86 | 34.00 |
| D + T | 99.13 | 99.59 | 86.00 | 99.07 | 99.03 | 100.00 | 98.40 | 99.10 | 78.00 | 99.20 | 99.31 | 96.00 | 97.20 | 98.34 | 64.00 | 98.33 | 98.97 | 80.00 | 99.00 | 99.10 | 96.00 |
| L | 99.40 | 99.45 | 98.00 | 99.53 | 99.52 | 100.00 | 96.27 | 96.14 | 100.00 | 100.00 | 100.00 | 100.00 | 98.80 | 98.76 | 100.00 | 94.67 | 94.48 | 100.00 | 100.00 | 100.00 | 100.00 |
| L + B | 98.07 | 99.24 | 64.00 | 99.87 | 99.93 | 98.00 | 96.47 | 99.38 | 12.00 | 99.27 | 99.59 | 90.00 | 95.87 | 97.59 | 46.00 | 96.33 | 99.59 | 2.00 | 98.47 | 99.59 | 66.00 |
| L + R | 97.73 | 99.45 | 48.00 | 98.47 | 99.93 | 56.00 | 96.80 | 99.45 | 20.00 | 98.20 | 99.24 | 68.00 | 96.87 | 98.90 | 38.00 | 96.33 | 99.59 | 2.00 | 97.93 | 99.72 | 46.00 |
| L + S | 96.00 | 98.07 | 36.00 | 97.20 | 99.17 | 40.00 | 96.00 | 98.97 | 10.00 | 97.47 | 99.59 | 36.00 | 95.80 | 98.48 | 18.00 | 96.47 | 99.45 | 10.00 | 96.73 | 98.07 | 58.00 |
| L + SB | 95.67 | 96.55 | 70.00 | 96.67 | 97.10 | 84.00 | 91.53 | 93.45 | 36.00 | 97.00 | 97.52 | 82.00 | 94.87 | 96.34 | 52.00 | 91.20 | 92.97 | 40.00 | 97.27 | 97.66 | 86.00 |
| L + T | 98.07 | 99.45 | 58.00 | 99.20 | 99.66 | 86.00 | 96.00 | 98.69 | 18.00 | 99.53 | 99.66 | 96.00 | 97.93 | 99.66 | 48.00 | 95.27 | 98.55 | 0.00 | 99.60 | 99.79 | 94.00 |
| N | 99.87 | 99.93 | 98.00 | 100.00 | 100.00 | 100.00 | 99.07 | 99.03 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 98.33 | 98.28 | 100.00 | 100.00 | 100.00 | 100.00 |
| N + B | 98.33 | 99.66 | 60.00 | 98.73 | 99.59 | 74.00 | 96.93 | 99.24 | 30.00 | 99.67 | 100.00 | 90.00 | 97.47 | 98.62 | 64.00 | 95.67 | 98.90 | 2.00 | 98.80 | 99.66 | 74.00 |
| N + R | 98.40 | 99.59 | 64.00 | 99.53 | 100.00 | 86.00 | 95.67 | 98.97 | 0.00 | 97.67 | 99.45 | 46.00 | 95.33 | 97.86 | 22.00 | 95.60 | 98.90 | 0.00 | 98.13 | 99.59 | 56.00 |
| N + S | 97.60 | 98.55 | 70.00 | 99.27 | 99.93 | 80.00 | 97.60 | 99.52 | 42.00 | 98.13 | 99.45 | 60.00 | 95.80 | 98.34 | 22.00 | 96.87 | 99.72 | 14.00 | 98.47 | 99.17 | 78.00 |
| N + SB | 96.33 | 97.59 | 60.00 | 97.33 | 98.00 | 78.00 | 92.47 | 93.93 | 50.00 | 96.53 | 96.97 | 84.00 | 94.47 | 96.76 | 28.00 | 88.53 | 90.14 | 42.00 | 96.73 | 97.52 | 74.00 |
| N + T | 99.33 | 99.45 | 96.00 | 99.67 | 99.66 | 100.00 | 99.07 | 99.38 | 90.00 | 100.00 | 100.00 | 100.00 | 99.07 | 99.17 | 96.00 | 96.60 | 99.38 | 16.00 | 100.00 | 100.00 | 100.00 |
| O | 99.20 | 99.31 | 96.00 | 100.00 | 100.00 | 100.00 | 99.93 | 99.93 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 99.87 | 99.86 | 100.00 | 100.00 | 100.00 | 100.00 |
| O + B | 96.73 | 98.90 | 34.00 | 97.53 | 99.93 | 28.00 | 96.60 | 99.93 | 0.00 | 98.00 | 99.86 | 44.00 | 97.20 | 99.38 | 34.00 | 96.33 | 99.66 | 0.00 | 97.80 | 100.00 | 34.00 |
| O + R | 99.47 | 99.86 | 88.00 | 99.67 | 100.00 | 90.00 | 96.60 | 99.93 | 0.00 | 98.93 | 99.86 | 72.00 | 96.53 | 98.90 | 28.00 | 96.27 | 99.59 | 0.00 | 99.00 | 100.00 | 70.00 |
| O + S | 98.73 | 99.45 | 78.00 | 99.47 | 99.86 | 88.00 | 96.27 | 99.45 | 4.00 | 98.07 | 99.24 | 64.00 | 95.27 | 98.00 | 16.00 | 96.33 | 99.66 | 0.00 | 98.20 | 98.83 | 80.00 |
| O + SB | 95.87 | 97.31 | 54.00 | 96.93 | 96.90 | 98.00 | 87.93 | 89.45 | 44.00 | 96.00 | 96.41 | 84.00 | 92.87 | 94.90 | 34.00 | 84.67 | 86.55 | 30.00 | 96.13 | 96.76 | 78.00 |
| O + T | 99.33 | 99.66 | 90.00 | 100.00 | 100.00 | 100.00 | 98.40 | 98.76 | 88.00 | 99.93 | 99.93 | 100.00 | 98.80 | 98.83 | 98.00 | 95.47 | 98.62 | 4.00 | 99.67 | 99.66 | 100.00 |
| Mean | 98.08 | 99.00 | 71.13 | 99.08 | 99.53 | 86.27 | 96.72 | 98.31 | 50.87 | 98.84 | 99.40 | 82.53 | 96.84 | 98.37 | 52.60 | 96.27 | 98.07 | 44.00 | 98.22 | 99.08 | 73.27 |
| Kappa | 70.14 | 85.79 | 49.17 | 81.93 | 50.97 | 42.07 | 72.34 | ||||||||||||||
| DP | 98.40 | 99.08 | 96.72 | 98.85 | 97.80 | 95.58 | 98.36 | ||||||||||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rzecki, K.; Sośnicki, T.; Baran, M.; Niedźwiecki, M.; Król, M.; Łojewski, T.; Acharya, U.R.; Yildirim, Ö.; Pławiak, P. Application of Computational Intelligence Methods for the Automated Identification of Paper-Ink Samples Based on LIBS. Sensors 2018, 18, 3670. https://doi.org/10.3390/s18113670
Rzecki K, Sośnicki T, Baran M, Niedźwiecki M, Król M, Łojewski T, Acharya UR, Yildirim Ö, Pławiak P. Application of Computational Intelligence Methods for the Automated Identification of Paper-Ink Samples Based on LIBS. Sensors. 2018; 18(11):3670. https://doi.org/10.3390/s18113670
Chicago/Turabian StyleRzecki, Krzysztof, Tomasz Sośnicki, Mateusz Baran, Michał Niedźwiecki, Małgorzata Król, Tomasz Łojewski, U Rajendra Acharya, Özal Yildirim, and Paweł Pławiak. 2018. "Application of Computational Intelligence Methods for the Automated Identification of Paper-Ink Samples Based on LIBS" Sensors 18, no. 11: 3670. https://doi.org/10.3390/s18113670
APA StyleRzecki, K., Sośnicki, T., Baran, M., Niedźwiecki, M., Król, M., Łojewski, T., Acharya, U. R., Yildirim, Ö., & Pławiak, P. (2018). Application of Computational Intelligence Methods for the Automated Identification of Paper-Ink Samples Based on LIBS. Sensors, 18(11), 3670. https://doi.org/10.3390/s18113670







