A Novel Method and an Equipment for Generating the Standard Moisture in Gas Flowing through a Pipe
Abstract
1. Introduction
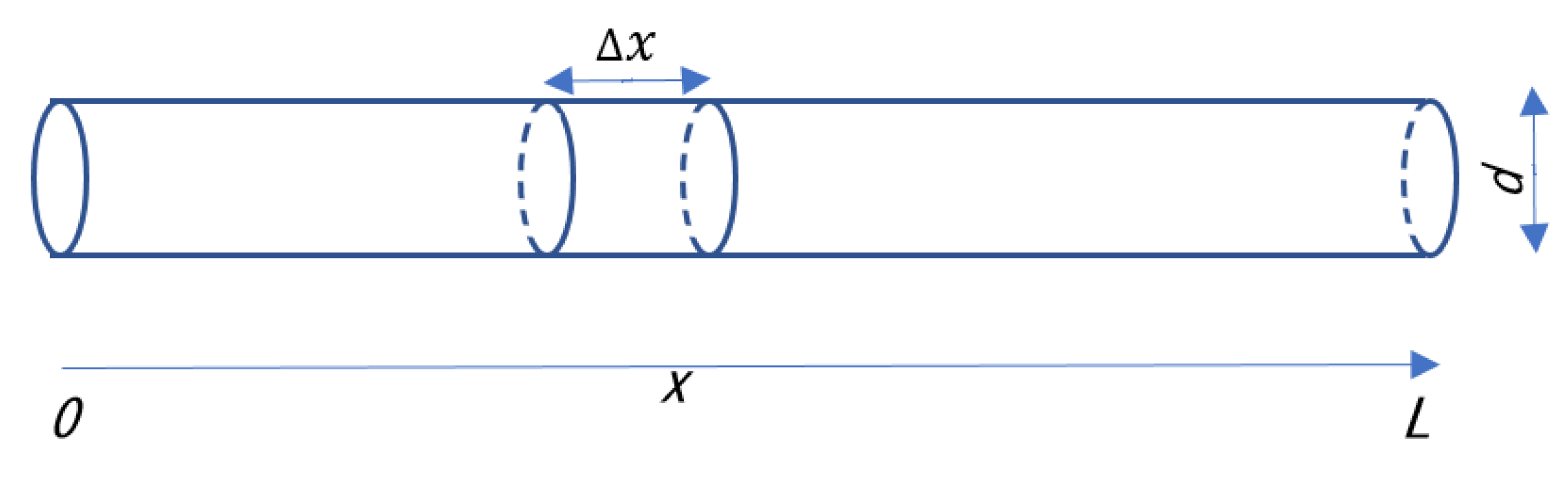
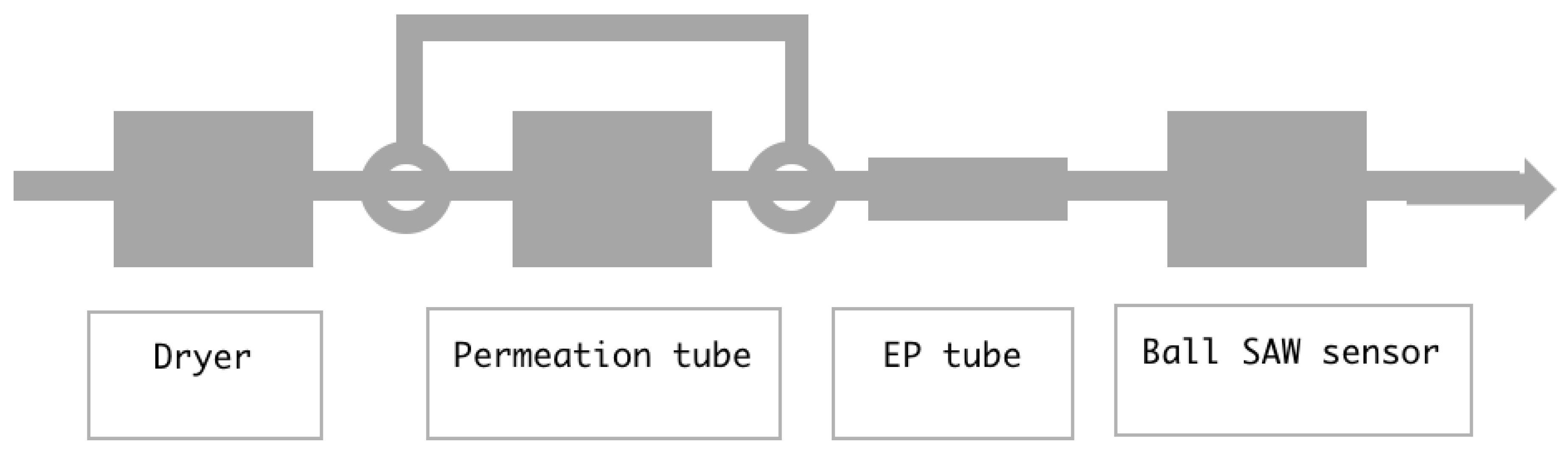
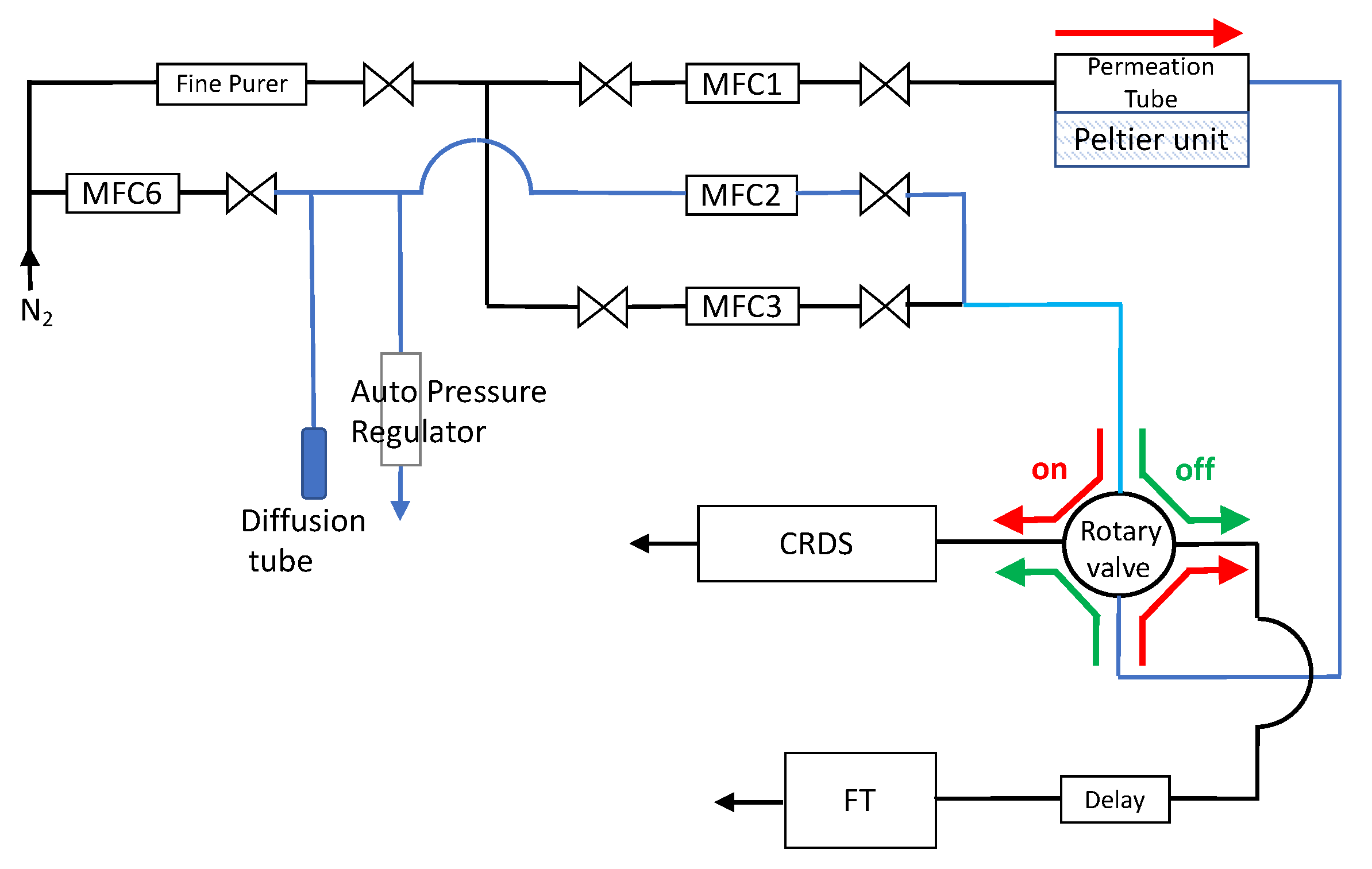
2. Moisture in a Gas Flowing through a Pipe
3. Theoretical Analysis
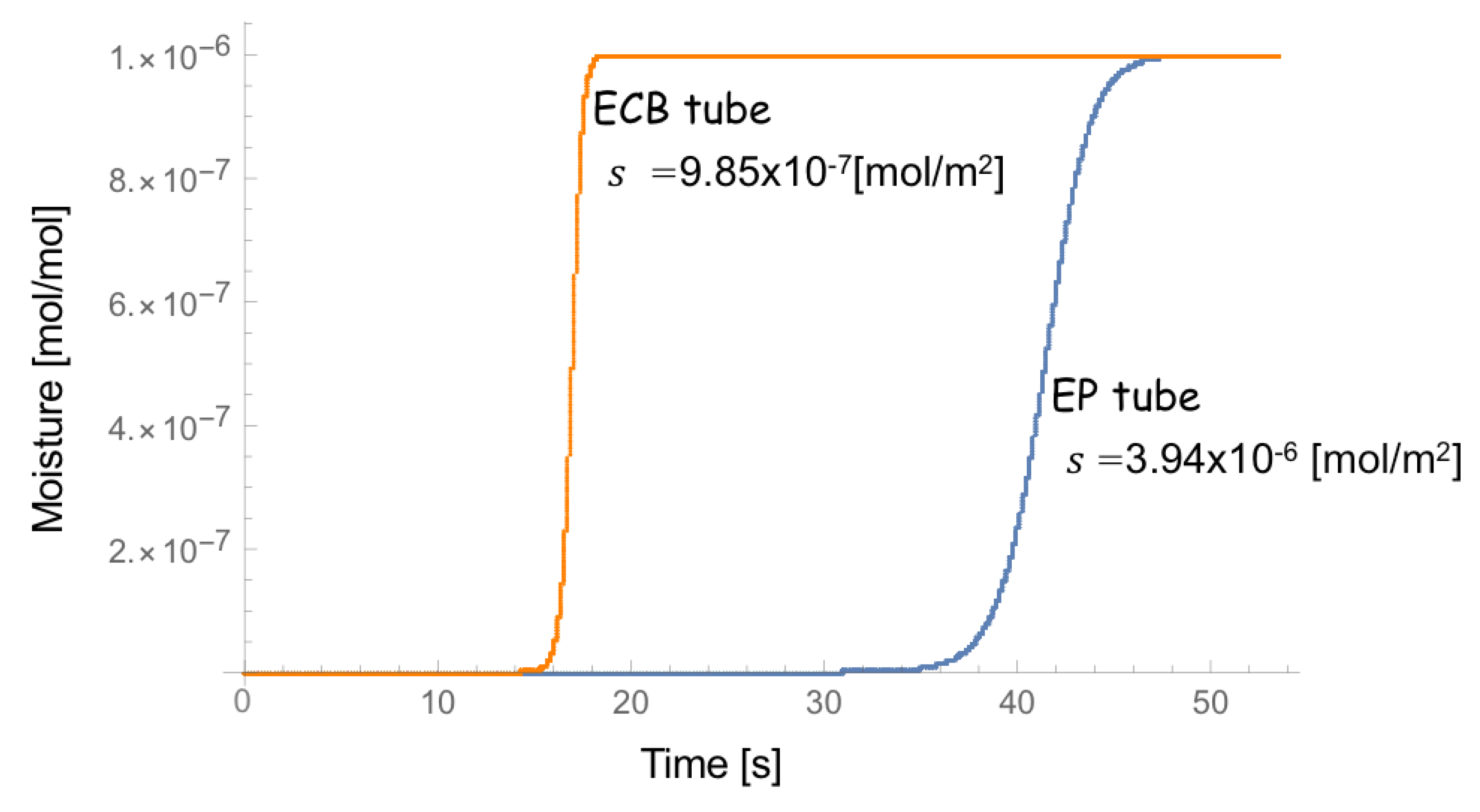
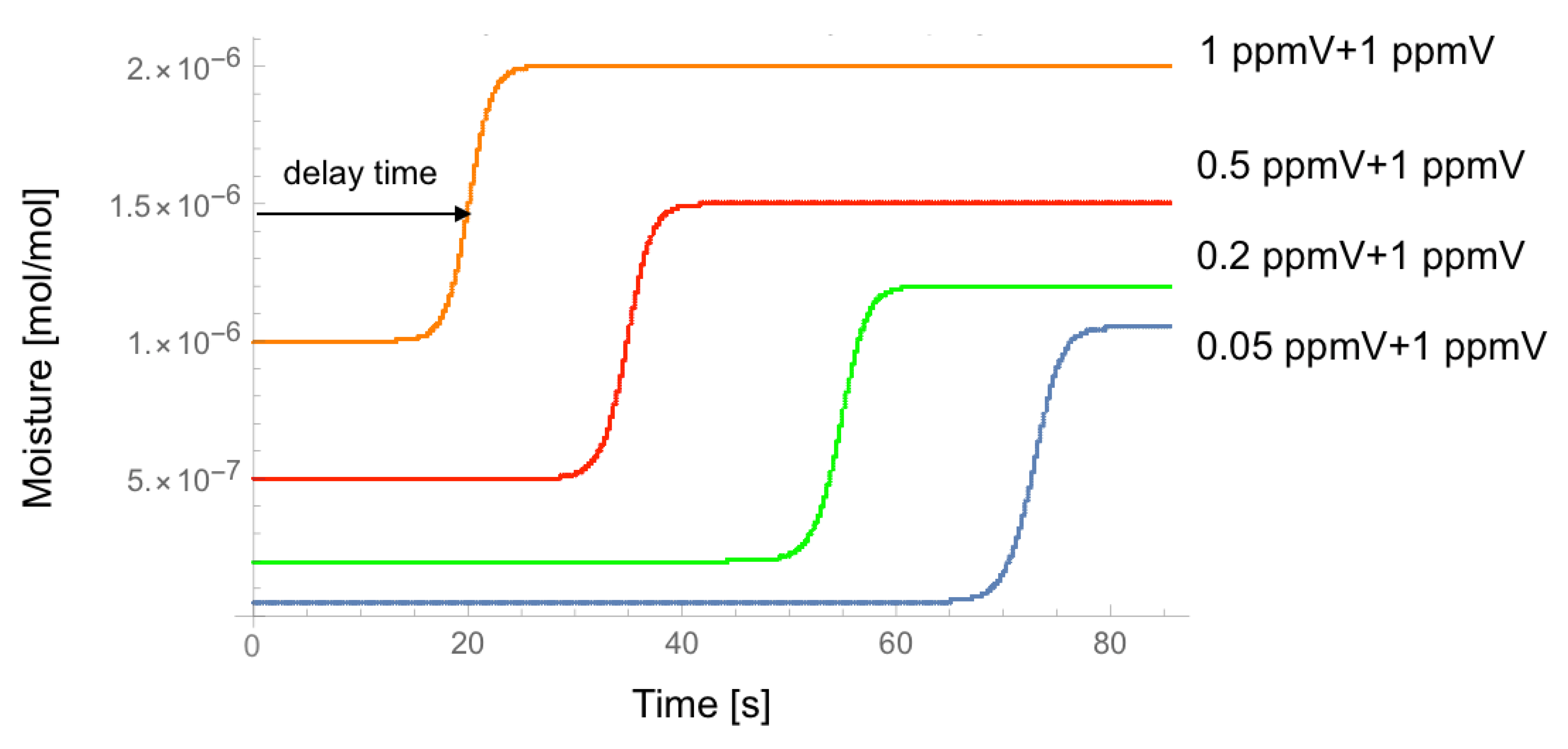
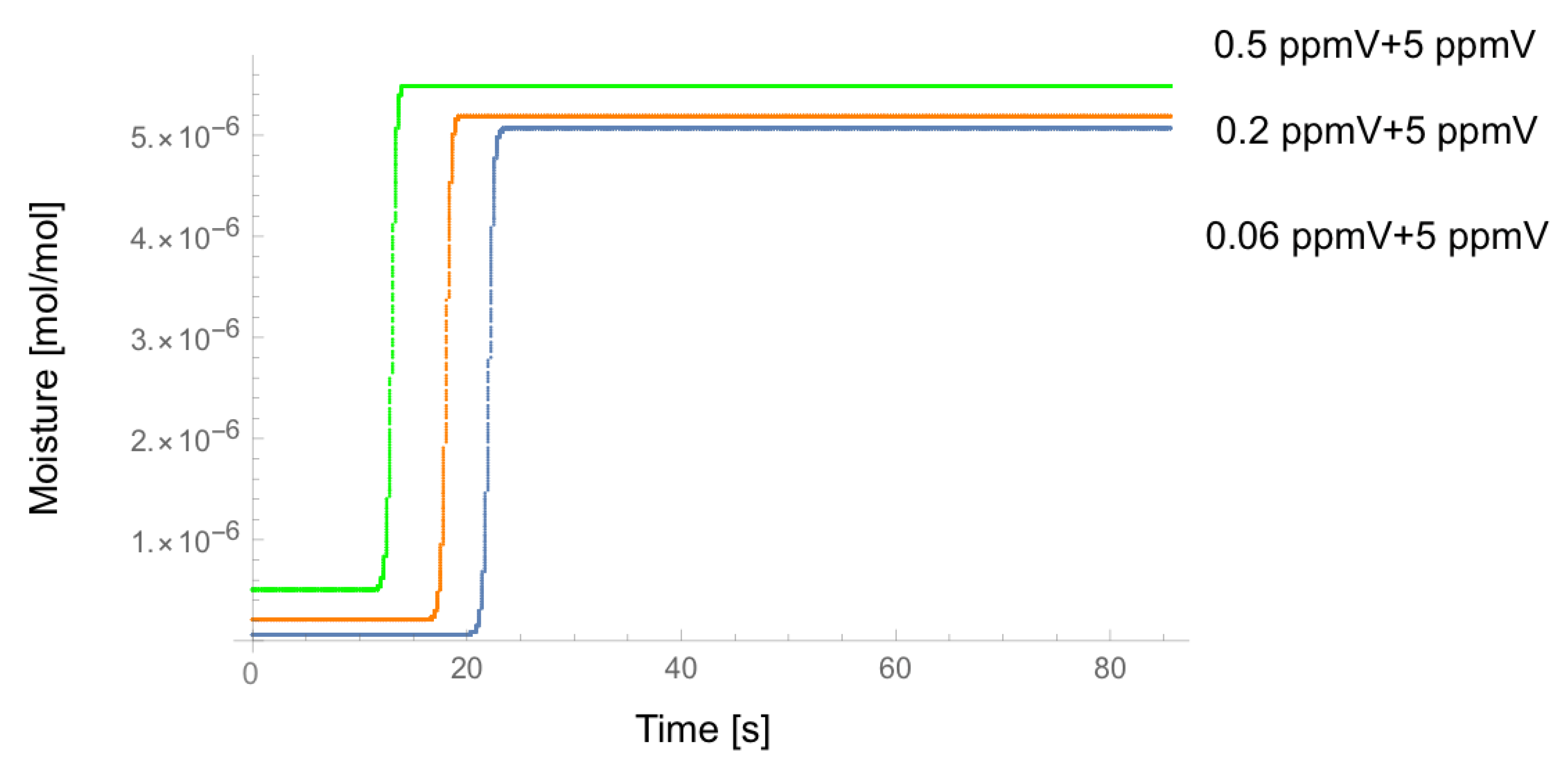
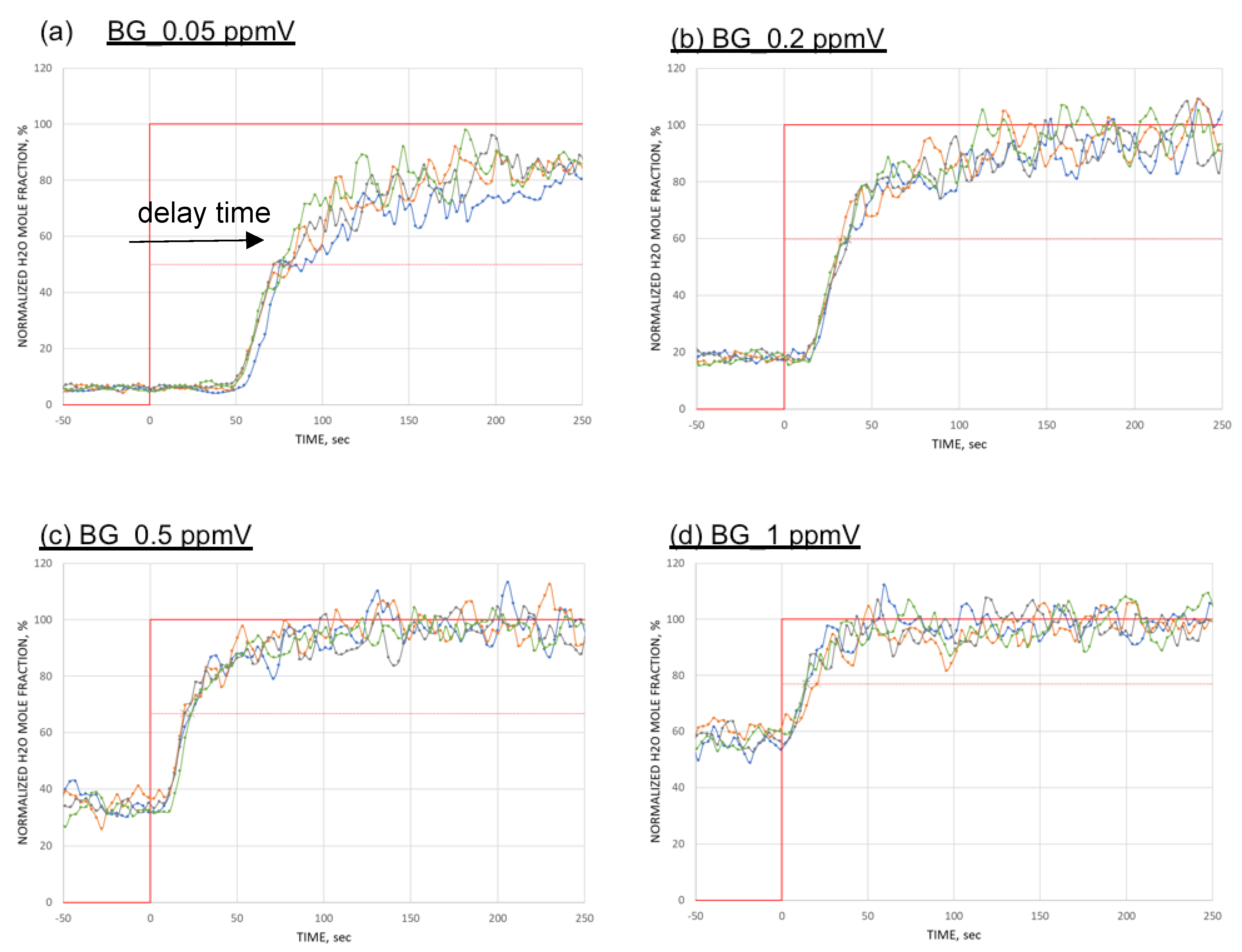
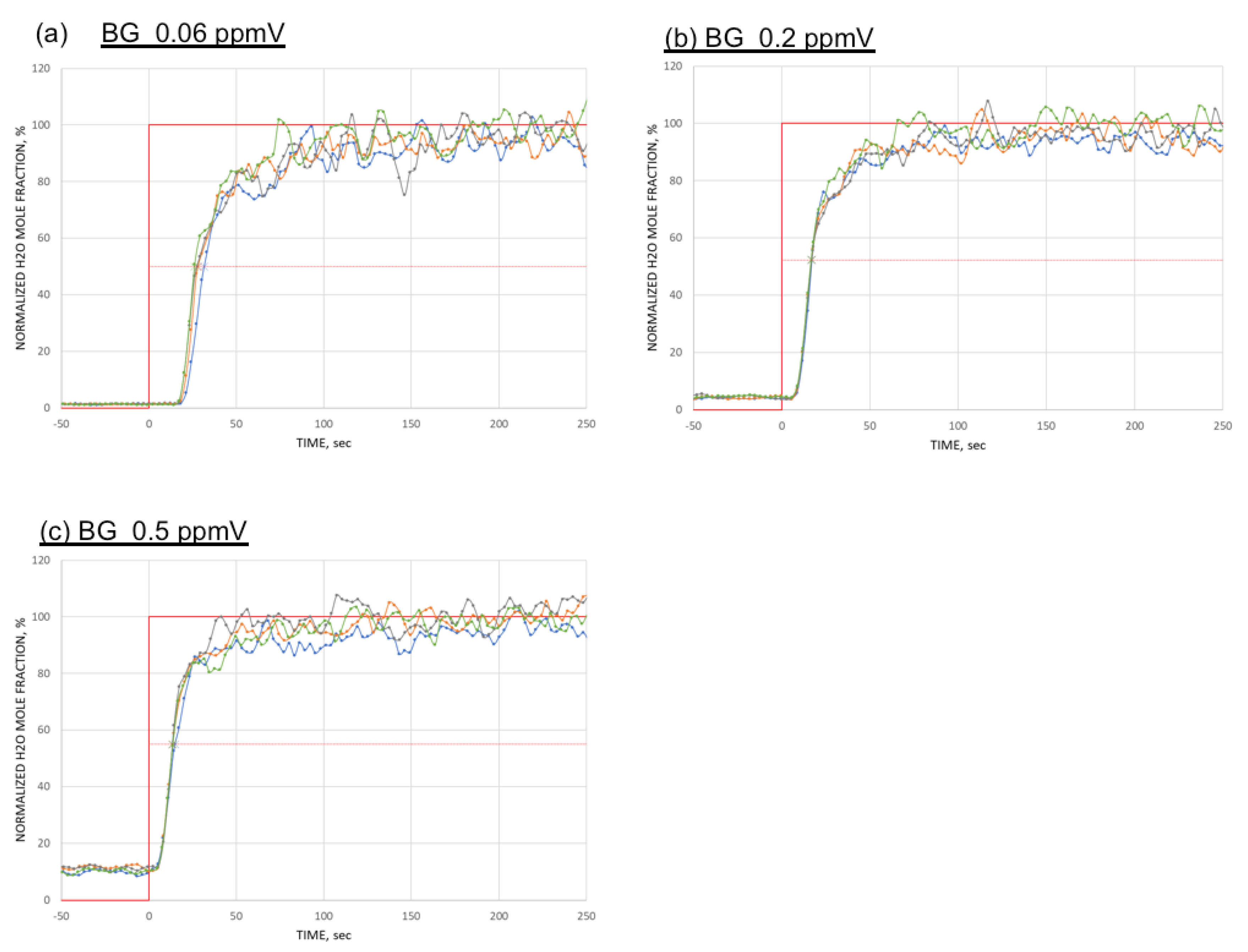
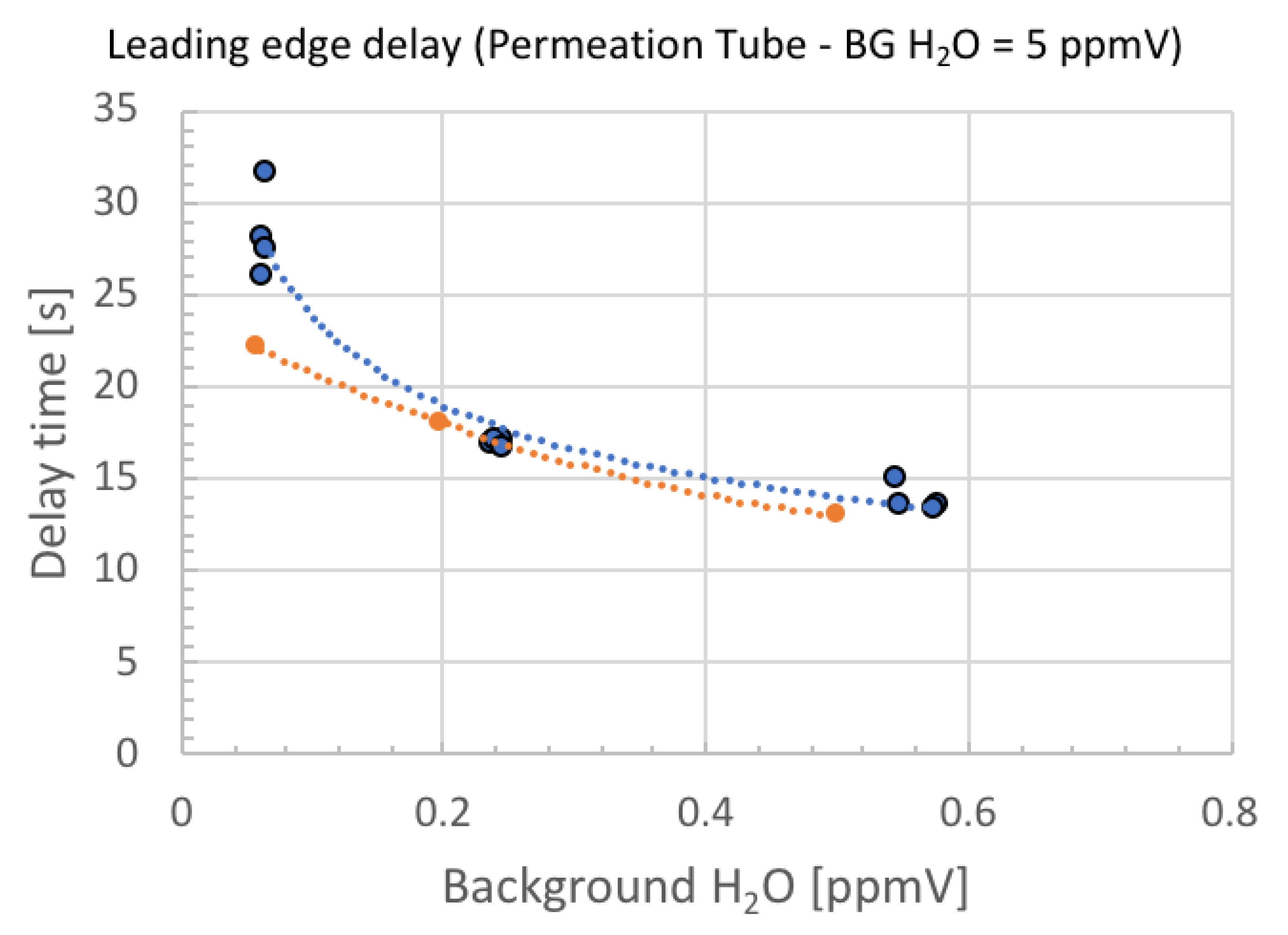
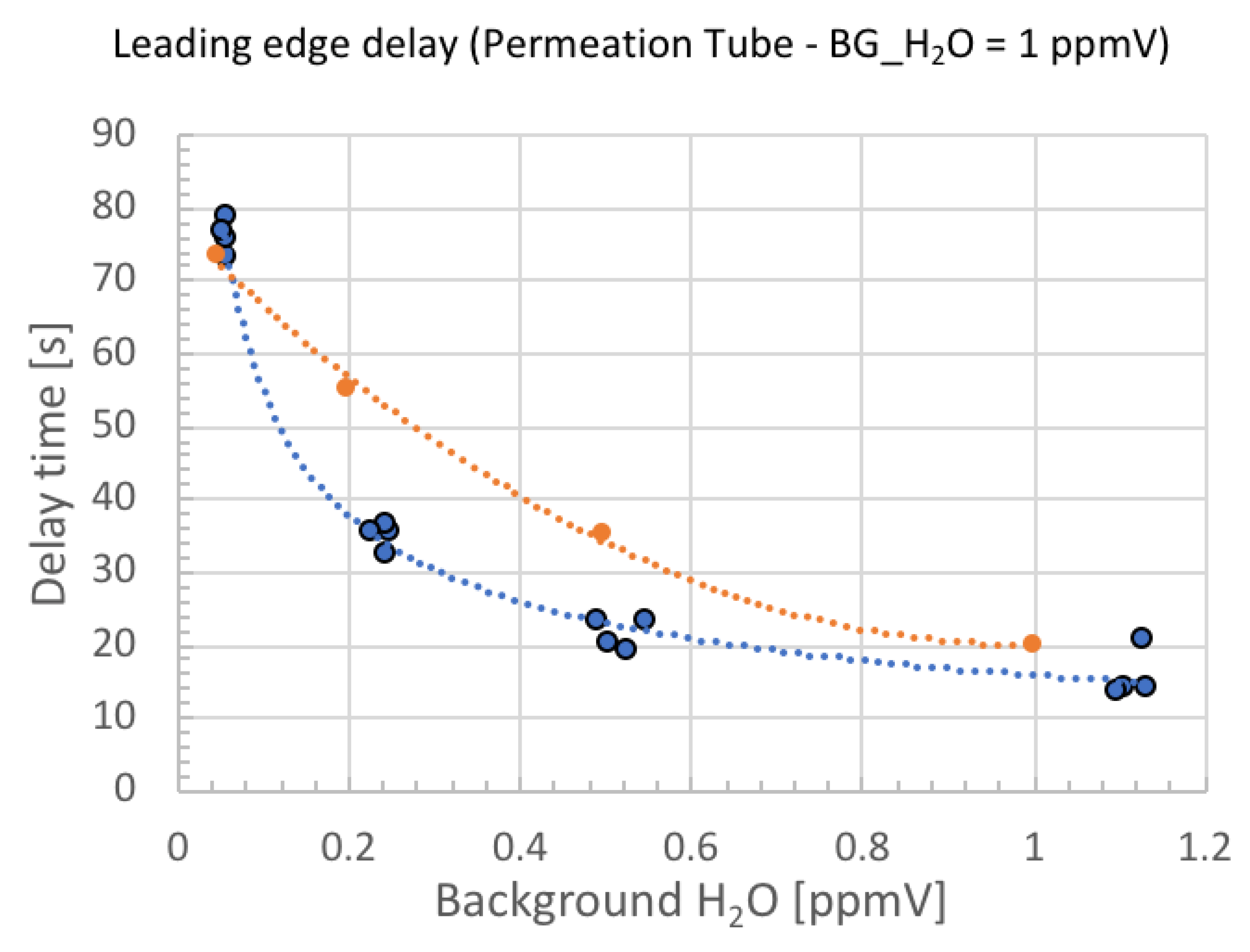
4. Result
5. Discussion
Author Contributions
Conflicts of Interest
Appendix A
References
- Funke, H.H.; Grissom, B.L.; McGrew, C.E.; Raynor, M.W. Techniques for the measurement of trace moisture in high-purity electronic specialty gases. Rev. Sci. Instrum. 2003, 74, 3909. [Google Scholar] [CrossRef]
- Cecil, O.B. Aluminum oxide humidity sensor. U.S. Patent 3,440,372, 22 April 1969. [Google Scholar]
- Zhou, X.; Liu, X.; Jeffries, J.B.; Hanson, R.K. Development of a sensor for temperature and water concentration in combustion gases using a single tunable diode laser. Meas. Sci. Technol. 2003, 14, 1459. [Google Scholar] [CrossRef]
- Demtroeder, W. Laser Spectroscopy, 4th ed.; Springer: Berlin, Germany, 2008; p. 22. [Google Scholar]
- Takeda, N.; Motozawa, M. Extremely Fast 1 μmol·mol−1 Water-Vapor Measurement by a 1 mm Diameter Spherical SAW Device. Int. J. Thermophys. 2012, 33, 1642. [Google Scholar] [CrossRef]
- Tsuji, T.; Oizumi, T.; Takeda, N.; Akao, S.; Tsukahara, Y.; Yamanaka, K. Temperature compensation of ball surface acoustic wave sensor by two-frequency measurement using undersampling. Jpn. J. Appl. Phys. 2015, 54, 07HD13. [Google Scholar] [CrossRef]
- Abe, H.; Yamada, K.M.T. Performance evaluation of a trace-moisture analyzer based on cavity ring-down spectroscopy: Direct comparison with the NMIJ trace-moisture standard. Sens. Actuators A Phys. 2011, 165, 230. [Google Scholar] [CrossRef]
- McKeogh, G.; Sparages, N.J.D. 16-McKeogh-1. In Proceedings of the GAS2017, Rotterdam, The Netherlands, 13 June 2017. [Google Scholar]
- Abe, H.; Kitano, H. Development of humidity standard in trace-moisture region: Characteristics of humidity generation of diffusion tube humidity generator. Sens. Actuators A Phys. 2006, 128, 202. [Google Scholar] [CrossRef]
- Stevens, M.; Bell, S.A. The NPL standard humidity generator: an analysis of uncertainty by validation of individual component performance. Meas. Sci. Technol. 1992, 3, 943. [Google Scholar] [CrossRef]
- O’Keeffe, A.E.; Ortman, G.C. Primary standards for trace gas analysis. Anal. Chem. 1966, 38, 760. [Google Scholar] [CrossRef]
- Ohmi, T. Ultra clean processing. Microeclectr. Eng. 1991, 10, 163. [Google Scholar] [CrossRef]
- Ohmi, T.; Nakagawa, Y.; Nakamura, M.; Ohki, A.; Koyama, T. Formation of chromium oxide on 316L austenitic stainless steel. J. Vac. Sci. Technol. A 1996, 14, 2505. [Google Scholar] [CrossRef]
- Tsuji, T.; Akao, S.; Oizumi, T.; Takeda, N.; Tsukahara, Y.; Yamanaka, K. Moisture adsorption desorption characteristics of stainless steel tubing measured by ball surface acoustic wave trace moisture analyzer. Jpn. J. Appl Phys. 2017, 56, 07JC03. [Google Scholar] [CrossRef]
- Jaulmes, A.; Vidal-Madjar, C.; Ladurelli, A.; Guiochon, G. Study of peak profiles in nonlinear gas chromatography. 1. Derivation of a theoretical model. J. Phys. Chem. 1984, 88, 5379. [Google Scholar] [CrossRef]
- Jaulmes, A.; Vidal-Madjar, C.; Ladurelli, A.; Guiochon, G. Study of peak profiles in nonlinear gas chromatography. 2. Determination of the curvature of isotherms at zero surface coverage on graphitized carbon black. J. Phys. Chem. 1984, 88, 5385. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsukahara, Y.; Hirayama, O.; Takeda, N.; Oizumi, T.; Fukushi, H.; Sato, N.; Tsuji, T.; Yamanaka, K.; Akao, S. A Novel Method and an Equipment for Generating the Standard Moisture in Gas Flowing through a Pipe. Sensors 2018, 18, 3438. https://doi.org/10.3390/s18103438
Tsukahara Y, Hirayama O, Takeda N, Oizumi T, Fukushi H, Sato N, Tsuji T, Yamanaka K, Akao S. A Novel Method and an Equipment for Generating the Standard Moisture in Gas Flowing through a Pipe. Sensors. 2018; 18(10):3438. https://doi.org/10.3390/s18103438
Chicago/Turabian StyleTsukahara, Yusuke, Osamu Hirayama, Nobuo Takeda, Toru Oizumi, Hideyuki Fukushi, Nagisa Sato, Toshihiro Tsuji, Kazushi Yamanaka, and Shingo Akao. 2018. "A Novel Method and an Equipment for Generating the Standard Moisture in Gas Flowing through a Pipe" Sensors 18, no. 10: 3438. https://doi.org/10.3390/s18103438
APA StyleTsukahara, Y., Hirayama, O., Takeda, N., Oizumi, T., Fukushi, H., Sato, N., Tsuji, T., Yamanaka, K., & Akao, S. (2018). A Novel Method and an Equipment for Generating the Standard Moisture in Gas Flowing through a Pipe. Sensors, 18(10), 3438. https://doi.org/10.3390/s18103438



