A New Bias Error Prediction Model for High-Precision Transfer Alignment
Abstract
1. Introduction
2. Materials and Methods
2.1. TA Approach
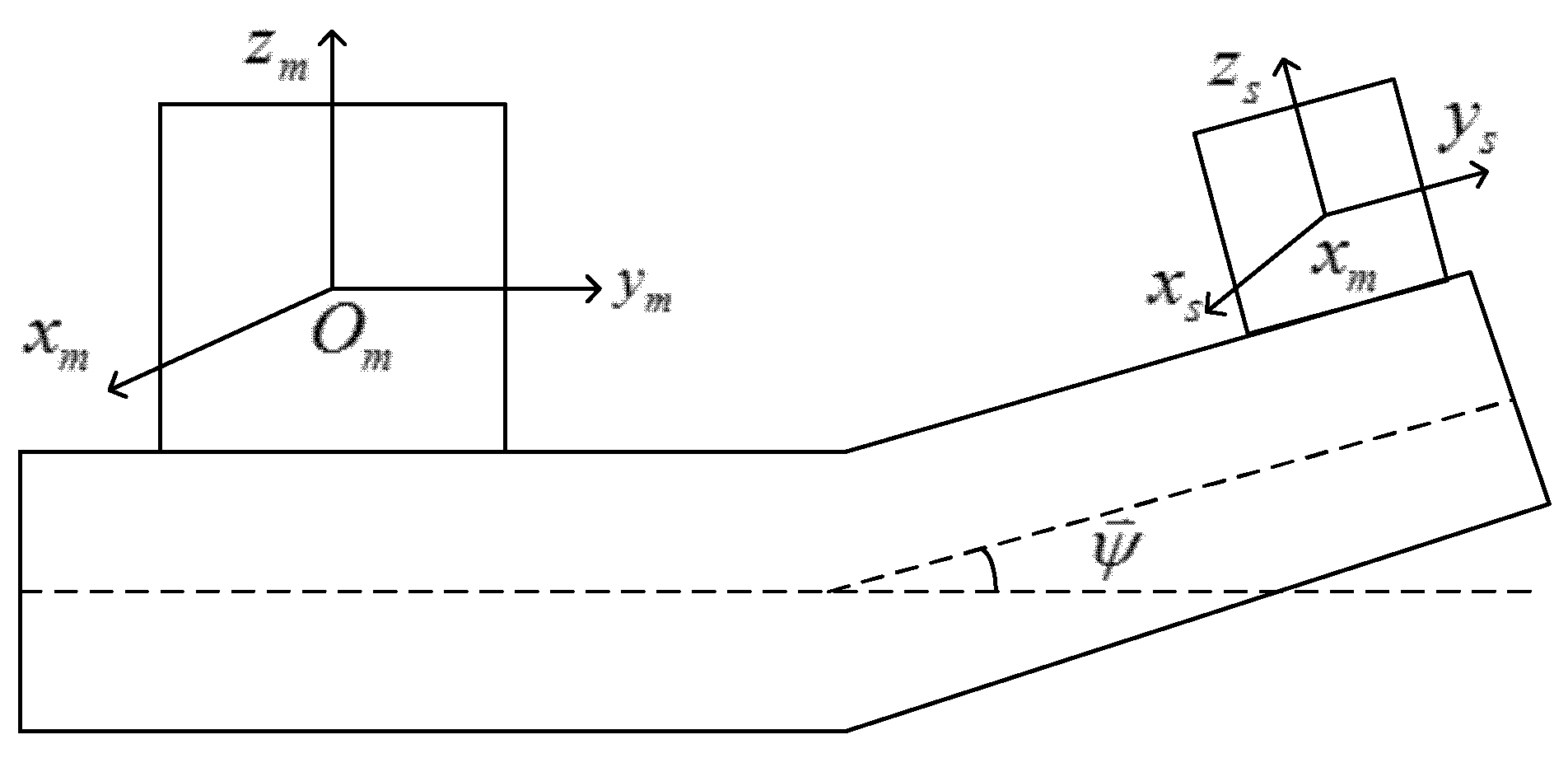
2.1.1. Introduction to the Coordinate Frame
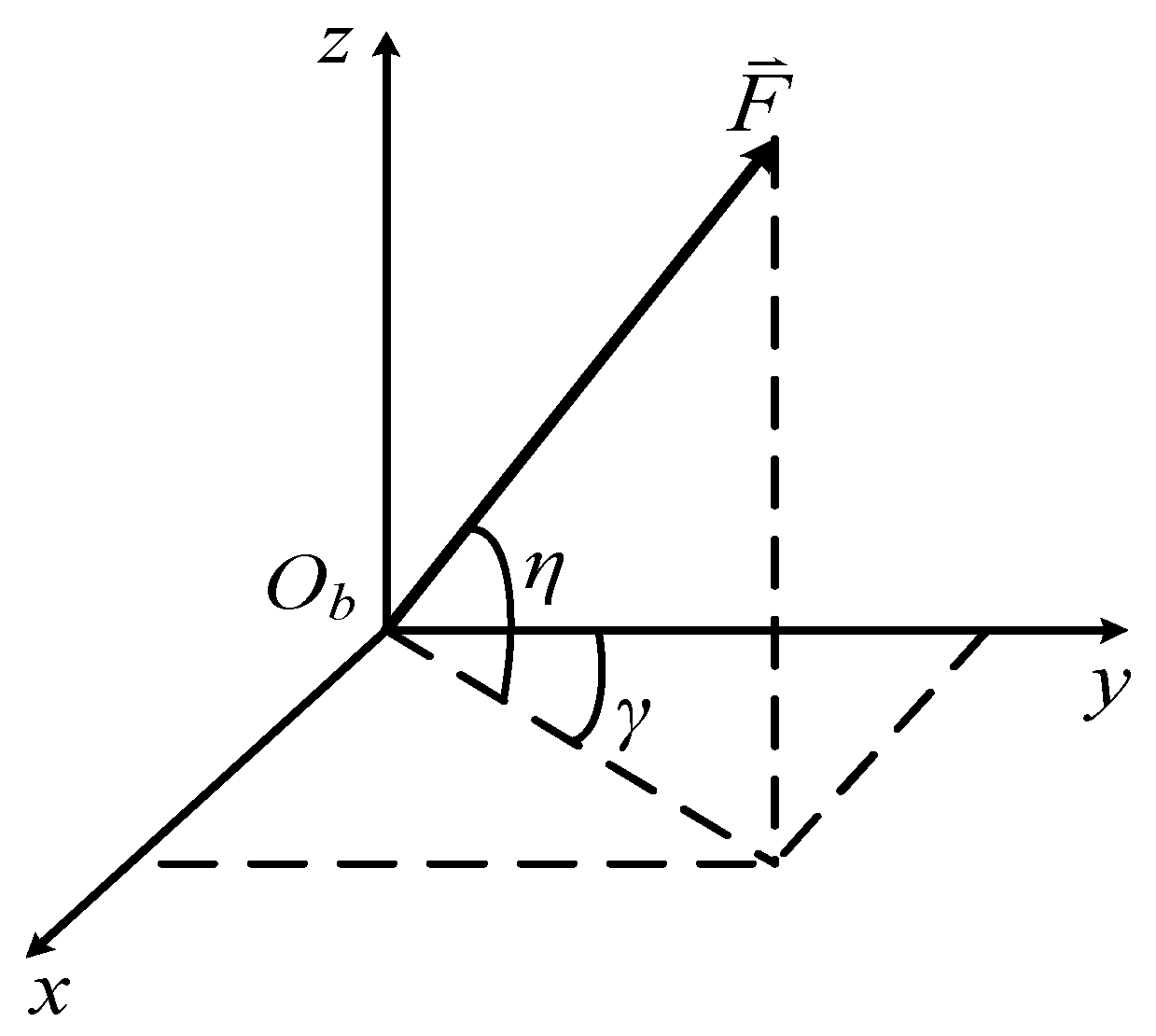
2.1.2. Acceleration Matching Function
2.1.3. Kalman Filtering Formulation
2.2. Correlation Between Linear Motion and Dynamic Lever-Arm
2.2.1. Bernoulli-Euler Beam Model
2.2.2. Beam Linear Motion and Dynamic Lever-arm Model
2.3. Bias Error Analysis and Modeling
2.3.1. Bias Error Analysis
2.3.2. Bias Error Prediction Model
3. Experiment Validation
3.1. Simulation Conditions and Model Establishment
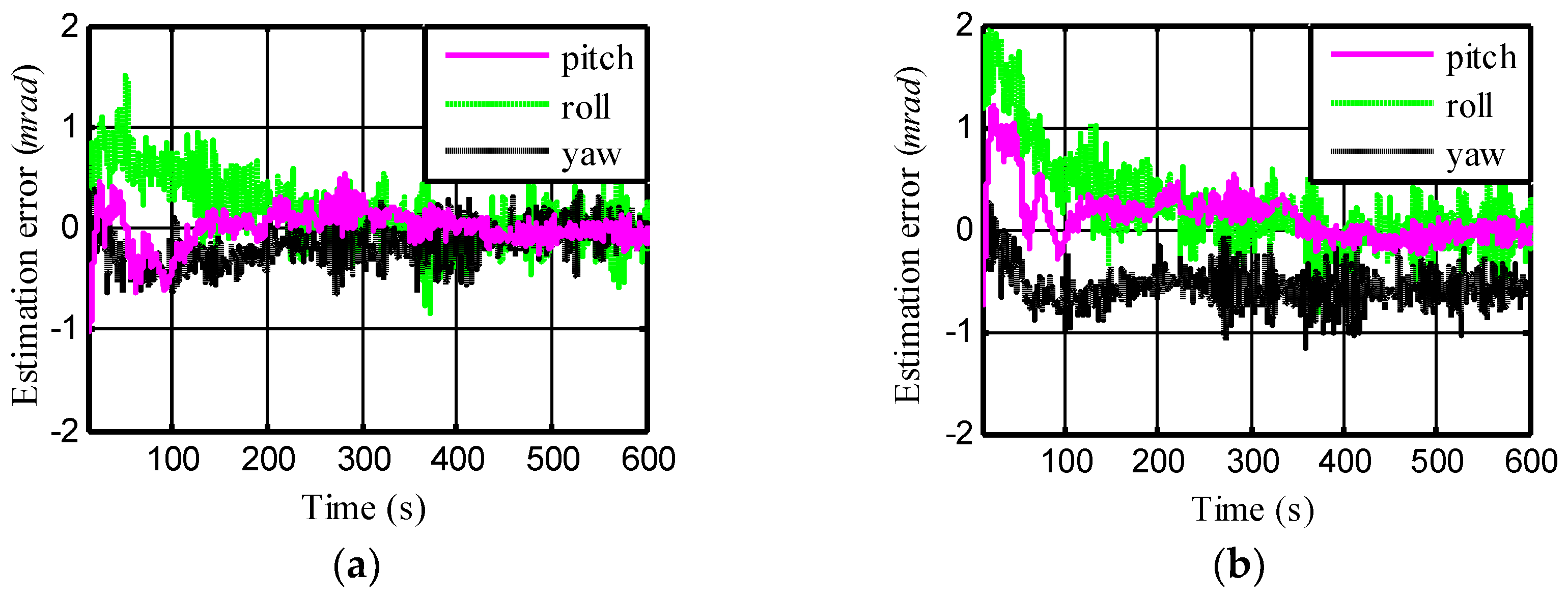
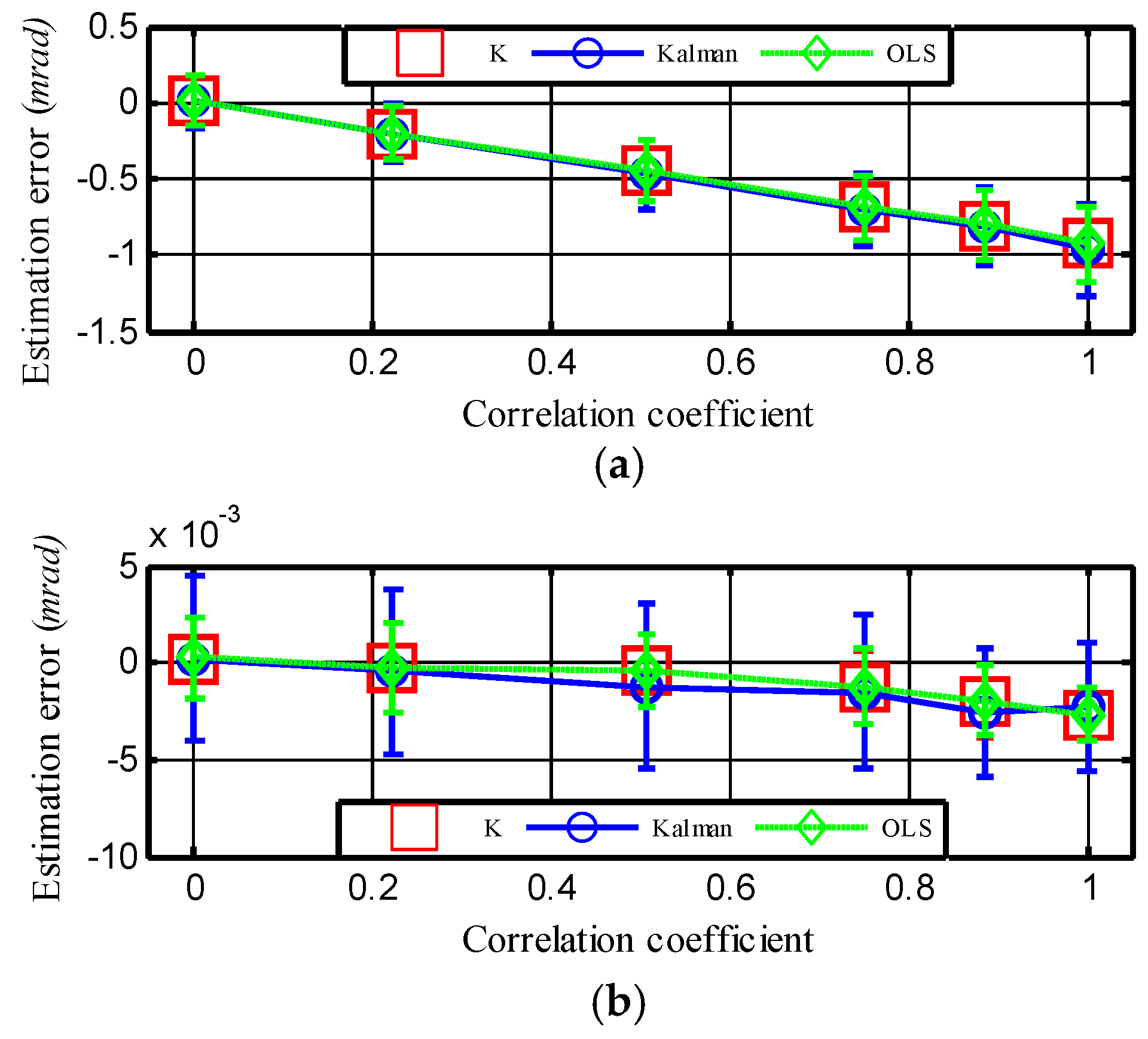
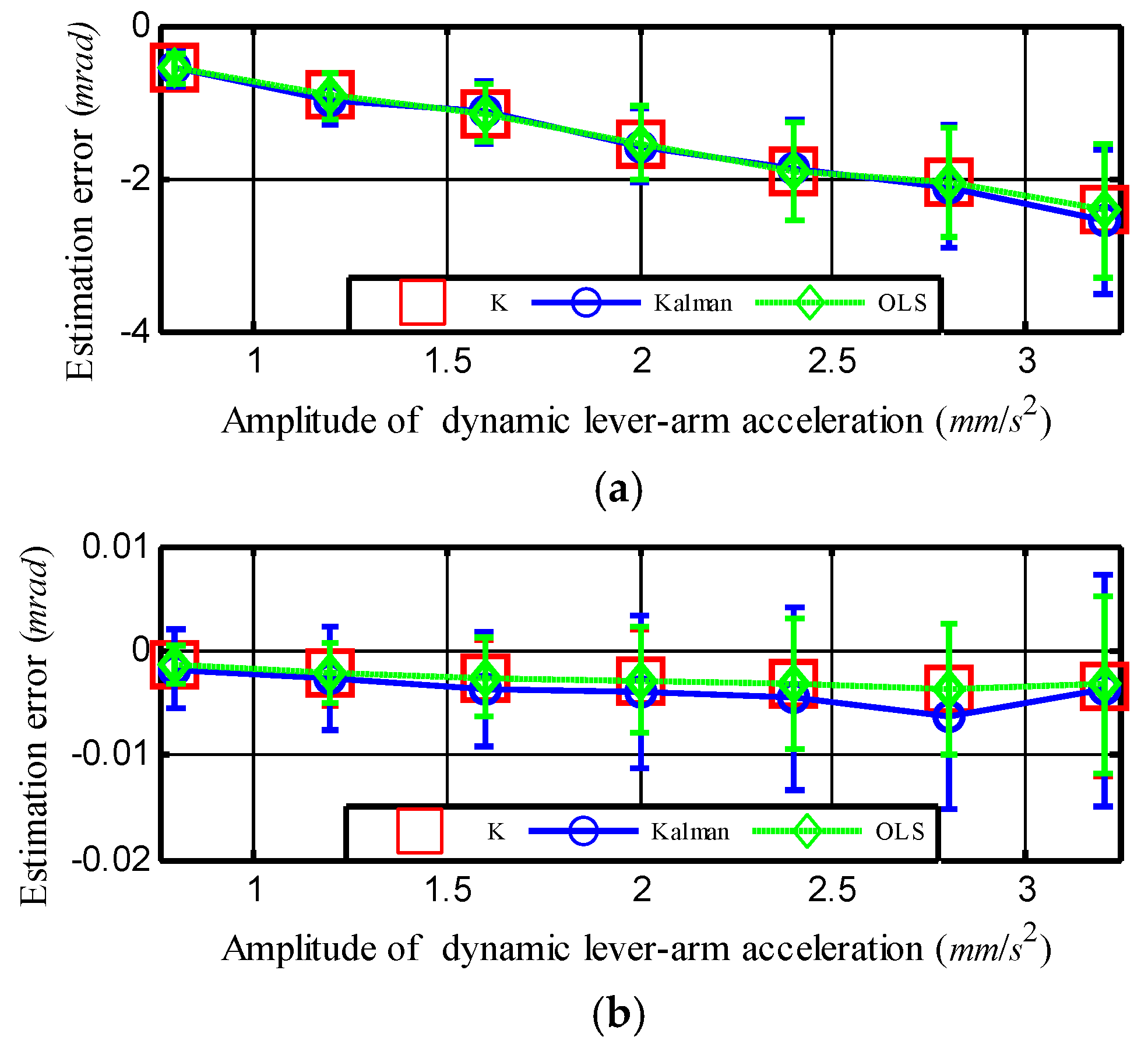
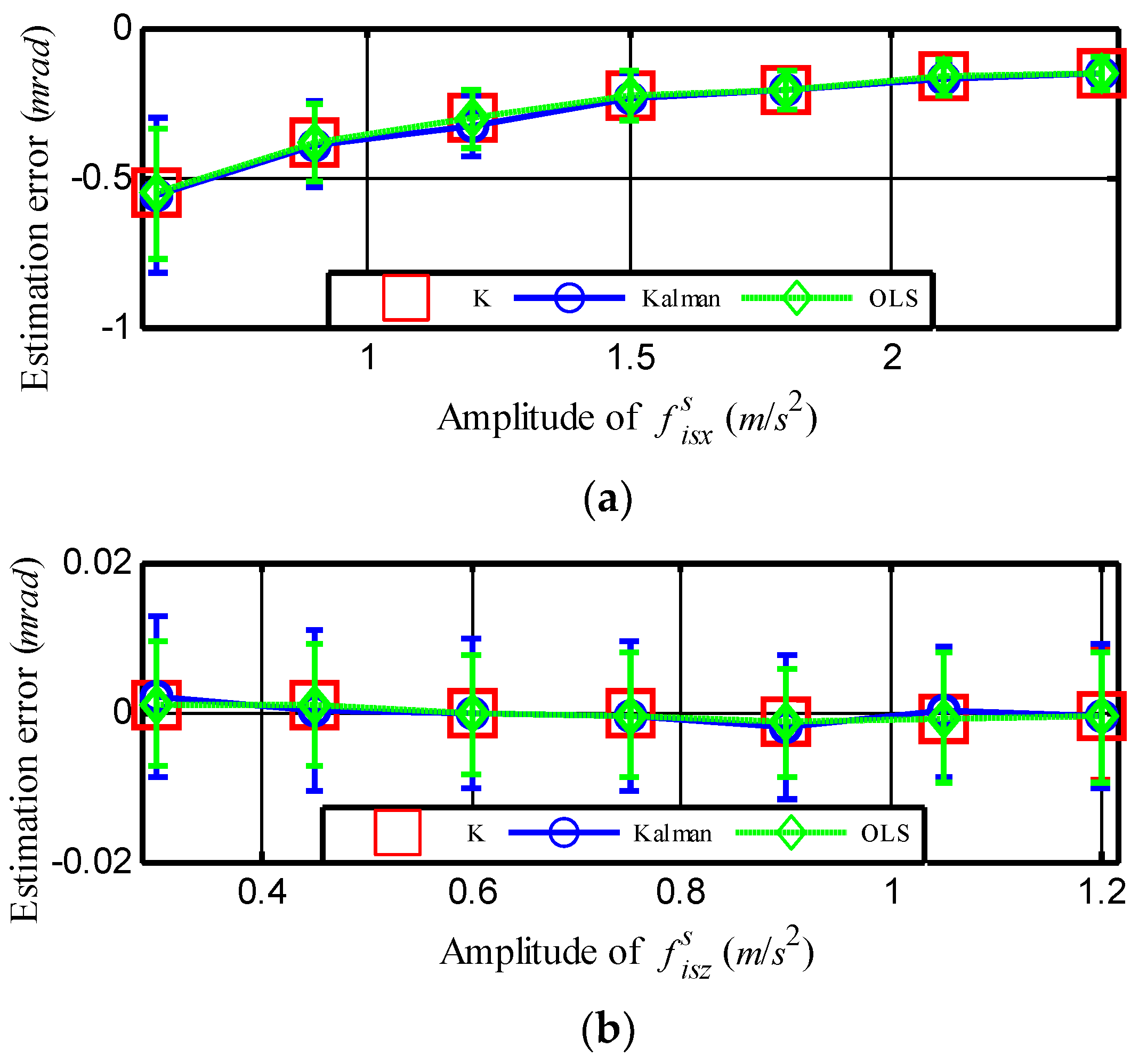
3.2. Result and Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kain, J.; Cloutier, J. Rapid Transfer Alignment for Tactical Weapon Applications. In Proceedings of the Guidance, Navigation and Control Conference, Boston, MA, USA, 14–16 August 1989. [Google Scholar]
- Schneider, A.M. Kalman Filter Formulations for Transfer Alignment of Strapdown Inertial Units. J. Navig. 1983, 30, 72–89. [Google Scholar] [CrossRef]
- Berke, L. Master reference system for rapid at sea alignment of aircraft inertial navigation systems. In Proceedings of the Guidance and Control Conference, Seattle, WA, USA, 15–17 August 1966. [Google Scholar]
- Browne, B.H.; Lackowski, D.H. Estimation of Dynamic Alignment Errors in Shipboard Firecontrol Systems. In Proceedings of the Conference on Decision and Control including the 15th Symposium on Adaptive Processes, Clearwater, FL, USA, 1–3 December 1976. [Google Scholar]
- Spalding, K. An Efficient Rapid Transfer Alignment Filter. In Proceedings of the Astrodynamics Conference on Guidence, Navigation and Control Conference, Hilton Head Island, SC, USA, 10–12 August 1992. [Google Scholar]
- Wu, W.; Chen, S.; Qin, S.Q. Online estimation of ship dynamic flexure model parameters for transfer alignment. IEEE Trans. Control Syst. Technol. 2013, 21, 1666–1678. [Google Scholar] [CrossRef]
- Hagan, C.E.; Lofts, C.S. Accelerometer based alignment transfer. In Proceedings of the IEEE PLANS 92 Position Location and Navigation Symposium Record, Monterey, CA, USA, 23–27 March 1992. [Google Scholar]
- Sinpyo, H.; Man Hyung, L.; Ho-Hwan, C.; Sun-Hong, K.; Speyer, J.L. Experimental study on the estimation of lever arm in GPS/INS. IEEE Trans. Veh. Technol. 2006, 55, 431–448. [Google Scholar]
- Chattaraj, S.; Mukherjee, A.; Chaudhuri, S.K. Transfer alignment problem: Algorithms and design issues. Gyroscopy Navig. 2013, 4, 130–146. [Google Scholar] [CrossRef]
- Xiong, Z.; Peng, H.; Liu, J.Y.; Wang, J.; Sun, Y. Online calibration research on the lever arm effect for the hypersonic vehicle. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2014. [Google Scholar]
- Gao, W.; Zhang, Y.; Sun, Q.; Ben, Y. Error analysis and compension for lever-arm effect in transfer anlgnment. Chin. J. Sci. Instrum. 2013, 34, 560–564. [Google Scholar]
- Yang, D.; Wang, S.; Li, H.; Liu, Z.; Zhang, J. Performance Enhancement of Large-Ship Transfer Alignment: A Moving Horizon Approach. J. Navig. 2012, 66, 17–33. [Google Scholar] [CrossRef]
- Gao, W.; Ben, Y.; Sun, F.; Xu, B. Performance comparison of two filtering approaches for INS rapid transfer alignment. In Proceedings of the 2007 International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007. [Google Scholar]
- Qingwei, G.; Guorong, Z.; Xibin, W.; Fang, W. Incorporate modeling and simulation of transfer alignment with flexure of carrier and lever-arm effect. Chin. J. Aeronaut. 2009, 11, 2172–2177. [Google Scholar]
- Chen, W.; Zeng, Q.; Liu, J.; Wang, H. Research on shipborne transfer alignment under the influence of the uncertain disturbance based on the extended state observer. Opt. Int. J. Light Electron Opt. 2017, 130, 777–785. [Google Scholar] [CrossRef]
- Groves, P.D.; Wilson, G.G.; Mather, C.J. Robust rapid transfer alignment with an INS/GPS reference. In Proceedings of the 2002 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 28–30 January 2002. [Google Scholar]
- Mochalov, A.V. Optical Gyros and Their Application. In A System for Measuring Deformations of Large-Sized Objects; LouKianov, D., Rodloff, R., Sorg, H., Stieler, B., Eds.; Canada Communication Group Inc.: Hull, QC, Canada, 1999; pp. 1–9. [Google Scholar]
- Groves, P.D. Optimising the Transfer Alignment of Weapon INS. J. Navig. 2003, 56, 323–335. [Google Scholar] [CrossRef]
- Petovello, M.G.; Keefe, K.O.; Lachapelle, G.; Cannon, M.E. Measuring aircraft carrier flexure in support of autonomous aircraft landings. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 523–535. [Google Scholar] [CrossRef]
- Pehlivanoğlu, A.G.; Ercan, Y. Investigation of Flexure Effect on Transfer Alignment Performance. J. Navig. 2012, 66, 1–15. [Google Scholar] [CrossRef]
- Wu, W.; Qin, S.; Chen, S. Coupling influence of ship dynamic flexure on high accuracy transfer alignment. Int. J. Model. Ident. Control 2013, 19, 224–234. [Google Scholar] [CrossRef]
- Heffes, H. The effect of erroneous models on the Kalman filter response. IEEE Trans. Autom. Control 1966, 11, 541–543. [Google Scholar] [CrossRef]
- Abei, X.; Qingming, G.; Songhui, H. Analysis of model error effect on kalman filtering. J. Geod. Geodyn. 2008, 28, 101–104. [Google Scholar]
- Kailath, T. An innovations approach to least-squares estimation—Part I: Linear filtering in additive white noise. IEEE Trans. Autom. Control 1968, 13, 646–655. [Google Scholar] [CrossRef]
- Kailath, T.; Frost, P. An innovations approach to least-squares estimation—Part II: Linear smoothing in additive white noise. IEEE Trans. Autom. Control 1968, 13, 655–660. [Google Scholar] [CrossRef]
- Sorenson, H.W. Least-squares estimation: From Gauss to Kalman. IEEE Spectr. 1970, 7, 63–68. [Google Scholar] [CrossRef]
- Ishihara, J.Y.; Terra, M.H.; Campos, J.C.T. Robust Kalman filter for descriptor systems. IEEE Trans. Autom. Control 2006, 51, 1354. [Google Scholar] [CrossRef]
- Luo, X.; Wang, H. Robust Adaptive Kalman Filtering—A method based on quasi-accurate detection and plant noise variance–covariance matrix tuning. J. Navig. 2016, 70, 137–148. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T.; Marshall, L.R. Nonlinear Coupling of Pitch and Roll Modes in Ship Motions. J. Hydronaut. 1973, 7, 145–152. [Google Scholar] [CrossRef]
- Juncher Jensen, J.; Dogliani, M. Wave-induced ship full vibrations in stochastic seaways. Mar. Struct. 1996, 9, 353–387. [Google Scholar] [CrossRef]
- Lee, J.; Whaley, P.W. Prediction of the Angular Vibration of Aircraft Structures. J. Sound Vib. 1976, 49, 541–549. [Google Scholar] [CrossRef]
- Huddle, J.R.; Chueh, V.K. Transfer Alignment of Navigation Systems. U.S. Patent 7206694B2, 16 July 2004. [Google Scholar]
| (mrad) | (Hz) | (1/s) | |
|---|---|---|---|
| X-axis | 0.0776 | 0.16 | 0.1 |
| Y-axis | 0.1551 | 0.19 | 0.1 |
| Z-axis | 0.1551 | 0.18 | 0.1 |
| (mrad/s) | (Hz) | (1/s) | |
|---|---|---|---|
| X-axis | 4.7 | 0.17 | 0.1 |
| Y-axis | 7.2 | 0.16 | 0.1 |
| Z-axis | 2.2 | 0.18 | 0.1 |
| (mm/s2) | (Hz) | (1/s) | |
|---|---|---|---|
| X-axis | 3.1 | 0.17 | 0.1 |
| Y-axis | 0.77 | 0.16 | 0.1 |
| Z-axis | 1.5 | 0.17 | 0.1 |
| (mm/s2) | (Hz) | (1/s) | |
|---|---|---|---|
| X-axis | 0.6 | 0.16 | 0.1 |
| Y-axis | 0.4 | 0.17 | 0.1 |
| Z-axis | 0.3 | 0.17 | 0.1 |
| X-Direction | Y-Direction | Z-Direction | |
|---|---|---|---|
| Ship inertial angular velocity () | WNx | WNy | WNz |
| Dynamic misalignment angle () | WNx | WNy | WNz |
| Dynamic lever-arm acceleration () | WNx | WNy | WNz |
| SINS acceleration data () | (1 − ξ)*WNx + ξ*WNy | WNy | (1 − ξ)*WNz + ξ*WNy |
| MINS | SINS | |||
|---|---|---|---|---|
| Bias | White Noise | Bias (mGal) | white Noise (SD) (mGal) | |
| X | 0 | 0 | 30 | 10 |
| Y | 0 | 0 | 30 | 10 |
| Z | 0 | 0 | 30 | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, S.; Qin, S.; Hu, F.; Wu, W. A New Bias Error Prediction Model for High-Precision Transfer Alignment. Sensors 2018, 18, 3277. https://doi.org/10.3390/s18103277
Zhang Y, Yang S, Qin S, Hu F, Wu W. A New Bias Error Prediction Model for High-Precision Transfer Alignment. Sensors. 2018; 18(10):3277. https://doi.org/10.3390/s18103277
Chicago/Turabian StyleZhang, Yutong, Shuai Yang, Shiqiao Qin, Feng Hu, and Wei Wu. 2018. "A New Bias Error Prediction Model for High-Precision Transfer Alignment" Sensors 18, no. 10: 3277. https://doi.org/10.3390/s18103277
APA StyleZhang, Y., Yang, S., Qin, S., Hu, F., & Wu, W. (2018). A New Bias Error Prediction Model for High-Precision Transfer Alignment. Sensors, 18(10), 3277. https://doi.org/10.3390/s18103277





