Vision-Based Real-Time Traversable Region Detection for Mobile Robot in the Outdoors
Abstract
:1. Introduction
- A new method is proposed to robustly estimate a vanishing point, which outperforms the state-of-the-art considering tradeoff of time efficiency and accuracy. The vanishing point is detected by voting of a few line segments formed with some dominant pixels rather than by voting of all pixels in most existing methods.
- A fast, self-supervised segmentation scheme is proposed for unstructured traversable region detection. An appearance model based on multivariate Gaussian is constructed from the sample region adaptively determined by the vanishing point and dominant borders in the input image. This scheme allows real-time performance on a mobile robot.
2. Methods
2.1. Traversable Region Detection
2.2. Vanishing Point Estimation
| Algorithm 1. Vanishing Point Estimation |
|
|
|
|
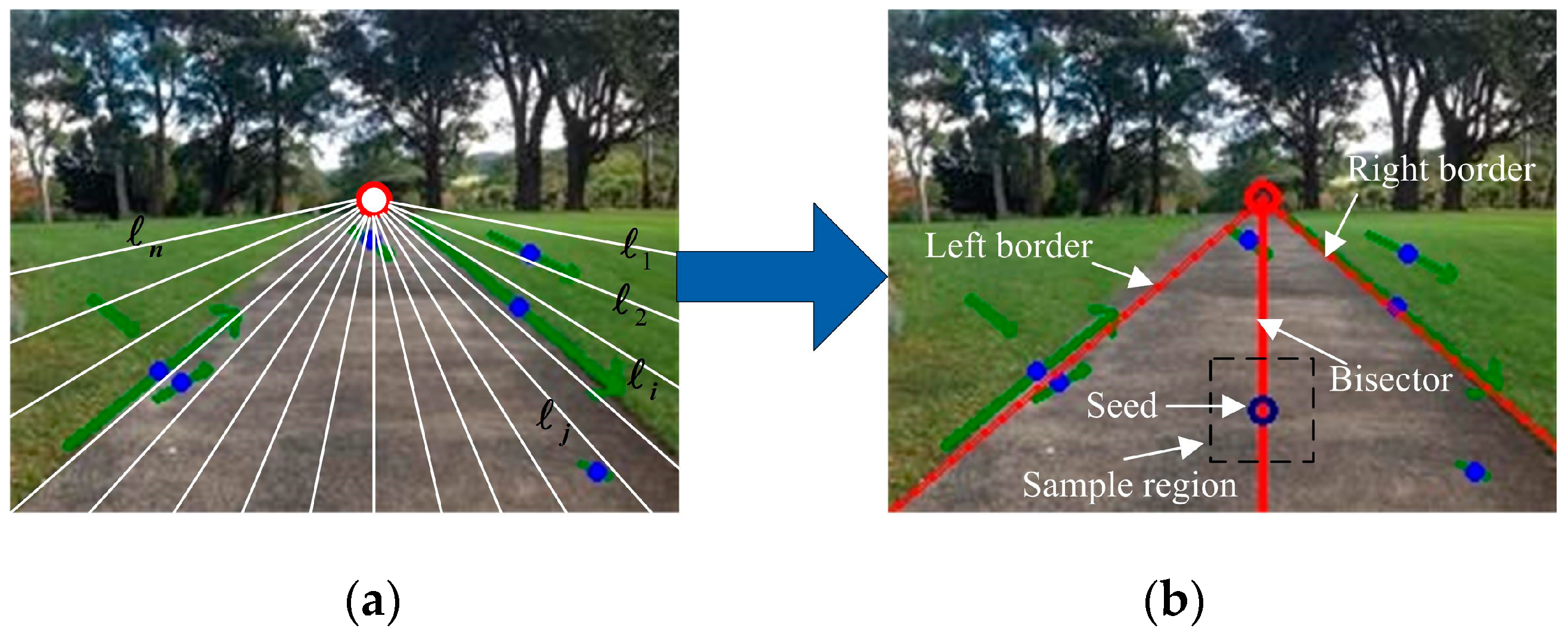
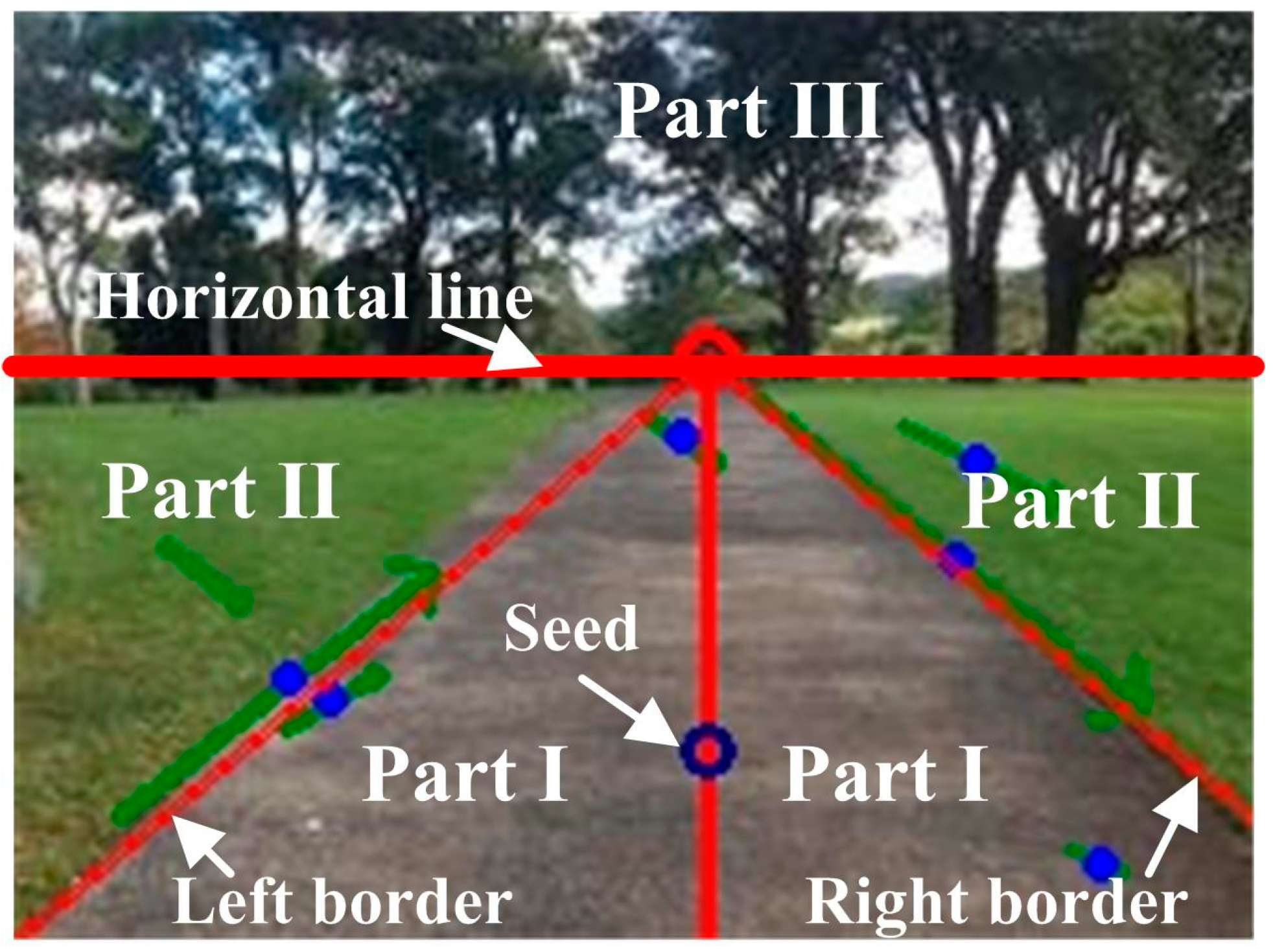
2.3. Sample Region Selection
2.4. Segmentation Method
| Algorithm 2. Traversable Region Segmentation |
|
|
|
|
3. Experimental Results and Discussion
3.1. Vanishing Point Detection
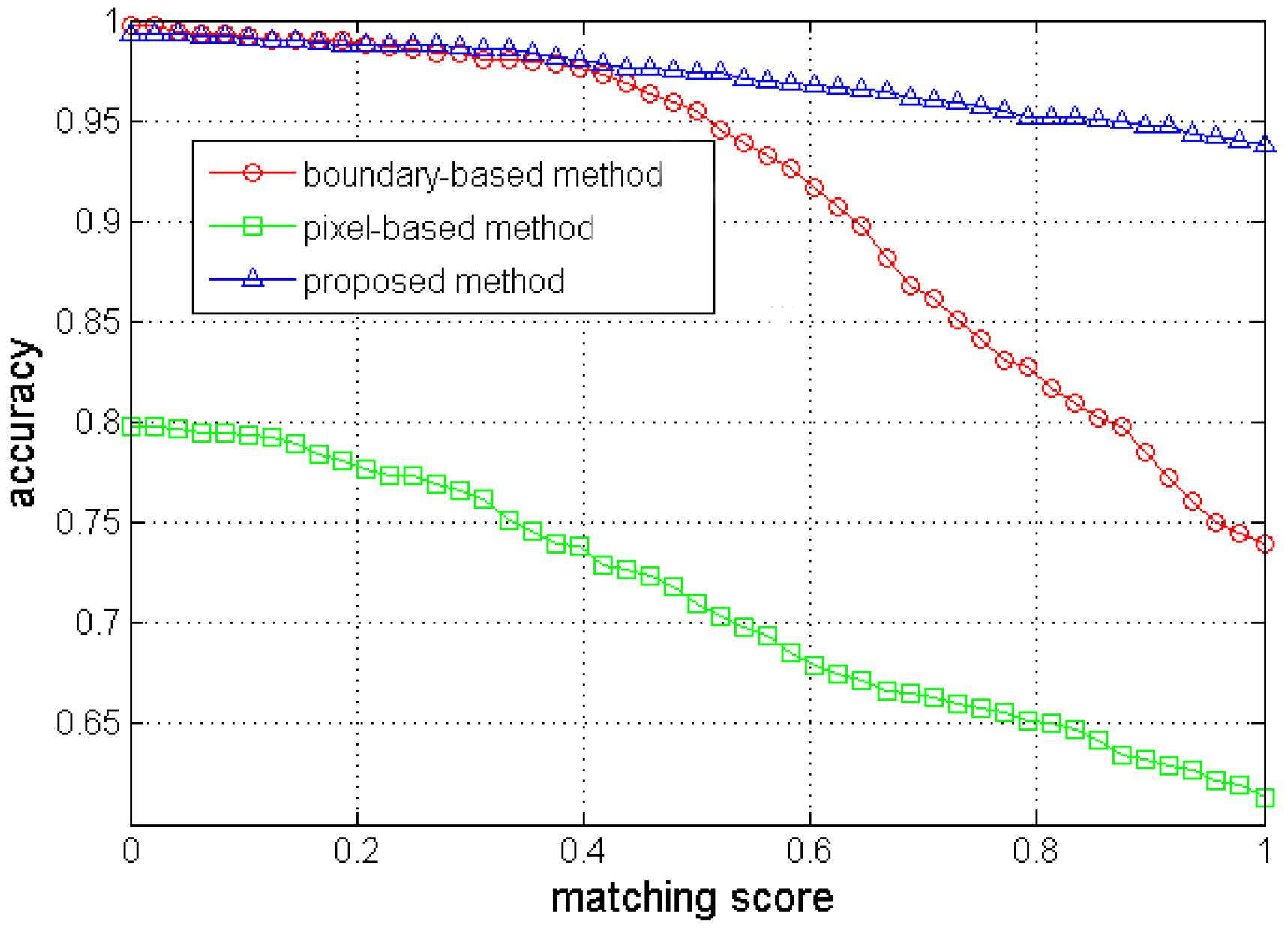
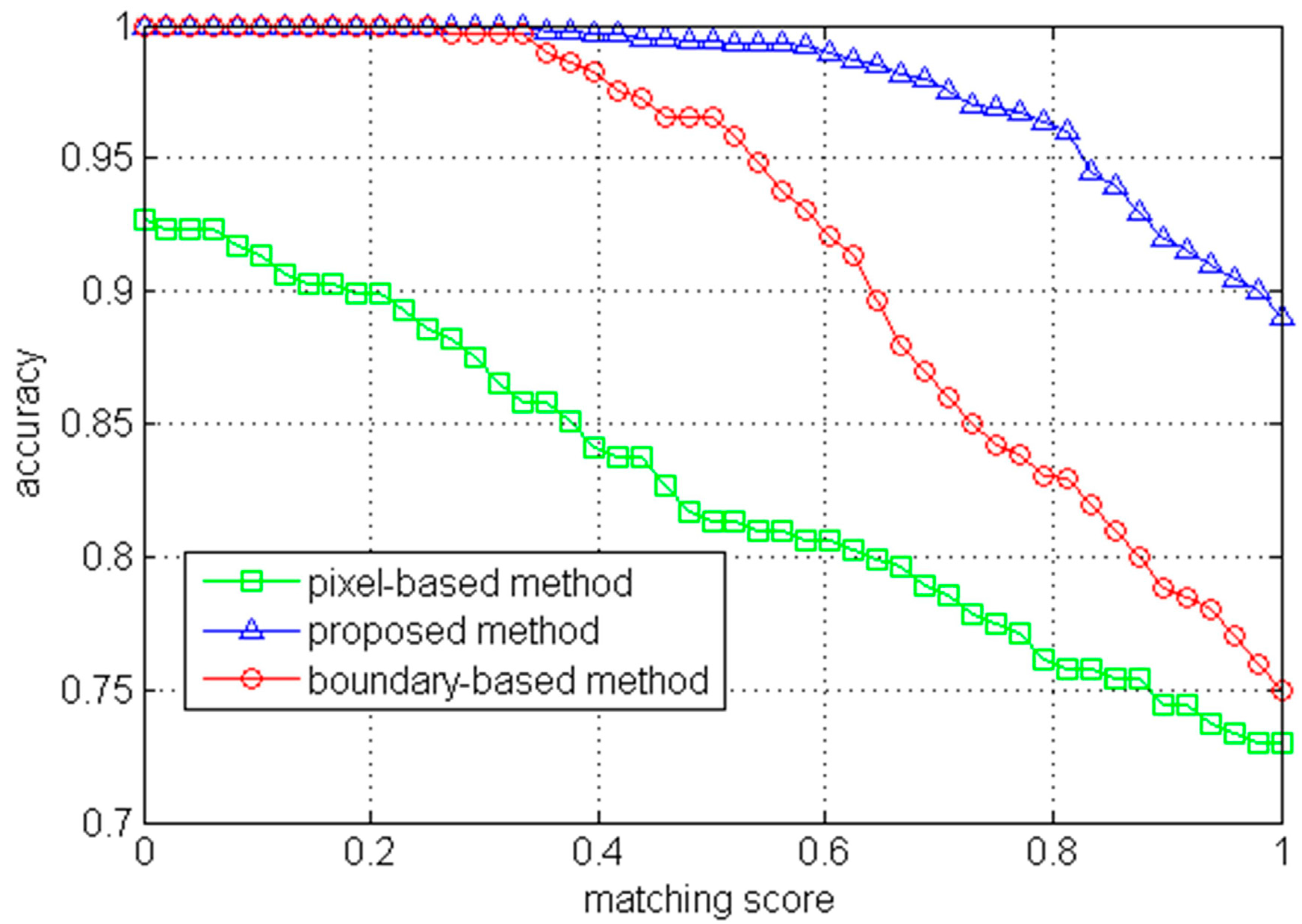
3.2. Traversable Region Segmentation
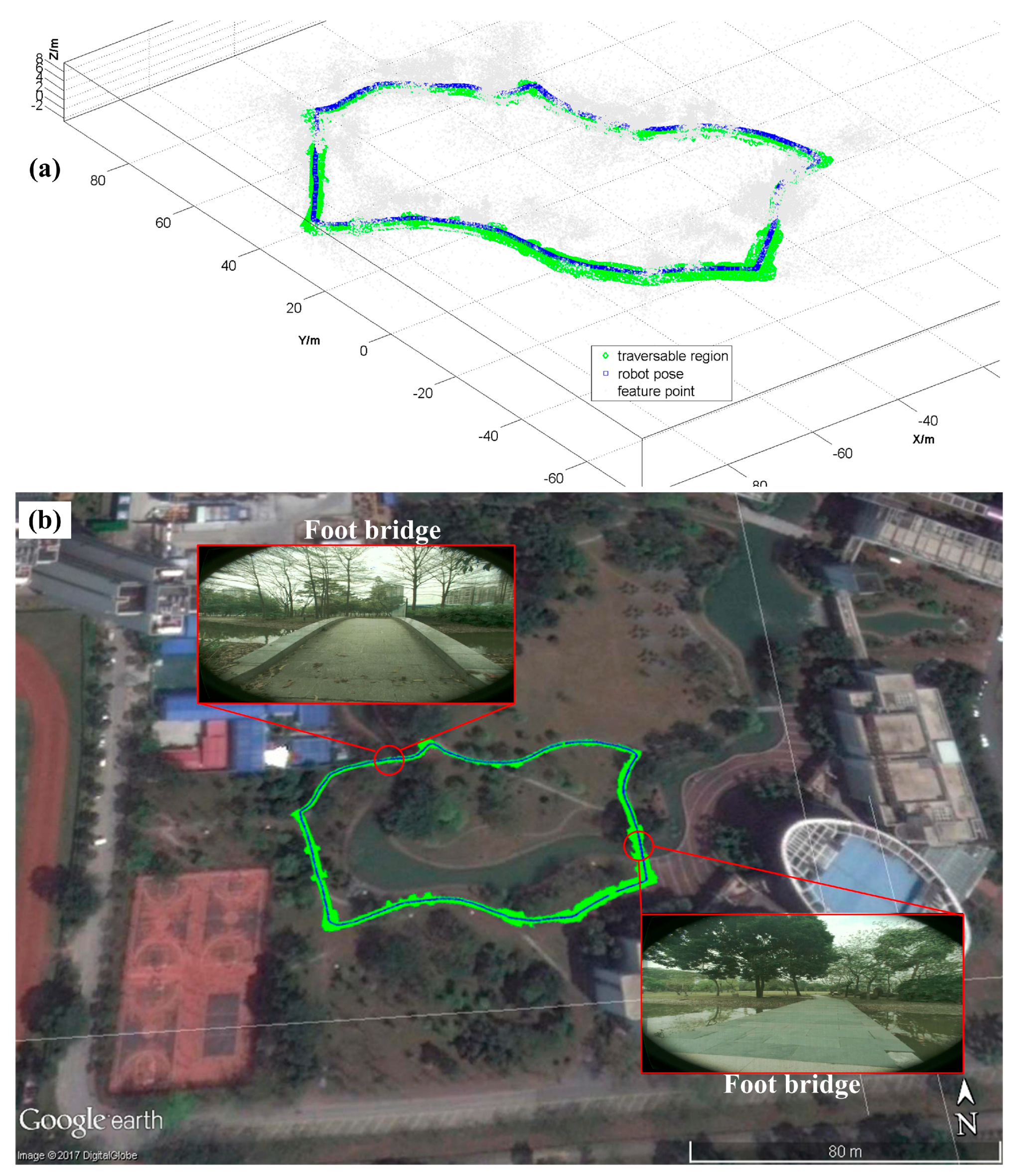
3.3. Real Time Implementations for Robot Navigation
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Phung, S.L.; Le, M.C.; Bouzerdoum, A. Pedestrian road detection in unstructured scenes for assistive navigation. Comput. Vis. Image Underst. 2016, 149, 186–196. [Google Scholar] [CrossRef]
- Cristóforis, P.D.; Nitsche, M.A.; Krajník, T.; Mejail, M. Real-time monocular image-based path detection. J. Real Time Image Proc. 2016, 11, 335–348. [Google Scholar]
- Kong, H.; Audibert, J.; Ponce, J. General road detection from a single image. IEEE Trans. Image Process. 2010, 19, 2211–2220. [Google Scholar] [CrossRef] [PubMed]
- Moghadam, P.; Starzyk, J.A.; Wijesoma, W.S. Fast Vanishing-Point Detection in Unstructured Environments. IEEE Trans. Image Process. 2012, 21, 425–430. [Google Scholar] [CrossRef] [PubMed]
- Miksik, O. Rapid vanishing point estimation for general road detection. In Proceedings of the IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012. [Google Scholar]
- Tan, C.; Tsai, H.; Chang, T.; Shneier, M. Color model-based real-time learning for road following. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Toronto, ON, Canada, 17–20 September 2006. [Google Scholar]
- Ramstrom, O.; Christensen, H. A method for following unmarked roads. In Proceedings of the IEEE Intelligent Vehicles Symposium, Las Vegas, NV, USA, 6–8 June 2005. [Google Scholar]
- Álvarez, J.M.; Ĺopez, A.M. Road detection based on illuminant invariance. IEEE Trans. Intell. Transp. Syst. 2011, 12, 184–193. [Google Scholar] [CrossRef]
- Lu, X. Self-supervised road detection from a single image. In Proceedings of the IEEE International Conference on Image Processing, Quebec City, QC, Canada, 27–30 September 2015. [Google Scholar]
- Miksik, O.; Petyovsky, P.; Zalud, L.; Jura, P. Robust detection of shady and high-lighted roads for monocular camera based navigation of UGV. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Álvarez, J.M.; Ĺopez, A.M.; Gevers, T.; Lumbreras, F. Combining priors, appearance, and context for road detection. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1168–1178. [Google Scholar] [CrossRef]
- Lee, H.; Kwak, K.; Jo, S. An incremental nonparametric Bayesian clustering-based traversable region detection method. Auton. Robot 2017, 41, 795–810. [Google Scholar] [CrossRef]
- Xiao, L.; Dai, B.; Liu, D.X.; Zhao, D.W.; Wu, T. Monocular road detection using structured random forest. Int. J. Adv. Robot. Syst. 2016, 13, 1–13. [Google Scholar] [CrossRef]
- Alvarez, J.M.; Gevers, T.; LeCun, Y.; Lopez, A.M. Road scene segmentation from a single image. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Mohan, R. Deep deconvolutional networks for scene parsing. arXiv, 2014; arXiv:1411.4101. [Google Scholar]
- Oliveira, G.L.; Burgard, W.; Brox, T. Efficient deep models for monocular road segmentation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Tai, L.; Liu, M. Deep-learning in Mobile Robotics—From Perception to Control Systems: A Survey on Why and Why not. arXiv 2017, arXiv:1612.07139. [Google Scholar]
- Ghurchian, R.; Hashino, S. Shadow compensation in color images for unstructured road segmentation. In Proceedings of the 9th IAPR Conference on Machine Vision Applications, MVA 2005, Tsukuba, Japan, 16–18 May 2005; pp. 598–601. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Lee, T. Image representation using 2D Gabor wavelets. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 959–971. [Google Scholar]
- Von Gioi, R.G.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A fast line segment detector with a false detection control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef] [PubMed]
- KITTI Dataset. Available online: http://www.cvlibs.net/datasets/kitti/eval_road.php (accessed on 31 August 2017).
- Wang, Y.; Teoh, E.K.; Shen, D.G. Road detection and tracking using B-Snake. Image Vis. Comput. 2004, 22, 269–280. [Google Scholar] [CrossRef]
- Humenberger, M.; Zinner, C.; Weber, M.; Kubinger, W.; Vincze, M. A fast stereo matching algorithm suitable for embedded real-time systems. Comput. Vis. Image Underst. 2010, 114, 1180–1202. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Point Cloud Library. Available online: http://pointclouds.org/ (accessed on 31 August 2017).






| Method | Average Error | Times (s) | |
|---|---|---|---|
| PLVP Dataset | Challenge Dataset | ||
| Gabor-based method | 0.0812 ± 0.1042 | 0.0909 ± 0.1010 | 11.712 a |
| Hough-based method | 0.1463 ± 0.1353 | 0.2464 ± 0.1464 | 0.009 b |
| Proposed method | 0.0734 ± 0.0858 | 0.1023 ± 0.1085 | 0.021 c |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, F.; Zhu, X.; He, C. Vision-Based Real-Time Traversable Region Detection for Mobile Robot in the Outdoors. Sensors 2017, 17, 2101. https://doi.org/10.3390/s17092101
Deng F, Zhu X, He C. Vision-Based Real-Time Traversable Region Detection for Mobile Robot in the Outdoors. Sensors. 2017; 17(9):2101. https://doi.org/10.3390/s17092101
Chicago/Turabian StyleDeng, Fucheng, Xiaorui Zhu, and Chao He. 2017. "Vision-Based Real-Time Traversable Region Detection for Mobile Robot in the Outdoors" Sensors 17, no. 9: 2101. https://doi.org/10.3390/s17092101
APA StyleDeng, F., Zhu, X., & He, C. (2017). Vision-Based Real-Time Traversable Region Detection for Mobile Robot in the Outdoors. Sensors, 17(9), 2101. https://doi.org/10.3390/s17092101




