Reduction of the Influence of Laser Beam Directional Dithering in a Laser Triangulation Displacement Probe
Abstract
:1. Introduction
2. Effect of the Laser Beam Directivity on the Measurement Accuracy
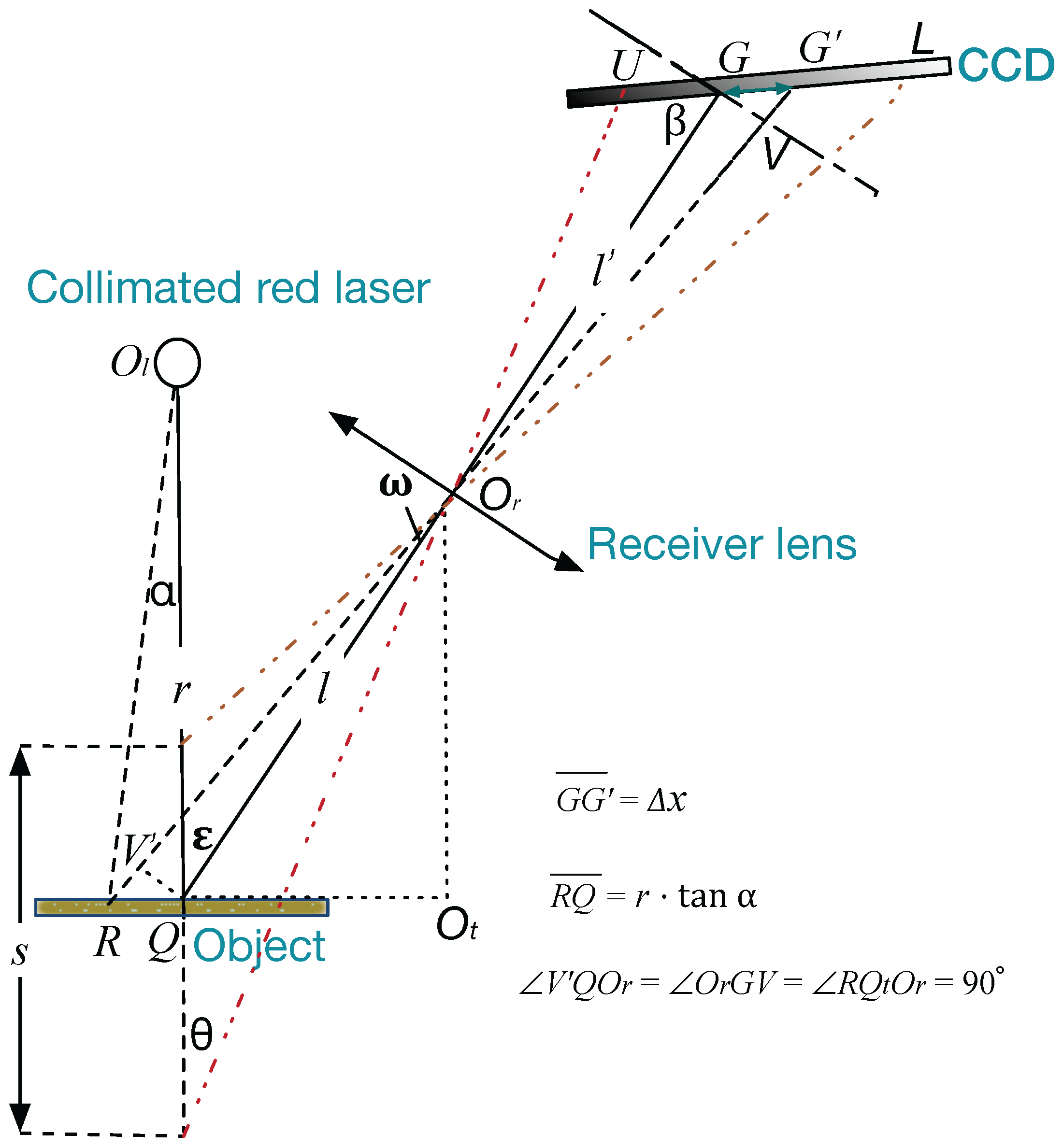
3. Measurement Methodology
3.1. Basic Layout
3.2. Laser Dithering Compensation Algorithm
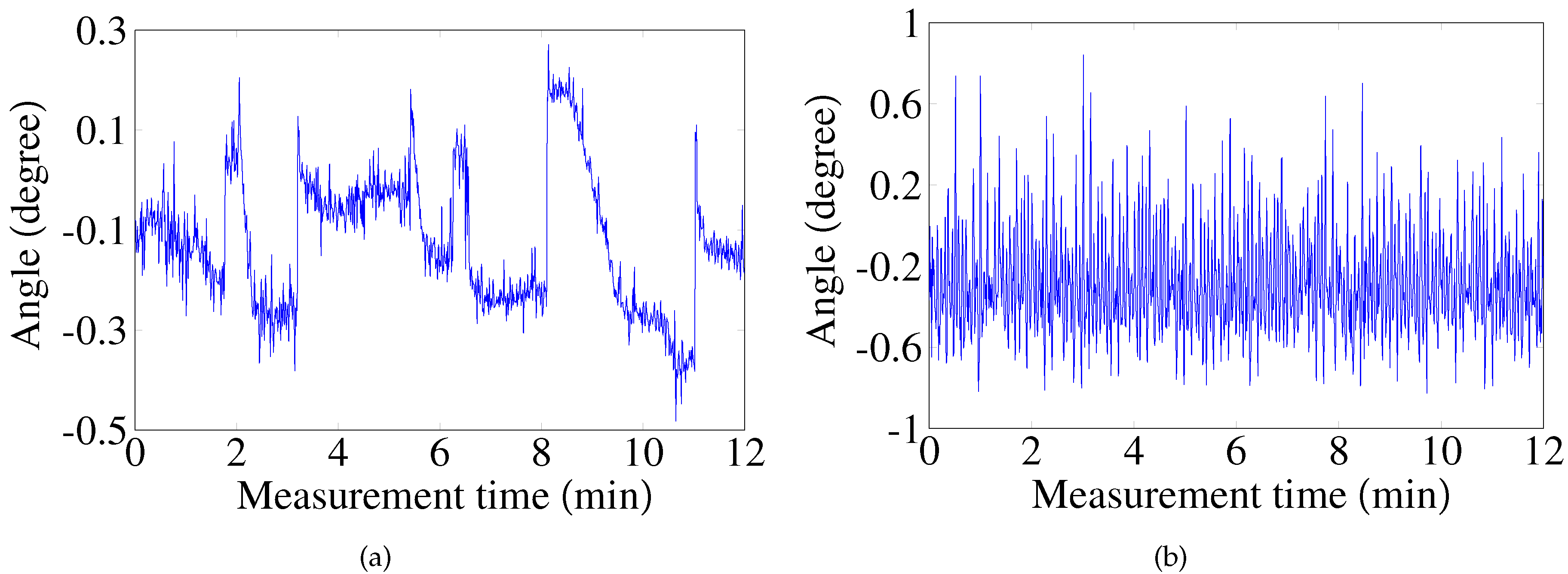
4. Experimental Test
4.1. Presetting
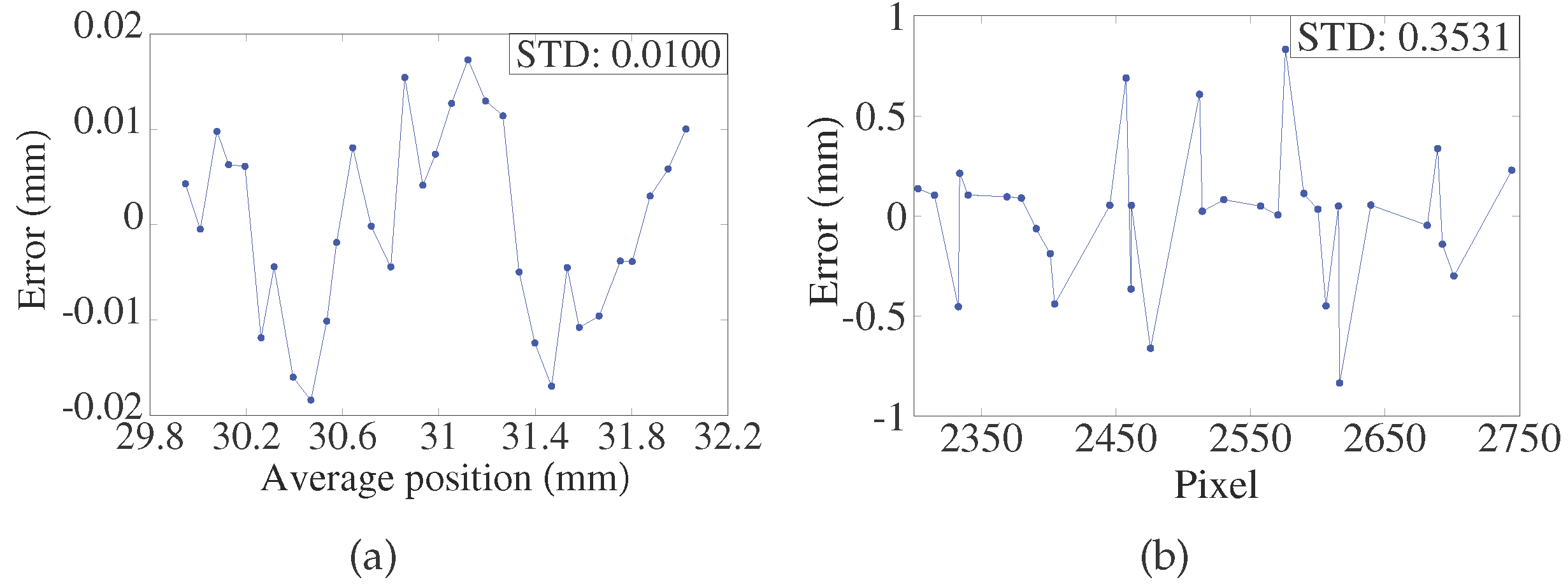
4.2. Verification of the Laser Dithering Compensation Algorithm
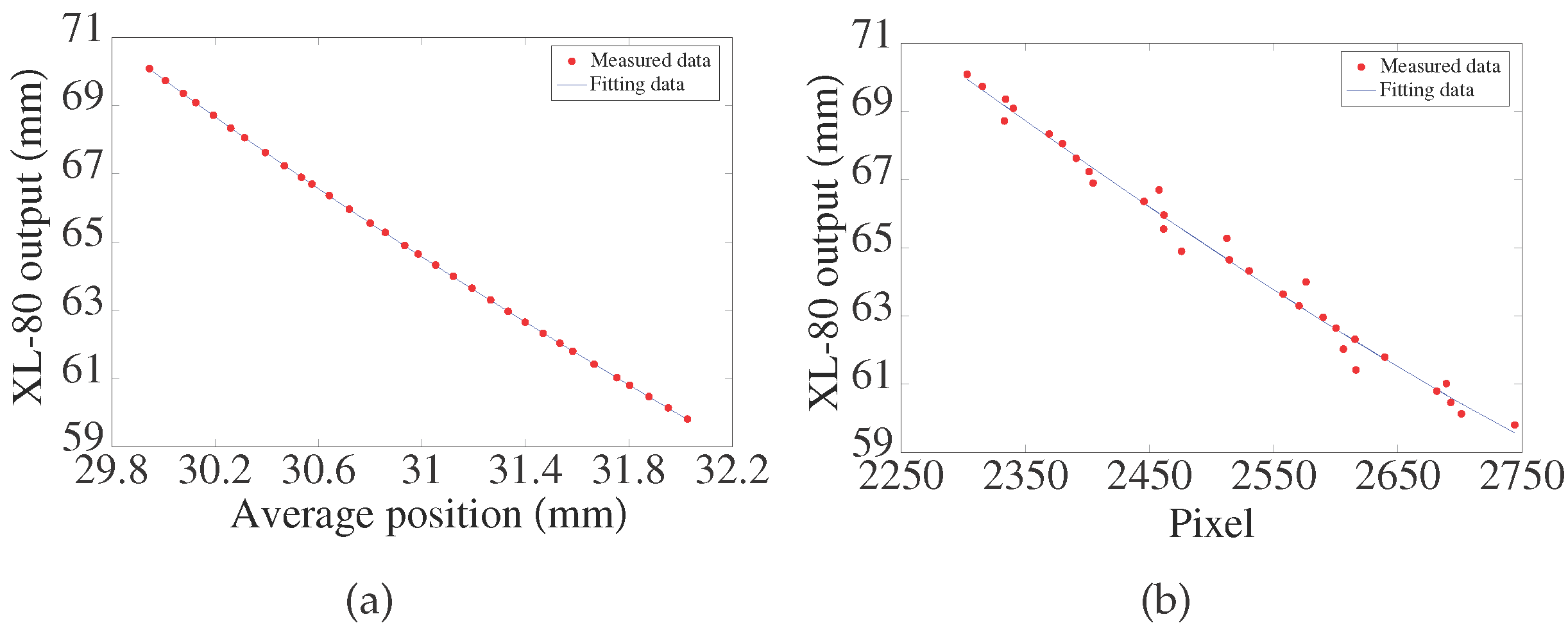
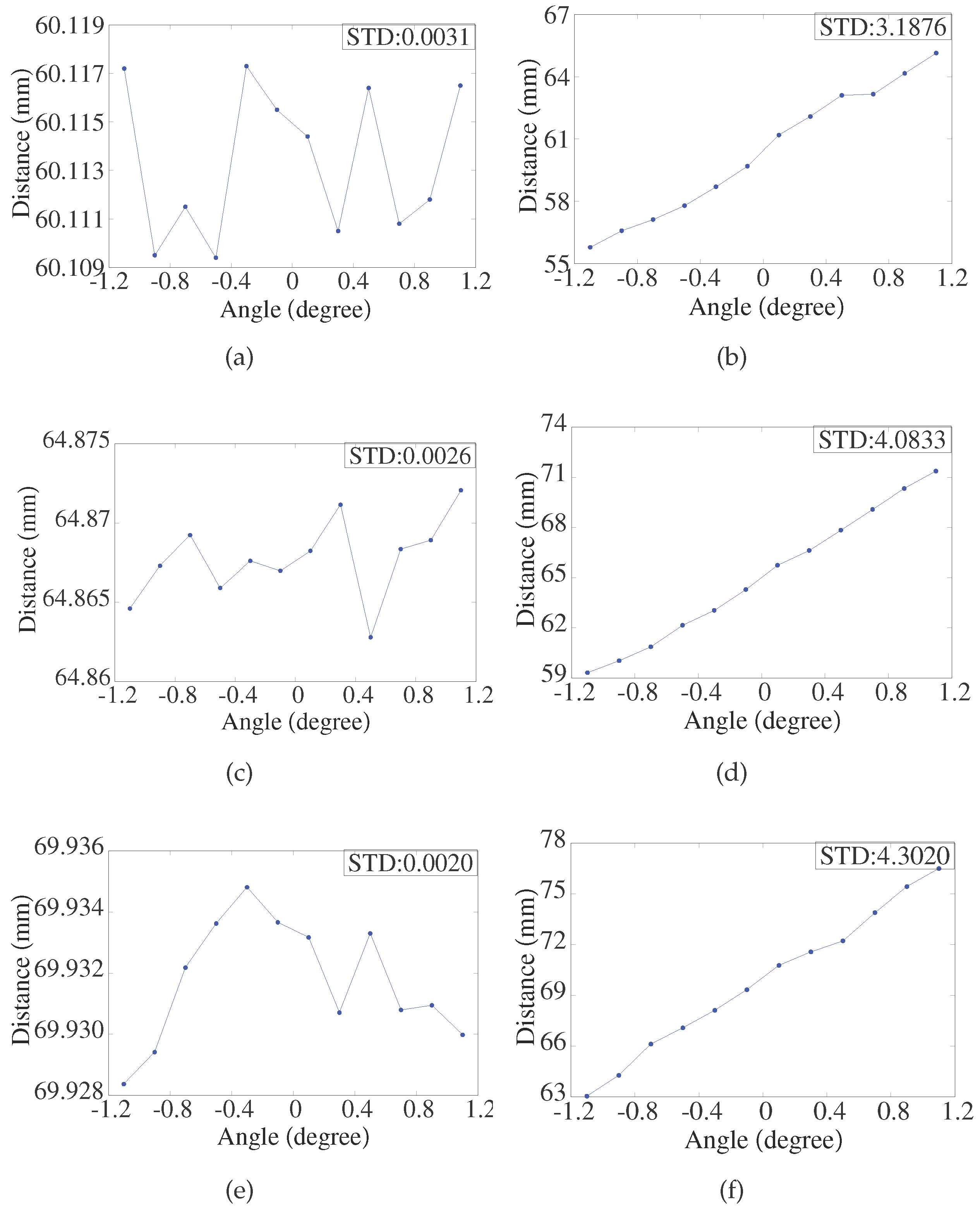
4.3. Calibration
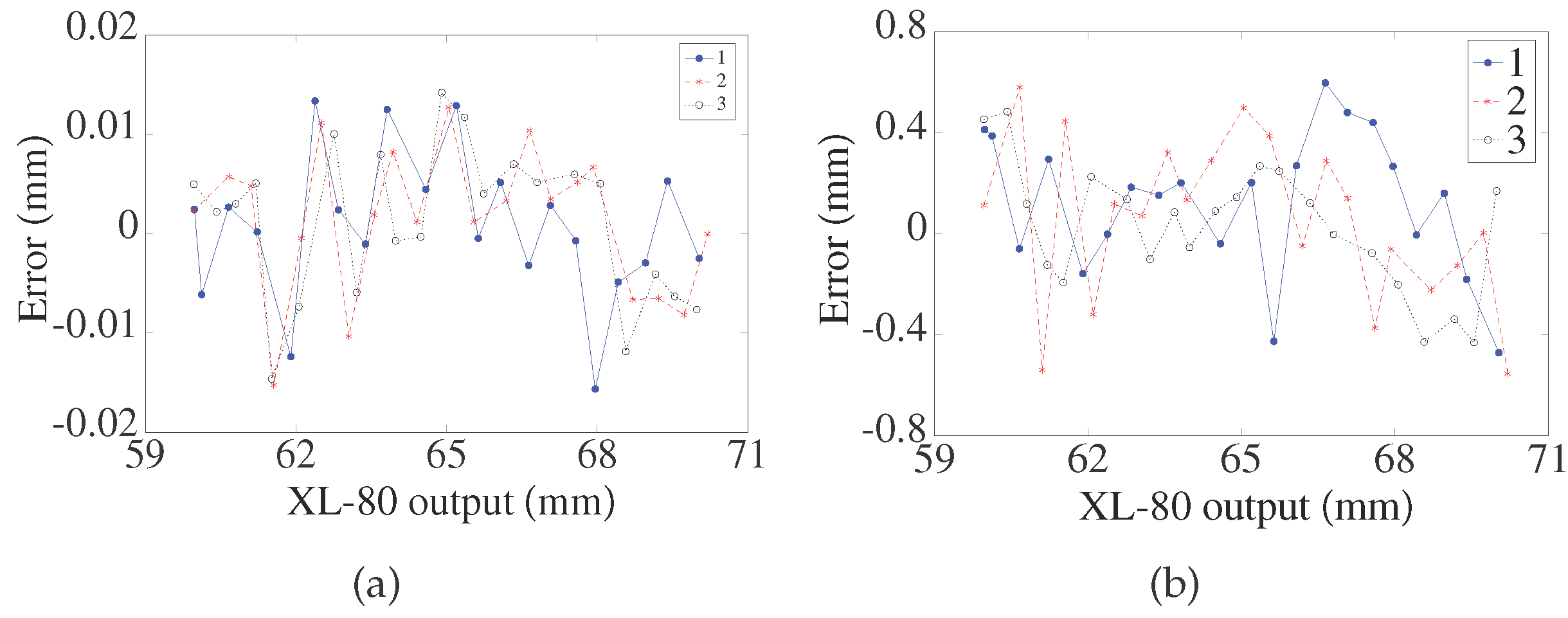
4.4. Repeatability Test
4.5. Nonlinearity Test
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, F.; Qu, X.; Ouyang, J. An automated inner dimensional measurement system based on a laser displacement sensor for long-stepped pipes. Sensors 2012, 12, 5824–5834. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Wang, Z.; Wu, Z.; Li, X.; Wang, L.; Liu, C. Calibration of Laser Beam Direction for Inner Diameter Measuring Device. Sensors 2017, 17, 294. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Li, B. A Rapid Method to Achieve Aero-Engine Blade Form Detection. Sensors 2015, 15, 12782–12801. [Google Scholar] [CrossRef] [PubMed]
- Scheimpflug, T. Method of Distorting Plane Imaged by Means of Lens or Mirrors. US Patent 751,347, 2 February 1904. [Google Scholar]
- Dorsch, R.G.; Häusler, G.; Herrmann, J.M. Laser Triangulation: Fundamental Uncertainty in Distance Measurement. Appl. Opt. 1994, 33, 1306–1314. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.K.; Kang, S.G.; Nam, J.S.; Park, K.H. Intensity Control of Triangulation Based PSD Sensor Independent of Object Color Variation. Sens. J. 2011, 11, 3311–3315. [Google Scholar] [CrossRef]
- Daneshpanah, M.; Harding, K. Surface sensitivity reduction in laser triangulation sensors. Procceedings of Dimensional Optical Metrology and Inspection for Practical Applications, San Diego, CA, USA, 21 August 2011. [Google Scholar]
- Shen, L.; Li, D.; Luo, F. A study on laser speckle correlation method applied in triangulation displacement measurement. Optik 2013, 124, 4544–4548. [Google Scholar] [CrossRef]
- Miks, A.; Novak, J.; Novak, P. Analysis of imaging for laser triangulation sensors under Scheimpflug rule. Opt. Expr. 2013, 21, 18225–18235. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Kim, K.C.; Kim, S.H.; Kwak, Y.K. Resolution enhancement using a diffraction grating for optical triangulation displacement sensors. In Proceedings of the Testing, Reliability, and Applications of Optoelectronic Devices, San Jose, CA, USA, 20 January 2001; pp. 102–108. [Google Scholar]
- Blais, F. Review of 20 years of range sensor development. J. Electron. Imaging 2004, 13, 231–243. [Google Scholar] [CrossRef]
- Loranger, F.; Laurendeau, D.; Houde, R. A fast and accurate 3-D rangefinder using the Biris technology: The TRID sensor. In Proceedings of the International Conference on Recent Advances in 3-D Digital Imaging and Modeling, Washington, DC, USA, 12–15 May 1997; pp. 51–58. [Google Scholar]
- Keyence Co., Ltd. Laser Displacement Sensor Technology Book. 2008. Available online: http://www1.keyence.com/topics/vision/lkg/book.php (accessed on 5 May 2017).
- Žbontar, K.; Podobnik, B.; Povše, F.; Mihelj, M. On-machine laser triangulation sensor for precise surface displacement measurement of various material types. In Proceedings of the Dimensional Optical Metrology and Inspection for Practical Applications II, San Diego, CA, US, 25 August 2013. [Google Scholar]
- Stalmashonak, A.; Zhavoronkov, N.; Hertel, I.V.; Vetrov, S.; Schmid, K. Spatial control of femtosecond laser system output with submicroradian accuracy. Appl. Opt. 2006, 45, 1271–1274. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Patel, K.; Govindarajan, J.; Kumar, A. Fuzzy logic based feedback control system for laser beam pointing stabilization. Appl. Opt. 2010, 49, 5143–5147. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, P.V. Fast Steering Mirror Technology: Active Beam Stabilization. 2001. Available online: http://optical-filters.newport.com/Support/MagazineFeatures/pdf/10390-578.pdf (accessed on 5 May 2017).
- Ibaraki, S.; Kitagawa, Y.; Kimura, Y.; Nishikawa, S. On the limitation of dual-view triangulation in reducing the measurement error induced by the speckle noise in scanning operations. Int. J. Adv. Manuf. Technol. 2016, 88, 731–737. [Google Scholar] [CrossRef]
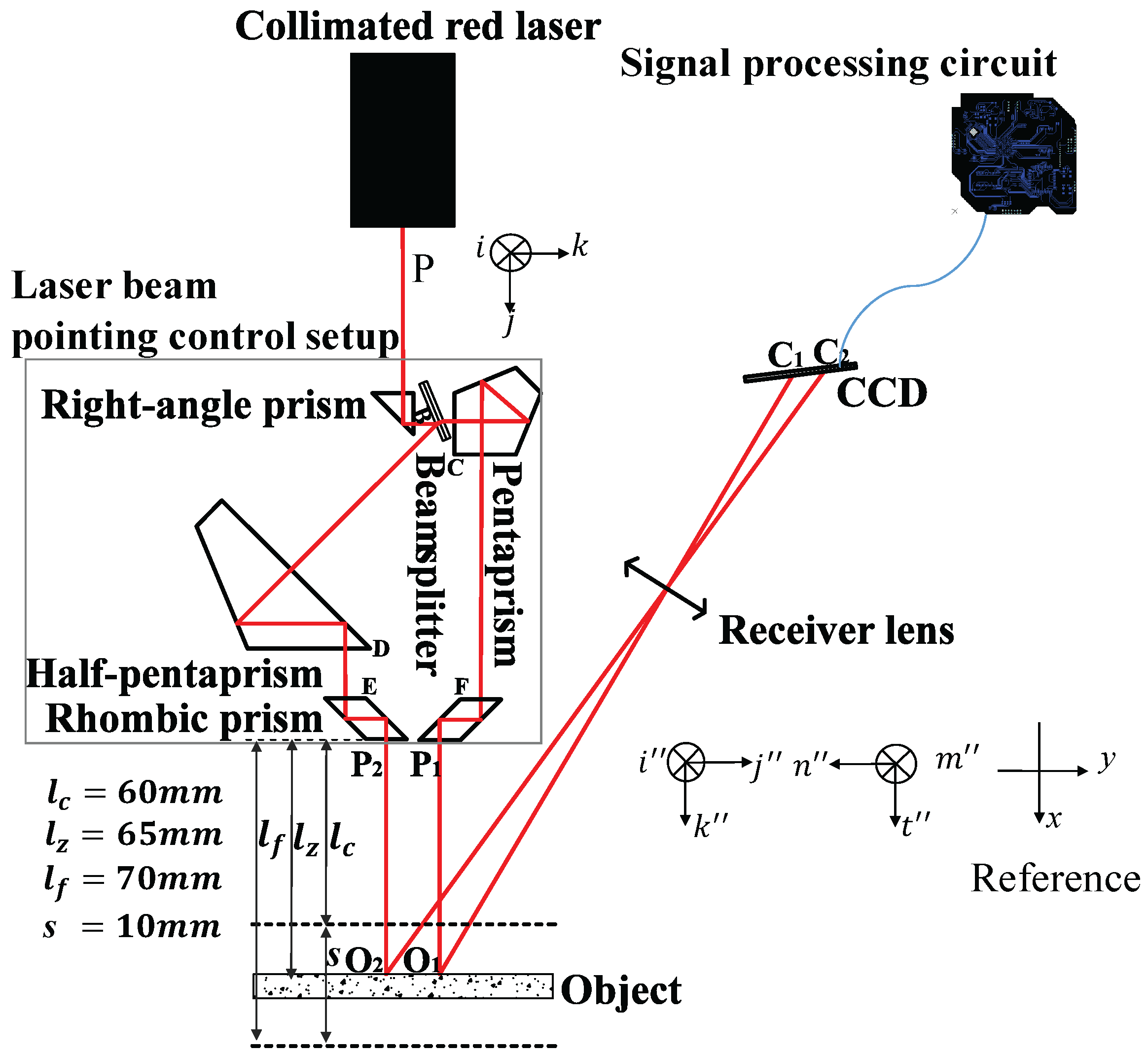




| Device | Manufacturer | Type | Major Parameters |
|---|---|---|---|
| CCD | Toshiba | TCD2566BFG | Resolution 5.25 |
| Ceramic gauge block | Seeman | WB02 | Size |
| Red collimated laser | / | KYL635N10-X1240 | |
| Right-angle prism | Fuyu Optics | / | Size |
| Pentaprism | XJT | WJ-151515 | Size |
| Half-pentaprism | Daheng Optics | / | Size |
| Rhombic prism | Union Optic | RBP0010 | Size |
| Beam splitter | / | / | Size |
| Receiver lens | / | / | Focus 26.054 |
| Rotational devices | Thorlabs | PRM/M | / |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Tao, W.; Zhang, Z.; Zhao, S.; Yin, X.; Zhao, H. Reduction of the Influence of Laser Beam Directional Dithering in a Laser Triangulation Displacement Probe. Sensors 2017, 17, 1126. https://doi.org/10.3390/s17051126
Yang H, Tao W, Zhang Z, Zhao S, Yin X, Zhao H. Reduction of the Influence of Laser Beam Directional Dithering in a Laser Triangulation Displacement Probe. Sensors. 2017; 17(5):1126. https://doi.org/10.3390/s17051126
Chicago/Turabian StyleYang, Hongwei, Wei Tao, Zhengqi Zhang, Siwei Zhao, Xiaoqia Yin, and Hui Zhao. 2017. "Reduction of the Influence of Laser Beam Directional Dithering in a Laser Triangulation Displacement Probe" Sensors 17, no. 5: 1126. https://doi.org/10.3390/s17051126
APA StyleYang, H., Tao, W., Zhang, Z., Zhao, S., Yin, X., & Zhao, H. (2017). Reduction of the Influence of Laser Beam Directional Dithering in a Laser Triangulation Displacement Probe. Sensors, 17(5), 1126. https://doi.org/10.3390/s17051126






