Operating Point Self-Regulator for Giant Magneto-Impedance Magnetic Sensor
Abstract
:1. Introduction
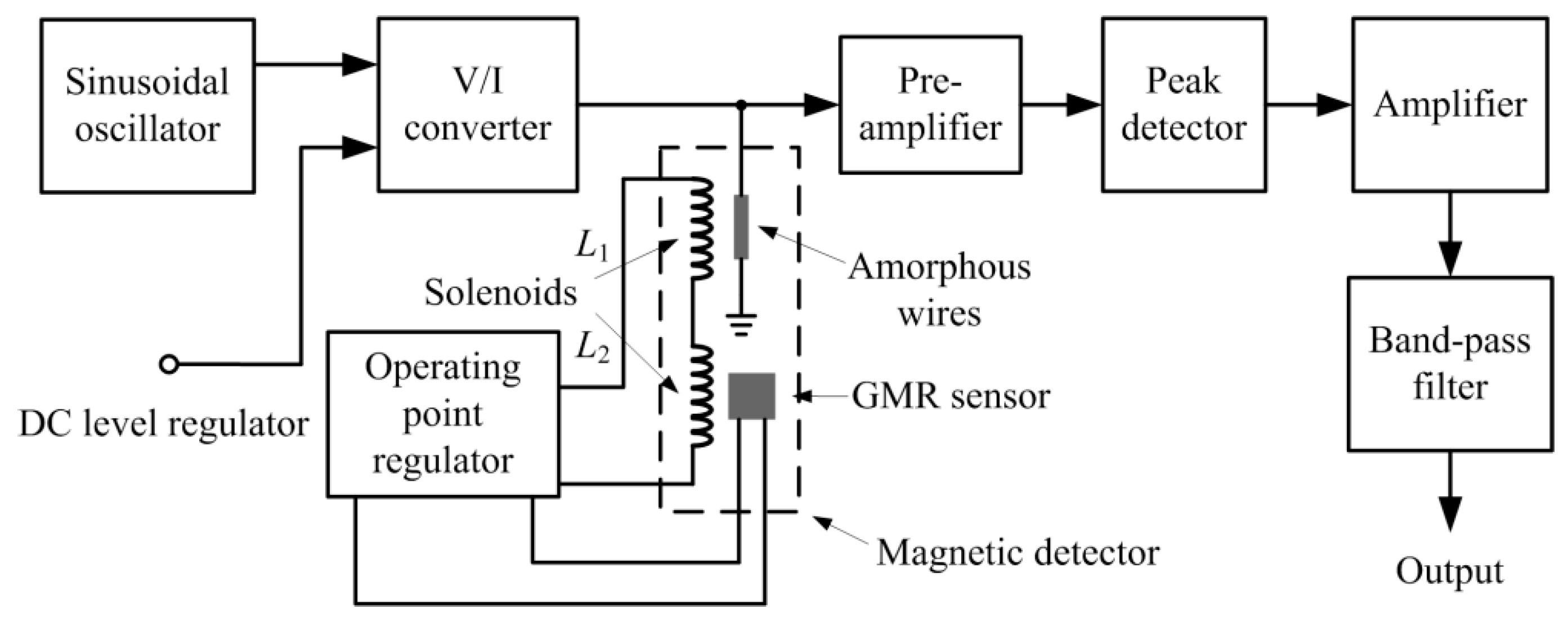
2. The Structure of GMI Sensor
2.1. The Structure of Magnetic Detector
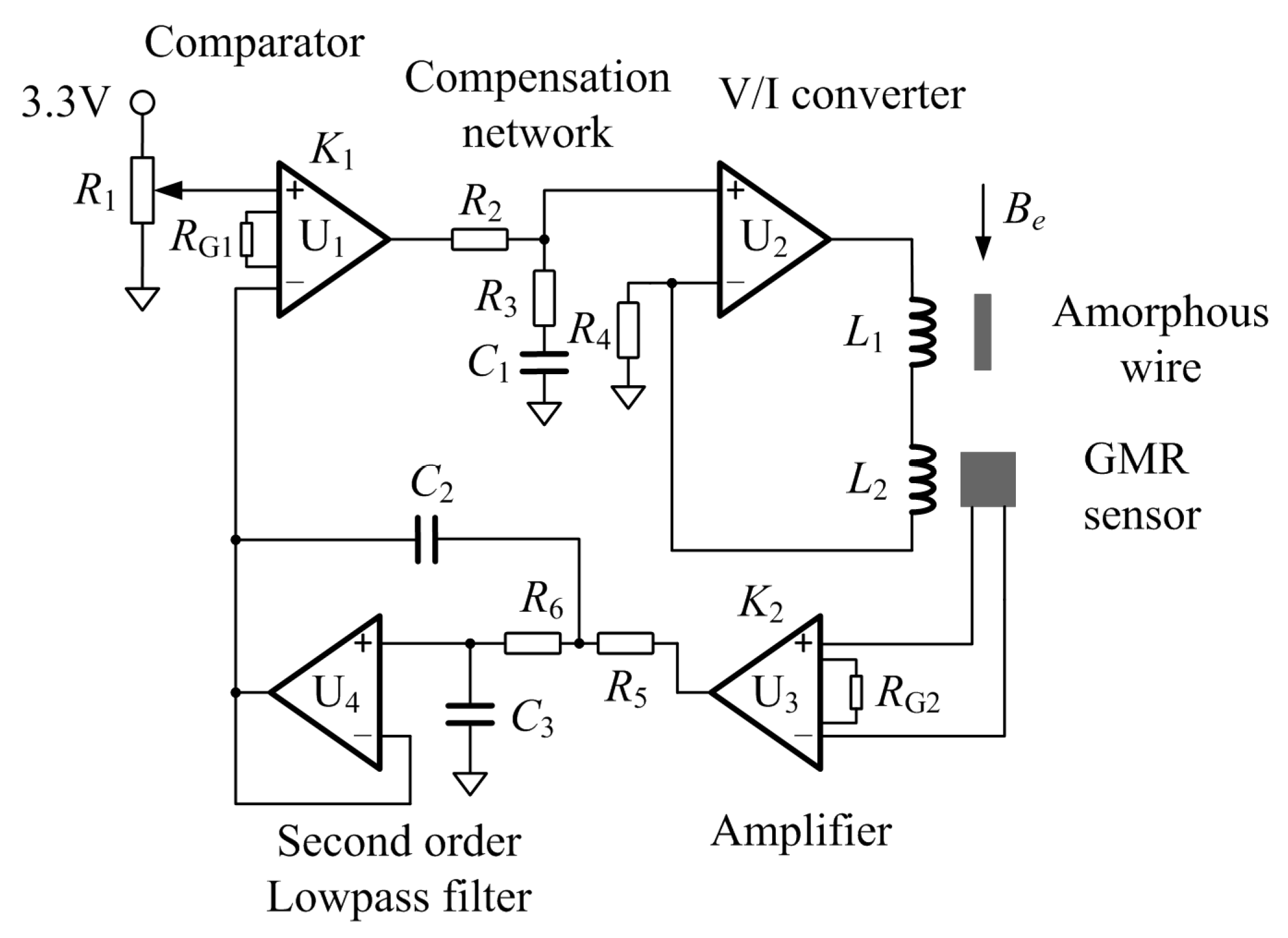
2.2. The Design of GMI Sensor
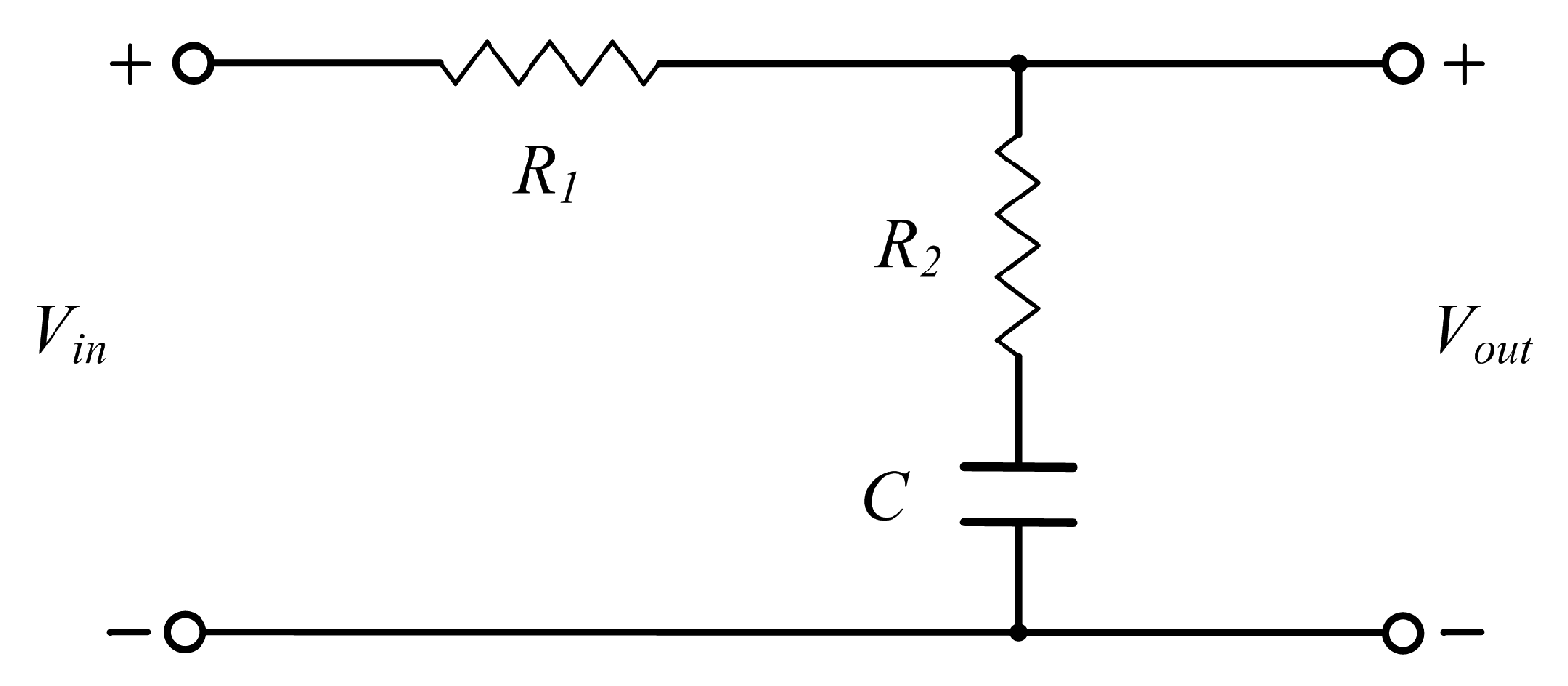
2.3. The Operating Point Self-Regulator and the Passive Phase-Lag Compensation Network
3. Results and Discussion
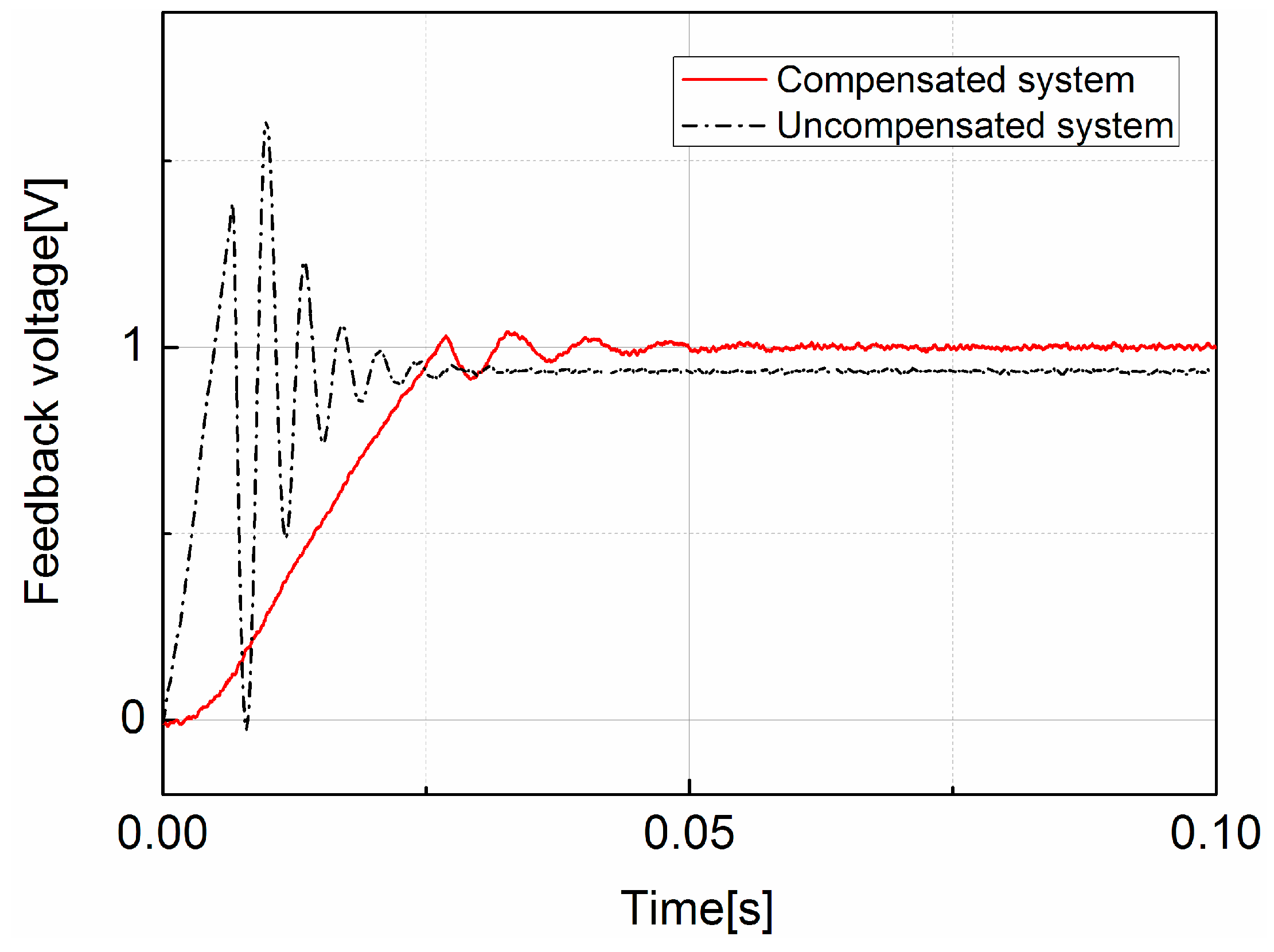
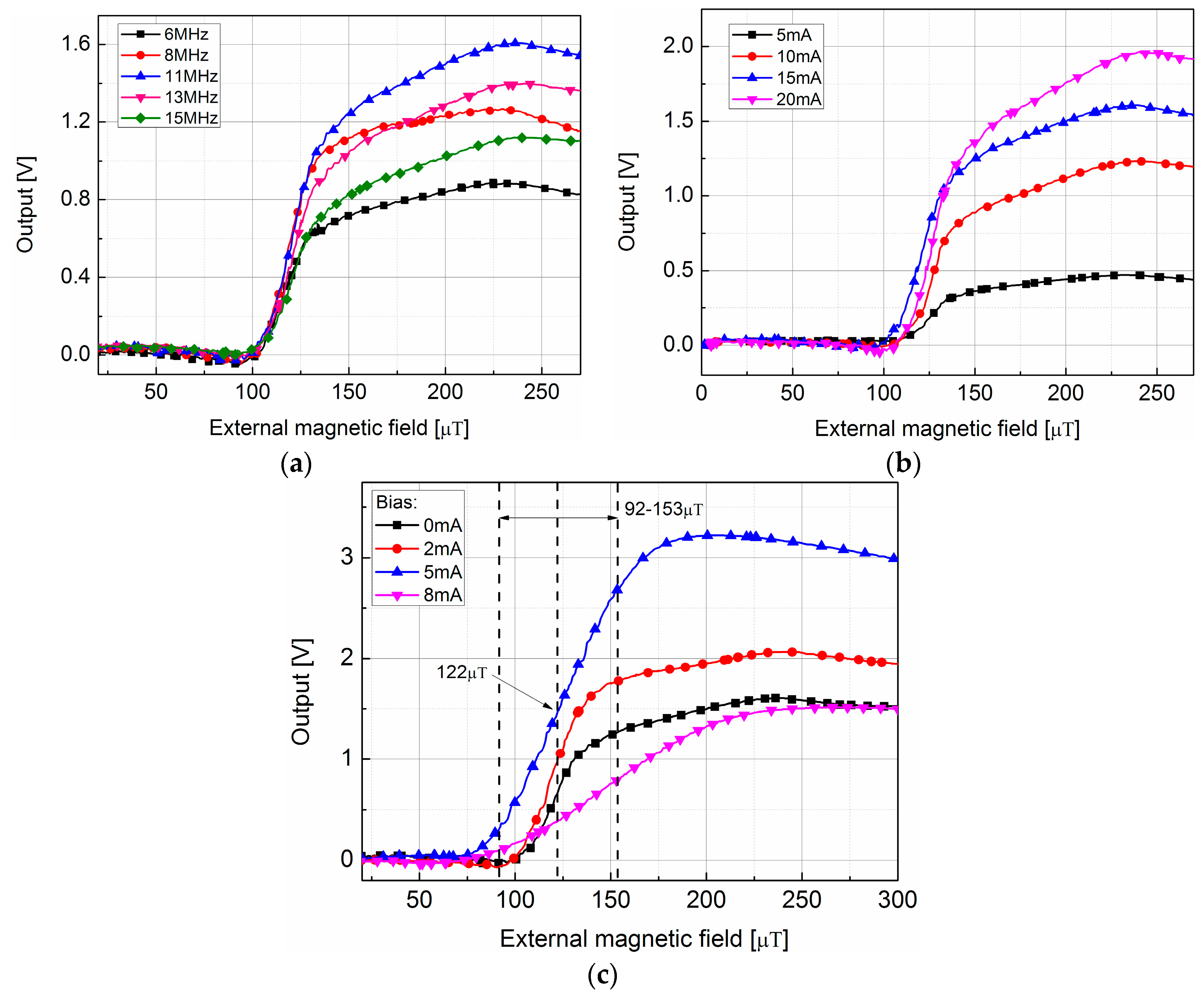
3.1. The Perfromance of the Operating Point Self-Regulator
3.2. The Decision of the Operating Point
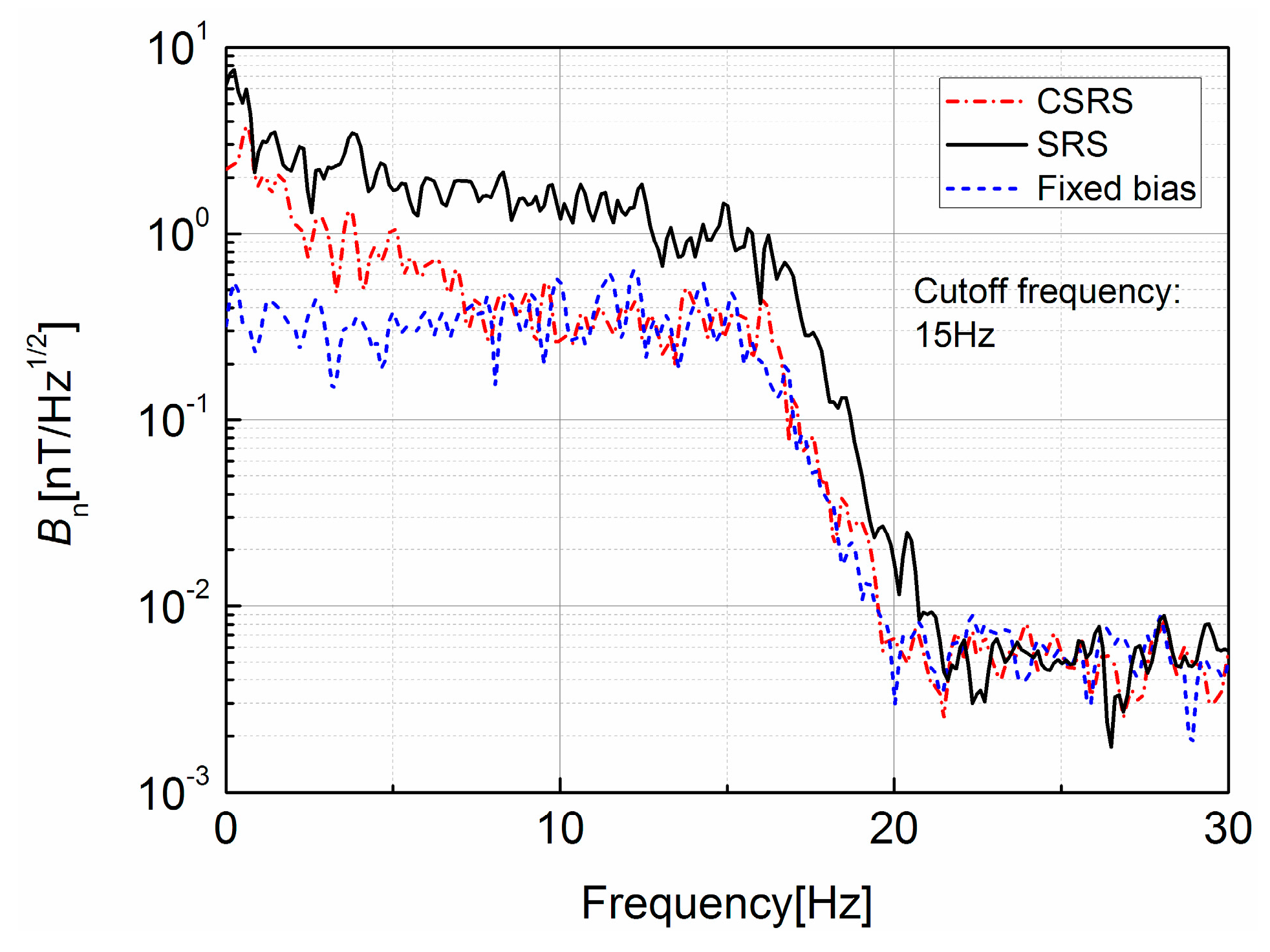
3.3. The GMI Sensor with the Compensated Self-Regulating System
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Phan, M.-H.; Peng, H.-X. Giant magnetoimpedance materials: Fundamentals and applications. Prog. Mater. Sci. 2008, 211, 980–985. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Shen, L.P.; Cai, C.M.; Panina, L.V. Sensitive micro magnetic sensor family utilizing magneto-impedance (MI) and stress-impedance (SI) effects for intelligent measurements and controls. Sens. Actuators A Phys. 2001, 91, 85–90. [Google Scholar] [CrossRef]
- Olivera, J.; Cruz-Blas, C.A.; Gomez-Polo, C. Comprehensive analysis of a micro-magnetic sensor performance using amorphous microwire MI element with pulsed excitation current. Sens. Actuators A Phys. 2011, 168, 90–94. [Google Scholar] [CrossRef]
- Knobel, M.; Pirota, K.R. Giant magnetoimpedance: Concepts and recent progress. J. Magn. Magn. Mater. 2002, 242–245, 33–40. [Google Scholar] [CrossRef]
- Mohri, K.; Panina, L.V.; Uchiyama, T.; Bushida, K.; Noda, M. Sensitive and quick response micro magnetic sensor utilizing magneto-impedance in Co-rich amorphous wire. IEEE Trans. Magn. 1995, 31, 1266–1275. [Google Scholar] [CrossRef]
- Kuzminski, M.; Nesteruk, K.; Lachowicz, H.K. Magnetic field meter based on the giant magnetoimpedance effect. Sens. Actuators A Phys. 2008, 141, 68–75. [Google Scholar] [CrossRef]
- Das, T.K.; Mitra, A.; Mandal, S.K.; Roy, R.K.; Banerji, P.; Panda, A.K. Parametric controls on gaint magnetoimpedance (GMI) behaviour of CoFeSiBCr amorphous wires for prospective sensor applications. Sens. Actuators A Phys. 2014, 220, 382–387. [Google Scholar] [CrossRef]
- Asfour, A.; Yonnet, J.-P.; Zidi, M. Toward a novel digital electronic conditioning for the GMI magnetic sensors: The software defined radio. IEEE Trans. Magn. 2015, 51, 4001004. [Google Scholar] [CrossRef]
- Uchiyama, T.; Mohri, K.; Honkura, Y.; Panina, L.V. Recent advances of Pico-Tesla resolution magneto-impedance sensor based on amorphous wire CMOS IC MI sensor. IEEE Trans. Magn. 2012, 48, 3833–3839. [Google Scholar] [CrossRef]
- Melo, L.G.C.; Menard, D.; Yelon, A.; Ding, L.; Saez, S.; Dolabdjian, C. Optimization of the magnetic noise and sensitivity of giant magnetoimpedance sensors. J. Appl. Phys. 2008, 103, 033903. [Google Scholar] [CrossRef]
- Kollu, P.; Jin, L.; Kim, K.W.; Yoon, S.S.; Kim, C.G. One-dimensional AGMI sensor with Co66Fe4Si15B15 ribbon as sensing element. Appl. Phys. A 2008, 90, 533–536. [Google Scholar] [CrossRef]
- Zhang, D.S.; Pan, Z.M.; Zhou, H.; Zhang, W.N. Magnetic sensor based on giant magneto-impedance effect using the self-regulating technology on the bias magnetic field. Sens. Actuators A Phys. 2016, 249, 225–230. [Google Scholar] [CrossRef]
- Yu, G.L.; Bu, X.Z.; Xiang, C.; Xu, H. Design of a GMI magnetic sensor based on longitudinal excitation. Sens. Actuators A Phys. 2010, 161, 72–77. [Google Scholar]
- Liu, J.S.; Sun, J.F.; Xing, D.W.; Xue, X. Twin-detector sensor of Co-rich amorphous microwires to overcome GMI fluctuation induced by ambient temperature. IEEE Trans. Magn. 2012, 48, 2449–2454. [Google Scholar] [CrossRef]
- Peng, H.-X.; Qin, F.X.; Phan, M.-H. Ferromagnetic Microwire Composites—From Sensors to Microwave Applications; Springer: Manchester, UK, 2016. [Google Scholar]
- Ipatov, M.; Zhukova, V.; Zhukov, A.; Gonzalez, J. Expanding the longitudinal magnetoimpedance sensor range by direct bias current. J. Appl. Phys. 2013, 113, 203902. [Google Scholar] [CrossRef]
- Asfour, A.; Zidi, M.; Yonnet, J.P. High frequency amplitude detector for GMI magnetic sensors. Sensors 2014, 14, 24502–24522. [Google Scholar] [CrossRef] [PubMed]
- Sandacci, S.; Makhnovskiy, D.; Panina, L.; Mohri, K.; Honkura, Y. Off-diagonal impedance in amorphous wires and its application to linear magnetic sensors. IEEE Trans. Magn. 2004, 40, 3505–3511. [Google Scholar] [CrossRef]
- Gudoshnikov, S.; Usov, N.; Nozdrin, A.; Ipatov, M.; Zhukov, A.; Zhukova, V. Highly sensitive magnetometer based on the off-diagonal GMI effect in Co-rich glass-coated microwire. Phys. Status Solidi A 2014, 211, 980–985. [Google Scholar] [CrossRef]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems; Addison Wesley Publishing Co.: Boston, MA, USA, 1995. [Google Scholar]
- Silva, E.C.; Gusmao, L.A.P.; Barbosa, C.R.H.; Monteiro, E.C.; Machado, F.L.A. High sensitivity giant magnetoimpedance (GMI) magnetic transducer: Magnitude versus phase sensing. Meas. Sci. Technol. 2011, 22, 035204. [Google Scholar] [CrossRef]






| Uncompensated System | Compensated System | |
|---|---|---|
| Controller | Gain, K1 | Phase-lag network |
| Step overshoot | 72.2% | 4.2% |
| Settling time (milliseconds) | 23 | 35 |
| Steady-state error for step | 5.6% | 2% |
| Magnetic Field (μT) | 43.4 | 62 | 80.6 | 99.2 | 117.9 | 136.5 |
| Output (increase) (V) | 0.4346 | 0.5207 | 0.6086 | 0.699 | 0.7987 | 0.8890 |
| Output (decrease) (V) | 0.435 | 0.5260 | 0.6125 | 0.7026 | 0.7989 | 0.8909 |
| Magnetic Field (μT) | 155 | 173.7 | 192 | 210.9 | 229.5 | 248.1 |
| Output (increase) (V) | 0.9827 | 1.0834 | 1.1790 | 1.2768 | 1.3773 | 1.4887 |
| Output (decrease) (V) | 0.9843 | 1.0846 | 1.1833 | 1.2849 | 1.3834 | 1.4887 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Pan, Z.; Zhang, D. Operating Point Self-Regulator for Giant Magneto-Impedance Magnetic Sensor. Sensors 2017, 17, 1103. https://doi.org/10.3390/s17051103
Zhou H, Pan Z, Zhang D. Operating Point Self-Regulator for Giant Magneto-Impedance Magnetic Sensor. Sensors. 2017; 17(5):1103. https://doi.org/10.3390/s17051103
Chicago/Turabian StyleZhou, Han, Zhongming Pan, and Dasha Zhang. 2017. "Operating Point Self-Regulator for Giant Magneto-Impedance Magnetic Sensor" Sensors 17, no. 5: 1103. https://doi.org/10.3390/s17051103
APA StyleZhou, H., Pan, Z., & Zhang, D. (2017). Operating Point Self-Regulator for Giant Magneto-Impedance Magnetic Sensor. Sensors, 17(5), 1103. https://doi.org/10.3390/s17051103





