1. Introduction
The global navigation satellite system (GNSS) plays an increasingly important role in military and civil areas; however, the risk caused by the vulnerability of GNSS signals is getting more and more serious. Therefore, interference mitigation techniques are absolutely essential to ensure the reliability, accuracy and continuity of GNSS services. In terms of the characteristics of the GNSS, one way of enhancing its ability of mitigating radio frequency interferences is to improve the design of navigation satellites [
1], for example optimizing the structure of signals and increasing the power of transmitters; but, these methods are too costly in terms of the design cycle and material resources. The other way is to improve the anti-jamming performance of GNSS receivers, which has attracted significant attention due to its low cost, high flexibility and great scalability.
The interference mitigation techniques for GNSS receivers can be classified into the time-domain, transform-domain, spatial and spatial-time processing [
2]. On account of the characteristics of interferences in the time-domain and transform-domain, many methods have been extensively studied (e.g., [
3,
4,
5,
6]). The time-domain and frequency-domain processing methods are mainly used for suppressing fewer stationary narrow-band interferences. The time-frequency processing is one of the most powerful methods for suppressing the interfering signal, which has more concentrated energy distribution in the time-frequency domain than GNSS signals. For example, Chien et al. proposed to generate a reference signal by using wavelet-packet-transform-based adaptive predictors and subtracting the refined interfering signal from the received signal [
7]. Additionally, it is effective to combat chirp interferences and single-tone interferences with a high interference-to-signal power ratio. However, when they are used to combat wideband interferers whose time-frequency characteristics are irregular (such as Gaussian interferers) or multiple interferences whose time and frequency characteristics are varied and vary rapidly in the frequency domain, their performance degrades seriously.
The space-based methods utilizing an antenna array are able to effectively mitigate narrowband and wideband interferences no matter what their time and frequency characteristics are. For example, the minimum variance distortionless response (MVDR) beamformer [
8] is one of the most powerful spatial processing methods, which has a distortionless response for the desired signal while rejecting all interferences arriving from other directions. Additionally, the spatial processing has been mainly used for interference mitigation in GNSS applications [
9]. According to the energy of GNSS signals in the receiver being less than that of the thermal noise, [
10] drew the attention to mitigating interferences whose power is significantly higher than that of global position system signals by employing the minimum power distortionless response (MPDR) beamformer. Additionally, its effectiveness is doubtless as a verified method by practice. Nevertheless, the number of interferences that can be dealt with is limited to the number of antenna elements. Antenna design complexity increases with the number of elements, and so does the cost. In addition to that, given a limited physical space, placing several antenna elements close to each other could lead to undesired interactions, which will degrade the performance. In order to deal with more interferences with a limited number of antenna elements, the spatial temporal adaptive processing (STAP) is introduced [
11]. By combining time and spatial processing, it is possible to increase the number of suppressed narrowband interfering signals without extra elements in the array. Although their superior advantages are obvious and desirable, the STAP may introduce cross-correlation function biases and distortions, which can result in inferior position estimates [
11,
12,
13]. This is mainly because of the temporal part of filtering [
14] and the non-linearity behavior of its frequency response [
15]. These biases and distortions vary according to the direction of arrival (DOA) and the number of interfering signals. Additionally, each one of the distortions is unique for each desired signal. To obtain accurate position and time solutions, some methods reducing the distortions and biases have been studied [
16,
17]. They reduce the DoF of interferences mitigation and bring more complexity both in arithmetic and implementation.
In addition, since the jamming technology develops rapidly and the electromagnetic environment is increasingly complex, there may be multiple types of interfering signals presenting simultaneously rather than only one or one type of interfering signals in the receiving environment. Although existing interference mitigation methods are able to improve the performance of GNSS receivers in the presence of interferences, there are enormous challenges when they suppress multiple types of interferences: (1) the hardware or space costs are enormous; (2) when the DOA of the interference (especially for the wideband interference) is close to the GNSS signal, their performance degrades seriously; (3) the methods using both spatial and time-/frequency-domain processing may distort the GNSS signals.
To address the above problems, some cascaded multi-type interferences mitigation methods using frequency and spatial (or spatial-time) domains are introduced (e.g., [
18,
19]). These methods are “simple cascades” of existing techniques without considering the mutual overlaps of different signals. It is one of the obvious disadvantages that when the narrowband interfering signals fall in the wideband Gaussian interferences, the pre-stage methods may be invalid.
In the coexistence of multiple types of interfering signals, there may be overlaps among interfering signals in the time, frequency and spatial domains. It is an enormous challenge for existing methods to deal with multiple interferences. To address this problem, we introduce the signal sparse decomposition theory [
20] into array signal processing. The sparse decomposition theory is gaining significant attention due to its advantages in digital signal processing and has been successfully applied to many fields, for example signal detection [
21], clutter and jamming suppression [
22]. Then, a cascaded multi-type interferences mitigation method combining improved DCQGMP-based sparse decomposition and the MPDR beamformer is proposed in this paper. In the first stage, the single-tone (multi-tone) and linear chirp interfering signals can be detected and canceled by utilizing an improved DCQGMP-based sparse decomposition according to their sparsity in the over-complete dictionary. In order to reduce the running time and detect interference signals that may fall in the other wideband interferences effectively, a novel design strategy of the over-complete dictionary and MP algorithm is proposed, and DCQGA [
23] is used to approach the MP optimization problem. To solve the problems of slow convergence speed, low search precision and poor robustness in the traditional DCQGA, the encoding mode and rotation angle computing function are improved. In the second stage, the MPDR beamformer is adopted to suppress the residual interferences, which is able to enhance the steering gain of the DOA of GNSS signals while nullifying interferences. Finally, the performance of the improved DCQGA is verified by a simulation. Additionally, several simulation scenarios are considered to show the effectiveness of the proposed method for multi-type interferences mitigation, and the compared methods are the well-known MPDR beamformer [
10] and the distortionless space-time processor [
16].
2. Signal Model
The received signal should be an aggregate of GNSS signals, the receiver thermal noise and interfering signals. For the convention of description, suppose that there is only one GNSS signal contaminated by
K interferences and the thermal noise. Additionally, they are independent of each other and adhere to the narrowband model. Then, for the
m-th sampling time, the complex representation of the signal vector received by an arbitrary antenna array with
N elements can be expressed as:
where
is the sampling period,
, indicates the
-th interfering signal and
is the corresponding steering vector.
denotes the GNSS signal, and
represents the receiver thermal noise. Additionally,
a, representing the steering vector of the GNSS signal whose dimension is
, can be written as:
where
denotes the wavelength of received signals;
is a 3 × 1 unit vector representing the DOA of the GNSS signal;
,
is a 3 × 1 unit vector pointing to the
-th antenna element; ‘
’ denotes transpose.
The interfering signal can be classed into different types according to the interferers generating it. In this paper, interferences are considered to be in the class of continuous wave interferences (CWI) and wideband Gaussian noise signals, which can be written as:
where
denotes a Gaussian interfering signal with zero mean and
variance; and
,
represent the number of CWI and wideband Gaussian noise signals. In general, the CWI,
, usually is a frequency-modulated signal with an almost constant amplitude. The linear chirp and single-tone (or multi-tone) signals, which are the main types of CWI [
24], are considered in the following analysis. Their time-domain function can be expressed as:
where
A is the interfering signal amplitude;
B and
represent the bandwidth and frequency modulation period of the chirp signal, respectively;
is the time offset; and
represents the phase.
3. The Proposed Method
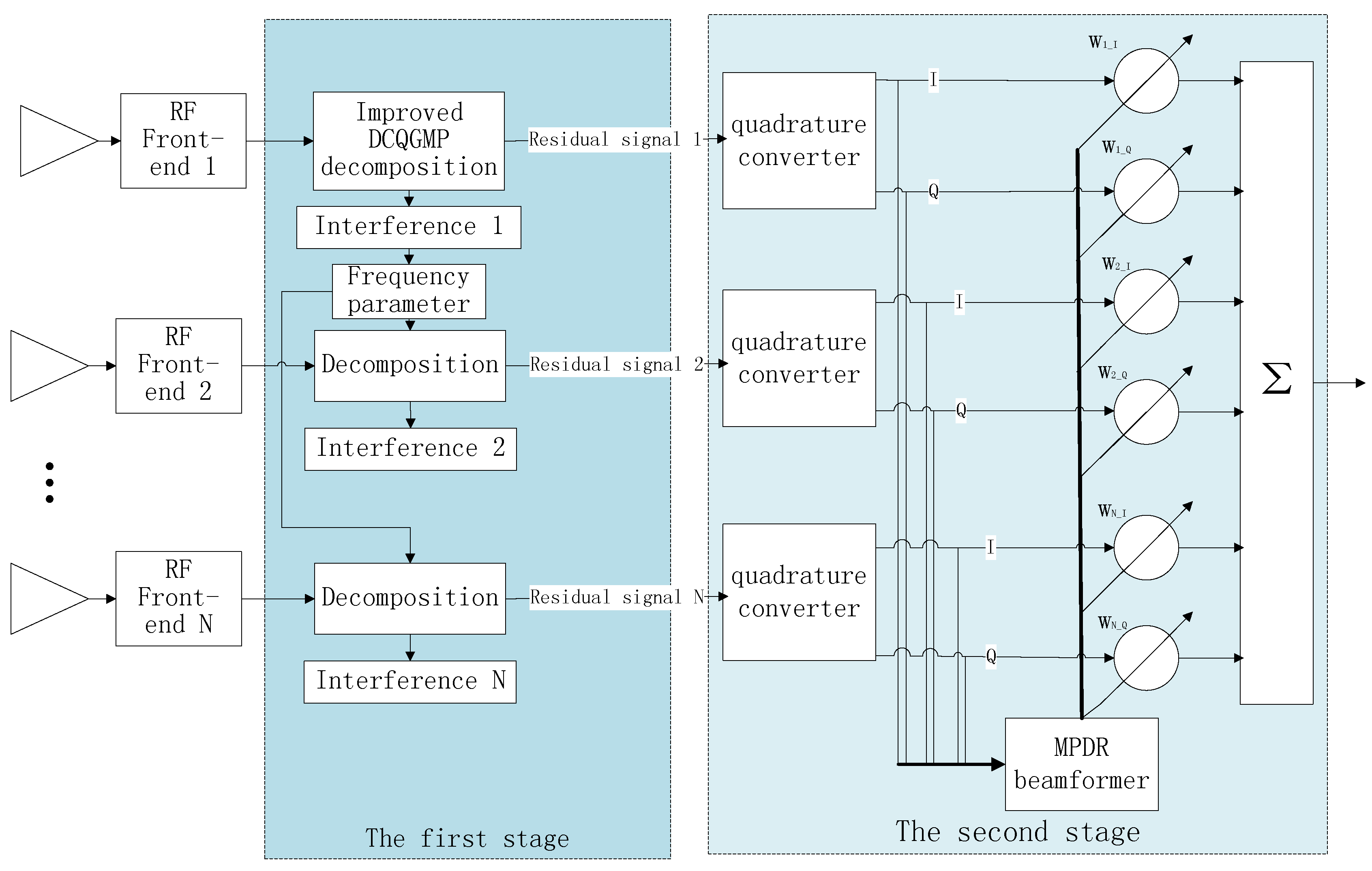
In the coexistence of multiple types of interfering signals, there may be overlaps among different interfering signals in the time, frequency and spatial domains. How to deal with these interferences according to their different characteristics in different dimensions is an enormous challenge for existing methods. Focusing on this issue, a cascaded multi-type interferences mitigation method combining improved DCQGMP-based sparse decomposition and the MPDR beamformer is introduced, whose block diagram is shown in
Figure 1. The signal model in
Section 2 is a complex expression; however, there are only real signals in physical circuits. The signals in the RF front-end are real, and the in-phase (I) and quadrature (Q) signals obtained by using a quadrature converter usually are treated as the real part and imaginary part of the complex expression for array processing, respectively. Although it is feasible to suppress the CWI before or after the quadrature converter since the envelopes of CWI signals are both continuous in the two parts, the calculation of detecting and canceling CWI before the quadrature converter is half of doing that after the quadrature converter. Accordingly, the CWI signals’ detection and suppression are applied before the orthogonal transformation. In the first stage as shown in
Figure 1, the received signals are sparsely decomposed to excise interfering signals, which can be sparse represented in the over-complete dictionary. We re-design the over-complete dictionary according to the characteristics of CWI signals to make the sparse decomposition suitable for multi-type interferences mitigation, and the necessary conditions for CWI signal detecting are analyzed, especially when the power of the CWI signals is lower than that of the wideband Gaussian interferences. In order to reduce the computation amount of the traditional MP algorithm, the DCQGA is used for MP optimization. Additionally, an improved DCQGA with the characteristic of high search density, adaptive step-size updating is suggested to improve the convergence rate and computational precision. Then, on the basis of these, a multi-channel signal interference suppression method based on the improved DCQGMP and a ratio terminate principle are proposed. In the second stage, the spatial DoF of the antenna array is employed to nullify the residuary interferences (such as Gaussian noise interferences) by utilizing the MPDR beamformer.
3.1. Multi-Channel Signal Interference Suppression Method Based on Improved DCQGAMP
3.1.1. Matching Pursuit Decomposition
The MP algorithm, dealing with the signal sparse decomposition effectively, is an iterative “greedy” algorithm [
21]. Compared with other sparse decomposition algorithms, it has flexibility and adaptability to signals. The key idea of this algorithm is that at each iteration, the best atom is selected and regarded as one of the components of the sparse representation.
Assume that is the signal to be decomposed, and define as the over-complete dictionary of functions, where is an atom and is the parameter set of atoms. The inner product of and is defined as the similarity measure function Z, i.e., . After l iterations, we will get a codebook . Additionally, the basic implementation steps of MP are as follows:
Initialization: ; ; .
Compute the inner products for all atoms; find the maximum amongst all inner products: ; and add to codebook B.
Compute the residual signal: ; if precision is reached, then stop; otherwise , and iterate to Step 2.
If the termination condition is reached after the
L steps’ decomposition, the signal can be expressed as:
where
is the residual signal.
3.1.2. Analysis of Interference Detection Performance
In order to facilitate the analysis, only one single-tone or linear chirp interfering signal is considered in the following analysis, and assume that there are
wideband Gaussian noise interfering signals. The GNSS signals are able to be ignored due to their relatively weak energy. Then, without considering the array steering vector, for
M snapshots, at the
n-th antenna, the signal before the quadrature frequency conversion can be written as:
in which:
where
p is the energy of the CWI signal and
represents the frequency parameter.
where
is the
i-th Gaussian interfering signal with zero mean and
variance and
represents the real part of the complex expression. Then,
ℵ can be regarded as a Gaussian noise with zero mean and
variance.
Suppressing interferences using MP-based sparse decomposition can be considered as a process by which the received signal is adaptively decomposed in an over-complete dictionary of functions, providing a sparse linear expansion of CWI signals and the residual signal in which there is no CWI. The detectability of the interference signal affects the performance of the method, which is mainly determined by the over-complete dictionary, the interfering signal energy and the number of snapshots.
The over-complete dictionary should be constructed according to the broadband of desired signals and the prior knowledge about the types of interfering signals that can be obtained by experience or other investigative means. The real representation of CWI signals can be expressed by a cosine model with bandwidth, modulation period, initial frequency, fixed frequency and phase parameters. Hence, the over-complete dictionary should contain the corresponding parameter space. Most simply, select a series of linear frequency-modulated signals as atoms in the over-complete dictionary, which could be expressed as:
where
is the normalized coefficient;
, in which
and
represent the bandwidth and the center frequency of the atoms, respectively;
,
and
represent the frequency modulation period, the time offset and the initial frequency of the atom, respectively. The values of
,
,
and
form the parameter set
, and they are selected at regular intervals according to their respective reasonable ranges and the number of atoms. The greater the number of atoms is, the higher the decomposition accuracy is.
The best atom is selected by looking for the maximum measure function
Z:
Assume that the best matching atom,
, is in the over-complete dictionary and has been known. Then:
where
and
represent the frequency spacing and the phase spacing, respectively. Additionally, since
M is large enough, we can suppose that the normalized coefficients,
, are equivalent to each other in the following analysis. In general digital signal processing,
satisfies the Nyquist sampling theorem or the bandpass sampling theorem, and
M is large enough, so the latter is much less than the former in the polynomial, then:
Additionally, the maximum value of
is the inner product of the signal to be decomposed, and the best matching atom:
Since
ℵ is the Gaussian noise with zero mean and
variance, then
is the Gaussian noise with zero mean and
variance. Additionally, about 99.997 percent of the values drawn from a normal distribution are within four standard deviations
away from the mean. Therefore, the necessary condition for detecting CWI signals is that the number of samples
M should satisfy:
then, that is:
3.1.3. The Mutual Influence of Multiple Signals
In the previous section, we have analyzed the interference detection performance of the MP-based sparse decomposition when there is one interfering signal. However, there may be multiple signals to be dealt with. Then, taking the scenario that there are two interfering signals as an example, we analyze the effects on the method due to the presence of multiple signals. The two interfering signals can be written as:
where
and
are the energy of Interfering Signals 1 and 2, respectively;
and
represent the frequency parameter of the two interfering signals, respectively.
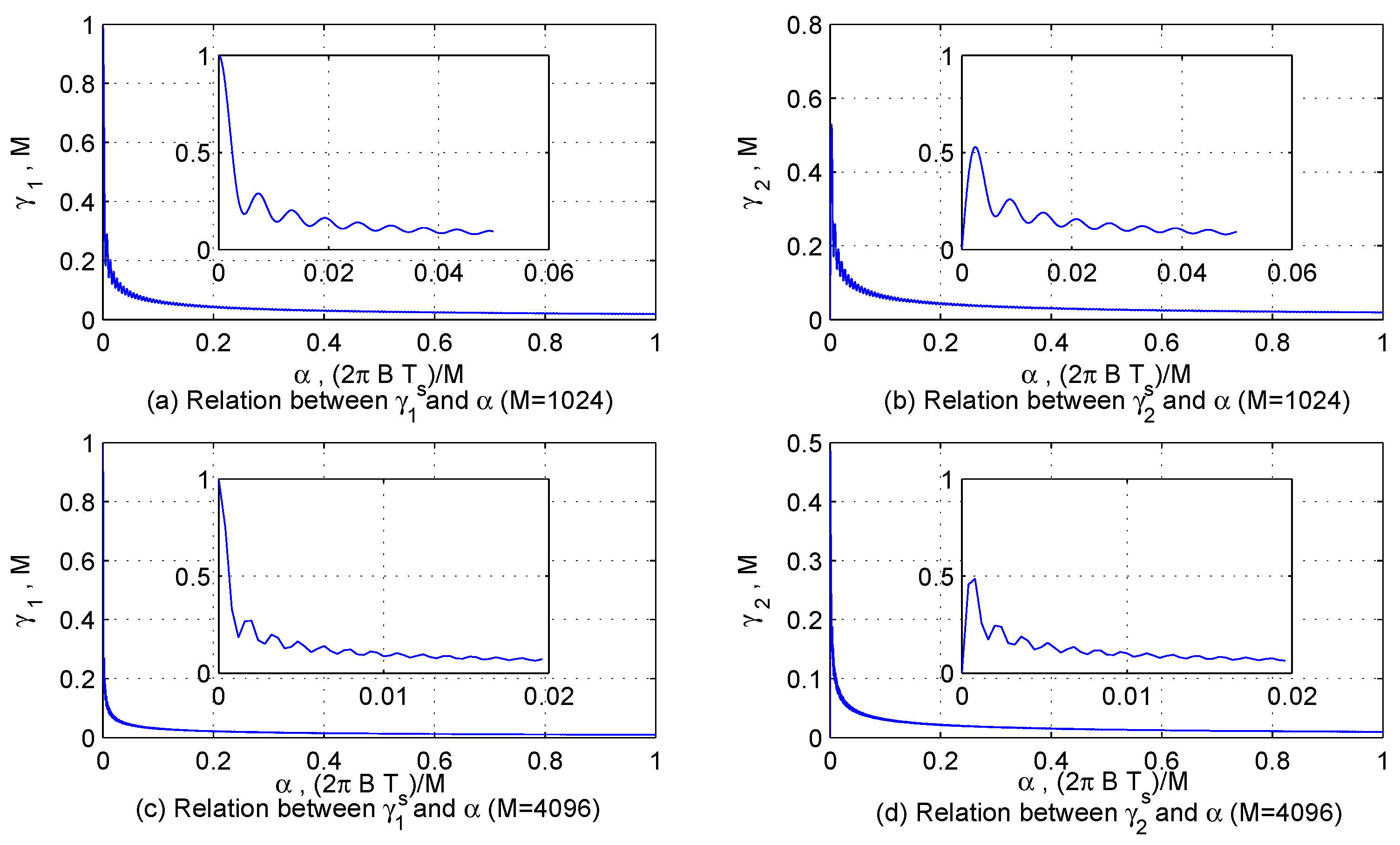
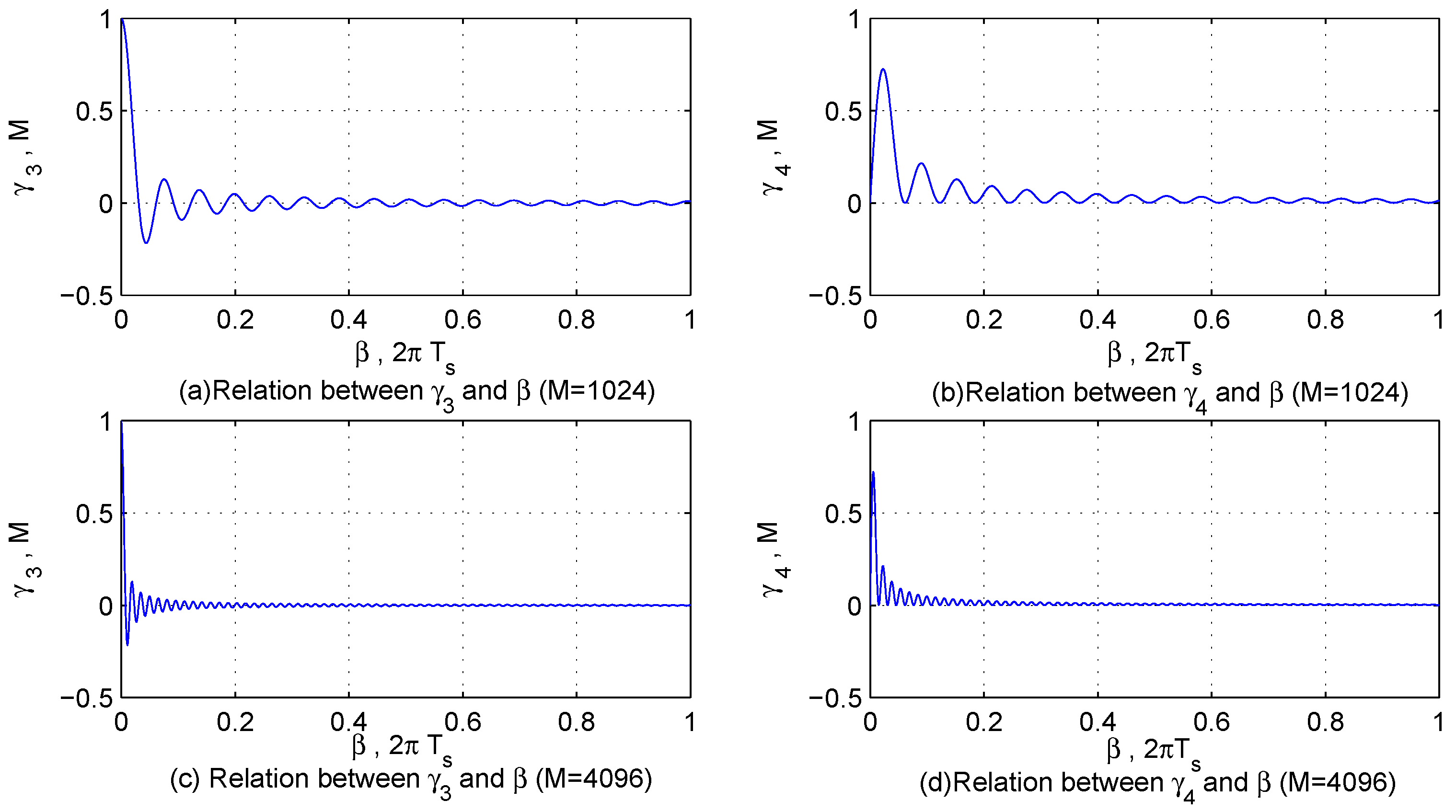
In order to describe the characteristics of
and
more intuitively, let
,
,
and
, and their features are displayed in
Figure 2 and
Figure 3. According to the characteristics of interfering signals and the sampling theorem,
and
are large enough to make
; however,
,
and
may be so small that the value of
is similar to
M.
In summary, the influence of Interfering Signal 2 on Interfering Signal 1 is mainly affected by the energy of Interfering Signal 2 and the difference of frequency parameters of the two signals. It shows a tendency to increase with the increase of the energy and the decrease of the difference of frequency parameters. From Equations (
14), (
23) and (
25), it is found that we can reduce the influence of multiple interfering signals by increasing the number of sampling points
M. Additionally, the conclusion can be extended to multiple interfering signals.
3.1.4. The Improved MP Algorithm and Design Strategy of the Over-Complete Dictionary
In the MP-based decomposition, most of the calculation is spent on finding the best atom, and the number of atoms has a significant positive correlation with the number of parameters. Therefore, the less the parameters that should be obtained by the MP algorithm, the better. Fortunately,
is a periodic function over
, and the period is
. In particular,
is a cosine function of
, so
can be obtained by the analytical method according to the periodicity and symmetry of
to reduce the the number of atoms. The detailed implementation way is as follows. Generate a group of atoms according to frequency parameters:
Additionally, calculate the corresponding
:
Additionally, we can work out
and the inner products corresponding to
as follows:
3.1.5. The Terminate Condition of MP
The conventional terminative condition of the MP algorithm is to judge whether the energy of the residual signal or the times of iterations meet the requirements. However, in the complicated electromagnetic environment, since the energy of the signals that can be sparse represented sometimes may be smaller than that of the other interferences, the energy of residual signal has little difference with the original signal energy; and because the number of signals that can have sparse representation is unknown, presetting the proper iterative number is also impossible. The existing terminative condition is not able to guarantee the effectiveness of the proposed method. Hence, a ratio terminate principle is introduced, which is to judge whether the ratio of the inner product of the best atom obtained and the signal to be decomposed in the
l iteration to the variance of the residual signal meets the threshold. It can be expressed mathematically as:
where
represents the variance function. Equations (16) and (17) show that when the signal to be decomposed contains the interference signal that can have sparse representation in the over-complete dictionary, inevitably there is a best atom making
.
3.1.6. The Improved Double Chain Quantum Genetic Algorithm
Because the decomposition accuracy is related to the number of atoms, the size of the dictionary D is usually large. Additionally, in MP-based decomposition, most of the calculation is spent on finding the best atom. As a consequence, if we perform the MP algorithm in the usual way, the computation complexity will be very high. Therefore, we need to consider the fast algorithm for MP. One way to reduce the running time is to approach the optimization problem by using evolutionary computing. DCQGA is a probability optimization algorithm combining the quantum computation and genetic algorithm, with good global search capability and highly efficient parallel computing performance [
25]. Another advantage of DCQGA is that its encoding space is continuous [
26,
27], which presents an effective approach to deal with continuous parameter spaces directly. Thus, the DCQGA can be used for the optimization problem in this paper, which will greatly reduce the amount of computation and improve the decomposition accuracy. Despite the effectiveness of DCQGA, it suffers from some disadvantages, such as: (1) the probability of searching for global optimum solutions is small due to the large coding space; (2) without considering the characteristics of the target function and the encoding mode, the conventional rotation angle computing function leads to low convergence speed and searching efficiency. To address that, a high density encoding mode and a cosine rotation angle computing function are proposed.
The conventional encoding method can be expressed as:
where
,
is a random number in
.
,
;
n and
m represent the colony size and the number of qubits, respectively.
It is noticed that the probability amplitude changes periodically, and the same solution appears two times in each gene chain. In other words, the traditional encoding method increases the number of global optimal solutions and sub-optimal solutions at the same time. Additionally, the increased number of sub-optimal solutions is much more than that of global optimal solutions. To solve this problem, compressing the traditional encoding space, let
, then the range of probability amplitude,
and
, is [0, 1]. In order to avoid that the probability amplitude value is not within [0, 1] when the phase exceeding the set range in the process of evolution, the encoding mode is improved as:
Each of probability amplitudes corresponds to an optimization variable in solution space. If the
j-th qubit on chromosome
is
, the corresponding variables in solution space
can be computed as follows:
Compared with the traditional encoding mode, although the reduction of the encoding space reduces the number of optimal solutions, it does not reduce the search probability of the optimal solution. On the contrary, the probability of finding the optimal solution is improved, and it is proven in the following analysis.
Let
be an arbitrarily small positive constant. The solution space can be divided into
subintervals. When the solution falls in the subinterval that contains the global optimum solution, we can think that the global optimal solution with precision of
is obtained. Without loss of generality, assume that there is one global optimum solution and
chromosomes. According to the traditional encoding method, the probability of obtaining the global optimal solution can be expressed as:
According to the proposed encoding method, the probability of obtaining the global optimal solution can be expressed as:
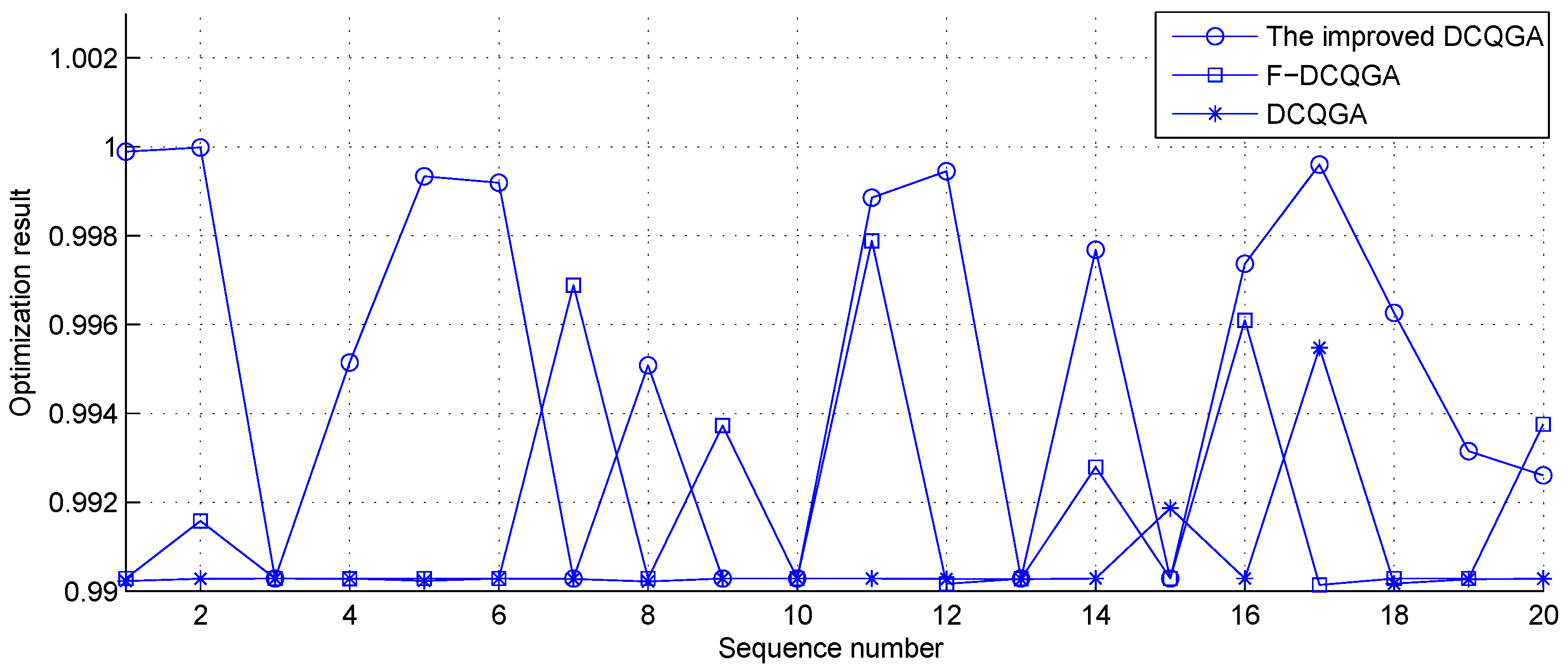
Then, . In other words, in the evolution of each generation, the probability of the improved DCQGA is higher than that of the traditional one to obtain the global optimal solution with precision of .
The conventional rotation angle computing function is written as:
where
is the changing trend of fitness function defined by Equations (
12)–(
14) in [
23].
The exponential function can not fit the change trend of the cosine/sine encoding function well, so replace it with a cosine function; the adaptive cosine rotation angle computing function is written as:
3.1.7. The Multi-Channel Signal Interference Suppression Method Based on Improved DCQGMP
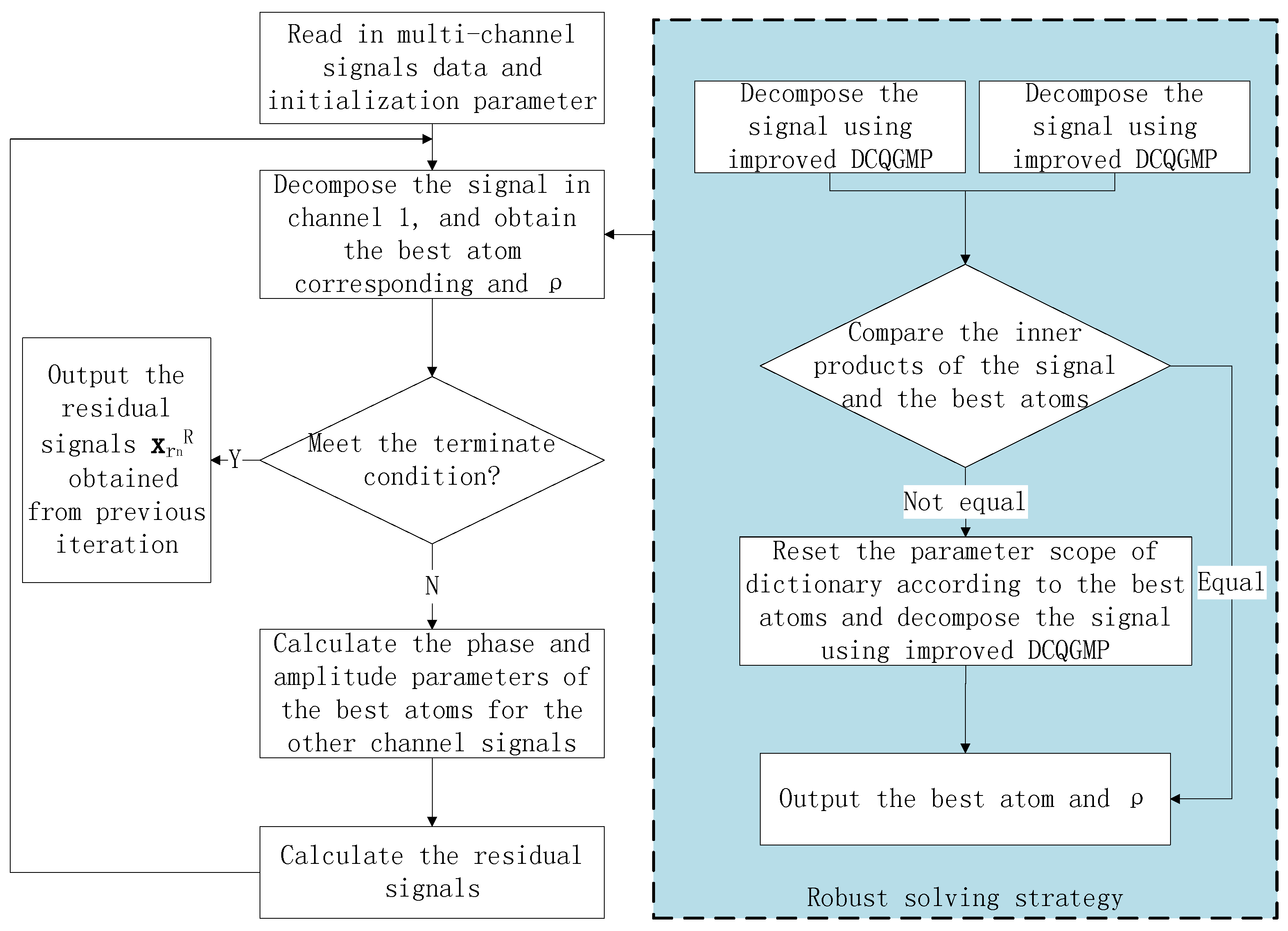
Because the GNSS receiver used in the proposed method is equipped with an array antenna, there are multi-channel signals to be dealt with. If these signals are decomposed independently, the calculation is very great. Fortunately, the array signal processing theory demonstrates that there is a potential correlation among the multi-channel signals. In particular, they have the same frequency, similar amplitude and distinct phases. Therefore, we propose a multi-channel signal interference suppression method based on the improved DCQGMP. Its rough flow chart is shown in
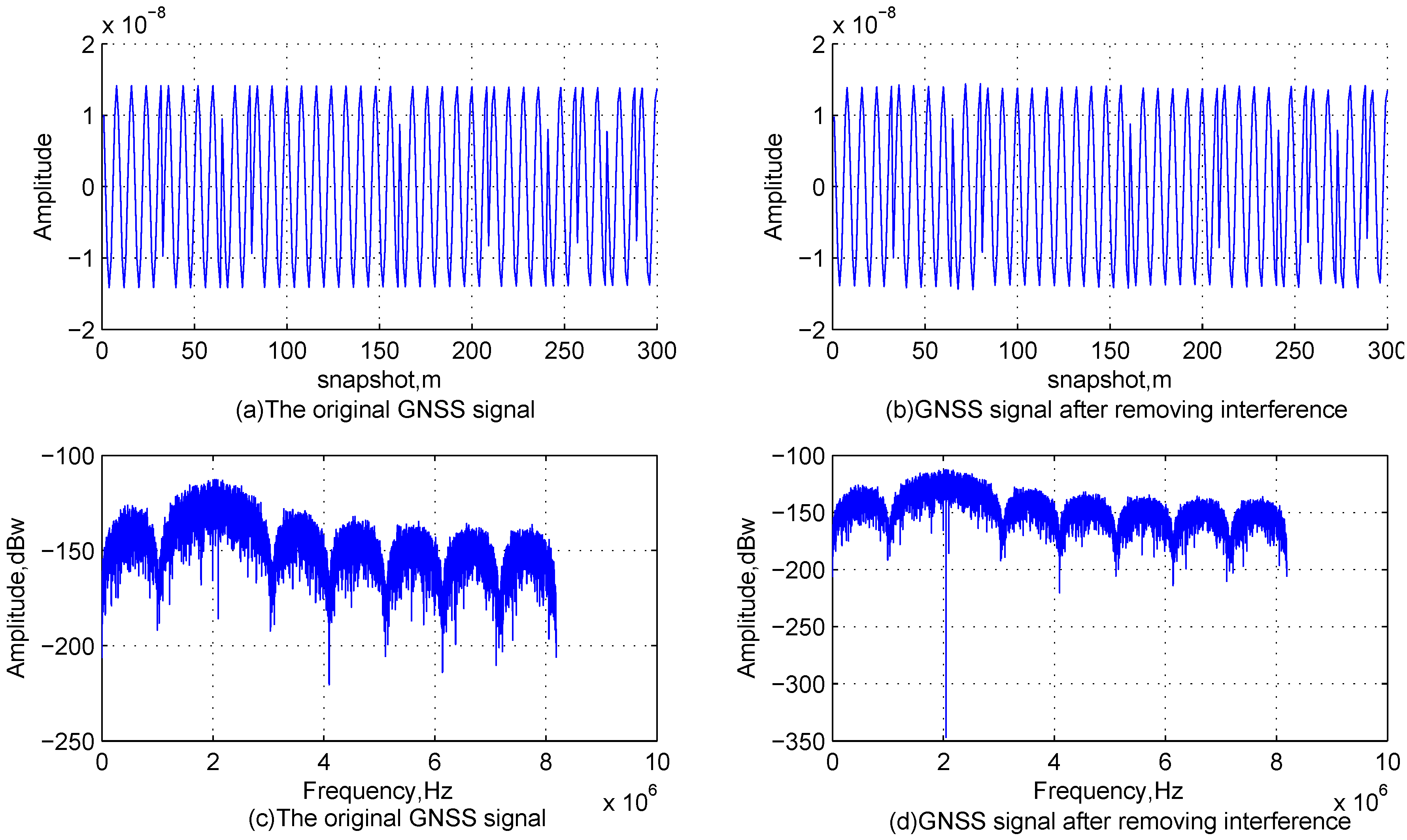
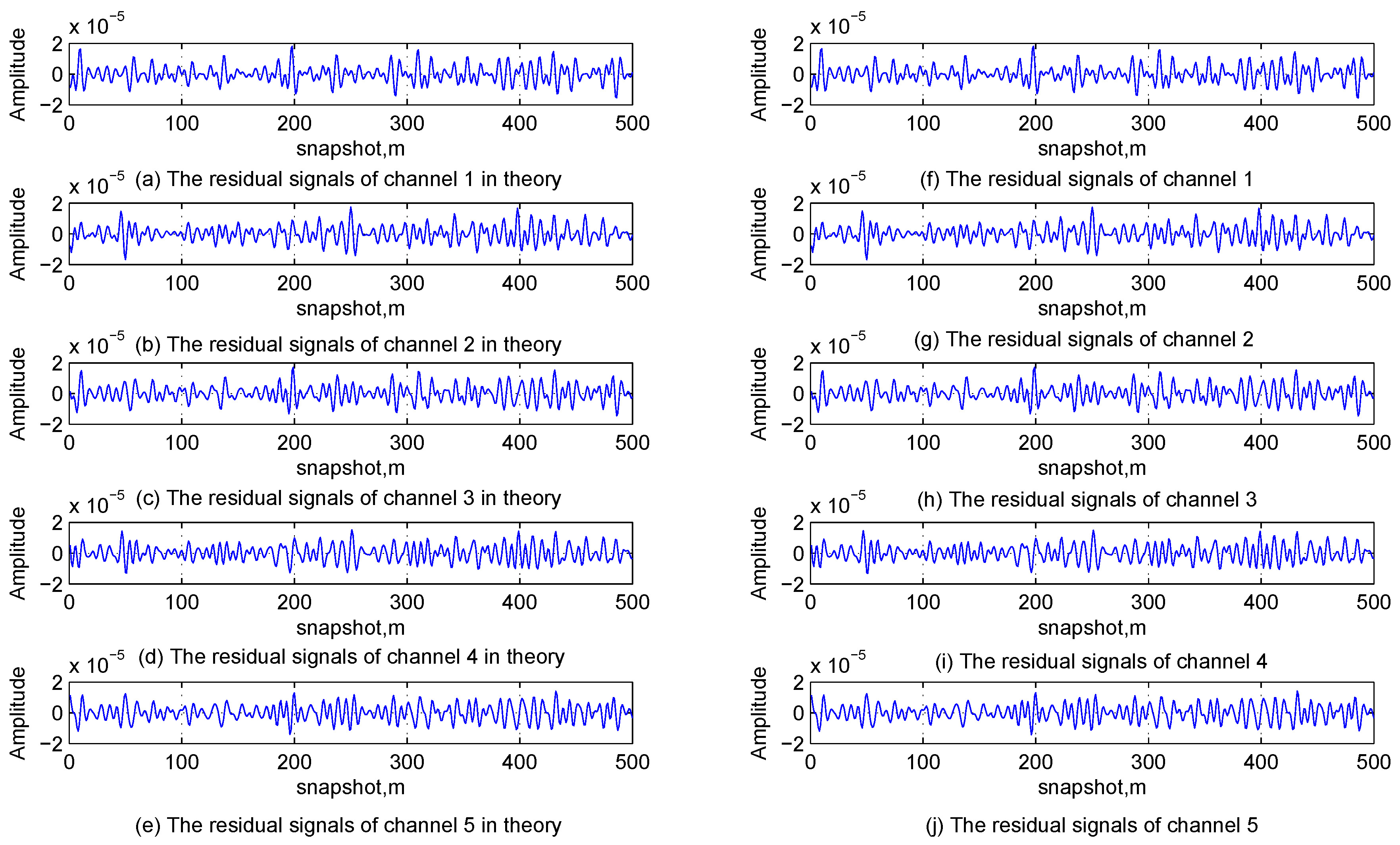
Figure 4. Since the phase parameter in each channel can be obtained by an analytical method, only one channel signal should be decomposed. Then, the phase parameters of signals in different channels are obtained according to the frequency parameters. Finally, the continuous wave interference signal is canceled.
As shown in the dashed box of
Figure 2, in order to avoid that the improved DCQGMP algorithm converges to a local optimal solution, a robust solving strategy is used. Firstly, the signal is decomposed using two improved DCQGMP whose initial population and evolution are independent of each other. Additionally, the fitness function is:
Secondly, compare their best fitness values. If they are equal, output the best atom and ; if not, select the atom with the larger fitness value as a suboptimal atom and come to the next step. Thirdly, reduce the search ranges of the parameters as of the original centered in the suboptimal atom, and decompose the signal again. Then, output the result.
3.2. MPDR Beamformer
In the second stage, the spatial filtering is applied, which can reject interferences and protect the GNSS signal by pointing the beam of receiver antenna array towards the GNSS satellite and away from interferers. In GNSS applications, the MPDR beamformer is one of the most powerful methods due to its effectiveness for interference suppression without considering the structure and direction of interfering signals. Additionally, the optimization problem for the space-only MPDR beamformer can be written as:
where
w represents the array weight vector;
a is defined by Equation (2);
denotes the spatial covariance matrix of the residual signals obtained by Stage 1, which can be expressed by:
where ‘
H’ denotes conjugate transpose, and
M is the size of snapshot data;
;
where
and
are the in-phase (I) and quadrature (Q) signals obtained by using the quadrature converter. Then, the optimal weight vector is:
5. Conclusions
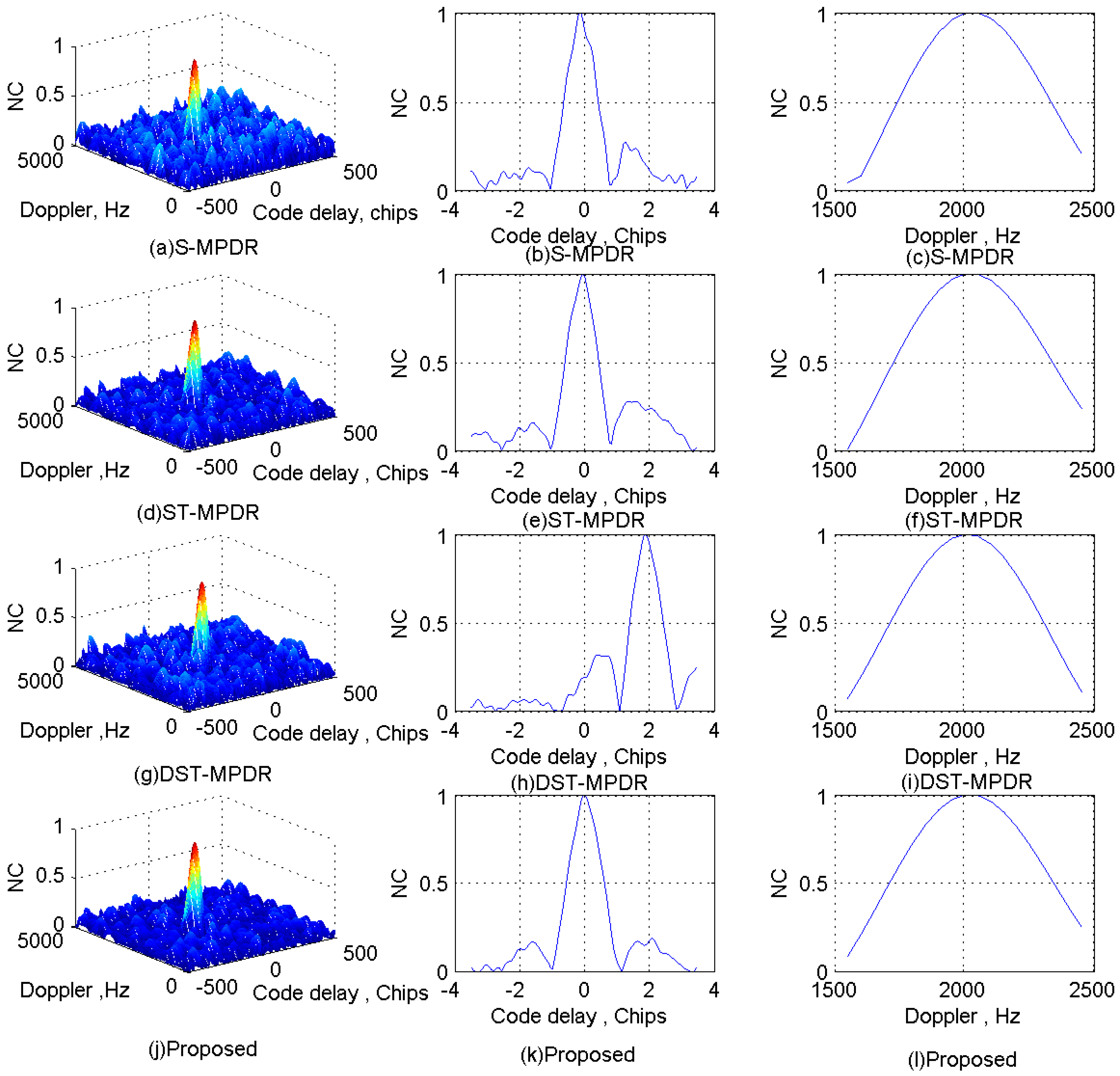
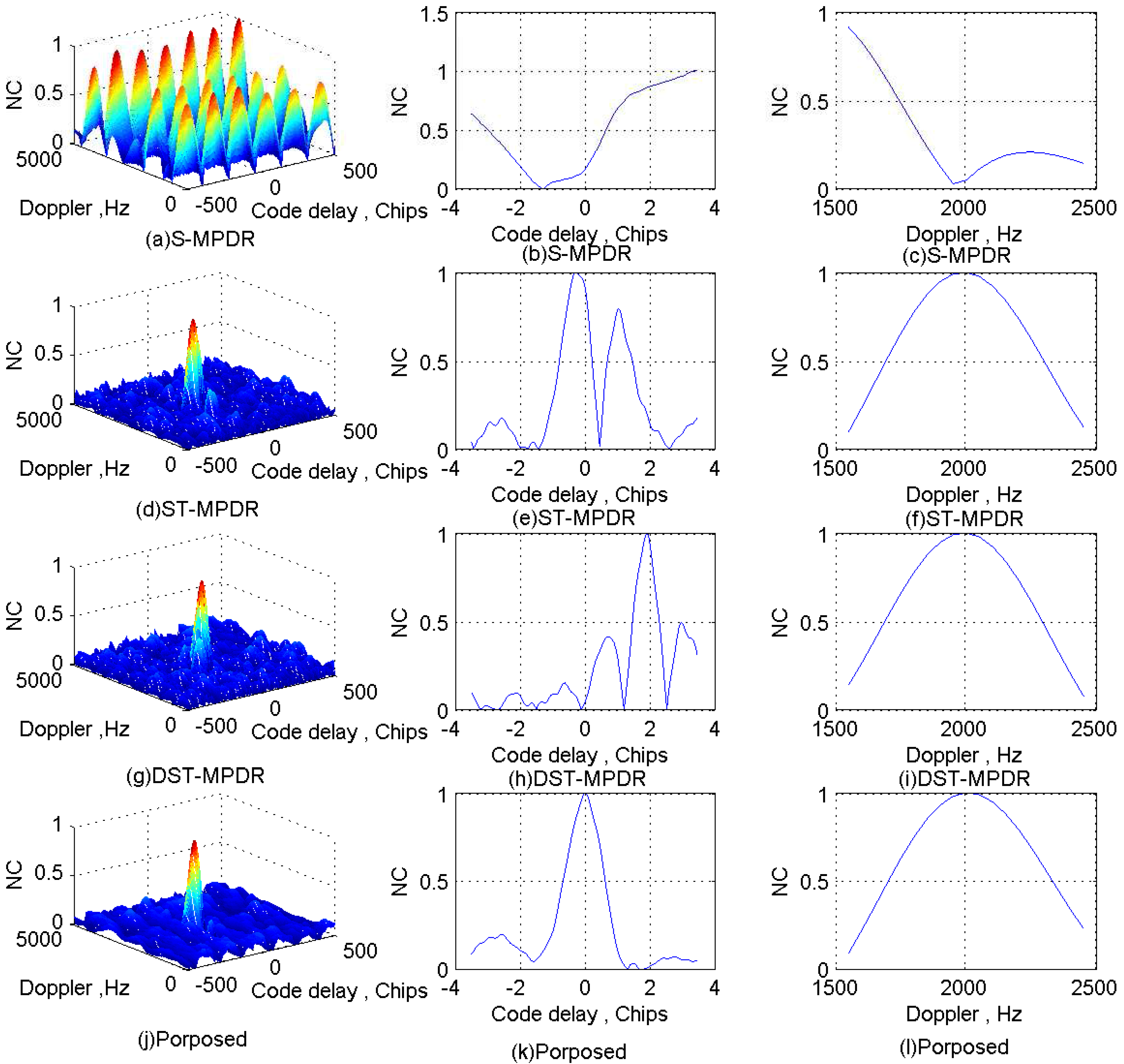
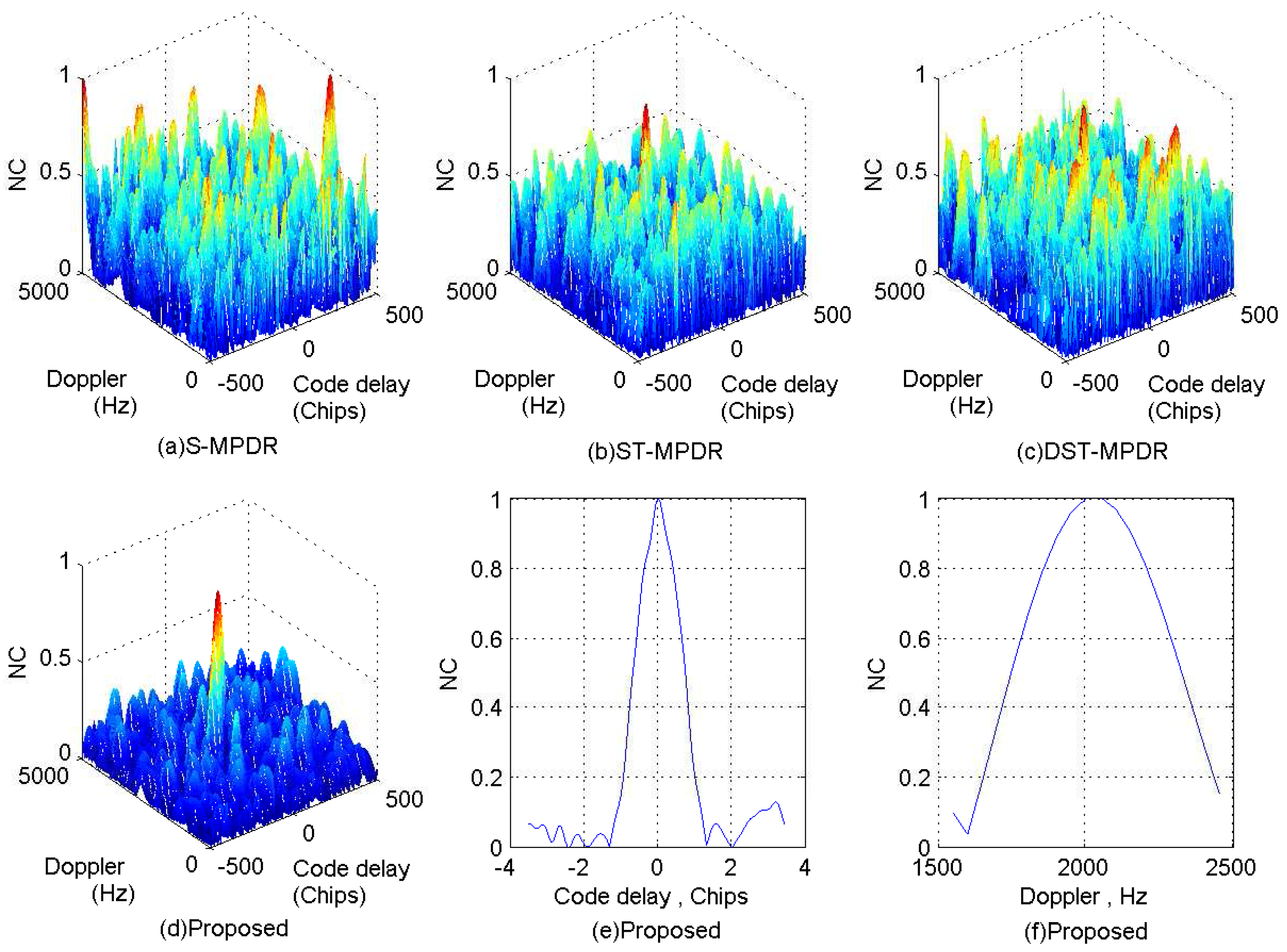
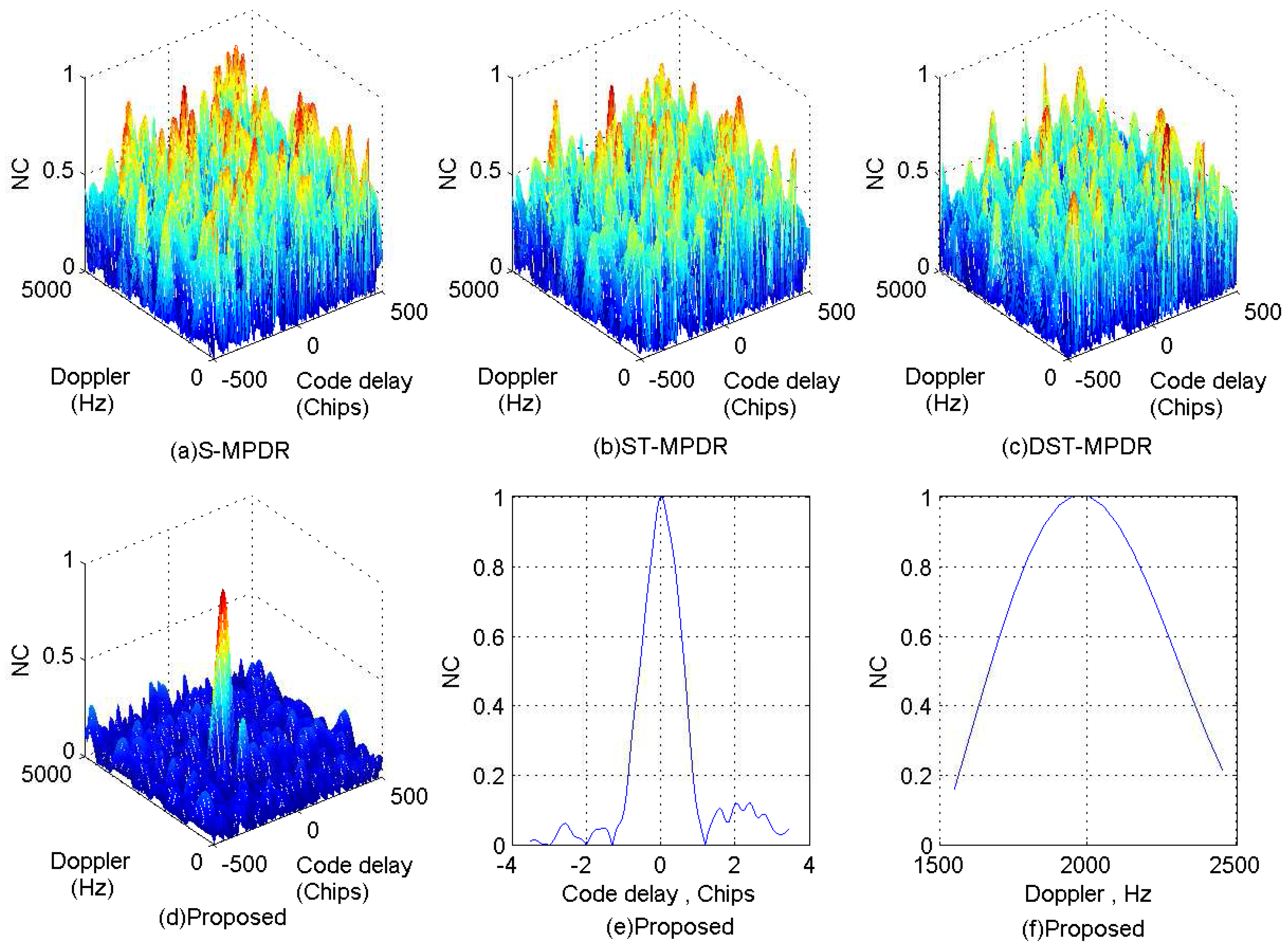
Focusing on the complex electromagnetic environment in which multiple types of interfering signals coexist at the same time, a novel cascaded multi-type interferences mitigation method using sparse decomposition and array processing is introduced and examined in this paper. To solve the problem that there are overlaps among different interfering signals, the sparsity of the CWI signals and the advantage of the spatial processing are used. Firstly, the detectability of single-tone (multi-tone) and linear chirp interfering signals using the MP-based sparse decomposition is analyzed, and to reduce the running time of signal decomposition, an improved DCQGMP is introduced. Then, the multi-channel signals interference suppression method based on the improved DCQGMP is proposed, which can economize the spatial DoF of the antenna array by effectively detecting and canceling the single-tone (multi-tone) and linear chirp interfering signals even when they vanish into Gaussian interferences. Secondly, the MPDR beamformer is employed to mitigate the residuary interferences (such as Gaussian noise interferences) by utilizing the spatial DoF. Numerical simulations show that the proposed cascade method can not only suppress more interferences, but also does not significantly affect the position and shape of the correlation peaks of GNSS signals. Compared with the S-MPDR beamformer, ST-MPDR beamformer and DST-MPDR, the proposed method is able to deal with multi-type interferences more effectively and can suppress interferences with the same DOA as the GNSS signal, which can be sparse represented in the over-complete dictionary. Therefore, the proposed method can be implemented in the coexistence of multiple types of interfering signals to effectively improve the interference suppression performance of GNSS receivers while reducing the cost of space and hardware.