Coastal Areas Division and Coverage with Multiple UAVs for Remote Sensing
Abstract
:1. Introduction
2. Related Work
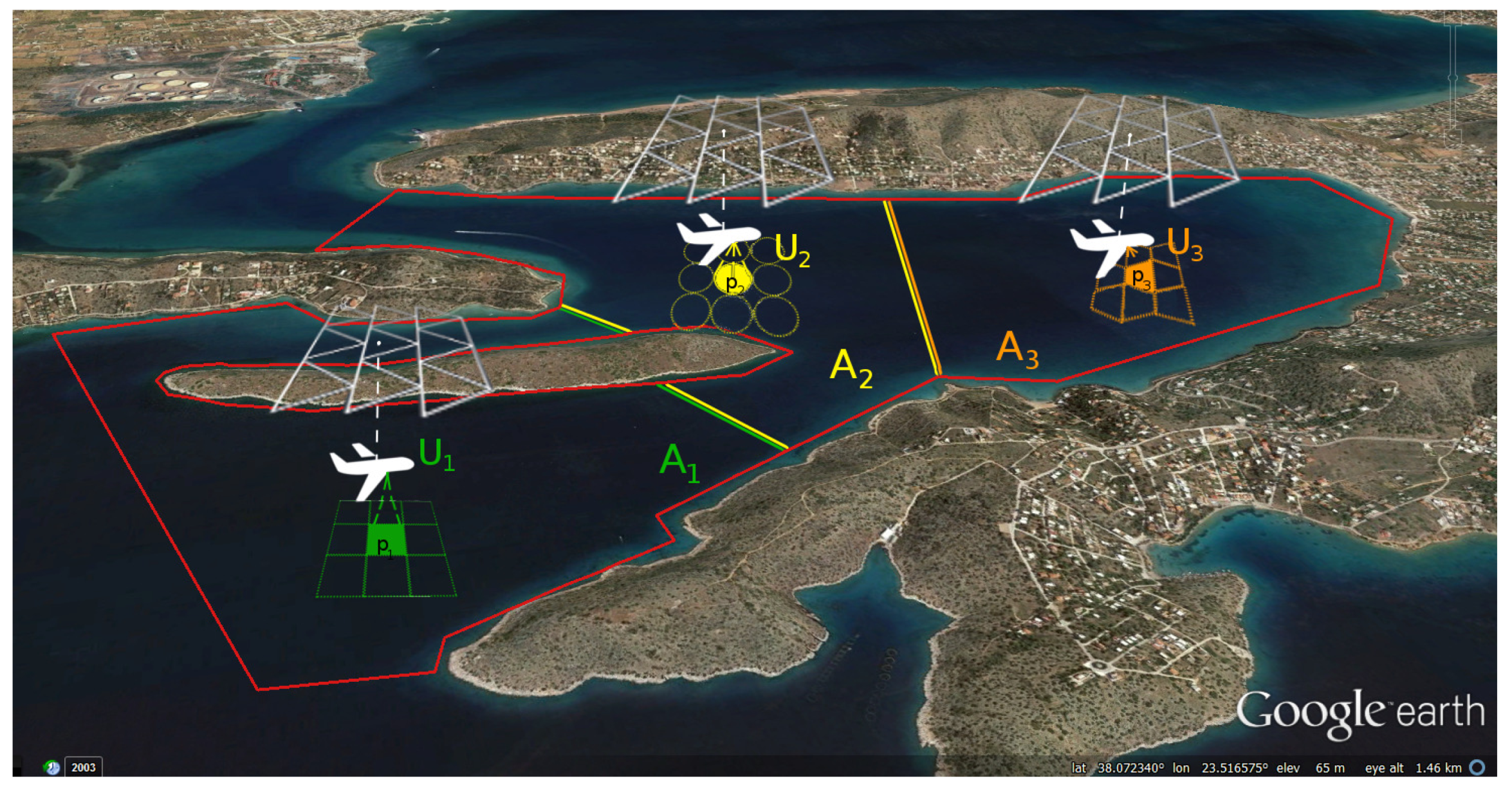
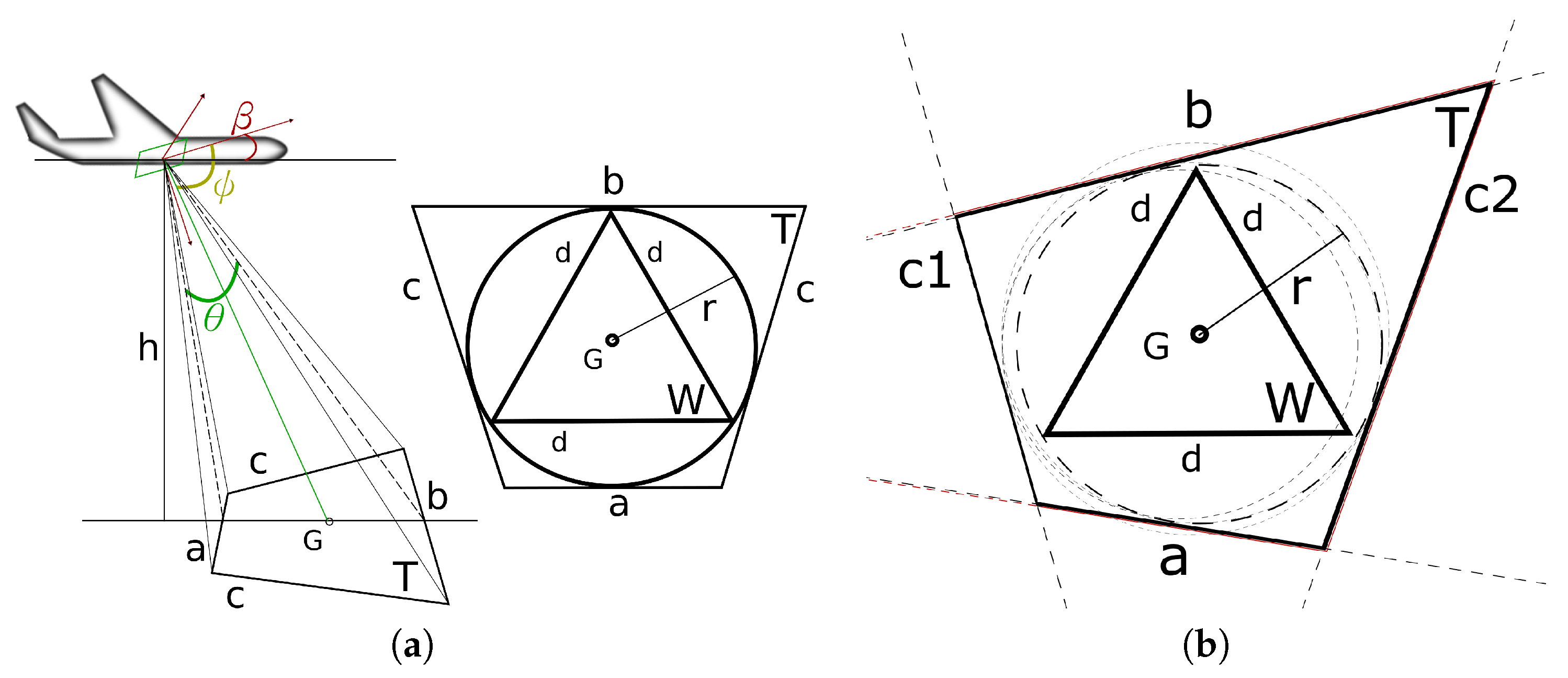
3. Problem Statement, Assumptions and Metrics Considered
- The closeness of the cells within to the initial location of the UAV in charge of searching that sub-area should be minimized. This can be achieved by minimizing the sum of distances between each center of cell from the set S and the initial locations :where is the number of cells of S inside .
- The size of should be as close as possible to for all of the UAVs. This can be achieved by minimizing the sum of differences:where represents the area of the cells inside .
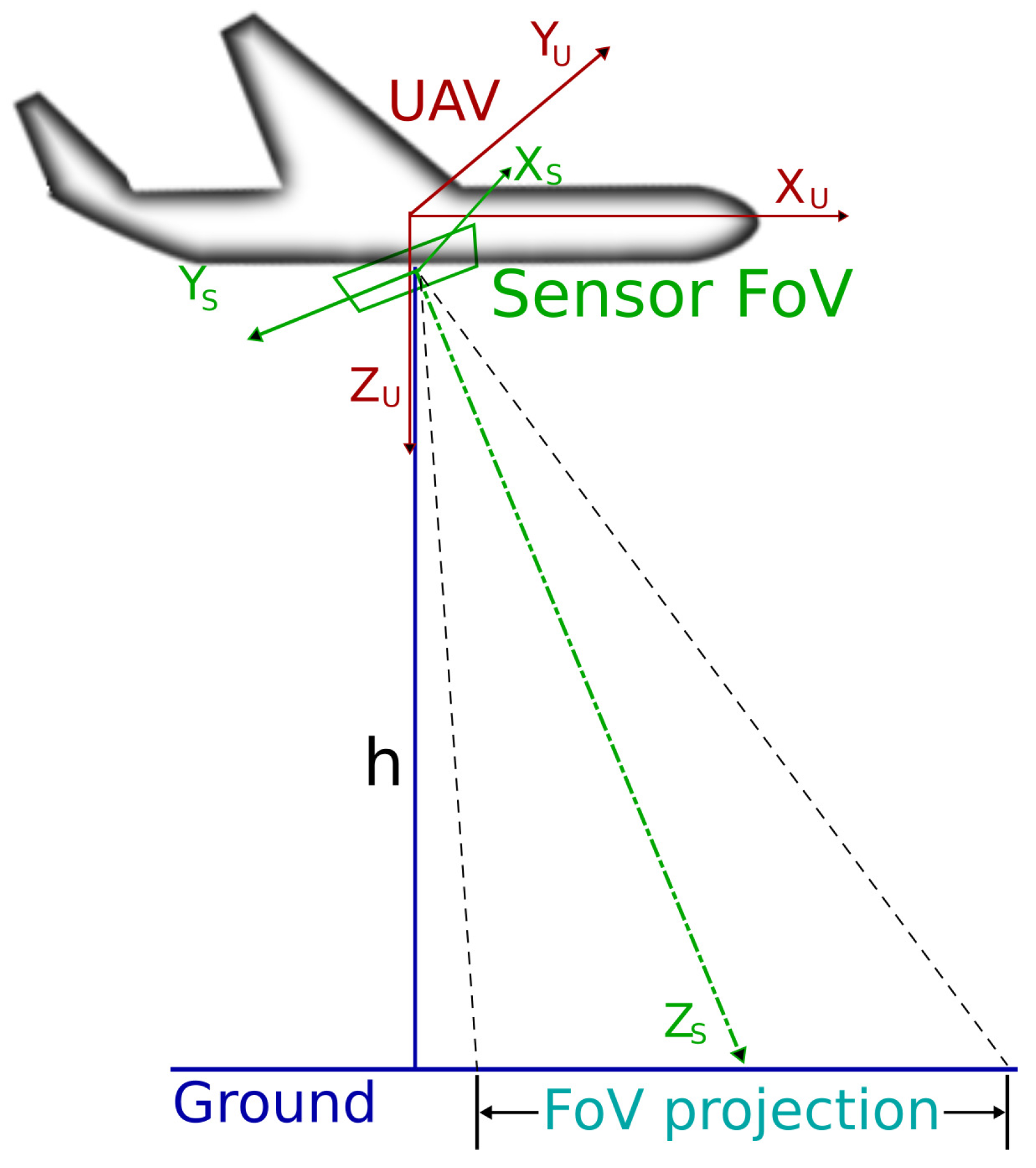
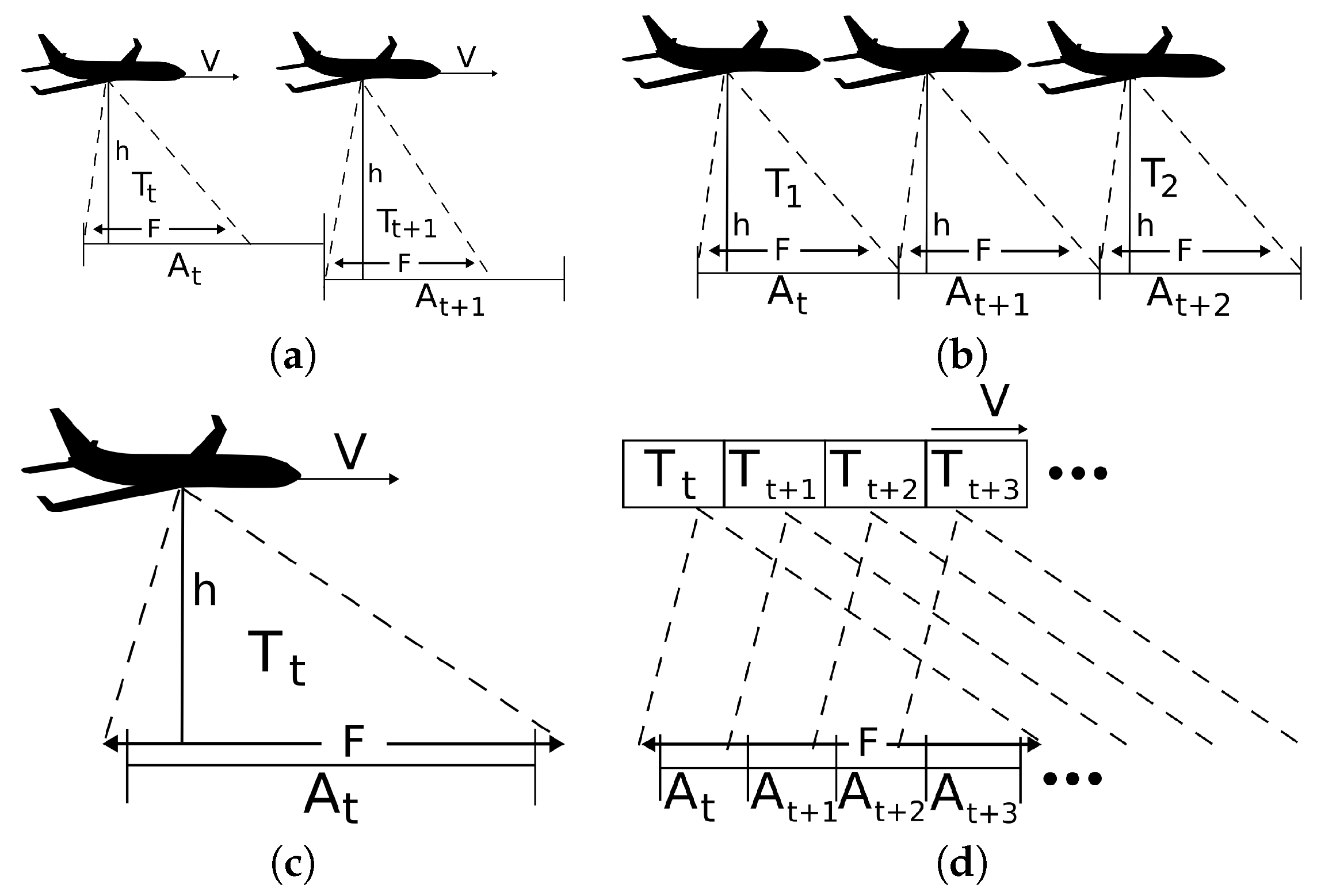
4. Model Considered for the On-Board Sensors
5. Area Decomposition and Partition in a Multi-UAV Context
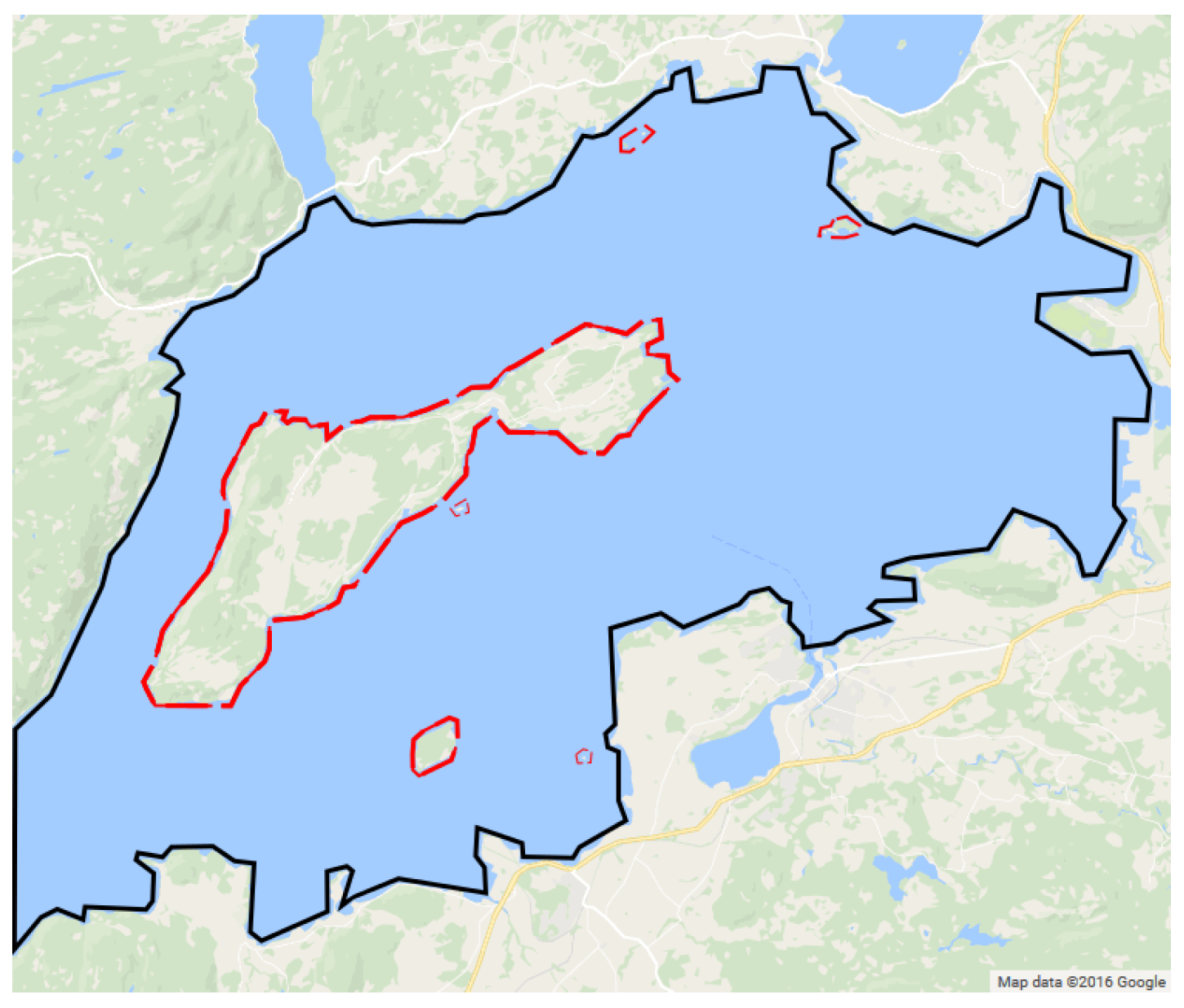
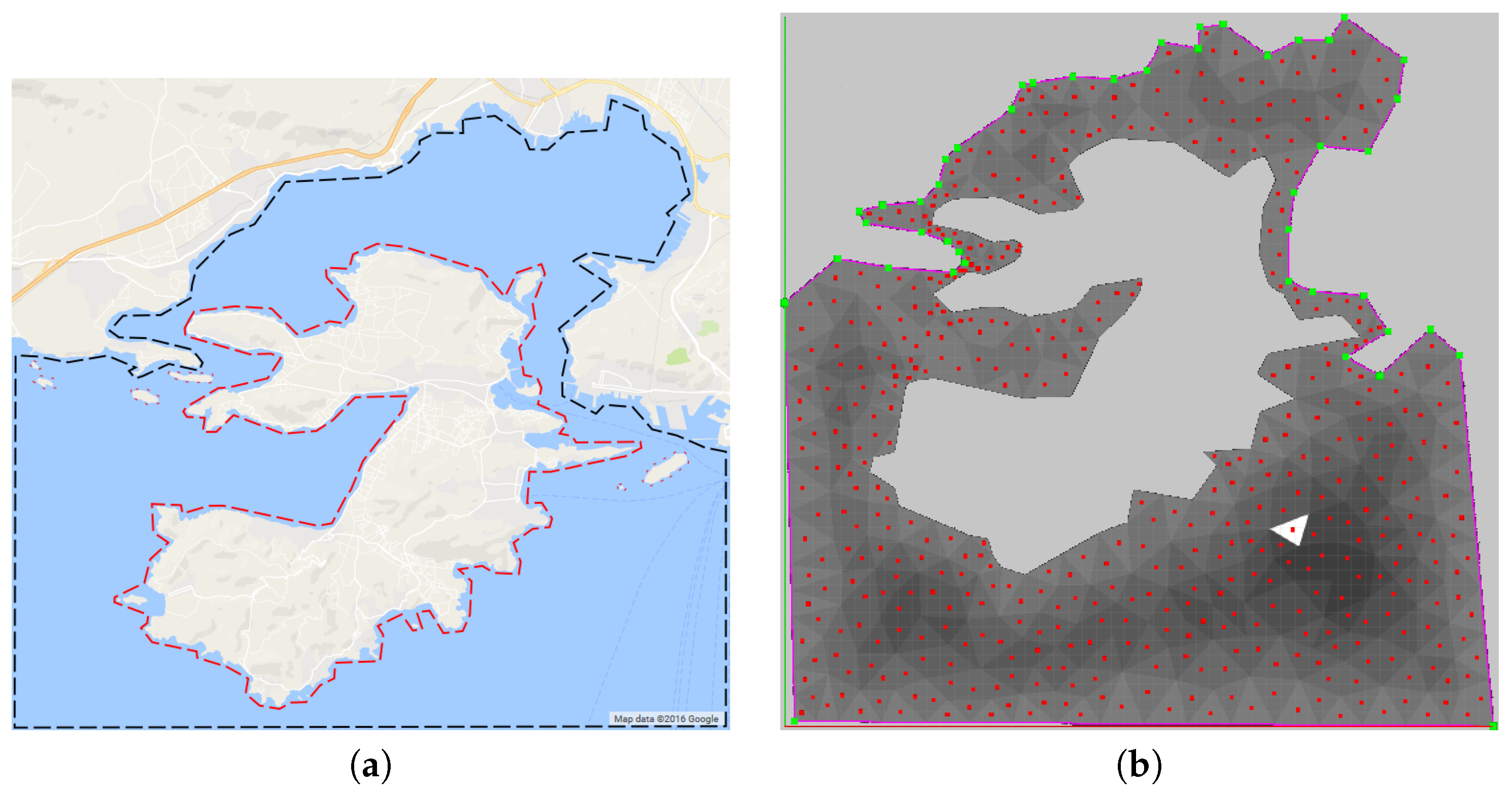
5.1. Exact Cell Decomposition
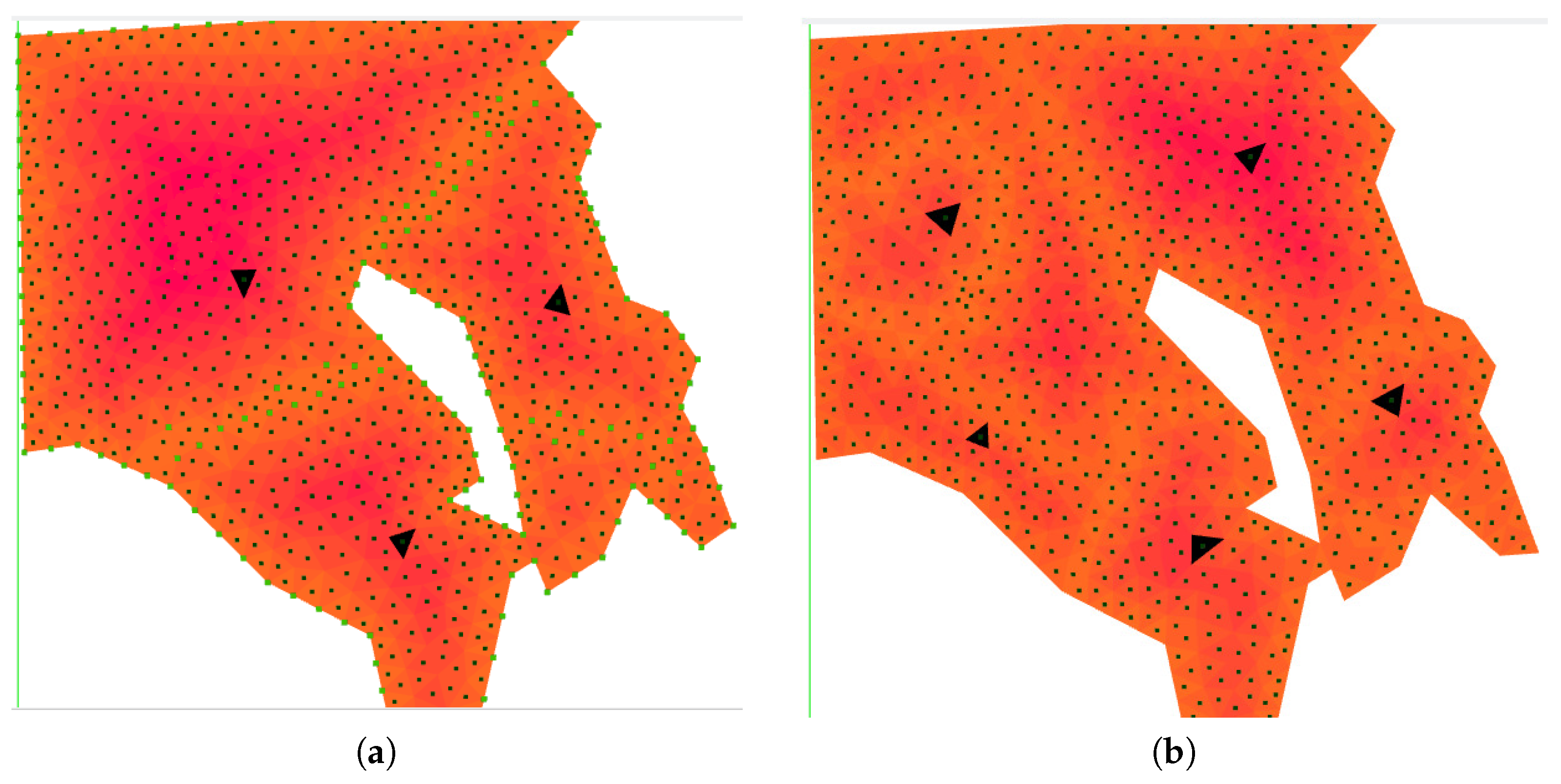
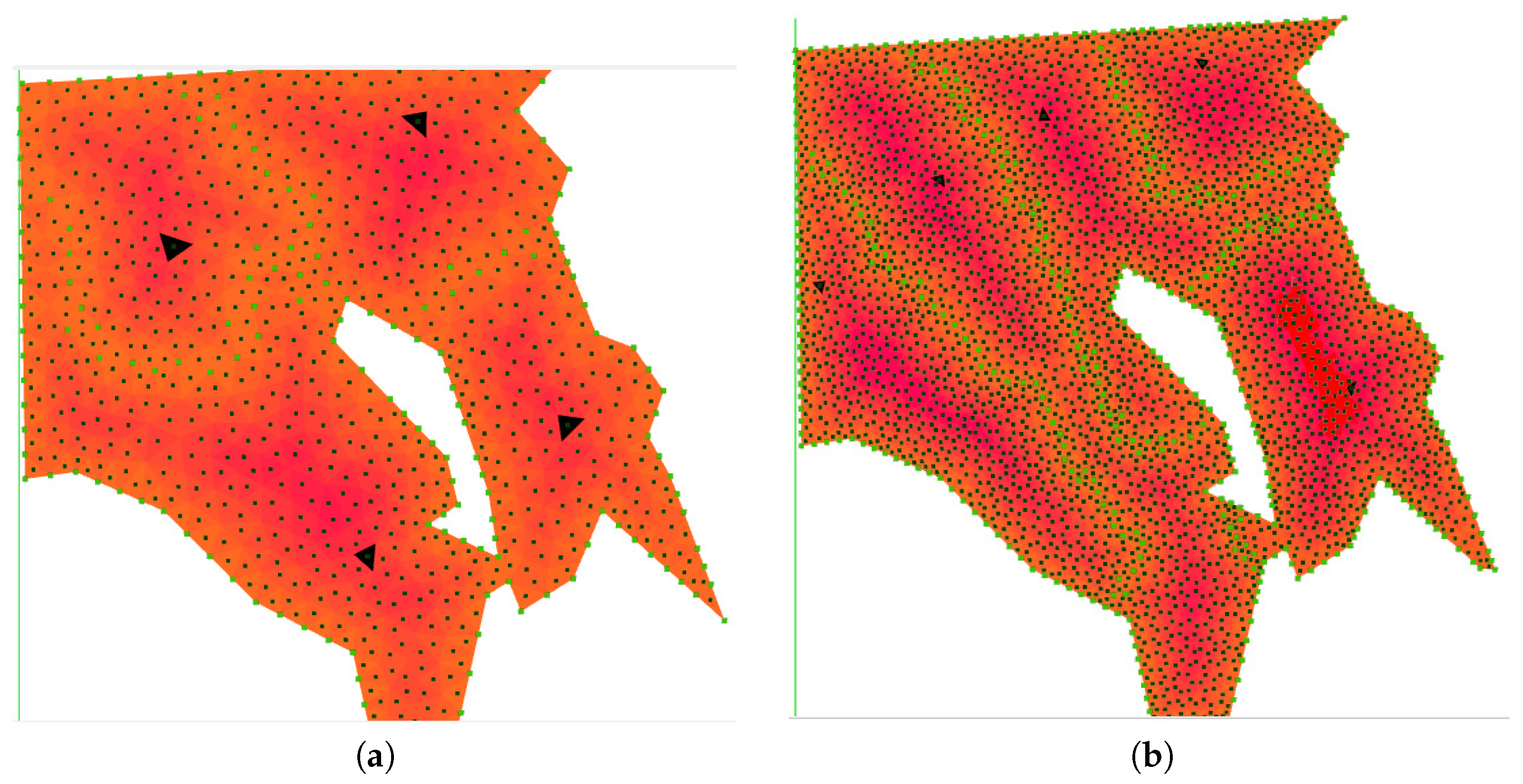
5.2. Baseline Area Partitioning Algorithm
| Algorithm 1: Antagonizing wavefront propagation algorithm that computes the baseline area partition. Q is a queue list managed as an FIFO by functions and . |
| : initial vertices/triangular cells for each UAV , : area size of triangular cells v, : the set of neighbors of vertex v, : the UAV identifier allocated to triangular cell v, : area coverage capability of UAV in square meters : area size of the smallest triangular cell in CDT  |
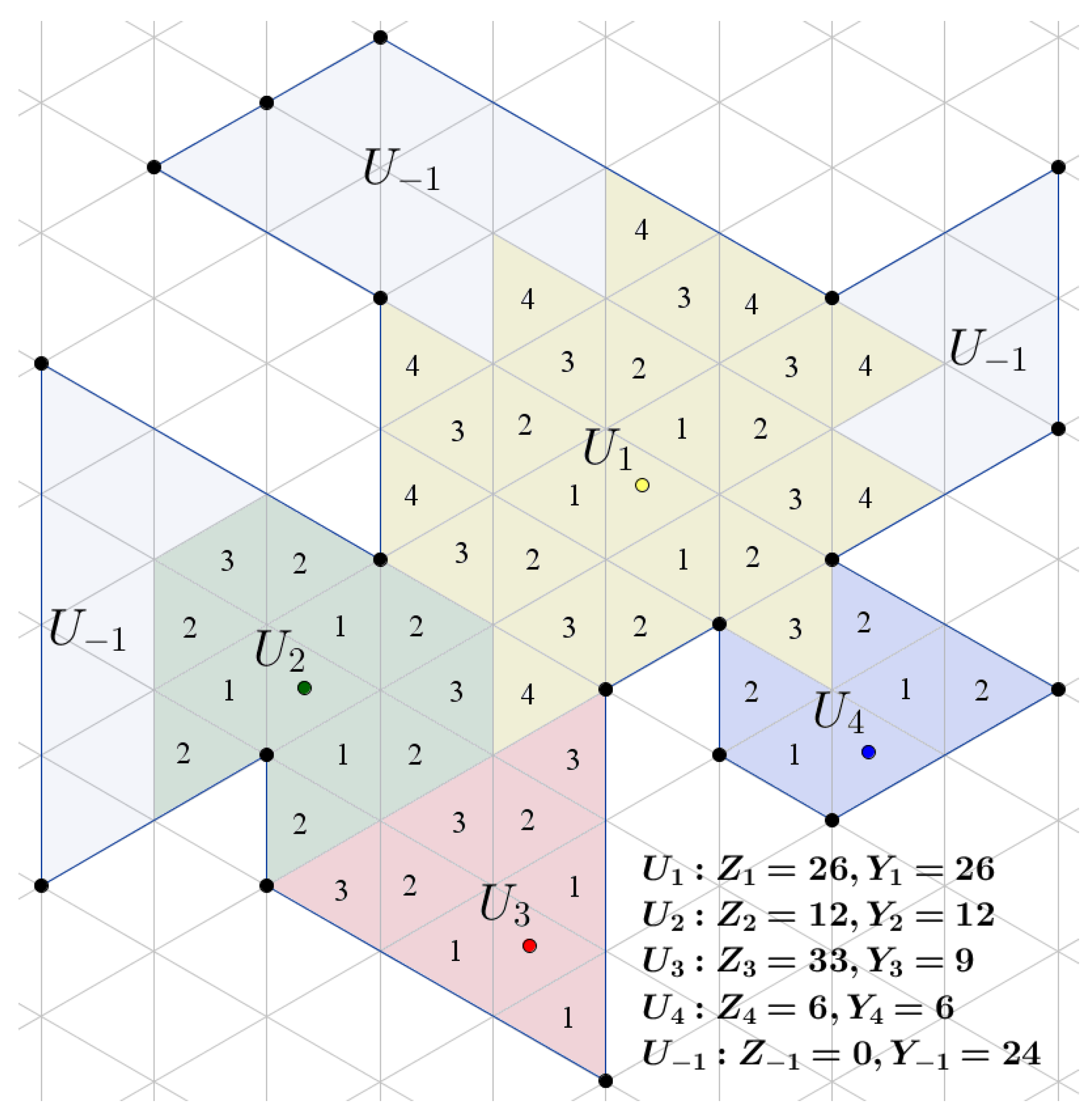
5.3. Reverse Watershed Schema
| Algorithm 2: RWS algorithm for the generation of the border-to-center cost attribute. Q is a queue list managed as an FIFO by functions and . |
| : the set of neighbors of vertex/triangular cell v, : the UAV identifier for triangular cell v  |
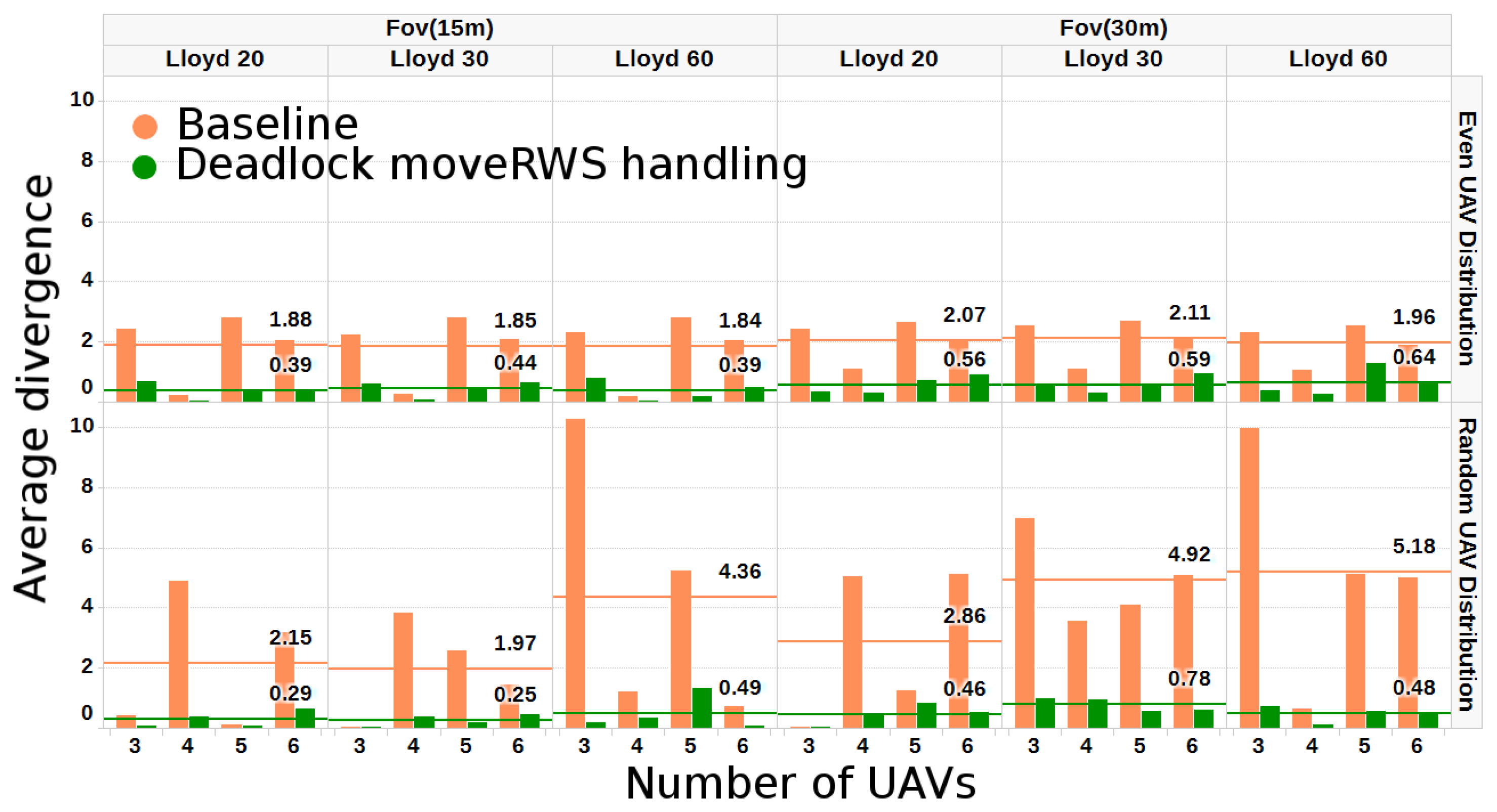
5.4. Adjustment Function for Deadlock Scenarios
| Algorithm 3: Multi-UAV partitioning Deadlock Handling (DLH) algorithm. Baseline partitioning is performed by Algorithm 1, whereas this method is for the sub-area size adjustment (if needed). Function gets a UAV identifier from list L that has an area surplus, whereas function gets the identifier of a UAV that has an area shortfall after Algorithm 1. Function finds a feasible transition sequence between UAV and , whereas the function performs the transfer between triangular cells. |
: area size of the smallest triangular cells in CDT  |
| Algorithm 4: MoveAWP algorithm. is the transition cost from the AWP algorithm (see Algorithm 1). Then, function finds the largest transition cost value triangular cell of UAV that is adjacent to UAV in the sequence. Then, function takes as variables an initial cell v, the area size that needs to be exchanged and the UAV identifier that needs to be exchanged from. The growing function is similar to Algorithm 1. |
| the transition sequence between and for triangular cells exchange, treated as a list : initial triangular cell for identifier exchange S: area size to be moved  |
| Algorithm 5: MoveRWS algorithm. Function finds a valid transition sequence, as can be seen in Figure 8. This function is also called before the initial recursion of the MoveRWS algorithm. Function makes use of the information of the RWS algorithm (see Algorithm 2), and it exchanges agent identifiers on two adjacent configuration spaces, by exchanging the amount of triangular cells that have the lowest coverage cost, but are adjacent. It also propagates and extends this cost. Function returns the remaining sequence for the specific transition, in order to initially transfer only the amount of triangular cells that are adjacent between i and until the final UAV. In case this happens, the requested area has not been exchanged yet, so the algorithm runs recursively, and the last line takes a step back in sequence traversal. |
| S area size to be moved the area size of adjacent triangular cells between UAV k and l the transition sequence between and for triangular cell exchange, treated as a list  |
6. Simulation Results
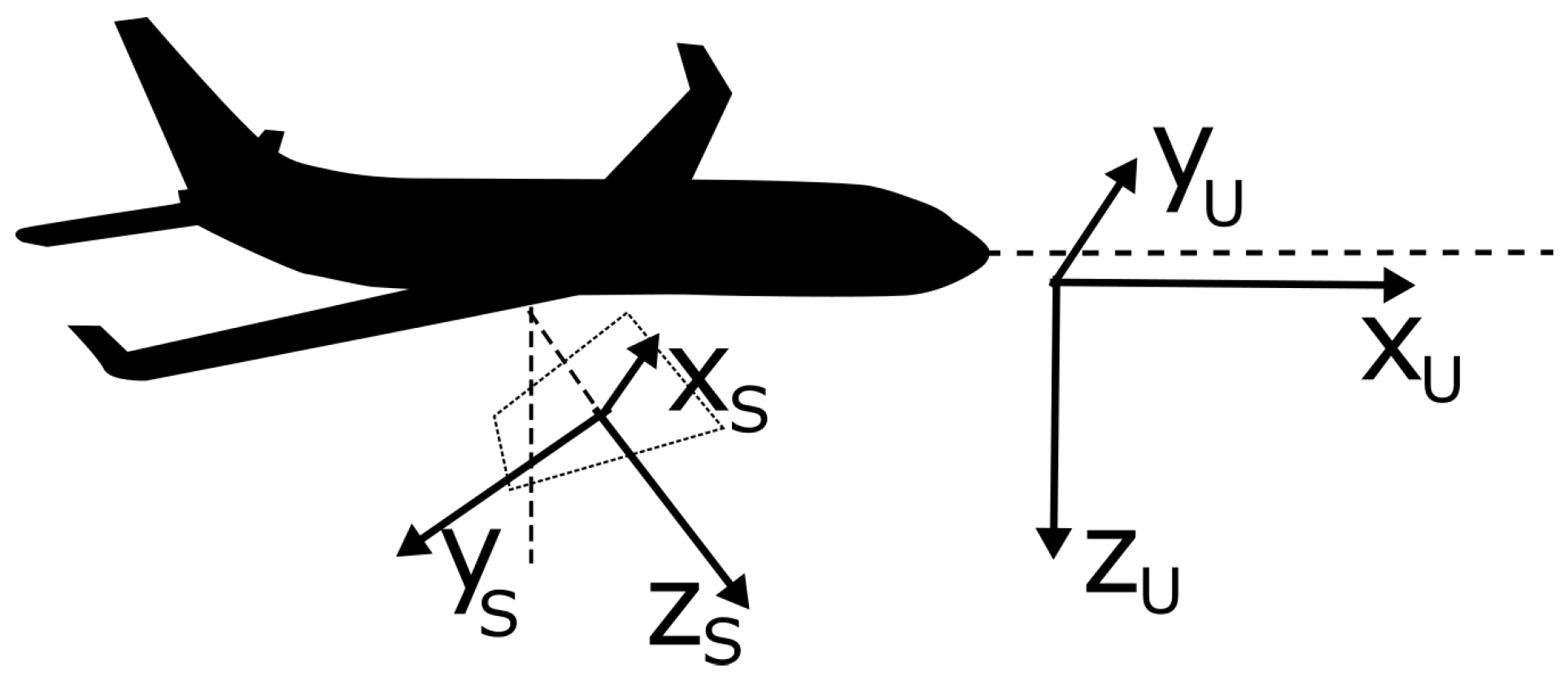
6.1. Coordinate Frames
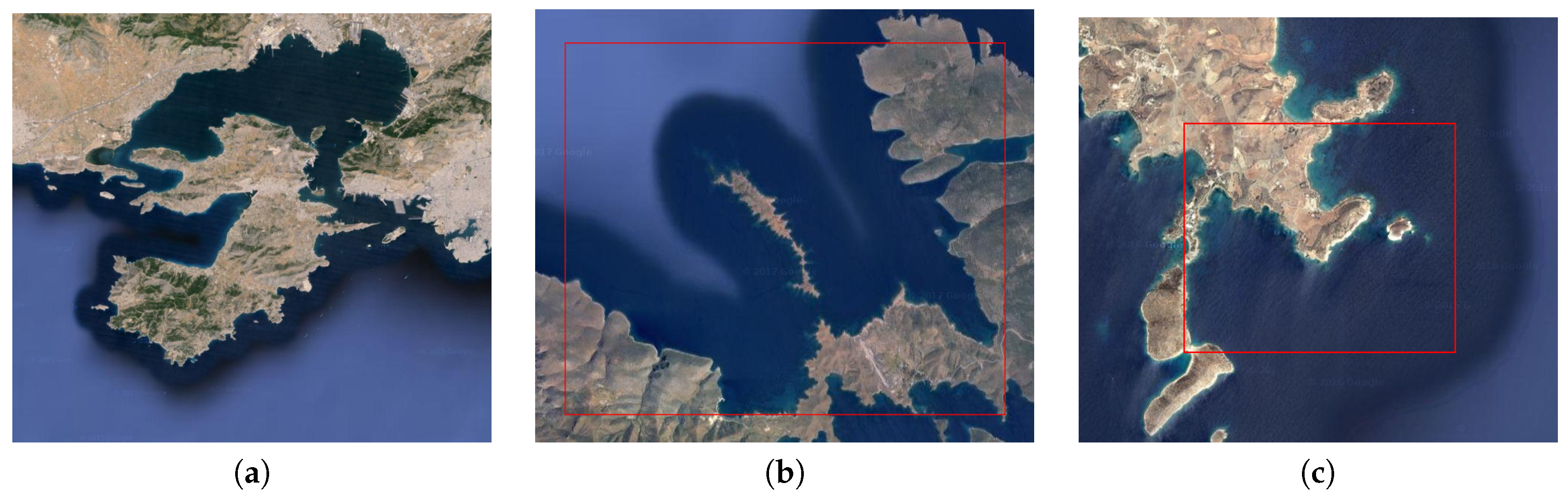
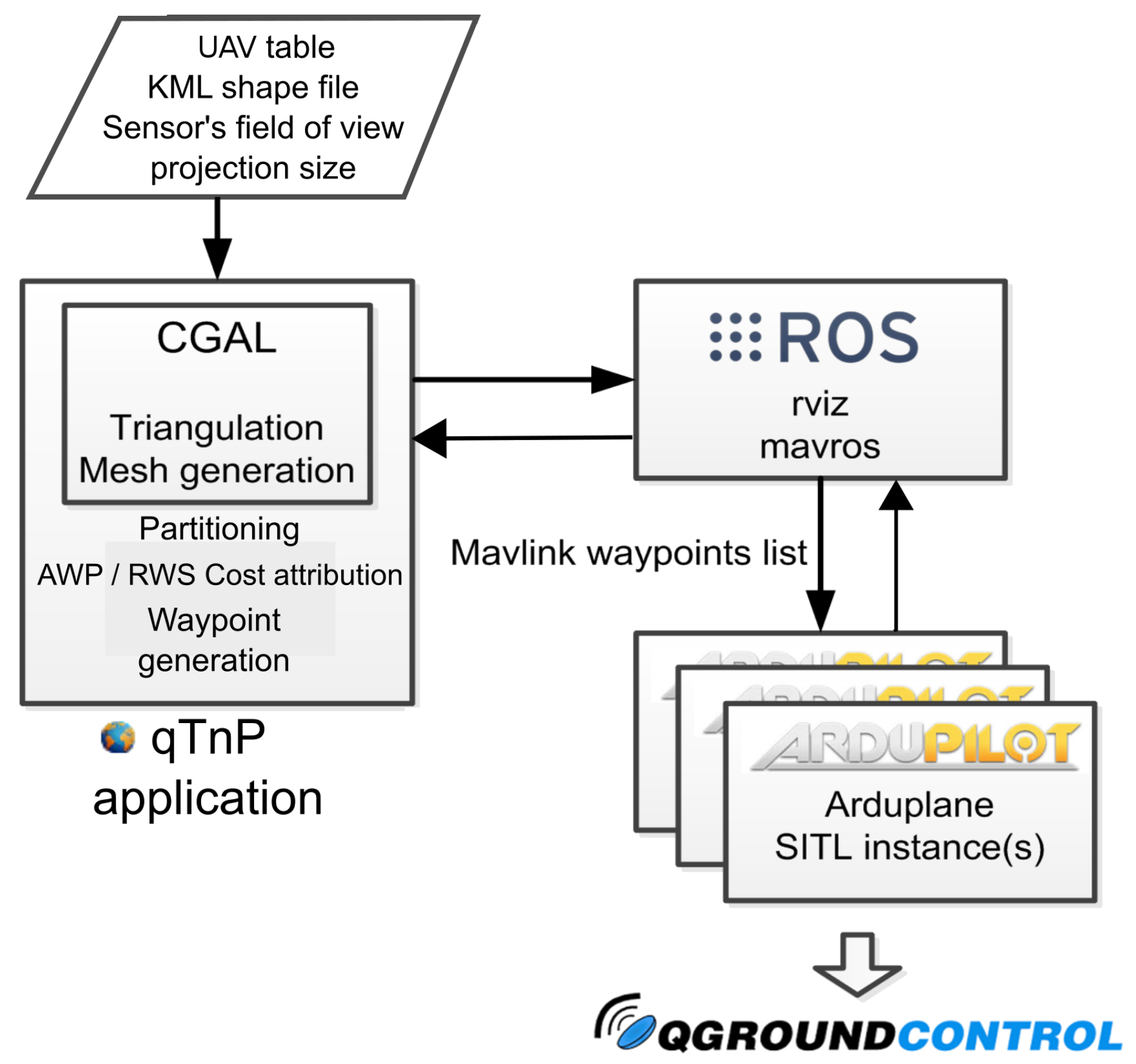
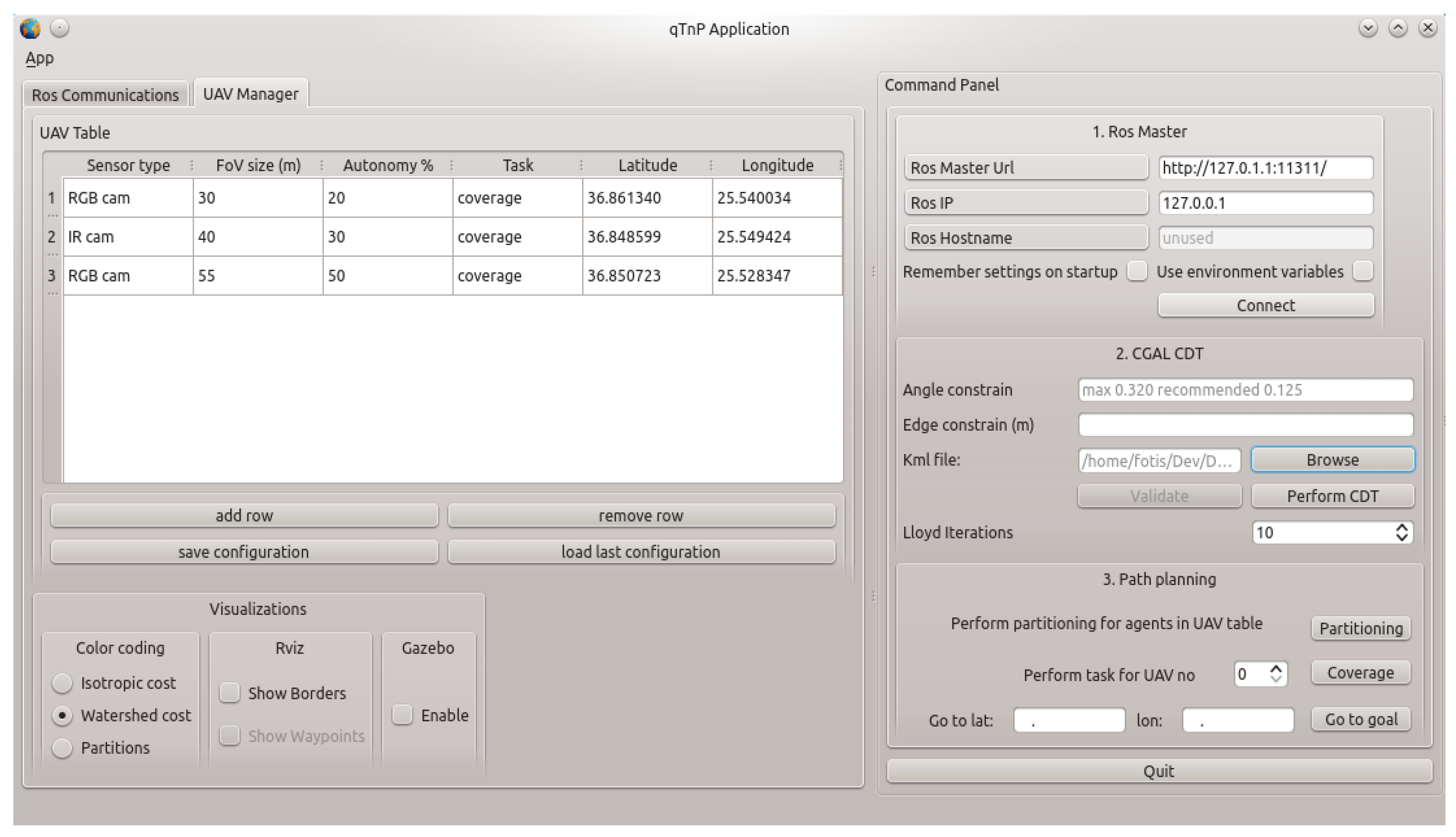
6.2. Simulation Architecture and Configuration
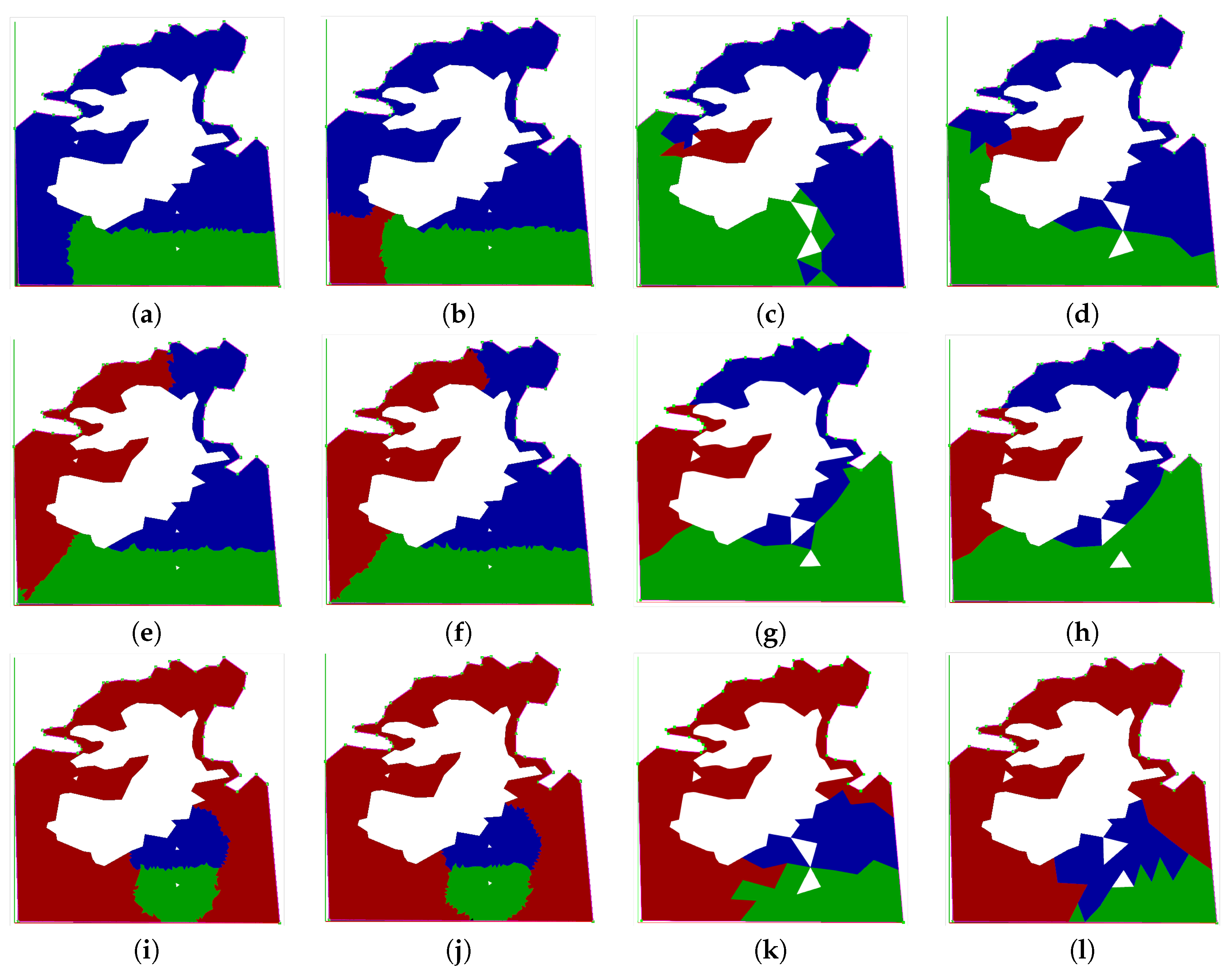
6.3. Partitioning Algorithms Comparison in Simulation
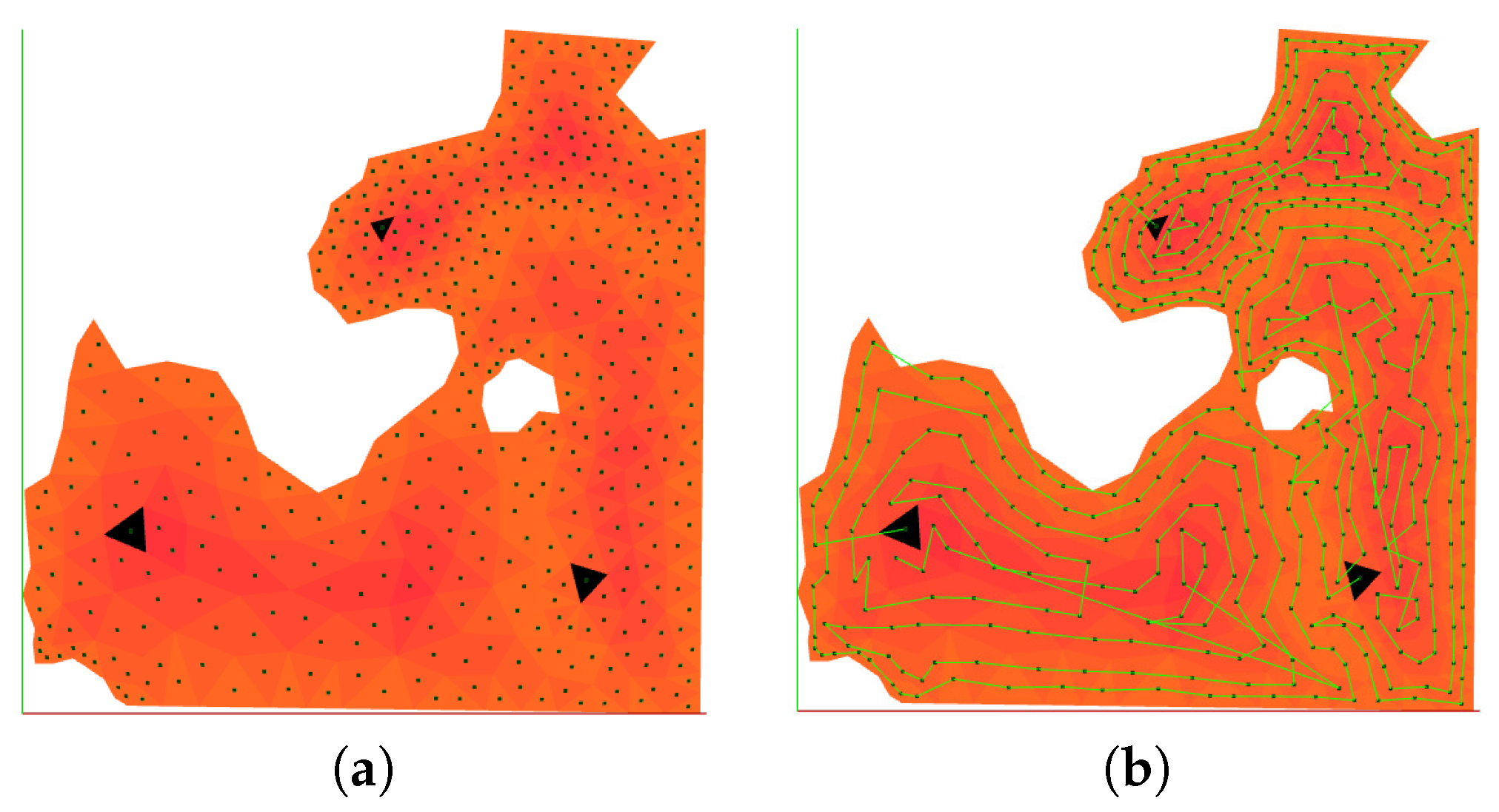
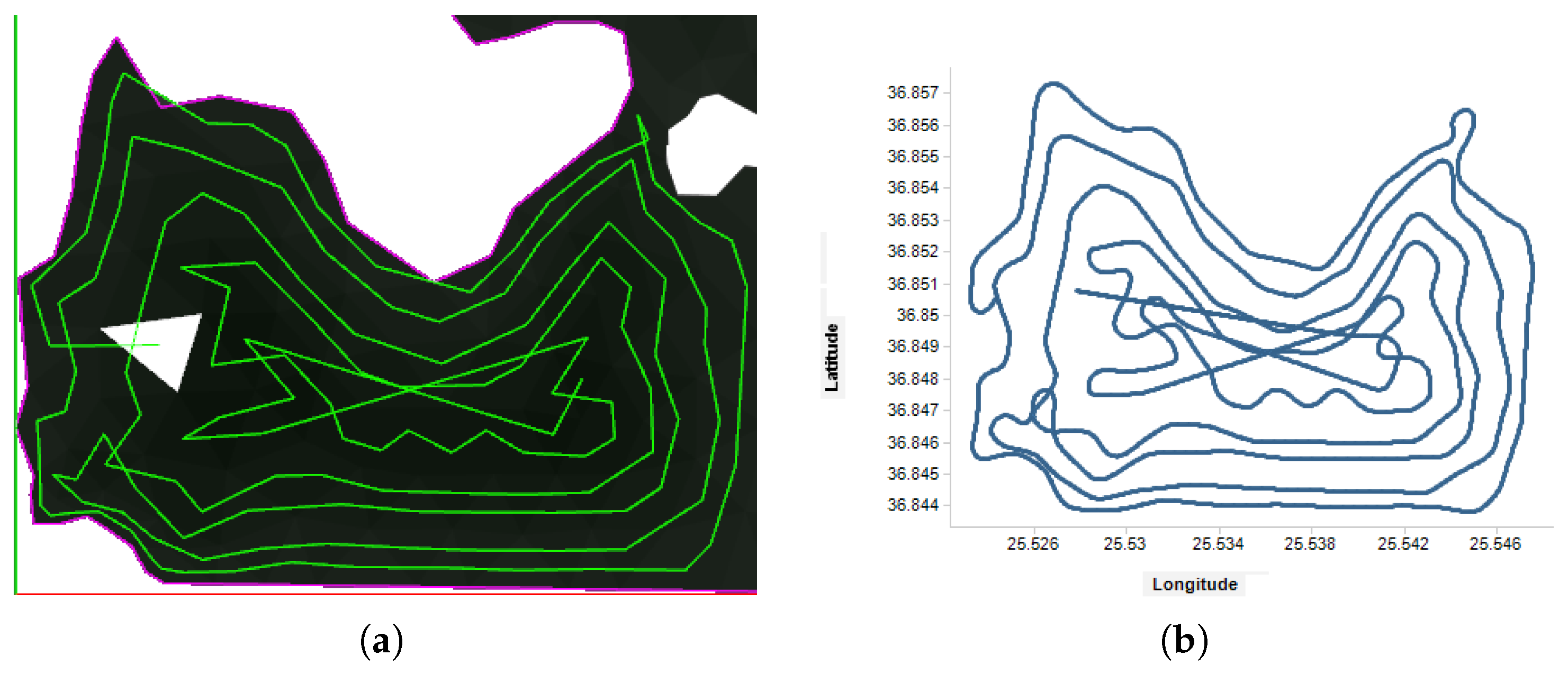
6.4. Coverage Path Planning Simulation Results
| Algorithm 6: Waypoint list computation for coverage. is an auxiliary variable with the current border-to-center cost in each step, whereas is the starting position of the UAV . Function finds the closest vertex to the current one that has its same border-to-center cost. is the sub-CDT for UAV . W is the produced waypoint list of vertices. |
| ; findClosest(); W.insert(v);  |
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| FoV | Field of View |
| CDT | Constrained Delaunay Triangulation |
| AWP | Antagonizing Wavefront Propagation |
| RWS | Reverse Watershed Schema |
| DLH | Deadlock Handling |
| ROS | Robotic Operating System |
| SITL | Software In The Loop |
References
- Quigley, M.; Conley, K.; Gerkey, B.P.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. Proceeddings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–13 May 2009. [Google Scholar]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Alitappeh, R.J.; Pimenta, L.C.A. Distributed Safe Deployment of Networked Robots. In Springer Tracts in Advanced Robotics; Chong, N.Y., Cho, Y.J., Eds.; Springer: Tokyo, Japan, 2016; Volume 112, pp. 65–77. [Google Scholar]
- Kapoutsis, A.C.; Chatzichristofis, S.A.; Kosmatopoulos, E.B. DARP: Divide Areas Algorithm for Optimal Multi-Robot Coverage Path Planning. J. Intell. Robot. Syst. 2017. [Google Scholar] [CrossRef]
- Korsah, G.A.; Stentz, A.; Dias, M.B. A comprehensive taxonomy for multi-robot task allocation. Int. J. Robot. Res. 2013, 32, 1495–1512. [Google Scholar] [CrossRef]
- Quaritsch, M.; Kruggl, K.; Wischounig-Strucl, D.; Bhattacharya, S.; Shah, M.; Rinner, B. Networked UAVs as aerial sensor network for disaster management applications. e & i Elektrotech. Inf. 2010, 127, 56–63. [Google Scholar]
- Li, Y.; Chen, H.; Joo Er, M.; Wang, X. Coverage path planning for UAVs based on enhanced exact cellular decomposition method. Mechatronics 2011, 21, 876–885. [Google Scholar] [CrossRef]
- Di Franco, C.; Buttazzo, G. Coverage Path Planning for UAVs Photogrammetry with Energy and Resolution Constraints. J. Intell. Robot. Syst. 2016, 83, 445–462. [Google Scholar] [CrossRef]
- Fazli, P.; Davoodi, A.; Mackworth, A.K. Multi-robot repeated area coverage. Auton. Robots 2013, 34, 251–276. [Google Scholar] [CrossRef]
- Bochkarev, S.; Smith, S.L. On minimizing turns in robot coverage path planning. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–24 August 2016; pp. 1237–1242. [Google Scholar]
- Kapanoglu, M.; Alikalfa, M.; Ozkan, M.; Parlaktuna, O. A pattern-based genetic algorithm for multi-robot coverage path planning minimizing completion time. J. Intell. Manufact. 2012, 23, 1035–1045. [Google Scholar] [CrossRef]
- Englot, B.; Hover, F.S. Three-dimensional coverage planning for an underwater inspection robot. Int. J. Robot. Res. 2013, 32, 1048–1073. [Google Scholar] [CrossRef]
- Mei, Y.; Lu, Y.H.; Hu, Y.C.; Lee, C.G. Energy-efficient motion planning for mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA’04), Barcelona, Spain, 18–22 April 2004; Volume 5, pp. 4344–4349. [Google Scholar]
- Barber, D.B.; Redding, J.D.; McLain, T.W.; Beard, R.W.; Taylor, C.N. Vision-based target geo-location using a fixed-wing miniature air vehicle. J. Intell. Robot. Syst. 2006, 47, 361–382. [Google Scholar] [CrossRef]
- Balampanis, F.; Maza, I.; Ollero, A. Area decomposition, partition and coverage with multiple remotely piloted aircraft systems operating in coastal regions. In Proceedings of the IEEE 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 275–283. [Google Scholar]
- Boissonnat, J.D.; Devillers, O.; Pion, S.; Teillaud, M.; Yvinec, M. Triangulations in CGAL. Comput. Geom. 2002, 22, 5–19. [Google Scholar] [CrossRef]
- CGAL—2D Conforming Triangulations and Meshes—2.5 Optimization of Meshes with Lloyd. Available online: https://doc.cgal.org/latest/Mesh2/index.htmlsecMesh2optimization (accessed on 9 November 2016).
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- The CGAL Project. In CGAL User and Reference Manual, 4.8.1 edition; CGAL Editorial Board, 2015.
- Autopilot Software in the Loop Simulation. Available online: http://ardupilot.org/dev/docs/sitl-simulator-software-in-the-loop.html (accessed on 20 December 2016).
- RVIZ—3D Visualization Tool for ROS. Available online: http://wiki.ros.org/rviz (accessed on 20 December 2016).
- MAVROS—MAVLink Extendable Communication Node for ROS with Proxy for Ground Control Station. Available online: http://wiki.ros.org/mavros (accessed on 9 November 2016).
- Fixed Wing Ardupilot Instance for Autopilot Hardware. Available online: http://ardupilot.org/plane/index.html (accessed on 9 November 2016).
- Jsbsim, the Open Source Flight Dynamics Model in C++. Available online: http://jsbsim.sourceforge.net/ (accessed on 19 December 2016).
- Qgroundcontrol - Ground Control Station for Small Air–Land–Water Autonomous Unmanned Systems. Available online: http://qgroundcontrol.org/ (accessed on 22 December 2016).
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A Node-Based Multithreaded Open Source Robotics Framework for Deeply Embedded Platforms. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 25–30 May 2015. [Google Scholar]


| FoV (15 m) | FoV (30 m) | ||||
|---|---|---|---|---|---|
| #UAVs | moveRWS | moveAWP | moveRWS | moveAWP | |
| Metric F (m) | 3 | 333,861.84 | 333,909.67 | 82,768.44 | 84,979.76 |
| Metric F (m) | 5 | 437,988.74 | 439,642.85 | 129,879.24 | 131,516.96 |
| FoV (15 m) | FoV (30 m) | ||||
|---|---|---|---|---|---|
| #UAVs | moveRWS | moveAWP | moveRWS | moveAWP | |
| Metric F (m) | 3 | 508,801.74 | 508,751.513 | 211,395 | 214,945.82 |
| Metric F (m) | 5 | 566,971.55 | 568,819.45 | 151,389.621 | 155,269.99 |
| UAV Capability % | FoV (15 m) | FoV (30 m) | ||||
|---|---|---|---|---|---|---|
| Lloyd Iterations | Lloyd Iterations | |||||
| 20 | 30 | 60 | 20 | 30 | 60 | |
| 50% | 0.5/0.92 | 0/0.62 | 0/0.92 | 0.35/0.3 | 0.35/0.18 | 0.05/0.3 |
| 30% | 6.74/0.14 | 6.74/0.89 | 6.88/1.21 | 6.95/0.21 | 7.19/0.65 | 6.86/0.25 |
| 20% | 0.01/1.04 | 0.01/0.26 | 0.01/0.28 | 0/0.49 | 0.03/0.82 | 0.05/0.54 |
| Average% | 2.41/0.69 | 2.25/0.59 | 2.29/0.80 | 2.43/0.32 | 2.52/0.55 | 2.32/0.36 |
| % | 7.25/2.1 | 6.75/1.78 | 6.89/2.42 | 7.3/0.99 | 7.57/1.66 | 6.96/1.09 |
| 20% | 0.02/0.02 | 0.02/0.08 | 0.02/0.06 | 0/0.41 | 0.05/0.12 | 0.05/0.45 |
| 40% | 0/0.06 | 0/0.11 | 0/0.05 | 3.89/0.28 | 3.91/0.59 | 3.6/0.49 |
| 20% | 0.96/0 | 1.11/0 | 0.78/0.06 | 0.48/0.17 | 0.48/0 | 0.62/0.12 |
| 20% | 0/0.02 | 0/0.17 | 0/0.03 | 0/0.29 | 0/0.48 | 0/0.07 |
| Average% | 0.25/0.03 | 0.28/0.09 | 0.2/0.05 | 1.09/0.37 | 1.11/0.3 | 1.07/0.28 |
| % | 0.98/0.12 | 1.13/0.35 | 0.8/0.2 | 4.37/1.11 | 4.44/1.18 | 4.27/1.13 |
| 20% | 0.15/0.38 | 0.15/0.6 | 0.18/0.01 | 0.15/0.11 | 0.11/0.59 | 0.11/1.36 |
| 30% | 13.73/0.34 | 13.75/0.31 | 13.72/0.15 | 13.1/0.24 | 12.98/0.76 | 12.63/1.64 |
| 20% | 0/0.31 | 0/0.42 | 0/0.08 | 0/1.6 | 0.3/0.81 | 0/0.66 |
| 10% | 0/0.41 | 0/0.86 | 0/0.41 | 0/0.71 | 0/0.3 | 0/1.21 |
| 20% | 0.21/0.65 | 0.05/0.14 | 0.21/0.36 | 0/1.01 | 0/0.36 | 0/1.61 |
| Average% | 2.81/0.42 | 2.79/0.47 | 2.28/0.35 | 2.65/0.92 | 2.68/0.56 | 2.55/0.9 |
| % | 14.09/2.1 | 13.95/2.33 | 14.11/1.01 | 13.25/3.69 | 13.39/2.81 | 12.74/4.5 |
| 10% | 0.15/0.21 | 0.15/0.73 | 0.15/0.41 | 0.11/0.72 | 0/0.18 | 0.11/0.29 |
| 20% | 0.3/1.04 | 0.3/1.37 | 0.3/1.35 | 0/1.83 | 0/1.37 | 0/0.43 |
| 10% | 0.15/0.23 | 0.15/0.16 | 0.15/0.23 | 0.11/0.14 | 0/0.97 | 0.11/0.39 |
| 30% | 11.26/0.38 | 11.45/0.69 | 11.2/0.53 | 11.94/0.84 | 12.64/0.83 | 10.75/0.96 |
| 20% | 0.3/0.51 | 0.3/0.36 | 0.3/0.33 | 0.24/0.8 | 0/0.98 | 0.24/0.55 |
| 10% | 0.15/0.19 | 0.15/0.47 | 0.15/0.15 | 0.11/1.04 | 0.11/1.25 | 0.11/0.98 |
| Average% | 2.05/0.41 | 2.08/0.63 | 2.04/0.5 | 2.09/0.9 | 2.13/0.93 | 1.89/0.6 |
| % | 12.32/2.47 | 12.5/3.78 | 12.25/3.01 | 12.51/5.36 | 12.75/5.58 | 11.32/3.59 |
| UAV Capability % | FoV (15 m) | FoV (30 m) | ||||
|---|---|---|---|---|---|---|
| Lloyd Iterations | Lloyd Iterations | |||||
| 20 | 30 | 60 | 20 | 30 | 60 | |
| 50% | 0/0.1 | 0/0 | 30.8/0.27 | 0/0 | 0/1.49 | 29.81/0.5 |
| 30% | 1.19/0.02 | 0.08/0.02 | 0.01/0.16 | 0.024/0.024 | 20.9/0.65 | 0.01/0.57 |
| 20% | 0.01/0.09 | 0.01/0.01 | 0.01/0.11 | 0.024/0.024 | 0.024/0.84 | 0.05/1.1 |
| Average% | 0.4/0.07 | 0.03/0.01 | 10.27/0.18 | 0.02/0.02 | 6.97/0.99 | 9.95/0.72 |
| % | 1.2/0.21 | 0.09/0.03 | 30.82/0.54 | 0.05/0.05 | 20.92/2.98 | 29.87/2.17 |
| 20% | 0/0.43 | 15.37/0.22 | 2.19/0.49 | 0/0.730 | 14.2/1.66 | 0.62/0.05 |
| 40% | 13.1/0.33 | 0/0.53 | 0/0.22 | 14/0.43 | 0/1.89 | 0.07/0.14 |
| 20% | 6.48/0.31 | 0/0.06 | 2.64/0.35 | 6.24/0.56 | 0/0.12 | 1.8/0.16 |
| 20% | 0/0.42 | 0/0.69 | 0/0.35 | 0/0.26 | 0/0.12 | 0.02/0.07 |
| Average% | 4.9/0.37 | 3.84/0.38 | 1.21/0.36 | 5.06/0.5 | 3.55/0.95 | 0.67/0.11 |
| % | 19.58/1.48 | 15.37/1.5 | 4.83/1.43 | 20.24/1.98 | 14.2/3.79 | 2.67/0.42 |
| 20% | 0.01/0.03 | 0.01/0.21 | 11.23/0.77 | 0/1.8 | 0.02/1.43 | 10.78/0.4 |
| 30% | 0.53/0.02 | 12.85/0.24 | 0.02/0.68 | 0/0.27 | 13.45/0.42 | 0.02/1.4 |
| 20% | 0.01/0.03 | 0.01/0.11 | 11.59/2.65 | 6.24/0.57 | 6.88/0.44 | 10.78/0.64 |
| 10% | 0.01/0.07 | 0.01/0.19 | 3.382/1.19 | 0/0.46 | 0.04/0.21 | 3.97/0.04 |
| 20% | 0.01/0.14 | 0.01/0.14 | 0.01/1.36 | 0/1.03 | 0.02/0.37 | 0.02/0.4 |
| Average% | 0.11/0.05 | 2.58/0.18 | 5.25/1.33 | 1.25/0.82 | 4.12/0.57 | 5.11/0.58 |
| % | 0.57/0.27 | 12.89/0.89 | 26.24/6.64 | 6.24/4.12 | 20.59/2.87 | 25.57/2.88 |
| 10% | 0.02/0.46 | 4.36/0.05 | 4.2/0.26 | 0.04/0.36 | 0.04/0.18 | 0.04/0.09 |
| 20% | 0.02/1.02 | 4.23/0.26 | 0.01/0.06 | 0.05/0.3 | 0.05/0.36 | 0.05/1.49 |
| 10% | 0.02/0.42 | 0.01/0.47 | 0.01/0.01 | 0.04/1.2 | 0/0.41 | 0.04/0.25 |
| 30% | 19.04/0.5 | 0.01/1.22 | 0.01/0.01 | 20.32/0.74 | 20/1.48 | 19.85/0.31 |
| 20% | 0.01/0.9 | 0.02/0.04 | 0.01/0.02 | 10.32/0.49 | 10.32/0.24 | 10.08/0.65 |
| 10% | 0.02/0.66 | 0.01/0.58 | 0.01/0.2 | 0.04/0.028 | 0/1.01 | 0.04/0.22 |
| Average% | 3.18/0.66 | 1.44/0.43 | 0.71/0.09 | 5.13/0.52 | 5.07/0.61 | 5.02/0.5 |
| % | 19.13/3.96 | 8.64/2.62 | 4.25/0.56 | 30.81/3.12 | 30.41/3.68 | 30.1/3.01 |
| UAV | FoV Projection Size (m) | (deg) | Altitude (m) | Relative Capability |
|---|---|---|---|---|
| UAV 1 | 30 | −45 | 100 | 20% |
| UAV 2 | 40 | −45 | 80 | 30% |
| UAV 3 | 55 | −45 | 120 | 50% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balampanis, F.; Maza, I.; Ollero, A. Coastal Areas Division and Coverage with Multiple UAVs for Remote Sensing. Sensors 2017, 17, 808. https://doi.org/10.3390/s17040808
Balampanis F, Maza I, Ollero A. Coastal Areas Division and Coverage with Multiple UAVs for Remote Sensing. Sensors. 2017; 17(4):808. https://doi.org/10.3390/s17040808
Chicago/Turabian StyleBalampanis, Fotios, Iván Maza, and Aníbal Ollero. 2017. "Coastal Areas Division and Coverage with Multiple UAVs for Remote Sensing" Sensors 17, no. 4: 808. https://doi.org/10.3390/s17040808
APA StyleBalampanis, F., Maza, I., & Ollero, A. (2017). Coastal Areas Division and Coverage with Multiple UAVs for Remote Sensing. Sensors, 17(4), 808. https://doi.org/10.3390/s17040808






