Acoustic NLOS Identification Using Acoustic Channel Characteristics for Smartphone Indoor Localization
Abstract
:1. Introduction
- An acoustic NLOS identification approach based on acoustic channel characteristics is proposed for smartphone indoor localization in the real world. This approach is suitable for the acoustic localization systems based on DOA, TOA and TDOA strategies.
- An efficient approach to estimate relative channel gain and delay based on the cross-correlation method is proposed, in order to mitigate the influence of the Doppler Effect and reduce the computational complexity.
- The differences and characteristics of acoustic relative channel gain and delay under LOS and NLOS conditions are investigated through extensive measurements in office rooms and lobby environment using COTS smartphones. Novel features are extracted from these characteristics that capture the salient properties based on time delay characteristics, waveform characteristics, Rician K-factor and frequency characteristics of relative channel gain.
- An optimal kernel function for an SVM classifier to realize acoustic NLOS identification is evaluated and chosen under the accuracy criterion, based on a data set with more than 10 thousand measurements. The best feature set of the SVM classifier for acoustic NLOS identification is investigated and proposed.
2. Characterization of the Acoustic Channel under LOS and NLOS Conditions
2.1. The Characteristics of Room Acoustic Propagation under LOS Condition
- . There is only one direct path between the transmitter and receiver, which is the LOS path. is the LOS condition, and 0 for the NLOS condition. and are decreased with the increase of path length, due to the air propagation attenuation.
- The length of the reflection path is definitely longer than the LOS path. With the increase of reflection time, becomes larger and larger, while is quickly decreased due to the acoustic absorption by air, walls and furniture. For the diffusion propagation path, the number of diffusion paths is usually very large. and are related to the shape of the diffusion surface, absorption coefficient, and the relative position between the transmitter, receiver and diffusion surface.
- Generally speaking, the energy of signals received from the LOS path and reflection path is larger than the signals received from the diffusion path, that is , > . However, the relationship between and is determined by ambient environment. It is common that the LOS signal is not the strongest, especially in large space environment.
2.2. The Characteristics of Acoustic Propagation under NLOS Condition
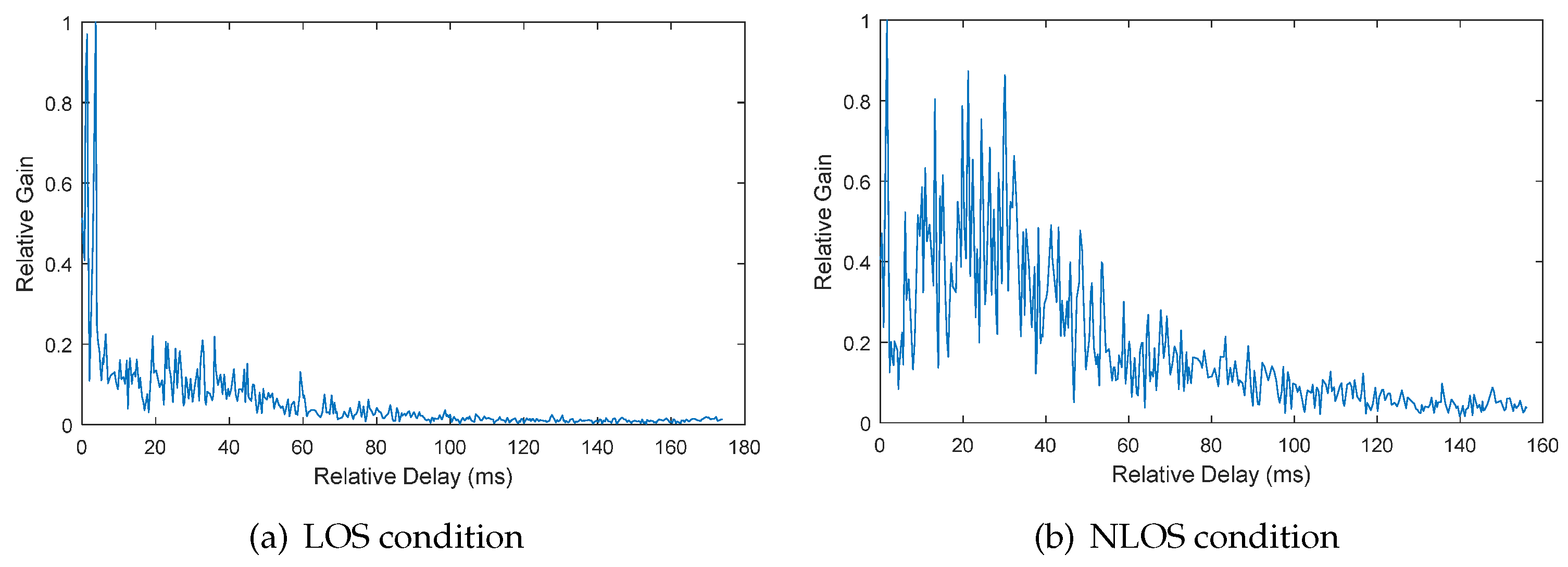
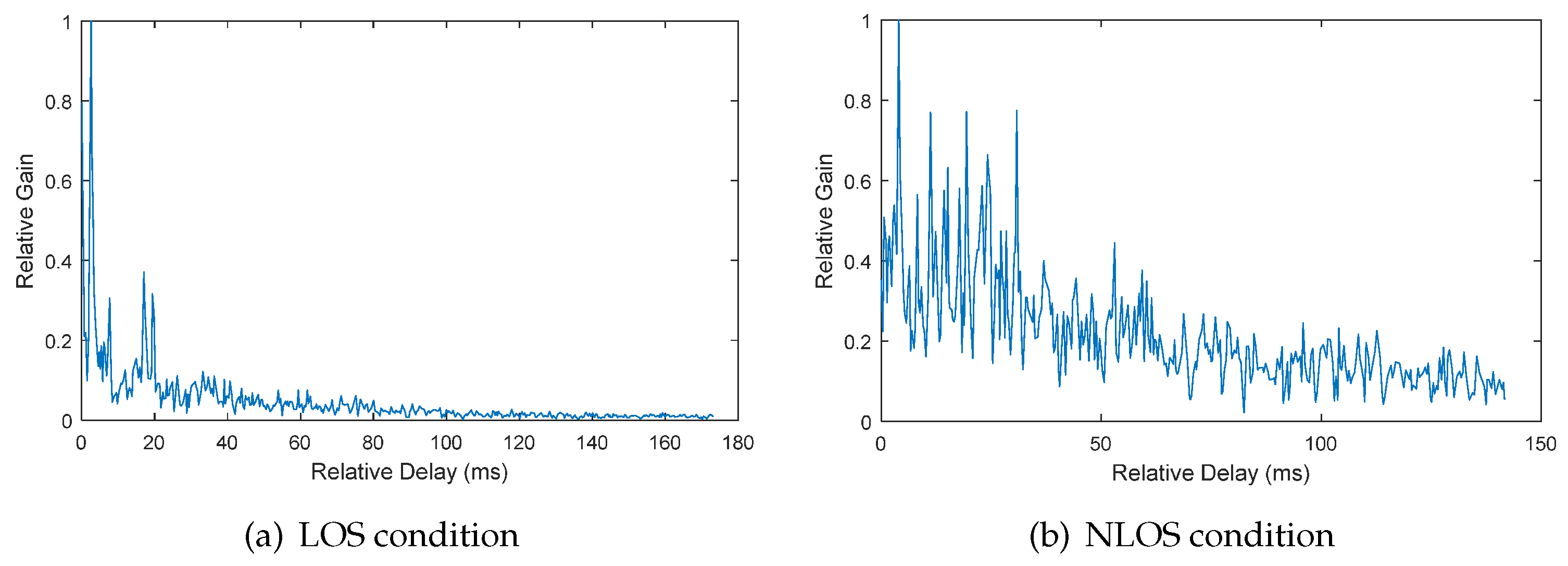
3. The Relative Channel Gain and channel Delay Estimation
3.1. Modelling of Received Signals
3.2. Estimation Approach
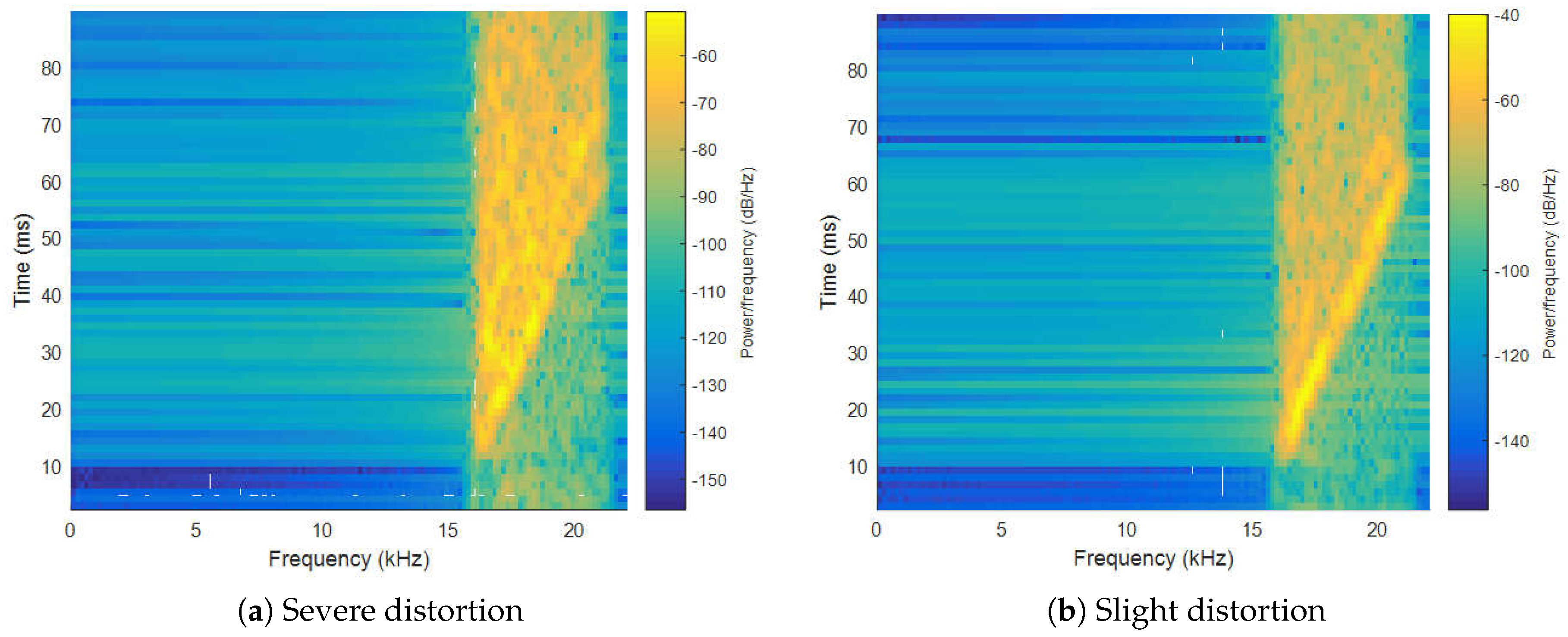
4. Data Acquisition and Features Extraction
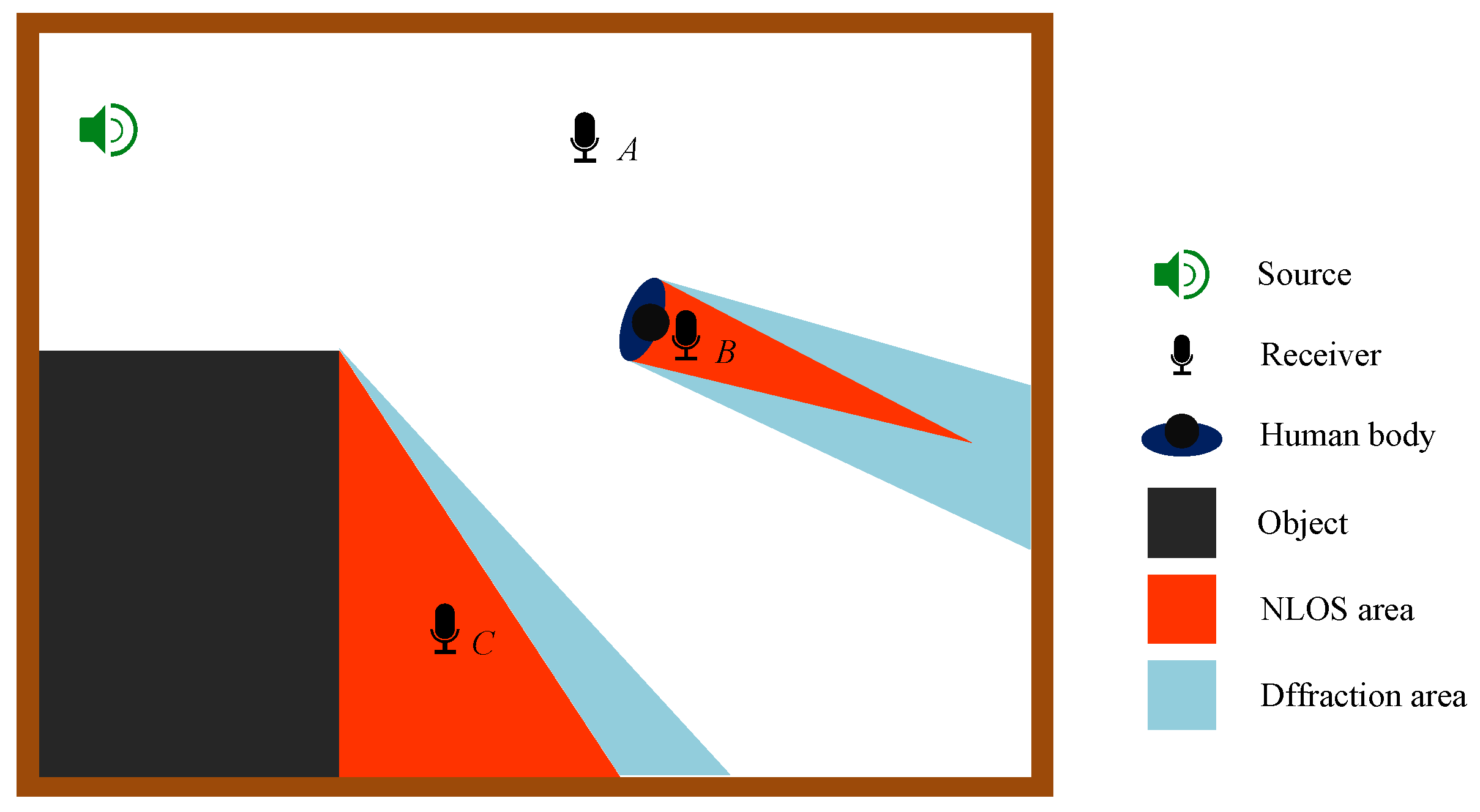
4.1. Experiment Deployment
A. Obstructions
B. Experiment Process
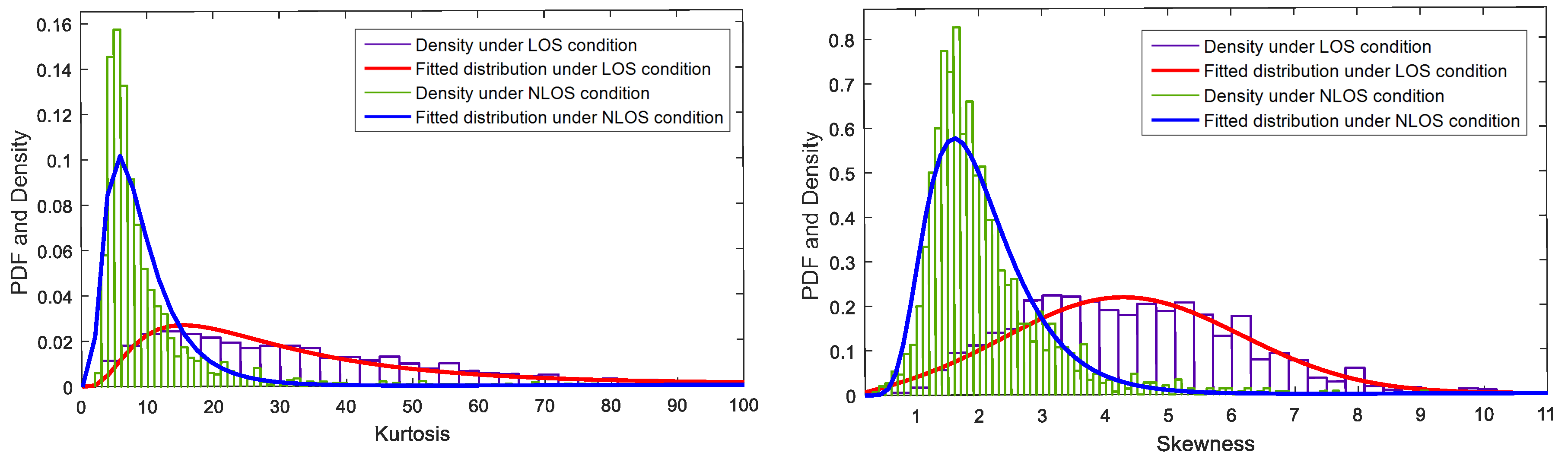
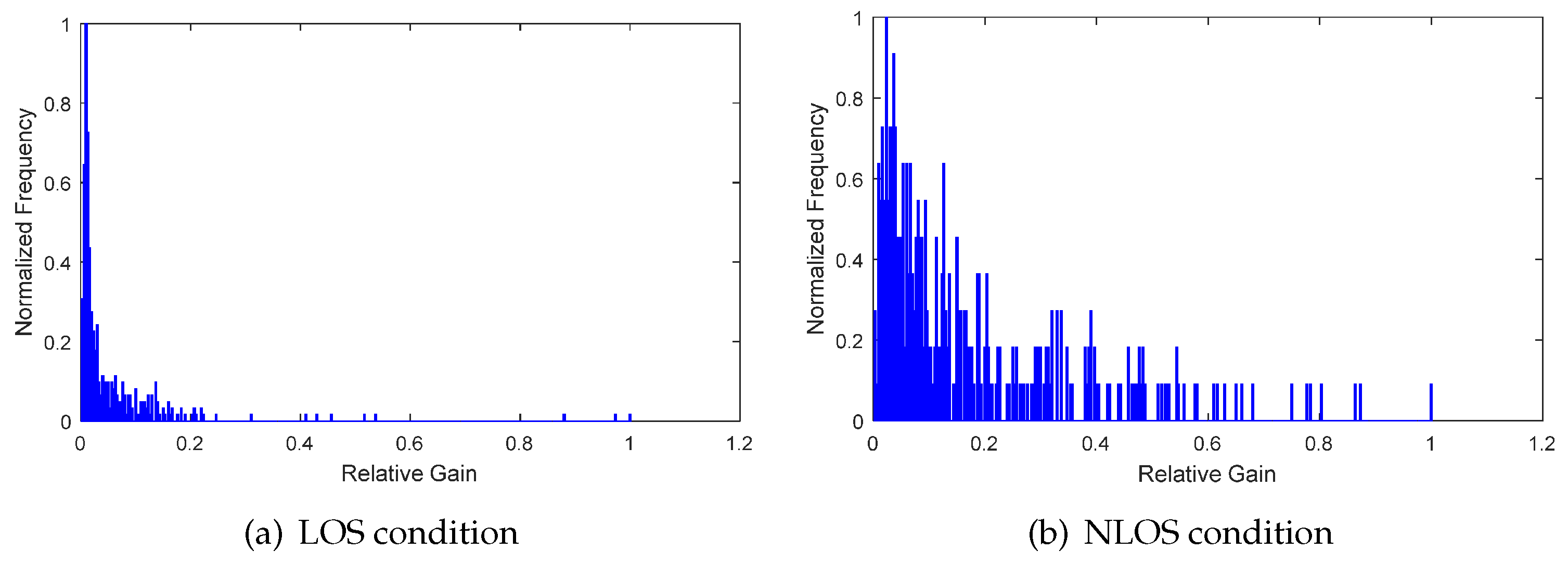
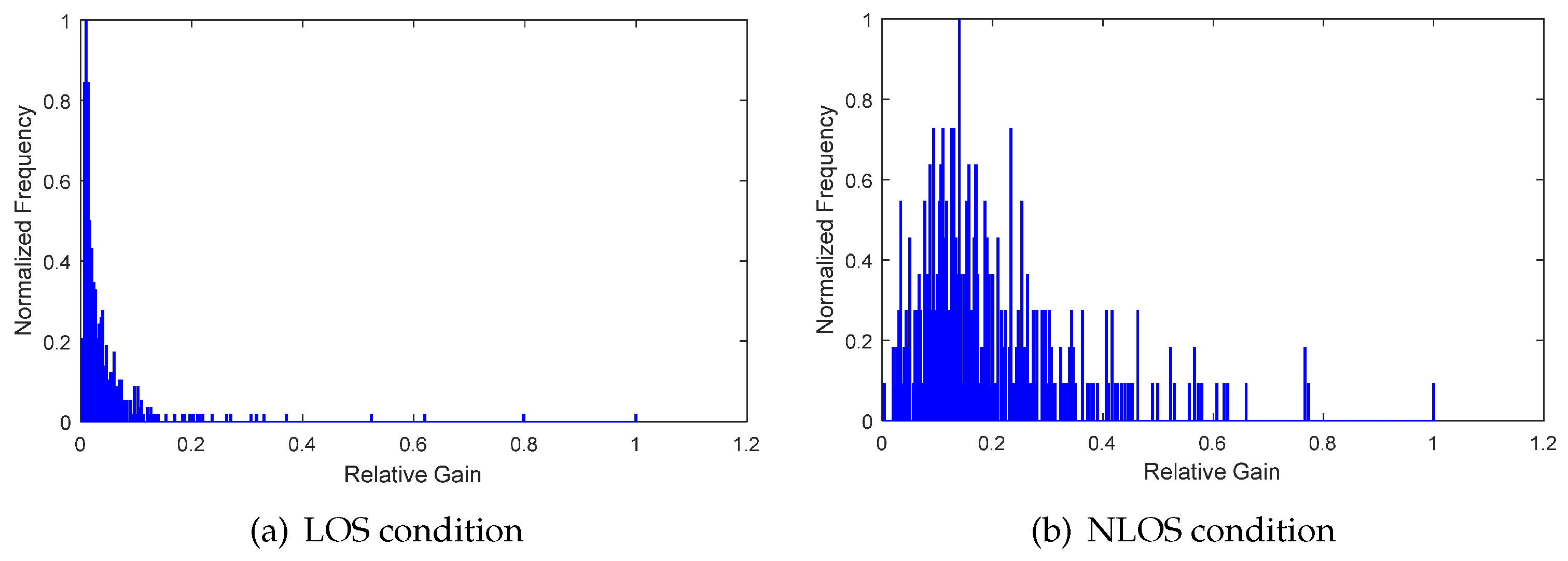
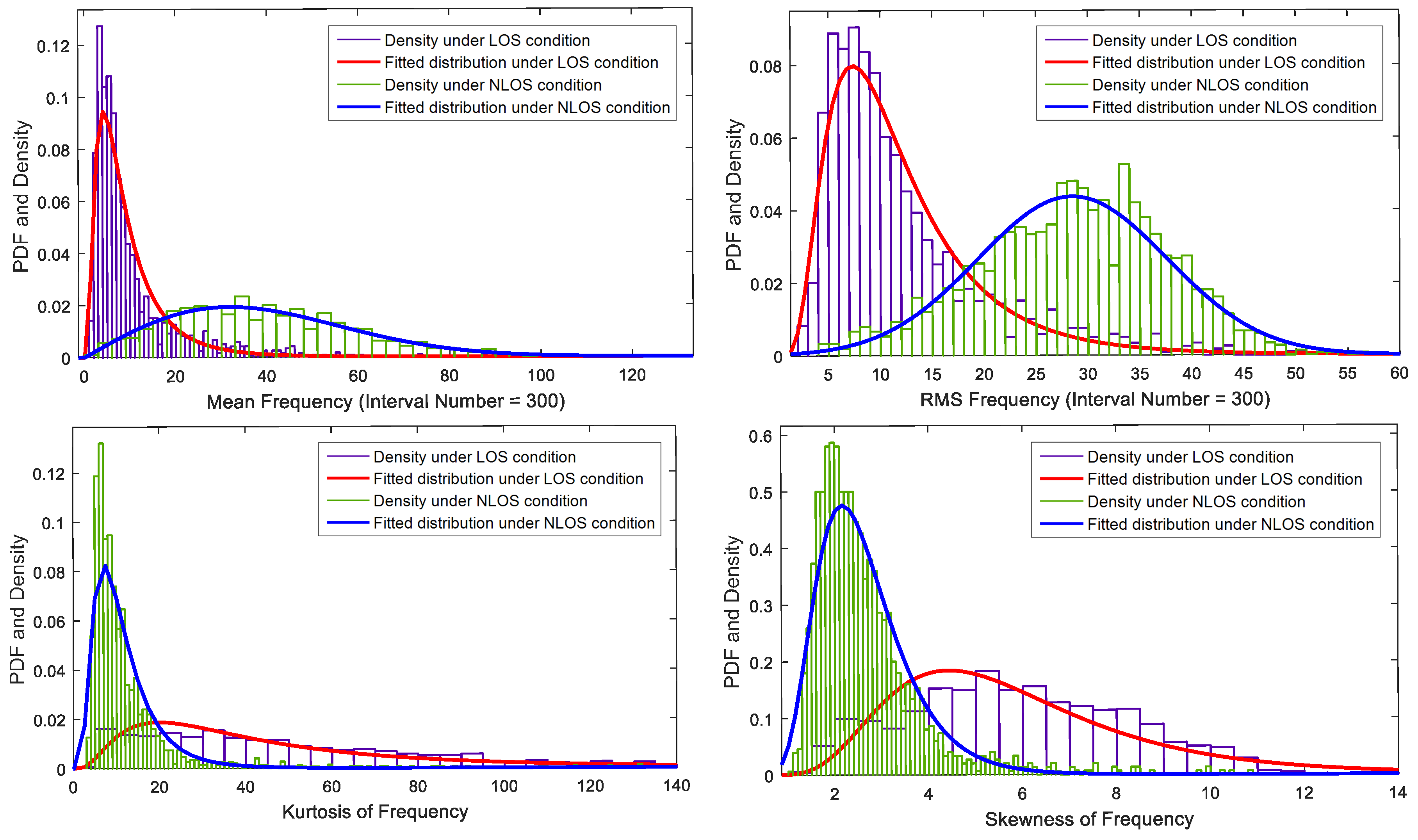
4.2. Features Extraction
5. NLOS Identification Based on SVM Classifiers
5.1. The SVM Classifier and Kernel Function
5.2. Cross-Validation and Evaluation Criteria
5.3. Test Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ens, A.; Höflinger, F.; Wendeberg, J.; Hoppe, J.; Zhang, R.; Bannoura, A.; Reindl, L.M.; Schindelhauer, C. Acoustic Self-Calibrating System for Indoor Smartphone Tracking. Int. J. Navig. Observ. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, C.; Liu, F.; Dong, Y.; Xu, X. Exponentially Weighted Particle Filter for Simultaneous Localization and Mapping Based on Magnetic Field Measurements. IEEE Trans. Instrum. Meas. 2017. [Google Scholar] [CrossRef]
- Zhuang, Y.; Yang, J.; Li, Y.; Qi, L.; El-Sheimy, N. Smartphone-based indoor localization with bluetooth low energy beacons. Sensors 2016, 16, 596. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Shen, G.; Zhang, Y. BeepBeep:A High-Accuracy Acoustic-based System for Ranging and Localization Using COTS Devices. ACM Trans. Embedded Comput. Syst. 2012, 11, 4. [Google Scholar] [CrossRef]
- Tan, C.; Zhu, X.; Su, Y.; Wang, Y.; Wu, Z.; Gu, D. A low-cost centimeter-level acoustic localization system without time synchronization. Measurement 2016, 78, 73–82. [Google Scholar] [CrossRef]
- Huang, W.; Xiong, Y.; Li, X.; Lin, H.; Mao, X.; Yang, P.; Liu, Y.; Wang, X. Swadloon: Direction finding and indoor localization using acoustic signal by shaking smartphone. IEEE Trans. Mob. Comput. 2015, 14, 2145–2157. [Google Scholar] [CrossRef]
- Liu, K.; Liu, X.; Li, X. Guoguo: Enabling Fine-Grained Smartphone Localization via Acoustic Anchors. IEEE Trans. Mob. Comput. 2016, 15, 1144–1156. [Google Scholar] [CrossRef]
- Lopes, S.I.; Vieira, J.M.N.; Reis, J.; Albuquerque, D.; Carvalho, N.B. Accurate smartphone indoor positioning using a WSN infrastructure and non-invasive audio for TDoA estimation. Pervasive Mob. Comput. 2015, 20, 29–46. [Google Scholar] [CrossRef]
- Microsoft Indoor Localization Competition---IPSN 2016. Available online: https://www.microsoft.com/en-us/research/event/microsoft-indoor-localization-competition-ipsn-2016/ (accessed on 11 April 2016).
- Packi, F.; Hanebeck, U.D. Robust NLOS Discrimination for Range-Based Acoustic Pose Tracking. In Proceedings of the International Conference on Information Fusion, Heidelberg, Germany, 9–12 July 2012; pp. 1601–1608. [Google Scholar]
- Güvenc, İ.; Chong, C.; Watanabe, F.; Inamura, H. NLOS identification and weighted least square localization for UWB systems using multipath channel statistics. EURASIP J. Adv. Signal Process. 2007. [Google Scholar] [CrossRef]
- Chan, Y.; Tsui, W.; So, H.; Ching, P. Time of arrival based localization under NLOS conditions. IEEE Trans. Veh. Technol. 2006, 55, 17–24. [Google Scholar] [CrossRef]
- Yu, K.; Dutkiewicz, E. NLOS Identification and Mitigation for Mobile Tracking. IEEE Trans. Aerospace Elctronic Syst. 2013, 49, 1438–1452. [Google Scholar] [CrossRef]
- Khodjaev, J.; Park, Y.; Malik, A.S. Survey of NLOS identification and error mitigation problems in UWB-based positioning algorithms for dense environments. Ann. Telecommun. 2010, 65, 301–311. [Google Scholar] [CrossRef]
- Venkatraman, S.; Caffery, J., Jr. A statistical approach to non-line-of-sight BS identification. In Proceedings of the International Symposium on Wireless Personal Multidedia Communications, Honolulu, HI, USA, 27–30 October 2002; Volume 1, pp. 296–300. [Google Scholar]
- Gezici, S.; Kobayashi, H.; Poor, H.V. Non-Parametric Non-Line-of-Sight Identification. In Proceedings of the IEEE Vehicular Technology Conference, Orlando, FL, USA, 6–9 October 2003; Volume 4, pp. 2544–2548. [Google Scholar]
- Yu, K.; Guo, Y.J. Statistical NLOS Identification Based on AOA, TOA and Signal Strength. IEEE Trans. Veh. Technol. 2009, 58, 274–286. [Google Scholar] [CrossRef]
- Lakhzouri, A.; Lohan, E.S.; Hamila, R.; Renfors, M. Extended Kalman Filter Channel Estimation for Line-of-Sight Detection in WCDMA Mobile Positioning. EURASIP J. Appl. Signal Process. 2003, 13, 1268–1278. [Google Scholar] [CrossRef]
- Xu, W.; Wang, Z.; Zekavat, S.A. Non-line-of-sight identification via phase difference statistics across two-antenna elements. IET Commun. 2011, 5, 1814–1822. [Google Scholar] [CrossRef]
- Maranò, S.; Gifford, W.M.; Wymeersch, H.; Win, M.Z. NLOS Identification and Mitigation for Localization Based on UWB Experimental Data. IEEE J. Sel. Areas Commun. 2011, 28, 1026–1035. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.; Watanabe, F. NLOS Identification and Mitigation for UWB Localization Systems. In Proceedings of the IEEE Wireless Communicaton and Networking Conference, Hong Kong, China, 11–15 March 2007; pp. 1571–1576. [Google Scholar]
- Diamant, R.; Tan, H.; Lampe, L. LOS and NLOS Classification for Underwater Acoustic Localization. IEEE Trans. Mob. Comput. 2014, 13, 311–323. [Google Scholar] [CrossRef]
- Kuttruff, H. Room Acoustic, 4th ed.; Spon Press: London, UK, 2006; pp. 89–114. [Google Scholar]
- Yang, G.; Yin, W.J.; Li, M.; Pan, R.Z.; Zhou, L.H. An effective Sine-Chirp signal for multi-parameter estimation of underwater acoustic channel. J. Acoustic Soc. Am. 2014, 135, 2201. [Google Scholar] [CrossRef]
- Chen, J.; Benesty, J.; Huang, Y. Time delay estimation in room acoustic environments: An overview. EURASIP J. Appl. Signal Process. 2006. [Google Scholar] [CrossRef]
- Doukas, A.; Kalivas, G. Rician K Factor Estimation for Wireless Communication Systems. In Proceedings of the International Conference on Wireless & Mobile Communications, Bucharest, Romania, 29–31 July 2006; pp. 69–74. [Google Scholar]
- Xiao, C.; Zheng, Y.R.; Beaulieu, N.C. Novel sum-of-sinusoids simulation model for Rayleigh and Rician fading channels. IEEE Trans. Wirel. Commun. 2006, 5, 3667–3679. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Wang, X.; Bi, D.; Ding, L.; Wang, S. Agent collaborative target localization and classification in wireless sensor networks. Sensors 2007, 7, 1359–1386. [Google Scholar] [CrossRef]
- Jiang, L.; Zhu, B.; Rao, X.; Berney, G.; Tao, Y. Discrimination of black walnut shell and pulp in hyperspectral fluorescence imagery using Gaussian kernel function approach. J. Food Eng. 2007, 81, 108–117. [Google Scholar] [CrossRef]
- Hossin, M.B.; Sulaiman, M.N. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1–11. [Google Scholar]
- Joshi, M.V. On evaluating performance of classifiers for rare classes. In Proceedings of the IEEE International Conference on Data Mining, Maebashi City, Japan, 9–12 December 2002; pp. 641–644. [Google Scholar]
- Kostadinov, D.; Bogdanova, S. Logistic Regression Classifier for Palmprint verification. In Proceedings of the International Conference on Systems, Signals and Image Processing (IWSSIP), Vienna, Austria, 11–13 April 2012; pp. 413–416. [Google Scholar]
- Alexandre-Cortizo, E.; Rosa-Zurera, M.; López-Ferreras, F. Application of Fisher Linear Discriminant Analysis to Speech/Music Classification. In Proceedings of the International Conference on Computer as a Tool, Belgrade, Serbia & Montenegro, 21–24 November 2005; pp. 1666–1669. [Google Scholar]




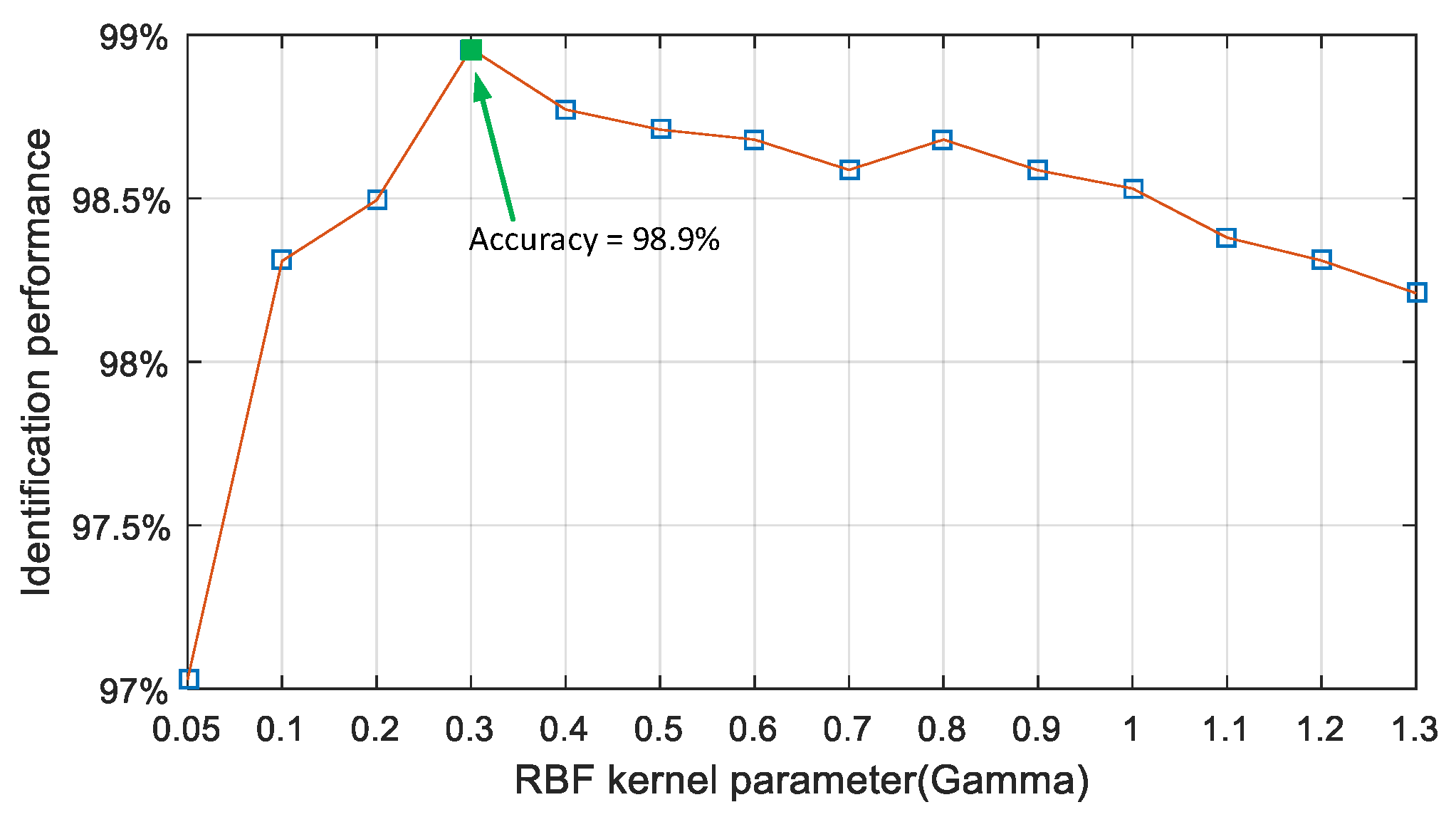
| RBF Kernel Function | Polynomial Kernel Function | ||||||
| Feature | Precision | Accuracy | F1-Measure | Feature | Precision | Accuracy | F1-Measure |
| 0.818 | 0.826 | 0.850 | 0.832 | 0.832 | 0.850 | ||
| 0.749 | 0.781 | 0.824 | 0.776 | 0.770 | 0.795 | ||
| k | 0.837 | 0.823 | 0.841 | k | 0.784 | 0.811 | 0.840 |
| s | 0.840 | 0.828 | 0.846 | s | 0.803 | 0.821 | 0.844 |
| 0.896 | 0.853 | 0.864 | 0.895 | 0.858 | 0.873 | ||
| 0.858 | 0.867 | 0.885 | 0.883 | 0.858 | 0.871 | ||
| 0.850 | 0.851 | 0.870 | 0.848 | 0.837 | 0.854 | ||
| 0.838 | 0.852 | 0.872 | 0.813 | 0.847 | 0.871 | ||
| 0.838 | 0.849 | 0.870 | 0.827 | 0.846 | 0.868 | ||
| Mean accuracy | 0.837 | Mean accuracy | 0.831 | ||||
| Median accuracy | 0.849 | Median accuracy | 0.837 | ||||
| Best feature | Best feature | ||||||
| Linear Kernel Function | Sigmoid Kernel Function | ||||||
| Feature | Precision | Accuracy | F1-Measure | Feature | Precision | Accuracy | F1-Measure |
| 0.825 | 0.826 | 0.848 | 0.564 | 0.564 | 0.721 | ||
| 0.783 | 0.763 | 0.789 | 0.559 | 0.559 | 0.717 | ||
| k | 0.778 | 0.800 | 0.834 | k | 0.566 | 0.566 | 0.723 |
| s | 0.813 | 0.819 | 0.846 | s | 0.289 | 0.205 | 0.290 |
| 0.876 | 0.849 | 0.862 | 0.512 | 0.456 | 0.625 | ||
| 0.884 | 0.861 | 0.874 | 0.549 | 0.549 | 0.709 | ||
| 0.859 | 0.852 | 0.869 | 0.559 | 0.559 | 0.717 | ||
| 0.810 | 0.844 | 0.870 | 0.544 | 0.544 | 0.705 | ||
| 0.827 | 0.847 | 0.868 | 0.397 | 0.297 | 0.430 | ||
| Mean accuracy | 0.829 | Mean accuracy | 0.478 | ||||
| Median accuracy | 0.844 | Median accuracy | 0.549 | ||||
| Best feature | Best feature | k | |||||
| SVM with RBF Kernel Function | ||||
| Best | Worst | Average | ||
| Feature combination | Accuracy | Feature combination | Accuracy | |
| 0.867 | 0.781 | 0.837 | ||
| 0.913 | 0.841 | 0.877 | ||
| 0.975 | 0.864 | 0.931 | ||
| 0.984 | 0.902 | 0.967 | ||
| 0.985 | 0.952 | 0.980 | ||
| 0.984 | 0.980 | 0.982 | ||
| 0.983 | 0.981 | 0.982 | ||
| 0.983 | 0.981 | 0.982 | ||
| 0.983 | 0.983 | 0.983 | ||
| Mean accuracy | 0.962 | |||
| Median accuracy | 0.983 | |||
| Best feature combination | ||||
| SVM with Polynomial Kernel Function | ||||
| Best | Worst | Average | ||
| Feature combination | Accuracy | Feature combination | Accuracy | |
| 0.858 | 0.770 | 0.831 | ||
| 0.873 | 0.827 | 0.853 | ||
| 0.886 | 0.830 | 0.860 | ||
| 0.889 | 0.842 | 0.863 | ||
| 0.890 | 0.843 | 0.868 | ||
| 0.895 | 0.848 | 0.873 | ||
| 0.896 | 0.853 | 0.880 | ||
| 0.903 | 0.866 | 0.891 | ||
| 0.892 | 0.892 | 0.892 | ||
| Mean accuracy | 0.887 | |||
| Median accuracy | 0.890 | |||
| Best feature combination | ||||
| SVM with Linear Kernel Function | ||||
| Best | Worst | Average | ||
| Feature combination | Accuracy | Feature combination | Accuracy | |
| 0.861 | 0.763 | 0.829 | ||
| 0.876 | 0.825 | 0.853 | ||
| 0.884 | 0.828 | 0.859 | ||
| 0.887 | 0.843 | 0.864 | ||
| 0.890 | 0.840 | 0.867 | ||
| 0.895 | 0.842 | 0.873 | ||
| 0.896 | 0.852 | 0.878 | ||
| 0.902 | 0.863 | 0.887 | ||
| 0.894 | 0.894 | 0.894 | ||
| Mean accuracy | 0.887 | |||
| Median accuracy | 0.890 | |||
| Best feature combination | ||||
| Logistic Regression | ||||
| Best | Worst | Average | ||
| Feature combination | Accuracy | Feature combination | Accuracy | |
| 0.860 | 0.776 | 0.830 | ||
| 0.882 | 0.803 | 0.850 | ||
| 0.882 | 0.828 | 0.858 | ||
| 0.893 | 0.837 | 0.862 | ||
| 0.889 | 0.839 | 0.866 | ||
| 0.903 | 0.839 | 0.874 | ||
| 0.895 | 0.839 | 0.878 | ||
| 0.895 | 0.877 | 0.886 | ||
| 0.890 | 0.890 | 0.890 | ||
| Mean accuracy | 0.888 | |||
| Median accuracy | 0.890 | |||
| Best feature combination | ||||
| LDA | ||||
| Best | Worst | Average | ||
| Feature combination | Accuracy | Feature combination | Accuracy | |
| 0.848 | 0.760 | 0.809 | ||
| 0.882 | 0.767 | 0.844 | ||
| 0.879 | 0.829 | 0.855 | ||
| 0.878 | 0.834 | 0.860 | ||
| 0.887 | 0.836 | 0.864 | ||
| 0.891 | 0.847 | 0.867 | ||
| 0.889 | 0.848 | 0.870 | ||
| 0.885 | 0.855 | 0.874 | ||
| 0.873 | 0.873 | 0.873 | ||
| Mean accuracy | 0.879 | |||
| Median accuracy | 0.882 | |||
| Best feature combination | ||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Huang, D.; Wang, X.; Schindelhauer, C.; Wang, Z. Acoustic NLOS Identification Using Acoustic Channel Characteristics for Smartphone Indoor Localization. Sensors 2017, 17, 727. https://doi.org/10.3390/s17040727
Zhang L, Huang D, Wang X, Schindelhauer C, Wang Z. Acoustic NLOS Identification Using Acoustic Channel Characteristics for Smartphone Indoor Localization. Sensors. 2017; 17(4):727. https://doi.org/10.3390/s17040727
Chicago/Turabian StyleZhang, Lei, Danjie Huang, Xinheng Wang, Christian Schindelhauer, and Zhi Wang. 2017. "Acoustic NLOS Identification Using Acoustic Channel Characteristics for Smartphone Indoor Localization" Sensors 17, no. 4: 727. https://doi.org/10.3390/s17040727
APA StyleZhang, L., Huang, D., Wang, X., Schindelhauer, C., & Wang, Z. (2017). Acoustic NLOS Identification Using Acoustic Channel Characteristics for Smartphone Indoor Localization. Sensors, 17(4), 727. https://doi.org/10.3390/s17040727





