The Electrochemical Behavior of Carbon Fiber Microelectrodes Modified with Carbon Nanotubes Using a Two-Step Electroless Plating/Chemical Vapor Deposition Process
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Reagents
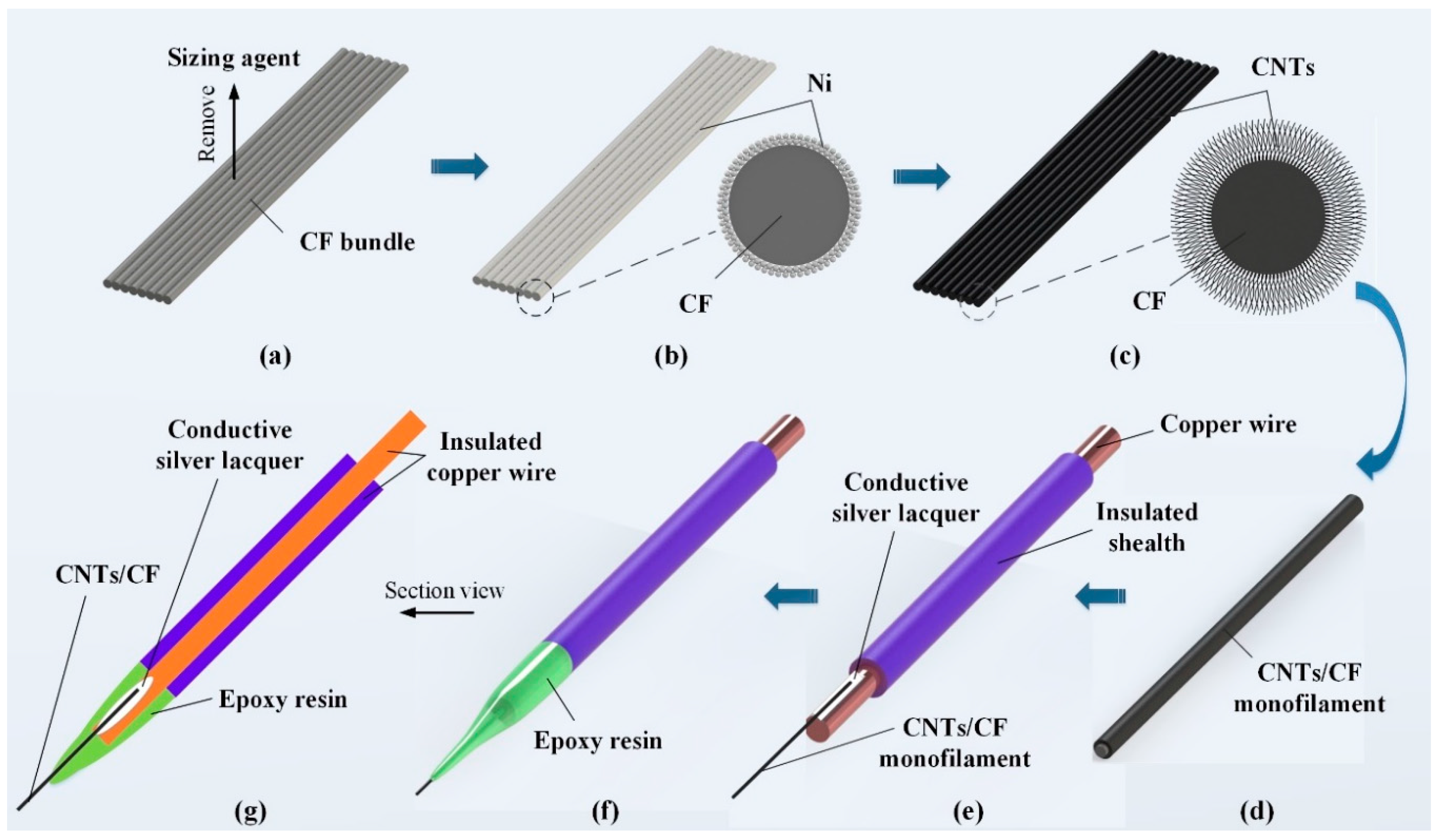
2.2. Preparation of CNTs/CFMEs
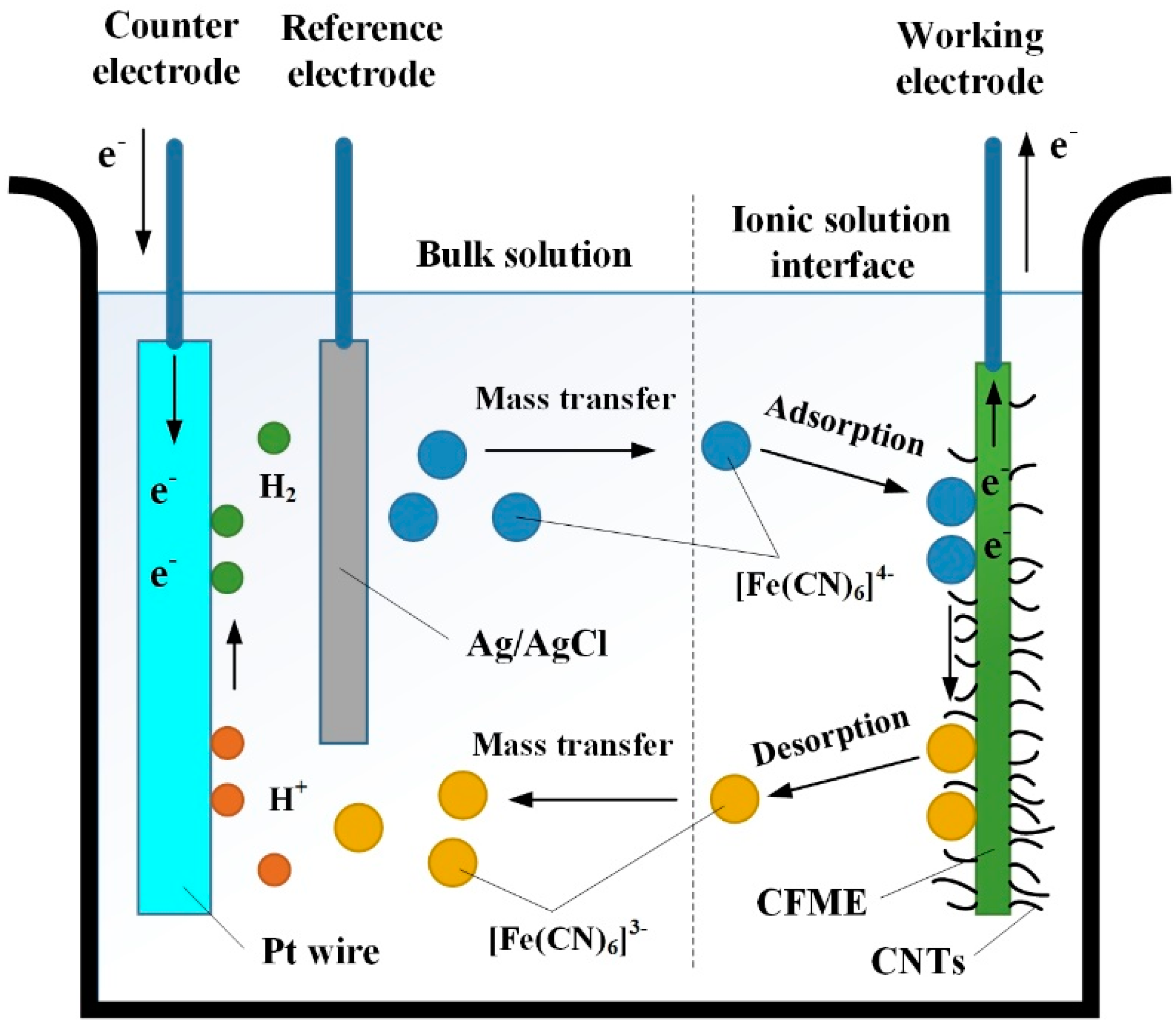
2.3. Performance Characterization
3. Results and Discussion
3.1. Morphology Observation of CNTs/CFs
3.2. Electrical Conductivity Analysis of CNTs/CFs
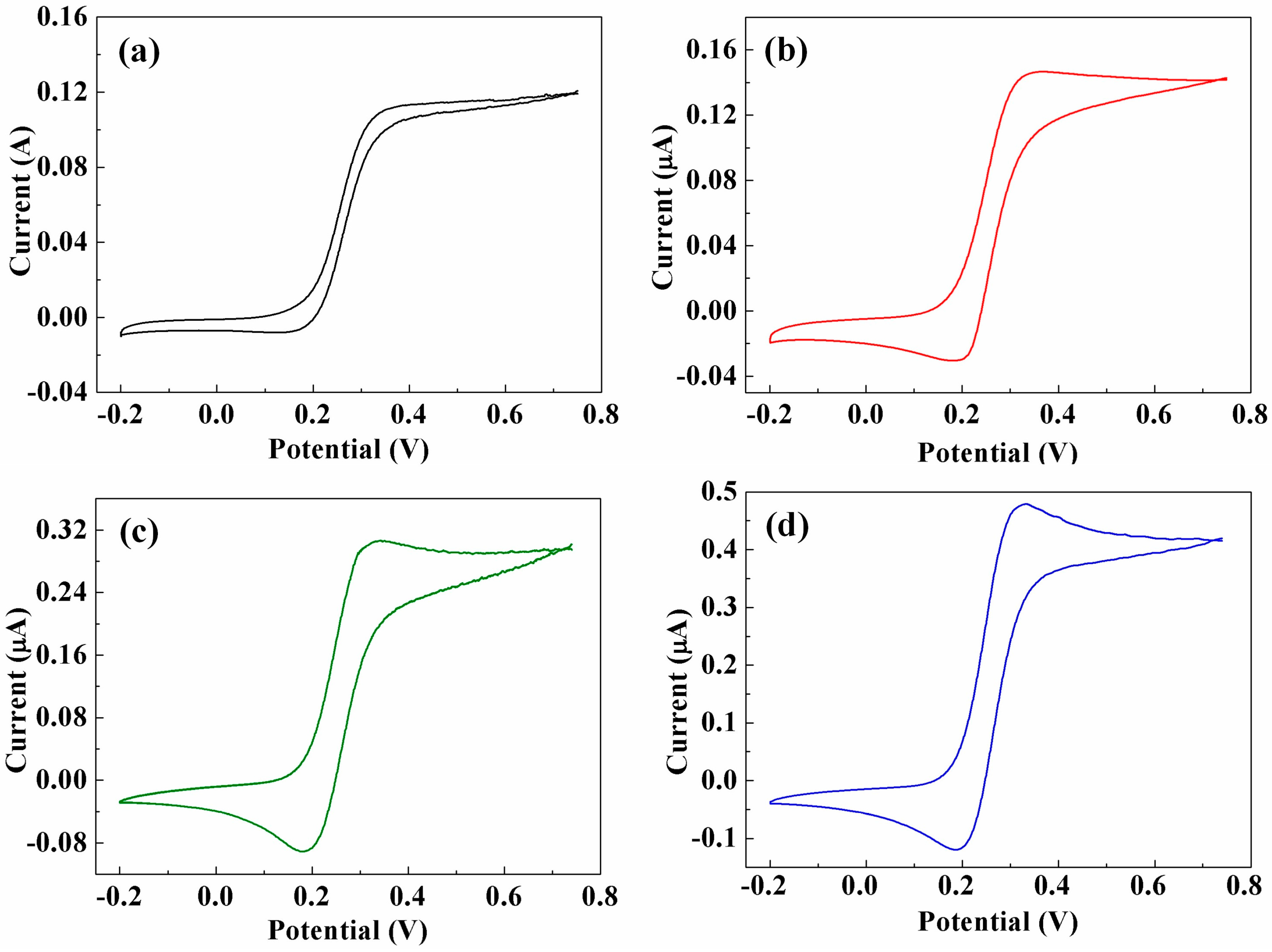
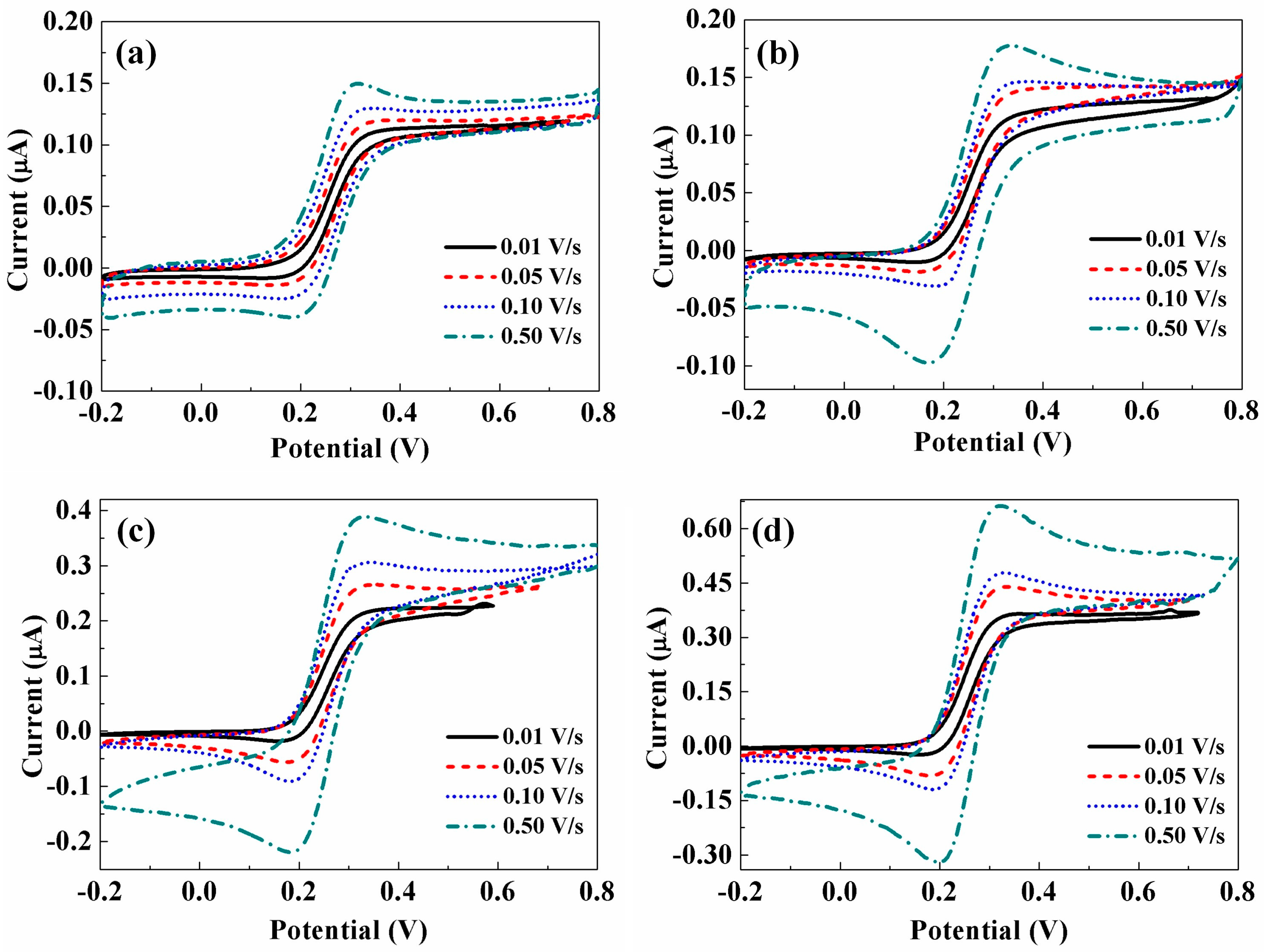
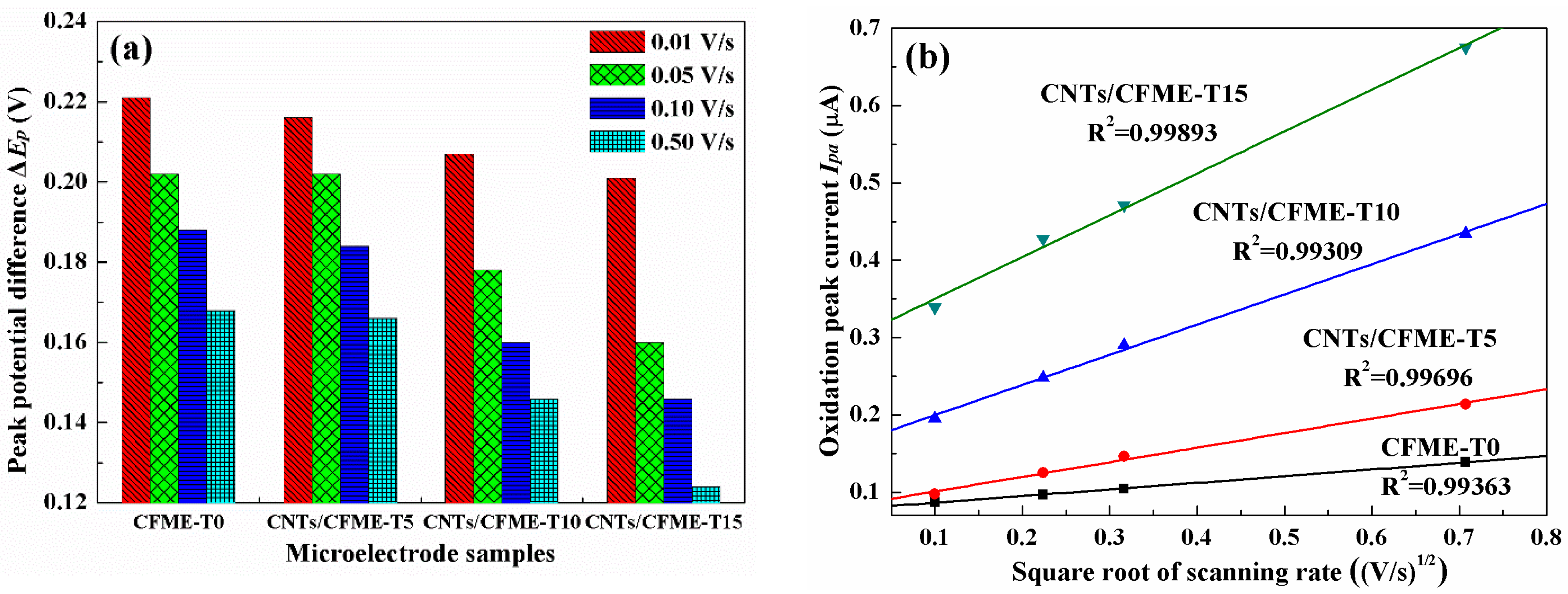
3.3. Cyclic Voltammetry (CV) Analysis of CNTs/CFMEs
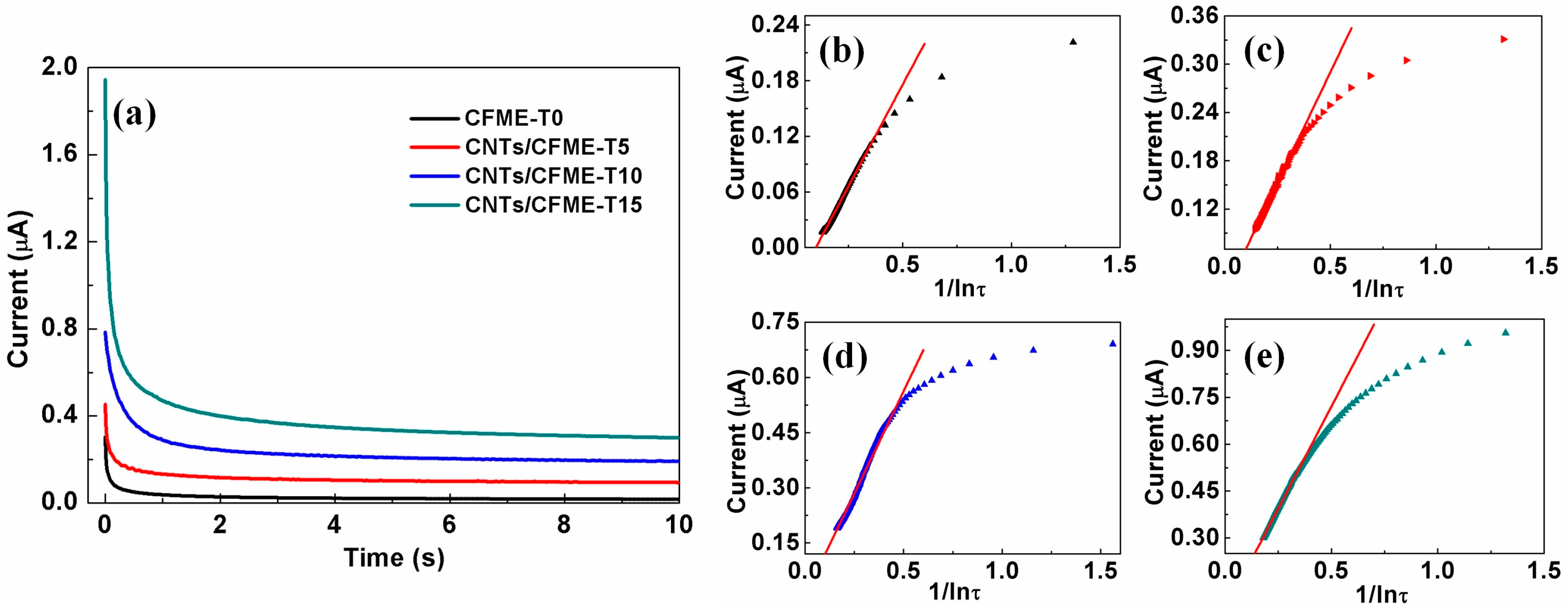
3.4. Electrocatalytic Activity of the Microelectrode
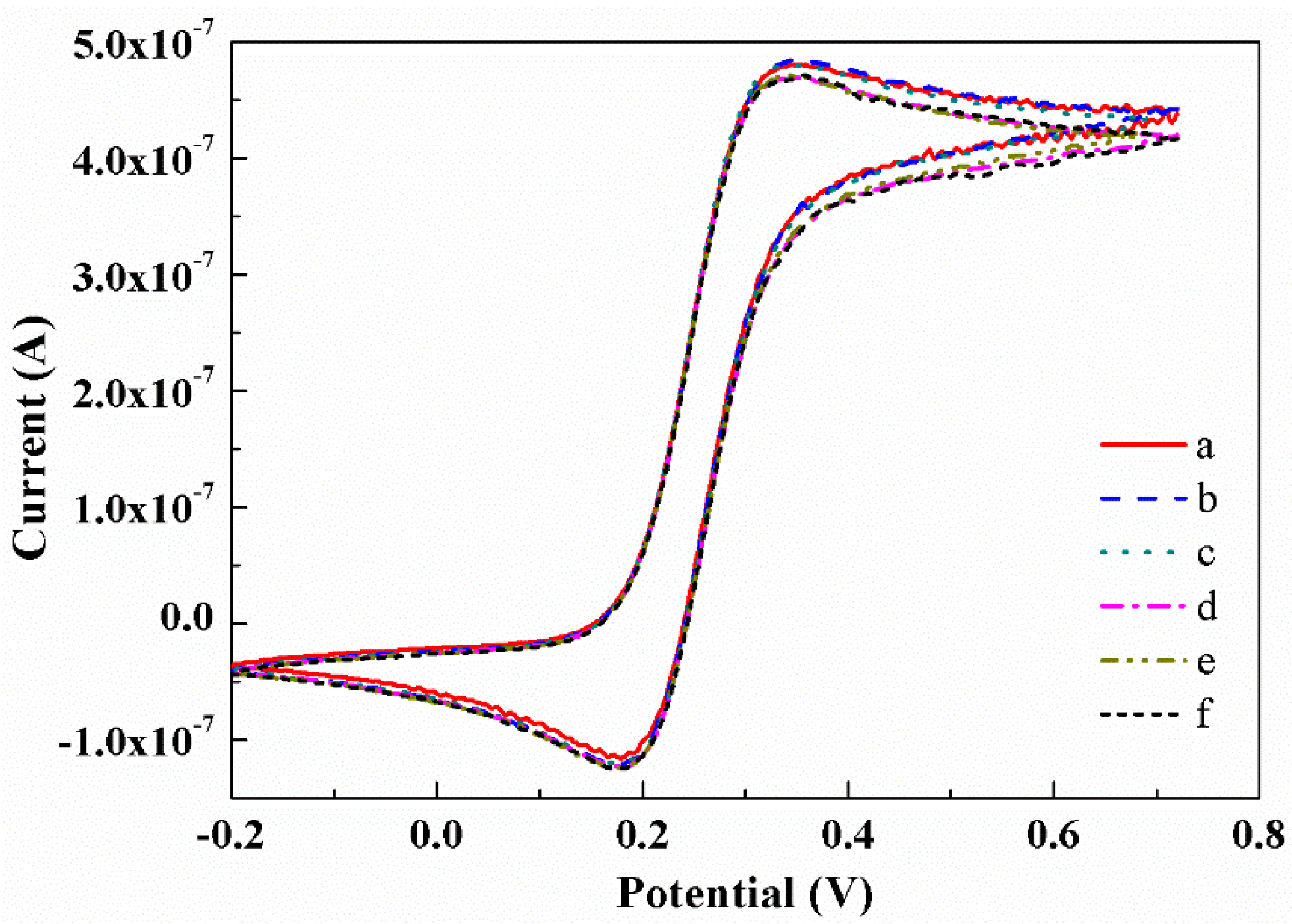
3.5. Reproducibility Analysis of the CNTs/CFME
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Forster, R. Micro- and Nanoelectrodes; Springer: New York, NY, USA, 2014; pp. 1248–1256. [Google Scholar]
- Lourenço, C.F.; Ledo, A.; Laranjinha, J.; Gerhardt, G.A.; Rui, M.B. Microelectrode array biosensor for high-resolution measurements of extracellular glucose in the brain. Sens. Actuators B Chem. 2016, 237, 298–307. [Google Scholar] [CrossRef]
- Lin, A.S.; Chen, J.; Huang, T. Electrochemical oxidation of dissolved carbon monoxide on rotating disk electrodes and micro-electrodes. Adv. Mater. Res. 2015, 1101, 144–148. [Google Scholar] [CrossRef]
- Pereira, A.R.; Souza, J.C.P.D.; Iost, R.M.; Sales, F.C.P.F.; Crespilho, F.N. Application of carbon fibers to flexible enzyme electrodes. J. Electroanal. Chem. 2016, 780, 396–406. [Google Scholar] [CrossRef]
- Njagi, J.; Chernov, M.M.; Leiter, J.C.; Andreescu, S. Amperometric detection of dopamine in vivo with an enzyme based carbon fiber microbiosensor. Anal. Chem. 2010, 82, 989–996. [Google Scholar] [CrossRef] [PubMed]
- Salazar, P.; Martín, M.; O’Neill, R.D.; González-Mora, J.L. Glutamate microbiosensors based on prussian blue modified carbon fiber electrodes for neuroscience applications: In Vitro characterization. Sens. Actuators B Chem. 2016, 235, 117–125. [Google Scholar] [CrossRef]
- Iost, R.M.; Sales, F.C.P.F.; Martins, M.V.A.; Almeida, M.C.; Crespilho, F.N. Glucose biochip based on flexible carbon fiber electrodes: In vivo diabetes evaluation in rats. Chemelectrochem 2015, 2, 518–521. [Google Scholar] [CrossRef]
- Daniele, S.; Bragato, C. From Macroelectrodes to Microelectrodes: Theory and Electrode Properties; Springer: New York, NY, USA, 2014; pp. 373–401. [Google Scholar]
- Yu, L.; Qi, Z.; Qin, X.; Jin, D.; Jin, G.; Li, K.; Hu, X. Electrochemical detection of nitrate in PM2.5, with a copper-modified carbon fiber micro-disk electrode. Talanta 2015, 143, 245–253. [Google Scholar] [CrossRef] [PubMed]
- Pak, H.; Yoo, Y.R. Surface treatment effect of carbon fiber fabric counter electrode in dye sensitized solar cell. J. Nanosci. Nanotechnol. 2012, 12, 1679–1683. [Google Scholar] [CrossRef] [PubMed]
- Kakhki, R.M. A review to recent developments in modification of carbon fiber electrodes. Arab. J. Chem. 2014, in press. [Google Scholar] [CrossRef]
- Ghoreishi, S.M.; Behpour, M.; Hajisadeghian, E.; Golestaneh, M. Voltammetric determination of resorcinol on the surface of a glassy carbon electrode modified with multi-walled carbon nanotube. Arab. J. Chem. 2012, 485, 1513–1516. [Google Scholar] [CrossRef]
- Xiang, L.; Yu, P.; Zhang, M.; Hao, J.; Wang, Y.; Zhu, L.; Dai, L.; Mao, L. Platinized aligned carbon nanotube-sheathed carbon fiber microelectrodes for in vivo amperometric monitoring of oxygen. Anal. Chem. 2014, 86, 5017–5023. [Google Scholar] [CrossRef] [PubMed]
- Swamy, B.E.K. Carbon nanotube-modified microelectrodes for simultaneous detection of dopamine and serotoninin vivo. Analyst 2007, 132, 876–884. [Google Scholar] [CrossRef] [PubMed]
- Ross, A.E.; Venton, B.J. Nafion-CNT coated carbon-fiber microelectrodes for enhanced detection of adenosine. Analyst 2012, 137, 3045–3051. [Google Scholar] [CrossRef] [PubMed]
- Du, F.; Huang, W.; Shi, Y.; Wang, Z.; Cheng, J. Real-time monitoring of NO release from single cells using carbon fiber microdisk electrodes modified with single-walled carbon nanotubes. Biosens. Bioelectron. 2008, 24, 415–421. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Lu, L.; Tang, Y.; Zhang, F.; Shen, C.; Zang, X.; Ding, X.; Cai, W.; Lin, L. Hierarchically nanostructured carbon fiber-nickel-carbon nanotubes for high-performance supercapacitor electrodes. Mater. Lett. 2017, 186, 70–73. [Google Scholar] [CrossRef]
- Zhu, S.; Su, C.H.; Lehoczky, S.L.; Muntele, I.; Ila, D. Carbon nanotube growth on carbon fibers. Diam. Relat. Mater. 2003, 12, 1825–1828. [Google Scholar] [CrossRef]
- Cesano, F.; Bertarione, S.D.; Scarano, A.; Zecchina, A. Connecting carbon fibers by means of catalytically grown nanofilaments: Formation of carbon−carbon composites. Chem. Mater. 2005, 17, 5119–5123. [Google Scholar] [CrossRef]
- Wong, K.H.; Pickering, S.J.; Rudd, C.D. Recycled carbon fiber reinforced polymer composite for electromagnetic interference shielding. Compos. A Appl. Sci. Manuf. 2010, 41, 693–702. [Google Scholar] [CrossRef]
- Sengupta, J.; Jacob, C. The effect of Fe and Ni catalysts on the growth of multiwalled carbon nanotubes using chemical vapor deposition. J. Nanopart. Res. 2010, 12, 457–465. [Google Scholar] [CrossRef]
- Brukh, R.; Mitra, S. Mechanism of carbon nanotube growth by CVD. Chem. Phys. Lett. 2006, 424, 126–132. [Google Scholar] [CrossRef]
- Birch, E.M.; Ruda, A.T.E.; Chai, M.; Andrews, R.; Hatfield, L.R. Properties that influence the specific surface areas of carbon nanotubes and nanofibers. Ann. Occup. Hyg. 2013, 57, 1148–1166. [Google Scholar] [PubMed]
- Dong, L.; Xu, C.; Yang, Q.; Fang, J.; Li, Y.; Kang, F. High-performance compressible supercapacitors based on functionally synergic multiscale carbon composite textiles. J. Mater. Chem. A 2015, 3, 4729–4737. [Google Scholar] [CrossRef]
- Matsumoto, S.; Yamanaka, K.; Ogikubo, H.; Akasaka, H.; Ohtake, N. Carbon nanotube dispersed conductive network for microbial fuel cells. Appl. Phys. Lett. 2014, 105, 083904. [Google Scholar] [CrossRef]
- Bartosova, Z.; Riman, D.; Halouzka, V.; Vostalova, J.; Simanek, V.; Hrbac, J.; Jirovsky, D. A comparison of electrochemically pre-treated and spark-platinized carbon fiber microelectrode. Measurement of 8-oxo-7, 8-dihydro-2′-deoxyguanosine in human urine and plasma. Anal. Chim. Acta 2016, 935, 82–89. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.S.; Huang, W.H.; Tong, H.; Wang, Z.L.; Cheng, J.K. Carbon fiber nanoelectrodes modified by single-walled carbon nanotubes. Anal. Chem. 2003, 75, 6341–6345. [Google Scholar] [CrossRef] [PubMed]
- Qing, W.; Liu, X.; Lu, H.; Liang, J.; Liu, K. Ensemble of carbon fiber ultra-microelectrodes modified with nanotubes, and its application to the determination of dopamine. Microchim. Acta 2008, 160, 227–231. [Google Scholar] [CrossRef]
- Radia, A.E.M.; Mostafa, M.R.; Elshafey, R.M.; Hegazy, T.A. Determination of Drimarene blue X-BLN at a glassy carbon electrode by differential pulse voltammetry. Collect. Czechoslov. Chem. Commun. 2011, 76, 1765–1773. [Google Scholar] [CrossRef]
- Aristov, N.; Habekost, A. Cyclic voltammetry—A versatile electrochemical method investigating electron transfer processes. World J. Chem. Educ. 2015, 3, 115–119. [Google Scholar]
- Xiang, L.; Yu, P.; Hao, J.; Zhang, M.; Zhu, L.; Dai, L.; Mao, L. Vertically aligned carbon nanotube-sheathed carbon fibers as pristine microelectrodes for selective monitoring of ascorbate in vivo. Anal. Chem. 2014, 86, 3909–3914. [Google Scholar] [CrossRef] [PubMed]
- Filotás, D.; Nagy, L.; Skoda-Földes, R.; Kollár, L.; Nagy, G. Electrochemical experimental study for the characterization of tetraferrocenyl-cavitand, synthetized in click-reaction. Electroanalysis 2015, 27, 38–41. [Google Scholar] [CrossRef]
- Fan, J.; Zhao, G.; Zhao, H.; Chai, S.; Cao, T. Fabrication and application of mesoporous Sb-doped SnO2 electrode with high specific surface in electrochemical degradation of ketoprofen. Electrochim. Acta 2013, 94, 21–29. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, Student Solutions Manual, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Szabo, A.; Cope, D.K.; Tallman, D.E.; Kovach, P.M.; Wightman, R.M. Chronoamperometric current at hemicylinder and band microelectrodes: Theory and experiment. J. Electroanal. Chem. 1987, 217, 417–423. [Google Scholar] [CrossRef]
- Konopka, S.J.; Mcduffie, B. Diffusion coefficients of ferri- and ferrocyanide ions in aqueous media, using twin-electrode thin-layer electrochemistry. Anal. Chem. 1970, 42, 1741–1746. [Google Scholar] [CrossRef]
- Álvarez-Martos, I.; Campos-Alfaraz, N.; Gómez-Plaza, D.; Fernández-Abedul, M.T. Electrochemical properties of spaghetti and forest like carbon nanotubes grown on glass substrates. Sens. Actuators B Chem. 2014, 192, 253–260. [Google Scholar] [CrossRef]


| Chemical | Formula | Amount (g·L−1) |
|---|---|---|
| Nickel sulfate | NiSO4·6H2O | 40 |
| Sodium hypophosphite | NaH2PO2·H2O | 20 |
| Sodium citrate | NaC6H5O7·2H2O | 100 |
| Ammonium chloride | NH4Cl | 50 |
| Ammonium hydroxide | NH3·H2O | pH adjustment |
| Microelectrode | The Fitted Linear Regression Equations | Coefficient of Determination |
|---|---|---|
| CFME-T0 | iqss = 4.39523 × 10−7 1/lnτ − 4.39466 × 10−8 | 0.99678 |
| CNTs/CFME-T5 | iqss = 5.49772 × 10−7 1/lnτ + 1.47824 × 10−8 | 0.9974 |
| CNTs/CFME-T10 | iqss = 1.11411 × 10−6 1/lnτ + 5.64842 × 10−9 | 0.99049 |
| CNTs/CFME-T15 | iqss = 1.3068 × 10−6 1/lnτ + 6.75016 × 10−8 | 0.99684 |
| Microelectrode | Effective Surface Area (cm2) | Quasi-Steady State Current Density (A/cm2) |
|---|---|---|
| CFME-T0 | 2.39036 × 10−5 | 0.751 × 10−3 |
| CNTs/CFME-T5 | 4.27135 × 10−5 | 2.19 × 10−3 |
| CNTs/CFME-T10 | 12.9838 × 10−5 | 1.47 × 10−3 |
| CNTs/CFME-T15 | 20.3059 × 10−5 | 1.48 × 10−3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Liang, L.; Teh, K.S.; Xie, Y.; Wan, Z.; Tang, Y. The Electrochemical Behavior of Carbon Fiber Microelectrodes Modified with Carbon Nanotubes Using a Two-Step Electroless Plating/Chemical Vapor Deposition Process. Sensors 2017, 17, 725. https://doi.org/10.3390/s17040725
Lu L, Liang L, Teh KS, Xie Y, Wan Z, Tang Y. The Electrochemical Behavior of Carbon Fiber Microelectrodes Modified with Carbon Nanotubes Using a Two-Step Electroless Plating/Chemical Vapor Deposition Process. Sensors. 2017; 17(4):725. https://doi.org/10.3390/s17040725
Chicago/Turabian StyleLu, Longsheng, Linsheng Liang, Kwok Siong Teh, Yingxi Xie, Zhenping Wan, and Yong Tang. 2017. "The Electrochemical Behavior of Carbon Fiber Microelectrodes Modified with Carbon Nanotubes Using a Two-Step Electroless Plating/Chemical Vapor Deposition Process" Sensors 17, no. 4: 725. https://doi.org/10.3390/s17040725
APA StyleLu, L., Liang, L., Teh, K. S., Xie, Y., Wan, Z., & Tang, Y. (2017). The Electrochemical Behavior of Carbon Fiber Microelectrodes Modified with Carbon Nanotubes Using a Two-Step Electroless Plating/Chemical Vapor Deposition Process. Sensors, 17(4), 725. https://doi.org/10.3390/s17040725





