Efficient Data Collection in Widely Distributed Wireless Sensor Networks with Time Window and Precedence Constraints
Abstract
:1. Introduction
- We consider the trajectory planning problem with time window and precedence constraints which evolves throughout time.
- We develop optimal algorithms to solve the trajectory planning of the mobile sink in the ideal case.
- We consider the situation cycles are changing dynamically and develop a greedy algorithm to solve it.
- We develop a method to calculate the optimal number of mobile sinks when the area is too large for a single mobile sink to serve.
2. System Background and Related Work
3. System Model and Problem Formulation
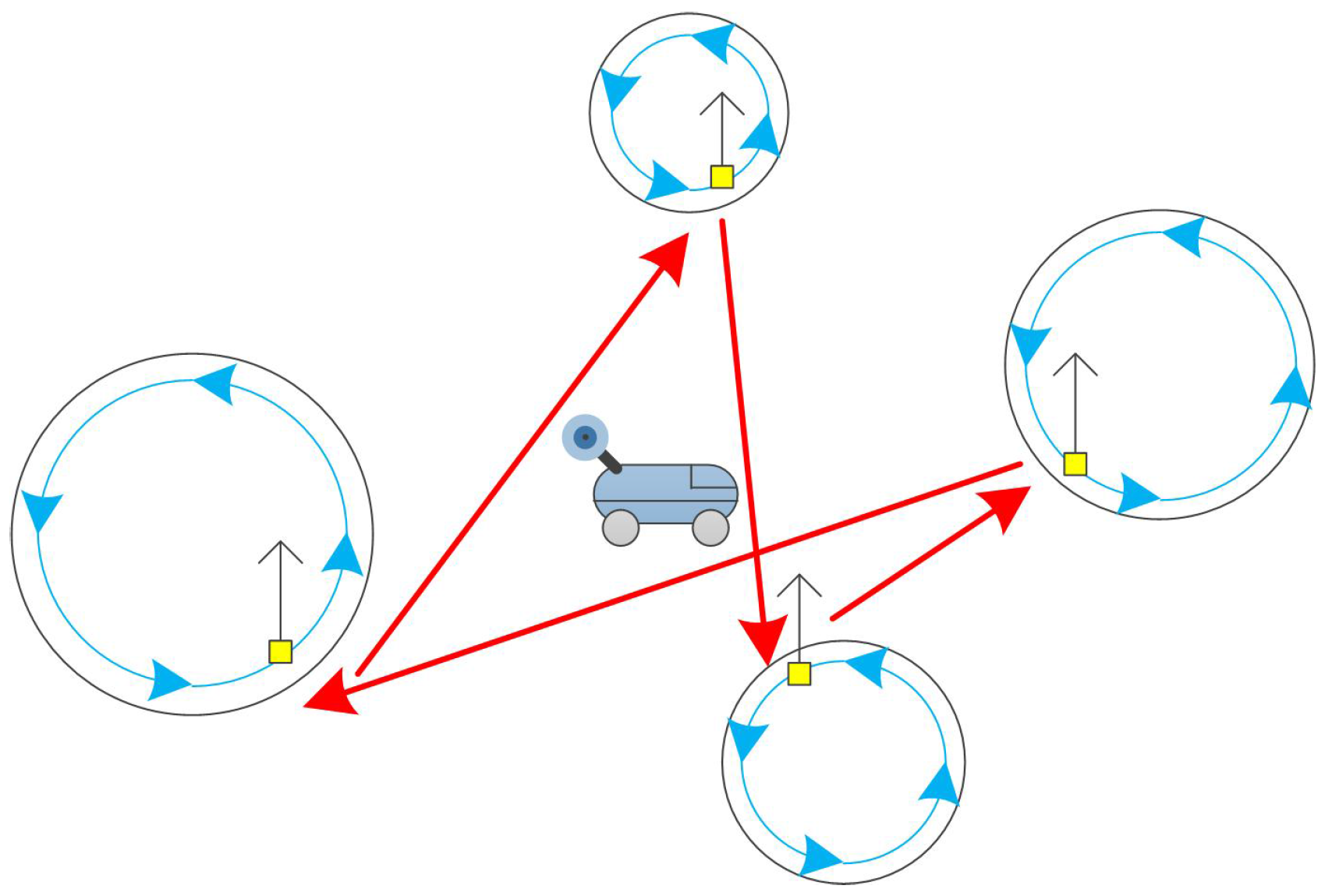
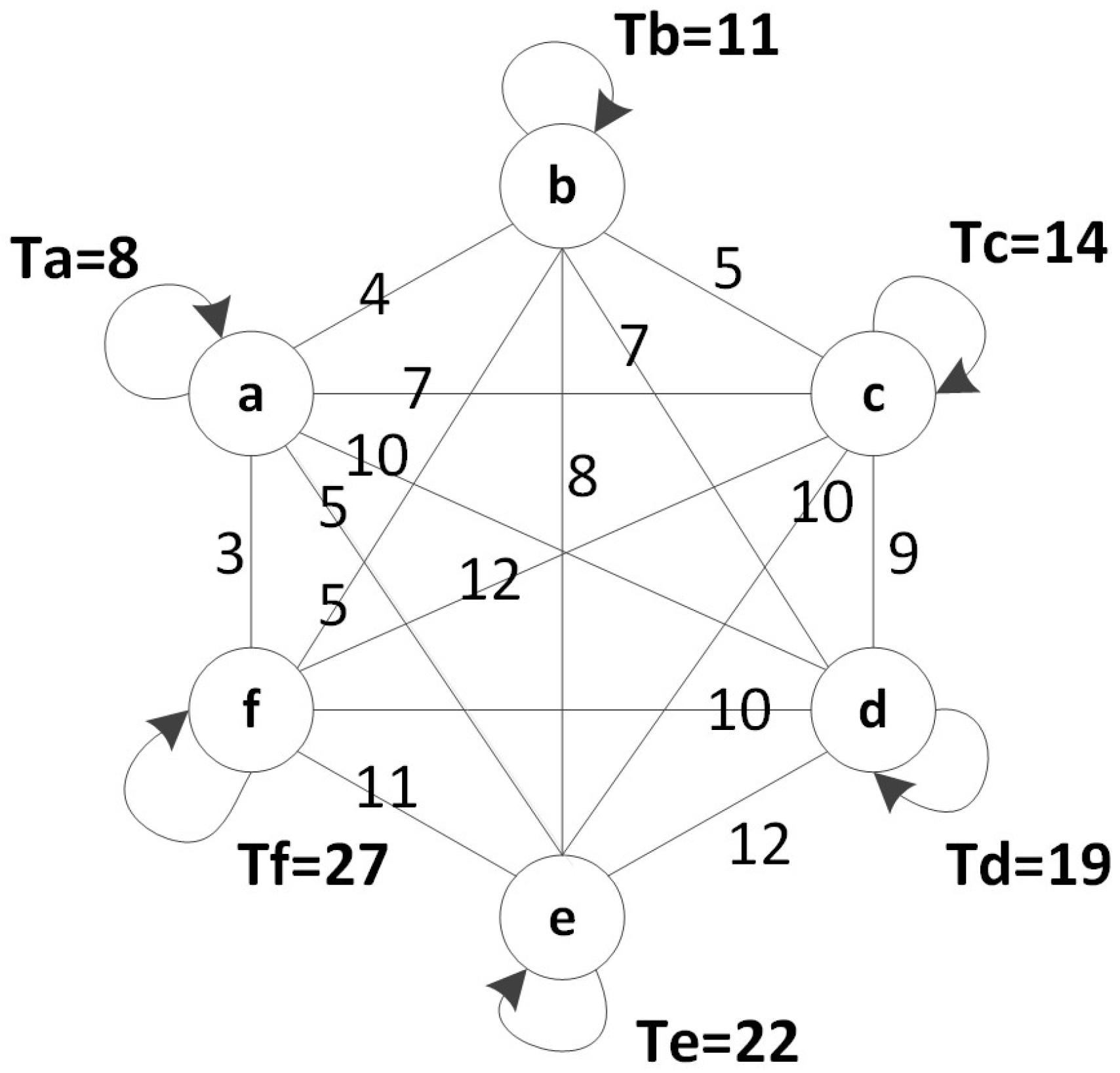
3.1. UGV Appearance Cycles
3.2. Mobile Sink Trajectory Planing
4. Optimizing Path Schedule of the Mobile Sink
4.1. The Ideal Case
| Algorithm 1 Complete path finding algorithm in the precedence graph |
| Require: adjacency matrix M Ensure: a point sequence forming a path.
|
| Algorithm 2 Optimal shortest path finding algorithm in the precedence graph |
| Require: adjacency matrix M Ensure: hop number of each point i and a point sequence forming a path. Initialize
|
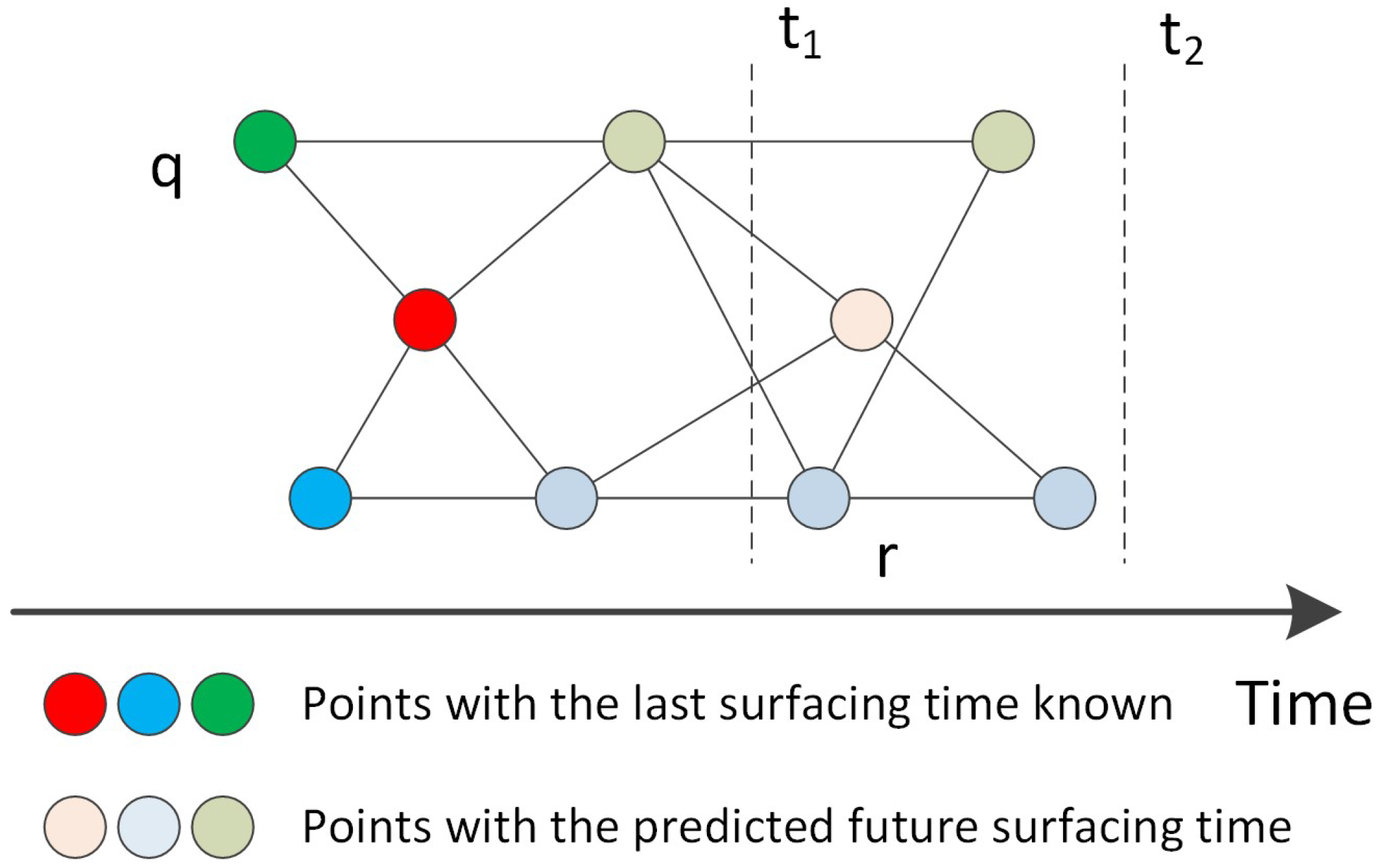
4.2. The Practice Case
| Algorithm 3 k-hop path finding algorithm in the precedence graph |
| Require: adjacency matrix M Ensure: a point sequence forming a path. Initialize
|
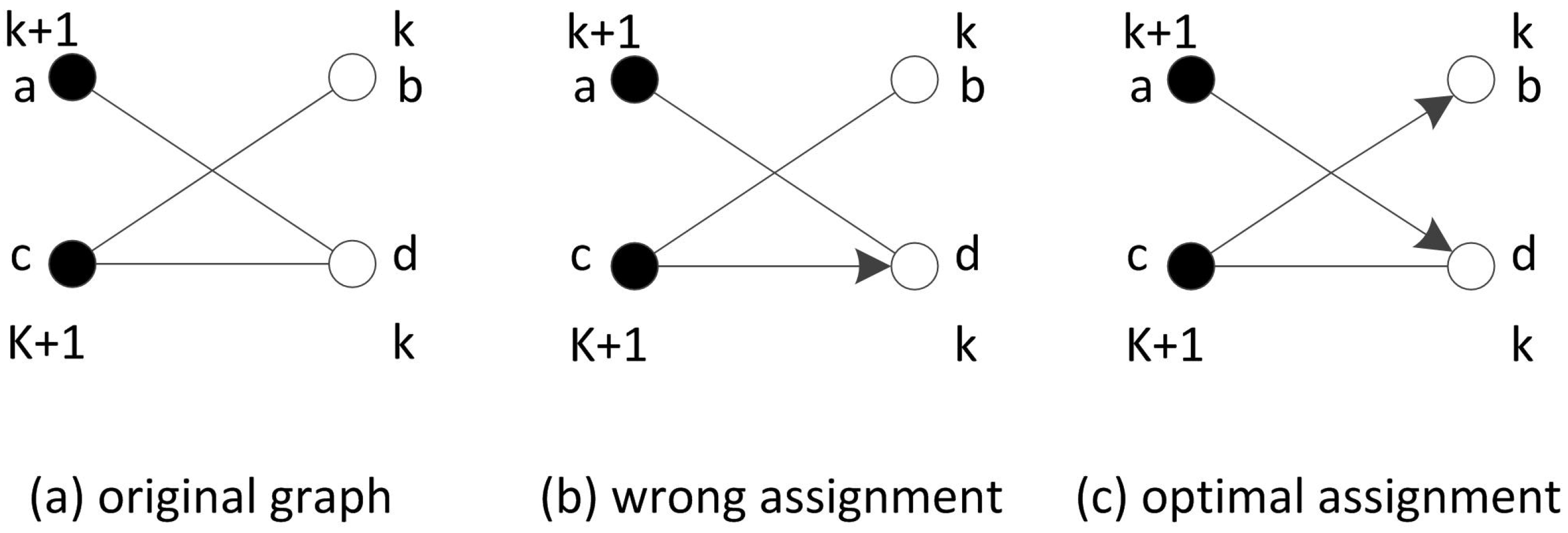
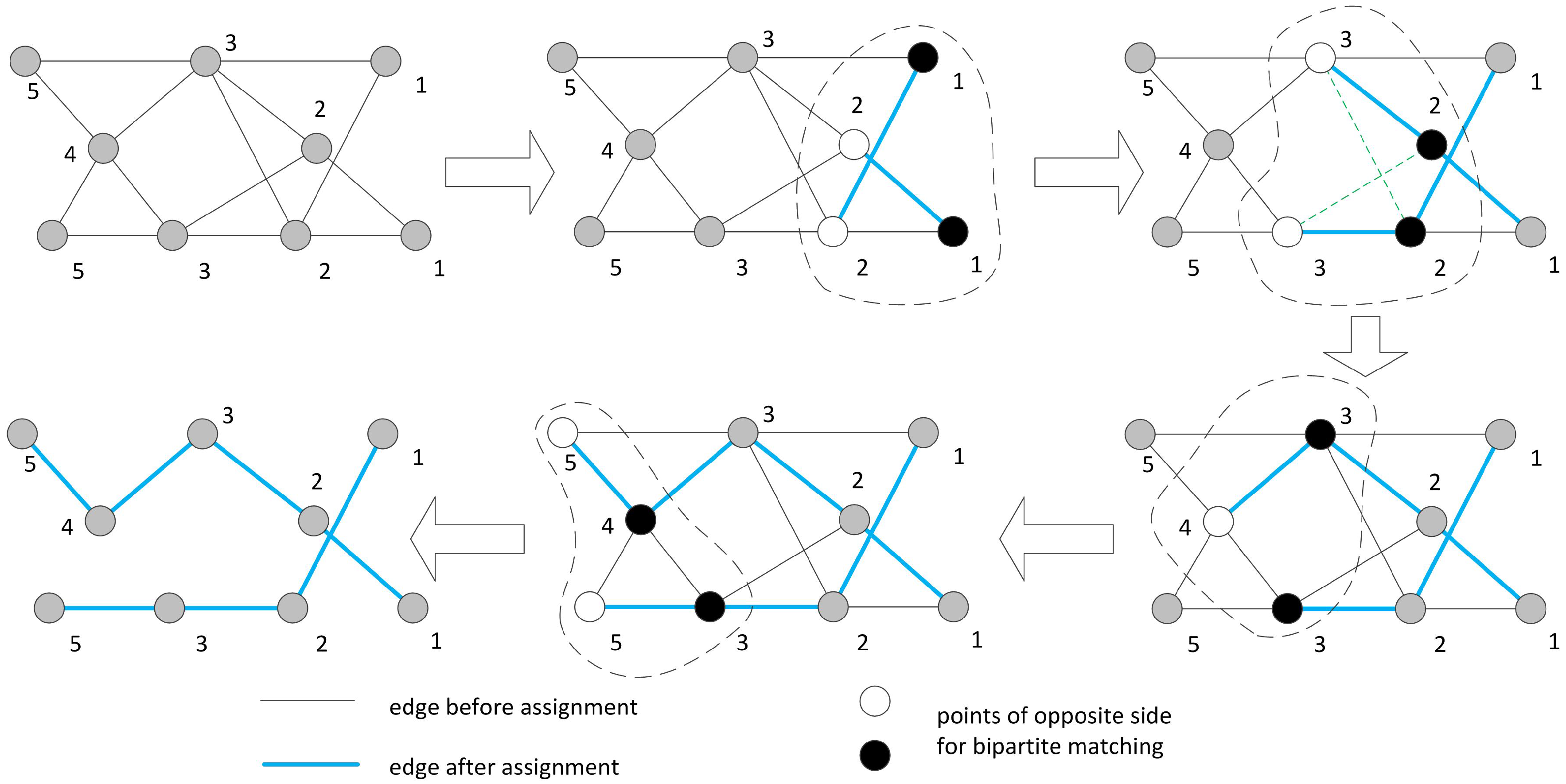
5. Optimizing the Number of Mobile Sinks and Their Paths
5.1. The Ideal Case
| Algorithm 4 Optimal number of mobile sinks in the ideal case |
| Require: points with hop number Ensure: optimal number of mobile sinks and the paths Initialize Set the weight of each edge as 1, and start from hop number 1 and 2 (k = 1) Assign
|
5.2. The Practice Case
| Algorithm 5 Finding the number of mobile sinks in the practice case |
| Require: k-hop graph Ensure: Number of mobile sinks
|
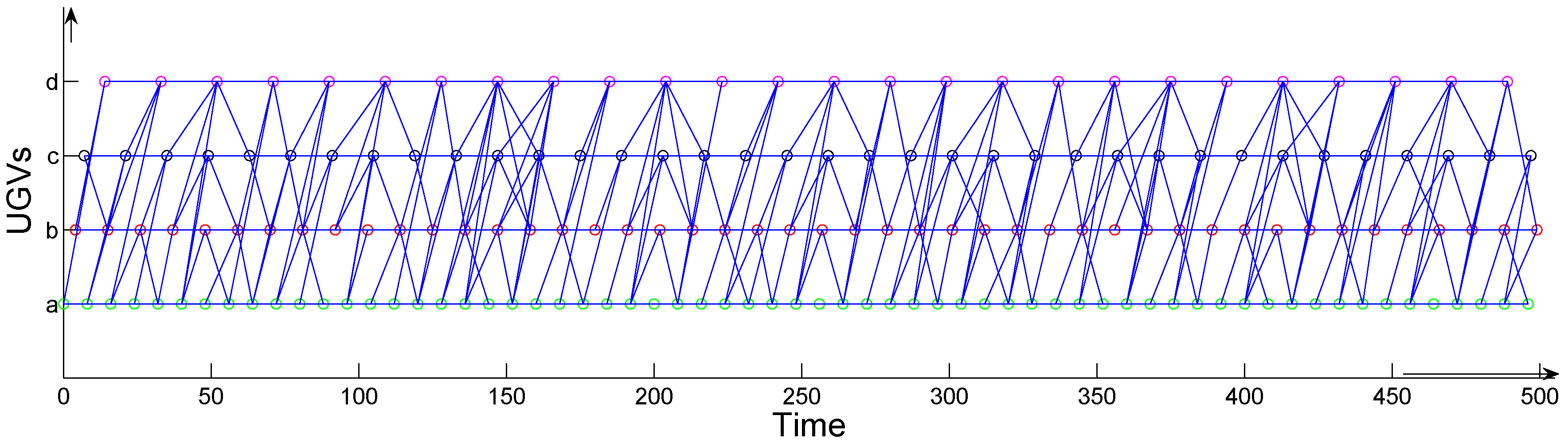
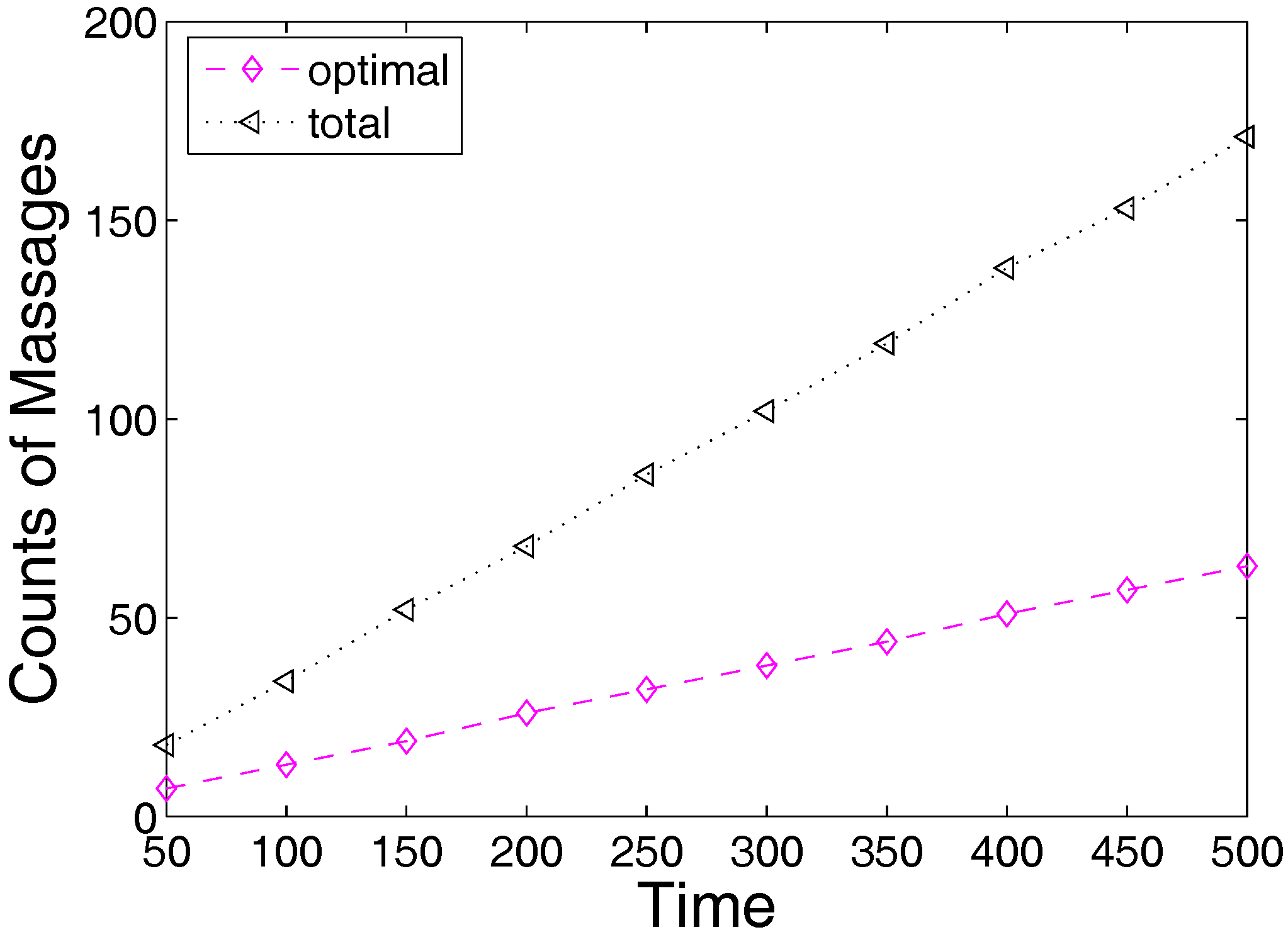
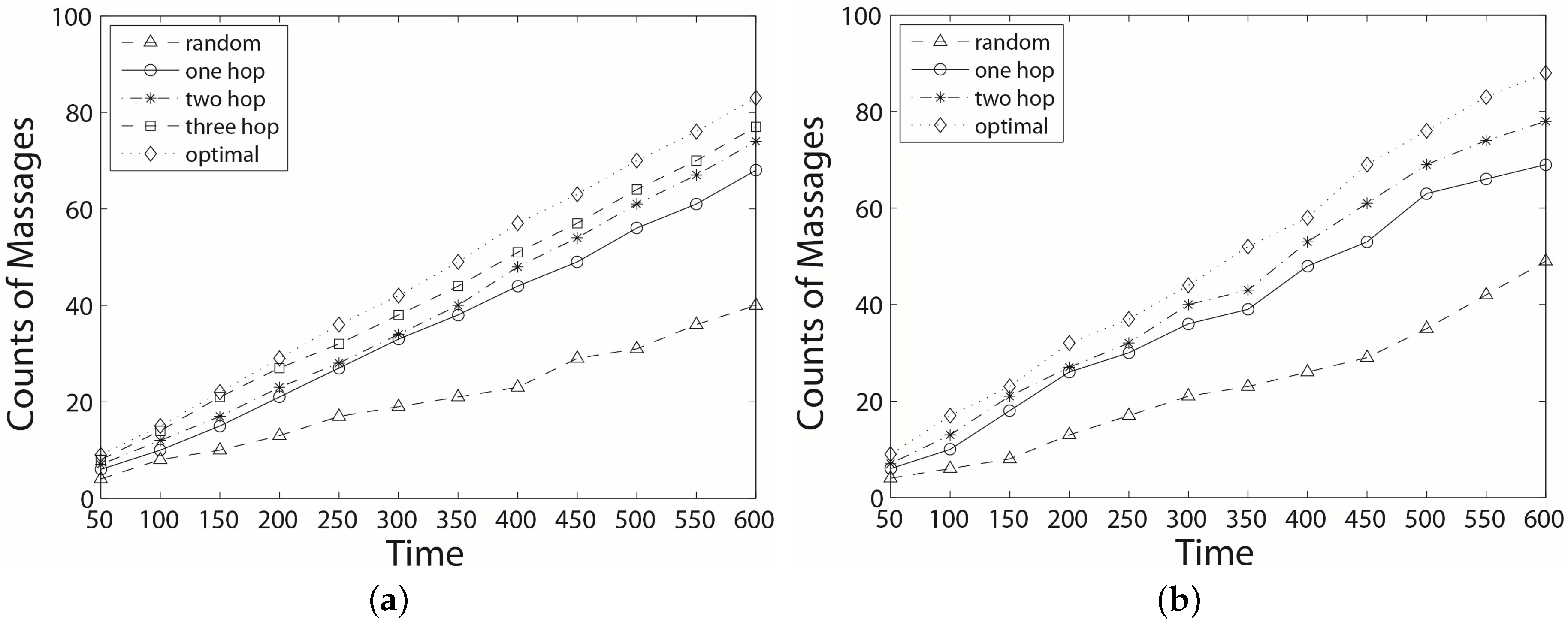
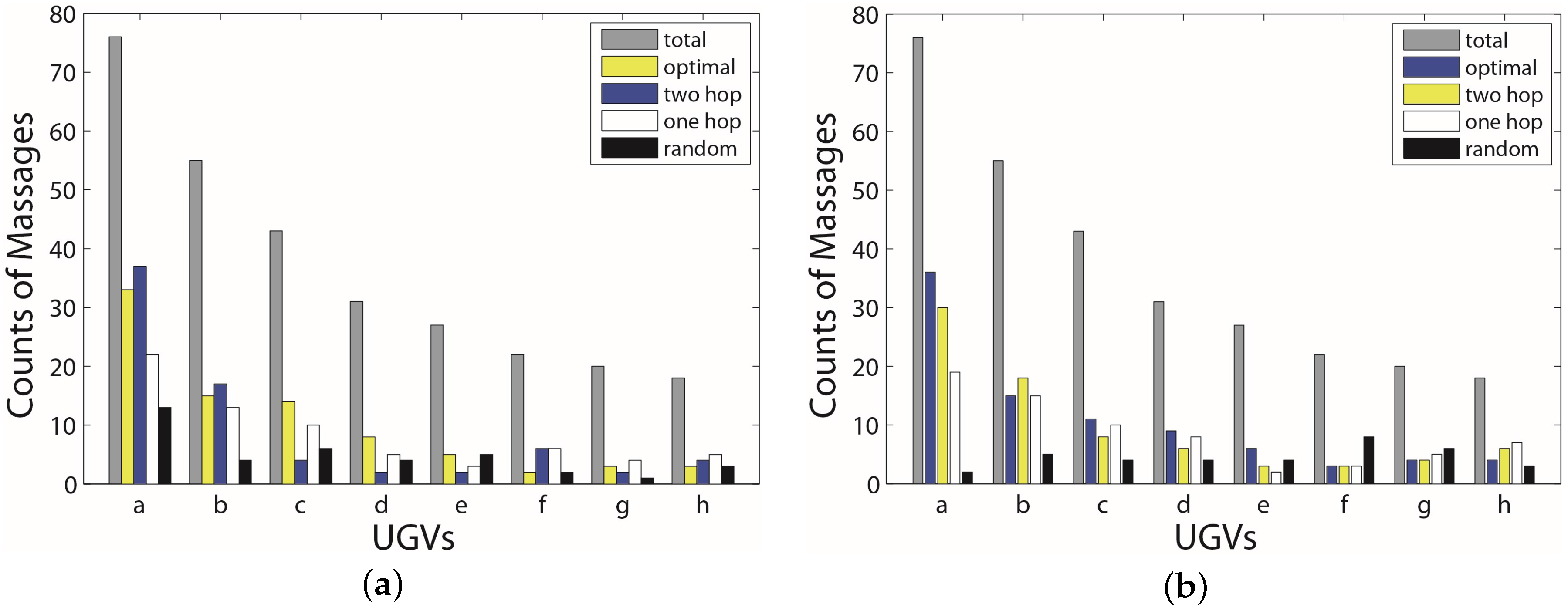
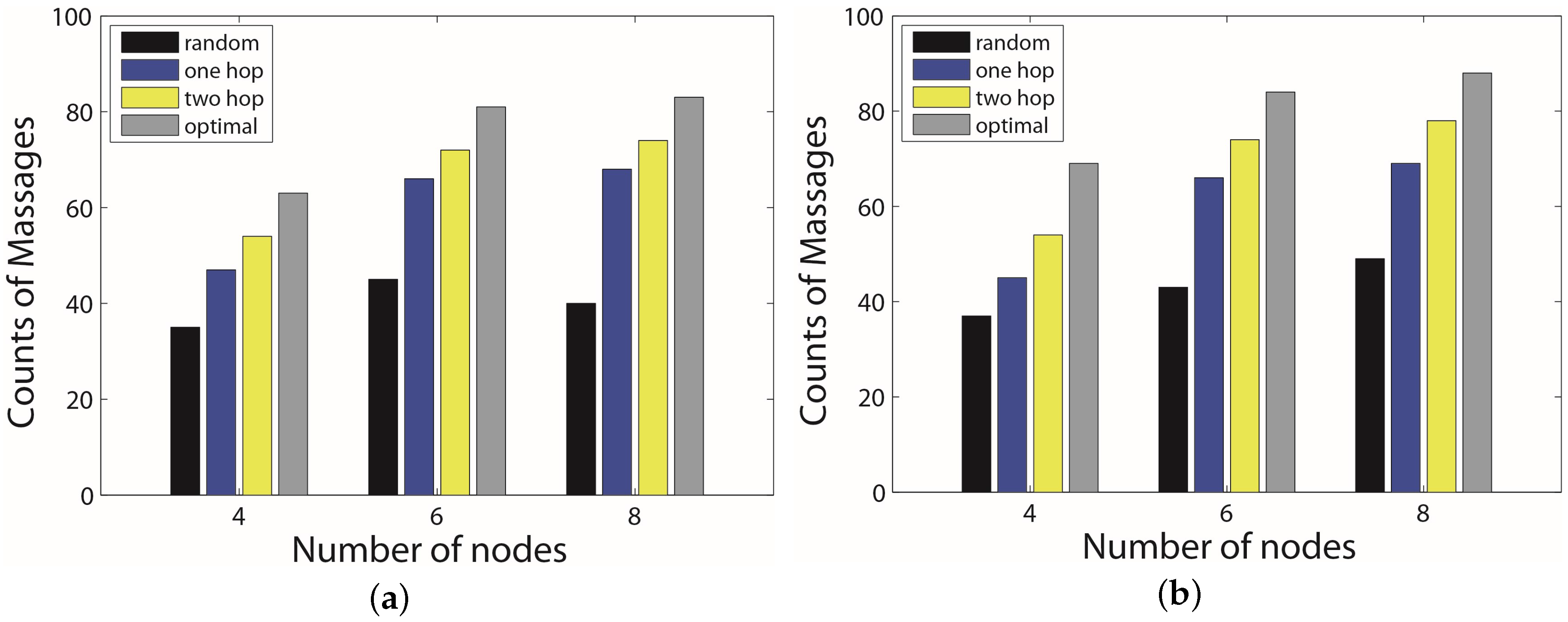
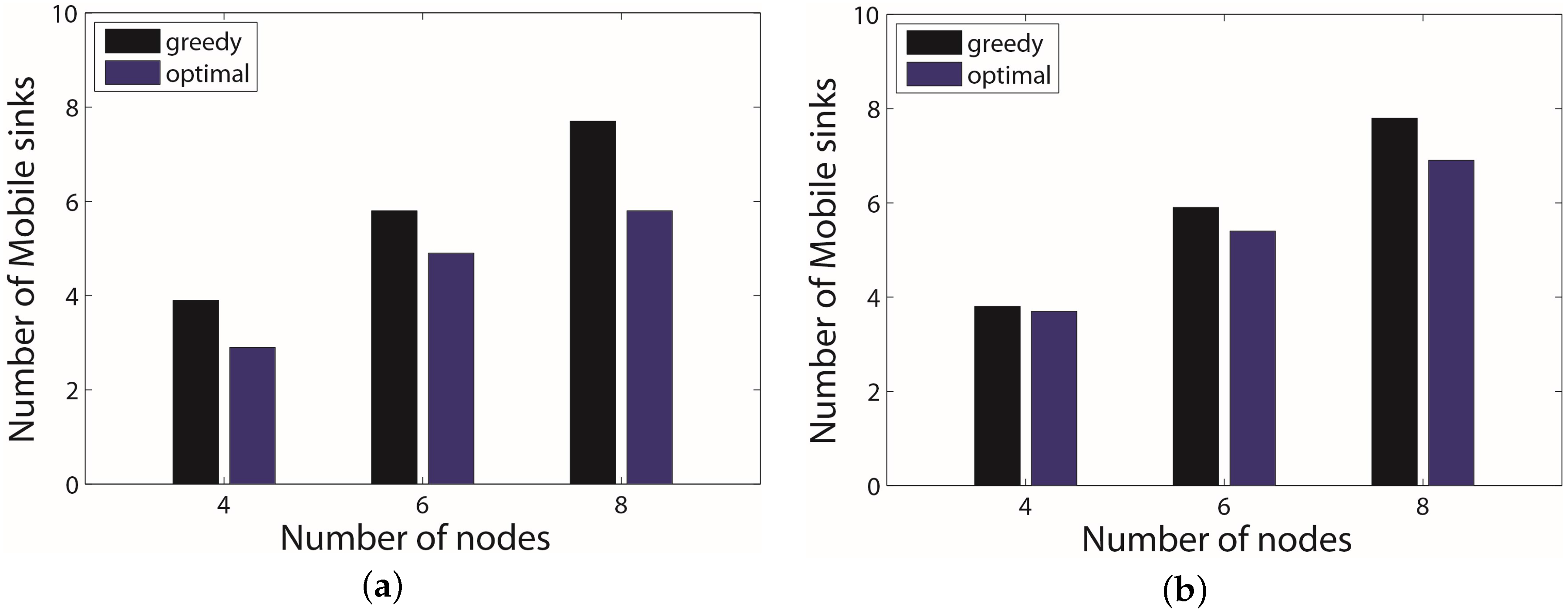
6. Experimental Section
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, Y.; Zhou, G.; Zhao, J.; Dai, G.; Li, X.Y.; Gu, M.; Ma, H.; Mo, L.; He, Y.; Wang, J. Long-term large-scale sensing in the forest: Recent advances and future directions of GreenOrbs. Front. Comput. Sci. China 2010, 4, 334–338. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, X.; He, Y.; Liu, K.; Gong, W.; Wang, J. CitySee: Not only a wireless sensor network. IEEE Netw. 2013, 27, 42–47. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, J. Data Collection and Event Detection in the Deep Sea with Delay Minimization. In Proceedings of the 2015 12th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Seattle, WA, USA, 22–25 June 2015; pp. 1–9.
- Li, W.; Farrell, J.A.; Pang, S.; Arrieta, R.M. Moth-inspired chemical plume tracing on an autonomous underwater vehicle. IEEE Trans. Robot. 2006, 22, 292–307. [Google Scholar] [CrossRef]
- Calvo, O.; Sousa, A.; Rozenfeld, A.; Acosta, G. Smooth path planning for autonomous pipeline inspections. In Proceedings of the 6th International Multi-Conference on Systems, Signals and Devices, Sharjah, UAE, 23–26 March 2009; pp. 1–9.
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Underwater acoustic sensor networks: Research challenges. Ad Hoc Netw. 2005, 3, 257–279. [Google Scholar] [CrossRef]
- Tokekar, P.; Hook, J.V.; Mulla, D.; Isler, V. Sensor planning for a symbiotic UAV and UGV system for precision agriculture. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 5321–5326.
- Yun, Y.; Xia, Y.; Behdani, B.; Smith, J.C. Distributed Algorithm for Lifetime Maximization in a Delay-Tolerant Wireless Sensor Network with a Mobile Sink. IEEE Trans. Mob. Comput. 2013, 12, 1920–1930. [Google Scholar] [CrossRef]
- Nesamony, S.; Vairamuthu, M.; Orlowska, M. On Optimal Route of a Calibrating Mobile Sink in a Wireless Sensor Network. In Proceedings of the Fourth International Conference on Networked Sensing Systems (INSS ’07), Braunschweig, Germany, 6–8 June 2007; pp. 61–64.
- Alnabelsi, S.H.; Almasaeid, H.M.; Kamal, A.E. Optimized sink mobility for energy and delay efficient data collection in FWSNs. In Proceedings of the IEEE Symposium on Computers and Communications (ISCC 2010), Riccione, Italy, 22–25 June 2010; pp. 550–555.
- Shi, Y.; Xie, L.; Hou, Y.T.; Sherali, H.D. On renewable sensor networks with wireless energy transfer. In Proceedings of the The 30th IEEE International Conference on Computer Communications (INFOCOM 2011), Shanghai, China, 10–15 April 2011; pp. 1350–1358.
- Kindervater, G.A.P.; Lenstra, J.K.; Savelsbergh, M.W.P. Sequential and Parallel Local Search for the Time-Constrained Travelling Salesman Problem; Technical Report; Technische Universiteit Eindhoven: Eindhoven, The Netherlands, 1990. [Google Scholar]
- Fagerholt, K.; Christiansen, M. A Travelling Salesman Problem with Allocation, Time window and Precedence constraints—An application to ship scheduling. Int. Trans. Oper. Res. 2000, 7, 231–244. [Google Scholar] [CrossRef]
- Zhu, Y. The Multi-Traveling Salesman Problem with Time Window and Precedence Constraints and Its Algorithm. Master’s Thesis, Fudan University, Shanghai, China, 2000. [Google Scholar]
- Mehrabi, A.; Kim, K. Maximizing Data Collection Throughput on a Path in Energy Harvesting Sensor Networks Using a Mobile Sink. IEEE Trans. Mob. Comput. 2016, 15, 690–704. [Google Scholar] [CrossRef]
- Rasul, A.; Erlebach, T. An Energy Efficient and Restricted Tour Construction for Mobile Sink in Wireless Sensor Networks. In Proceedings of the 2015 IEEE 12th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Dallas, TX, USA, 19–22 October 2015; pp. 55–63.
- Tashtarian, F.; Moghaddam, M.H.Y.; Sohraby, K.; Effati, S. On Maximizing the Lifetime of Wireless Sensor Networks in Event-Driven Applications With Mobile Sinks. IEEE Trans. Veh. Technol. 2015, 64, 3177–3189. [Google Scholar] [CrossRef]
- Tang, J.; Guo, S.; Yang, Y. Delivery latency minimization in wireless sensor networks with mobile sink. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 6481–6486.
- Luo, J.; Hubaux, J.P. Joint Sink Mobility and Routing to Maximize the Lifetime of Wireless Sensor Networks: The Case of Constrained Mobility. IEEE/ACM Trans. Netw. 2010, 18, 871–884. [Google Scholar] [CrossRef]
- Jo, Y. Communication Availability-Based Scheduling for Fair Data Collection with Path-Constrained Mobile Sink in Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2015, 2015. [Google Scholar] [CrossRef]
- Xie, G.; Pan, F. Cluster-Based Routing for the Mobile Sink in Wireless Sensor Networks With Obstacles. IEEE Access 2016, 4, 2019–2028. [Google Scholar] [CrossRef]
- Aldabbas, O.; Abuarqoub, A.; Hammoudeh, M.; Raza, U.; Bounceur, A. Unmanned Ground Vehicle for Data Collection in Wireless Sensor Networks: Mobility-aware Sink Selection. Open Autom. Control Syst. J. 2016, 2016. [Google Scholar] [CrossRef]
- Basagni, S.; Bölöni, L.; Gjanci, P.; Petrioli, C.; Phillips, C.A.; Turgut, D. Maximizing the value of sensed information in underwater wireless sensor networks via an autonomous underwater vehicle. In Proceedings of the IEEE INFOCOM 2014—IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 988–996.
- Mitrovic-Minic, S.; Krishnamurti, R. The multiple TSP with time windows: Vehicle bounds based on precedence graphs. Oper. Res. Lett. 2006, 34, 111–120. [Google Scholar] [CrossRef]
- Ng, K.Y.; Sancho, N.G. Precedence and Time Windows Constrained Travelling Salesman Problem (TSP) in Maritime Surveillance. J. Battlef. Technol. 2014, 17, 39–42. [Google Scholar]
- Assignment Problem and Hungarian Algorithm. Available online: https://www.topcoder.com/community/data-science/data-science-tutorials/assignment-problem-and-hungarian-algorithm/ (accessed on 9 February 2017).
- Bondy, J.; Murty, U. Graph Theory with Applications, 1st ed.; Elsevier Science Publishing Co., Inc.: New York, NY, USA, 1976. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Fu, T.; Xu, J.; Ding, Y. Efficient Data Collection in Widely Distributed Wireless Sensor Networks with Time Window and Precedence Constraints. Sensors 2017, 17, 421. https://doi.org/10.3390/s17020421
Liu P, Fu T, Xu J, Ding Y. Efficient Data Collection in Widely Distributed Wireless Sensor Networks with Time Window and Precedence Constraints. Sensors. 2017; 17(2):421. https://doi.org/10.3390/s17020421
Chicago/Turabian StyleLiu, Peng, Tingting Fu, Jia Xu, and Yue Ding. 2017. "Efficient Data Collection in Widely Distributed Wireless Sensor Networks with Time Window and Precedence Constraints" Sensors 17, no. 2: 421. https://doi.org/10.3390/s17020421
APA StyleLiu, P., Fu, T., Xu, J., & Ding, Y. (2017). Efficient Data Collection in Widely Distributed Wireless Sensor Networks with Time Window and Precedence Constraints. Sensors, 17(2), 421. https://doi.org/10.3390/s17020421




