Comparative Study of Different Methods for Soot Sensing and Filter Monitoring in Diesel Exhausts
Abstract
:1. Introduction
2. Materials and Methods
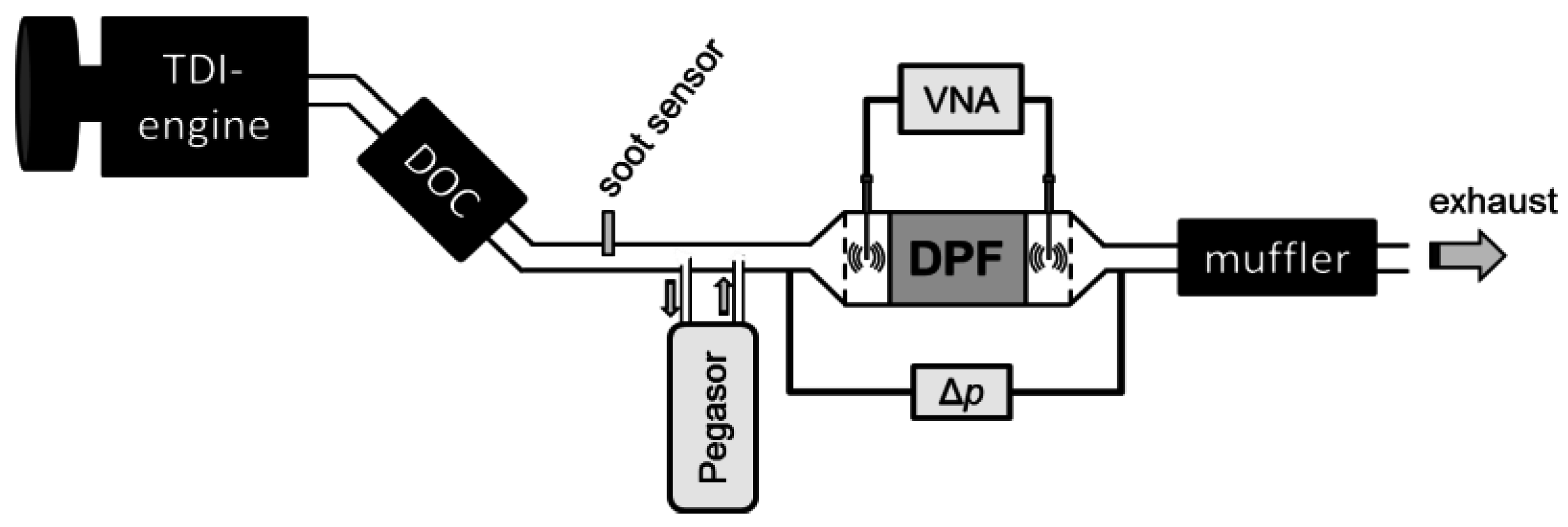
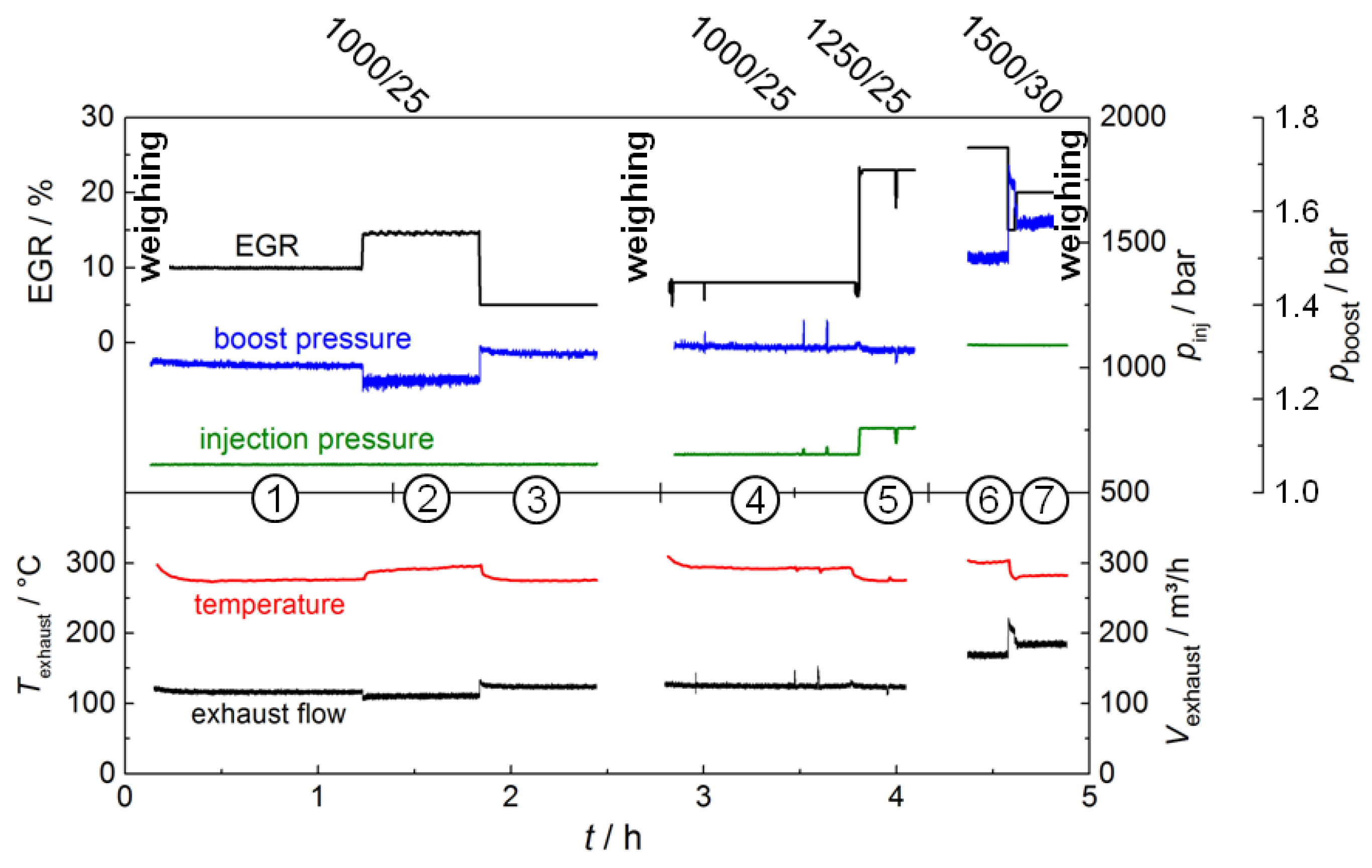
2.1. Experimental Setup and Procedure
2.2. Microwave-Based Method for Soot Load Determination
2.3. Resistive Soot Sensor
3. Results and Discussion
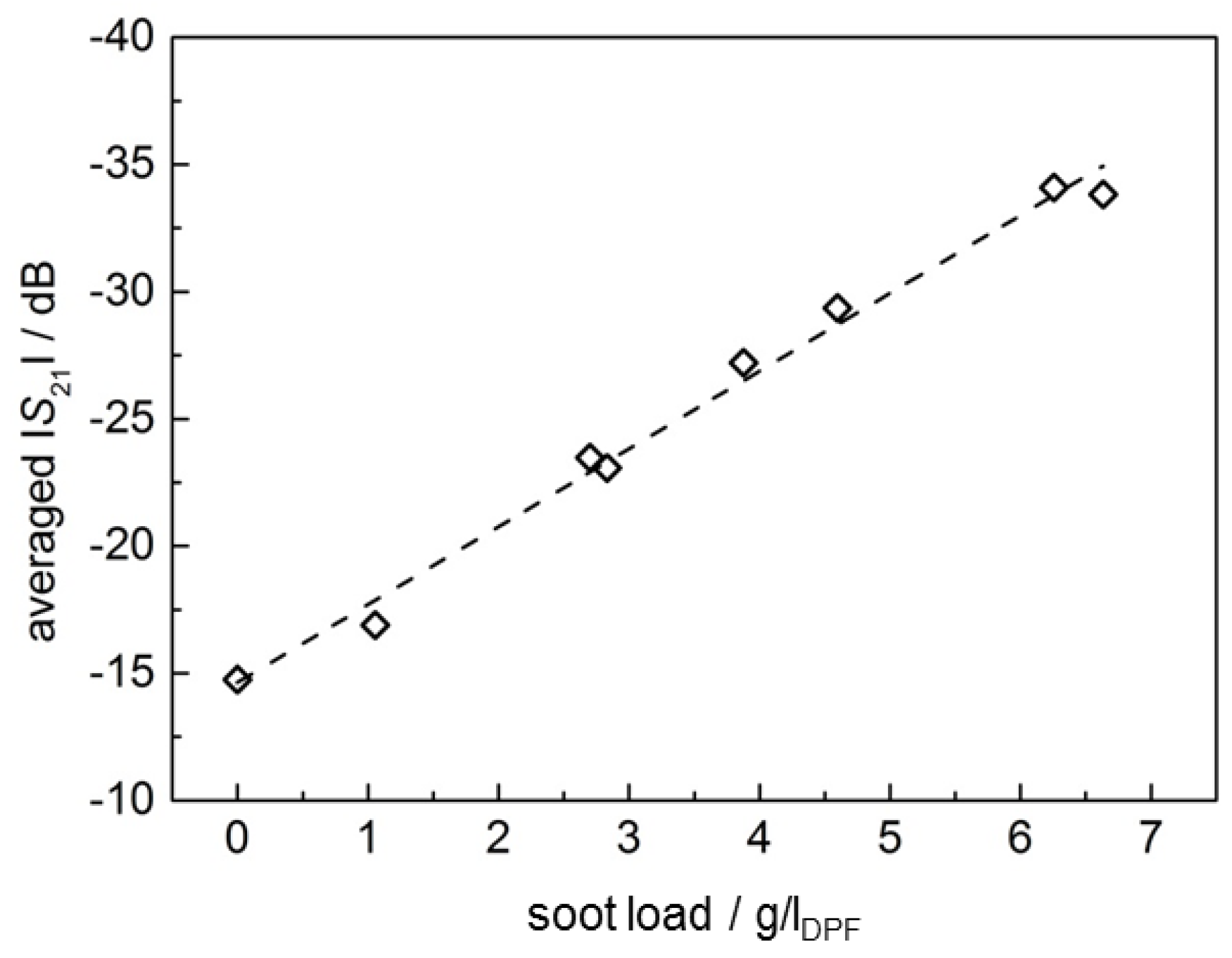
3.1. Soot Load Determination
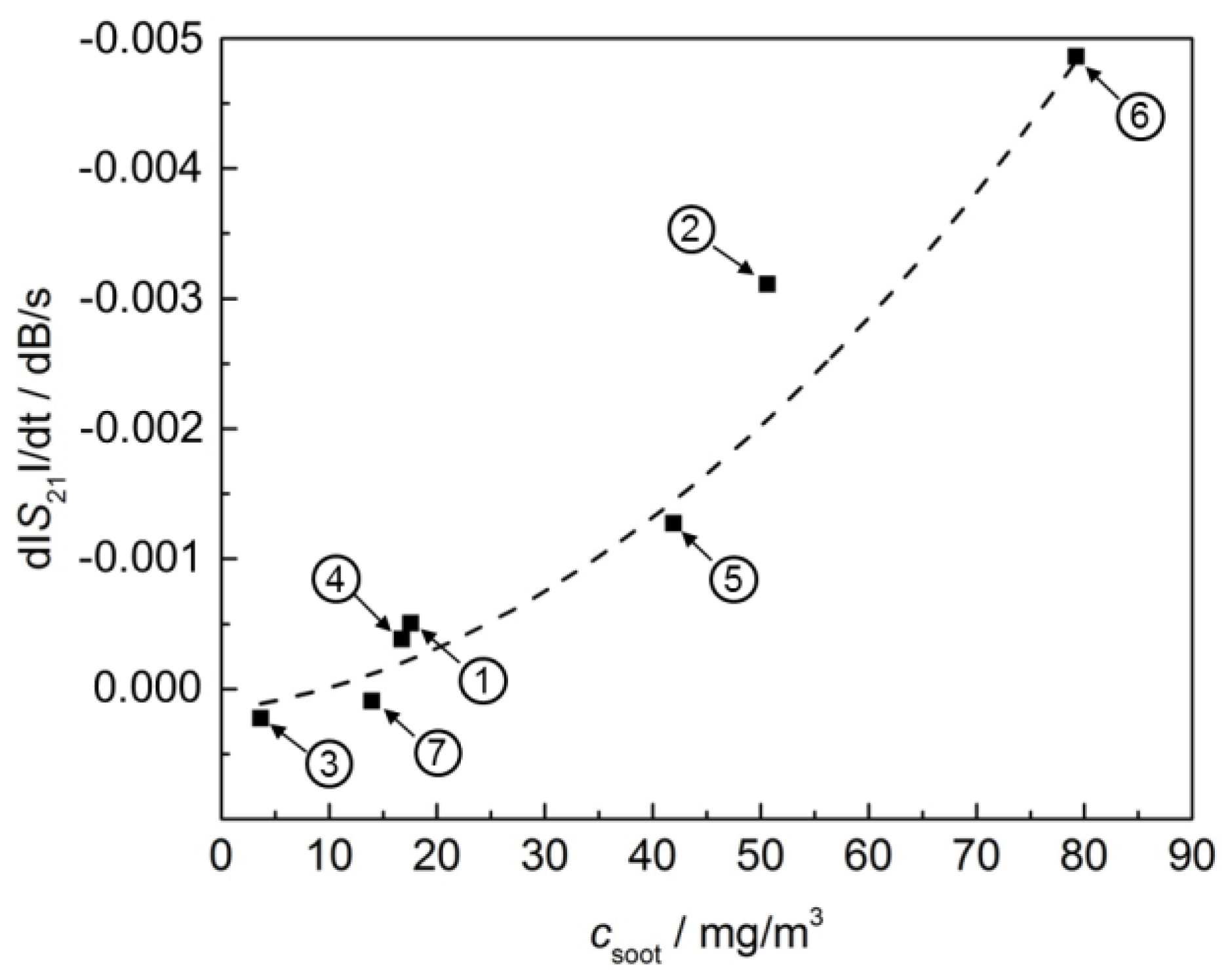
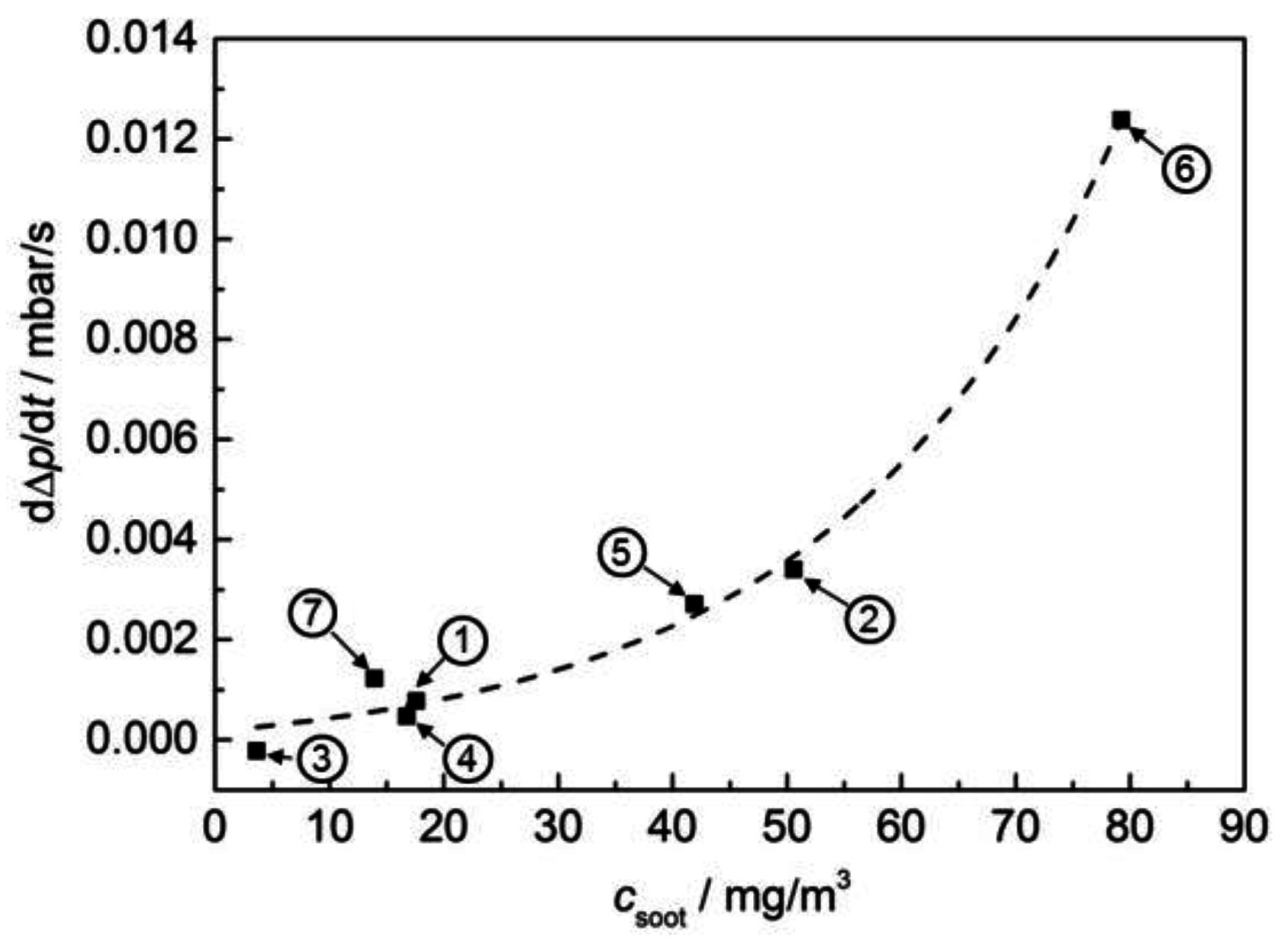
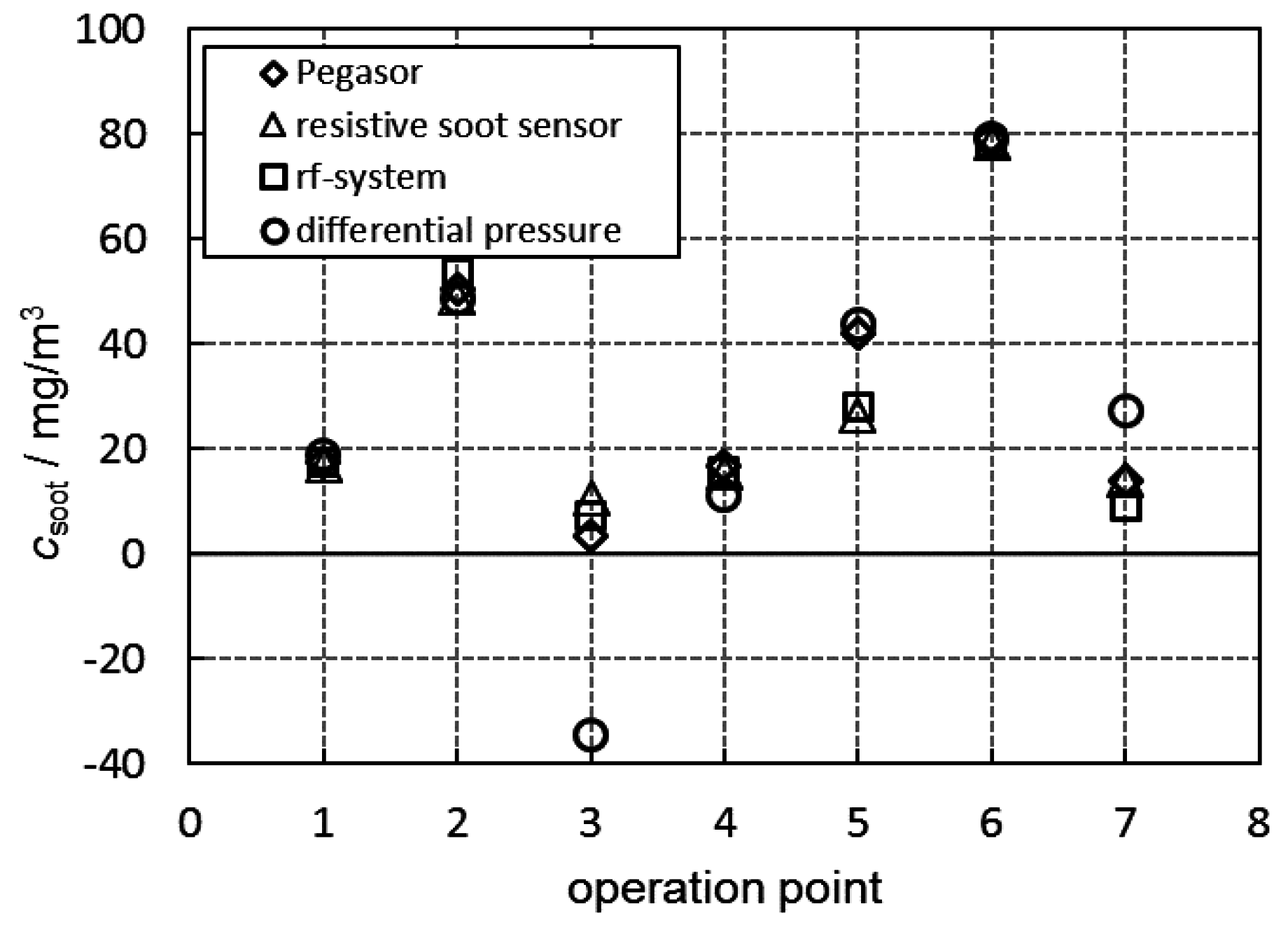
3.2. Soot Mass Concentration in the Exhaust Gas
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Twigg, M.V.; Phillips, P.R. Cleaning the air we breathe—Controlling diesel particulate emissions from passenger cars. Platin. Met. Rev. 2009, 53, 27–34. [Google Scholar] [CrossRef]
- Rose, D.; Boger, T. Different Approaches to Soot Estimation as Key Requirement for DPF Applications; SAE Technical Paper 2009-01-1262; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Feulner, M.; Hagen, G.; Piontkowski, A.; Müller, A.; Fischerauer, G.; Brüggemann, D.; Moos, R. In-Operation Monitoring of the Soot Load of Diesel Particulate Filters—Initial Tests. Top. Catal. 2013, 56, 483–488. [Google Scholar] [CrossRef]
- Sappok, A.; Bromberg, L.; Parks, J.; Prikhodko, V. Loading and Regeneration Analysis of a Diesel Particulate Filter with a Radio Frequency-Based Sensor; SAE Technical Paper 2010-01-2126; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Fischerauer, G.; Förster, M.; Moos, R. Sensing the Soot Load in Automotive Diesel Particulate Filters by Microwave Methods. Meas. Sci. Technol. 2010, 21, 035108. [Google Scholar] [CrossRef]
- Feulner, M.; Seufert, F.; Müller, A.; Hagen, G.; Moos, R. Influencing Parameters on the Microwave-Based Soot Load Determination of Diesel Particulate Filters. Top Catal. 2016, in press. [Google Scholar] [CrossRef]
- Sappok, A.; Ragaller, P.; Bromberg, L.; Prikhodko, V.; Storey, J.; Parks, J. Real-Time Engine and Aftertreatment System Control Using Fast Response Particulate Filter Sensors; SAE Technical Paper 2016-01-0918; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Marr, I.; Groß, A.; Moos, R. Overview on Conductometric Solid-State Gas Dosimeters. J. Sens. Sens. Syst. 2014, 3, 29–46. [Google Scholar] [CrossRef]
- Hagen, G.; Feistkorn, C.; Wiegärtner, S.; Heinrich, A.; Brüggemann, D.; Moos, R. Conductometric Soot Sensor for Automotive Exhausts: Initial Studies. Sensors 2010, 10, 1589–1598. [Google Scholar] [CrossRef] [PubMed]
- Ochs, T.; Schittenhelm, H.; Genssle, A.; Kamp, B. Particulate Matter Sensor for on Board Diagnostics (OBD) of Diesel Particulate Filters (DPF). SAE Int. J. Fuels Lubr. 2010, 3, 61–69. [Google Scholar] [CrossRef]
- Bartscherer, P.; Moos, R. Improvement of the sensitivity of a conductometric soot sensor by adding a conductive cover layer. J. Sens. Sens. Syst. 2013, 2, 95–102. [Google Scholar] [CrossRef]
- Husted, H.; Roth, G.; Nelson, S.; Hocken, L.; Fulks, G.; Racine, D. Sensing of Particulate Matter for on-Board Diagnosis of Particulate Filters. SAE Int. J. Engines 2012, 5, 235–247. [Google Scholar] [CrossRef]
- Lloyd Spetz, A.; Huotari, J.; Bur, C.; Bjorklund, R.; Lappalainen, J.; Jantunen, H.; Schütze, A.; Andersson, M. Chemical sensor systems for emission control from combustions. Sens. Actuators B Chem. 2013, 187, 184–190. [Google Scholar] [CrossRef]
- Weigl, M.; Roduner, C.; Lauer, T. Partikelfilter-Onboard-Diagnose mittels eines Soot-Sensors nach Partikelfilter. In Proceedings of the 6th International Exhaust Gas and Particulate Emissions Forum, Ludwigsburg, Germany, 9–10 March 2010; pp. 62–69.
- Brunel, O.; Duault, F.; Lavy, J.; Creff, Y.; Youssef, B. Smart Soot Sensor for Particulate Filter OBD. SAE Int. J. Passeng. Cars Electron. Electr. Syst. 2013, 6, 307–327. [Google Scholar] [CrossRef]
- Feulner, M.; Hagen, G.; Müller, A.; Schott, A.; Zöllner, C.; Brüggemann, D.; Moos, R. Conductometric Sensor for Soot Mass Flow Detection in Exhausts of Internal Combustion Engines. Sensors 2015, 15, 28796–28806. [Google Scholar] [CrossRef] [PubMed]
- Besch, M.C.; Thiruvengadam, A.; Kappanna, H.K.; Cozzolini, A.; Carder, D.K.; Gautam, M.; Tikkanen, M. Assessment of Novel in-line Particulate Matter Sensor with respect to OBD and Emissions Control Applications. In Proceedings of the ASME 2011 International Combustion Engine Division Fall Technical Conference, Morgantown, WV, USA, 2–5 October 2011.
- Masoudi, M; Sappok, A. Soot (PM) Sensors. DieselNet Technology Guide. Available online: http://dieselnet.com/tech/dpf_soot_sensors.php (accessed on 20 October 2015).
- Ragaller, P.; Sappok, A.; Bromberg, L.; Gunasekaran, N.; Warkins, J.; Wilhelm, R. Particulate Filter Soot Load Measurements using Radio Frequency Sensors and Potential for Improved Filter Management; SAE Technical Paper 2016-01-0943; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Amphenol. Thermometrics Accusolve Diesel Particulate Filter (DPF) Soot Sensor. Available online: http://amphenol-sensors.com/en/component/edocman/73-temperature-sensors/114-transportation-assemblies/127-automotive-temperature-sensors/210-thermometrics-accusolve-diesel-particulate-filter-dpf-soot-sensor (accessed on 14 February 2017).
- Grob, B.; Schmid, J.; Ivleva, N.P.; Niessner, R. Conductivity for Soot Sensing: Possibilities and Limitations. Anal. Chem. 2012, 84, 3586–3592. [Google Scholar] [CrossRef] [PubMed]
- Dunne, L.J.; Sarkar, A.K.; Kroto, H.W.; Munn, J.; Kathirgamanathan, P.; Heinen, U.; Fernandez, J.; Hare, J.; Reid, D.G.; Clark, D. Electrical, Magnetical and Structural Characterisation of Fullerene Soots. J. Phys. Condensed Matter 1996, 8, 2127–2141. [Google Scholar] [CrossRef]
- Hagen, G.; Spannbauer, C.; Feulner, M.; Kita, J.; Müller, A.; Brüggemann, D.; Moos, R. Conductometric Soot Sensors: Influence of Voltage and Temperature on the Soot Deposition. In Proceedings of the 16th International Meeting on Chemical Sensors (IMCS), Jeju, Korea, 10–13 July 2016.
- Groß, A.; Beulertz, G.; Marr, I.; Kubinski, D.J.; Visser, J.H.; Moos, R. Dual Mode NOx Sensor: Measuring Both the Accumulated Amount and Instantaneous Level at Low Concentrations. Sensors 2012, 12, 2831–2850. [Google Scholar] [CrossRef] [PubMed]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feulner, M.; Hagen, G.; Hottner, K.; Redel, S.; Müller, A.; Moos, R. Comparative Study of Different Methods for Soot Sensing and Filter Monitoring in Diesel Exhausts. Sensors 2017, 17, 400. https://doi.org/10.3390/s17020400
Feulner M, Hagen G, Hottner K, Redel S, Müller A, Moos R. Comparative Study of Different Methods for Soot Sensing and Filter Monitoring in Diesel Exhausts. Sensors. 2017; 17(2):400. https://doi.org/10.3390/s17020400
Chicago/Turabian StyleFeulner, Markus, Gunter Hagen, Kathrin Hottner, Sabrina Redel, Andreas Müller, and Ralf Moos. 2017. "Comparative Study of Different Methods for Soot Sensing and Filter Monitoring in Diesel Exhausts" Sensors 17, no. 2: 400. https://doi.org/10.3390/s17020400
APA StyleFeulner, M., Hagen, G., Hottner, K., Redel, S., Müller, A., & Moos, R. (2017). Comparative Study of Different Methods for Soot Sensing and Filter Monitoring in Diesel Exhausts. Sensors, 17(2), 400. https://doi.org/10.3390/s17020400




