Markov Chain Realization of Joint Integrated Probabilistic Data Association
Abstract
:1. Introduction
2. Target Tracking with JIPDA
2.1. Mathematical Models
2.2. JIPDA
3. Markov Chain Based JIPDA (MCJIPDA)
4. Design of Transition Probabilities for MCJIPDA
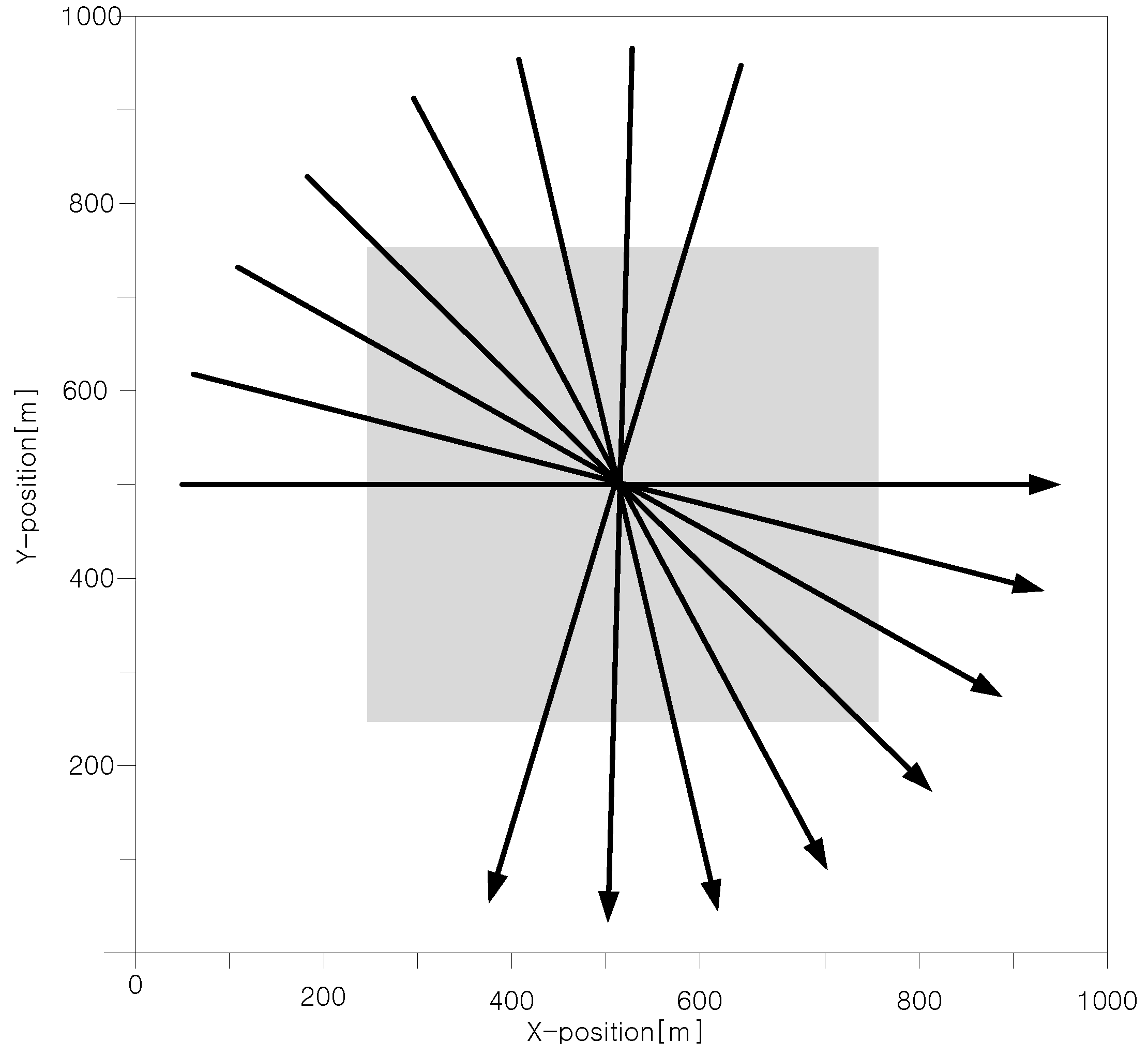
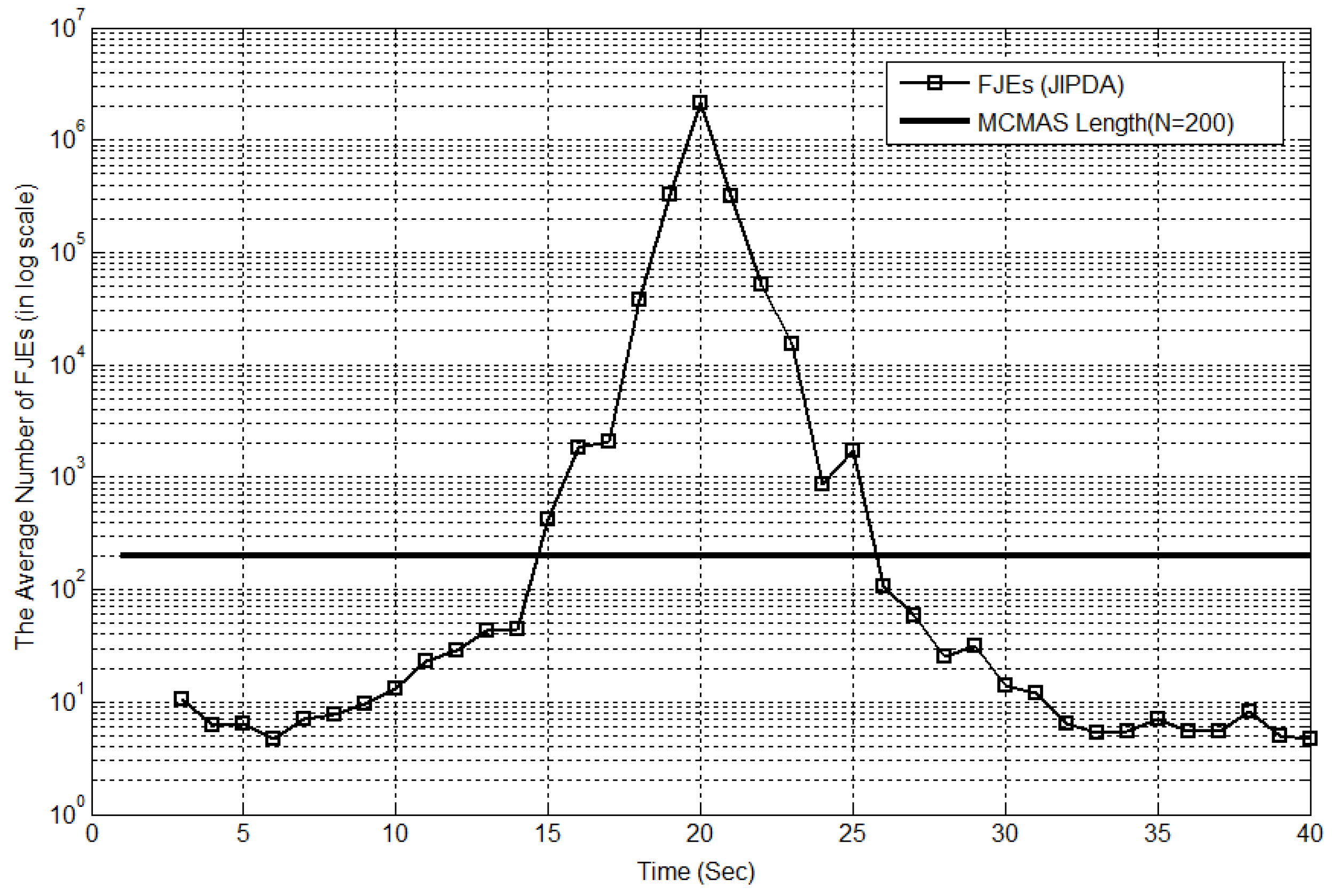
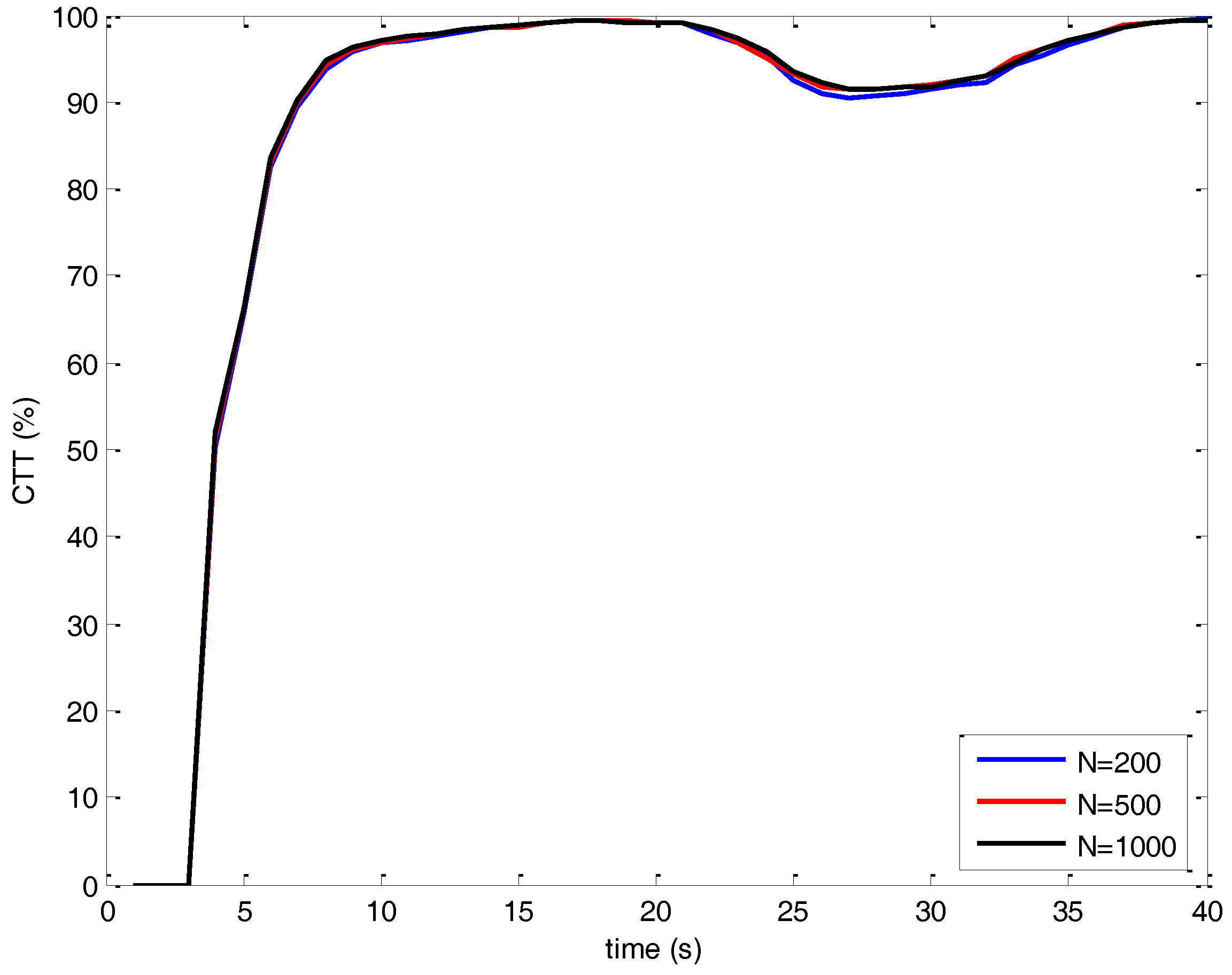
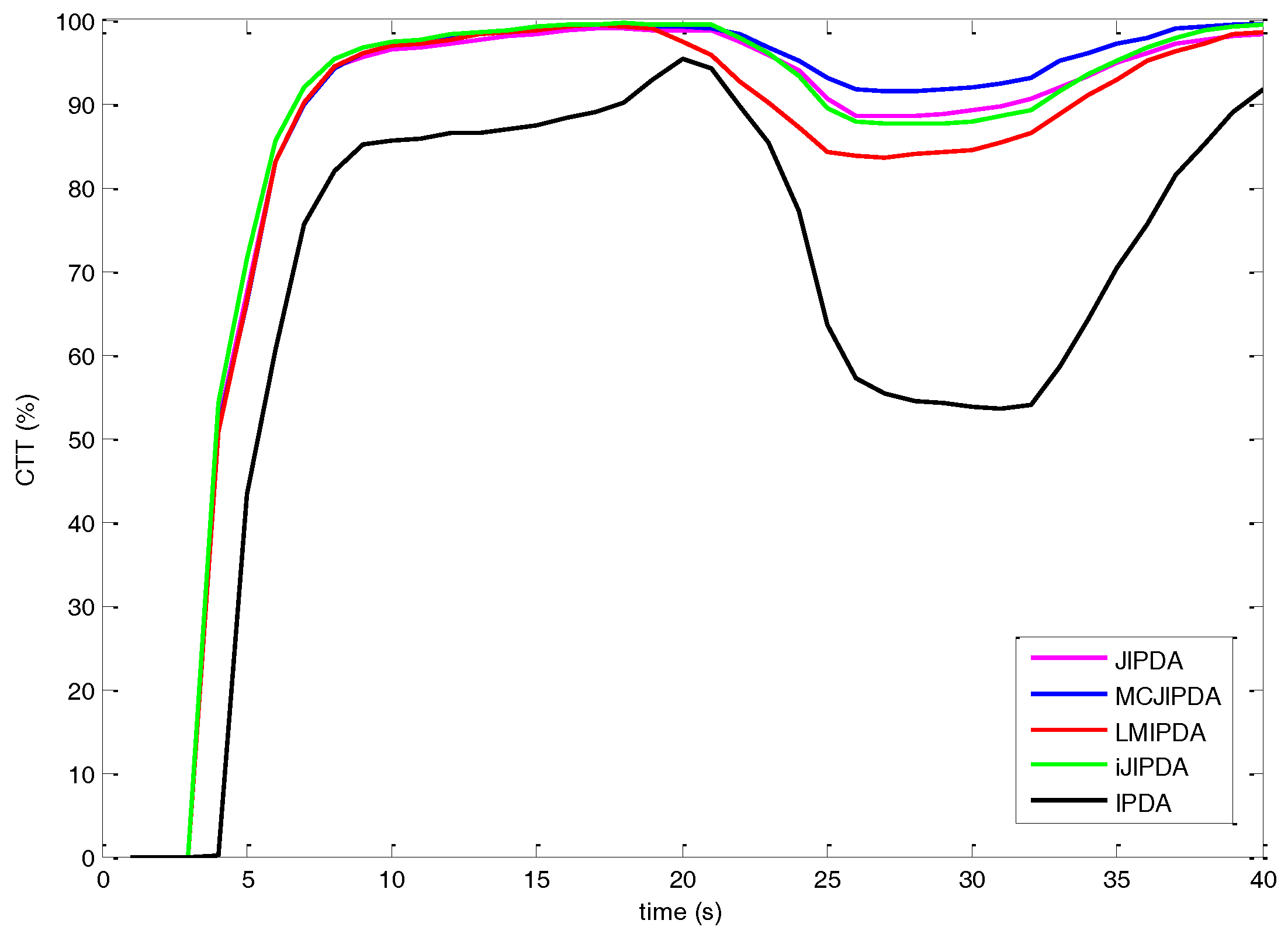
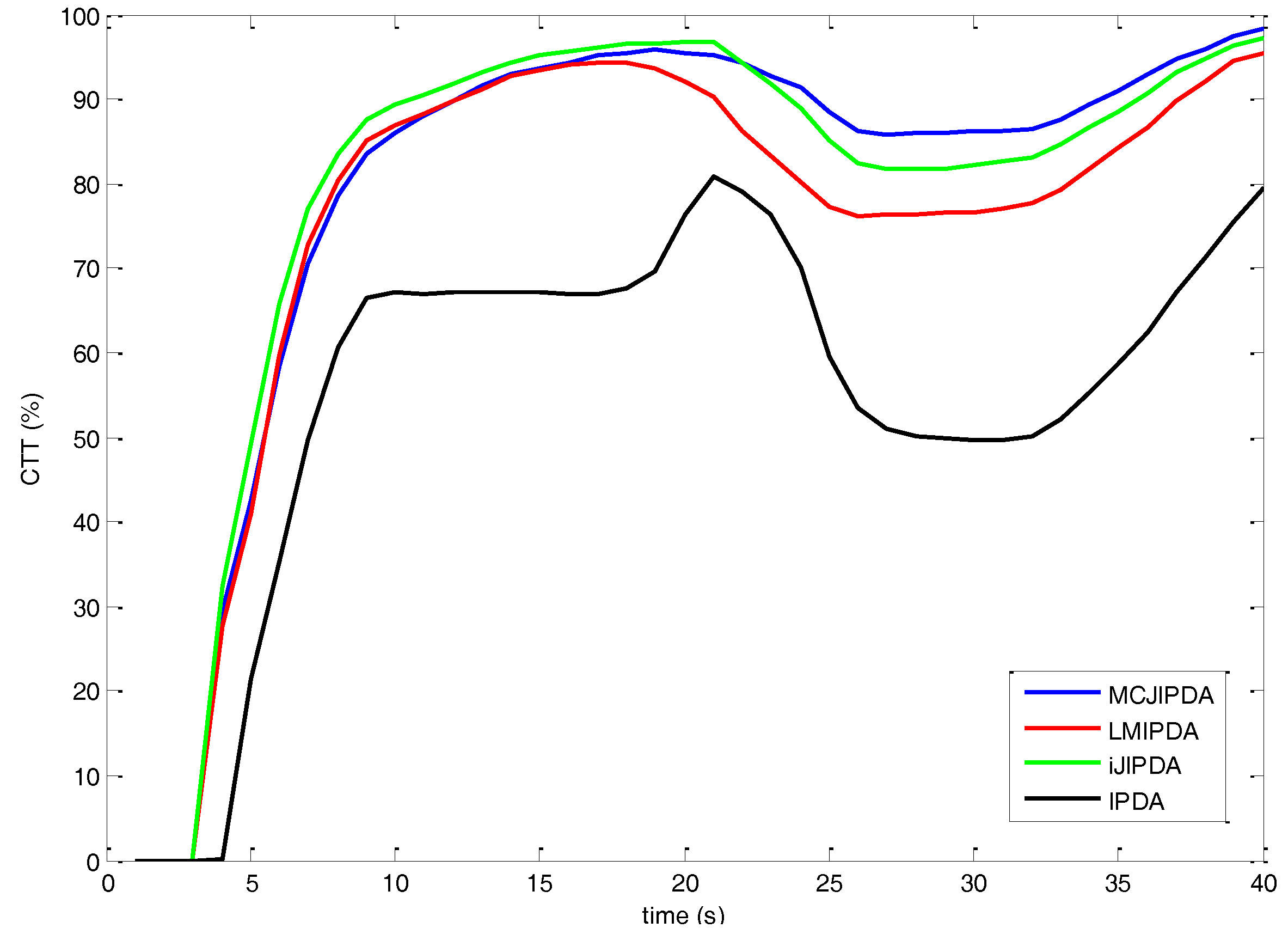
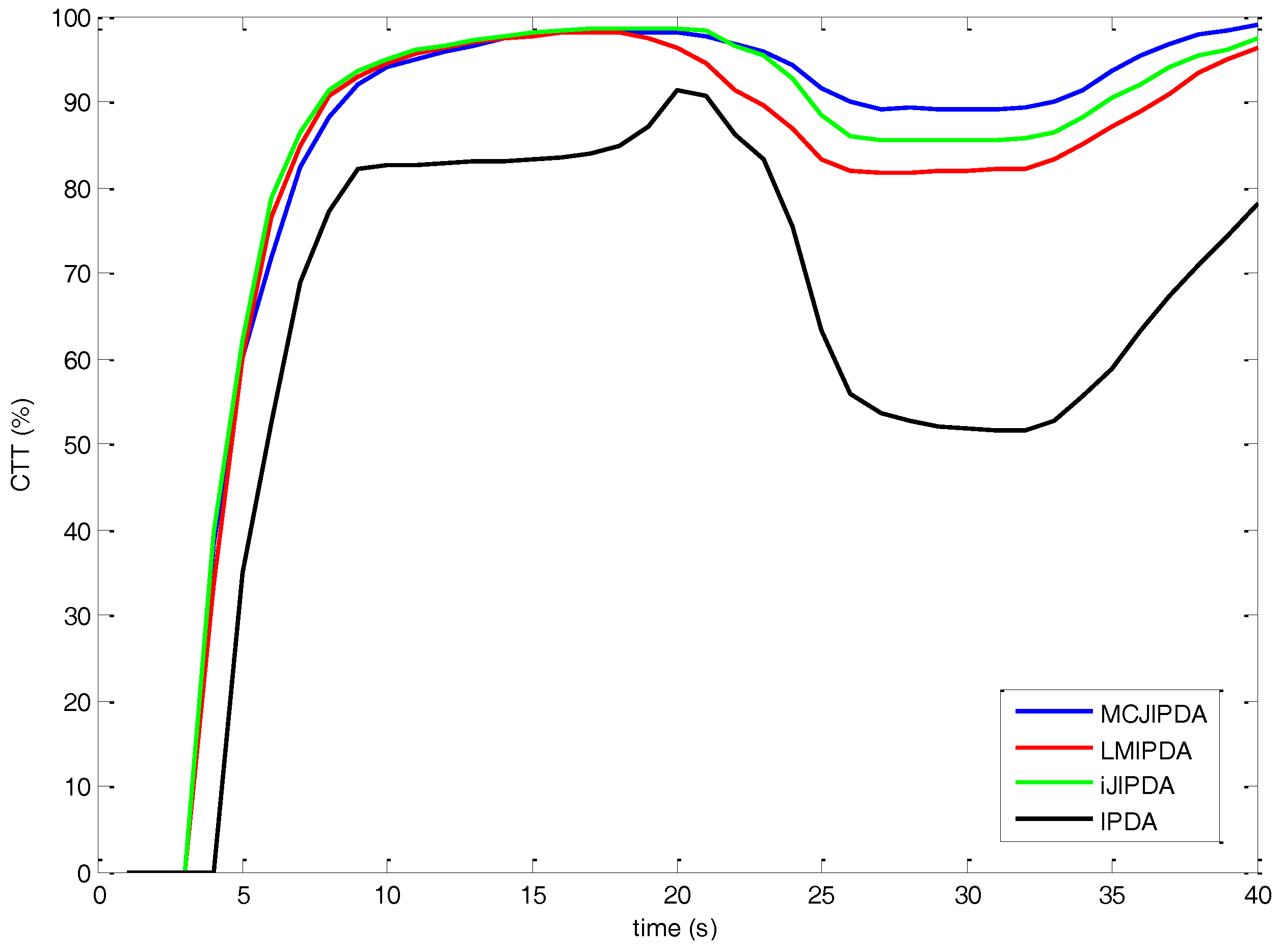
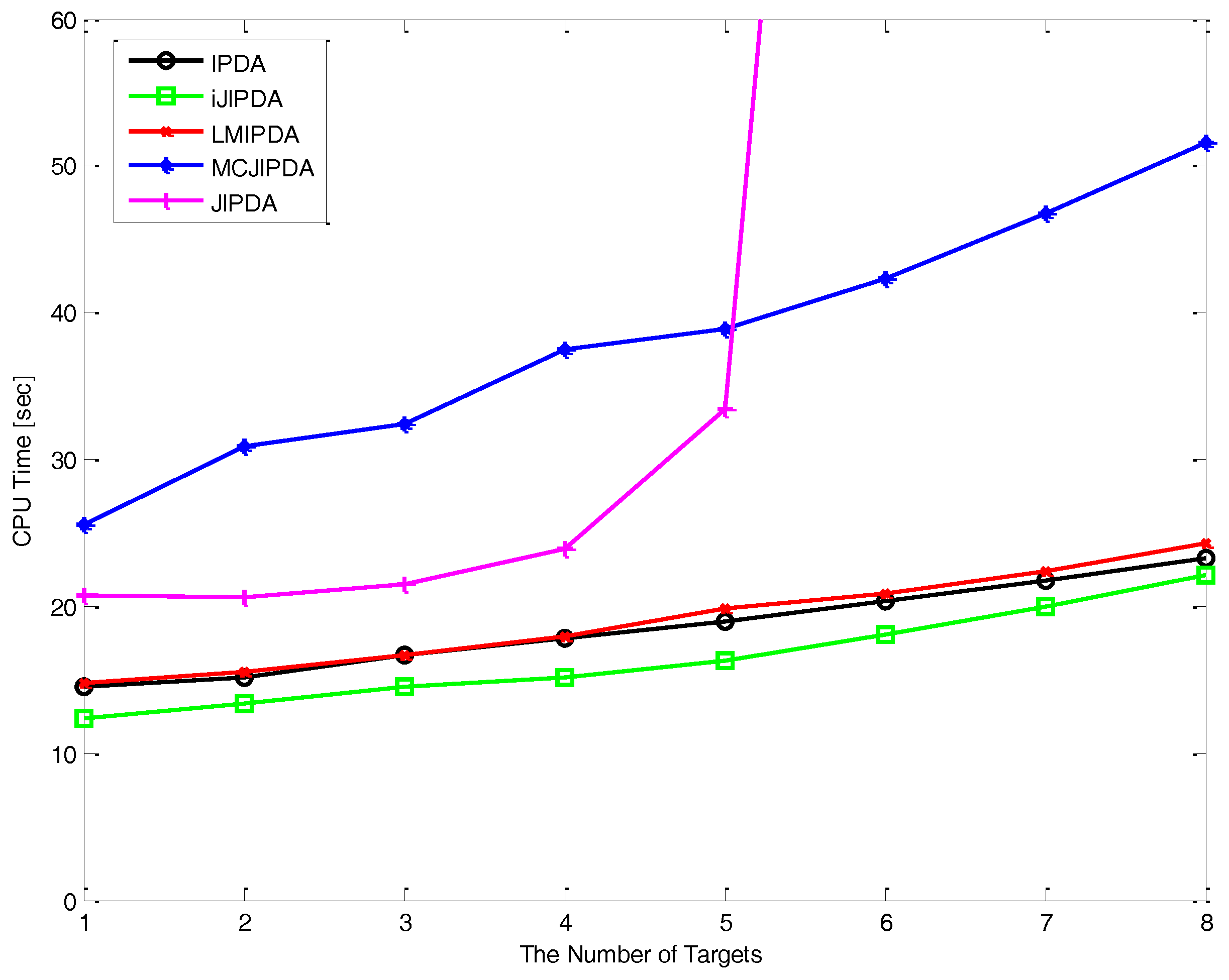
5. Simulations
- nCases: the total number of targets being followed by a confirmed track at scan 15;
- nOK: the number of “nCases” tracks that still follow their original tracks at scan 35;
- nSwitched: the number of “nCases” tracks that follow different targets at scan 35;
- nLost: the number of “nCases” tracks becoming false or terminated at scan 35;
- nMerge: the number of “nCases” tracks lost due to merging among “nCases tracks” at scan 35;
- nResult [CT]: the total number of targets being followed by a confirmed track at the last scan 40;
- CFT: the total number of confirmed false tracks during the entire simulation;
- CPU [sec]: the total CPU times for 300 Monte Carlo runs, in seconds, on a 3.6G Intel PC, running Windows 7, and C++ programs.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Challa, S.; Moreland, M.; Musicki, D.; Evans, R. Fundamentals of Object Tracking; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Zhang, Q.; Song, T.L. Improved Bearings-Only Multi-Target Tracking with GM-PHD Filtering. Sensors 2016, 16, 1469. [Google Scholar] [CrossRef] [PubMed]
- Mahler, R. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. Analytic implementations of the cardinalized probability hypothesis density filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The cardinality balanced multi-target multi-Bernoulli filter and its implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Bar-Shalom, Y.; Fortmann, T.E. Tracking and Data Association; Academic Press: New York, NY, USA, 1988. [Google Scholar]
- Bar-Shalom, Y.; Tse, E. Tracking in a cluttered environment with probabilistic data association. Automatica 1975, 11, 451–460. [Google Scholar] [CrossRef]
- Mušicki, D.; Evans, R.; Stanković, S. Integrated Probabilistic Data Association (IPDA). IEEE Trans. Autom. Control 1994, 39, 1237–1241. [Google Scholar] [CrossRef]
- Mušicki, D. Automatic Tracking of Maneuvering Targets in Clutter Using IPDA. Ph.D. Dissertation, University of Newcastle, New South Wales, Australia, 1992. [Google Scholar]
- Mušicki, D.; Evans, R. Joint Integrated Probabilistic Data Association: JIPDA. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1093–1099. [Google Scholar] [CrossRef]
- Mušicki, D.; Evans, R. Multi-scan multi-target tracking in clutter with integrated track splitting filter. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1432–1447. [Google Scholar] [CrossRef]
- Mušicki, D.; La Scala, B.; Evans, R. Multi-target tracking in clutter without measurement assignment. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 877–896. [Google Scholar] [CrossRef]
- Song, T.L.; Kim, H.W.; Mušicki, D. Iterative Joint Integrated Probabilistic Data Association. In Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 1714–1720. [Google Scholar]
- Song, T.L.; Kim, H.W.; Mušicki, D. Iterative Joint Integrated Probabilistic Data Association for Multitarget Tracking. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 642–653. [Google Scholar] [CrossRef]
- Roecker, J.A.; Phillis, G.L. Suboptimal joint probabilistic data association. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 510–517. [Google Scholar] [CrossRef]
- Romeo, K.; Crouse, D.F.; Bar-Shalom, Y.; Willett, P. The JPDA in practical system: Approximations. In Proceedings of the SPIE, Signal and Data Processing of Small Targets, Orlando, FL, USA, 16 April 2010. [Google Scholar]
- Reid, D.B. An algorithm for tracking multiple targets. IEEE Trans. Autom. Control 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Blackman, S.; Popolis, R. Design and Analysis of Modern Tracking Systems; Artech House: Boston, MA, USA, 1999. [Google Scholar]
- Reuter, S.; Vo, B.T.; Vo, B.N.; Dietmayer, K. The labelled multi-Bernoulli filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar]
- Oh, S.; Russel, S.; Sastry, S. Markov chain Monte Carlo Data Association for Multi-Target Tracking. IEEE Trans. Autom. Control 2009, 54, 481–497. [Google Scholar]
- Brereton, T. Stochastic Simulation of Processes, Fields and Structures; Institute of Stochastic: Ulm, Germany, 2014. [Google Scholar]
- Cortés, J.C.; Navarro-Quiles, A.; Romero, J.V.; Roselló, M.D. Randomizing the parameters of a Markov chain to model the stroke disease: A technical generalization of established computational methodologies towards improving real applications. J. Comput. Appl. Math. 2017, 324, 225–240. [Google Scholar] [CrossRef]

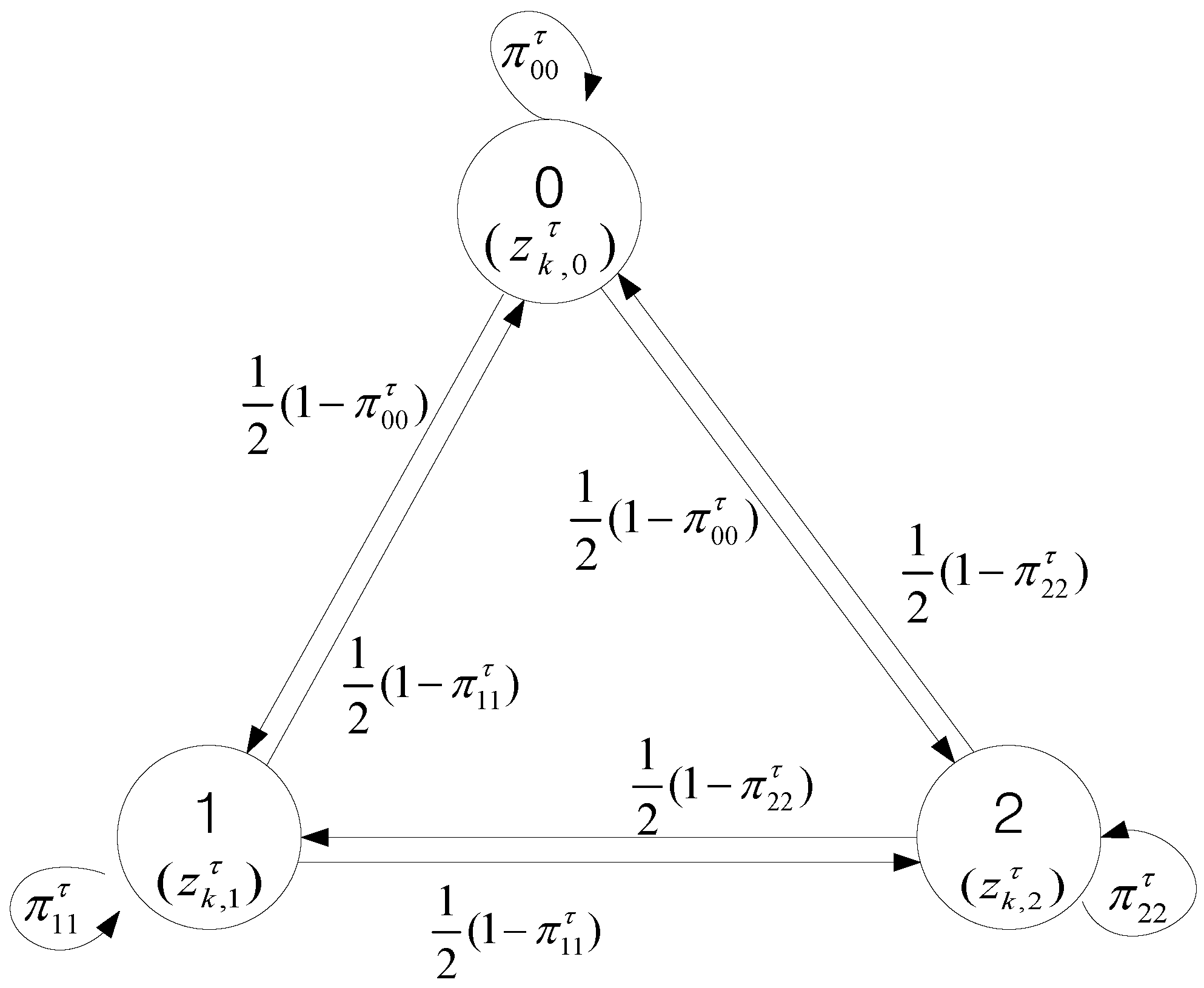
| j | (=1) | (=2) | |
|---|---|---|---|
| 1 | |||
| 2 | = | ||
| 3 | = | ||
| 4 | = | ||
| 5 | = | = | |
| 6 | = | = | |
| 7 | = | ||
| 8 | = | = |
| Case | |||
|---|---|---|---|
| #1 | 0.9 | ||
| #2 | 0.8 | ||
| #3 | 0.9 |
| MC Length | N = 200 | N = 500 | N = 1000 | |
|---|---|---|---|---|
| Statistics | ||||
| nCases | 2378 | 2380 | 2379 | |
| nOK | 1999 | 2035 | 2044 | |
| nSwitched | 155 | 142 | 133 | |
| nLost | 24 | 18 | 15 | |
| nMerged | 200 | 185 | 187 | |
| nResults | 2390 | 2385 | 2387 | |
| CFT | 73 | 74 | 74 | |
| CPU [sec] | 43.4 | 52.7 | 86.4 | |
| Measure Items | IPDA | LMIPDA | JIPDA | iJIPDA | MCJIPDA |
|---|---|---|---|---|---|
| nCases | 2121 | 2382 | 2370 | 2386 | 2380 |
| nOK | 979 | 1882 | 2039 | 2017 | 2035 |
| nSwitched | 135 | 105 | 60 | 64 | 142 |
| nLost | 7 | 3 | 5 | 7 | 18 |
| nMerged | 1000 | 392 | 266 | 298 | 185 |
| nResult[CT] | 2200 | 2363 | 2358 | 2386 | 2385 |
| C/F Track | 74 | 72 | 73 | 73 | 74 |
| CPU[sec] | 29.7 | 23.9 | 1120271 | 21.51 | 52.7 |
| Measure Items | IPDA | LM-IPDA | iJIPDA | MCJIPDA |
|---|---|---|---|---|
| nCases | 1608 | 2256 | 2293 | 2264 |
| nOK | 693 | 1629 | 1787 | 1762 |
| nSwitched | 129 | 159 | 121 | 214 |
| nLost | 7 | 5 | 6 | 38 |
| nMerged | 779 | 463 | 379 | 250 |
| nResult[CT] | 1906 | 2291 | 2331 | 2359 |
| C/F Track | 73 | 74 | 71 | 73 |
| CPU[sec] | 28.6 | 25.6 | 21.9 | 53.3 |
| Measure Items | IPDA | LM-IPDA | iJIPDA | MCJIPDA |
|---|---|---|---|---|
| nCases | 2002 | 2355 | 2360 | 2354 |
| nOK | 921 | 1849 | 1963 | 1984 |
| nSwitched | 105 | 84 | 56 | 127 |
| nLost | 9 | 4 | 7 | 27 |
| nMerged | 967 | 418 | 334 | 216 |
| nResult[CT] | 1872 | 2309 | 2336 | 2374 |
| C/F Track | 73 | 71 | 75 | 73 |
| CPU[sec] | 58.6 | 62.5 | 54.2 | 127.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.H.; Zhang, Q.; Song, T.L. Markov Chain Realization of Joint Integrated Probabilistic Data Association. Sensors 2017, 17, 2865. https://doi.org/10.3390/s17122865
Lee EH, Zhang Q, Song TL. Markov Chain Realization of Joint Integrated Probabilistic Data Association. Sensors. 2017; 17(12):2865. https://doi.org/10.3390/s17122865
Chicago/Turabian StyleLee, Eui Hyuk, Qian Zhang, and Taek Lyul Song. 2017. "Markov Chain Realization of Joint Integrated Probabilistic Data Association" Sensors 17, no. 12: 2865. https://doi.org/10.3390/s17122865
APA StyleLee, E. H., Zhang, Q., & Song, T. L. (2017). Markov Chain Realization of Joint Integrated Probabilistic Data Association. Sensors, 17(12), 2865. https://doi.org/10.3390/s17122865






