The Design and Characterization of a Prototype Wideband Voltage Sensor Based on a Resistive Divider
Abstract
:1. Introduction
2. Voltage Sensor
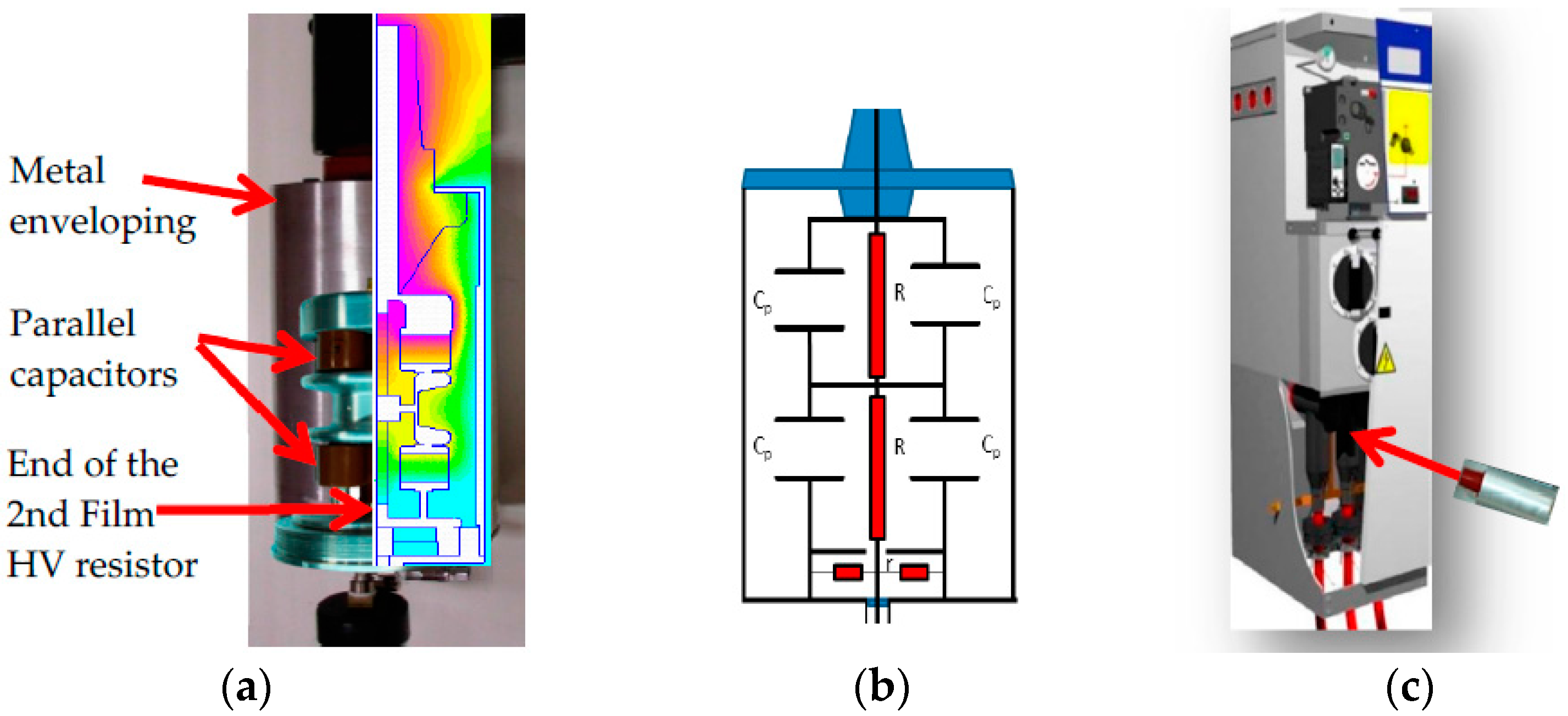
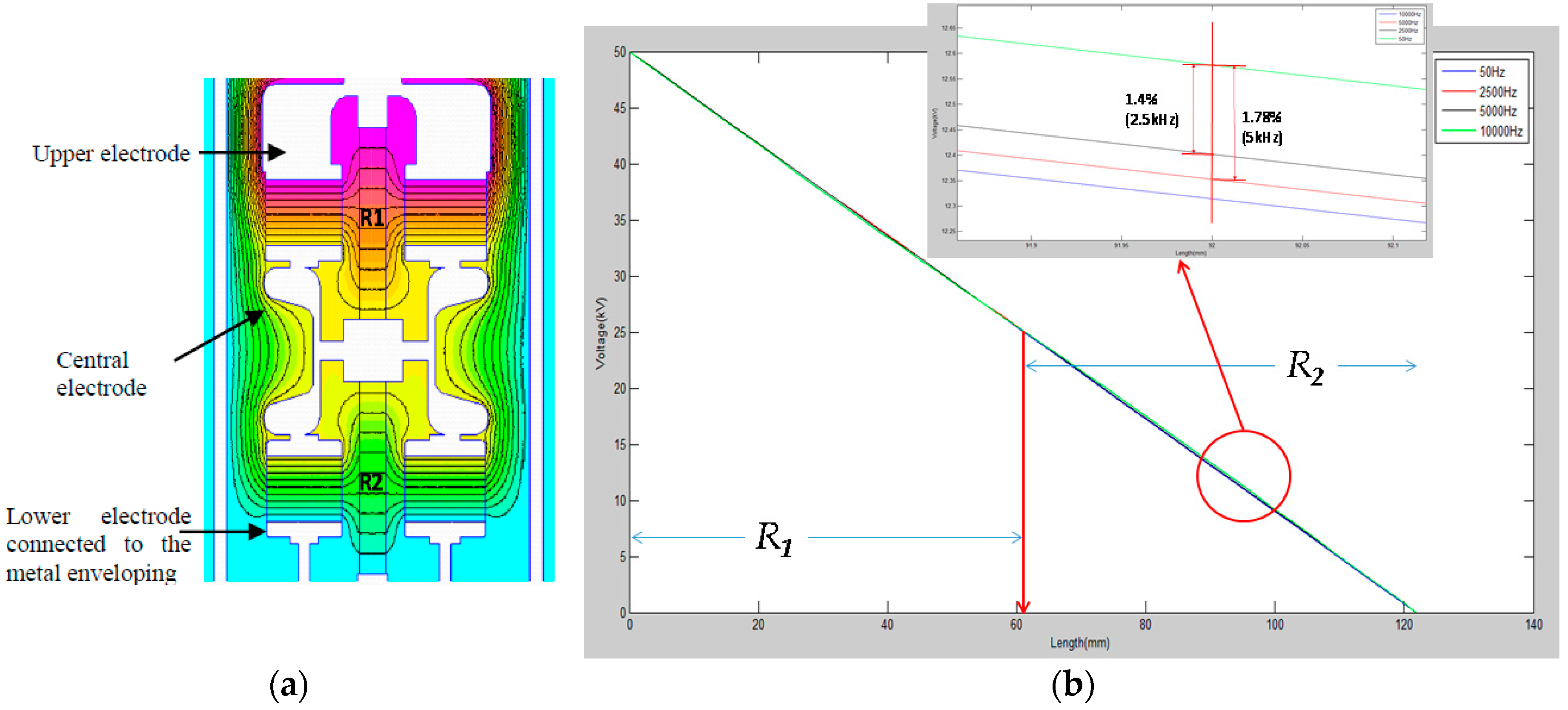
2.1. Physical Design
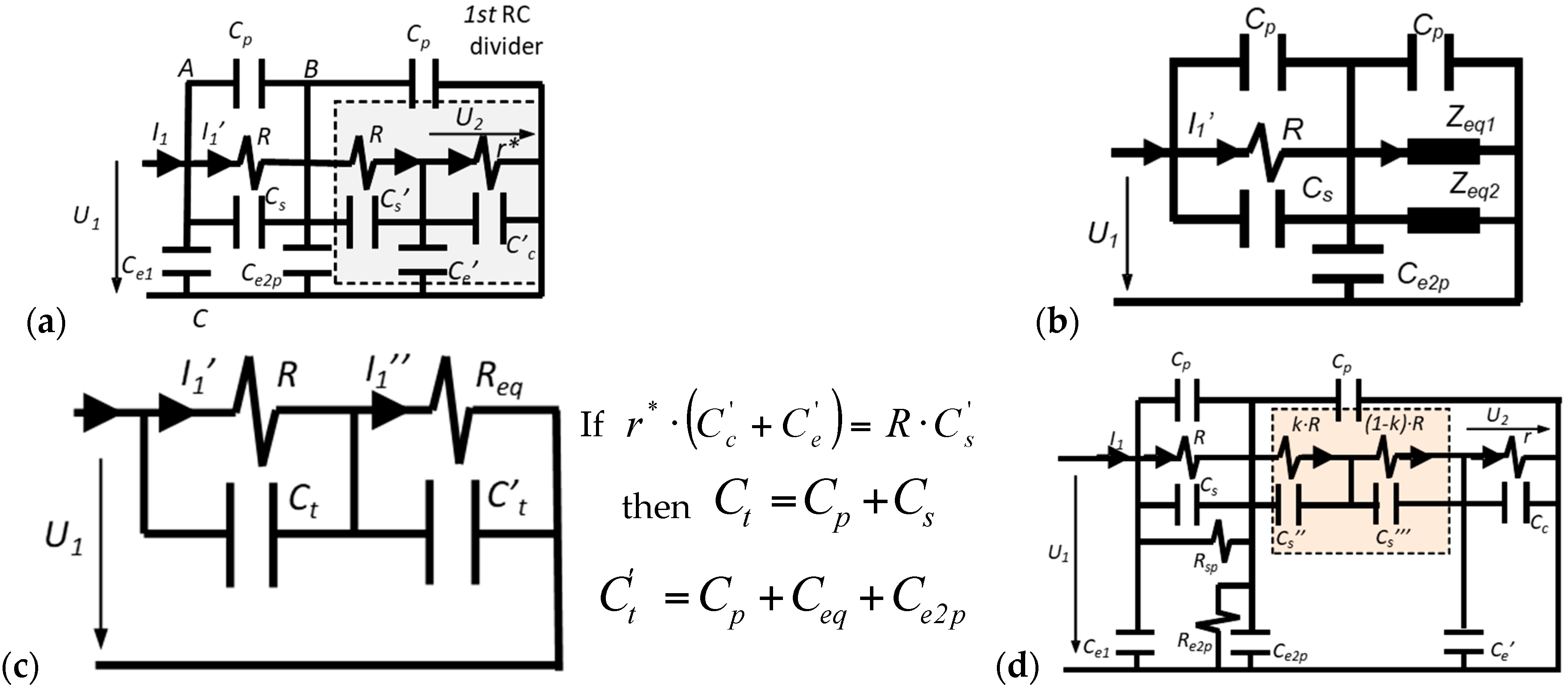
2.2. Simplified Electrical Model
3. Frequency Response Analysis
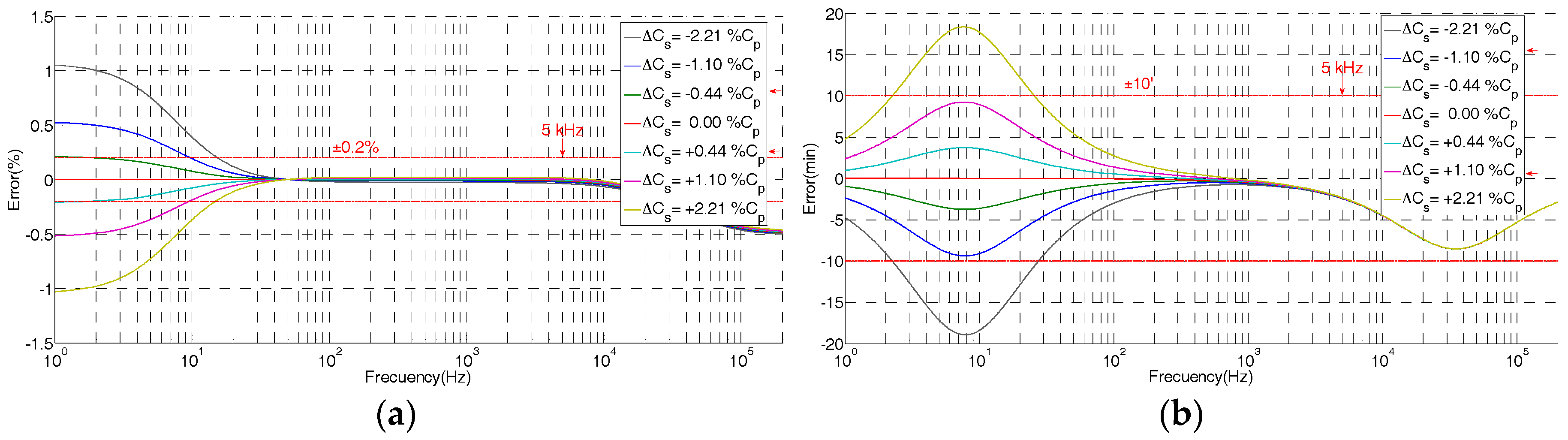
3.1. Frequency Response Analysis Using the Simplified Model
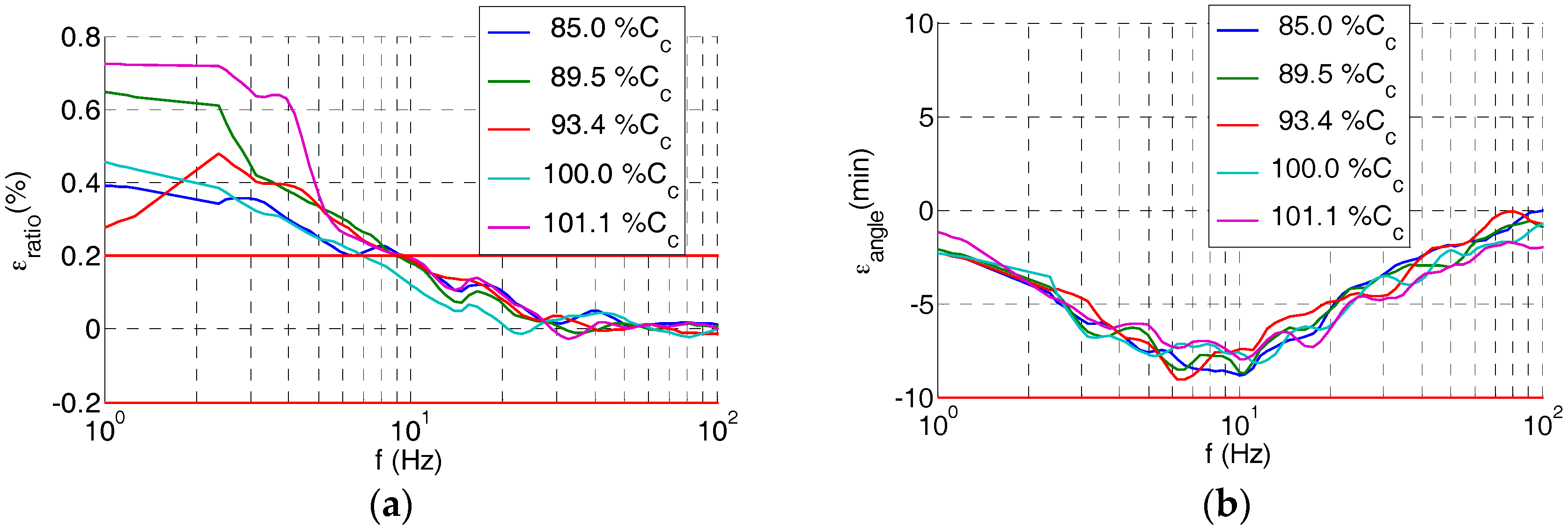
3.2. Measuring the Response Frequency of the Built Sensor
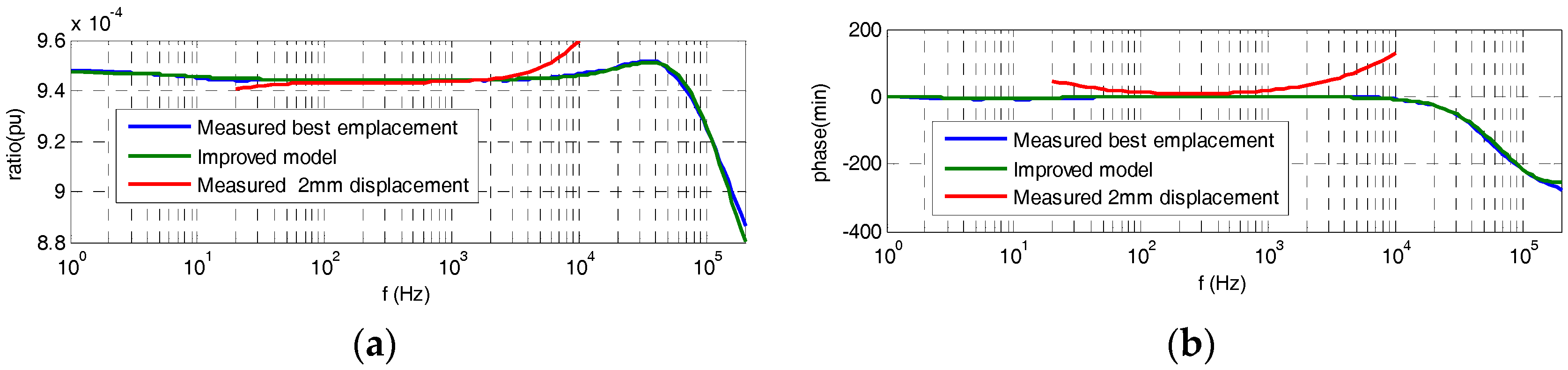
4. Improved Electrical Model
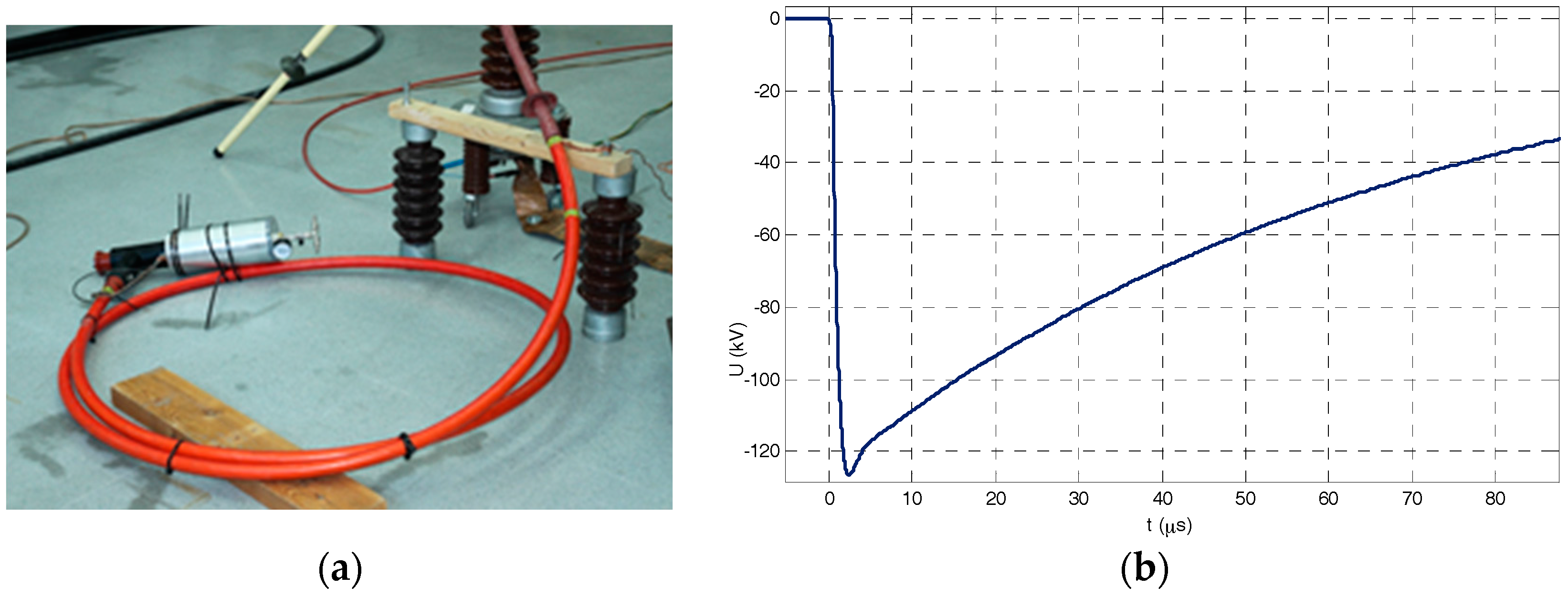
5. High-Voltage Calibration and Insulation Testing
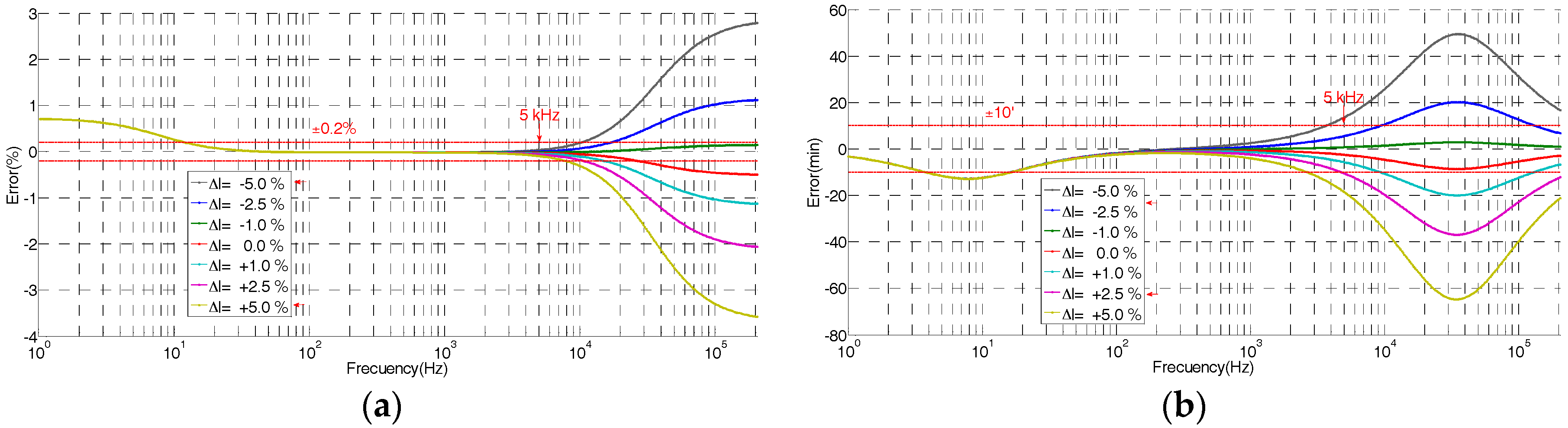
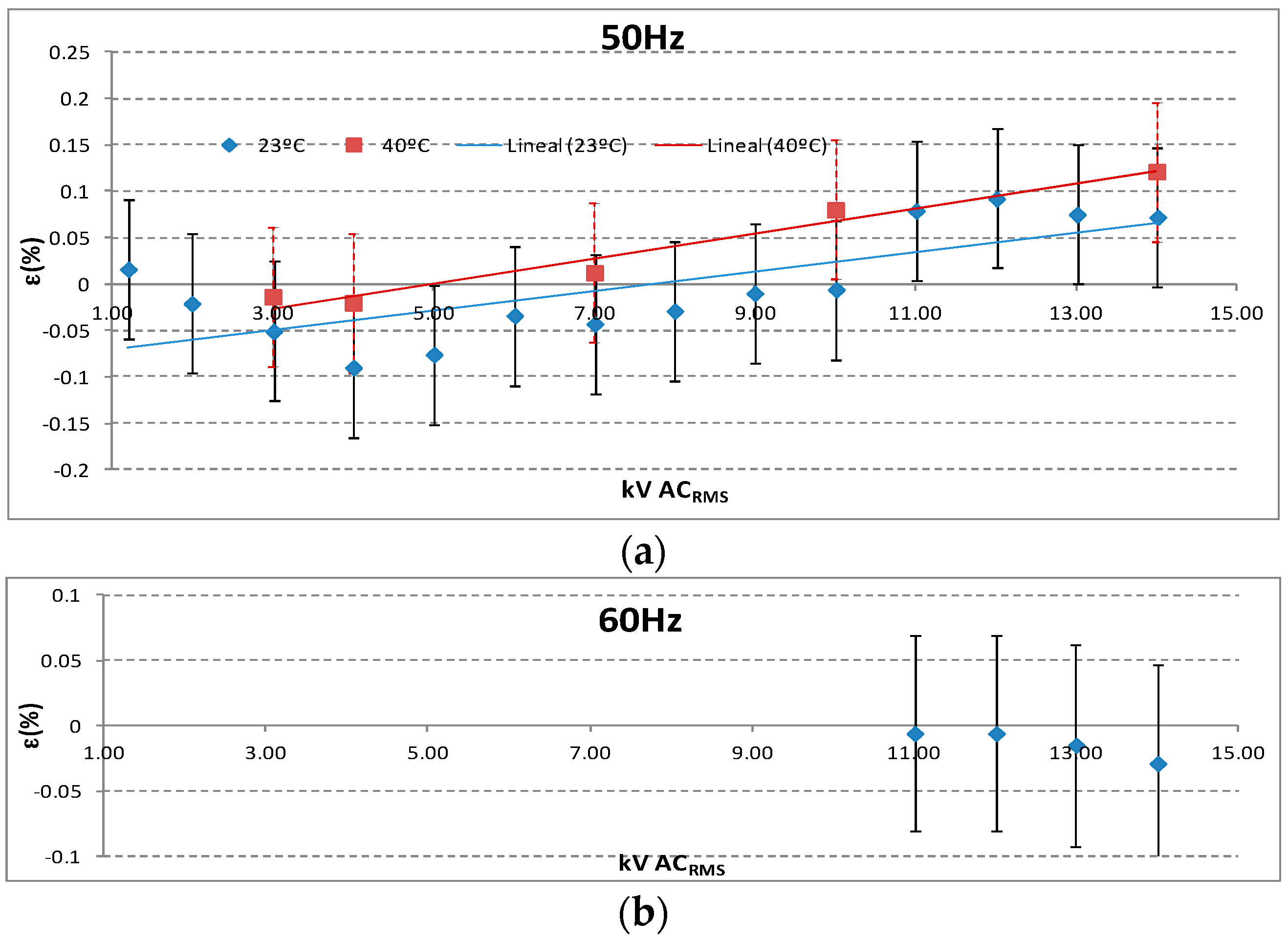
5.1. Ratio and Angle Errors
5.2. Insulation Tests
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- International Electrotechnical Commission. IEC 61869-1 Instrument Transformers—Part 1: General Requirements; IEC: Geneva, Switzerland, 2007. [Google Scholar]
- International Electrotechnical Commission. IEC 61869-3 Additional Requirements for Inductive Voltage Transformers; IEC: Geneva, Switzerland, 2011. [Google Scholar]
- International Electrotechnical Commission. IEC 60060-2 High Voltage Test Techniques—Part 2 Measuring Techniques; IEC: Geneva, Switzerland, 2010. [Google Scholar]
- International Electrotechnical Commission. IEC 61000 Electromagnetic Compatibility (EMC); IEC: Geneva, Switzerland, 1992. [Google Scholar]
- EN 50160 European Standard. Voltage Characteristics in Public Distribution Systems-Voltage Disturbances; CENELEC: Brussels, Belgium, 1999. [Google Scholar]
- Klatt, M.; Meyer, J.; Elst, M.; Schegner, P. Frequency Responses of MV voltage transformers in the range of 50 Hz to 10 kHz. In Proceedings of the 14th International Conference on Harmonics and Quality of Power (ICHQP), Bergamo, Italy, 26–29 September 2010. [Google Scholar]
- Seljeseth, H.; Saethre, E.A.; Ohnstad, T.; Lien, I. Voltage transformer frequency response. Measuring harmonics in Norwegian 300 kV and 132 kV power systems. In Proceedings of the 8th International Conference on Harmonics and Quality of Power, Athens, Greece, 14–16 October 1998; Volume 2, pp. 820–824. [Google Scholar]
- Kunde, K.; Däumling, H.; Huth, R.; Schlierf, H.W.; Schmid, J. Frequency Response of Instrument Transformers in the kHz Range. Available online: http://www.trench.at/content/download/1604/14169/file/Frequency%20Response%20of%20Instrument%20Transformers%20in%20the%20kHz%20range.pdf (accessed on 17 November 2017).
- Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M.; Modarres, M. Frequency response of MV voltage transformer under actual waveforms. IEEE Trans. Instrum. Meas. 2017, 66, 1146–1154. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. IEC 60044-7 Instrument Transformers—Part 7: Electronic Voltage Transformers. Additional Requirements for Electronic Voltage Transformers; IEC: Geneva, Switzerland, 1999. [Google Scholar]
- Hlavacek, J.; Draxler, K.; Styblikova, R. 20 kV AC Divider with ratio correction. In Proceedings of the 19th International Symposium on High Voltage Engineering, Pilsen, Czech Republic, 23–28 August 2015. [Google Scholar]
- Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M.; Modarres, M.; Zucca, M. Frequency compliance of MV voltage sensors for smart grid application. IEEE Sens. J. 2017, 17, 7621–7629. [Google Scholar] [CrossRef]



| Parameter | Primary Value | Determined By | Simplified Model Figure 3b | Simplified Model Figure 3b | Improved Model Figure 3d |
|---|---|---|---|---|---|
| R | 25 MΩ | Measurements | 25 MΩ | 25 MΩ | 25 MΩ |
| r | 50 kΩ | Measurements | - | - | - |
| Zr | 1 MΩ | Data Sheet | - | - | - |
| r* = r·Zr/(r + Zr) | - | Derived | 47.6 kΩ | 47.6 kΩ | 47.6 kΩ |
| Cp | 809.2 pF | Measurements | 809.2 pF | 809.2 pF | 809.2 pF |
| Cc (1) | 63.8 pF | Measurements | - | - | - |
| Cr | 20.0 pF | Data sheet | - | - | - |
| Cc′ = Cc + Cr | 83.8 pF | Derived | - | - | - |
| Ce′ | 12.1 pF | Measurements | 12.1 pF | 12.1 pF | 12.1 pF |
| Cc′′ = Cc′+ Ce′ | - | Derived | 95.9 pF | 95.9 pF | 95.9 pF |
| Ce1 (3) | 29.5 pF | Measurements | - | - | 29.5 pF |
| Ce2p | 12.5 pF | Measurements | 12.5 pF | 12.5 pF | 12.5 pF |
| Cs | 2.2 pF | Measurements | 2.2 pF (2) | 2.2 pF (2) | 2.2 pF (2) |
| Cs′ | 0.18 pF | Modeling | 0.18 pF | 0.18 pF | - |
| Cs′′/Cs′′′ | - | Modeling | - | - | 0.20/0.87 pF |
| Requ | - | Derived (5) | 25 048 kΩ | 25 048 kΩ | - |
| Cequ | - | Derived (6) | 0.15 pF | - | - |
| Ct | - | Derived (12) | 811.4 pF | - | |
| Ct’ | - | Derived (12) | - | 821.9 pF | - |
| Rs | - | Modeling | - | - | 865 MΩ |
| Re2 | - | Modeling | - | - | 658 MΩ |
| k | - | Modeling | - | - | 0.96 |
| Restriction of 1st RC Divisor | Equation (1) R·Cs′ = r*·(Cc′ + Ce′) | Restriction of 2nd RC Divisor | R·Ct = Req·Ct′ |
|---|---|---|---|
| R·Cs′ (kΩ·pF) | 4545 | R·Ct (kΩ·pF) | 20,284 |
| r*·(Cc' + Ce′) (kΩ·pF) | 4568 | Req·Ct' (kΩ·pF) | 20,587 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garnacho, F.; Khamlichi, A.; Rovira, J. The Design and Characterization of a Prototype Wideband Voltage Sensor Based on a Resistive Divider. Sensors 2017, 17, 2657. https://doi.org/10.3390/s17112657
Garnacho F, Khamlichi A, Rovira J. The Design and Characterization of a Prototype Wideband Voltage Sensor Based on a Resistive Divider. Sensors. 2017; 17(11):2657. https://doi.org/10.3390/s17112657
Chicago/Turabian StyleGarnacho, Fernando, Abderrahim Khamlichi, and Jorge Rovira. 2017. "The Design and Characterization of a Prototype Wideband Voltage Sensor Based on a Resistive Divider" Sensors 17, no. 11: 2657. https://doi.org/10.3390/s17112657
APA StyleGarnacho, F., Khamlichi, A., & Rovira, J. (2017). The Design and Characterization of a Prototype Wideband Voltage Sensor Based on a Resistive Divider. Sensors, 17(11), 2657. https://doi.org/10.3390/s17112657




